De novo prediction of protein folding pathways and structure using the principle of sequential stabilization

Abstract

Motivated by the relationship between the folding mechanism and the native structure, we develop a unified approach for predicting folding pathways and tertiary structure using only the primary sequence as input. Simulations begin from a realistic unfolded state devoid of secondary structure and use a chain representation lacking explicit side chains, rendering the simulations many orders of magnitude faster than molecular dynamics simulations. The multiple round nature of the algorithm mimics the authentic folding process and tests the effectiveness of sequential stabilization (SS) as a search strategy wherein 2° structural elements add onto existing structures in a process of progressive learning and stabilization of structure found in prior rounds of folding. Because no a priori knowledge is used, we can identify kinetically significant non-native interactions and intermediates, sometimes generated by only two mutations, while the evolution of contact matrices is often consistent with experiments. Moreover, structure prediction improves substantially by incorporating information from prior rounds. The success of our simple, homology-free approach affirms the validity of our description of the primary determinants of folding pathways and structure, and the effectiveness of SS as a search strategy.

Despite numerous advances since the original sequence-to-structure folding paradigm was proposed over 50 years ago (1), we still lack a general framework that enables simultaneous prediction of the folding mechanism and structure using only the amino acid (aa) sequence [notwithstanding recent successes of all-atom simulations to fold small, fast-folding proteins (2)]. An obvious obstacle is the astronomical number of conformations available to a polypeptide. Proteins overcome this obstacle by sampling a limited set of conformations, guided by the folding process itself. However, most successful structure prediction methods do not consider the folding mechanism when sampling conformations. Conversely, many methods for predicting folding mechanism rely on knowledge of the final structure (e.g., Gō models).

Another obstacle emerges because many non-native and near-native conformations often differ by only a few RT, which is at or beyond the ability of current energy functions to reliably distinguish. A related difficulty arises because the native state is the global free energy minimum even if three competing properties—local backbone torsional angle preferences, hydrogen bonded 2° structure, and 3° packing—are not individually optimized. For example, 3° context can overcome local biases in determining the final 2° structure (3). Hence, a successful framework should couple 3° context to 2° structure formation, rather than relying on a strict hierarchical approach.

Sequential stabilization (SS) provides one mechanism for coupling 2° and 3° structure formation during folding and guiding the search process (4, 5). Supported by native state hydrogen exchange experiments, ψ analysis, and other observations (6, 7), this view argues that proteins predominantly fold along one or a few low energy pathways determined by the stepwise addition of cooperative units of structure or foldons (e.g., a helix or a strand). Prior emergence of hydrogen bonded structure serves as a template for the formation of additional structure that may only exist as a minor population in isolation.

Here we describe an iterative framework, termed TerItFix, to test whether the combination of SS with basic principles of protein chemistry can be used to predict folding pathways and structure using only the sequence as input. The principle of SS is implemented by using the statistics of folding trajectories garnered from prior rounds of simulation to bias the subsequent sampling of backbone dihedral angles (8) and the energies of tertiary contacts and hydrogen bonds. The approach combines simple backbone torsional ϕ, ψ moves, a polypeptide chain with no side chains beyond C_β carbons, and multiple rounds of simulation with the progressive learning and building of 3° motifs through constraints imposed by data from prior rounds. We predict the 2° and 3° structures and pathways for 8 proteins using only approximately 10³ CPU hours per protein. The results are largely consistent with experimental data, even in the presence of kinetically significant non-native interactions.

Model

Initially, approximately 500 individual Monte Carlo Simulated Annealing (MCSA) folding simulations are performed using specialized ϕ, ψ backbone moves and energy functions appropriate for a reduced chain representation consisting of the backbone plus C_β heavy atoms, as discussed below. The best final structures (lowest energy quartile) are then examined for recurring 2° structures, backbone hydrogen bonding, and 3° contacts. After modifying the move set and energy functions to promote these recurring features, another round of approximately 500 folding simulations is performed. The passing of information from one round to another is repeated until convergence (Fig. S1). This iterative, multiround learning and biasing procedure equates to a search strategy involving sequential stabilization, as illustrated with the folding of ubiquitin (Fig. 1).

Fig. 1.

TerItFix protocol applied to Ub. 2° and 3° structure coevolve as the rounds proceed with local and nonlocal constraints derived from the prior round. The ϕ, ψ sampling distribution is initially obtained from a coil library. It contains angles from all regions of the Ramachandran map at a frequency given by the relative height of the blue, green, pink, and red bars, color coded according the legend in the lower left. The sampling distribution becomes more restricted as 2° structure is progressively fixed after each round; e.g., L43 preferentially adopts β conformations as the rounds progress and its distribution shifts to the β basin (left column). The contact maps identify the order of 3° structure formation along the pathway, which can be used to construct potential folding intermediates (bottom).

The folding simulations employ move sets and energy functions that are designed to describe three competing protein properties: ϕ, ψ preferences, 2° structure, and 3° packing. Angle preferences are incorporated by sampling conformational space using neighbor-dependent ϕ, ψ distributions derived from the PDB (Fig. S2). These angles are used for pivot moves, where only a single residue’s ϕ, ψ angles are changed, as well as for double crankshaft local moves, where two consecutive peptide groups are rotated (9, 10) (Fig. S3). In the initial round, angles are chosen from a coil library that accurately describes the structure of the chemically denatured state (11). Later rounds use information about the 2° structures garnered from the prior round to restrict the sampling distribution (see Methods).

Our energy function is composed of three statistical potentials and two biasing terms (SI Text, Fig. S4), which guide the formation of 2° structure and 3° packing. The first potential (8) describes the residue–residue interactions according to the distance distributions in the PDB, contingent on 2° structure and the relative orientation of the two residues’ C_α-C_β vectors (Fig. S4). The second potential describes each residue’s burial propensity, as calculated using the number of heavy atoms surrounding each C_β atom in an 11 Å hemisphere defined by the orientation of the C_α-C_β vector (glycines are ignored). The third term is associated with backbone desolvation and backbone hydrogen bonding. The desolvation term assigns a penalty for the loss of water-peptide hydrogen bonds when there is no compensating protein–protein hydrogen bond (Fig. S4).

Even for small proteins, the exploration of the folding landscape poses a formidable search problem, and thus requires additional constraints. The principle of SS provides a realistic method of guiding the search by continually refining the ϕ, ψ sampling distributions, which determine local structure, and biasing the energy for recurring motifs to guide 2° and 3° structure formation. After each round, the lowest energy quartile is evaluated to identify 2° structure preferences and popular 3° contacts and hydrogen bonding. These items are used to restrict the backbone sampling library (Fig. S2) and to generate two energetic biasing terms, E_contact and E_H-Bond, that are employed in the next folding round (see Methods).

This iterative process incrementally fixes 2° structure and biases 3° structure and hydrogen bonding as the rounds proceed, producing a series of sequential steps that may correspond to the authentic folding pathway (Fig. 1). Individual biases may strengthen or weaken in subsequent rounds because of the emergence of competing contacts. In principle, if no major kinetic traps impede the pathway, the final sampling distribution and contact probabilities should converge to produce the native 2° and 3° structures, respectively.

Results

We apply TerItFix to deduce the folding pathways of eight proteins and simultaneously to predict their 3° structures. The different levels of information accessible are demonstrated by studying the fast folding five helix subdomain of lambda repressor (λ_6–85) and comparing the predictions to experiments (12, 13) and molecular dynamics (MD) simulations (2, 14, 15). Next, TerItFix is applied to describe the folding pathways of two homologous immunity proteins, Im7 and Im9, along with a double point mutant, SIm9, to demonstrate that our method is sensitive enough to capture the kinetic consequences of slight aa variations and to predict the presence of kinetic intermediates. Finally, TerItFix is used to describe five other proteins, Ub, chymotrypsin inhibitor 2 (CI2), Protein L and two three helix bundle proteins, Protein A and the designed α3d.

λ_6–85.

Starting with a ϕ, ψ distribution generated from the coil library, a folding pathway emerges after five rounds of folding with a 4.3 Å Cα RMSD (best) structure (Fig. 2). The initial ϕ, ψ distribution provides little indication of the positions or propensities of the helices or their order of formation because most angles in the initial distribution are nonhelical. A clear pathway emerges as the rounds proceed, with helices H3 and H4 appearing first and interacting. As the probabilities of these two helices increase in progressive TerItFix rounds, H1 gradually appears and docks against the H3-H4 motif by round R3. While the number of helices remains largely unchanged after R3, the helices lengthen, and their contact probabilities continue to increase for the next few rounds, as evident by the evolution of the ϕ, ψ distributions, average contact maps, and the centroid of the largest cluster formed from the structures generated in each round (Fig. 2A). Although H2 and H5 appear in some trajectories, the population of structures containing these helices remains insufficient to justify restricting the sampling distributions in those positions to the helical basin.

Fig. 2.

λ_6–85. (A) The initial ϕ, ψ sampling distribution has low helical propensity. A pathway emerges with the docking of helices H3 and H4, followed by H1. By Round 6, H2 and H5 emerge, albeit weakly. Contact maps and illustrative structures are shown in the center and right columns, respectively. (B) The RMSD distribution of the endpoints of the approximately 500 trajectories improves with each round. (C) The reaches 70% of the native level in R4 and a representative, TS analog containing H1 + H3 + H4 + H5 is identified.

These simulations highlight the interplay between 2° and 3° structure formation. The helical probability for the residues of helix H2 in R1 exceeds that in subsequent rounds. This loss of native-like structure suggests that H1 and H2 initially interact, but 3° contacts between H1 with H3 and H4 dominate in later rounds. At the same time, the average contacts between H4 and H5 continue to rise until round R4, even though residues in H5 never become highly helical (Fig. S5). Besides predicting the pathway, incorporating the strategy of SS into TerItFix improves the predicted structures (Fig. 2B).

Although the TerItFix algorithm produces a folding pathway, identifying the TSE is not straightforward due to the multiround nature of the method. Using an observation deduced from our ψ analysis studies of four proteins that obey the correlation between log(k_fold) and relative contact order (RCO) (16–18), we identify a TSE by the condition RCO^TSE/RCO^Native ∼ 0.7. The number of long-range contacts in λ_6–85 sharply increases in the low energy structures of R4, and some achieve the 70% RCO level (Fig. 2C). Examination of such structures indicates that H1, H3, H4, and potentially H5 are present in this predicted TSE.

Using mutational ϕ analysis, Oas and coworkers suggest that H1 and H4 are formed in the TSE, while the presence of H2 and H3 is unclear (ϕ = 0.2 and 0.3) and the status of H5 is ambiguous (12). Our kinetic amide isotope effect data indicate that the TSE contains approximately 80% of the native helical hydrogen bonds, consistent with the TSE burying 70% of the total denaturant sensitive surface area (19, 20). This high level of hydrogen bond formation suggests that at least one more helix is present in the TSE, potentially H3 because ϕ^H3 = 0.3 > ϕ^H2 = 0.2. Hence, predictions from TerItFix appear to be largely consistent with experiment.

MD simulations by Shaw and coworkers find that the TSE contains H1–H4 and that these four helices are at least partially formed in the denatured state (2). The presence of H1 and H4 in the TSE is consistent across the TerItFix trajectories, MD simulations, and experiments. But the MD simulations appear to disagree with TerItFix and experiments (at 310 K) in predicting H2 to be significantly populated in the TS. This difference might be a consequence of the high helical propensity of H1–H4 in the unfolded state in the MD simulations (at 350 K). Experimentally, the helical content in an unfolded analog is approximately 16% at 310 K (21), which is much lower than the 42% helical content in the MD simulations but accords with the low approximately 15% helical angle content in TerItFix’s initial ϕ, ψ coil sampling library.

A Markov state analysis of 3265 relatively short (μsec) MD simulations identifies a TS structure (P_fold = 0.53) having only 1–2 turns of helices H1–H4 and two adjacent β strands (14). Another set of MD simulations using a new tempering method finds that H1–H3 are formed prior to H4 and H5 (15). Further experiments should be performed to permit more accurate assessments of the disparate results obtained by TerItFix and the three different MD simulations.

Im7,9.

The homologous immunity proteins Im7 and Im9 highlight a case where TerItFix is advantageous over native-biased methods. Im7 and Im9 display different folding kinetics despite being nearly identical four-helix bundles with approximately 60% sequence identity. Im7 folds in a three-state manner with an intermediate containing helices H1, H2 and H4, while Im9 folds in a two-state manner (22, 23). Im7’s three helix intermediate is misfolded in the sense that the three helices must at least partially separate in order to accommodate H3. The importance of sequence is further highlighted by the fact that only two conservative mutations in Im9 (“SIm9”) induce a three-state mechanism akin to Im7’s (24). That such slight variations of the aa sequence can alter the folding behavior reflects the challenge of reproducing these results.

After only three rounds of simulations, all four helices form and interact in Im9, whereas H3 fails to form in Im7 (Fig. 3A and Figs. S6 and S7). The sampling distribution for the residues in H3 of Im7 never evolves beyond the coil specification, and the protein becomes “trapped” in an intermediate structure containing H1, H2 and H4 (Fig. S6). Thus, TerItFix correctly captures the energetic frustration of the folding landscape of Im7 that is absent in Im9.

Fig. 3.

Im proteins. (A) Contact maps. By the last round, R3, TerItFix predicts that the H3 is formed in Im9 (green circle) whereas H3 is absent in Im7 and SIm9, as observed experimentally. (B) In SIm9, the interaction energy between V37L strengthens the H1-H2 contacts but destabilizes the H2-H3 contacts between V37L and I53.

Next, TerItFix is applied to the folding of SIm9 which has the conservative V37L and V71I substitutions in H2 and H4, respectively, and folds with the accumulation of the same three helix intermediates as Im7. Remarkably, the TerItFix results for SIm9 are very similar to those for Im7, successfully predicting the same three helix intermediate as observed experimentally (Fig. 3A) and demonstrating a high level of sensitivity of our method to changes in sequence and the energy landscape.

The origin of the sensitivity to two conservative mutations is deduced from the differences in the H1-H2 contacts for Im9 and SIm9 (Fig. S7B). SIm9’s two mutations promote docking of these helices in a geometry that precludes the addition of H3. Specifically, the two mutations alter the pairwise DOPE-PW energies between the helices (Fig. 3B). In SIm9, the interactions between V37L, which lies in H2, and residues in H1 are stronger, while the interactions between V37L and I53 in H3 are weaker. These two differences provide an explanation for the disparate folding mechanism induced by only two aa mutations.

Prediction of Early Events, Foldons and Non-native Contacts.

TerItFix simulations begin from a conformation devoid of regular structure. Hence, the method can provide insights by identifying motifs that form at the earliest stages of folding for five proteins: Ub, CI2, Protein L, α3d (25), and Protein A.

Ub is a 76 residue α/β protein with a relatively complex topology and a folding pathway that has been extensively characterized by ψ analysis and native state hydrogen exchange (5, 7, 16). The TSE contains four adjoining strands, β1–4, and part of the major α helix. Folding from the TSE to the native state occurs in a stepwise manner with the addition of the small 3₁₀ helix followed by the β5 strand. However, the early events leading to the TSE are difficult to identify due to the their intrinsic instability and the ensuing two-state kinetic folding behavior.

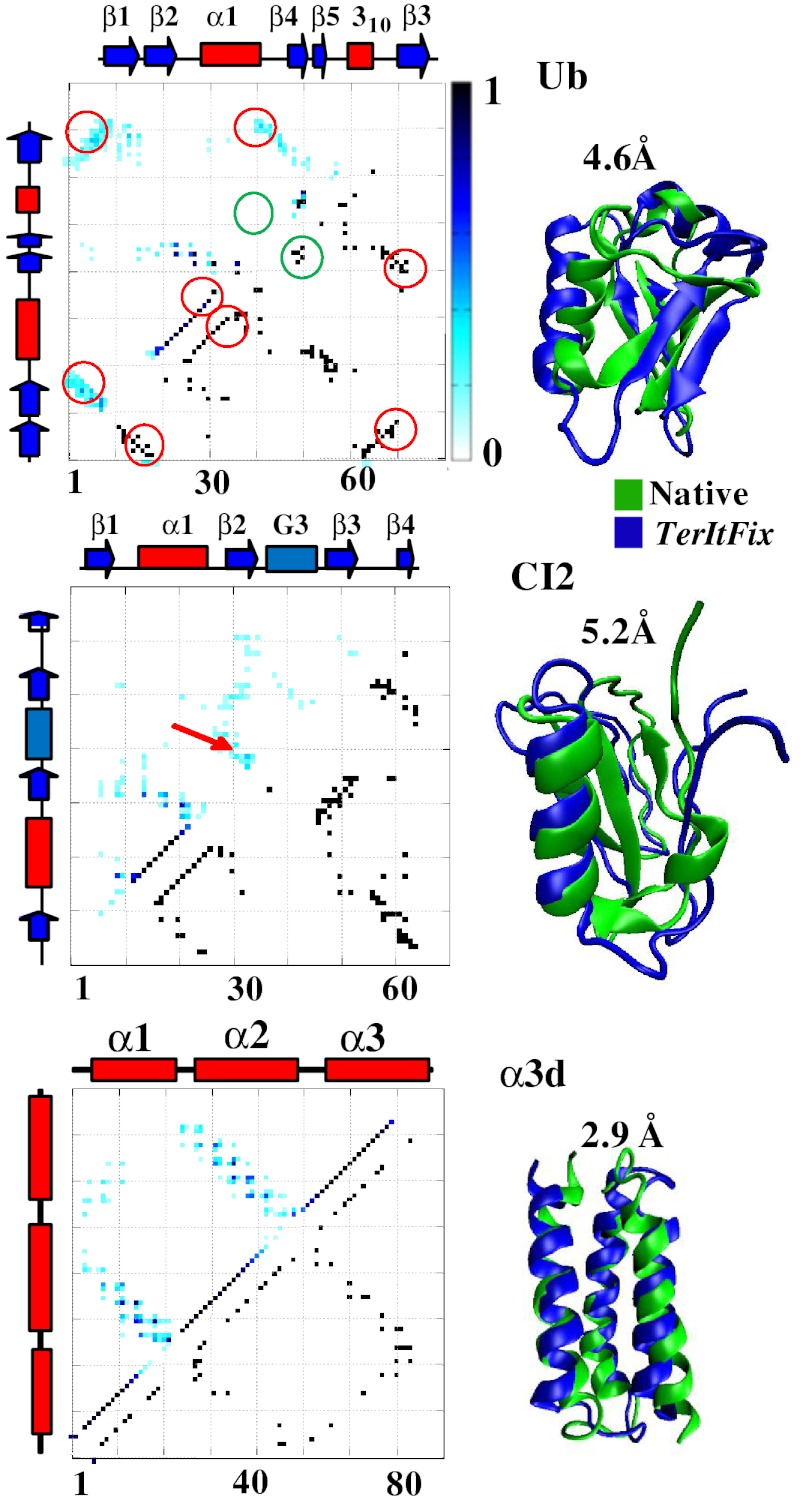
The first motif to form in the TerItFix simulations is the β1-β2 hairpin (Fig. 4 and Fig. S8), followed by the addition of the α helix and the interaction between the two terminal strands, β1-β3. The early interaction between the termini is significant because long-range contacts generally form with greater difficulty, especially when 30+ intervening residues are still unstructured. Although β1-β3 form a parallel arrangement in the native structure, we observe some non-native antiparallel arrangements. The subsequent steps include the formation of contacts between β3 and β4 and the strengthening of contacts between the helix and β4 in later rounds. By R6, both the 2° structure distribution and average contact maps plateau. While the two remaining foldons, the 3₁₀ helix and β5, maintain low populations in the contact maps, enough steps along the folding pathway are resolved to obtain the correct fold and a best Cα RMSD structure of 4.6 Å. The TerItFix results are consistent with experiments; in particular, the foldons known to be in the TSE are predicted to form prior to the two foldons known to fold after the transition state.

Fig. 4.

Ub, CI2 and α3d. The average contact maps in R5 (upper) are compared to the native contact maps (lower). For Ub, the contacts are circled according to experimental ψ values (green: ψ = 0, absent in TS; red: ψ = 1, present in the TS). For CI2, the non-native contacts are noted with the red arrow. The detailed pathways for the three proteins are in Figs. S1–S3.

CI2 contains both parallel and antiparallel β strands onto which a single helix and an active site loop G3 are packed. CI2 folds in a two state manner, with a TSE characterized using ϕ analysis (26, 27). The helix has the highest ϕ values, followed by strands β3 and β4. In the first TerItFix round, interactions appear throughout the protein (Fig. 4). By R2, the helix begins to emerge (Fig. S9), followed by the β3-G3-β4 motif. The β3-β4 interactions intensify as the carboxy terminus of the helix docks to β3, forming a hydrophobic cluster and stabilizing interactions between the helix and β3-β4. Both experiment and previous simulations (28) suggest that this motif is present in the TS. We concur that the helix forms first, followed by β3-β4. The experimental studies with double mutant cycles also implicate interactions between A17, L50, and I59 in the TSE. Although A17–I59 interactions are absent in our simulations, we observe interactions between residues around A17 and L50. By R4 of TerItFix, non-native contacts between the active site loop G3 and β3-β4 emerge because G3 forms a β-hairpin structure with either β3 or β4. This non-native signature is consistent with the previous simulations (28) and is rationalized by the native G3 loop having an extended geometry that can readily hydrogen bond with either the β3 or β4 strands.

TerItFix simulations for Protein L converge within three rounds, with the formation of hairpin 2 followed by the formation of hairpin 1, producing a best RMSD structure of 3.2 Å (Fig. 5 and Fig. S10). The TSE of Protein L has recently determined using ψ analysis to be extensive, consisting of all four strands (18). This result updates earlier ϕ analysis studies which indicate that the TSE is small and polarized (29). Our simulations predict a non-native registry for hairpin 2, consistent with the experimental finding of non-native structure in the TSE for this region of the protein. The non-native structure arises because the native turn for hairpin 2 consists of three unfavorable consecutive positive ϕ dihedral angles, whereas TerItFix predicts a canonical Type I β turn (Fig. 5). This result agrees with all atom simulations (18) and can explain the origin of the non-native behavior observed experimentally. However, the non-native register is never fully resolved in the TerItFix simulations.

Fig. 5.

Protein L. TerItFix produces a 3.2 Å C_α-RMSD structure albeit with a non-native register for hairpin 2. The TerItFix (red arrows) and native (green arrows) ϕ,ψ angles for the 3 turn residues are indicated.

The two 3-helix bundles are relatively easy targets for TerItFix. According to TerItFix, the pathway for the 73 aa α3d begins with the docking of H2 and H3 (Fig. 4 and Fig. S11). As the contacts between these helices increase, the amino terminus of H1 forms and docks against the other two helices. The lowest Cα RMSD of our best structure is 2.9 Å, in fact, slightly better than the 3.1 Å obtained in the Shaw MD simulations (2). Protein A’s three helices form almost simultaneously within three TerItFix rounds, producing a lowest RMSD structure of 2.9 Å (Fig. S12). Notably, H2 is kinked at the center in R2, but is corrected by R3.

Discussion

The aa sequence of a protein codes for its structure as well as the energy landscape that guides it to that structure. Thus, a fundamental challenge is to identify the basic principles that enable the prediction of folding pathways and structure from sequence alone. The present work is notable in the integration of the prediction of both structure and folding pathways, and in producing agreement with experiments for diverse systems beginning from a realistic unfolded state and using a computationally rapid model lacking explicit side chains.

The three primary components of protein structure—local backbone propensities, hydrogen bonding and 3° packing—are combined with the principle of SS to guide the search process by iteratively fixing 2° and 3° structure. The use of energy functions specifically designed to capture the major stereo-chemical properties (e.g., orientational dependence of pairwise interactions, backbone desolvation, neighbor effects on dihedral preferences) enables the method to describe subtle influences of the primary sequence on the energetic landscape.

Previous methods also have used hierarchical approaches to build protein structures, while others, including our own (8), integrate 2° and 3° structure prediction (30–34). A hybrid version of TerItFix utilizing sequence but not structural homology (3) has been validated in CASP8 and 9 and ranks as one of the best groups in the CASP9 refinement category that involves improving template-based models to solve the crystallographic phase problem (10). Nonetheless, these methods still primarily focus on one aspect, either structure prediction or the folding mechanism.

Our approach departs from Gō-like methods that require knowledge of the native state and invoke the assumption that folding is driven by native interactions on funneled energy landscapes with minimal energetic frustration (35). While the Gō landscape might describe many features of folding, its predictive power can be limited when non-native interactions are important (18, 36, 37), or when slight changes in the aa sequence can drastically alter the folding properties (24), as occurs for the Im proteins discussed here. Gō variants exist that employ sequence dependence and even all-atom representations (38–42), but knowledge of the native state is still required.

Most proteins considered here highlight TerItFix’s ability to identify interesting features of the folding landscapes. Unlike most homology-free structure prediction algorithms, TerItFix invokes no assumptions about 2° structure or uses fragments, while running many orders of magnitude faster than MD simulations (CPU hours compared to CPU weeks). In the absence of major kinetic traps, we expect that TerItFix can predict the native structure for many small proteins. A further test emerges from additional simulations for the set of 12 fast-folding proteins recently investigated by the DE Shaw group using all-atom MD simulations (43). As will be described elsewhere, we obtain an average Cα-RMSD_best of 2.7 ± 1.2 Å as compared to 2.0 ± 1.3 Å from the MD simulations, with TerItFix producing lower values for 5 of the 12 targets. However, proteins with complicated folds such as SH3 still pose a challenge for TerItFix.

While the detection of kinetic traps is one success of our method, resolving them remains difficult. To counter this difficulty, we refold the protein in every round starting from an extended conformation, but using the information garnered from the previous round in the form of sampling and energetic biases. Because the prior information is implemented as biases, rather than as enforced contacts, both native and non-native contacts can weaken in successive rounds. For example, the native-like contacts between H1-H2 in λ repressor form early, are lost in middle rounds, and then reappear in later rounds. Im7, however, provides an example where the new contacts cannot override the earlier, non-native ones, and the protein becomes trapped in an intermediate state. A signature of a kinetic trap in our simulations is the presence of region(s) whose structural diversity varies within and between rounds. Potentially, the threshold for fixing 2° structure assignments and biasing 3° contacts can be reduced to drive the escape from the trap.

Another impediment to modeling protein folding is the inherent difficulty of correctly balancing the energies associated with different types of contacts and backbone geometries. Small errors in the energy function, or the lack of explicit hydrogen bonds and backbone ϕ, ψ dihedral angles, can greatly impact the order of structure formation and the location of the TSE on the reaction surface. These issues contribute to the inability of nearly all prior methods to accurately describe the TSE of Protein L(18) and Protein A (17).

The TerItFix algorithm’s central feature of coupling the 2° and 3° structure by iterative fixing and SS helps identify low energy pathway(s) with the proper order of structure formation. Nevertheless, we experience difficulty identifying the TSE for Protein L and Protein A. Even though simulations for both these proteins converge within three rounds, ascertaining the TSE is difficult and requires auxiliary information. Our prior ψ analysis studies of four proteins with disparate RCO levels indicate that their TSEs acquire a similar fraction of native topology, RCO^TSE ≈ 0.7·RCO^Native (5, 16–18). Accordingly, we cluster all structures from the TerItFix simulations whose RCOs are between 60% and 80% of the native value to identify a TSE (Fig. S13). The major cluster for Protein L has both hairpins folded, in agreement with experiment. But the amino portion of the helix is also folded, which is not observed experimentally (18). Overestimation of the helical content in Protein L’s TSE is typical of other methods as well (18). The TerItFix-determined TSE for Protein A has H1 and H3 along with a kinked helix H2. This structure is close to experiment, except that in the experimental studies, the ends of H1 and H3 are frayed and H2 is not kinked.

Conclusion

We present TerItFix, a holistic approach for predicting pathways and structure that couples basic principles of protein chemistry with a realistic and robust search strategy involving sequential stabilization to find low-energy folding routes. Central to the TerItFix folding algorithm is the progressive learning and biasing of 2° structure, 3° contacts, and backbone hydrogen bonding. Information learned in one round of folding simulations is used in the following round. This work demonstrates that the empirical principle of SS can be applied as a computational strategy to predict both pathways and structure.

By unifying the determination of folding mechanism and prediction of structure, this work has positive implications for both areas. Because no knowledge about the native state is required, we can predict non-native kinetic traps and structures. Our nature-inspired computational search strategy can benefit the prediction of larger proteins, one of the major frontiers of the field. Finally, our work is equally applicable to fast or slow folding proteins and thus provides a suitable alternative for cases that are outside the range of current MD simulations. Moving forward, we plan to use TerItFix predicted steps as an initial path to launch MD simulations, which could then be connected using Markov-state models or network analysis to obtain the energy surface and a more complete description of the kinetics, including timescales and barrier heights.

Methods

2° Structure-Fixing Protocol.

The frequencies of helix, strand, and coil structure, as determined by the Dictionary of Protein Secondary Structure (44), are used to update the consensus 2° structure assignments. At each position, one of the three types is eliminated as a sampling option when its frequency falls below a threshold; e.g., remove helix if frequency lies below 1%. The consensus 2° structure restricts the ϕ, ψ sampling library employed in the subsequent folding round (Fig. S2).

3° Structure Fixing.

The frequency of contacts between residues i and j, E_contact,i<j, in the lowest energy quartile serves as a bias for the next round, with a contact defined by a C_β,i-C_β,j separation below 7.5 Å (only for |i - j| > 3). A similar hydrogen bonding bias between residues i and j is given by -E_{H-Bond i,j} = 25p_i,j + 2(1 - p_i), where p_ij is the probability that the NH of residue i bonds to the CO of residue j, and (1-p_i) is the probability that the NH of residue i lacks a hydrogen bond. This functional form ensures a minimal contribution even when p_i is low in the prior round. The total energy is given as the weighted sum of the E_contact, E_H-Bond, plus the three statistical potentials (SI Text, Table S1).

Each trajectory comprises two stages, with the first stage having higher contributions from the two biasing terms. This stage produces partially structured conformations that form the starting points for the second stage in which the weights of the statistical potentials are increased. Each stage concludes with a refinement step where the minimization is rerun using the double crankshaft local move.