Alternative ground states enable pathway switching in biological electron transfer

Abstract

Electron transfer is the simplest chemical reaction and constitutes the basis of a large variety of biological processes, such as photosynthesis and cellular respiration. Nature has evolved specific proteins and cofactors for these functions. The mechanisms optimizing biological electron transfer have been matter of intense debate, such as the role of the protein milieu between donor and acceptor sites. Here we propose a mechanism regulating long-range electron transfer in proteins. Specifically, we report a spectroscopic, electrochemical, and theoretical study on WT and single-mutant Cu_A redox centers from Thermus thermophilus, which shows that thermal fluctuations may populate two alternative ground-state electronic wave functions optimized for electron entry and exit, respectively, through two different and nearly perpendicular pathways. These findings suggest a unique role for alternative or “invisible” electronic ground states in directional electron transfer. Moreover, it is shown that this energy gap and, therefore, the equilibrium between ground states can be fine-tuned by minor perturbations, suggesting alternative ways through which protein–protein interactions and membrane potential may optimize and regulate electron–proton energy transduction.

Long-range electron transfer (ET) reactions lie at the heart of bioenergetic pathways in all living organisms (1). Nature has evolved specialized proteins and cofactors performing ET with high efficiency over distances as long as 20 Å (2). The role of the protein milieu between the donor and acceptor sites and its fine-tuning has been matter of intense debate in the past two decades (3). Marcus theory predicts that, in the nonadiabatic regime, ET rates are determined by the product of two terms: a Franck–Condon factor that accounts for the ability of thermal fluctuations to induce energetic degeneracy of donor and acceptor, and the electronic matrix element or coupling 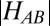that represents the probability of electron tunneling between the degenerate states. Most structure-based ET coupling theories include parameters describing details of the donor and acceptor state electronic structure (4, 5). However, information needed to assess these parameters is unknown in most cases, and treatments often assume only one donor (and acceptor) electronic wave function involved, i.e., the so called redox-active molecular orbital, thereby emphasizing the role of the bridge. It has been shown that structural fluctuations of the bridge between donor and acceptor modulate 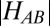(6, 7), leading to different regimes depending on the time scale of the fluctuations with respect to the lifetime of the resonant donor-acceptor state. The structural features of the protein (and water) bridging donor and acceptor redox centers define the tunneling rates, even for large coupling fluctuations (8, 9). Prytkova et al. (10) have considered thermal averages over multiple ligand field states of Fe in heme proteins.

Here we report an example of a biological redox metal center (Cu_A) in which thermal fluctuations may populate two alternative ground-state electronic wave functions optimized for electron entry and exit, respectively, through two different and nearly perpendicular pathways. Moreover, we propose that biologically relevant perturbations may shift the equilibrium between both ground states, thus contributing to the directionality of ET reactions in Cu_A-containing enzymes.

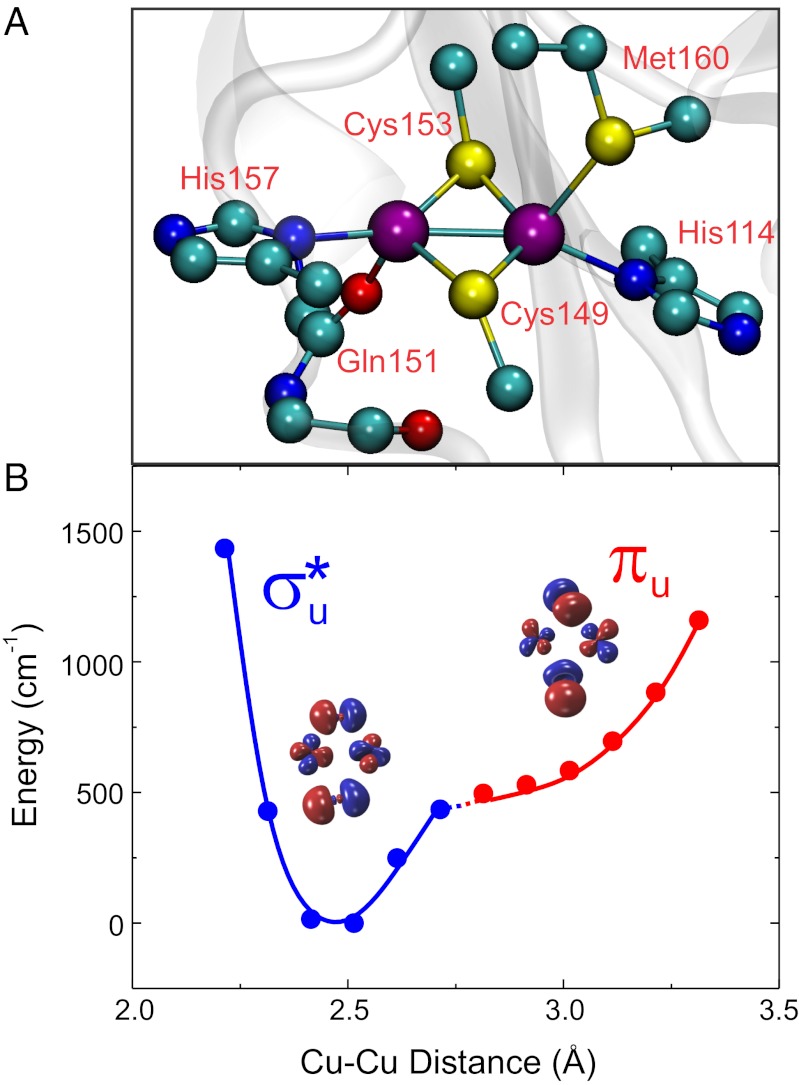
Cu_A is a binuclear copper site that acts as an optimized hub for long-range ET in terminal oxidases and in N₂O reductases (11). The two copper ions are bridged by two cysteine ligands, forming a nearly planar Cu₂S₂ diamond core characterized by a short Cu—Cu distance (2.4 Å; Fig. 1A). The coordination sphere of the metal site is completed by two terminal histidine residues and two weakly coordinated axial ligands provided by a methionine sulfur and a backbone carbonyl (Fig. 1A). Electrons shuttled by a soluble cytochrome c (Cyt) are delivered to the Cu_A site in subunit II of the oxidase and from there to the catalytic site embedded in subunit I, where O₂ is reduced to water. These steps involve two long, nearly perpendicular pathways through the protein milieu. Despite the low driving forces, ET takes place with high rates along these two pathways (12–14). This efficiency has been attributed to the unique coordination features of the Cu_A site (Fig. 1A), which were suggested to yield both a low reorganization free energy (λ) and an electronic structure that enhances superexchange coupling by means of a high Cu—S_Cys covalency (15). In its oxidized form, Cu_A is a fully delocalized mixed-valence species (Cu^1.5+Cu^1.5+) whose electronic structure can be described by a double-well potential energy surface as a function of the Cu—Cu distance, with two ground states, a σ_u* and a π_u level, with minima at ∼2.4 and ∼2.9 Å, respectively (Fig. 1B) (16, 17). NMR studies have revealed a fast interconversion between the σ_u* and π_u ground states (18–20). However, the σ_u* ground state is considered as the only redox-active orbital in ET, based on (i) the low population of the π_u ground state at physiological temperature, and (ii) the higher λ value predicted for the π_u ground state, making its involvement in ET unlikely (16, 17).

Fig. 1.

(A) The Cu_A site from Thermus thermophilus ba₃ oxidase (rendered from PDB ID 2CUA) (35). (B) Double-well potential describing the ground-state symmetry as a function of the Cu—Cu distance, including the calculated σ*_u (blue) and π_u (red) molecular orbitals. The large splitting between both states yields an adiabatic surface along the coordinate.

We recently reported that engineering of the weak axial ligand at position 160 of the Cu_A site of Thermus thermophilus (Cu_A hereafter) results in minor perturbations that tune the reduction potential (21) of the metal site. Here we show that these perturbations can also shift the fluctuating equilibrium between the σ_u* and π_u ground states in the Cu_A site, favoring the population of the π_u ground state, and, that far from being detrimental to the ET reaction, a large increase in the superexchange coupling through an alternative pathway compensates the larger λ measured for this ground state. Thus, we propose that thermally accessible ground states of different wave function symmetry can be switched, allowing for efficient directional long-range inter- and intraprotein ET with minor changes in the nuclear configuration at a low energy cost.

Results and Discussion

Effect of Axial Mutations on the Geometric and Electronic Structure of Cu_A Sites.

X-ray absorption spectra (XAS) were collected on samples of WT Cu_A and the M160H and M160Q mutants. Data analysis reveals that the metal–metal and metal–ligand distances in the Cu₂S₂ core are largely unaltered by the mutations (SI Appendix, Table S1 and Fig. S1). In addition, the structural differences between the oxidized and reduced forms are subtle in all cases. Addition of a S(Met) scatterer at 2.9 Å in the WT variants was consistent with the data, but did not improve significantly the fit. Instead, inclusion of an additional O/N scatterer definitely improved the fit for the mutants’ spectra, suggesting that the engineered axial ligands bind the copper center. Thus, introduction of axial ligands able to bind the copper ion do not give rise to dramatic structural changes in the Cu₂S₂ core.

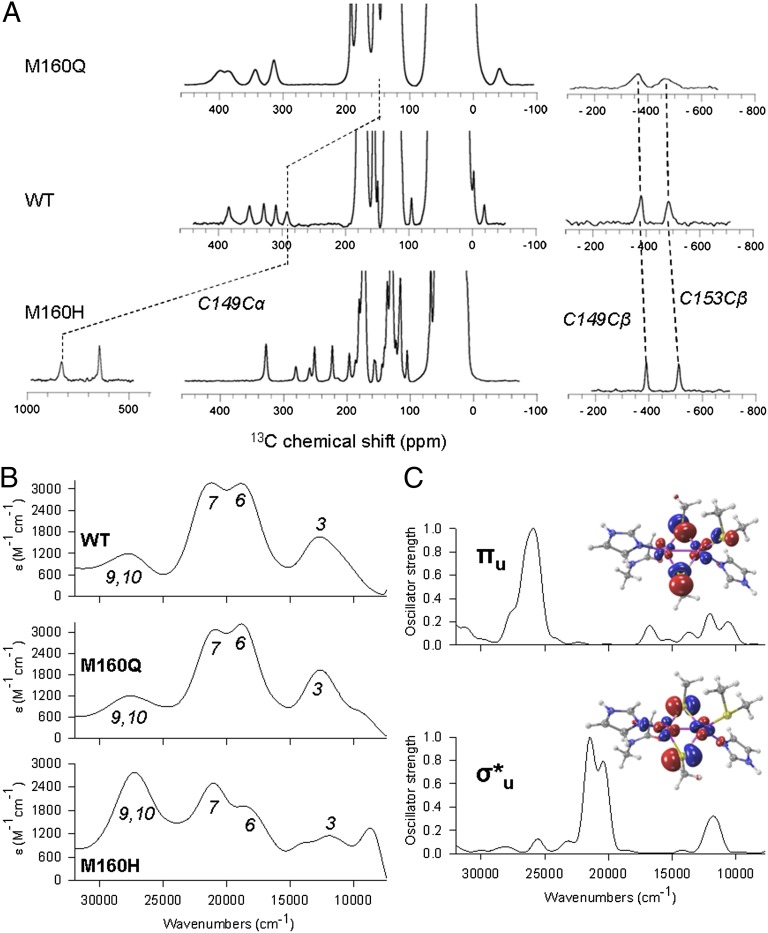
The absorption and CD spectra of oxidized Cu_A centers are dominated by two intense S_Cys→Cu charge transfer (CT) bands at 21,270 and 18,700 cm⁻¹, and N_His→Cu CT transitions at 28,000 and 25,800 cm⁻¹ (Fig. 2B; SI Appendix, Fig. S4 and Table S3) (22). The low-energy feature at 12,650 cm⁻¹ is an intervalence transition (ψ→ψ*) whose energy reflects the electronic coupling between the two copper ions, being sensitive to the ground-state identity (23). The absorption spectrum of M160Q closely resembles that of the WT protein, with a ψ→ψ* band at 12,750 cm⁻¹, consistent with a σ_u* ground state for both protein variants (Fig. 2 B and C). The electronic spectrum of the M160H mutant, instead, presents some perturbations (Fig. 2B; SI Appendix, Fig. S4). To aid in the interpretation, we performed quantum mechanics (QM) calculations at the time-dependent density functional theory (TDDFT) level on this mutant, obtaining the spectra corresponding to both the σ_u* and π_u ground state, shown in Fig. 2. The calculations show that the experimental UV-Vis spectral features result from contributions of both ground states. Specifically, for the π_u ground state, the S_Cys→Cu CT bands blue-shift to ∼28,000 cm⁻¹, partially overlapping with the N_His→Cu CT transitions, whereas the intervalence band appears at 12,100 cm⁻¹, reflecting a decrease in the Cu—Cu interaction with respect to the WT protein. Thus, we can conclude that the perturbation of the weak axial ligand shifts the equilibrium toward the π_u ground state, favoring its thermal accessibility (Fig. 2C; SI Appendix, Fig. S5). Resonance Raman (RR) spectra of the WT, M160Q, and M160H proteins recorded by exciting at 514 nm (19,455 cm⁻¹) are almost identical (SI Appendix, Fig. S6 and Table S4), despite the fact that the absorption spectrum of M160H differs significantly from those of WT and M160Q. This finding is consistent with our QM calculations, which reveal that Cu_A sites with π_u ground state do not present any significant absorption at the excitation wavelength and, thus, the similarity of the RR spectra reflects the structural identity of the three proteins in the σ_u* ground state. Coincidentally, the structural similarities between all studied species observed by extended X-ray absorption fine structure (EXAFS) is due to the accessibility of only the σ_u* state at the cryogenic temperatures used for these experiments (SI Appendix, Fig. S13). The electronic spectrum of M160H at room temperature is therefore consistent with the binding of His160 (as detected by XAS), with a larger impact in the electronic structure of the site compared with the M160Q mutation.

Fig. 2.

(A) ¹³C NMR spectra highlighting resonances from the cysteine residues in WT Cu_A and the M160H and M160Q mutants. (B) Experimental absorption spectra for WT Cu_A and the M160H and M160Q mutants. (C) Simulated spectra for σ*_u and π_u ground states on the WT geometry.

The electron spin density on ¹H, ¹⁵N, and ¹³C nuclei on the metal ligands was determined by NMR spectroscopy on the oxidized, paramagnetic forms of the WT protein and the M160Q and M160H mutants. The high Cu—S_Cys covalency is preserved in all cases, as evidenced by the position of the β¹³C Cys resonances (Fig. 2A), which are sensitive probes of the unpaired spin density on the Cys S γ atoms. The NMR spectra of M160Q reveal specific perturbations in the signals from His114 (bound to the same copper ion as M160) and little effect on His157. On the contrary, in M160H the signals from both His114 and His157 are perturbed, with a reduced spin density in their imidazole rings. In this mutant, we identified a third spin system corresponding to an imidazole moiety with net unpaired spin density (SI Appendix, Figs. S2 and S3), which we attribute to His160. We conclude that His160 is tightly bound to the copper ion (supporting EXAFS data), and we attribute the unpaired electron spin density on His160 to the presence of d_z² character in the molecular orbital containing the unpaired electron. This phenomenon is unique for M160H, for the axial ligands in the WT protein (Met) and in M160Q (Gln) do not exhibit any unpaired spin density.

NMR allows to quantitate the populations of the σ_u* and π_u ground states at room temperature. The chemical shifts of the β-¹H of Cys153, and the α-¹³C from Cys149 are very sensitive to the σ_u*–π_u energy gap because they present dramatic differences in their electron spin densities in the two possible ground states. These two nuclei display S-S-Cβ-Hβ /Cα dihedral angles of nearly 90°, resulting in minimal spin density delocalization in the σ_u* state, and a large spin delocalization in the π_u ground state (Fig. 2A). These resonances show large differences between the studied proteins (Fig. 2; SI Appendix, Fig. S2). Analysis of the temperature dependences of their chemical shifts based on a Boltzmann distribution in a two-state model allowed us to determine the σ_u*–π_u energy gaps of the WT, M160H, and M160Q proteins at 600, 200, and 900 cm⁻¹, respectively (Table 1). These values imply that, at 25 °C, the population of the π_u state is ∼30% in M160H and 1% in M160Q, compared with 5% for the WT protein. These results agree with the experimental and QM calculated absorption spectra, which indicate that the π_u ground state is more accessible in M160H (Fig. 2B). Consistently, the sharper NMR lines in M160H can be accounted for by a more-accessible π_u level, whereas the opposite holds for M160Q (Fig. 2).The electron paramagnetic resonance spectra of the different variants further confirm this trend (21). The g_// values reflect the spin-orbit coupling of the σ_u* level with the π_u excited state at the equilibrium geometry of the σ_u* ground state (∼2.5 Å; Fig. 1) and follow the trend M160Q > WT > M160H, consistent with the stabilization of the π_u level provided by the axial His (Table 1). These data clearly demonstrate that the axial ligand tunes the energy gap between the σ_u* and the π_u levels, and that the latter can be significantly populated upon this minor structural perturbation.

Table 1.

Summary of experimental and theoretical results for WT, M160Q, and M160H

CuA variant	E(GSπu)–E(GSσu*), cm−1†	Populations at 25 °C, σu*:πu	E(ESπu)–E(GSσu*), cm−1‡	Eψ→ψ*, cm−1§	ε, mV¶	kET, s−1||	λexp, eV††	λcalc, eV‡‡		ΔG# = λexp/4, cm−1
								σu*	πu
M160H	200	72:28	3,970	6,050	148	0.81	0.63	0.26	0.48	1,270
WT	600	95:5	4,690	6,325	293	2.03	0.46	0.32	0.63	928
M160Q	900	99:1	4,810	6,375	158	1.65	0.45	0.41	0.57	907

^†Calculated from fits of the temperature dependences of the NMR signals. GS, ground state.

^‡Calculated from the g_// values reported by Ledesma et al. (21) as done by Gorelsky et al. (16). ES, excited state

^§Calculated as half the energy of the intervalence band.

^¶Reported by Ledesma et al. (21).

^||Determined from electrochemical measurements (this work).

^††Determined from the temperature dependences of k_ET.

^‡‡Obtained from QM calculations.

Population of the π_u Ground State May Be Achieved by Different Small Structural Fluctuations.

Mixed-valence model complexes reported in the literature are characterized by a π_u ground state and a Cu—Cu distance of 2.9 Å, which is reflected in a red-shift of the intervalence band to 5,560 cm⁻¹. This picture differs greatly from the one reported here, because the calculated and experimental position of the intervalence band for M160H exhibit much smaller red-shifts. The lack of evidence in favor of a long Cu—Cu distance prompted us to explore, through QM calculations, other reaction coordinates able to yield a π_u ground state. We found that the σ_u*–π_u energy gap is very sensitive to changes in the His114/His157 dihedral angle (with the highest occupied molecular orbital symmetry changing at an angle of ∼25°; SI Appendix, Fig. S10) and to deformations that disrupt the planarity of the Cu₂S₂ diamond core (SI Appendix, Fig. S11). None of these distortions is associated with a significant lengthening of the Cu—Cu distance, as depicted in Fig. 1. Moreover, the application of electric fields of biologically relevant magnitudes, which may act as an external perturbation, results in increased σ_u*–π_u energy gaps along the Cu—Cu coordinate (SI Appendix, Fig. S12). We conclude that the alternative π_u ground state may be populated through different reaction coordinates, all requiring approximately the same (low) energy and involving relatively minor geometric fluctuations that do not necessarily imply such a long Cu—Cu distance. Moreover, the energy gap (and the relative populations of each ground state) might be affected by perturbations such as mutations of the weak axial ligand and the presence of a biologically relevant electric field.

Protein Film Voltammetry.

The λ values of the WT Cu_A site and mutants were determined by cyclic voltammetry (CV) of protein samples adsorbed on biomimetic electrodes. Two types of independent experiments and data treatments were performed. In one case, CVs were recorded at constant temperature as a function of the scan rate, and λ values were obtained from simulations of the voltammograms in terms of the Marcus equation integrated to account for the density of states of the metal electrode (24). The second type of experiment consisted of CVs recorded as a function of temperature in a nonisothermal cell at variable scan rates. Rate constants in the latter case were obtained using Laviron’s formalism (24, 25), and λ was estimated from Arrhenius plots in a temperature range (15–40 °C) that, as shown in SI Appendix, Fig. S13, does not affect the relative population of both ground states. Despite the different uncertainties and sources of errors, both approaches yielded nearly identical results, with λ values of 0.46 (WT), 0.45 (M160Q), and 0.63 eV (M160H) (Table 1; SI Appendix, Figs. S7 and S8). The measured λ values for M160Q and WT Cu_A are expected to correspond to the σ_u* ground state, largely predominant in both variants in the temperature range of the experiments. This conclusion is confirmed by our QM calculations, which for WT Cu_A in σ_u* and π_u ground-state configurations yield inner sphere λ values (λ_in) of 0.32 and 0.63 eV, respectively (Table 1). In contrast, the population of the π_u ground state is 28% in the M160H mutant, implying that two species should be electrochemically distinguishable if both ground states were redox-active. However, only a single redox couple is detected over a large range of scan rates (10–10,000 mV⋅s⁻¹) and temperatures, indicating that only one of the ground states is active in this mutant. The QM-calculated λ_in values for M160H are 0.26 eV and 0.48 eV for the σ_u* and π_u ground states, respectively, suggesting that the measured λ value (0.63 eV) corresponds to the π_u ground state. The similarity between calculated λ_in and experimental λ values and their sensitivity to the nature of the ground state suggests that in all cases, λ_out represents a small contribution.

The σ_u*–π_u energy gaps for WT and M160Q are within the same range of the activation free energy (ΔG^# ∼ λ/4) for ET of these variants, i.e., 0.12 eV (900 cm⁻¹). Given that at room temperature the population of the σ_u* ground state is ≥95% in both cases, we conclude that the σ_u* state is the electrochemically detected species for WT and M160Q. Instead, for M160H ΔG^# (0.16 eV) is 6.5× larger than the σ_u*–π_u energy gap. This observation suggests that the crossing point between reactants and products can only be achieved for the π_u state along the adiabatic surface, thereby supporting the conclusion that the π_u state is the only redox-active species in this mutant (SI Appendix, Fig. S9 and accompanying text).

Of great significance, the measured ET rate for M160H is only 2.5-fold lower than in WT, thus revealing that the larger λ value (which would imply a sevenfold drop in k_ET), is compensated by an increase in |H_AB|, as a consequence of populating the alternative π_u ground state (SI Appendix, Fig. S7).

Interplay Between Electronic Coupling and Reorganization Free Energy.

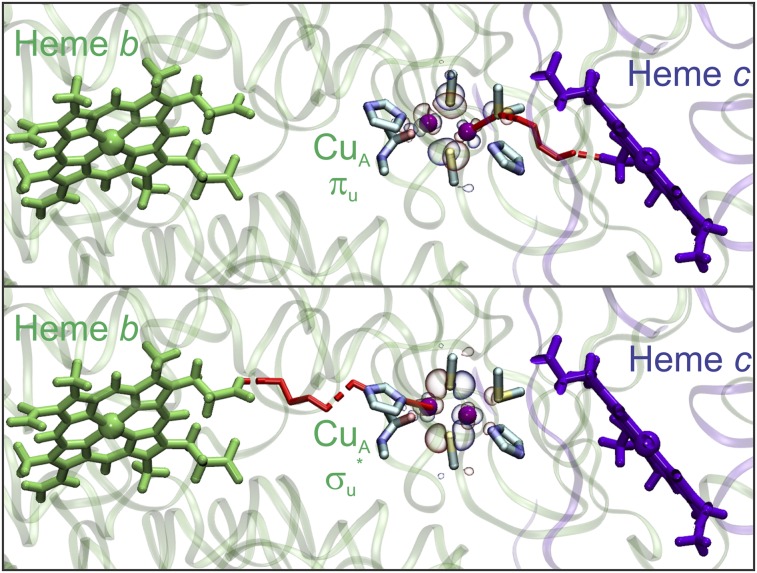
The current picture for ET in terminal oxidases assumes that the protein framework forces the Cu_A site into the σ_u* ground state to avoid a detrimental increase of λ. However, here we have shown that the population of the π_u state can be achieved through minor structural perturbations, and that this transition exerts a low impact on the value of λ. Previous pathways calculations considering only the σ_u* ground state weighted by metal–ligand covalencies suggested that the Cys ligands act as the electron access point (26). However, our pathways analysis in the ET complex between cytochrome c₅₅₂ (Cyt c₅₅₂) and the Cu_A domain of T. thermophilus (13) reveals that the axial Met160 ligand provides the favored electron entry point to the Cu_A site (SI Appendix, Tables S6 and S7). Even though the metal–ligand covalency is very low for the axial Cu—S_Met bond in the σ_u* ground state (Fig. 3), our QM calculations predict a 10-fold increase in the π_u ground state (SI Appendix, Table S8), which is supported by the finding of net electron spin density in the axial His ligand in M160H due to population of the π_u level. Thus, a π_u ground state provides an efficient electron entry pathway by means of an increased superexchange coupling along the Cu—S_Met bond (Fig. 3). This effect results in an enhancement in the ET rate of up to two orders of magnitude, overriding the increase in λ when going from a σ_u* to a π_u ground state. Met160 is not only in the preferred entry pathway, but it is also located next to the hydrophobic patch where Cyt c₅₅₂ binds the Cu_A domain (Fig. 3) (13).

Fig. 3.

(Upper) Optimal ET pathway (red) from cytochrome c to Cu_A in the π_u state, and (Lower) from Cu_A in the σ_u* state to the ba₃ group of the oxidase. Rendered from the structure of T. thermophilus ba₃ oxidase (PDB ID code 1XME) (41) and the model complex between the Cu_A domain and cytochrome c₅₅₂ (PDB ID code 2FWL) (13).

The most efficient pathways for subsequent ET from reduced Cu_A to heme b involve His157 as the electron exit point. Our QM calculations on the reduced Cu_A site reveal that the covalency of the Cu—N(His157) bond is doubled in the σ_u* state compared with the π_u state, suggesting that ET to heme b is favored through the σ_u* orbital. Thus, optimal interprotein ET from Cyt c₅₅₂ to Cu_A involves a π_u ground state as redox-active orbital, whereas subsequent ET from Cu_A is optimized for the σ_u* ground state of the reduced Cu_A (Fig. 3).

Implications for Biological ET.

Based on the present results, we propose that the availability of two alternative redox-active ground states enables efficient directional ET through the Cu_A site, which in the σ_u* and π_u states is able to couple effectively with “upstream” and “downstream” redox partners, respectively. Although it cannot be completely ruled out for the in vivo process, such a pathway-switching mechanism does not necessarily imply a diode-like charge flow. However, the efficiency and directionality of the process depends on the σ_u*–π_u equilibrium, which in turn might be regulated by minor perturbations. Specifically, transient binding of Cyt to CcO might induce structural perturbations populating the π_u state, thus turning its associated pathway on. After the ET reaction takes place, the reduced state does not exhibit an energy minimum of π_u symmetry, so the system relaxes toward the σ_u* ground state, which is optimized for subsequent intramolecular ET reactions. In line with this proposal, a recent study has provided evidence of a direct vibrational coupling between an ET metal site and the protein surface, suggesting that formation of a transient interprotein complex could be transmitted to the metal site (27). Moreover, transient binding of redox protein partners is known to modify the reduction potential of donor and acceptor sites (28) and to induce geometrical distortions of copper redox centers (29, 30). In fact, the study of the Cyt₅₅₂—Cu_A complex reveals subtle structural perturbations at the Cu_A site in a redox state-dependent fashion (13). In addition, the prediction that moderate electric fields alter the barrier for σ_u*–π_u interchange suggests that the local membrane potential could exert regulation on the electroprotonic energy transduction, as previously proposed based on different evidence (31, 32). Of utmost importance, however, even in the absence of external perturbations, the enhanced superexchange coupling of the π_u state renders it suitable for participating in the ET reaction, even if poorly populated.

In summary, here we show that population of alternative electronic states can be favored by subtle perturbations, and suggest that their different covalencies could allow for directional ET. The involvement of transiently and lowly populated, or “invisible,” conformations has been recently recognized crucial for the function of a number of proteins (33, 34). In this respect, the finding that minor perturbations may favor the population of the otherwise invisible (but redox-active) π_u state of Cu_A reveals a previously unidentified role for alternative electronic ground states in directional ET.

Materials and Methods

Protein Preparation.

Samples of WT and mutant Cu_A-soluble fragments from subunit II of the cytochrome ba₃ from T. thermophilus were produced as described previously (18) and stored in 100 mM phosphate buffer (pH 6.0) with 100 mM KCl.

Resonance Raman.

RR spectra were recorded with 514 nm excitation (13 mW; Coherent Innova 70c) in backscattering geometry using a confocal microscope coupled to a single-stage spectrograph (JobinYvon XY 800) equipped with a CCD detector. Protein samples (1 mM) were placed into a rotating quartz cell for the measurements.

Electrochemical Determinations.

Cyclic voltammetry was performed with a Gamry REF600 potentiostat in a nonisothermal cell equipped with a polycrystalline gold bead working electrode, a Pt wire auxiliary electrode, and a Ag/AgCl reference electrode. Modification of the Au electrodes and measurement conditions are described in SI Appendix.

NMR Spectroscopy.

NMR experiments were carried out on a Bruker Avance II Spectrometer (600.13 MHz ¹H frequency) as described in SI Appendix and in our previous work on WT CuA (18).

X-Ray Absorption Spectroscopy.

Cu K-edge (8.9 keV) EXAFS and X-ray absorption near-edge structure data were collected at the Stanford Synchrotron Radiation Laboratory operating at 3 GeV with currents between 100 and 80 mA on beam line 9-3. See SI Appendix for further details.

Optical Spectroscopy.

Absorption and circular dichroism spectra were acquired with Jasco V-670 and J-810 equipment, respectively, using thermostatized chambers and quartz cells.

Computational Methods.

Models were built from PDB ID code 2CUA (35) by replacing Met160 to generate the mutant structures, which were relaxed with AMBER 11 (36). QM and QM/molecular mechanics calculations were performed with Gaussian09 (37) and SIESTA/Hybrid (38, 39). Donor–acceptor electronic couplings were computed with the Pathways (40) plug-in for the Visual Molecular Dynamics program. See SI Appendix for further details.