Active, motor-driven mechanics in a DNA gel

Abstract

Cells are capable of a variety of dramatic stimuli-responsive mechanical behaviors. These capabilities are enabled by the pervading cytoskeletal network, an active gel composed of structural filaments (e.g., actin) that are acted upon by motor proteins (e.g., myosin). Here, we describe the synthesis and characterization of an active gel using noncytoskeletal components. We use methods of base-pair-templated DNA self assembly to create a hybrid DNA gel containing stiff tubes and flexible linkers. We then activate the gel by adding the motor FtsK50C, a construct derived from the bacterial protein FtsK that, in vitro, has a strong and processive DNA contraction activity. The motors stiffen the gel and create stochastic contractile events that affect the positions of attached beads. We quantify the fluctuations of the beads and show that they are comparable both to measurements of cytoskeletal systems and to theoretical predictions for active gels. Thus, we present a DNA-based active gel whose behavior highlights the universal aspects of nonequilibrium, motor-driven networks.

Living cells display a range of interesting mechanical activities, including the ability to change shape, to translocate, and to apply stress to their surroundings. All of these activities can be stimulated by external mechanical or chemical signals. Some do not rely on a genetic response, but rather a response at the level of the cytoskeleton, the primary mechanical system of the cell (1, 2). This suggests that some of the cell’s mechanical activities can be reproduced by a relatively simple artificial soft-matter system that lacks genetic control. Such a system would be useful both as a model for testing the physical principles underlying cytoskeletal behavior and as a material with potential technological applications.

To design such a system, we must consider the key components of the cytoskeleton itself: Many cellular mechanical activities are due to a network of actin filaments that gains an active, nonequilibrium character through internal stresses generated by myosin motor proteins. These motors transduce chemical energy (through ATP hydrolysis) into mechanical work. In both muscle and nonmuscle cells, the main mechanical role of myosin is to contract the filaments, creating stress that propagates through the actin gel (3). This leads to a stiffening of the cell (4) along with enhanced mechanical fluctuations (5). These two behaviors have also been seen in reconstituted networks that only contain myosin and cross-linked actin (6–9), supporting the notion that these two components are the minimum needed to recapitulate active cell mechanics.

What other motors and filaments can be used to form a gel with active mechanics? There are many biomolecular and synthetic fibers that can match the structural stiffness and cross-linking capabilities of actin (if not its active polymerization traits). The motor proteins are not so easily replaced, as can be judged by the limited capabilities of synthetic molecular motors in comparison to their biological counterparts (10). However, there is one large class of noncytoskeletal motor proteins available: those that work on DNA. Due to DNA’s extreme biological importance, a wide variety of motor proteins exist that replicate, transcribe, repair, or segregate the genome. Further, DNA itself is an attractive structural component, as sequence-directed self-assembly can be exploited to control gel morphology and mechanics.

Here, we show that certain active mechanical traits of the cytoskeleton can be reproduced in a DNA-based material. We use sequence-directed self-assembly to create a gel of DNA then activate it with a bacterial motor protein. The gel is a hybrid of stiff DNA nanotubes (11, 12) cross-linked by long, flexible double-stranded DNA linkers. The motor protein is FtsK50C (13), a construct derived from the bacterial protein FtsK, a bifunctional cell division/chromosome segregation machine (14, 15). Single-molecule experiments have demonstrated that FtsK50C is capable of contracting single DNA strands (16, 17). Here, this contractile activity serves to replace that of myosin and leads to an active DNA gel that stiffens and exhibits active mechanical fluctuations in a quantitatively similar fashion to the cytoskeleton.

Experimental Methods

Design of the DNA Gel.

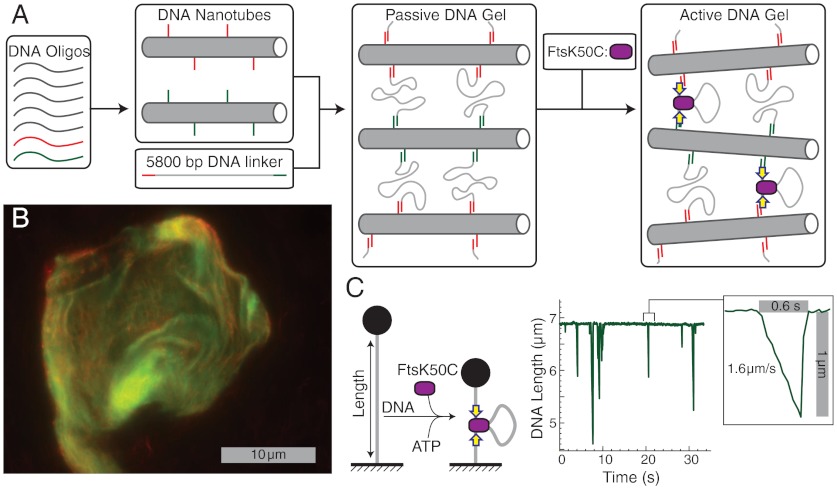
In the cytoskeleton, actin serves as both a stiff structural filament and a motor protein substrate. In a DNA system, it is difficult for a single filament to play both roles because the substrates of all DNA-based motors, single- or double-stranded DNA (ss/dsDNA), are relatively flexible. We overcame this limitation by designing a hybrid gel comprised of DNA nanotubes linked to one another by long dsDNAs: The DNA nanotubes play the role of stiff structural filaments while the dsDNA linkers serve as motor substrates (Fig. 1A). The nanotubes are assembled from DNA oligos (Fig. S1 and Table S1), forming hollow, cylindrical bundles of 12–14 double-helices with a ≈10 nm radius, and lengths of 5 to 10 μm (12). Neighboring helices are bound to each other every two or four helical turns by crossover junctions, where strands switch between helices. Such nanotubes have persistences lengths of several microns, similar to actin (and roughly 100-fold stiffer than dsDNA) (11, 12).

Fig. 1.

Components and synthesis of an active DNA gel. (A) Schematic of gel synthesis and activation, in which base-pair-programmed self-assembly is used first to create two types of rigid DNA nanotubes decorated with sticky ends then to cross-link the tubes with long linker DNAs. The gel is activated by addition of the motor protein construct FtsK50C. (B) Confocal fluorescent image of a DNA gel. The gel contains two types of nanotubes containing, respectively, red and green dyes. (C) Sketch and data demonstrating the contractile activity of FtsK50C on a single, stretched DNA strand; data shown are adapted from ref. 17.

To form a gel, two sets of mechanically identical nanotubes are synthesized separately, each containing a different fluorescent dye and presenting a different 10-base unpaired ssDNA strand on its surface. The ssDNA protrusions are complementary to single-stranded sequences at either end of a 5,800 bp dsDNA linker (Fig. S2). The two types of DNA nanotubes are mixed with the linker, the mixture is concentrated by spin filtration to promote hybridization, and then ligated. The two types of nanotubes are labeled, respectively, with red and green fluorescent dyes, permitting imaging of the gels on a two-color confocal microscope (Fig. 1B). Those images reveal colocalization and intermixing of the two types of nanotubes, indicating successful synthesis of base-pair-linked gels with typical dimensions of 3–10 μm on a side.

The Motor FtsK50C.

In our DNA gel, we replace the contractile activity of myosin with the motor FtsK50C (13) (Fig. 1C). The FtsK50C construct is derived from the bacterial protein FtsK, which is a bifunctional protein: The N-terminal domain is an essential cell division protein, whereas the C-terminal domain forms a hexameric motor protein that encircles and translocates DNA in order to assist chromosome segregation (14, 15, 18). FtsK50C is a truncation that includes the C-terminal motor domain along with 50 amino acids from the N terminus that promote multimerization (13). Although FtsK50C is not the only FtsK truncation that displays in vitro translocase activity (19), it is unique in exhibiting a DNA contraction activity. FtsK50C forms multimotor complexes capable of binding DNA in multiple places. Motor translocation then leads to the extrusion of loops of DNA and contraction of the bound strand (16, 17). Contraction of a DNA strand can occur transiently and repetitively, with the motor suddenly releasing the extruded loop between events (17) (Fig. 1C); alternatively, the motor can hold a strand in the contracted state for a long duration in a mode termed “reeling in” (16).

FtsK50C is a notably strong and fast motor, capable of generating 50 pN of force and translocating at speeds of ≥5,000 bp/s ≈ 1.7 μm/s (16, 17); these characteristics help achieve the maximally active DNA gel. FtsK activity is also sequence-dependent: The C-terminal γ domain binds to the 8 bp FtsK orienting polar sequence (KOPS), which promotes and orients motor activity (20–22). Here, we enhance motor activity by incorporating an inwardly oriented triple KOPS sequence (23) at either end of the DNA linker.

Results and Discussion

Mechanics of the Passive Gel.

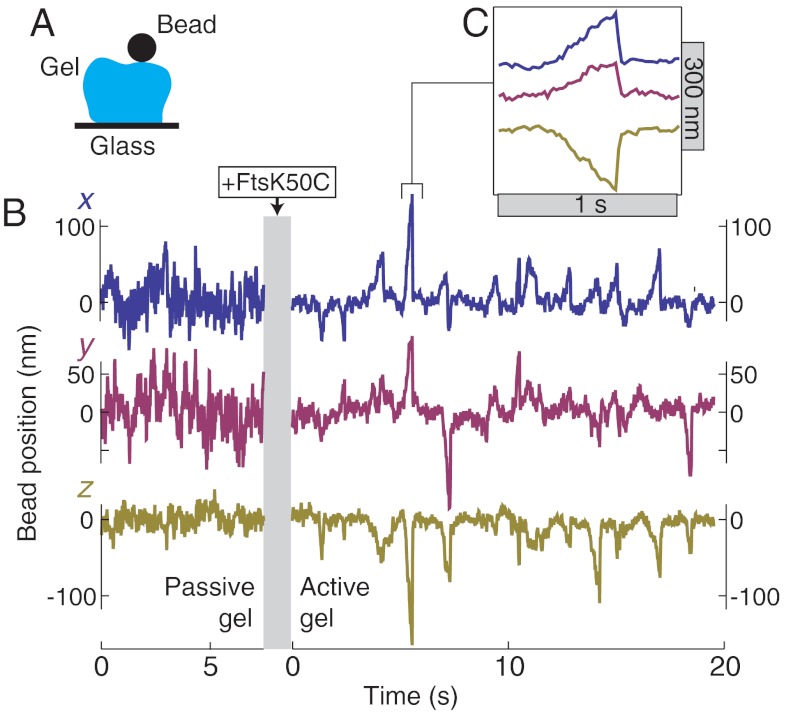
We characterize the active and passive mechanical properties of DNA gels by immobilizing gel fragments on a glass coverslip, attaching 1 μm diameter beads to the tops of the fragments, and tracking the three-dimensional trajectory of the beads in a microscope (Fig. 2A). In this way, we have measured five gel fragments in both the active and passive states. A typical trajectory of a bead attached to a passive DNA gel (i.e., prior to activation by the motor protein) is shown in Fig. 2B. We analyze the trajectories by calculating, first, the van Hove correlation function P(Δx(τ)); this is the distribution of displacements, Δx(τ) = x(τ + t) - x(τ) for a given lag time τ. In the passive gel, P(Δx(τ)) is gaussian for all lag times and in all three dimensions (Fig. 3, blue points), as expected for a thermally fluctuating particle in a harmonic potential. We further investigate gel dynamics by calculating the ensemble-averaged mean-squared displacement versus τ, 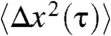. In all three dimensions, the mean-squared displacement (MSD) rises for short times, and plateaus at long times, with a plateau value of about 300 nm² in the z axis, and 1,000–1,500 nm² in the lateral dimensions (Fig. 4A).

Fig. 2.

Trajectories of a bead attached to a passive and active DNA gel. (A) Sketch of experimental geometry, in which a DNA gel is attached to a glass surface and a 1 μm diameter bead, and the bead’s position is tracked over time. (B) Representative x, y, and z trajectories of a bead attached to the same gel fragment before and after activation by the motor FtsK50C. To simplify the comparison of fluctuations, the passive and active trajectories are offset to share the same baseline value. (C) Highlight of one second of trajectory showing the sawtooth shape of an individual motor-induced bead excursion.

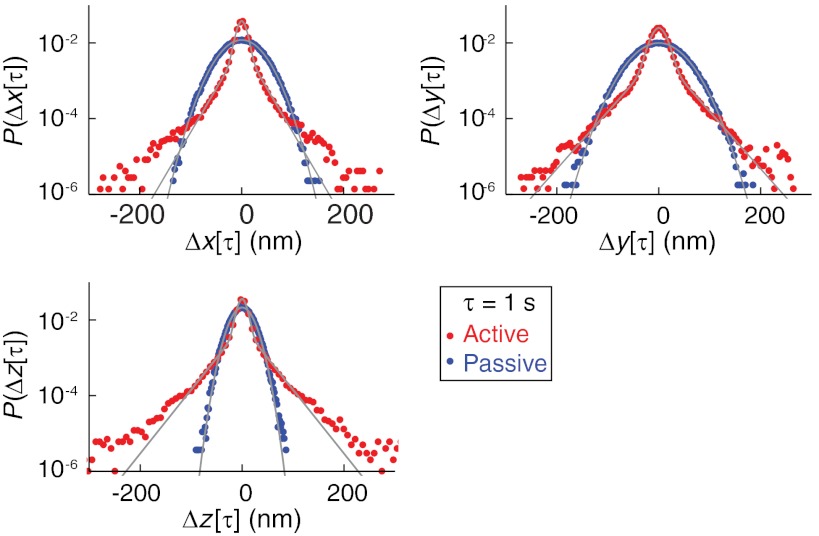
Fig. 3.

Van Hove correlation functions, P(Δr(τ)), of active and passive gel fluctuations in each dimension, r = x, y, or z. P(Δr(τ)) was calculated from the three-dimensional trajectory of a bead attached to the same gel in both the passive and active state. The gray lines show the best fits to either the normal distribution (passive data) or a summed normal/exponential distribution (active data).

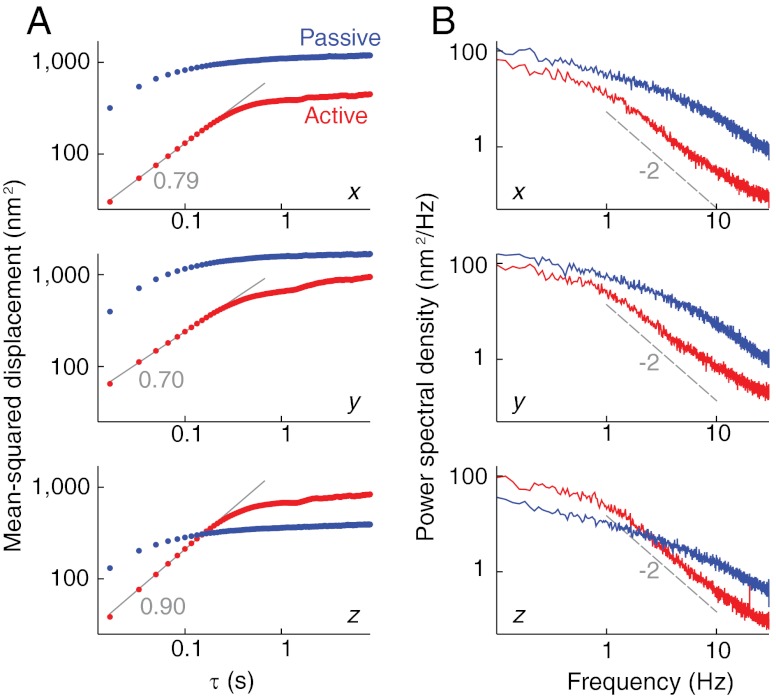
Fig. 4.

Dynamics of the active and passive gel. (A) Mean-squared displacement vs. lag time, τ, for a bead attached to a passive (blue) and active (red) gel. The small-τ active gel data are fit to a power law (gray lines), with the best-fit exponent noted. (B) Power spectral density of the positions of the same bead. The dashed line is an overlay (not a fit) indicating the 1/f² behavior expected for a freely diffusing particle.

Bead fluctuations in the (x,y,z) directions permit an estimate of the gel’s elastic moduli, i.e., the shear moduli E_x and E_y, and the tensile modulus E_z. The small size of the gel precludes exact measurement of E due to imprecise knowledge of gel shape and the similar sizes of the gel and the probe particle. However, we can obtain a rough, order-of-magnitude estimate by noting that only thermal fluctuations are present and applying equipartition to find the modulus in dimension r as , where k_BT is the thermal energy, A is the gel’s cross-sectional area and z₀ is the slab thickness. We estimate z₀ from the particle tracking data and A from fluorescent images of the gel. For the data shown in Fig. 4, the ratio A/z₀ ≈ 3 μm. Using the plateau MSD values from Fig. 4, we find E_x ≈ E_y ≈ 1 Pa, and E_z ≈ 3 Pa. Moduli estimates for other gel fragments are within a factor of three of these values.

A modulus of order 1 Pa is consistent with a slab dominated by the elasticity of the DNA linkers: The stiffness of a homogenous gel of long polymers derives from the entropic elasticity of the network strands and is roughly 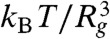, where R_g is the radius of gyration of the strands. This estimate assumes a strand density of 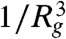, consistent with expectations that linker strand packing is limited by the large entropic penalty for interpenetration of random walk polymers. Here, the 5,800 bp DNA linkers have R_g ≈ 150 nm (24), which gives a modulus of E ≈ 1 Pa. Our measurement thus indicates that the bead fluctuations arise from the flexible linker compliance rather than the much-stiffer elasticity of the nanotubes. This agrees with the basic expectation that the compliance of a system will be dominated by its most flexible components.

Bead Trajectories in the Active Gel.

Adding FtsK50C and ATP leads to qualitative changes in the position and trajectory of a bead attached to a DNA gel; see Fig. 2B. Across the five measured gels, the mean bead height (and thus gel thickness) decreases by 200–1,100 nm, corresponding to a decrease of 20–40% of the total bead height, whereas the lateral bead positions shift by 200–900 nm. We attribute the stable shifts in bead position to near-permanent contraction of many linker dsDNAs by the motor in its reeling in mode (16).

Bead dynamics also significantly change upon activation: The trajectory in all three dimensions exhibits a decreased baseline noise value (discussed below) along with large intermittent excursions. The excursions have a characteristic sawtooth shape (Fig. 2C), with a constant-slope leading edge terminated by a sudden jump back to the initial position. Similar sawtooth events are also seen in measurements of the end-to-end extension of a single, stretched DNA upon contraction by an FtsK50C complex (Fig. 1C); in that case, the slope of the leading edge indicates the translocation velocity of the motor as it extrudes a DNA loop, and the sudden jump is from motor unbinding and fast relaxation back to the initial extension (17). Thus, we attribute each excursion of beads in the gel to a single contraction-and-release event caused by a single motor complex. That the leading-edge slope is constant indicates that the restoring force from the gel is not sufficient to slow the motor, consistent with FtsK50C’s known large stall force (16, 17). Finally, that individual excursions can clearly be resolved is indicative of only intermittent and nonoverlapping motor activity within the entire gel; however, the gel as a whole shows a significant contraction, indicative of widespread motor activity. We conclude that in the active gel a relatively large number of linker strands are held in a contracted, reeled-in state, accounting for the contraction, whereas a few motors display the repetitive contractile events that cause bead excursions.

Although similar in shape, the motor events in the gel differ quantitatively from those on a single DNA strand; these differences can be attributed to the distribution of motors throughout the bulk of the gel. On a single stretched DNA strand, the motor only affects the bead position along the axis of stretching. In contrast, in the gel, contractile events move the bead in the ± x, ± y, and -z directions (Fig. 2B). This is expected, as motors can randomly bind anywhere in the gel, contract, and pull the bead closer, moving the bead in both the lateral and vertical directions. The lack of +z events is simply due to the placement of beads on top of the gels. Further, the speed of bead motion during contractile events in the gel varies between 100–1,000 nm/s; in contrast, the speed of contraction on a single strand is slightly faster, ≈1,500 nm/s, but varies only by ≈20% (17). This is again consistent with motors located at various positions relative to the bead: The coupling of motor contraction to bead motion will decrease with their separation distance and vary with the connectivity of the intervening network. Thus, the bead speed will be reduced relative to the single-motor speed and exhibit a larger variance due to the random spatial distribution of motors.

Van Hove Analysis of Active Fluctuations.

We analyze fluctuations in the active gel by, first, calculating the van Hove correlation function P(Δr(τ)) for each dimension r. Whereas the passive gel always displays gaussian van Hove distributions, the active system shows, in all three dimensions, two clear fluctuation domains (Fig. 3): Small displacements are distributed normally, whereas P(Δr(τ)) shows a significantly enhanced tail for larger displacements. For moderate displacements (≲100 nm), this tail is exponential. Significantly, qualitatively similar van Hove distributions were found in in vitro actin/myosin systems (9), indicating universal traits shared by both systems.

In the active gel, both motors and thermal effects drive bead fluctuations. These effects can be separated using active microrheological techniques (6) whose application here is precluded by the small gel dimensions. Thus, to proceed, we surmise that the two types of fluctuations correspond to the two observed van Hove regimes. That is, we hypothesize that the central normal component arises from thermal fluctuations and that the tail arises from motor fluctuations. If this is true, then the small variance of the normal component indicates that the active gel is significantly stiffer than the passive gel. We quantify this by extracting the variance of the normal component by fitting the van Hove distributions to a function that is the normalized sum of an exponential and a gaussian distribution; this probability distribution fits the data well for small and moderate displacements (see Fig. 3). We then use the normal component variance to estimate the increase in active gel modulus relative to the passive gel. This estimate ignores the change in shape of the gel, which is appropriate because the change in gel thickness, ≈30%, indicates that shape changes are relatively small. Across five fragments, we find that gel activation typically decreases the normal component variance by roughly a factor of 10 in each dimension; in particular, the variance decreases by between 4 and 30-fold in each dimension, with a median decrease of 12-fold in x, 18-fold in y, and 11-fold in z. Thus, the gel becomes roughly 10 times stiffer upon activation; this is best viewed as a lower-bound because motor fluctuations are likely to broaden the normal component of the active van Hove distribution (9). As noted above, our estimate of absolute modulus is imprecise due to the small size of the gels. However, we emphasize that our observation of gel stiffening is robust because the stiffening estimate is based on a differential measurement of the exact same gel fragment in the two states, which removes ambiguities arising from the gel size.

Our estimate of a 10-fold stiffening can be directly compared to two in vitro studies of actin networks, both of which measured a maximal 100-fold stiffening upon activation by myosin motors (6, 8). That stiffening was interpreted to be caused by the nonlinear elastic response of individual actin filaments to myosin-derived forces: Actin filaments are fixed in the gel at an extension near their persistence length before being stressed, and so greatly rigidify under tension (25–27). In contrast, the mechanics of our DNA gel are well explained by the linear response of the long, flexible linkers, whose unstressed extension is a small fraction of their total contour length. Thus, forces from the motors should not stiffen our system, because, for small strains, linearly responsive elements do not change their stiffness with applied force; this explains why our DNA gel shows a smaller stiffening than the cytoskeletal system. That said, we do observe some stiffening. We attribute the stiffening to a structural change rather than a change due to motor forces: The reeled-in DNA strands will act as much shorter linkers, with correspondingly larger stiffnesses. Indeed, a model of a mixture of compliant, protein-free linkers with stiff, contracted linkers can reproduce the measured stiffening of the gel, if, e.g., 1% of the linkers become 1,000-fold stiffer upon contraction (SI Text). A 1,000-fold stiffening of individual linkers is reasonable because the initial entropic stiffness is very weak and because the motor’s long processivity will allow contraction of nearly the entirely linker, effectively removing the linker’s entropic compliance and replacing it with the much stiffer compliance of a short protein/DNA rod (SI Text).

The non-gaussian portion of the van Hove distributions is roughly exponential for moderate displacements. This originates in the exponential kinetics of the motor itself: Single FtsK50C complexes translocate a random, exponentially distributed distance per contraction event (17). Motor kinetics were also interpreted as creating an exponential van Hove tail in cytoskeletal systems (9). In that work, the authors noted that large displacements must arise from a few nearby motors (perhaps just one), because the activity of motors far from the probe will not extend into the tails of the distribution. Our work serves to reinforce this point: The gel we use is quite small [3–10 μm in extent, compared to > 50 μm for the actin gels (9)], and so does not contain any motors far from the probe; yet, we still observe a partially exponential distribution, indicating that a few nearby motors suffice to produce it.

The extreme tail of all the van Hove distributions consistently deviates above the best-fit exponential, and terminates at ≈200 nm. We attribute this to the finite length of the linker DNA: FtsK50C contracts, on average, 6,000 bp of DNA per event when opposed by a 10 pN force (17), and likely travels even longer against lower forces. Thus, the linker length (5,800 bp) is comparable to the mean event length, so many events will contract the entire linker. The initial extent of a linker is of order R_g ≈ 150 nm. Thus, because a significant fraction of events will contract an entire linker, we expect an excess in bead displacements of roughly 150 nm at the tail of the van Hove distribution, as observed.

Diffusive Behavior of Beads in the Active Gel.

We next calculate the MSD from the active-gel bead trajectories, and compare to those in the passive gel (Fig. 4A). In most cases, the active MSD is smaller than the passive MSD when compared for the same lag time, τ. This decrease is consistent with a stiffening of the gel upon motor activation, which will curtail bead motion. The addition of motor fluctuations, which would increase the MSD, does not outweigh the decrease caused by stiffening, except in the z direction at long lag times. This slight difference in the lateral and vertical MSDs is likely due to the assymetry induced by the proximity of the gel to the solid glass surface.

In all dimensions, the active MSD increases monotonically with time up to τ ≈ 0.5 s; this is in contrast to the passive MSD, which reaches a plateau at a much earlier time (≈0.1 s). Further, in all dimensions, the active MSD increases as a power-law, 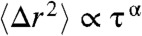, with a typical exponent of 0.7 ≤ α ≤ 0.9, which is near the exponent expected for a freely diffusing particle (α = 1). In fact, the proximity of a long-time plateau will lead to underestimates in the exponent of a short-time power-law, as can be seen in toy calculations (Fig. S3). Thus, we conclude that our measured exponents are consistent with the emergence of a diffusive regime upon activating the gel. This occurs despite the general stiffening of the gel which, if only thermal fluctuations were present, would act to decrease the regime of diffusive behavior.

That a bead attached to a stiffer gel shows diffusive dynamics over a larger time-scale is counterintuitive, but can be explained by the dynamics of motor fluctuations. As predicted by MacKintosh and Levine (28, 29), free diffusion and active-gel fluctuations show similar dynamics for complementary reasons. This is most easily understood in the frequency domain: Free diffusion is driven by spectrally white noise (Langevin forces), and counteracted by the dissipation of hydrodynamic drag, which has a 1/f signature. Active-gel fluctuations are driven by motor activity, which has a 1/f signature arising from the sudden release at the end of each contraction event, while being counteracted by the elastic response of the gel, which is roughly flat at low frequencies. The power spectrum of displacement, which is the square of the product of driving force and response, thus has a 1/f² shape for both free diffusion and active-gel fluctuations, which leads to a linear increase of MSD with time in both situations. In the active gel, this increase stops at τ ≈ 0.5 s, which corresponds to the timescale of motor events.

To confirm this picture, we calculate the power-spectral density (PSD) of bead fluctuations in both the active and passive gels, as shown in Fig. 4B. The passive gel has a roughly Lorentzian PSD, with a corner frequency of f ≈ 10 Hz. The active-gel PSD shows the clear emergence of a low-frequency corner at f ≈ 1 Hz, followed by a regime where the PSD decreases as ≈1/f², as predicted (28, 29). This emergent low-frequency corner cannot be explained by gel stiffening alone, which would lead to an increase in the Lorentzian corner frequency seen in the passive gel.

Both time-domain and frequency-domain analyses of displacement fluctuations in cytoskeletal active gels have also shown diffusive behavior (5, 7). Lau et al. used two-particle microrheology in living cells, and found a 1/f² fluctuation spectrum (5). Brangwynne et al. created in vitro cytoskeletal networks and characterized them by imaging the fluctuations of individual filaments, finding a linear increase of MSD with time (7). Our DNA-based active gel shows the same dynamics as these systems, again indicating universal aspects of motor-driven active gel behavior.

Conclusion

We have described the design, synthesis, and characterization of an active gel composed of DNA strands and a DNA-based motor protein. We designed the gel with two components, stiff DNA nanotubes and flexible dsDNA cross-linkers, so as to both mimic the cytoskeletal actin network and allow a DNA-based motor access to its native substrate. We have shown that resulting gel mechanics are largely controlled by the linkers: The measured ≈1 Pa elastic modulus in the absence of the motors indicates that compliance is dominated by the linear response of the flexible linkers. This is corroborated by the relatively small motor-induced stiffening of the gel because a linear elastic network will not stiffen in response to small strains; this can be directly contrasted with the larger motor-induced stiffening measured in networks of semirigid cytoskeletal filaments (6, 8).

The active dynamics of our DNA-based gel match those of both in vivo and vitro cytoskeletal systems, indicating the chemistry-independent, universal physical features of motor-driven active gels. Those features are: 1) the exponential tail in the van Hove correlation functions [seen in in vitro actin/myosin networks (9)]; 2) An enhanced regime in which mean-squared displacements rise linearly (diffusively) with time [seen in in vitro actin/myosin networks (7)]; and 3) Power spectra with a 1/f² component [seen in in vivo fluctuation probes (5)]. Further, the latter two observations match theoretical predictions of the dynamics of motor-activated gels (28, 29).

DNA-based active gels have the potential to be important model systems in which to investigate nonequilibrium network behavior and thus key points of comparison for other such networks, such as the cytoskeleton. Indeed, the results presented here lend support to prevailing models of active cytoskeletal mechanics in which the key component is a contractile motor that suddenly releases its substrate.

Active gels further represent a unique class of bioinspired materials whose functions have potential technological utility. The main challenge in exploiting these functions is the transfer of active mechanics out of the cytoskeleton and into an artificial material (30). We have shown that this transfer can be carried out successfully by using DNA to synthesize the gel and activating it with a DNA-based motor protein. Generally, making such materials with DNA is likely to be a powerful approach both due to the ability to control DNA sequence, which permits control both of gel structure and of sequence-dependent protein behavior, and because of the significant design flexibility inherent in the broad spectrum of existing DNA-based motor proteins.

Materials and Methods

Gel Synthesis and Activation.

Synthesis of two types of nanotubes with protruding sticky ends was based on a prior 5-oligo nanotube design (11), and is depicted in Fig. S1. One oligo from that prior work was split in two, and one half was extended by 10 bases (GTAA CGA CTC for type-1 nanotubes, GCCA ATG CAC for type-2) to form the sticky ends (see Table S1 for all oligo sequences). The resulting 6-oligo nanotubes were formed by mixing 1 μM of each oligo in buffer (40 mM Tris acetate, 1 mM EDTA, 12.5 mM magnesium acetate, pH 8.3) in a total volume of 50 μL, then annealing from 95 °C to room temperature over 40 h. Type-1 (type-2) nanotubes were fluorescently labled with fluorescein amidite (Cy5).

The dsDNA linker was constructed from the plasmid pMal-p5×, which was synthesized by molecular cloning, then cut with the restriction enzyme AvaI. The cut plasmid was then annealed and ligated, at each end, to short double-stranded segments containing a 3× overlapping KOPS sequence (23), and terminating in 10 base sticky ends complementary to those on the nanotubes; a schematic of the nanotube/linker assembly is shown in Fig. S2. Three types of linkers were prepared: unlabeled, biotinylated, and digoxigenin labeled.

The gel was made in a five-step process using a microcentrifuge filter (Microcon Ultracel YM-100). Each step consisted of successively adding 100 μL of solution to the filter, then spinning for 12 min at 500  × g. The sequence of added solutions was: 0.01 μM digoxigenin-labeled linker; 0.1 μM type-1 nanotube, 0.09 μM unlabeled linker, 0.1 μM type-2 nanotube, and 0.01 μM biotinylated linker. After the last centrifugation, the filter was inverted and centrifuged into a new tube for 3 min at 1,000  × g to unbind DNA from the filter. The resulting gel solution was then added to a digoxigenin-coated flow cell, and streptavidin-coated beads were flowed in to attach to the tops of the gel fragments.

Bead positions were tracked over time to characterize the DNA-only (passive) gel. Then, motor protein was added by flushing the flow cell with 50 μL of solution containing 400 nM FtsK 50C, 20 mM ATP, 10 mM MgCL₂, 50 mM NaCl, 10 mM Tris-HCl, 1 mM DTT, pH 7.9. All solutions in the flow cell contained a small amount of surfactant (0.01% Pluronics F127 and 0.01% Tween 20) to prevent nonspecific adhesion of beads or gels to the surface.

Bead Tracking.

Bead positions were tracked by placing the flow cell in an inverted light microscope, imaging the beads onto a 60 Hz CCD camera, and calculating the bead position with nanometer accuracy using existing image-analysis routines (31, 32). To remove common-mode drift, both experimental (gel-attached) beads, and reference beads (attached to the glass surface) were tracked; the reported trajectories correspond to the difference between the experimental and reference traces.