Counting single photoactivatable fluorescent molecules by photoactivated localization microscopy (PALM)

Abstract

We present a single molecule method for counting proteins within a diffraction-limited area when using photoactivated localization microscopy. The intrinsic blinking of photoactivatable fluorescent proteins mEos2 and Dendra2 leads to an overcounting error, which constitutes a major obstacle for their use as molecular counting tags. Here, we introduce a kinetic model to describe blinking and show that Dendra2 photobleaches three times faster and blinks seven times less than mEos2, making Dendra2 a better photoactivated localization microscopy tag than mEos2 for molecular counting. The simultaneous activation of multiple molecules is another source of error, but it leads to molecular undercounting instead. We propose a photoactivation scheme that maximally separates the activation of different molecules, thus helping to overcome undercounting. We also present a method that quantifies the total counting error and minimizes it by balancing over- and undercounting. This unique method establishes that Dendra2 is better for counting purposes than mEos2, allowing us to count in vitro up to 200 molecules in a diffraction-limited spot with a bias smaller than 2% and an uncertainty less than 6% within 10 min. Finally, we demonstrate that this counting method can be applied to protein quantification in vivo by counting the bacterial flagellar motor protein FliM fused to Dendra2.

Knowing the state of oligomerization of molecules can help to establish their structural organization in space and ultimately unravel their function. Electron microscopy, cryo-EM, and crystallography are the methods of choice to elucidate macromolecular structures at intermediate and high resolution, respectively, but these techniques often involve elaborate sample preparation or require isolating the protein complexes from their natural environment. Optical microscopy with fluorescent proteins provides a much less invasive alternative and allows quantification of proteins with single molecule sensitivity (1, 2). However, the resolution of conventional microscopy is diffraction-limited to approximately 250 nm, a dimension much larger than the size of protein complexes.

In photoactivated localization microscopy (PALM), multiple fluorescent molecules spatially closer than the diffraction limit can be resolved by separating their contributions in time (3). PALM can, in principle, be used to count single molecules located within a diffraction-limited spot in the image. Ideally, any irreversibly photoactivatable fluorescent protein (PA-FP) can be used as a tag to count, for example, the number of proteins of a particular kind inside a cell, by simply tallying the number of emission bursts (4–6). In practice, however, the potential counting error incurred by the fluorescent blinking of PA-FPs in their photoactivated form (3, 6, 7) has been a major obstacle to the use of PALM for molecular counting. Although a semiempirical approach to correct the artifact due to the mEos2 photoblinking was recently proposed (8), systematic guidelines have not been established yet for quantitative PALM applications.

In this work, we present a comprehensive method for accurate counting of PA-FPs by PALM, from the choice of a PA-FP to data acquisition and analysis. Specifically, we characterized the fluorescent blinking properties of mEos2 and Dendra2 via single molecule in vitro experiments and proposed a kinetic model to describe their emission, blinking, and photobleaching behavior. We found that Dendra2 is a more suitable tag than mEos2 for protein counting by PALM. Furthermore, we developed a unique photoactivation scheme and an analysis algorithm to quantify and minimize the counting error and to improve the accuracy of molecular identification. Finally, we applied our counting method to quantify the bacterial flagellar motor protein, FliM, in live cells and we obtained the expected number of molecules per motor for this protein (9–11).

Results

mEos2 and Dendra2 Blink in Their Photoactivated Red Form.

To elucidate and characterize the blinking behavior of mEos2 and Dendra2, we developed a single molecule assay. Biotinylated mEos2 molecules were immobilized on a streptavidin-coated glass coverslip in a manner such that oligomerization was negligible and molecules were spatially separated enough to be detected individually (SI Materials and Methods). To investigate their red fluorescence emission properties, we photoconverted all the mEos2 to the activated form by illuminating them with a 405 nm laser for 2 min; thereafter the sample was excited with a 561 nm laser (SI Materials and Methods).

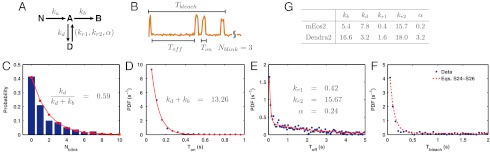
The mean distance between mEos2 molecules on the glass coverslip was much greater than the full width at half maximum, approximately 302 nm, of the point spread function of the instrument, thus eliminating the uncertainty of observing single molecules (Fig. 1A and Fig. S3 A–C). An example time trace of the integrated emission intensity of one molecule shows three peaks within the first 2 s, followed by a low background that persists for at least 2 min (Fig. 1B). We interpret this pattern as the single mEos2 molecule blinking two times in the red form before photobleaching (6). The possibility of those three peaks arising from activation of three mEos2 molecules at different moments can be excluded because mEos2 molecules were synchronized to the red form. Moreover, the spatial positions of these three individual emission bursts (Fig. 1C) were indistinguishable within the localization uncertainty yielded by PALM analysis (Fig. 1D) (12).

Fig. 1.

mEos2 blinks in its photoactivated red form. (A) Single-molecule fluorescence detected with an EMCCD camera shows spatially distinct individual molecules. (Scale bar, 1 μm.) (B) Time trace of emission intensity (orange line) and (C) EMCCD images of a single mEos2 (red box from A) show two transitions to dark states, followed by photobleach. (D) Localized positions (+ symbol) of each of the three images from C are spatially indistinguishable within the localization uncertainty (white circle, 1σ). (Scale bar, 10 nm.)

We also performed the experiment with Dendra2 molecules under identical conditions. The results showed that Dendra2 blinked in its activated red form as well.

Kinetic Model of PA-FP Blinking.

To use mEos2 or Dendra2 for counting purposes, it is necessary to understand the blinking and the photoactivation behaviors of these PA-FP molecules. Here, we propose a phenomenological kinetic model (Fig. 2A) to describe the fluorescence behavior of PA-FPs and validate the model by experimental data. This model describes the transitions between four states: nonactive (N), active (A), dark (D), and photobleach (B).

Fig. 2.

Quantification of blinking and photoactivation of mEos2 and Dendra2. (A) Kinetic model. Nonactive form N of PA-FP is converted to the active form A with rate, k_a, upon 405 nm laser illumination. In the presence of 561 nm laser, the molecule emits light and can go either to dark D or to bleach B states with rates k_d and k_b, respectively. Molecules recover from D to A state with two rates k_r1 and k_r2; α is the ratio between the contributions of the fast recovery rate k_r2 and the slow recovery rate k_r1 (see text). (B) The kinetic rates were obtained by measuring four parameters from single molecules emission traces. (C–F) mEos2 (653 molecules) blinking characteristics under 561 nm excitation laser (22 W/mm²). (C) Distribution of N_blink fits well to a geometric distribution (red line, Eq. 1). (D) T_on distribution of mEos2 (blue dots) follows a single exponential decay (red line), whereas (E) T_off distribution (blue dots) fits well to a double exponential (red line). (F) The measured distribution (blue dots) of T_bleach shows a good agreement with the model prediction (SI Text, Eqs. S24–S26) without extra fitting parameters. (G) Summary of fluorescence kinetic rates of mEos2 and Dendra2. Rate unit is s^-1.

The proposed kinetic model quantitatively describes the probability distributions of four random variables that are measured from the single mEos2 molecules emission traces (Fig. 2B): The number of times the molecule blinks (N_blink) before a photobleaching event, the fluorescence-on time (T_on) before the molecule goes into the dark state or it photobleaches, the fluorescence-off time (T_off) or the time the molecule spends in the dark state, and the photobleach time (T_bleach). The measured probability distribution of N_blink fits well (R² = 0.98) to the predicted geometric distribution (SI Text)

[1]

where η = k_d/(k_d + k_b) is the probability of transition to the dark state (Fig. 2C) and k_d and k_b are the rates of transition to the dark and the photobleach states, respectively. The probability density function (PDF) of T_on fits well (R² = 0.99) to a single exponential function, with the fitted decay rate providing k_b + k_d (Fig. 2D). In contrast to T_on, the PDF of T_off fits well to a double exponential function, p(t) = (k_r1e^-k_r1t + αk_r2e^-k_r2t)/(1 + α), (R² = 0.95), whereas the trial of single exponential functions results in a poor fit (R² = 0.65) (Fig. 2E). The measurement of three quantities, N_blink, T_on, and T_off, is sufficient to determine all the rate constants concerning the red fluorescence of mEos2 (Fig. 2G). Once the rates are determined, all the other measurable quantities are redundant and should be predictable by the kinetic model itself. For example, Fig. 2F shows a good agreement between the measurement and the model prediction of T_bleach (SI Text, Eqs. S24–S26), which further validates the model.

The single molecule data of Dendra2, which is dimmer than mEos2 (Fig. S3), also fits well to the kinetic model (Fig. S4) and the determined rate constants are listed in Fig. 2G, in comparison with those of mEos2. The photobleach rate (k_b) of Dendra2 is about three times faster, whereas the transition rate to the dark state (k_d) is more than twice slower than that of mEos2. Accordingly, Dendra2 blinks on average seven times less than mEos2 [k_d/k_b ∼ 0.2 and approximately 1.4, respectively (SI Text, Eq. S12)]. Also, the slow rate of recovery from the dark state (k_r1) is four times faster for Dendra2 than for mEos2, and the ratio (α) between the events of fast (k_r2) and slow (k_r1) recovery is 16 times greater for Dendra2 than for mEos2.

In summary, Dendra2 blinks less (20% of the population versus 60% for mEos2) and additionally it recovers from the dark state faster than mEos2. Therefore, Dendra2 is a better PALM tag than mEos2 for counting purposes.

Overcounting Error Decreases with the Blinking Tolerance Time τ_c.

The fluorescence blinking of PA-FPs induces an overcounting error if every emission burst is naively considered as coming from a different molecule. Even for a PA-FP with a low blinking probability like Dendra2 (η = 0.16, Fig. S4B), the counting error can be as significantly large as 19% (mean number of blinks, k_d/k_b), because for a given molecule, each single blink adds a 100% overcounting error. Previous PALM studies took account of this problem, despite lack of a systematic analysis, by introducing a blinking tolerance time interval, τ_c: All bursts of emission observed within the localization uncertainty of the instrument and time window τ_c were attributed to the blinking of the same molecule (3, 6, 7, 13). However, the value of τ_c was determined in a purely empirical manner. Recently, the idea of fitting the counting results obtained through various values of τ_c with an empirical function was also proposed (8).

Here, we investigate the effect of τ_c in detail and with mathematical rigor. We consider the probability that the number of blinks 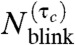by the same molecule, with the dwell time in the dark state longer than τ_c, is n. For the kinetic model in Fig. 2A, this probability distribution is given by

[2]

where

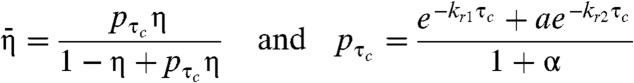[3]

(SI Text). Eq. 2 is still formally a geometric distribution, like Eq. 1. The dark state transition probability η, however, is reduced by a factor p_τc; i.e., the probability of T_off being greater than τ_c. This probability decays exponentially with τ_c at rates k_r1 and k_r2, which are the rates of recovery from the dark state (Eq. 3). Therefore, the introduction of τ_c has the same apparent effect as reducing the probability of entrance to the dark state. Moreover, we can take advantage of the exponential sensitivity by incorporating τ_c into the single molecule identification algorithm to effectively diminish the overcounting error caused by fluorescence blinking.

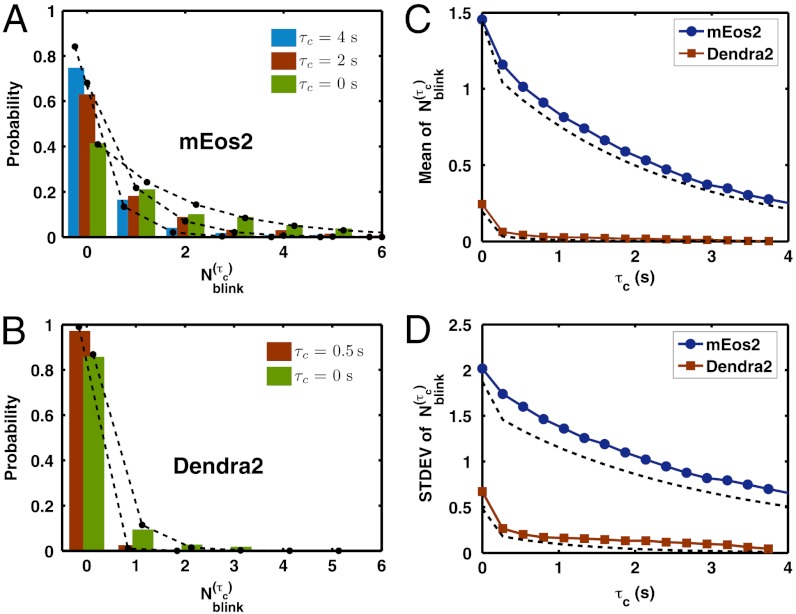
The theory predicts well the experimentally obtained probability distributions of 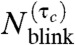as τ_c increases for both mEos2 and Dendra2 (Fig. 3 A and B). The overall behavior of the distributions can be better understood by their means and standard deviations (Fig. 3 C and D). In the case of Dendra2, a τ_c of just 0.5 s reduces the mean apparent number of blinks to approximately 0.05 with a standard deviation of approximately 0.2. Whereas, for mEos2, the mean apparent number of blinks decays much more slowly with τ_c, because of its small k_r1. This stronger dependence of 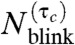on τ_c and the smaller number of blinks (Fig. 2G) make Dendra2 a better dye than mEos2 for counting purposes.

Fig. 3.

Single molecule overcounting error due to blinking decreases exponentially with the introduction of τ_c. The measured (A) mEos2 and (B) Dendra2 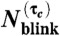distributions (bars) and their (C) means and (D) standard deviations (solid line) at different values of τ_c are well-predicted (dashed line) by the kinetic model, Eqs. 2 and 3.

Estimation of Molecular Counting Error.

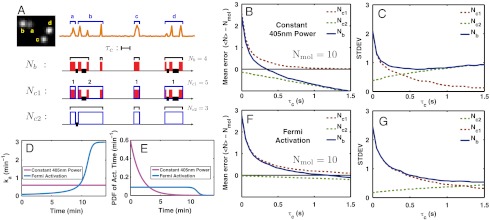
To evaluate the error made when counting multiple spatially indistinguishable mEos2 or Dendra2 molecules by PALM, we developed an analysis method, as follows: First, we randomly pick a certain number of molecules detected on the electron multiplying charge coupled device (EMCCD) field of view (Fig. 4A) and group them. Thereafter, we construct a temporal emission pattern by placing the individual emission traces of the group on the same time axis and superimposing them into a time trace (Fig. 4A). This procedure imitates the emission pattern from spatially indistinguishable molecules, as can be encountered in more realistic and general situations. Then, we count molecules by simply tallying the groups of emission bursts that are separated by more than τ_c, and define this quantity as N_b. The crucial element for this analysis is that, in this constructed dataset, the identity and the number of the chosen molecules are exactly known a priori because they are spatially well-separated on the CCD image (Fig. 4A and Fig. S3 A–C). Therefore, we can quantify the error of our counting method by comparing, for a given value of τ_c, the value of N_b to the actual number of molecules in the group, N_mol.

Fig. 4.

Error in counting multiple Dendra2 molecules in vitro. Dendra2 molecules were illuminated simultaneously with both 405 nm and 561 nm lasers. (A) A constructed multiple-molecule emission pattern (orange line) by grouping together the emission traces of four spatially separated molecules (a, b, c, and d, Left). Two molecules blinked (b and d) and the other two did not (a and c). N_mol is the actual number of molecules, there are four in this example. N_b is the number of molecules counted from this constructed emission pattern by our counting method. (N_c1 - N_mol) and (N_c2 - N_mol) represent the overcounting error due to blinking and undercounting error due to mixing, respectively. N_b, N_c1, and N_c2 are calculated as explained in the text. A red band represents an emission burst and a blue box encloses emission bursts of one molecule identified by using the spatial information from the EMCCD image on the left. Thick black lines mark the time intervals shorter than the value of the τ_c (represented by the length of a line segment). A black bracket encloses the bursts that belong to the presumed single molecule when our counting test is applied. Hence, the error of counting or molecular identification can be quantified by comparing the black brackets with the blue boxes. (B) Mean and (C) standard deviation to count 10 Dendra2 molecules by using N_b, N_c1, and N_c2 for 405 nm laser power fixed to 3.5 mW/mm² employing different values of τ_c (Fig. S5 for distributions). (D and E) Fermi activation produces an almost uniform PDF of activation time, which temporally separates emissions of different molecules most efficiently, thus decreasing the counting error. (F and G) Counting test for Fermi activation with t_F = 670 s and T = 20 s.

In the example shown in Fig. 4A, the introduction of τ_c reduced the value of N_b from eight to four molecules, totally eliminating, in this case, the counting error. However, notice that the identification of molecules a and b was actually incorrect; a mixture of the a-burst and the first two b-bursts was misidentified as one molecule whereas the last (third) b-burst was identified as a separate molecule. This example clearly demonstrates that N_b contains two sources of counting error; i.e., the overcounting due to blinking and the undercounting due to mixing. Here, τ_c reduces the overcounting error but at the same time induces undercounting.

We can separate the two types of counting errors by introducing two quantities, N_c1 and N_c2. N_c1 is calculated as N_mol plus the number of blinking events, within the emission trace of a single molecule, that are temporally separated by more than τ_c. It represents the total overcounting by blinking for a given value of τ_c. N_c2, on the other hand, focuses on the temporal separation between the photobleach moment of a molecule and the moment of subsequent photoactivation of another molecule. N_c2 is calculated as N_mol minus the number of molecules that have their emission traces separated by less than τ_c. Therefore, (N_c1 - N_mol) and (N_c2 - N_mol) represent the overcounting error due to blinking and the undercounting error due to mixing, respectively. By definition, N_c1 is greater than or equal to N_mol, whereas N_c2 is smaller than or equal to N_mol. Obtaining N_c1 and N_c2 requires spatial separation of molecules to identify individual molecules, and therefore are not useful for practical counting purposes. Rather, they are introduced to help better understand the behavior of N_b.

Imagine that we use PALM to interrogate a number of molecules that are photoactivated, blink, and eventually photobleach. Suppose, moreover, that we repeat this experiment several times. Because the behavior of the PA-FP; i.e., their activation, emission, blinking, and photobleaching, is stochastic, every experiment will produce a variable set of events similar to those in Fig. 4A for the same τ_c. The various molecule groupings that correspond to each experiment result in a distribution of N_b, N_c1, and N_c2. Fig. 4 B and C shows how their mean and standard deviation change with τ_c for the case of N_mol equal to 10 molecules (Fig. S5 for the full distributions), calculated by repeating this procedure on many constructed emission patterns. For small values of τ_c, the overcounting error by blinking dominates and so N_b is almost identical to N_c1. The increase of τ_c rapidly reduces this overcounting error. However, it also increases the chance of undercounting, eventually making this error dominant. Thus, N_b approaches to N_c2 asymptotically for large values of τ_c (Fig. 4 B and C and Fig. S5). In this case, the undercounting error induced by emission mixing is what determines the ultimate error of molecular counting by PALM. In Fig. 4B, although τ_c ∼ 1 s suppresses the mean blinking-induced error 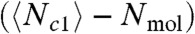down to approximately 0.25 molecule, fluorescence mixing among multiple particles becomes significant at this value of τ_c, biasing the mean of N_b by approximately -0.7 molecule and keeping its standard deviation above approximately 1 molecule (Fig. 4C).

Fermi Photoactivation.

The extent of the undercounting error depends on the power of the activation laser. The fixed power (3.5 mW/mm²) of the 405 nm laser gives rise to exponentially distributed activation times with the rate k_a = 0.6 min^-1 (Fig. 4 D and E and Fig. S6). Therefore, the majority of molecules are activated in the first few minutes of the experiment, hence there is a high probability that photoactivations are poorly separated in time.

Ideally, the most efficient separation of the photoactivation events would be achieved with uniformly distributed activation times. Previous PALM studies (3–5, 7) tried to approximate such a uniform PDF by visually estimating the number of activated molecules per unit time and manually increasing the activation laser power in a stepwise fashion. Instead, we propose to vary the activation rate k_a by continuously modulating the activation laser power in such a way that the photoactivation times are distributed following a Fermi function, a smooth approximation of a uniform distribution, as follows:

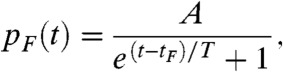[4]

where A is a normalization constant, t_F is the time for the Fermi function to drop to half of its maximum value, and T is the fall-off time of the Fermi function. Such a PDF corresponds to a time-varying activation rate k_a(t) given by

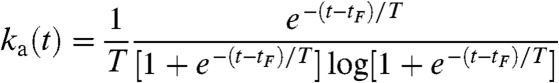[5]

(SI Text). This formula is combined with a calibration curve of the effect of the activation laser power on k_a (Fig. S6C) to obtain the required power modulation scheme. An example of the Fermi activation scheme with t_F = 670 s and T = 20 s is shown in Fig. 4 D and E.

Molecular counting tests show that the Fermi activation significantly improves the temporal separation of photoactivations, and therefore that the distribution of N_c2 stays centered around N_mol with a small standard deviation for a wider range of τ_c(Fig. 4 F and G). This small standard deviation makes it possible, by using a larger value of τ_c, to correct the overcounting error due to blinking, without introducing a significant undercounting error. It is thus possible to lower the error in N_b.

Optimal Molecular Counting.

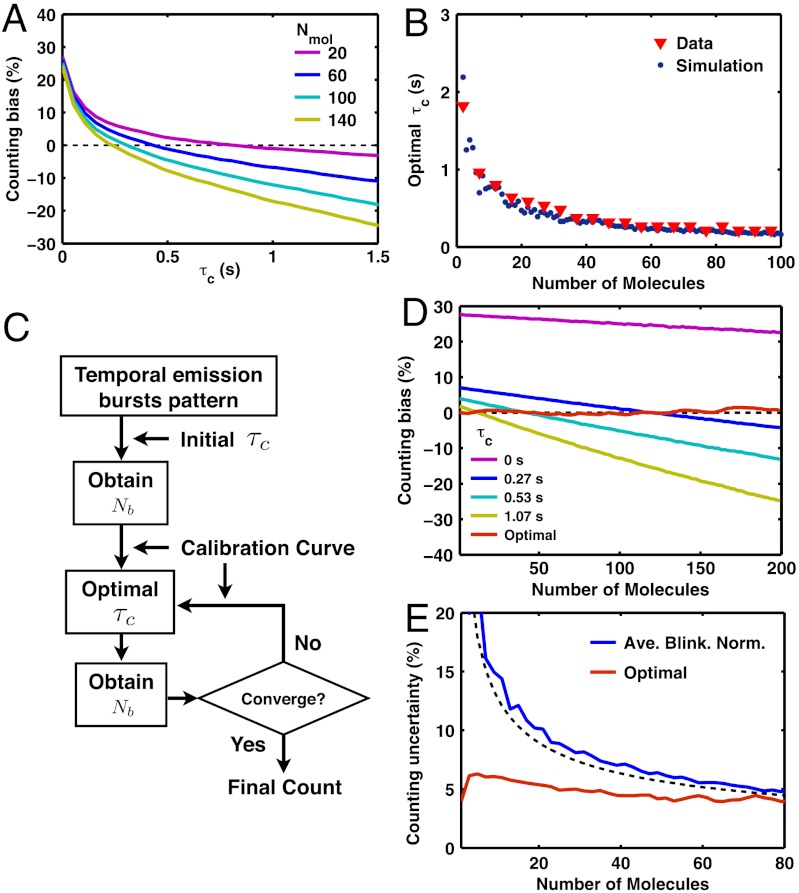
The accuracy of counting molecules by PALM depends on a variety of factors. To optimize this accuracy, we first choose Dendra2 for its minimal blinking properties and adopt the Fermi activation scheme for optimal temporal separation of the photoactivation of different molecules. But the counting accuracy also depends on both the value of τ_c and the number of molecules. To understand how different molecular densities affect the counting error, we repeated the in vitro counting test, as previously described in Fig. 4, for numbers of molecules, N_mol, ranging up to 200 molecules (Fig. 5). As N_mol increases, N_b gets biased more downward for the same value of τ_c because the temporal separation between photoactivations among different molecules gets smaller overall, thus increasing the chance of undercounting multiple molecules by fluorescence mixing (Fig. 5A).

Fig. 5.

Method of iterative optimal-τ_c molecular counting. (A) Dendra2 under Fermi activation with t_F = 670 s and T = 20 s shows that a large value of τ_c and a large number of molecules tend to bias down the counting; i.e., the mean of N_b gets smaller than N_mol (dashed black line). (B) For a given number of molecules, there exists an optimal value of τ_c in which the bias error is eliminated by balancing the over- and undercounting error. The simulation result (blue dots, see text) shows a good agreement with the τ_c obtained from the experimental data (red triangles). (C) Iterative optimal-τ_c counting algorithm that achieves a minimal bias error (see text). (D) Optimal counting method removes the bias error (≤ 2%) for counting between 1 and 200 Dendra2 molecules. In contrast, the use of constant values of τ_c shows significant bias errors. (E) With the bias error eliminated, the final counting error is given by the counting uncertainty; i.e., the standard deviation (≤ 6.2%) for iterative optimal-τ_c counting (red line, only shown up to 80 molecules). In comparison, the result of average-blinking normalization method (see text) provides unbiased counting with a reasonably small uncertainty, although less accurate than the iterative optimal-τ_c method (blue line, data; black dashed line, SI Text, Eq. S45). All the results, except the simulation data in B, were obtained from the counting tests (Fig. 4) on Dendra2 in vitro experimental data.

An inappropriate choice of τ_c results in a significant deviation of the mean value of N_b from N_mol, which leads to systematic over- or underestimation (Fig. 5A). Therefore, we seek to find the optimal value of τ_c that balances the overcounting and the undercounting so that the mean value of N_b is as close as possible to N_mol. Experimental curves such as those in Fig. 5A yield the value of this optimal τ_c for each value of N_mol. In principle, it can also be predicted by the kinetics in Fig. 2A and the measured rate constants of Dendra2 (Fig. 2G). To confirm this assertion, we performed stochastic simulations (SI Materials and Methods) of the kinetic model to compute the optimal τ_c curve. The results of the simulation of the optimal τ_c showed an excellent agreement with the experimental values (Fig. 5B). Thus, the optimal values of τ_c can be determined as long as the kinetic rates are measured.

Note, however, that the optimal value of τ_c depends on the number of molecules, which is precisely the unknown that we wish to determine. Therefore, we introduce a simple iterative method to count molecules with minimal systematic error (Fig. 5C). We start with an initial choice of τ_c = 0 and use it to compute N_b. We take that value of N_b as the first estimate for N_mol, and choose—off the calibration curve (Fig. 5B)—a new value of τ_c that corresponds to the optimal value for that number of molecules. We then repeat the procedure until convergence, which in practice occurs quickly, and independently of the initial choice. Remarkably, when tested on our in vitro Dendra2 data with t_F = 670 s and T = 20 s, this iterative optimal-τ_c counting method yields a distribution of N_b with a mean offset by less than 2% from the correct answer, for N_mol ranging from 1 to 200 molecules (Fig. 5D and Fig. S7). As the bias error is eliminated in this way, the final counting error is determined only by the counting uncertainty; i.e., the standard deviation of N_b, which arises from the intrinsic stochasticity of the photoactivation and blinking kinetics. For the above-mentioned tests, the uncertainty in the number of molecules is less than approximately 6% when counting up to 200 molecules using iterative optimal-τ_c counting (Fig. 5E). Moreover, the method also allowed to identify multiple bursts as coming from the same molecule with good accuracy (Fig. S8). On the contrary, previous PALM studies that use a fixed empirical value of τ_c (3, 7, 13), have shown that this approach has a very narrow working range of number of molecules, and the bias error gets significantly large (tens of percent) outside this range (Fig. 5D).

Alternatively, dividing the total number of emission bursts (counted with τ_c = 0) by the 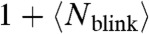per molecule (1.2 for Dendra2, 2.4 for mEos2, Fig. 2, and Fig. S4) also accomplishes unbiased counting (SI Text). This simple method of normalization by average blinking has a reasonably small counting uncertainty for Dendra2 (Fig. 5E) and can thus be used as a quick and easy estimate of the number of molecules. However, it does not address the correct identification of single molecules, and is less accurate than the iterative optimal-τ_c counting method. In general, the iterative method presented should be preferred if both optimal counting and identification are needed.

Counting of Flagellar Motor Protein FliM.

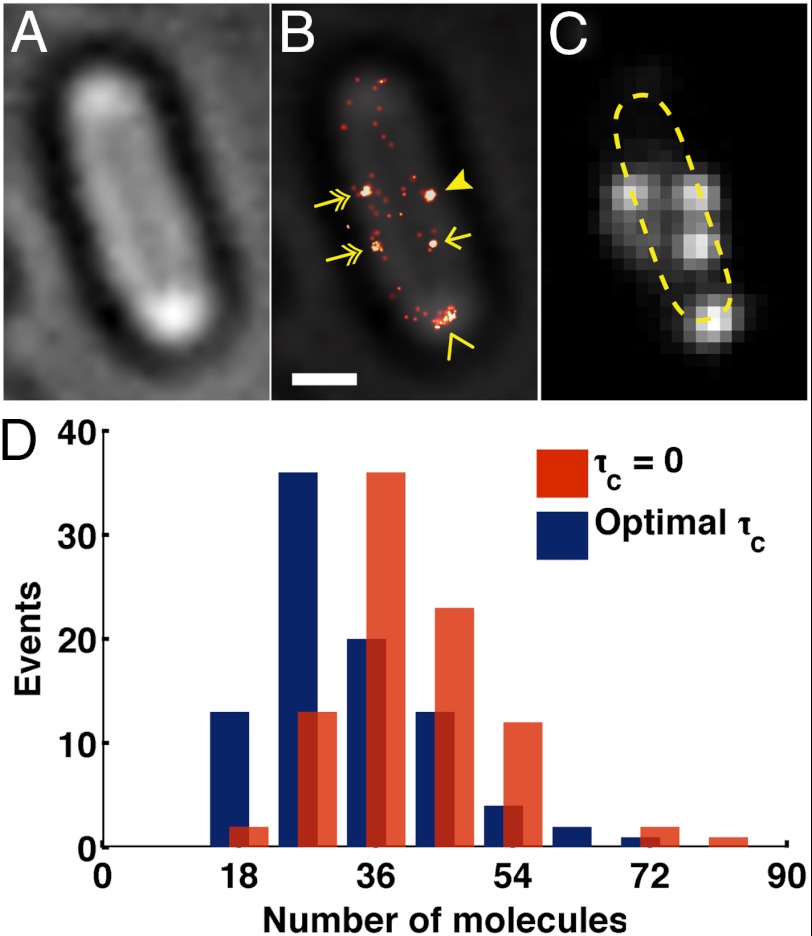
To validate in vivo our molecular counting method, we quantified a flagellar motor protein, FliM, in bacterial cells. FliM is ideal as a counting standard because the number of the molecules within a single mature flagellar motor is known, 34 and 30 ± 6 determined by electron microscopy (9, 10) and photobleaching method (11), respectively. Moreover, a single protein complex is practically immobile once the motor matures; the exchange rate of the cytoplasmic and the motor FliM molecules is low (approximately one molecule in 10 min) (14); and, finally, FliM fused to a fluorescent protein is functional in terms of the localization pattern in cells and swimming and swarming ability (11, 14, 15).

To count FliM protein by PALM we expressed FliM fused to Dendra2 using a medium copy number plasmid under the control of the pBAD promoter (SI Materials and Methods), with an induction level that gives FliM a physiological expression level (14, 15) in the ΔfliM strain (16). FliM-Dendra2 mainly localized as clusters at the cell periphery when the cells were focused at the midplane and the illumination was pseudo-total internal reflection fluorescence (pseudo-TIRF) (Fig. 6). The number of clusters per cell (between one and six) and the clusters localization were similar to those described previously for flagellar motors. Using our optimal τ_c counting method, we quantified 33 ± 1 (mean ± SEM) FliM-Dendra2 molecules per motor, which is within the error of previously reported 34 molecules per flagellar motor (9–11).

Fig. 6.

Counting the number of FliM-Dendra2 molecules in the flagellar motor expressed in ΔfliM strain. (A) Bright-field and (B) FliM-Dendra2 PALM overlay image show that the motor proteins mainly localize as clusters at the cell membrane. Clusters located at the lateral periphery of the cells (arrow head) were selected for the molecular counting, with the exclusion of clusters that were elongated (chevron), located at the cell pole (chevron), or off the periphery (arrow), and surrounded by dispersed molecules (two-headed arrow). (Scale bar, 500 nm.) (C) Diffraction-limited FliM-Dendra2 image. Dashed line, contour of the cell. (D) Iterative optimal-τ_c counting method estimates 33 ± 1 (mean ± SEM) FliM-Dendra2 molecules per cluster, which is similar to the previously quantified number of 34 molecules per flagellar motor. In contrast, the blinking noncorrected method (τ_c = 0) estimates 40 ± 1. A total of 89 clusters were analyzed.

Discussion

In this study, we showed how the blinking properties of PA-FPs Dendra2 and mEos2 quantitatively affect their use in PALM as fluorescent tags for single molecule identification and molecular counting. We introduced a kinetic scheme to explain these properties and measured all the kinetic rates via single molecule experiments (Fig. 2). Our measured two rates of recovery from the dark state for mEos2 are similar to those from Annibale et al. (6, 8). The existence of the dark state is well-known in the PALM literature (3, 7, 13), and current PALM image reconstruction techniques deal with it using a fixed blinking tolerance time that attributes close consecutive emission bursts to the same molecule. We have shown that to achieve unbiased counting, the tolerance time must actually be fine-tuned according to the kinetics of the molecule, the number of molecules and the duration of the experiment (Fig. 5 and Fig. S7).

The ultimate goal of our protein quantification method is to count molecules in a cellular environment where multiple molecules of interest are located within the localization precision of PALM. Therefore, our study used only the temporal emission patterns together with the measured in vitro blinking rates of PA-FP. Although we did not measure the blinking rates of Dendra2 in cells, the in vivo molecular counting of flagellar motor protein FliM fused to Dendra2, was very close to the previously reported values using independent methods (9–11). This result suggests that either the Dendra2 blinking rates in vivo are similar to those in vitro or our protein counting method is not too sensitive to variations in the blinking rates. A test of the counting method’s robustness by simulation (Fig. S9), show that the method is indeed quite insensitive to the actual values of the kinetic parameters.

Our approach can also help to improve PALM imaging. If blinking and intermolecular mixing (Fig. 4) are not well-accounted for, some of the Gaussian spots obtained in a reconstructed PALM image will actually not represent a single molecule. Error in molecular identification (Fig. S8) and counting can lead to artifacts in PALM images (6). Therefore, the use of a correct tolerance time τ_c becomes critical. Moreover, good molecular identification also improves the spatial resolution of PALM because multiple emission bursts can then be correctly attributed to the blinking of a single molecule, and can be combined to improve the localization accuracy (Fig. S3 D and E).

Another available method for protein quantification using fluorescence microscopy with subdiffraction resolution is a photobleaching experiment where the sequential bleaching of individual dyes is detected through the stepwise decrease of the total fluorescence intensity, thus achieving subdiffraction resolution (2, 17, 18). However, this method is limited to small numbers of proteins. On the other hand, Annibale et al. recently developed a method for molecular counting by PALM by fitting a semiempirical formula to the measured N_b(τ_c) for several values of small τ_c, in the regime where overcounting is dominant (8); but the valid range of τ_c for the fitting was chosen subjectively, which could potentially bias the counting significantly.

In conclusion, we have shown that the blinking behavior of photoactivatable proteins such as Dendra2 and mEos2 leads to an overcounting error, and that an overcompensation of this effect by the use of a blinking tolerance time can lead to an undercounting error. We propose to use a unique photoactivation scheme, Fermi photoactivation, to improve identification of individual molecules in a spatially unresolvable confinement. We also developed an iterative method to minimize the counting error with the optimal tolerance time, τ_c, which depends on the kinetic rates of the fluorescent tags. Finally, as a proof of principle, we applied this method to count the number of FliM proteins in the flagellar motor, whose number is known through independent measurements. We show that we have developed a robust method for counting Dendra2 in vivo that potentially can be applied to numerous questions of cellular biology.