Advantages of a dual-tracer model over reference tissue models for binding potential measurement in tumors

Abstract

The quantification of tumor molecular expression in vivo could have a significant impact for informing and monitoring immerging targeted therapies in oncology. Molecular imaging of targeted tracers can be used to quantify receptor expression in the form of a binding potential (BP) if the arterial input curve or a surrogate of it is also measured. However, the assumptions of the most common approaches (reference tissue models) may not be valid for use in tumors. In this study, the validity of reference tissue models is investigated for use in tumors experimentally and in simulations. Three different tumor lines were grown subcutaneously in athymic mice and the mice were injected with a mixture of an epidermal growth factor receptor- (EGFR-) targeted fluorescent tracer and an untargeted fluorescent tracer. A one-compartment plasma input model demonstrated that the transport kinetics of both tracers were significantly different between tumors and all potential reference tissues, and using the reference tissue model resulted in a theoretical underestimation in BP of 50 ± 37%. On the other hand, the targeted and untargeted tracers demonstrated similar transport kinetics, allowing a dual-tracer approach to be employed to accurately estimate binding potential (with a theoretical error of 0.23 ± 9.07%). These findings highlight the potential for using a dual-tracer approach to quantify receptor expression in tumors with abnormal hemodynamics, possibly to inform the choice or progress of molecular cancer therapies.

1. Introduction

Quantification of in vivo tissue biomarker expression is an ultimate aim of many molecular imaging approaches. In general, quantification is carried out by targeting an imaging tracer to a specific molecular marker in tissue, injecting that targeted tracer systemically, and then imaging its uptake in one or more regions-of-interest (ROIs). The idea behind this approach is that the receptor density in an ROI plays a key role in the uptake and retention of a targeted tracer. However, many other factors can also influence the uptake dynamics: such as the rate of tracer delivery (hemodynamics), the vascular permeability, the interstitial pressure, the integrity of lymphatic drainage, non-specific binding, or cellular internalization. In applications where negligible non-specific binding and cellular internalization can be expected, it is possible, in principle, to account for variability in other factors by measuring the plasma input curve (Mintun et al., 1984).

The difficulty with plasma input approaches is that they require invasive arterial blood sampling to measure the plasma input curve. In response, the neurotransmitter positron emission tomography community has developed and often employs a reference tissue model that incorporates the uptake of the targeted tracer in a region of interest void of targeted receptor as a surrogate for the plasma input curve (Lammertsma and Hume, 1996; Logan et al., 1996; Gunn et al., 1997; Ichise et al., 2003). Reference tissue models are based on the assumption that the ratio of the tracer extravasation and tissue efflux rates are roughly equal in both the region of interest and in the reference region. While this has been shown to be true for many neurotransmitter studies (Parsey et al., 2000), there have only been a handful of studies employing versions of these models in tumors (Daghighian et al., 1993; Ferl et al., 2009; Zhang et al., 2006) and the validity of this assumption has not been fully investigated (Tomasi et al., 2012). It should also be noted that majority of plasma input model applications have also utilized a reference tissue to normalize out tracer delivery effects on uptake, finding that it improved the reproducibility of measures of tracer binding (Volkow et al., 1993).

Both plasma input and reference tissue models of this sort are typically used in applications employing a reversible-binding tracer to measure the “binding potential”, a product of the tracer affinity for a targeted receptor and the concentration of available receptor in a region of interest. This in turn offers powerful insight into the pathophysiology of that region of interest. In particular, binding potential could be used to monitor the molecular progression of disease and has the potential to guide new biological therapies (Weissleder and Pittet, 2008).

An alternative non-plasma requiring approach to quantifying binding potential is to employ a dual-tracer method, similar to the reference tissue approach but for which the reference tissue input is replaced by the uptake of a simultaneously injected, untargeted tracer in the same region of interest as the targeted tracer (Tichauer et al., 2011; Pogue et al., 2010). Therefore with the dual-tracer method, as long as the targeted and untargeted tracers are chosen such that they exhibit similar vascular transport kinetics, tracer binding potential can theoretically be determined in tumors or any organ without requiring a reference tissue that has similar hemodynamic and vascular permeability characteristics. In this study, the suitability of a reference tissue input and the proposed dual-tracer input model were investigated and compared in the context of imaging binding potential in mice inoculated with one of three difference tumor lines. The tumor lines were chosen to exhibit various levels of epidermal growth factor receptor (EGFR), a cell-surface receptor overexpressed in many cancers (Herbst and Langer, 2002), and the two models were applied to the simultaneous uptakes of an EGFR-targeted fluorescent tracer and an untargeted fluorescent tracer (each fluorescent at different near-infrared wavelengths of light), which were serially imaged in the tumors and in surrounding tissues over 1 h after tracer injection.

2. Methods and Materials

2.1 Compartment models for tracer kinetic analyses

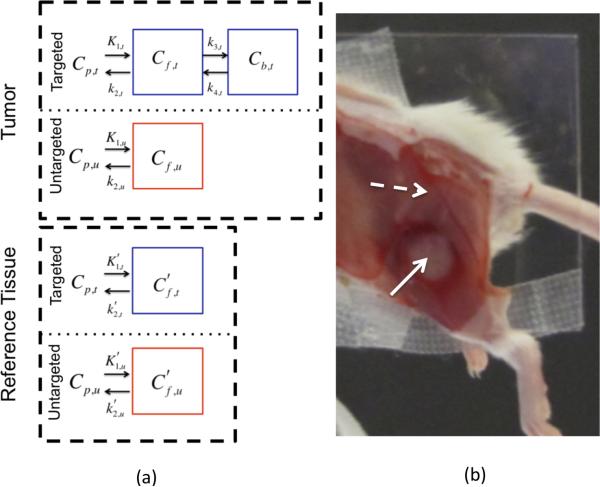
Many tracer kinetic models require compartmentalization of a tracer's distribution in tissue to limit modeling of tracer uptake dynamics to the factors that carry the most influence. The reference tissue input and the dual-tracer input models investigated in this study were based on the compartment models depicted in Fig. 1. The models describe targeted and untargeted tracer uptake in two tissues: a “tumor” tissue (a tissue with some density of targeted receptors) and a “reference” tissue (a tissue devoid of targeted receptors). In each tissue, uptake is driven by a plasma input, which for rigor is labeled differently for each tracer: denoted as C_p,t for the targeted tracer and C_p,u for the untargeted tracer. Both tracers were assumed to interact with at least one distinct tissue-compartment in the tumor and the reference tissues: an interstitial “free” space compartment, C_f,x, where x = t for the targeted tracer and x = u for the untargeted tracer. A superscript tick mark is used to denote that the parameter is associated with the reference tissue as opposed to the tumor tissue. In the absence of targeted binding, and assuming first order tracer kinetics, the following differential equation can be constructed to model the relationship between a tracer's concentration in the plasma compartment and the free compartment as a function of time, t:

$$\frac{d{C}_{f,x}\left(t\right)}{dt}=K_{1,x}{C}_{p,x}\left(t\right)-k_{2,x}{C}_{f,x}\left(t\right),$$ (1)

where K_1,x is the rate constant governing the extravasation of the tracer from the plasma to the free space and k_2,x is the rate constant governing efflux of the tracer from the free space back into the plasma space. K_1,x is capitalized to symbolize the different units it has from the other kinetic parameters, since C_p,x is typically represented as a blood concentration (i.e., with respect to volume of blood), while tissue compartments are represented as a tissue concentration (i.e., with respect to volume of tissue).

Figure 1.

In (a) the compartment models for a targeted tracer in a cancerous region and a reference region (one void of specific receptor) are presented in blue boxes in the “Tumor” and “Reference Tissue” labeled dashed black line boxes, respectively. The compartment models for an untargeted tracer in the two regions are presented in red boxes. A white light image of the experimental mouse setup is provided in (b). The skin is removed from the tumor (identified by the solid white arrow) and the surrounding potential reference tissues (the dashed white arrow is pointing to muscle adjacent to the tumor, presumably void of epidermal growth factor receptor).

Eq. 1 was used to describe the uptake of the targeted and untargeted tracers in the reference tissue and the untargeted tracer in the tumor tissue. In the presence of binding, such as for the uptake of the targeted tracer in the tumor tissue, an additional tissue compartment was added to the structure of Eq. 1: a specific binding compartment, C_b,t, requiring a slightly more complex set of differential equations:

$$\begin{array}{cc}\hfill \frac{d{C}_{f,t}\left(t\right)}{dt}& =K_{1,t}{C}_{p,t}\left(t\right)-(k_{2,t}+k_{3,t})C_{f,t}\left(t\right)+k_{4,t}{C}_{b,t}\left(t\right)\hfill \\ \hfill \frac{d{C}_{b,t}\left(t\right)}{dt}& =k_{3,t}{C}_{f,t}\left(t\right)-k_{4,t}{C}_{b,t}\left(t\right),\hfill \end{array}$$ (2)

where k_3,t and k_4,t are the rate constants governing the transit of the tracer between the free space and the specific-receptor bound space.

2.2 Binding potential estimation

It is possible to solve the differential equations in Eqs. 1 and 2 analytically and use non-linear fitting approaches to estimate the rate constants governing tracer uptake if the uptake of the tracer in the tissue is measured and the plasma input function is known (Watabe et al., 2006; Gunn et al., 2001; Mintun et al., 1984). However, generally these solutions are simplified to better estimate the binding potential, BP, which is defined as:

$$BP=\left(\frac{k_3}{k_4}\right).$$ (4)

The significance of BP can be demonstrated by expanding Eq. 4 in the context of second order enzyme kinetics (Innis and Carson, 2007). In this case, k₃ is equivalent to B_avail·k_on, i.e., the product of the available receptor concentration (B_avail) and the association rate constant (k_on); and k₄ is equivalent to k_off, the disassociation rate constant. By substituting these definitions into Eq. 4, BP can be re-expressed as:

$$BP=\frac{B_{avail}\cdot k_{on}}{k_{off}}.$$ (5)

Eq. 5 can be re-expressed further by acknowledging that the ratio of k_on/k_off is, by definition, the affinity of the tracer for its specific receptor, often referred to as the K_A, and in the limit where the concentration of the tracer used is much lower than the available receptor concentration, B_avail can be approximated as the total concentration of receptor in a region of interest, B_max. Therefore the parameter, BP, is an estimate of the product of the receptor density in a region of interest and the tracer affinity for that receptor (BP = B_max·K_A). Since tracer affinity can be characterized in vitro, BP can be used to estimate receptor concentration, the salient parameter of interest in targeted molecular imaging studies. It should be noted that in the absence of receptor or available receptor for binding (blocking experiments) BP will approach zero.

As mentioned, reference tissue (Gunn et al., 1997; Ichise et al., 2003; Lammertsma and Hume, 1996; Logan et al., 1996) and dual-tracer (Pogue et al., 2010; Tichauer et al., 2011) approaches have been developed to avoid invasive procedures required to measure the plasma input functions. Reference tissue input models assume that the uptake of a targeted tracer in a region of interest and a reference region are measured, while dual-tracer models assume that the uptake of a targeted and an untargeted tracer are measured simultaneously in the same region of interest. Each method requires unique assumptions, however, they can be employed with the same solutions to the differential equations in Eq. 1 and 2. In this study the simplified reference tissue model first described by Lammertsma and Hume (Lammertsma and Hume, 1996) was employed as a scaffold to measure BP in animal studies, written as follows:

$$RO{I}_T\left(t\right)=R_1\cdot REF\left(t\right)+\left\{k_{2,t}-\frac{R_1{k}_{2,t}}{1+BP}\right\}REF\left(t\right)\ast e^{\frac{-k_{2,t}t}{1+BP}},$$ (6)

where * represents the convolution operation, ROI(t) is the uptake of the targeted tracer in the region of interest as a function of time, and $R_1=K_{1,t}∕K_{1,t}^{\prime }$ for the reference tissue model and R₁ = K_1,t / K_1,u for the dual-tracer model. REF represents either the uptake of the targeted tracer in a reference region for the reference tissue approach, or the uptake of the untargeted tracer in the region of interest for the dual-tracer model.

The reference tissue version of Eq. 6 assumes that $K_{1,t}∕k_{2,t}=K_{1,t}^{\prime }∕k_{2,t}^{\prime }$, i.e., that the ratio of the transport kinetics of the targeted tracer in the region of interest is equal to that in the reference tissue; whereas the dual-tracer version of Eq. 6 assumes that K_1,t k_2,t =K_1,u k_2,u, i.e., that the ratio of the transport kinetics of the targeted tracer in the region of interest is equal to that of the untargeted tracer in the same region of interest. The applicability of each of these models for use in tumors was investigated in vivo in mouse models (Sections 2.3 and 2.4) using Eq. 6 to estimate BP accuracy and using a Kety model to directly estimate the transport kinetic assumptions as described in Section 2.5.

2.3 Animal preparation

One of three different tumor lines, each expressing a different level of epidermal growth factor receptor (EGFR) were implanted into twenty-one immune-deficient mice (Charles River, Wilmington, MA). Six mice were inoculated with a rat gliosarcoma (9L-GFP; supplied by Dr. Bogdanov, Dartmouth Medical School), a cell line known to express very little EGFR (Gibbs-Strauss et al., 2010); nine mice were inoculated with a human neuronal glioblastoma (U251; supplied from Dr. Mark Israel, Norris Cotton Cancer Center, Dartmouth-Hitchcock Medical Center), a cancer cell line known to express moderate levels of EGFR (Gibbs-Strauss et al., 2010; Smith et al., 1987); and another six mice were inoculated with a human epidermoid carcinoma (A431; ATCC, Manassas, VA), known to express a very large amount of EGFR (Wikstrand et al., 1997). In all cases, the tumors were introduced by injecting 1×10⁶ tumor cells in Matrigel® (BD Biosciences, San Jose, CA) into the subcutaneous space on the left thigh of the mice. The tumors were then allowed to grow to a size of approximately 150 mm³ before imaging.

2.4 Imaging protocol

The mice were anesthetized with ketamine-xylazine (100 mg/kg:10 mg/kg i.p.) and the superficial tissue surrounding the tumors was removed. Each mouse was then placed tumor-side down on a glass slide and loosely secured with surgical tape (Fig. 1b). Once plated, the mice were positioned onto the imaging plane of an Odyssey Scanner (LI-COR Biosciences, Lincoln, NE). The Odyssey Scanner employs raster scanning and two lasers (one emitting at 685 nm and another at 785 nm) to excite two fluorophores simultaneously, pixel-by-pixel, and utilizes a series of dichroic mirrors to decouple fluorescence from the LI-COR 680 or 700 nm fluorescent tracers and the LI-COR 800 nm fluorescent tracer, respectively. All mice were injected with a cocktail of 1 nanomole of an EGFR targeted fluorescent tracer and 1 nanomole of an untargeted fluorescent tracer: the untargeted tracer was a carboxylate form of the IRDye 700DX NHS Ester (LI-COR Biosciences, Lincoln, NE) and the targeted tracer was IRDye 800CW-EGF (LI-COR Biosciences, Lincoln, NE). The mice were then imaged at approximately 3-min intervals for 1 h after injection of the fluorescent tracers. The ratio of measured fluorescence from the targeted and untargeted tracers at all time points were normalized to the ratio of fluorescence measured using the imaging system from a region of interest on the leg known to be void of EGFR to account for intensity differences due to quantum yield, relative tracer concentrations, and imaging efficiency differences at the two wavelength bands.

2.5 Estimating K₁ and k₂

The kinetic parameters, K₁ and k₂, were calculated in the tumor and in the reference tissue by fitting the analytical solution to a one-compartment model (Eq. 7), also known as the Kety model (Kety, 1951) to the uptake curves of the untargeted tracer in each tissue. For the tumor, the expression used was:

$$RO{I}_U\left(t\right)={\nu }_p\cdot C_{p,u}\left(t\right)+(1-{\nu }_p)\cdot K_{1,u}{C}_{p,u}\ast e^{-k_{2,u}t},$$ (7)

where ROI_U represents the uptake of the untargeted tracer in the region of interest, ν_p is the blood volume in the tumor that was assumed to be 5% of the total tissue volume, and a blood sampling experiment blood curve from a previous study was used to represent C_p,u (Samkoe et al., 2011). Eq. 7 was also used to estimate transport rate constants of both the targeted and the untargeted tracers, substituting REF_U or REF_T, the uptake of the untargeted or targeted tracer in the reference tissue, respectively, for ROI_U, and $K_{1,u}^{\prime }$ and $k_{2,u}^{\prime }$ or $K_{1,t}^{\prime }$ and $k_{2,t}^{\prime }$ for K_1,u and k_2,u, respectively. This same thing was also done to investigate the transport kinetics of the targeted tracer in three of the U251 mice by blocking the EGFR binding sites with a 30-nanomole intravenous injection of free human recombinant EGF (Millipore, Temecula, CA) 15 min prior to injecting the targeted and untargeted tracers.

3. Results

One assumption made by reference tissue models is that the ratio of K₁/k₂ in the reference tissue and the region of interest are the same. When the region of interest is a tumor, finding a suitable reference tissue may be difficult or impossible, since tumors often have irregular and variable hemodynamics and vascular infrastructure. Fig. 2a demonstrates the average uptake kinetics of the injected untargeted tracer for all tumor groups and in a reference tissue (the leg muscle, which was chosen as a potential “reference tissue” since it does not express the targeted receptor, EGFR). A repeated-measures ANOVA with tissue-type as a between-subjects factor and time as a within-subjects factor demonstrated that the temporal dynamics of the tracer uptake was significantly different between all tissue/tumor types (p < 0.05). In general, the uptake and the washout rates of the untargeted tracer in the reference tissue were slower than in the tumors (i.e., K₁ and k₂ were lower in the reference tissue). Amongst the tumor lines, A431 had the slowest washout (lowest k₂), followed by the U251 tumors, and then the 9L-GFP tumors. The 9L-GFP and A431 had similar uptake rates (K₁), while the uptake rate of the tracer in the U251 was slightly higher (not statistically significant).

Figure 2.

Average (mean ± SE) temporal normalized uptakes of untargeted fluorescence in the three tumor lines (red = human epidermoid carcinoma, A431; blue = human glioblastoma, U251; green = rat gliosarcoma, 9L-GFP) and in a reference tissue (purple = leg muscle) are presented in (a). The untargeted tracer K₁/k₂ ratio in each mouse for each tumor type (red = A431; blue = U251; green = 9L-GFP) is plotted against the untargeted K₁/k₂ ratio in a corresponding reference tissue in (b). The line of identity is indicated by the solid black line and the range for which the agreement between the tumor and reference tissue K₁/k₂ ratios would theoretically lead to an error in binding potential (BP) estimation of less than 50% is contained between the dashed black lines.

Though the shapes of the untargeted tracer uptake curves were significantly different between the reference tissue and all tumor lines, it is the ratio of K₁/k₂ that is important to determine whether a given tissue input will be suitable for reference tissue modeling analysis. Fig. 2b demonstrates a scatter-plot comparing the K₁/k₂ ratio for each tumor plotted against the K₁/k₂ of the corresponding reference tissue in the same mouse, for all mice. No statistically significant correlation was found between these two parameters when including all tumor lines, with K₁/k₂ generally being overestimated in the reference tissue compared to in the corresponding tumor. When each tumor line was treated separately, there were weak correlations between the K₁/k₂ ratios in the tumor and reference tissues; however, the data points did not fall near the line of identity, which is expected in reference tissue input models. Simulation results using the full solution to the two-tissue compartment model and an assumed plasma input from experimental results (Fig. 5b) suggested there is a linear relationship between the error in BP estimation and the mismatch in K₁/k₂ between the tumor and reference tissues when utilizing the reference tissue adaptation of Eq. 6 (results not shown). In accordance with this, Fig. 2b demonstrates that for the vast majority of the tumors imaged in this study, use of the reference tissue model would result in an underestimation in BP of more than 50%, with an average error of −57 ± 37%.

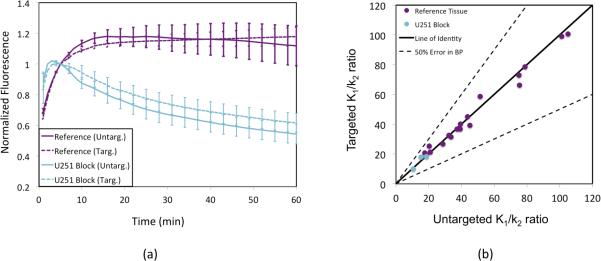
Fig. 3 explores the feasibility of utilizing the dual-tracer model instead of the reference tissue model to estimate BP in tumors. Fig. 3a depicts the temporal uptake and washout dynamics of both the EGFR-targeted tracer and the untargeted tracer in the reference tissue and in the U251 tumor group that was administered a large dose of EGF to block the sites of targeted tracer binding prior to tracer injection. For both the tumors and the reference tissues independently, there was no significant difference between the uptakes of the targeted and untargeted tracers, suggesting that the uptake of the specific untargeted tracer used in this study may be a good surrogate for the transport kinetics of the chosen targeted tracer. Fig. 3b further supports this contention, demonstrating a strong correlation (p < 0.001, r = 0.99) between the K₁/k₂ of the targeted tracer and that of the untargeted tracer in the blocked tumor and in the reference tissue (tissues that are void of available targeted receptor, EGFR). The slope of the correlation was 0.93 ± 0.11, not significantly different from the line of identity, which represents an ideal match for estimating BP with Eq. 6, and no data points fell outside of the 50% BP error range, with the average expected error in BP estimation equal to 0.23 ± 9.07%.

Figure 3.

Average (mean ± SE) temporal normalized uptakes of untargeted (solid lines) and targeted (dashed lines) fluorescence in the blocking study mice (cyan = human glioblastoma, U251) and in a reference tissue (purple = leg muscle) are presented in (a). The targeted tracer K₁/k₂ ratio in each blocking study mouse (cyan = U251) and in all reference tissues (purple data) is plotted against untargeted tracer K₁/k₂ ratio in the same tissues in (b). The line of identity is indicated by the solid black line and the range for which the agreement between the tumor and reference tissue K₁/k₂ ratios would theoretically lead to an error in binding potential (BP) estimation of less than 50% is contained between the dashed black lines.

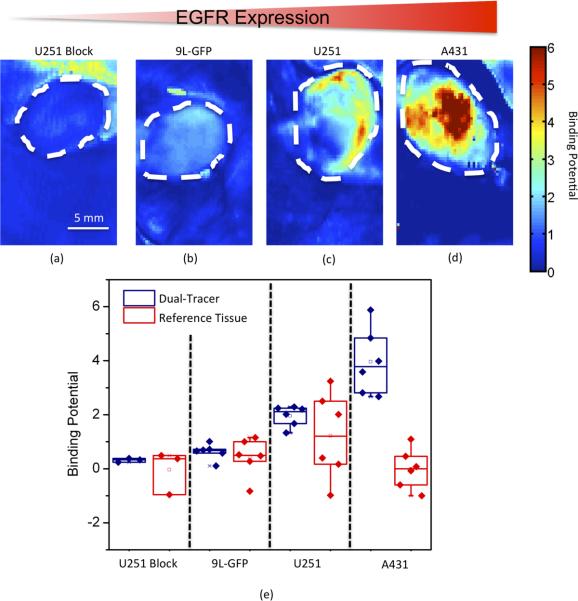
Fig. 4e presents binding potential estimates using both the reference tissue and the dual-tracer models, respectively. In general, the dual-tracer BP estimations had much less variation within each tumor group than the estimations resulting from the reference tissue model. Moreover, the average BP estimation using the dual-tracer model was significantly different between each group (p < 0.05), and followed the trend of expected EGFR expression for the different tumor lines. No significant differences were observed between the different tumor groups with respect to the BP estimations made by the reference tissue model. Furthermore, as expected from the results of Fig 2b, the reference tissue model BP estimates seemed to significantly underestimate BP in the U251 and A431 tumor groups. The ability of the dual-tracer model to be used in mapping BP on a pixel-by-pixel basis while continuing to demonstrate the relative difference in expected EGFR expression between the different tumor groups is demonstrated in Fig. 4a–d.

Figure 4.

Typical dual-tracer derived binding potential map examples are presented for each tumor group: blocked human glioblastoma, U251 Block (a); rat gliosarcoma, 9L-GFP (b); unblocked U251 (c); and human epidermoid, A431. The maps are depicted from left to right in order of increasing expected epidermal growth factor receptor (EGFR) expression, noted by the gradient red triangle at the top. A boxplot is also presented, including the average binding potential from each mouse, separated into different groups. The binding potential from each tumor is presented using both the dual-tracer method (“tracer”: navy blue data) and the reference tissue method (“tissue”: red data). The data is ordered from left to right in increasing expected EGFR expression as with the maps.

While the dual-tracer model demonstrated a better ability to estimate tumor BP in this study compared to a reference tissue model, it does require an additional stipulation that is not necessary for reference tissue approaches: that the plasma input functions of both the targeted and untargeted tracers be the same. Typical plasma curves of IRDye 800CW-EGF and IRDye 700DX (the targeted and untargeted tracers employed in the mouse experiments) from an independent blood collection study (Samkoe et al., 2011) were fitted with a four-parameter biexponential fit of the form, ae^−t/b+ce^−t/d (Tofts and Kermode, 1991), yielding parameters a–d of 0.14, 3.6 min⁻¹, 0.05, and 44.2 min⁻¹ for the IRDye 800CW-EGF tracer and 0.14, 3.5 min⁻¹, 0.05, and 47.4 min⁻¹ for the IRDye 700DX tracer. The effect of the minor differences between the plasma curves of the two tracers on BP estimation was investigated using a one-compartment plasma input analytical model (Kety, 1951) and a two-compartment plasma input model (Lammertsma et al., 1996) to create theoretical uptake curves for both the untargeted and targeted tracers, respectively. The raw experimental plasma curves of the two tracers were used as inputs, K₁ and k₂ were assumed to be 1 ml.min⁻¹.ml blood⁻¹ and 0.04 min⁻¹, respectively, which were roughly the average values acquired from the Kety analysis of the tumor experimental data presented in Fig. 3 (y-axis). For the targeted uptake simulation, BP was assumed to be 3, similar to value found in the A431 tumor group, with a k₄ = 0.1 min⁻¹, (Zhou et al., 1993). Applying the dual-tracer binding potential model to the resulting simulated targeted and untargeted tissue uptake curves resulted in an underestimation in BP of less than 5%.

4. Discussion

The ability to quantify biomarker expression in tumors with molecular imaging is a key goal in cancer research. Specifically, it could be used to predict the effectiveness of proposed cancer therapies on a patient-by-patient basis to guide personalized medicine and to inform drug discovery and development (Weissleder and Pittet, 2008). While there is an enormous number of studies that employ various molecular imaging approaches to measure the uptake of biomarker targeted tracers in tumors, very few studies have taken the extra step to try to quantify biomarker expression. However, this can be an important step since the uptake of a targeted tracer is not only dependent on the density of receptors, but is also dependent on a number of other factors that include the tracer delivery characteristics of the tissue (blood flow, vascular permeability), the potential for the tracer to be released back into the blood stream (which could be influenced by the interstitial pressure of the tissue (Jain, 1990b, a)), non-receptor mediated retention of the tracer (common in tumors (Wang et al., 2007; Maeda et al., 2000)), nonspecific binding of the tracer, and cellular internalization of the tracer. Conventional approaches of measuring binding potential - a direct correlate of receptor expression - employ either a plasma input (Mintun et al., 1984) or a reference tissue input (Lammertsma and Hume, 1996; Logan et al., 1996; Gunn et al., 1997; Ichise et al., 2003) to account for the tracer delivery and tissue efflux effects in a tissue. The majority of these studies have been carried out in the neurotransmitter imaging community; however, there are a handful of studies that have employed a variation of one of these two approaches in tumors (Chernomordik et al., 2010; Daghighian et al., 1993; Zhang et al., 2006; Ferl et al., 2009; Thurber and Weissleder, 2011). While these approaches have been demonstrated to have some success in quantifying biomarker expression in tumors, they may not work for all tumors. For the reference tissue input approaches and the majority of plasma input approaches that also employ a reference tissue, the kinetics of tumors can be highly variable and distinct from normal tissue; therefore, it may be difficult to find a suitable reference tissue. Furthermore, neither the plasma nor the reference tissue input approaches can account for tumor-specific non-receptor mediated retention and uptake of the tracer, which may be significant effects in some tumors (Maeda et al., 2000).

To better account for the non-receptor mediated factors that influence targeted tracer uptake in tumors, some groups have explored the possibility of referencing the uptake of the targeted tracer to the uptake of an untargeted tracer (Goldenberg et al., 1980; Hine et al., 1980; Liu et al., 2009; McLarty et al., 2009; Pogue et al., 2010). Our group has recently employed simplified tracer kinetics models (Lammertsma and Hume, 1996; Logan et al., 1996) in the context of this dual-tracer approach to quantify binding potential (Tichauer et al., 2011). In this study, the validity of these dual-tracer models was investigated in comparison to a simplified non-linear fitting interpretation (Lammertsma and Hume, 1996) of a reference tissue input approach using simulated and experimental data, particularly with respect to variations in the tracer delivery kinetics between the tumor and reference tissues, the equivalency of which is a requisite of both approaches: reference tissue approaches require K₁/k₂ be equal between the region of interest and the reference tissue, while the dual-tracer approach requires K₁/k₂ be equal between the targeted and untargeted tracers within the same tissues.

Tumors are known to have irregular and highly heterogeneous tracer delivery characteristics, which can vary from tumor to tumor and within individual tumors (Dewhirst et al., 1989). Therefore it is not obvious that a reference tissue approach for estimating targeted tracer binding potential will be suitable for use in tumor imaging since these approaches require a reference tissue void of receptors that matches the physiology of the region of interest. In this study, the uptake dynamics of an untargeted fluorescent tracer were imaged in three different tumor lines grown subcutaneously on the hind leg of athymic mice and in the muscle surrounding the tumor. The temporal uptake curves (Fig. 2a) were found to be significantly different (p < 0.05) amongst each tumor line and the reference tissue, suggesting that the delivery kinetics of a tracer can differ substantially from one tumor or tissue type to another. While the curves presented in Fig. 2a hint at the difficulty in finding a suitable reference tissue for BP estimation studies in tumors, the requirements of the reference tissue model are such that the shape of the uptake between the region of interest and the reference tissue can differ as long as the ratios of K₁/k₂ in the two regions are equal. By applying a one-tissue compartment model (Kety, 1951) to the uptake curve of the untargeted tracer in each tissue type (using an average plasma curve as an input (Samkoe et al., 2011)), it was possible to estimate the ratio of K₁/k₂. The results of the Kety analysis demonstrated that K₁/k₂ was about 60% lower in the tumors compared to the corresponding reference tissue, leading to a theoretical underestimation in BP estimation of about 60% using the simplified reference tissue model. It should be noted, that a number of different reference tissues were investigated for their ability to match the transport kinetics of the tumors, including skin, pancreas tissue, kidney, and liver, and in no cases were the K₁/k₂ measured in these tissues within 50% of that measured in the corresponding tumor. It should be noted that the Kety model employed assumed a blood volume of 5%, a parameter that could be highly variable amongst tumors; however, the results were found to be very insensitive to the assumed value in blood volume and a further investigation into the affect of blood volume on BP estimation found that changing the blood volume from 0 to 20% resulted in a BP underestimation of only 2% (results not shown).

By applying the same Kety model to the uptake of the targeted tracer in the reference tissue, the ratio of K₁/k₂ for the targeted tracer can also be estimated since the two-tissue compartment model used to approximate the distribution of the targeted tracer simplifies to a one-tissue compartment model in the absence of available receptor (Fig. 1a). This analysis can also be carried out for the targeted tracer uptake in the U251 tumor blocking study. Therefore, in both the reference tissue and the blocked U251 tumor tissues, it was possible to estimate K₁/k₂ for both the targeted and untargeted tracers to investigate the potential to use an untargeted tracer to act as a surrogate of the plasma input in Lammertsma and Hume's reference model (Lammertsma and Hume, 1996) as opposed to a reference tissue input. Fig. 3 demonstrated that while tracer uptakes differed significantly between the blocked tumor and the reference tissues, the uptake of the untargeted and targeted tracers was very similar within the same tissues, and the results of the Kety analysis showed an strong, statistically significant correlation between the ratio of K₁/k₂ for each tracer in all reference and blocked U251 tissues (Fig. 3b). These results supported the contention that a dual-tracer model could potentially outperform a reference tissue model for estimating BP in tumors. Fig. 4 adds further support, demonstrating that BP could be mapped on a pixel-by-pixel level in tumors using the dual-tracer approach and that the average BPs for each tumor line matched the expected level of expression of the targeted receptor, EGFR (a more involved validation of this dual-tracer model can be found elsewhere (Tichauer et al., 2011)). On the other hand, the reference tracer model BP estimates tended to underestimate BP as expected, exhibiting no discernable correlation with the level of expected EGFR expression.

While the dual-tracer model displayed a more accurate estimate of tumor BP than a reference tissue model in this study, it is important to note that this result is specific to the particular pair of tracers chosen for this study, and will not necessarily hold for just any targeted and untargeted tracer pair. Specifically, it is critical to confirm that any differences in the plasma kinetics between the two tracers employed will not cause significant errors on binding potential estimations. In this study, the targeted/untargeted tracer pair did exhibit minor differences between their plasma kinetics, but the estimated effect of binding potential estimation was less than 5%. The fact that the minor differences in the plasma input curves did not have a strong influence on the measured binding potential does highlight a potential for using fixed plasma input curves in plasma input models that do not require a reference tissue input, as long as inter-subject variability in the study is sufficiently low.

This study demonstrates, both in simulations and experimentally, that a dual-tracer can provide an ideal representation of non-receptor mediated tracer uptake effects on a targeted tracer's uptake in a tumor. In light of this, the dual-tracer approach was shown to be capable of isolating the binding characteristics of a targeted tracer's uptake in a tissue, irrespective of the tissue's tracer delivery or retention characteristics (which in tumors may be very different from any normal tissue). These findings highlight the importance of using a dual-tracer to quantify tumor receptor expression, which could be used to inform the choice or progress of biological therapies that target the same receptors. While the experimental results in this study were carried out using a fluorescence imaging modality to measure the uptake of the targeted and untargeted tracers, this dual-tracer approach could potentially be scaled to clinical use with dual-isotope single photon emission tomography (Fujii et al., 1979) instruments that can discriminate signal from two different tracers.