Action understanding and active inference

Abstract

We have suggested that the mirror-neuron system might be usefully understood as implementing Bayes-optimal perception of actions emitted by oneself or others. To substantiate this claim, we present neuronal simulations that show the same representations can prescribe motor behavior and encode motor intentions during action–observation. These simulations are based on the free-energy formulation of active inference, which is formally related to predictive coding. In this scheme, (generalised) states of the world are represented as trajectories. When these states include motor trajectories they implicitly entail intentions (future motor states). Optimizing the representation of these intentions enables predictive coding in a prospective sense. Crucially, the same generative models used to make predictions can be deployed to predict the actions of self or others by simply changing the bias or precision (i.e. attention) afforded to proprioceptive signals. We illustrate these points using simulations of handwriting to illustrate neuronally plausible generation and recognition of itinerant (wandering) motor trajectories. We then use the same simulations to produce synthetic electrophysiological responses to violations of intentional expectations. Our results affirm that a Bayes-optimal approach provides a principled framework, which accommodates current thinking about the mirror-neuron system. Furthermore, it endorses the general formulation of action as active inference.

1 Introduction

An exciting electrophysiological discovery is the existence of mirror neurons that respond to emitting and observing the same motor act (Di Pellegrino et al. 1992; Rizzolatti and Craighero 2004). Recently, we suggested that the representations encoded by these neurons are consistent with hierarchical Bayesian inference about states of the world generating sensory signals (Kilner et al. 2007a,b): See Grafton and Hamilton (2007) and Tani et al. (2004), who also consider action observation in terms of hierarchical inference. In these treatments, mirror neurons represent motor intentions (goals) and generate predictions about the proprioceptive and exteroceptive (e.g. visual) consequences of action, irrespective of agency (self or other). Casting mirror neurons in this representational role may explain why they appear to possess the properties of motor and sensory units in different contexts. This is because the content of the representation (action) is the same in different contexts (agency). Crucially, the idea that neurons represent the causes of sensory input also underlies predictive coding and active inference. In predictive coding, neuronal representations are used to make predictions, which are optimised during perception by minimizing prediction error. In active inference, action tries to fulfill these predictions by minimizing sensory (e.g. proprioceptive) prediction error. This enables intended movements (goal directed acts) to be prescribed by predictions, which action is enslaved to fulfill. This account of action suggests that mirror neurons are mandated in any Bayes-optimal agent that acts upon its world. We try to illustrate this, using simulations of optimal behavior that reproduce the basic empirical phenomenology of the mirror-neuron system.

Humans can infer the intentions of others through observation of their actions (Gallese and Goldman 1998; Frith and Frith 1999; Grafton and Hamilton 2007), where action comprises a sequence of acts or movements with a specific goal. Little is known about the neural mechanisms underlying this ability to ‘mind read’, but a likely candidate is the mirror-neuron system (Rizzolatti and Craighero 2004). Mirror neurons discharge not only during action execution but also during action–observation. Their participation in action execution and observation suggests that these neurons are a possible substrate for action understanding. Mirror neurons were first discovered in the premotor area, F5, of the macaque monkey (Di Pellegrino et al. 1992; Gallese et al. 1996; Rizzolatti et al. 2001; Umilta et al. 2001) and were identified subsequently in an area of inferior parietal lobule, area PF (Fogassi et al. 2005).

The premise of this article is that mirror neurons emerge naturally in any agent that acts on its environment to avoid surprising events. We have discussed the imperative of minimizing surprise in terms of a free-energy principle (Friston et al. 2006; Friston 2009). The underlying motivation is that adaptive agents maintain low entropy equilibria with their environment. Here, entropy is the average surprise of sensory signals, under the agent’s model of how those signals were generated. Another perspective on this imperative comes from the fact that surprise is mathematically the same as the negative log-evidence for an agent’s model. This means the agent is trying to maximise the evidence for its model of its world by minimizing surprise. Under some simplifying assumptions, surprise reduces to the difference between the model’s predictions and the sensations sampled (i.e. prediction error). In this formulation, action corresponds to selecting sensory samples that conform to predictions, while perception involves optimizing predictions by updating posterior (conditional) beliefs about the state of the world generating sensory signals. Both result in a reduction of prediction error (see Friston 2009 for a heuristic summary). The resulting scheme is called active inference (Friston et al. 2009, 2010a), which, in the absence of action, is formally equivalent to evidence accumulation in predictive coding (Mumford 1992; Rao and Ballard 1998).

Active inference provides a slightly different perspective on the brain and its neuronal representations, when compared to conventional views of the motor system. Under active inference, there are no distinct sensory or motor representations, because proprioceptive predictions are sufficient to furnish motor control signals. This obviates the need for motor representations per se: High-level representations encode beliefs about the state of the world that generate both proprioceptive and exteroceptive predictions. Motor control and action emerge only at the lowest levels of the hierarchy, as suppression of proprioceptive prediction error; for example, by classical motor reflex arcs. In this scheme, complex sequences of behavior can be prescribed by proprioceptive predictions, which peripheral motor systems try to fulfill. This means that the central nervous system is concerned solely with perceptual inference about the hidden states of the world causing sensory data. The primary motor cortex is no more or less a motor cortical area than striate (visual) cortex. The only difference between the motor cortex and visual cortex is that one predicts retinotopic input, while the other predicts proprioceptive input from the motor plant (see Friston et al. 2010a for discussion). In this picture of the brain, neurons represent both cause and consequence: They encode conditional expectations about hidden states in the world causing sensory data, while at the same time causing those states vicariously through action. In a similar way, they report the consequences of action because they are conditioned on its sensory sequelae. In short, active inference induces a circular causality that destroys conventional distinctions between sensory (consequence) and motor (cause) representations. This means that optimizing representations corresponds to perception or intention, i.e. forming percepts or intents. It is this bilateral view of neuronal representations we exploit in the theoretical treatment of the mirror-neuron system below.

A key aspect of the free-energy formulation is that hidden states and causes in the world are represented in terms of their generalised motion (Friston 2008). In this context, a generalised state corresponds to a trajectory or path through state-space that contains the variables responsible for generating sensory data. Neuronal representations of generalised states pertain not just to an instant in time but to a trajectory that encodes future states. This means that the implicit predictive coding is predictive in an anticipatory or generalised sense. This is only true of generalised predictive coding: Usually, the ‘predictive’ in predictive coding is not about what will happen but about predicting current sensations, given their causes. However, in generalised predictive coding, prediction can be used in both its concurrent and anticipatory sense. The trajectories one might presume are represented by the brain are itinerant or wandering. Obvious examples here are those encoding locomotion, speech, reading and writing. A useful concept here is the notion of a stable heteroclinic channel. This simply means a path through state-space that visits a succession of (unstable) fixed points. Heteroclinic channels and their associated itinerant dynamics are easy to specify in generative models and have been used to model the recognition of speech and song (e.g. Afraimovich et al. 2008; Rabinovich et al. 2008; Kiebel et al. 2009a,b). Conceptually, they can be thought of as encoding dynamical movement ‘primitives’ (Ijspeert et al. 2002; Schaal et al. 2007; Namikawa and Tani 2010) or perceptual and motor ‘schema’ (Jeannerod et al. 1995; Arbib 2008). In this article, we will use itinerant dynamics to both generate and recognise handwriting. During action these dynamics play the role of prior expectations that are fulfilled by action to render them posterior beliefs about what actually happened. In action–observation, these priors correspond to dynamical templates for recognizing complicated and itinerant sensory trajectories. In what follows, we will exploit both perspectives using the same neuronal instantiation of itinerant dynamics to generate action and then recognise the same action executed by another agent. The only difference between these two scenarios is whether the proprioceptive signals generated by action are sensed by the agent. It is this simple change of context (agency) that enables the same inferential machinery to generate and recognise the perceptual correlates of itinerant (sequential) behaviour.

This article comprises four sections. In Sect.2, we briefly reprise the free-energy formulation of active inference to place what follows in a general setting and illustrate that action–observation rests on exactly the same principles underlying perceptual inference, learning and attention. In Sect. 3, we describe a generative model based on Lotka–Volterra dynamics (Afraimovich et al. 2008) that generate handwriting. We use this model to illustrate the basic properties of active inference and how prior expectations can induce realistic motor behavior. This section is based on the principles established by Sect.2. Our focus will be on the interpretation of posterior or conditional expectations about hidden states of the world (the trajectory of joint angles in a synthetic arm) as intended movements, which action fulfils. In the Sect.4, we take the same model and make one simple change: We retain the visual input caused by action but ‘switch off’ proprioceptive input. This simulates action–observation and appeals to the same contextual gating we have used previously to model attention (Friston 2009; Feldman and Friston 2010). In this context, the observed movement is exactly the same as the self-generated movement. However, because the agent does not distinguish between perceptions and intentions, it still predicts and perceives the movement trajectory. In other words, it infers the trajectory intended by the (other) agent; provided the other agent behaves like the observer. The final section illustrates the implicit capacity to encode the intentions of others by reversing the movement during the course of the predicted sequence. We then examine the agent’s conditional representations for evidence that this violation has been detected. To do this, we look at the prediction errors and associate these with synthetic event related potentials of the sort observed electrophysiologically. We conclude with a brief discussion of this formulation of action–observation for the mirror-neuron system and motor control in general. The purpose of this paper is to provide proof of principle that active inference can account for both action and its understanding. We therefore focus on motivating the underlying scheme from basic principles and providing worked examples. However, we include an Appendix for people who want to implement and extend the simulations themselves.

2 Free-energy and active inference

In this section, we review briefly the free-energy principle and how it translates into action and perception. We have covered this material in previous publications (Friston et al. 2006; Friston 2008, 2009; Friston et al. 2009, 2010a,b). It is reprised here intuitively to describe the formulism on which later simulations are based.

The free-energy formalism for the brain has three basic ingredients. We start with the free-energy principle per se, which says that adaptive agents minimise a free-energy bound on surprise (or the negative log evidence for their model of the world). The free-energy is induced by something called a recognition density, encoded by the conditional expectations of hidden states causing sensory data (henceforth, expected states). Under the assumption that agents minimise free-energy (and implicitly surprise) using gradient descent, we end up with a set of differential equations describing how action and neuronal representations of expected states change with time. The second ingredient is the agent’s model of how sensory data are generated (Gregory 1968, 1980; Dayan et al. 1995). This model is necessary to specify what is surprising. We use a very general dynamical model with a hierarchical form that we assume is used by the brain. The third ingredient is how the brain implements the free-energy principle. This involves substituting the particular form of the generative model into the differential equations describing action and perception. The resulting scheme, when formulated in terms of prediction errors, corresponds to predictive coding (cf., Mumford 1992; Rao and Ballard 1998; Friston 2008). The scheme is essentially a set of differential equations describing the activity of two populations of cells in the brain (encoding expected states and prediction error, respectively). This generalised predictive coding is used in the simulations of subsequent sections. Furthermore, it is exactly the same scheme used in previous illustrations of perceptual inference (Kiebel et al. 2009a), perceptual learning (Friston 2008), reinforcement learning (Friston et al. 2009), active inference (Friston et al. 2010a) and attentional processing (Feldman and Friston 2010). The quantities and variables used below are summarised in Table 1.

Table 1.

Generic variables and quantities in the free-energy formation of active inference, under the Laplace assumption (i.e. generalised predictive coding)

Variable	Description
$m\mathrm{\in }ℳ$	Generative model or agent: In the free-energy formulation, each agent or system is taken to be a model of the environment in which it is immersed. $m\mathrm{\in }ℳ$ corresponds to the form (e.g. degrees of freedom) of a model entailed by an agent, which is used to predict sensory signals.
$a\subset \vartheta$	Action: These variables are states of the world that correspond to the movement or configuration of an agent (i.e. its effectors).
$\mathit{s̃}\left(t\right)=s\oplus s\prime \oplus s\prime \prime \oplus ...\mathrm{\in }S$	Sensory signals: These generalised sensory signals or samples comprise the sensory states, their velocity, acceleration and temporal derivatives to high order. In other words, they correspond to the trajectory of an agent’s sensations.
$\mathcal{L}(\tilde{s}\mid m)=-\ln p(\tilde{s}\mid m)$	Surprise: This is a scalar function of sensory samples and reports the improbability of sampling some signals, under a generative model of how those signals were caused. It is sometimes called (sensory) suprisal or self-information. In statistics it is known as the negative log-evidence for the model.
$H(S\mid m)\propto \int dt\mathcal{L}(\tilde{s}\left(t\right)\mid m)$	Entropy: Sensory entropy is, under ergodic assumptions, proportional to the long-term time average of surprise.
$\mathcal{G}(\tilde{s},\vartheta )=-\ln p(\tilde{s},\vartheta \mid m)$	Gibbs energy: This is the negative log of the density specified by the generative model; namely, surprise about the joint occurrence of sensory samples and their causes.
$\mathcal{F}(\tilde{s},q)=\mathcal{G}(\tilde{s},\mu )+\frac{1}{2}\ln \mid {\mathcal{G}}_{\mu \mu }\mid \ge \mathcal{L}(\tilde{s}\mid m)$	Free-energy: This is a scalar function of sensory samples and a recognition density, which upper bounds surprise. It is called free-energy because it is the expected Gibbs energy minus the entropy of the recognition density. Under a Gaussian (Laplace) assumption about the form of the recognition density, free-energy reduces to the simple function of Gibbs energy shown.
$S(\tilde{s},q)=\int \mathrm{d}t\mathcal{F}(\tilde{s},q)\ge H(S\mid m)$	Free-action: This is a scalar functional of sensory samples and a recognition density, which upper bounds the entropy of sensory signals. It is the time or path integral of free-energy.
$q\left(\vartheta \right)=\mathcal{N}(\mu ,\mathcal{C})$	Recognition density: This is also know as a proposal density and becomes (approximates) the conditional density over hidden causes of sensory samples, when free-energy is minimised. Under the Laplace assumption, it is specified by its conditional expectation and covariance.
$$\begin{gathered} \vartheta =\left\{\mathbf{u}\text{,}\mathrm{\phi }\text{,}a\right\} \\ \vartheta =\left\{\mathit{u}\text{,}\mathrm{\phi }\right\} \\ u=\left\{\mathit{x}\text{,}\mathit{v}\right\} \\ \varphi =\left\{\theta \text{,}\mathit{\mu }\right\} \end{gathered}$$	True (bold) and hidden (italics) causes: These quantities cause sensory signals. The true quantities exist in the environment and the hidden homologues are those assumed by the generative model of that environment. Both are partitioned into time-dependent variables and time-invariant parameters.
$\theta \subset \varphi \subset \vartheta$	Hidden parameters: These are the parameters of the mappings (e.g. equations of motion) that constitute the deterministic part of a generative model.
$\alpha \subset \varphi \subset \vartheta$	Log-precisions: These parameters control the precision (inverse variance) of fluctuations that constitute the random part of a generative model.
$x\left(t\right)=x^{\left(1\right)}\oplus x^{\left(2\right)}\oplus \dots \subset u\subset \vartheta$	Hidden states: These hidden variables encode the hierarchical states in a generative model of dynamics in the world.
$v\left(t\right)=v^{\left(1\right)}\oplus v^{\left(2\right)}\oplus \dots \subset u\subset \vartheta$	Hidden causes: These hidden variables link different levels of a hierarchical generative model.
$$\begin{gathered} f^{(i,v)}\left(x^{\left(i\right)},v^{\left(i\right)},\theta \right) \\ {f}^{(i,x)}\left(x^{\left(i\right)},v^{\left(i\right)},\theta \right) \end{gathered}$$	Deterministic mappings: These are equations at the ith level of a hierarchical generative model that map from states at one level to another and map hidden states to their motion within each level. They specify the deterministic part of a generative model.
$$\begin{gathered} {\omega }^{(i,v)} \\ {\omega }^{(i,x)} \end{gathered}$$	Random fluctuations: These are random fluctuations on the hidden causes and motion of hidden states. Gaussian assumptions about these fluctuations furnish the probabilistic part of a generative model.
${\Pi }^{(i,v)}={\mathit{R}}^{(i,v)}\otimes {\mathit{I}}^{(i,v)}\exp \left({\gamma }^{(i,v)}\right){\Pi }^{(i,x)}={\mathit{R}}^{(i,x)}\otimes {\mathit{I}}^{(i,x)}\exp \left({\gamma }^{(i,x)}\right)$	Precision matrices: These are the inverse covariances among (generalised) random fluctuations on the hidden causes and motion of hidden states.
$$\begin{gathered} R^{(i,v)} \\ {R}^{(i,x)} \end{gathered}$$	Roughness matrices: These are the inverses of the matrices encoding serial correlations among (generalised) random fluctuations on the hidden causes and motion of hidden states.
${\tilde{\epsilon }}^{(i,v)}={\tilde{v}}^{(i-1)}-{\tilde{f}}^{(i,v)}{\tilde{\epsilon }}^{(i,x)}=\mathcal{D}{\tilde{x}}^{\left(i\right)}-{\tilde{f}}^{(i,x)}$	Prediction errors: These are the prediction errors on the hidden causes and motion of hidden states evaluated at their current conditional expectation.
${\xi }^{(i,v)}={\tilde{\Pi }}^{(i,v)}{\tilde{\epsilon }}^{(i,v)}{\xi }^{(i,x)}={\tilde{\Pi }}^{(i,x)}{\tilde{\epsilon }}^{(i,x)}$	Precision-weighted prediction errors: These are the prediction errors weighted by their respective precisions.

See main text for details

2.1 Action and perception from basic principles

The starting point for the free-energy principle is that biological systems (e.g. agents) resist a natural tendency to disorder; under which fluctuations in their states cause the entropy (dispersion) of their ensemble density to increase with time. Probabilistically, this means that agents must minimise the entropy of their states and, implicitly, their sensory samples of the world. More formally, any agent or model, m, must minimise the average uncertainty (entropy) about its generalised sensory states, s̃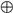 = s s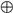’ s″ … S (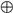 means concatenation). Generalised states (designated by the tilde) comprise the states per se and their generalised motion (velocity, acceleration, jerk, etc). Generalised motion is (in principle) of infinite order; however, it can be truncated to a low order (four in this paper); because the precision of high order motion is very small. This is covered in detail in Friston (2008). The average uncertainty about generalised states is

$$H(S\mid m)=-\int p(\tilde{s}\mid m)\ln p(\tilde{s}\mid m)d\tilde{s}\propto \int \mathrm{d}t\mathcal{L}(s\left(t\right)\mid m)$$ (1)

Under ergodic assumptions, this is proportional to the long-term average of surprise, also known as negative log-evidence, $\mathcal{L}(\tilde{s}\mid m)=-\ln p(\tilde{s}\mid m)$ . Essentially, sensory entropy negative log-evidence over time. Minimising sensory entropy therefore corresponds to maximizing the accumulated log-evidence for the agent’s model of the world. Although, sensory entropy cannot be minimised directly, we can create an upper bound S(s̃, q) ≥ H(S|m) that can be minimised. This bound is a function of a time-dependent recognition density q (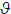) on the causes (i.e. environmental states and parameters) of sensory signals. The requisite bound is the path-integral of free-energy $\mathcal{F}$ , which is created simply by adding a non-negative function of the recognition density to surprise:

$$\begin{array}{cc}\hfill \mathcal{S}=& \int \mathrm{d}t\mathcal{F}(\tilde{s},q)\hfill \\ \hfill \mathcal{F}=& \mathcal{L}+D(q\left(\vartheta \right)\mid \mid p(\vartheta \mid \tilde{s},m))\hfill \\ \hfill =& {\langle \mathcal{G}\rangle }_q-\mathcal{H}\hfill \\ \hfill \mathcal{L}=& -\ln p(\tilde{s}\mid m)\hfill \\ \hfill \mathcal{G}=& -\ln p(\tilde{s},\vartheta \mid m)\hfill \\ \hfill \mathcal{H}=& -{\langle \ln q\left(\vartheta \right)\rangle }_q\hfill \end{array}$$ (2)

This function is a Kullback–Leibler divergence D(·||·) and is greater than zero, with equality when q(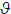) = p(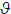|s̃, m) is the true conditional density. This means that minimizing free-energy, by changing the recognition density, makes it an approximate posterior or conditional density on sensory causes. This is Bayes-optimal perception. The free-energy can be evaluated easily because it is a function of the recognition density and a generative model entailed by m: Eq. 2 expresses free-energy in terms of $\mathcal{H}$ , the negentropy of q (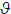) and an energy $\mathcal{G}=-\ln p(\tilde{s},\vartheta \mid m)$ expected under q(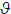). This expected (Gibbs) energy rests on a probabilistic generative model; p(s̃, |m). If we assume that the recognition density $q\left(\vartheta \right)=\mathcal{N}(\tilde{\mu },\mathcal{C})$ is Gaussian (known as the Laplace assumption), we can express free-energy in terms of the conditional mean or expectation of the recognition density $\tilde{\mu }\left(t\right)$ , where omitting constants

$$\mathcal{F}(\tilde{s}\left(a\right),\tilde{\mu })=\mathcal{G}(\tilde{s},\tilde{\mu })+\frac{1}{2}\ln \mid {\mathcal{G}}_{\tilde{\mu }\tilde{\mu }}\mid$$ (3)

Here, the conditional precision (inverse covariance) is ${\mathcal{C}}^{-1}=\mathcal{P}={\mathcal{G}}_{\tilde{\mu }\tilde{\mu }}$ . Crucially, this means the free-energy is a function of the expected states and sensory samples, which depend on how they are sampled by action. The action a(t) and expected states $\tilde{\mu }\left(t\right)$ that minimise free-energy are the solutions to the following differential equations

$$\begin{array}{cc}\hfill \stackrel{.}{a}=& -{\mathcal{F}}_a\hfill \\ \hfill \dot{\tilde{\mu }}=& \mathcal{D}\tilde{\mu }-{\mathcal{F}}_{\tilde{\mu }}\hfill \end{array}$$ (4)

In short, the free-energy principle prescribes optimal action and perception. Here $\mathcal{D}$ is a derivative matrix operator with identity matrices above the leading diagonal, such that $\mathcal{D}\tilde{\mu }={\mu }^{\prime }\oplus {\mu }^{\prime \prime }\oplus \cdots$ . Here and throughout, we assume all gradients (denoted by subscripts) are evaluated at the mean. The stationary solution of Eq. 4 ensures that when free-energy is minimised the expected motion of the states is the motion of the expected states; that is ${\mathcal{F}}_{\tilde{\mu }}=0\Rightarrow \dot{\tilde{\mu }}=\mathcal{D}\tilde{\mu }$ . The recognition dynamics in Eq. 4 can be regarded as a gradient descent in a frame of reference that moves with the expected motion of the states (cf., surfing a wave). More general formulations of Eq. 4 make a distinction between time-varying environmental states u and time-invariant parameters φ (see Friston et al. 2010a,b). In this article, we will assume that only the states are unknown or hidden from the agent and ignore the learning of φ

Action can only reduce free-energy by changing sensory signals. This changes the first (log-likelihood) part of Gibb’s energy $\mathcal{G}=-\ln p(\tilde{s}\mid \vartheta ,m)-\ln p(\vartheta \mid m)$ that depends on sensations. This means that action will sample sensory signals that are most likely under the recognition density (i.e. sampling selectively what one expects to experience). In other words, agents must necessarily (if implicitly) make inferences about the causes of their sensations and sample signals that are consistent with those inferences.

2.2 Summary

In summary, we have derived action and perception dynamics for expected states (in generalised coordinates of motion) that cause sensory samples. The solutions to these equations minimise free-energy and therefore minimise surprising sensations or, equivalently, maximise the evidence for an agent’s model of the world. This corresponds to active inference, where predictions guide active sampling of sensory data. Active inference rests on the notion that “perception and behavior can interact synergistically, via the environment” to optimise behavior (Verschure et al. 2003) and is an example of self-referenced learning (Porr and Wörgötter 2003; Wörgötter and Porr 2005). The precise form of active inference depends on the energy at each point in time $\mathcal{G}=-\ln p(\tilde{s},\vartheta \mid m)$ that rests on a particular generative model. In what follows, we review dynamic models of the world.

2.3 Hierarchical dynamic models

We now introduce a general model based on the models discussed in Friston (2008). We will assume that sensory data are modeled with a special case of

$$\begin{array}{cc}\hfill s=& f^{\left(\nu \right)}(x,\nu ,\theta )+{\omega }^{\left(\nu \right)}:{\omega }^{\left(\nu \right)}~\mathcal{N}(0,{\Sigma }^{\left(\nu \right)}(x,\nu ,\gamma ))\hfill \\ \hfill \stackrel{.}{x}=& f^{\left(x\right)}(x,\nu ,\theta )+{\omega }^{\left(x\right)}:{\omega }^{\left(x\right)}~\mathcal{N}(0,{\Sigma }^{\left(x\right)}(x,\nu ,\gamma ))\hfill \end{array}$$ (5)

The nonlinear functions f^(u) : u , x represent the deterministic part of the model and are parameterised by θ φ. The variables v u are referred to as hidden causes, while hidden states x u meditate the influence of the causes on sensory data and endow the model with memory. Equation 5 is just a state-space model, where the first (sensory mapping) function maps from hidden variables to sensory data and the second represents equations of motion for hidden states (where the hidden causes can be regarded as exogenous inputs). We assume the random fluctuations ω^(u) are analytic, such that the covariance of the generalised fluctuations ${\tilde{\omega }}^{\left(u\right)}$ is well defined. These fluctuations represent the stochastic part of the model. This model allows for state dependent changes in the amplitude of random fluctuations and introduces a distinction between the effect of states on the flow and dispersion of sensory trajectories. Under local linearity assumptions, the generalised motion of the sensory response and hidden states can be expressed compactly as

$$\begin{array}{cc}\hfill \tilde{s}=& {\tilde{f}}^{\left(\nu \right)}+{\tilde{z}}^{\left(\nu \right)}\hfill \\ \hfill \mathcal{D}\tilde{x}=& {\tilde{f}}^{\left(x\right)}+{\tilde{z}}^{\left(x\right)}\hfill \end{array}$$ (6)

where the generalised predictions are

$${\tilde{f}}^{\left(u\right)}=\left[\begin{array}{c}{f}^{\left(u\right)}=f^{\left(u\right)}\hfill \\ f^{{\prime }^{\left(u\right)}}=f_x^{\left(u\right)}{x}^{\prime }+f_{\nu }^{\left(u\right)}{\nu }^{\prime }\hfill \\ f^{{″}^{\left(u\right)}}=f_x^{\left(u\right)}{x}^{″}+f_{\nu }^{\left(u\right)}{\nu }^{″}\hfill \\ ⋮\hfill \end{array}\right]$$ (7)

Equation 5 means that Gaussian assumptions about the fluctuations specify a generative model in terms of a likelihood and empirical priors on the motion of hidden states

$$\begin{array}{cc}\hfill p(\tilde{s}\mid \tilde{x},\tilde{\nu },\phi ,m)& =\mathcal{N}\left({\tilde{f}}^{\left(\nu \right)},{\tilde{\Sigma }}^{\left(\nu \right)}\right)\hfill \\ \hfill p(\mathcal{D}\tilde{x}\mid x,\tilde{\nu },\phi ,m)& =\mathcal{N}\left({\tilde{f}}^{\left(x\right)},{\tilde{\Sigma }}^{\left(x\right)}\right)\hfill \end{array}$$ (8)

These probability densities are encoded by their covariances ${\tilde{\Sigma }}^{\left(u\right)}$ or precisions (inverse covariances) ${\tilde{\Pi }}^{\left(u\right)}≔\tilde{\Pi }(x,\nu ,{\gamma }^{\left(u\right)})$ with precision parameters γ φ that control the amplitude and smoothness of the random fluctuations. Generally, the covariances factorise: ${\tilde{\Sigma }}^{\left(u\right)}=V^{\left(u\right)}\otimes {\Sigma }^{\left(u\right)}$ into a covariance among different fluctuations and a matrix of correlations V^(u) over different orders of motion that encodes their smoothness. Given this generative model we can now write down the energy as a function of the conditional means, which has a simple quadratic form (ignoring constants)

$$\begin{array}{cc}\hfill \mathcal{G}=& {\mathcal{G}}^{\left(\nu \right)}+{\mathcal{G}}^{\left(x\right)}\hfill \\ \hfill {\mathcal{G}}^{\left(\nu \right)}=& \frac{1}{2}{\tilde{\epsilon }}^{\left(\nu \right)T}{\tilde{\Pi }}^{\left(\nu \right)}{\tilde{\epsilon }}^{\left(\nu \right)}-\frac{1}{2}\ln \mid {\tilde{\Pi }}^{\left(\nu \right)}\mid \hfill \\ \hfill {\mathcal{G}}^{\left(x\right)}=& \frac{1}{2}{\tilde{\epsilon }}^{\left(x\right)T}{\tilde{\Pi }}^{\left(x\right)}{\tilde{\epsilon }}^{\left(x\right)}-\frac{1}{2}\ln \mid {\tilde{\Pi }}^{\left(x\right)}\mid \hfill \\ \hfill {\tilde{\epsilon }}^{\left(\nu \right)}=& \tilde{s}-{\tilde{f}}^{\left(\nu \right)}\hfill \\ \hfill {\tilde{\epsilon }}^{\left(x\right)}=& \mathcal{D}{\tilde{\mu }}^{\left(x\right)}-{\tilde{f}}^{\left(x\right)}\hfill \end{array}$$ (9)

Here, the auxiliary variables ${\tilde{\epsilon }}^{\left(u\right)}:u\in \nu ,x$ , are prediction errors for sensory data and motion of the hidden states. We next consider hierarchical forms of this model. These are just special cases of Eq. 6, in which we make certain conditional independencies explicit. Although, the examples in the next section are not hierarchical, we briefly consider hierarchical forms here, because they provide an important empirical Bayesian perspective on inference that may be exploited by the brain. Furthermore, they provide a nice link to the connectionist scheme of Tani et al. (2004). Hierarchical dynamic models have the following form

$$\begin{array}{cc}\hfill s=& f^{(1,\nu )}(x^{\left(1\right)},{\nu }^{\left(1\right)}\theta )+{\omega }^{(1,\nu )}\hfill \\ \hfill {\stackrel{.}{x}}^{\left(1\right)}=& f^{(1,x)}(x^{\left(1\right)},{\nu }^{\left(1\right)},\theta )+{\omega }^{(1,x)}\hfill \\ \hfill & ⋮\hfill \\ \hfill {\nu }^{(i-1)}=& f^{(i,\nu )}(x^{\left(i\right)},{\nu }^{\left(i\right)},\theta )+{\omega }^{(i,\nu )}\hfill \\ \hfill {\stackrel{.}{x}}^{\left(i\right)}=& f^{(i,x)}(x^{\left(i\right)},{\nu }^{\left(i\right)},\theta )+{\omega }^{(i,x)}\hfill \end{array}$$ (10)

As above, f^(i,u) : u v, x are nonlinear functions, the random terms ω^(i,u) : u v, x are conditionally independent and enter each level of the hierarchy. They play the role of sensory noise at the first level and induce random fluctuations in the states at higher levels. The hidden causes v = v⁽¹⁾ v⁽²⁾ … link levels, whereas the hidden states x = x⁽¹⁾ x⁽²⁾ … link dynamics over time. In hierarchical form, the output of one level acts as an input to the next. This input can enter nonlinearly to produce quite complicated generalised convolutions with deep (hierarchical) structure. Crucially, when these top-down inputs act as control parameters for the hidden states in the level below, they correspond to ‘parametric biases’ in the connectionist scheme of Tani et al. (2004). Hierarchical structure appears in the energy as empirical priors ${\mathcal{G}}^{(i,u)}:u\in x,\nu$ where, ignoring constants

$$\begin{array}{cc}\hfill \mathcal{G}=& \sum _i{\mathcal{G}}^{(i,\nu )}+\sum _i{\mathcal{G}}^{(i,x)}\hfill \\ \hfill {\mathcal{G}}^{(i,\nu )}=& \frac{1}{2}{\tilde{\epsilon }}^{(i,\nu )T}{\tilde{\Pi }}^{(i,\nu )}{\tilde{\epsilon }}^{(i,\nu )}-\frac{1}{2}\ln \mid {\tilde{\Pi }}^{(i,\nu )}\mid \hfill \\ \hfill {\mathcal{G}}^{(i,x)}=& \frac{1}{2}{\tilde{\epsilon }}^{(i,x)T}{\tilde{\Pi }}^{(i,x)}{\tilde{\epsilon }}^{(i,x)}-\frac{1}{2}\ln \mid {\tilde{\Pi }}^{(i,x)}\mid \hfill \\ \hfill {\tilde{\epsilon }}^{(i,\nu )}=& {\tilde{\nu }}^{(i-1)}-{\tilde{f}}^{(i,\nu )}\hfill \\ \hfill {\tilde{\epsilon }}^{(i,x)}=& {{\mathcal{D}}_{\tilde{x}}}^{\left(i\right)}-{\tilde{f}}^{(i,x)}\hfill \end{array}$$ (11)

2.4 Summary

In summary, these models are as complicated as one could imagine; they comprise hidden causes and states, whose dynamics can be coupled with arbitrary (analytic) nonlinear functions. Furthermore, these states can be subject to random fluctuations with state-dependent changes in amplitude and arbitrary (analytic) autocorrelation functions. A key aspect is their hierarchical form, which induces empirical priors on the causes. In the next section, we look at the recognition dynamics entailed by this form of generative model, with a particular focus on how recognition might be implemented in the brain.

2.5 Action and perception under hierarchical dynamic models

If we now write down the recognition dynamics (Eq. 4) using precision-weighted prediction errors ${\xi }^{(i,u)}={\tilde{\Pi }}^{(i,u)}{\tilde{\epsilon }}^{(i,u)}$ from Eq. 11, one can see the hierarchical message-passing entailed by this scheme (ignoring the derivatives of the energy curvature):

$$\begin{array}{cc}\hfill {\dot{\tilde{\mu }}}^{(i,\nu )}=& {{\mathcal{D}}_{\tilde{\mu }}}^{(i,\nu )}+{\tilde{f}}_{\tilde{\nu }}^{i,\nu }{\xi }^{(i,\nu )}+{\tilde{f}}_{\tilde{\nu }}^{i,x}{\xi }^{(i,x)}-{\xi }^{(i+1,\nu )}\hfill \\ \hfill {\dot{\tilde{\mu }}}^{(i,x)}=& {{\mathcal{D}}_{\tilde{\mu }}}^{(i,x)}+{\tilde{f}}_{\tilde{x}}^{i,\nu }{\xi }^{(i,\nu )}+{\tilde{f}}_{\tilde{x}}^{i,x}{\xi }^{(i,x)}-{\mathcal{D}}^T{\xi }^{(i,x)}\hfill \\ \hfill {\xi }^{(i,\nu )}=& {\tilde{\Pi }}^{(i,\nu )}{\tilde{\epsilon }}^{(i,\nu )}={\tilde{\Pi }}^{(i,\nu )}\left({\tilde{\mu }}^{(i-1,\nu )}-{\tilde{f}}^{(i,\nu )}\right)\hfill \\ \hfill {\xi }^{(i,x)}=& {\tilde{\Pi }}^{(i,x)}{\tilde{\epsilon }}^{(i,x)}={\tilde{\Pi }}^{(i,x)}\left({{\mathcal{D}}_{\tilde{\mu }}}^{(i,x)}-{\tilde{f}}^{(i,x)}\right)\hfill \end{array}$$ (12)

For simplicity, we have assumed the amplitude of the random fluctuations does not depend on the states and can be parameterised in terms of log-precisions γ^(i,u) : u v, x, where the precision of the generalised fluctuations is ${\tilde{\Pi }}^{(i,u)}=R^{(i,u)}\otimes I^{(i,u)}\exp \left({\gamma }^{(i,u)}\right)$ . Here, R^(i,u) is the inverse of the correlation matrix V^(i,u) above and I (i,u) is the identity matrix.

It is difficult to overstate the generality and importance of Eq. 12: It grandfathers nearly every known statistical scheme, under parametric assumptions about noise. These range from ordinary least squares to advanced variational deconvolution schemes (see Friston 2008). Equation 12 is generalised predictive coding and follows simply from the generalised gradient decent in Eq. 4, where the freeenergy gradients reduce to linear mixtures of prediction errors. This simplicity rests on Gaussian assumptions about the random fluctuations and the form of the recognition density.

Equation 12 shows how recognition dynamics can be implemented by relatively simple message-passing between (neuronal) states encoding conditional expectations and prediction errors. The motion of conditional expectations is driven in a linear fashion by prediction error, while prediction error is a nonlinear function of conditional expectations. In neural network terms, Eq. 12 says that error-units encoding (precision-weighted) prediction error receive messages from the state-units encoding conditional expectations in the same level and the level above. Conversely, state-units are driven by error-units in the same level and the level below. Crucially, perception requires only the (precision-weighted) prediction error from the lower level ξ^(i,v) and the level in question ξ^(i,x), ξ(i+1,v). These constitute bottom-up and lateral messages that drive the conditional expectations ${\tilde{\mu }}^{i,u}$ towards a better prediction. These top-down and lateral predictions correspond to ${\tilde{f}}^{i,u}$ . This is the essence of recurrent message passing between hierarchical levels to optimise free-energy or suppress prediction error (see Friston 2008 for a more detailed discussion).

Equation 12 also tells us that the precisions modulate the responses of the error-units to their presynaptic inputs. This translates into synaptic gain control in principal cells (superficial pyramidal cells; Mumford 1992) elaborating prediction errors and fits comfortably with modulatory bias effects that have been associated with attention (Desimone and Duncan 1995; Schroeder et al. 2001; Salinas and Sejnowski 2001; Fries et al. 2008; see Feldman and Friston 2010). We will use precisions later to contextualise recognition under action or observation.

Since action can only affect the free-energy by changing sensory data, it can only affect sensory prediction error. From Eq. 4, we have

$$\begin{array}{cc}\hfill \stackrel{.}{a}=& -{\tilde{\epsilon }}_a^{\left(\nu \right)}{\xi }^{\left(\nu \right)}\hfill \\ \hfill {\tilde{\epsilon }}_a^{\left(\nu \right)}=& f_{\tilde{x}}^{\left(\nu \right)}\sum _j{\mathcal{D}}^{-j}{\left(f_{\tilde{x}}^{\left(x\right)}\right)}^{j-1}{f}_a^{\left(x\right)}\hfill \end{array}$$ (13)

The second equality expresses the change in prediction error with action in terms of the effect of action on successively higher order motions of the hidden states. In biologically plausible instances of this scheme, the partial derivatives in Eq. 13 would have to be computed on the basis of a mapping from action to sensory consequences, which is usually quite simple, e.g. activating an intrafusal muscle fiber elicits stretch receptor activity in the corresponding spindle (see Friston et al. 2010a for discussion).

2.6 Summary

In summary, we have derived equations for the dynamics of action and perception using a free-energy formulation of adaptive (Bayes-optimal) exchange with the world and a generative model that is both generic and biologically plausible. In what follows, we will use Eqs. 12 and 13 to simulate neuronal responses under action and observation. A technical treatment of the material in section will be found in Friston et al. (2010b), which provides the details of the scheme used to integrate (solve) Eq. 12 to produce the simulations in the next section.

3 Simulations: action

In this section, we describe a generative model of handwriting and then use the generalised predictive coding scheme of the previous section to simulate neuronal dynamics and behavior. To create these simulations, all we have to do is specify the equations of the generative model and the precision of random fluctuations. Action and perception are then prescribed by Eqs. 12 and 13, which simulate neuronal and behavioral responses respectively. Our agent was equipped a simple (one-level) dynamical model of its sensorium based on a Lotka–Volterra model of itinerant dynamics. The particular form of this model has been discussed previously as the basis of putative speech decoding (Kiebel et al. 2009b). Here, it is used to model a stable heteroclinic channel (Rabinovich et al. 2008) encoding successive locations to which the agent expects its two-jointed arm to be attracted. The resulting trajectory was contrived to simulate synthetic handwriting.

A stable heteroclinic channel is a particular form of (stable) itinerant trajectory or orbit that revisits a sequence of (unstable) fixed points. In our model, there are two sets of hidden states. The first set α = [α₁, …, α₆]^T x corresponds to the state-space of a Lotka–Volterra system. This is an abstract (attractor) state-space, in which a series of attracting points are visited in succession. The second set {x₁, x₂, x′₁, x′₂} x corresponds to the (angular) positions and velocities of the two joints in (two dimensional) physical space. The dynamics of both sets are coupled through the agent’s prior expectation that the arm will be drawn to a particular location, ℓ^*(α) specified by the attractor states. This is implemented simply by placing a (virtual) elastic band between the tip of the arm and the attracting location in physical space. The hidden states basically draw the arm’s extremity (finger) to a succession of locations to produce an orbit or trajectory, under classical Newtonian mechanics. We chose the locations so that the resulting trajectory looked like handwriting. These hidden states generate both proprioceptive and visual (extroceptive) sensory data: The proprioceptive data are the angular positions and velocities of the two joints {_x1, x₂, x₁′, x₂′}, while the visual information was the location of the arm in Cartesian space {ℓ₁, ℓ₁+ℓ₂},where ℓ₂(x₁, x₂) is the displacement of the finger from the location of the second joint ℓ₁(x₁) (see Fig. 1 and Table 2). Crucially, because this generative model generates two (proprioceptive and visual) sensory modalities, solutions to the equations of the previous section (i.e. perception) implement Bayes-optimal multisensory integration. However, because action is also trying to reduce prediction errors, it will move the arm to reproduce the expected trajectory (under the constraints of the motor plant). In other words, the arm will trace out a trajectory prescribed by the itinerant priors. This closes the loop, producing autonomous self-generated sequences of behavior of the sort described below. Note that the real world does not contain any attracting locations or elastic bands: The only causes of observed movement are the self-fulfilling expectations encoded by the itinerant dynamics of the generative model. In short, hidden attractor states essentially entail the intended movement trajectory, because they generate predictions that action fulfils. This means expected states encode conditional percepts (concepts) about latent abstract states (that do not exist in the absence of action), which play the role of intentions. We now describe the model formally. In this model, there is only one hierarchical level, and we can drop the hierarchical superscripts.

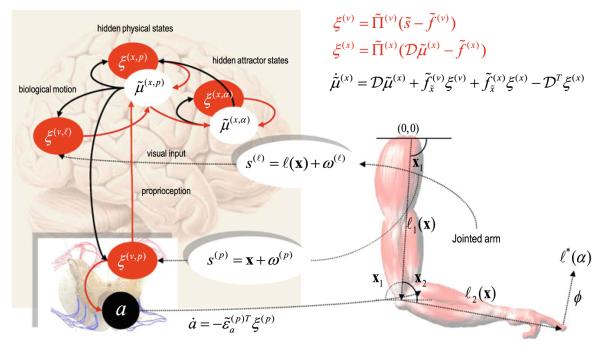
Fig. 1.

This schematic details the simulated mirror neuron system and the motor plant that it controls (left and right, respectively). The right panel depicts the functional architecture of the supposed neural circuits underlying active inference. The filled ellipses represent prediction error-units (neurons or populations), while the white ellipses denote state-units encoding conditional expectations about hidden states of the world. Here, they are divided into abstract attractor states (that supports stable heteroclinic orbits) and physical states of the arm (angular positions and velocities of the two joints). Filled arrows are forward connections conveying prediction errors and black arrows are backward connections mediating predictions. Motor commands are emitted by the black units in the ventral horn of the spinal cord. Note that these just receive prediction errors about proprioceptive states. These, in turn, are the difference between sensed proprioceptive input from the two joints and descending predictions from optimised representations in the motor cortex. The two jointed arm has a state space that is characterised by two angles, which control the position of the finger that will be used for writing in subsequent figures. The equations correspond to the expressions in the main text and represent a gradient decent on free-energy. They have been simplified here by omitting the hierarchical subscript and dynamics on hidden causes (which are not called on in this model)

Table 2.

Variables and quantities specific to the writing example of active inference (see main text for details)

Variable	Description
$\alpha \left(t\right)\in {\Re }^6\subset x$	Hidden attractor states: A vector of hidden  states that specify the current location  owards which the agent expects its arm to  be pulled.
$x_i\left(t\right)\in \Re \subset x$ $x_i^{\prime }\left(t\right)\in \Re \subset x$	Hidden effector states: Hidden states that  specify the angular position and velocity of  the i-th joint in a two-jointed arm.
${\ell }_1\left(x_1\right)\in {\Re }^2$ ${\ell }_2(x_1,x_2)\in {\Re }^2$	Joint locations: Locations of the end of the  two arm parts in Cartesian space. These are  functions of the angular positions of the  joints.
${\ell }^{\ast }\left(\alpha \left(t\right)\right)\in {\Re }^2$	Attracting location: The location towards  which the arm is drawn. This is specified by  the hidden attractor states.
$\varphi (x,\alpha )\in {\Re }^2$	Newtonian force: This is the angular force on  the joints exerted by the attracting location.
$A\in {\Re }^{6\times 6}\subset \theta$	Attractor parameters: A matrix of parameters  that govern the (sequential Lotka–Volterra)  dynamics of the hidden attractor states.
$L\in {\Re }^{2\times 6}\subset \theta$	Cartesian parameters: A matrix of  parameters that specify the attracting  locations associated with each hidden  attractor state.

3.1 The generative model

The model used in this section concerns a two-joint arm. When simulating active inference, it is important to distinguish between the agent’s generative model and the actual dynamics generating sensory data. To make this distinction clear, we will use bold for true equations and states, while those of the generative model will be written in italics. Proprioceptive input corresponds to the angular position and velocity of both joints, while the visual input corresponds to the location of the extremities of both parts of the arm.

$${\mathbf{f}}^{\left(\nu \right)}=f^{\left(\nu \right)}=\left[\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\hfill \\ \hfill x_1^{\prime }\hfill \\ \hfill x_2^{\prime }\hfill \\ \hfill {\ell }_1\left(x\right)\hfill \\ \hfill {\ell }_1\left(x\right)+{\ell }_2\left(x\right)\hfill \end{array}\right]$$ (14)

We ignore the complexities of inference on retinotopically mapped visual input and assume the agent has direct access to locations of the arm in visual space. The kinetics of the arm conforms to Newtonian laws, under which action forces the angular position of each joint. Both joints have an equilibrium position at 90°; with inertia m_l 8, 4 and viscosity κ_i 4, 2, giving the following equations of motion

$$\mathbf{x}=\left[\begin{array}{c}\hfill {\mathbf{x}}_1\hfill \\ \hfill {\mathbf{x}}_2\hfill \\ \hfill {\mathbf{x}}^{\prime 1}\hfill \\ \hfill {\mathbf{x}}^{\prime 2}\hfill \end{array}\right]{\mathbf{f}}^{\left(x\right)}=\left[\begin{array}{c}\hfill {\mathbf{x}}^{\prime 1}\hfill \\ \hfill {\mathbf{x}}^{\prime 2}\hfill \\ \hfill \frac{\left(a_1+{\mathbf{v}}_1-\frac{1}{4}({\mathbf{x}}_1-\frac{\pi }{2})-{\kappa }_1{\mathbf{x}}_1^{\prime }\right)}{m_1}\hfill \\ \hfill \frac{\left(a_2+{\mathbf{v}}_2-\frac{1}{4}({\mathbf{x}}_2-\frac{\pi }{2})-{\kappa }_2{\mathbf{x}}_2^{\prime }\right)}{m_2}\hfill \end{array}\right]$$ (15)

However, the agent’s empirical priors on this motion have a very different form. Its generative model assumes the finger is pulled to a (goal) location ${\ell }^{\ast }\left(\alpha \left(t\right)\right)\in {\Re }^2$ by a force $\varphi (x,\alpha )\in {\Re }^2$ , which implements the virtual elastic band above (1₆ is a column vector of ones):

$$\begin{array}{cc}\hfill x=& \left[\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\hfill \\ \hfill x_1^{\prime }\hfill \\ \hfill x_2^{\prime }\hfill \\ \hfill \alpha \hfill \end{array}\right]f^{\left(x\right)}=\left[\begin{array}{c}\hfill x_1^{\prime }\hfill \\ \hfill x_2^{\prime }\hfill \\ \hfill \frac{({\varphi }^T{\ell }_2{\ell }_2^{T}O{\ell }_1-\frac{1}{16}(x_1-\frac{\pi }{2})-k_1{x}_1^{\prime })}{m_1}\hfill \\ \hfill \frac{({\varphi }^{T}O{\ell }_2-\frac{1}{16}(x_2-\frac{\pi }{2})-k_2{x}_2^{\prime })}{m_2}\hfill \\ \hfill A\sigma \left(\alpha \right)-\frac{1}{8}\alpha +1_6\hfill \end{array}\right]\hfill \\ \hfill {\ell }_1\left(x\right)=& \left[\begin{array}{c}\hfill \cos \left(x_1\right)\hfill \\ \hfill \sin \left(x_1\right)\hfill \end{array}\right]\hfill \\ \hfill {\ell }_2\left(x\right)=& \left[\begin{array}{c}\hfill -\cos (-x_2-x_1)\hfill \\ \hfill \sin (-x_2-x_1)\hfill \end{array}\right]O=\left[\begin{array}{cc}0\hfill & -1\hfill \\ 1\hfill & 0\hfill \end{array}\right]\hfill \\ \hfill \varphi (x,\alpha )=& \frac{1}{2}({\ell }^{\ast }-{\ell }_1-{\ell }_2)\hfill \\ \hfill {\ell }^{\ast }\left(\alpha \right)=& Ls\left(\alpha \right)\hfill \\ \hfill \alpha \left({\alpha }_i\right)=& \frac{1}{1+e^{2{\alpha }_i}}\hfill \\ \hfill s\left({\alpha }_i\right)=& \frac{e^{2{\alpha }_i}}{\sum _j{e}^{2{\alpha }_j}},\hfill \end{array}$$ (16)

Heuristically, these equations of motion mean that the agent thinks that changes in its world are caused by the dynamics of hidden states $\stackrel{.}{\alpha }=A\sigma \left(\alpha \right)-\frac{1}{8}+1_6+{\omega }^{\left(\alpha \right)}$ in an abstract (conceptual) space. These dynamics conform to an attractor, which ensures points in attractor space are revisited in sequence and that only one attractor-state is active at any time. The currently active state selects a location ℓ^*(α) in the physical (Cartesian) space of the agent’s world, which exerts a force 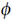(x, α) on the agent’s finger. The first four equations of motion in Eq. 16 pertain to the resulting motion of the agent’s arm in Cartesian space, while the last equation mediates the attractor dynamics driving these movements.

More formally, the (Lotka–Volterra) form of the equations of motion for the hidden attractor states ensures that only one has a high value at any one time and imposes a particular sequence on the underlying states. Lotka–Volterra dynamics basically induce competition among states that no state can win. One can see this intuitively by noting that when any state’s value is high, the negative effect on its motion can now longer be offset by the upper bounded function σ(α). The resulting winnerless competition rests on the (logistic) function σ(α), while the sequence order is determined by the elements of the matrix

$$A=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill -\frac{1}{2}\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill \cdots \hfill \\ \hfill -\frac{3}{2}\hfill & \hfill 0\hfill & \hfill -\frac{1}{2}\hfill & \hfill -1\hfill & \hfill \hfill \\ \hfill -1\hfill & \hfill -\frac{3}{2}\hfill & \hfill 0\hfill & \hfill -\frac{1}{2}\hfill & \hfill \ddots \hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill -\frac{3}{2}\hfill & \hfill 0\hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \ddots \hfill \end{array}\right]$$ (17)

Each attractor state has an associated location in Cartesian space, which draws the arm towards it using classical Newtonian mechanics. The attracting location is specified by a mapping ℓ^*(α) = Ls(α) from attractor space $\alpha \in {\Re }^6$ to Cartesian space $\ell \in {\Re }^2$ , which weights the locations L θ:

$$L=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 1.1\hfill & \hfill 1.0\hfill & \hfill 1\hfill & \hfill 1.4\hfill & \hfill 0.9\hfill \\ \hfill 1\hfill & \hfill 1.2\hfill & \hfill 0.4\hfill & \hfill 1\hfill & \hfill 0.9\hfill & \hfill 1.0\hfill \end{array}\right]$$ (18)

with a softmax function s(α) of the attractor states. The location parameters were specified by hand but could, in principle, be learnt as described in Friston et al. (2009, 2010a). The inertia and viscosity of the arm were chosen some what arbitrarily to reproduce realistic writing movements over 256 time bins, each corresponding to roughly 8ms (i.e. a second). Unless stated otherwise, we used a log-precision of four for sensory noise and eight for fluctuations in the motion of hidden states.

Movement is caused by action, which is trying to minimise sensory prediction error. A subtle but important constraint in these simulations was that action only had access to proprioceptive prediction error. In other words, action only minimised the difference between the expected and sensed angular location and velocity of the joints. This is important because it resolves a potential problem with active inference; namely that action or command signals need to know how they affect sensory input to minimise prediction error. The argument here is that the mapping from action to its proprioceptive consequences is sufficiently simple that it can be relegated (by evolution) to peripheral motor systems (perhaps even the spinal cord). In this example, complicated (handwriting) behavior is prescribed just by proprioceptive (generalised joint position) prediction errors. Here the mapping between action (changing the generalised joint position) and proprioceptive input is very simple. However, this does not mean that visual information (prediction errors) cannot affect action. Visual information is crucial when optimizing conditional beliefs (expected states) that prescribe predictions in both proprioceptive and visual modalities. This means that visual input can influence action vicariously, through high level (intentional) representations that predict a (unimodal) proprioceptive component (Fig. 1). See also Todorov et al. (2005). In short, although the perception or intention of the agent integrates proprioceptive and visual information in a Bayes-optimal fashion, action is driven just by proprioceptive prediction errors. This will become important in the next section, where we remove proprioceptive input but retain visual stimulation to simulate action observation.

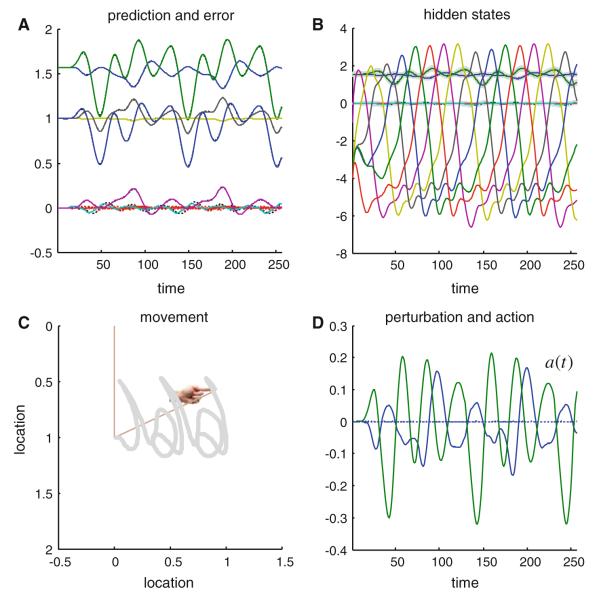
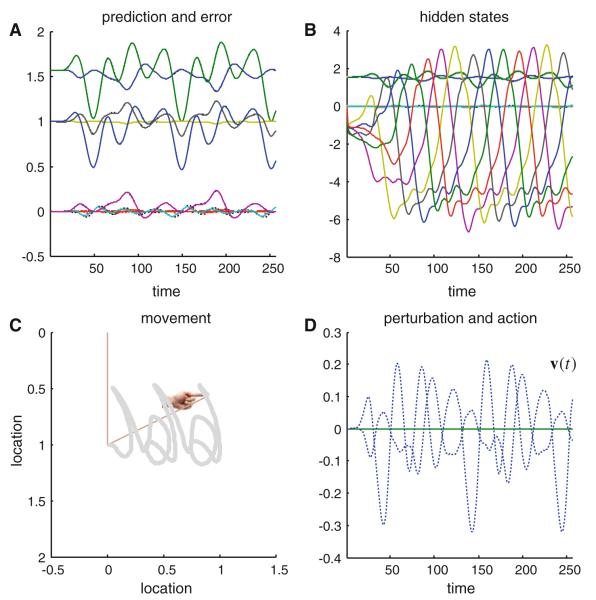
Figure 2 shows the results of integrating the active inference scheme of the previous section using the generative model above. The top right panel shows the hidden states; here the attractor states embodying Lotka–Volterra dynamics (the hidden joint states are smaller in amplitude). These generate predictions about the position of the joints (upper left panel) and consequent prediction errors that drive action. Action is shown on the lower right and displays intermittent forces that move the joint positions to produce a motor trajectory. This trajectory is shown on the lower left as a function of Cartesian location traced over time. This trajectory or orbit is translated as a function of time to reproduce the implicit handwriting. Although this is a pleasingly simple way of simulating an extremely complicated motor trajectory, it should be noted that this agent has a very limited repertoire of behaviors; it can only reproduce this sequence of graphemes, and will do so ad infinitum. Having said this, any exogenous perturbations or random forces on the arm have very little effect on the accuracy of its behavior; because action automatically compensates for unpredicted excursions from its trajectory (see Friston et al. 2009).

Fig. 2.

This figure shows the results of simulated action (writing), under active inference, in terms of conditional expectations about hidden states of the world (b), consequent predictions about sensory input (a) and the ensuing behavior (c) that is caused by action (d). The autonomous dynamics that underlie this behavior rest upon the expected hidden states that follow Lotka–Volterra dynamics: these are the six (arbitrarily) colored lines in b. The hidden physical states have smaller amplitudes and map directly on to the predicted proprioceptive and visual signals (a). The visual locations of the two joints are shown as blue and green lines, above the predicted joint positions and angular velocities that fluctuate around zero. The dotted lines correspond to prediction error, which shows small fluctuations about the prediction. Action tries to suppress this error by ‘matching’ expected changes in angular velocity through exerting forces on the joints. These forces are shown in blue and green in d. The dotted line corresponds to exogenous forces, which were omitted in this example. The subsequent movement of the arm is traced out in c; this trajectory has been plotted in a moving frame of reference so that it looks like synthetic handwriting (e.g. a succession of ‘j’ and ‘a’ letters). The straight lines in c denote the final position of the two jointed arm and the hand icon shows the final position of its extremity. (Color figure online)

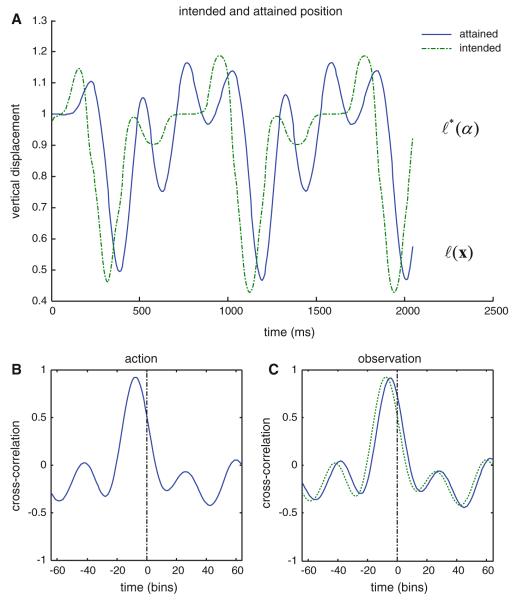
To highlight the fact that the hidden attractor states anticipate the physical motor trajectory, we plotted the expected and true locations of the finger. Figure 3 shows how conditional expectations about hidden states of the world antedate and effectively prescribe subsequent behavior. The upper panel shows the intended location of the finger. This is a nonlinear function ℓ^∗(u^(α)) of the attractor states (the states shown in Fig. 2). The subsequent location of the finger is shown as a solid blue line and roughly reproduces the desired position, with a lag of about 80ms. This lag can be seen clearly if we look at the cross-correlation function between the intended and attained positions shown on the lower left. One can see that the peak correlation occurs at about ten time bins or 80ms prior to a zero lag. These dynamics reinforce the notion that conditional beliefs (expected states) constitute an intentional representation.

Fig. 3.

This figure illustrates how conditional expectations about hidden states of the world antedate and effectively prescribe subsequent behavior. a shows the intended position of the arms extremity. This is a nonlinear function of the attractor states (the expected states shown in Fig. 2). The subsequent position of the finger is shown as a solid line and roughly reproduces the expected position, with a lag of about 80ms. This lag can be seen more clearly in the cross-correlation function between the intended and attained positions shown in b. One can see that the peak correlation occurs at about 10 time bins or 80 ms prior to a zero lag. Exactly the same results are shown in c but here for action–observation (see Fig. 5). Crucially, the perceived attractor states (a perceptual representation of intention) are still expressed some 50-60ms before the subsequent trajectory or position is evident. Interestingly, there is a small shift in the phase relationship between the cross-correlation function under action (dotted line) and action observation (solid line). In other words, there is a slight (approximately 8 ms) delay under observation compared to action, in the cross-correlation between representations of intention and motor trajectories

Empirically, the correlation between movements and their internal representations would suggest detectable coherence between muscle and cerebral activity. The time-courses in Fig. 2 suggest this coherence would predominate in the theta (4–10Hz) range. Interestingly, Jerbi et al. (2007) found significant phase-locking between slow (2–5Hz) oscillatory activity in the contralateral primary motor cortex and hand speed. They also reported “long-range task-related coupling between primary motor cortex and multiple brain regions in the same frequency band.” (Jerbi et al. 2007). Evidence for localised oscillations or coherence during writing (or writing observation) is sparse; however, Butz et al. (2006) were able to show that “coherence between cortical sources and muscles appeared primarily in the frequency of writing movements (3–7Hz), while coherence between cerebral sources occurred primarily around 10Hz (8–13Hz)”. Interestingly, they found coupling between ipsilateral cerebellum and the contralateral posterior parietal cortex (in normal subjects). This sort of finding may point to the specific neuronal systems (e.g. cerebellum and posterior parietal cortex) that sustain itinerant dynamics encoding complex motor behavior. Note there are dense connections between the ventral premotor and intraparietal cortex (Luppino et al. 1999).

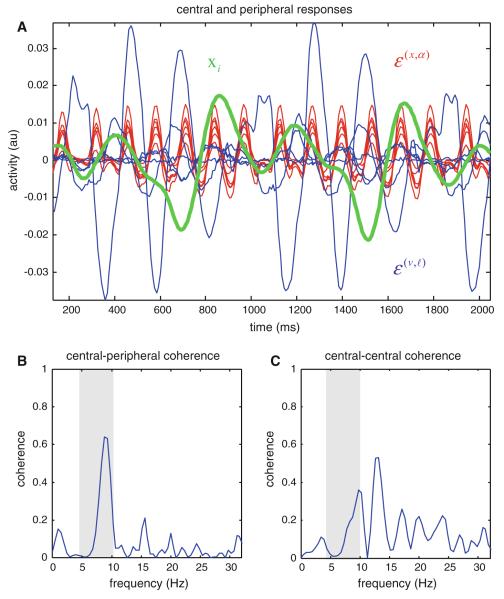
In fact, it was relatively easy to reproduce (roughly) the findings of Butz et al. (2006), using the simulated responses in Fig. 2. The upper panel of Fig. 4 shows the activity of prediction error units (red—attractor states; blue—visual input) and the angular position of a joint (green). These can be regarded as proxies for central and peripheral electrophysiological responses. This is because the main contribution to electroencephalographic (EEG) measures is thought to come from superficial pyramidal cells, and it is these that are believed to elaborate prediction error (Mumford 1992; Friston 2008). The lower left panel shows the coherence between the central (sum of errors on attractor states) and peripheral (arm movement) responses, while the lower right panel shows the equivalent coherence between the two populations of (central) error-units. The main result here is that central to peripheral coherence lies predominantly in the theta range (grey region) and reflects the quasiperiodic motion of the motor system, while the coherence between central measures lies predominately above the range (in the alpha range). This agrees qualitatively with the empirical results of Butz et al. (2006).

Fig. 4.

a The activity of prediction error units (red attractor states, blue visual input) and the angular position of the first joint (green). These can be regarded as proxies for central and peripheral electrophysiological responses; b shows the coherence between the central (sum of errors on red attractor states) and peripheral (green arm movement) responses, while c shows the equivalent coherence between the two populations of (central red and blue) error-units. The main result here is that central to peripheral coherence lies predominantly in the theta range (4–10Hz; grey region), while the coherence between central measures lies predominately above this range. (Color figure online)

3.2 Summary

In this section, we have covered the functional architecture of a generative model whose autonomous (itinerant) expectations prescribe complicated motor sequences through active inference. This rests upon itinerant dynamics (stable heteroclinic channels) that can be regarded as a formal prior on abstract causes in the world. These are translated into physical movements through classical Newtonian mechanics, which correspond to the physical states of the model. Action tries to fulfill predictions about proprioceptive inputs and is enslaved by autonomous predictions, producing realistic behavior. These trajectories are both caused by neuronal representations of abstract (attractor) states and cause those states in the sense that they are conditional expectations. Closing the loop in this way ensures a synchrony between internal expectations and external outcomes. Crucially, this synchrony entails a consistent lag between anticipated and observed movements, which highlights the prospective nature of generalised predictive coding. In short, active inference suggests a biological implementation of motor control that; (i) makes testable predictions about behavioral and neurophysiological responses; (ii) provides simple solutions to complex motor control problems, by enslaving action to perception; and (iii) is consistent with the known organization of the mirror-neuron system. In the next section, we will make a simple change which means that movements are no longer caused by the agent. However, we will see that the conditional expectations about attractor states are relatively unaffected, which means that they still anticipate observed movements.

4 Simulations: action–observation

In this section, we repeat the simulations of the previous section but with one small but important change. Basically, we reproduced the same movements as above but the proprioceptive consequences of action were removed, so that the agent could see but not feel the arm moving. From the agent’s perspective, this is like seeing an arm that looks like its own arm but does not generate proprioceptive input (i.e. the arm of another agent). However, the agent still expects the arm to move with a particular itinerant structure and will try to predict the trajectory with its generative model. In this instance, the hidden states still represent itinerant dynamics (intentions) that govern the motor trajectory but these states do not produce (precise) proprioceptive prediction errors and therefore do not result in action. Crucially, the perceptual representation still retains its anticipatory or prospective aspect and can therefore be taken as a perceptual representation of intention, not of self, but of another. We will see below that this representation is almost exactly the same under action–observation as it is during action.

Practically speaking, to perform these simulations, we simply recorded the forces produced by action in the previous simulation and replayed them as exogenous forces (hidden causes v(t) in Eq. 15) to move the arm in the current simulations. This change in context (agency) was modeled by down-weighting the precision of proprioceptive signals. This reduction appeals to exactly the same mechanism that we have used to model attention, in terms of perceptual gain (Feldman and Friston 2010). In this setting, reducing the precision of proprioceptive prediction errors precludes them from having any influence on perceptual inference (i.e. the agent cannot feel changes in its joints). Furthermore, action is not compelled to reduce these prediction errors because they have no (or trivial) precision. In these simulations, we reduced the log-precision of proprioceptive prediction errors from eight to minus eight.

The results of these simulations are shown in Fig. 5 using the same format as Fig. 2. The key thing to take from these results is that there is very little difference in terms of the inferred hidden states (upper right panel) or predictions and their errors (upper left panel). Furthermore, there is no difference in the actual movement (lower left panel). Having said this, there is small but important difference in inference at the onset of movement: Comparison with Fig. 2 shows that the hidden states take about 400ms (50 time bins) before ‘catching up’ with the equivalent trajectory under action. This means it takes a little time before the perceptual dynamics become entrained by the sensory input that they are trying to predict (note these simulations used the same initial conditions)

Fig. 5.

This shows exactly the same results as Fig. 2. However, in this simulation we used the forces from the action simulation to move the arm exogenously. Furthermore, we directed the agent’s attention away from proprioceptive inputs, by decreasing their precision to trivial values (a log precision of minus eight). From the agent’s point of view, it therefore sees exactly the same movements but in the absence of proprioceptive information. In other words, the sensory inputs produced by watching the movements of another agent. Because we initialised the expected attractor states to zero, sensory information has to entrain the hidden states so that they predict and model observed motor trajectories. The ensuing perceptual inference, under this simulated action observation, is almost indistinguishable from the inferred states of the world during action, once the movement trajectory and its temporal phase have been inferred correctly. Note that in these simulations the action is zero, while the exogenous perturbations are the same as the action in Fig. 2

The largest difference between Figs. 2 and 5 is in terms of action (sold lines) and the exogenous forces (dotted lines). Here, action has collapsed to zero and has been replaced by exogenous forces on the agent’s joints. These forces (hidden causes) correspond to the action of another agent that is perceived by the agent we are simulating. If one returns to Fig. 3 (lower right panel), one can see that the cross-correlation function, between the expected and the true or attained position, has retained its phase-lag and anticipates the intended movement of the other agent (although there is a slight shift in lag in comparison to action—dotted line). These simulations are consistent with motor activation prior to observation of a predicted movement (Kilner et al. 2004). This is the key behavior that we wanted to demonstrate; namely, that exactly the same neuronal representation can serve as a prescription for self-generated action, while, in another context, it encodes a perceptual representation of the intentions of another. The only thing that changes here is the context in which the inference is made. In these simulations, this contextual change was modeled by simply reducing the precision of proprioceptive errors. We have previously discussed this modulation of proprioceptive precision in terms of selectively enabling or disabling particular motor trajectories, which may be a potential target for the pathophysiology of Parkinson’s disease (Friston et al. 2009). Here, we use it to encode a change in context implicit in observing ones own arm, relative to observing another’s. The connection with formal mechanisms of attentional gain (Feldman and Friston 2010) is interesting here, because it means that we could regard this contextual manipulation as an attentional bias to exteroceptive signals (caused by others) relative to interoceptive signals (caused by oneself).

In terms of writing, “humans are able to recognise handwritten texts accurately despite the extreme variability of scripts from one writer to another. This skill has been suggested to rely on the observer’s own knowledge about implicit motor rules involved in writing” (Longcamp et al. 2006). Using magnetoencephalography (MEG), Longcamp et al. (2006) observed that 20-Hz oscillations were more suppressed after visual presentation of handwritten than printed letters, “indicating stronger excitation of the motor cortex to handwritten scripts”. This fits comfortably with the functional anatomy of active inference: The motor cortex is populated with multimodal neurons that respond to visual, somatosensory and auditory cues in peri-personal space (Graziano 1999; see also Graziano 2006). It is the ‘activation’ of these sorts of units that one would associate with the proprioceptive predictions in our model (see Fig. 1). Note that these predictions are still generated under action–observation; however, the precision (gain) of the ensuing prediction errors is insufficient to elicit motor acts.

4.1 Place-cells and oscillations

It is interesting to think about the attractor states as representing trajectories through abstract representational spaces (cf., the activity of place cells; O’Keefe 1999; Tsodyks 1999; Burgess et al. 2007). Figure 6 illustrates the sensory or perceptual correlates of units representing expected attractor states. The left hand panels show the activity of one (the fourth) hidden state unit under action, while the right panels show exactly the same unit under action–observation. The top rows show the trajectories in visual space, in terms of horizontal and vertical displacements (grey lines). The dots correspond to the time bins in which the activity of the hidden state unit exceeded an amplitude threshold of two arbitrary units. They key thing to take from these results is that the activity of this unit is very specific to a limited part of Cartesian space and, crucially, a particular trajectory through this space. The analogy here is between directionally selective place-cells of the sort studied in hippocampal recordings (Battaglia et al. 2004): In tasks involving goal-directed, stereotyped trajectories, the spatially selective activity of hippocampal cells depends on the animal’s direction of motion. Battaglia et al. (2004) were able to show “that sensory cues can change the directional properties of CA1 pyramidal cells, inducing bidirectionality in a significant proportion of place cells. For a majority of these bidirectional place cells, place field centers in the two directions of motion were displaced relative to one another, as would be the case if the cells were representing a position in space 5–10cm ahead of the rat”. This anticipatory aspect is reminiscent of the behavior of simulated responses shown in Fig. 3. A further interesting connection with hippocampal dynamics is the prevalence of theta rhythms during action (Dragoi and Buzsáki 2006): “Driven either by external landmarks or by internal dynamics, hippocampal neurons form sequences of cell assemblies. The coordinated firing of these active cells is organised by the prominent “theta” oscillations in the local field potential (LFP): place cells discharge at progressively earlier theta phases as the rat crosses the respective place field (phase precession)” (Geisler et al. 2010). Quantitatively, the dynamics of the hidden state-units in Fig. 2 (upper left panel) show quasiperiodic oscillations in the (low) theta range. The notion that quasiperiodic oscillations may reflect stable heteroclinic channels is implicit in many treatments of episodic memory and spatial navigation, which “require temporal encoding of the relationships between events or locations” (Dragoi and Buzsáki 2006), and may be usefully pursued in the context of active inference under itinerant priors.

Fig. 6.

These results illustrate the sensory or perceptual correlates of units representing expected hidden states. The left hand panels (a, c) show the activity of one (the fourth attractor) hidden state-unit under action, while the right panels (b, d) show exactly the same unit under action–observation. The top rows (a, b) show the trajectory in Cartesian (visual) space in terms of horizontal and vertical position (grey lines). The dots correspond to the time bins during which the activity of the state-unit exceeded an amplitude threshold of two arbitrary units. They key thing to take from these results is that the activity of this unit is very specific to a limited part of visual space and, crucially, a particular trajectory through this space. Notice that the same selectivity is shown almost identically under action and observation. The implicit direction selectivity can be seen more clearly in the lower panels (c, d), in which the same data are displayed but in a moving frame of reference to simulate writing. They key thing to note here is that this unit responds preferentially when, and only when, the motor trajectory produces a down-stroke, but not an up-stroke

4.2 Conserved selectivity under action and observation

Notice that the same ‘place’ and ‘directional’ selectivity is seen under action and observation (Fig. 6 right and left columns). Direction selectivity can be seen more clearly in the lower panels, in which the same data are displayed but in a moving frame of reference (to simulate writing). They key thing to note here is that this unit responds preferentially when, and only, when the motor trajectory produces a downstroke, but not an up-stroke. There is an interesting dissociation in the firing of this unit under action and action–observation: during observation the unit only starts responding to down-strokes after it has been observed once. This reflects the finite amount of time required for visual information to entrain the perceptual dynamics and establish veridical predictions (see Fig. 5).

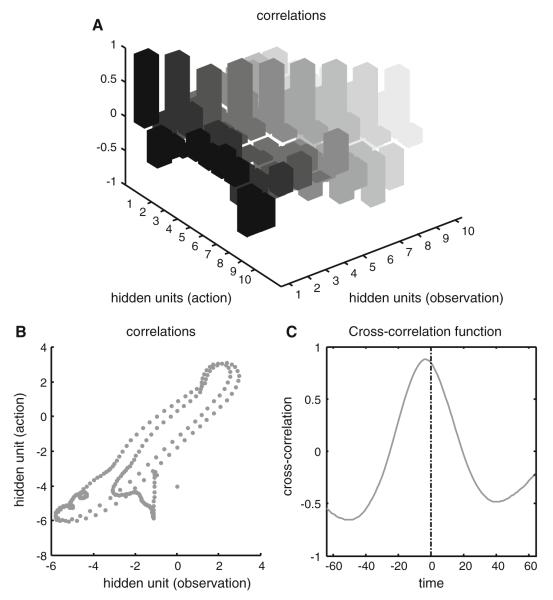
Figure 7 illustrates the correlations between the representations of hidden states under action and observation. The upper panel shows the cross-correlation (at zero lag) between all ten hidden state units. The first four correspond to the positions and velocities of the joint angles, while the subsequent six encode the attractor dynamics that represent trajectories during writing. The important thing here is that the leading diagonal of correlations is nearly one, while the off diagonal terms are distributed about zero. This means that the stimulus (visual) evoked responses of these units are highly correlated between action and observation and would be inferred, empirically, to be representing the same thing. To provide a simpler perspective on these correlations, the lower left panel plots the response of a single hidden state unit (the same depicted in Fig. 6) under observation and action, respectively, to show the high degree of correlation. Note that these correlations rest upon the fact that the same motion is expressed during action and action observation. The cross-correlation function is shown on the lower right. Interestingly, there is a slight phase-shift, suggesting that, under action, the activity of this unit occurs slightly earlier (about 4–8ms). We would expect this, given that this unit is effectively a consequence of motion in the visual field under observation, as opposed to a cause under action.

Fig. 7.

This figure illustrates the correlations between representations of hidden states under action and observation. a The cross-correlation (at zero lag) between all ten hidden state-units. The first four correspond to the positions and velocities of the joint angles, while the subsequent six encode the attractor dynamics that represent movement trajectories during writing. The key thing to note here is that the leading diagonal of correlations is nearly one, while the off-diagonal terms are distributed about zero. This means that the stimulus (visual) input-dependent responses of these units are highly correlated under action and observation; and would be inferred, by an experimenter, to be representing the same thing. To provide a simpler illustration of these correlations, b plots the response of a single hidden state unit (the same depicted in the previous figure) under observation and action, respectively. The cross-correlation function is shown in c. Interestingly, there is a slight phase shift suggesting that under action the activity of this unit occurs slightly later (about 4-8ms)

4.3 Summary

In summary, we have used exactly the same simulation as in the previous section to show that the same neuronal infra-structure can predict and perceive motor trajectories that are caused by another agency. Empirically, this means that if we were able to measure the activity of units encoding expected states, we would see responses of the same neurons under action and action–observation. We simulated this empirical observation by looking at the cross-correlation function between the last attractor state unit from the simulations of this section and the previous section; namely under action–observation and action. Although these traces are not identical, they have a profound correlation which is expressed maximally around zero lag. This is despite the fact that in the first simulation the states caused behavior (whereas in the second simulation they were caused by behavior). In Sect.6 we repeat the simulations of this section but introduce a deliberate violation of the exogenous forces to see if we could simulate an (intentional) violation response.

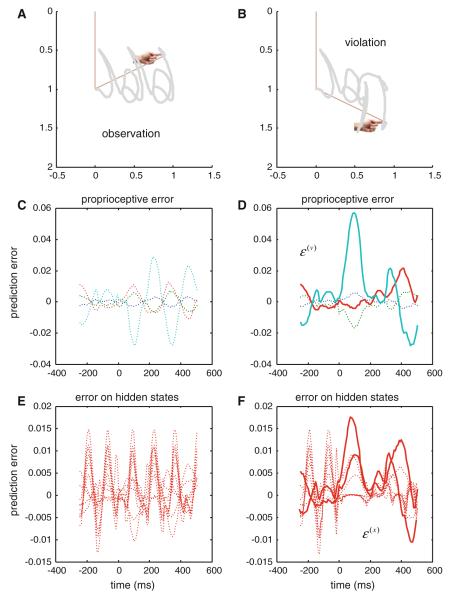
5 Simulations: violation-related responses

Here, we repeated the above simulation but reversed the exogenous forces moving the joints halfway through the executed movement. This produces a physically plausible movement but not one the agent can infer (perceive). We hoped to see an exuberant expression of prediction error following this perturbation. This is important because it demonstrates the agent has precise predictions about what was going to happen and was able to register the violations of these predictions. In other words, if the agent was simply inferring the current state of the world, there should be no increase in prediction error at the point of deviation from its prior expectations. To relate these simulations to empirical electrophysiology, we assume that the sources of prediction errors are superficial pyramidal cells that send projections to higher cortical levels.

Figure 8 shows simulated responses to violations of the expected trajectory (intention). The top panels show the stimuli presented to the agent, as in Fig. 5. The bottom panels show the synthetic electrophysiological responses that would be observed if we recorded cells reporting (proprioceptive) prediction errors about the joints (middle row) or about the motion of hidden states (lower row). We can associate these with local field potentials or event related potentials (ERPs). The left column show the stimuli and prediction errors under canonical or expected movements, whereas the right column shows the same results under violation. This violation was modeled by simply reversing the exogenous forces halfway through the trajectory. The lower panels show increased production of prediction error for both proprioceptive and hidden-state error-units following a violation of expectations. In both cases, it can be seen that there are early phasic and delayed components at about 100 and 400ms respectively for some units (highlighted with bold). These results may correspond to the electrophysiological violation or surprise responses seen electrophysiologically in other contexts (e.g. the N1, Mangun and Hillyard 1991; the mismatch negativity, Näätänen et al. (2001) and the P3, Donchin and Coles (1988)). A ubiquitous late positive component it the P3b with a parietal (posterior) distribution seen in oddball paradigms and is thought to represent a context-updating operation (Donchin and Coles 1988; Friedman et al. 2001; Gómez et al. 2008).

Fig. 8.

This figure shows simulated electrophysiological responses to violations of expected movements. The top panels (a, b) show the stimuli presented to the agent as in Fig. 5. The lower panels show the synthetic electrophysiological responses of units reporting prediction error (c, d proprioceptive errors; e, f errors on the motion of hidden states). The left panels (a, c, e) show the stimuli and prediction errors under canonical or expected movements, whereas the right panels (b, d, f) show the same results with a violation. This violation was modeled by simply reversing the exogenous forces halfway through the writing. The exuberant production of prediction error is shown in d and e. It can be seen here that there is an early phasic and delayed components at about 100 and 400ms for at least one proprioceptive and hidden state error-unit (sold lines). In c and d, errors on the angular positions are show in blue and green, while errors on angular velocities are in red and cyan. All errors on hidden states are shown in red in e and f. (Color figure online)

We are currently characterizing empirical responses to violations in the context of action–observation (Kilner et al., – in preparation). Although, we were not able to find any electrophysiological studies in the literature, Buccino et al. (2007) used fMRI to assess brain responses when the actions of others do or do not reflect their intentions: “volunteers were presented with video-clips showing actions that did reflect the intention of the agent (intended actions) and actions that did not (non-intended actions). Observation of both types of actions activated a common set of areas including the inferior parietal lobule, the lateral premotor cortex and mesial premotor areas. The contrast non-intended versus intended actions showed activation in the right temporo-parietal junction, left supramarginal gyrus, and mesial prefrontal cortex”. The authors conclude “that our capacity to understand non intended actions is based on the activation of areas signaling unexpected events in spatial and temporal domains, in addition to the activity of the mirror neuron system”. From the perspective of our model, the greater expression of prediction error under violation (i.e. non-intended action) would suggest fMRI activation (as opposed to deactivation) in those areas reporting prediction errors on biological motion and proprioception. These would probably involve the parietal and temporal cortex (as reported in Buccino et al. 2007).

5.1 Summary

In this section, we simulated violation responses in terms of synthetic ERPs. These responses speak to an empirical handle on action–observation responses, particularly in relation to how they rest upon encoding the intentions (anticipated trajectory) of motor movements. Crucially, these responses should be observed in exactly the same neuronal populations responsible for generating predictions that drive the same behavior during action. Although a simple set of simulations, they address a potentially important empirical approach to the study of mirror-neuron system.

6 Discussion

In this article, we have tried to show that the mirror-neuron system is entirely consistent and understandable in the context of (Bayes-optimal) active inference under the free-energy principle. Put simply, under this formulation, the brain does not represent intended motor acts or the perceptual consequences of those acts separately; the constructs represented in the brain are both intentional and perceptual: They are amodal inferences about the states of the world generating sensory data that have both sensory and motor correlates, depending upon the context in which they are made. The predictions generated by these representations are modality-specific, prescribing both exteroceptive (e.g. visual) and interoceptive (e.g. proprioception) predictions, which action fulfils. The functional segregation of motor and sensory cortex could be regarded as a hierarchical decomposition, in the brain’s model of its world, which provides predictions that are primarily sensory (e.g. visual cortex) or proprioceptive (motor and premotor cortex). If true, this means that high level representations can be used to furnish predictions in either visual or proprioceptive modalities, depending upon the context in which those predictions are called upon.

The ideas in this article can be regarded as a generic Bayesian (free-energy) perspective on the connectionist scheme introduced by Tani (2003); see also Tani et al. (2004) and Weber et al. (2006). Using robotic experiments, Tani et al. (2004) show that multiple behavioral schemata can be learned by recurrent neural networks in a distributed and hierarchical manner. Hierarchical (parametric) biases in the network play an essential role in both generating and recognizing behavioral patterns. “They act as a mirror system by means of self-organizing adequate memory structures”. We have pursued the same basic idea; that hierarchical generative models of the (interoceptive and exteroceptive) sequelae of action can be used to generate and recognise action and exploit this idea to understand what mirror neurons may encode.

The simulations in this article suggest that in the context of self-agency, proprioceptive predictions are afforded a high bias or precision, whereas when observing another this bias is suppressed (gated). Exactly the same sort of bias has been proposed for action selection by fronto-striatal loops (e.g. Bogacz and Gurney 2007; Frank et al. 2007; Hazy et al. 2007). Interestingly these proposals call upon classical neuromodulators (like dopamine and noradrenalin), whose role in modulating synaptic efficacy is exactly what would be required to implement expected precision in generalised predictive coding (see Eq. 12 and Friston 2008). Formally related mechanisms proposed for attention (e.g. Reynolds and Heeger 2009; Friston 2008; Feldman and Friston 2010) may also depend on modulatory neurotransmission (Clark et al. 1989; Coull 1998; Dalley et al. 2001; Davidson and Marrocco 2000; Hasselmo and Giocomo 2006; Herrero et al. 2008) and indeed the basal forebrain (Voytko et al. 1994). This means that we can use the same generative model, under action or observation, by selectively attending to visual or proprioceptive information (depending upon whether visual movement is caused by ourselves or others). The only difference, from the point of view of inference, is that movements caused by others do not have proprioceptive components. This provides a simple but mechanistic account of mirror neuron responses in the context of Bayes-optimal inference. Note that the gating of the proprioceptive prediction errors does not imply that the primary and secondary somatosensory areas are quiescent during action observation. Rather, that any observed activity in these areas should be suppressed relative to higher somatosensory processing. This is precisely what has been observed. In a meta-analysis of activations in primary and secondary somatosensory cortices during observation of touching actions: Keysers et al. (2010) report that areas OP1 and OP4 that constitute the secondary somatosensory area are consistently found to be active when observing actions. Areas BA1 and BA2—of the primary somatosensory cortex are sometimes found to be active—whereas area BA3 of the primary somatosensory cortex has never been shown to be active during observation of an action. Area BA3 is the primary area for somatosensory input where as BA1 and BA2 receive their inputs from BA3.

6.1 Active inference and motor control

There have been several accounts of forward and inverse models in action–observation in the motor control literature (Wolpert et al. 2003; Flanagan et al. 2003; Miall 2003; Keysers and Perrett 2004): “Skilled motor behavior relies on the brain learning both to control the body and predict the consequences of this control. Prediction turns motor commands into expected sensory consequences, whereas control turns desired consequences into motor commands. To capture this symmetry, the neural processes underlying prediction and control are termed the forward and inverse internal models, respectively” (Flanagan et al. 2003). Forward and inverse models (e.g. Wolpert et al. 1995) have been discussed in relation to imitation: The logic here is that the inverse model (mapping from sensory consequences to motor commands) can be used as a recognition model to infer the cause of an observed action. Once the cause is inferred the action can then be imitated. Although these proposals for forward-inverse models in imitation and social interactions (Wolpert et al. 2003) are exciting; they are formally very different from active inference and related connectionist schemes (Tani et al. 2004; Friston et al. 2010a). In active inference (and predictive coding), there are no inverse models or controllers; a generative model mapping from intention (cause) to sensation (consequence) is inverted by suppressing prediction error. If this suppression calls on action, then the intention is the generated action. If not, the intention (of another) is recognised. The implicit inversion depends on self-organizing, reciprocal exchange of signals among hierarchical levels of the brain’s generative model (see Fig. 1 and Tani et al. 2004). Crucially, active inference does not invoke any ‘desired consequences’, its rests only on experience-dependent learning and inference: Experience induces prior expectations, which guide perceptual inference and action:

Although our focus has been on the implications of active inference for the mirror-neuron system and vice versa, the approach taken in this work also has implications for conventional theories of motor control. In conventional approaches, one usually starts with some desired states or end points of the control process and uses an inverse model to compute the optimal control signals. These control signals are some-times finessed with corrections based upon a forward model (mapping from the control signals to expected sensory signals). This is a more complicated architecture than that used in active inference, where predictions control movement and obviate the need for an explicit control signal. This simplifies things greatly and resolves a series of issues in the motor control literature, which we have not emphasised in this article. For example, the problem of how to control a motor plant with many degrees of freedom becomes rather trivial. Here, it was solved by an invisible elastic band connecting the finger to the desired location. The ensuing scheme is a formal extension of the equilibrium point hypothesis that suggests “action and perception are accomplished in a common spatial frame of reference” (Feldman 2009). We generalise equilibrium points to cover trajectories through the use of generalised motion (generalised predictive coding). From the perspective of inferring the motor intentions of others, generalised predictive coding has an interesting implication. It suggests that an agent will only be able to predict (in the generalised or anticipatory sense) the trajectories or intentions of another, if the observed agent has the same sort of motor apparatus. In short, one should be much better at inferring the intended behavior of con-specifics, because the exteroceptive predictions are based on a veridical model of the other’s motor plant. This is not to say that we cannot predict the behavior of other creatures; however, it is unlikely that the neurons involved will show mirror neuron like properties, because they cannot predict our own proprioceptive inputs. This may provide an interesting empirical prediction; in that one would expect fewer violation responses when observing the same biological motion subtended by agents that do and do not look like ourselves (cf., Miura et al. 2010).

6.2 Functional anatomy

In describing these simulations, we have portrayed itinerant (attractor) dynamics as encoding motor intentions (anticipated or expected motor trajectories), while considering their role during action–observation as consequent on their role in specifying behavior. However, from a neurodevelopmental perspective the converse may be true. In other words, the form and structure of these neural attractor networks may be optimised during experience-dependent learning by watching other con-specifics (cf., Lee et al. 2010; see also Del Giudice et al. 2009). By subsequently attending to proprioceptive inputs one can see how learning to act through imitation could exploit the amodal role of high-order (intentional) representations. Clearly, this rests upon representations that predict the visual consequences of movement (of others): Neurons in the superior temporal sulcus (STS), respond selectively to biological movement (Grossman et al. 2000), both in monkeys (Oram and Perrett 1994) and humans (Allison et al. 2000). These neurons are not mirror neurons because they do not discharge during action execution. Nevertheless, they are often considered part of the mirror-neuron system (Keysers and Perrett 2004). Although mirror neurons were first discovered in macaque monkeys, using single-cell recordings, there is evidence for a homologous system in humans: Functional magnetic resonance imaging and positron emission tomography studies demonstrate that areas of frontal cortex, inferior parietal lobule (and posterior parietal cortex) and STS are active during action–observation (e.g. Decety et al. 1997; Grèzes et al. 2001; Hamilton and Grafton 2006).

We have deliberately tried to keep our simulations as simple as possible to highlight the underlying ideas. There are many things that one could nuance to make these simulations more realistic; for example, using a hierarchy of stable heteroclinic channels (cf., Tani et al. 2004; Kiebel et al. 2009b) and providing explicit contextual cues about whether one was observing ones own body or another’s. However, the basic results would not change and, even under this simple model, there is an easy mapping to known neurobiology. For example, we could associate the dynamics encoding itinerant motor sequences with prefrontal neurons (e.g. F5 in monkeys or Broca’s area in man). Many people have noted that the same form of itinerant trajectories used to predict complex motor sequences may also be involved in the prediction of speech (see Arbib 2010; Borghi et al. 2010). The hidden states subtending biological motion may correspond to neuronal populations in V5 complex and superior temporal sulcus (Allison et al. 2000; Takahashi et al. 2008), while low level proprioceptive and visual predictions could be associated with the activity of units in the motor cortex and early visual system respectively. The distributed anatomical arrangement of these representations speaks to a mirror-neuron system that implicates both executive systems and cortical systems involved in the processing of biological motion, which we have previously discussed in relation to mirror-neuron responses and inference about the intention of others (Kilner et al. 2007a,b). In conclusion, we hope to have sub-stantiated previous conjectures about the mirror-neuron system in the context of Bayesian inference, using simulations to disclose some operational and mechanistic details.

7 Appendix (software note)

This article has focused on the heuristics and basic equations that underlie active inference. However, we anticipate that people may want to reproduce and extend the simulations presented in this paper. In principle, this is fairly straightforward because active inference just entails integrating (solving) Eq. 4. The particular form of Eq. 4 rests on the free-energy gradients, which are specified completely by the generative model (specified as the equations of motion and Gaussian priors on the parameters of those equations). The numerics underlying the integration of Eq. 4 are described in Friston et al. 2010a (Eq. A3.2) and the form of the gradients can be found in Feldman and Friston (2010): See Appendix 1: Integrating the recognition dynamics (generalised filtering); using exactly the same notion as in this article. A more technical account can be found in Friston et al. (2010b) that describes recognition dynamics in terms of generalised filtering. Active inference can be regarded as supplementing generalised filtering (recognition dynamics) with the action dynamics in Eq. 13.

For people who want to reproduce the simulations and see how they work at a technical level, we recommend that they start with the Matlab code used in this article: All the requisite routines are available as part of the SPM software (academic freeware released under a GNU license; http://www.fil.ion.ucl.ac.uk/spm). In particular, the graphics in this paper can be reproduced from a graphical user interface (GUI) in the DEM toolbox that is invoked by typing DEM_demo at the Matlab prompt. When the GUI appears, depress the action observation button. The GUI provides the option to run or view/edit routines that serve as a pseudo-code specification of the ideas in the main text. DEM stands for dynamic expectation maximization, which is a variant of generalised filtering that uses a mean-field approximation (see Friston et al. 2010b for details). The GUI and the scripts are annotated in a way that should help clarify how the simulations are assembled.

It may seem strange to bundle simulation routines with a data analysis package; however, there are several reasons for doing this. (i) Active inference (as implement in spm_ADEM.m) uses exactly the same architecture and sub-routines as the equivalent DEM and generalised filtering schemes that omit action (spm_DEM.m and spm_LAP.m, respectively). These schemes are used routinely to analyze empirical time-series as part of the analysis software. This highlights the fact that active inference appeals to exactly the same fundaments of evidence-based model optimization (and variational techniques) as state-of-the-art Bayesian filtering for empirical data. (ii) Because the neurobiological simulation and data analysis routines call on the same numerics and sub-functions it is easier to bundle them together. This has the advantage that improvements to the code (and debugging) are seen by both application domains. One of the reasons we encourage people to start with this code is that it has been tested extensively through worldwide dissemination in the neuroimaging community. (iii) We have established a protocol within SPM, where people can create links to their own SPM compatible toolboxes, which is a nice way to disseminate ideas and developments. This may prove useful for people interested in the computational aspects of active inference in the future. (iv) Finally, the simulations are themselves used as part of data analysis; where recognition dynamics are used to explain evoked electromagnetic brain signals (see spm_dcm_dem.m).