Double Cohesion in Structural DNA Nanotechnology

Abstract

Double cohesion has proved to be a useful tool to assemble robust 2D arrays of large tiles. Here we present a variety of examples showing the utility of this approach. We apply this principle to the 3 types of 2D lattice sections of arrays whose individual tiles are inherently 3 dimensional, because they contain three vectors that span 3-space. This application includes motifs which are based on the tensegrity triangle, the six-helix bundle motif and on three skewed triple crossover molecules. All of these designs have the potential to form 3 dimensional structures if all three directions of propagation are allowed. If one direction is blunted, 2D arrays form, and all 3 combinations are presented here. In addition, a large parallelogram array that was not attainable previously using single duplex cohesion was also constructed using double cohesion. For comparison, arrays which use another type of double cohesion, double paranemic (PX) cohesion are also presented. Double cohesion of sticky ends proved to be the more effective tool to assemble large motifs into arrays.

Introduction

One of the key aims of structural nanotechnology is to design and construct robust structures that have the ability to self-assemble into periodic arrays.¹ Owing to its well-known structure and predictable intermolecular interactions, DNA is widely used to make such constructs. Reciprocal strand exchange between DNA double helices, similar to the DNA Holliday junction, has led to branched systems with multiple helical domains that contain many strands. Simple procedures enable one to program the relationship between sequence and structure.¹ Complementary sticky ends allow for programmable intermolecular cohesion, and have been used to construct a variety of objects, periodic arrays, and nanomechanical devices.² The predictable geometry of sticky-ended cohesion³ enables one to program specific intermolecular structural features, such as patterns and cavities, on the nanometer scale. In previous work, 2D crystalline DNA arrays have been constructed from a variety of motifs including double crossovers (DX),^4,5 triple crossovers (TX),⁶ DNA parallelograms,⁷ and a four-by-four structure.⁸

Recently, we reported a trigonal motif that incorporated double cohesion.⁹ This means that each sticky end is replaced by a pair of sticky ends. The individual units were constructed using DX rather than linear duplex DNA. The DX molecule is about twice as stiff as double helical DNA,^10,11 so the resulting unit is inherently quite rigid. In addition, the system assembles with double sticky-ended intermolecular interactions instead of single sticky ends (Figure 1). Double intermolecular interactions seem to compensate for errors in twist between succeeding components, thus making the connections less susceptible to individual variations. Trigonal lattices, which were not previously attainable using other motifs with single helical connections, were produced by this approach; indeed, a control in which only single cohesion was used failed to produce the target lattice. Here, we have expanded on this observation in a DNA parallelogram system, with the same result. We demonstrate that double cohesion is of value, not only in producing target arrays, but also in demonstrating flaws in 2D sections of 3D arrays. It is sufficiently robust that the arrays cohere, even when there are inherent problems in the design. In addition, we show that the alternative of double PX cohesion is less effective than double sticky-ended cohesion for assembling 2D lattices of DX triangles.

Figure 1. Single and Double Sticky-Ended Cohesion.

The cohesive nucleotides are indicated by orange base pairs. (a) Single Sticky Ended Cohesion. A single helix coheres with another helix through a single sticky-end pair. (b) Double Sticky-Ended Cohesion. Two branched molecules are shown, and they cohere with each other twice. Note that these molecules show only one half of each of the DX molecules that they represent; otherwise the junctions would not form two collinear arrangements.

RESULTS

All the individual tiles discussed below are robust, in the sense that blunt-ended versions of them migrate as single bands on non-denaturing gels (data not shown), indicating that our starting material is pure, homogenous and monodisperse. It is necessary to make blunt-ended versions of the tiles, for this type of assay, because sticky-ended versions can cohere in non-denaturing gels, leading to the appearance of multiple species. The need for blunt-ended versions of motifs to establish their robustness has been known for about a decade.¹⁰

DX Parallelograms

The simple DNA parallelogram consists of four Holliday junctions fused to form a parallelogram.⁷ In each direction there is a length of DNA corresponding to the side of the parallelogram and a second length corresponding to the part between parallelograms when an array is formed: For example, in the first parallelogram reported,⁹ six turns of DNA were used in each direction, with overhangs of one turn on each side, leading to four turns on each edge within the parallelogram, described by a notation of (4+2) × (4+2); thus, the periodic array contains a 4 × 4 turn parallelogram, a 4 × 2 turn parallelogram, a 2 × 4 turn parallelogram and a 2 × 2 turn parallelogram. The same paper reported a larger parallelogram, (6+2) × (4+2).⁷

We have tried to extend parallelogram arrays to somewhat larger dimensions. We have been partially successful with simple parallelograms of slightly larger dimensions; Figure 2a illustrates an array that is (4+4) × (4+4), and a second array that is (6+2) × (6+2).¹⁶ Attempts to achieve larger arrays were unsuccessful when we used single helical domains for each direction. Given the success of the DX motif in producing trigonal arrays, we tried a DX parallelogram. Our target has been an (8+4) × (8+4) parallelogram array. A schematic of the motif used is shown in Figure 2c. We tried two different motifs, one in which all of the crossovers forming the DX motifs were separated by even numbers of half-turns (termed PDX-E-E), and a second, where the DX crossovers within the boundaries of the square were separated by odd numbers of half-turns (PDX-E-O). All sticky ends contain six nucleotides. Figure 2d shows that a somewhat fragmentary small, array forms with the PDX-E-E motif, and that it displays the target periodicity, 40 nm. However, the PDX-E-O motif is much more successful. Figure 2e illustrates a large array, also with a periodicity of 40 nm. Figure 2f is a zoom of that image, and Figure 2g is the autocorrelation function of the image in Figure 2e, showing an angle of 50 between domains. As will be seen below, arrays that mix odd and even crossover separations are more successful than arrays the contain only even crossover separations. What is the basis for the success of the arrays? Is it the robustness of the DX-parallelogram, or is it the double cohesion? We performed the same control that we did in the case of the DX triangle, with the same result: No array formation is seen, only an individual parallelogram can be discerned from the most successful AFM image, illustrated in Figure 2h.

Figure 2. Experiments with Parallelogram Arrays. (a) A ( 4+4) × (4+4) Single Cohesion Parallelogram Array.

The dimensions of the image are 310 × 310 nm. The pseudo periodicity is 13 nm (both inside and outside the parallelogram are the same size) in agreement with expected values. The angle between directions is 68°, established from the autocorrelation function (not shown). (b) A ( 6+2) × (6+2) Single Cohesion Parallelogram Array. The dimensions of the image are 1500 × 1500 nm. The repeat distance is 27 nm and the angle found is 60. (c) Schematic of the PDX-E-O Motif. The relationship of the four different DX molecules and their constituent strands is visible. (d) An Array Formed by the PDX-E-E Motif. The image dimensions are 800 × 800 nm. The periodicity is 40 nm. (e) An Array Formed by the PDX-E-O motif. The image dimensions are 1500 × 750 nm. (f) A Zoom of the Array shown in (e). This image has been rotated 90 from the view in (e). The dimensions are 200 × 100 nm. (g) The Autocorrelation Function of the Image in (f). The dimensions are 150 × 150 nm. The periodicity is 40 nm and the angle between directions is 50. (h) A Control Experiment with Single Cohesion. This is the same self-assembly as in panels (e–g), but with only a single sticky end in each direction. The dimensions of this image are 200 × 200 nm. Other than a single box-like image slightly left of center, there is nothing reminiscent of the arrays seen in the successful self-assemblies.

3-Space-Spanning Motifs

The 3D-DX Triangle

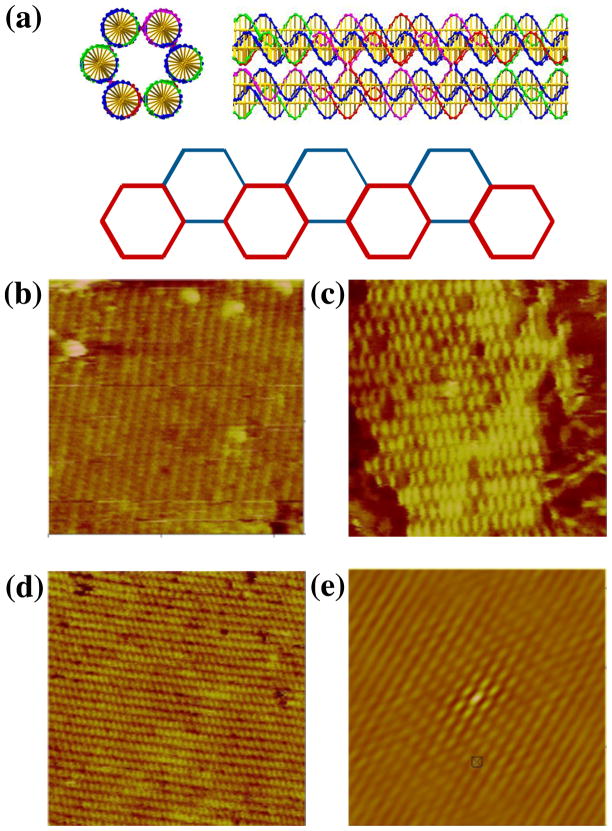
A key goal of DNA nanotechnology is the construction of well-ordered 3D DNA periodic crystals.¹ It is possible to produce 3D arrays by combining planar motifs that are rotated relative to each other by angles that are not full- or half-rotations. However, there are a number of problems associated with motifs that potentially can form first one plane, and then another that must be inserted into it. Consequently, motifs that span 3-space inherently appear to be a promising direction for achieving the goal of 3D self-assembled arrays. The first such motif was produced by Mao and his colleagues,¹² and it is known as the tensegrity triangle; it consists of three interwoven single-helical domains connected by Holliday junctions. The robustness of DX motifs has led us to produce a DX version of this motif, termed the 3D-DX triangle, shown in Figure 3a. Each edge is below one DX and above another, thereby creating a motif that spans 3-space.

Figure 3. Arrays of 3D-DX Molecules. (a) A Schematic of the 3D-DX Motif.

Note that each of the directions corresponds to a DX molecule. The nearly horizontal DX at the top is above the adjacent DX on the left and below the one on the right. (b–d) Three Independent Periodic Sections of the 3D-DX Motif with Even Numbers of Half-Turns Between All Crossovers. The dimensions of the square panel edges are 2113, 2203 and 2192 nm, respectively. Note the extensive curling in all three panels, although there is a nice flat image, as well, in panel (c). (e–g) Three Independent Periodic Sections of the 3D-DX Motif with Alternating Even and Odd Numbers of Half-Turns Between Crossovers. These images are in the same order as in panels (b–d). The dimensions of the square panel edges are 1926, 2501 and 2291 nm, respectively. Note the lack of curling relative to (b–d). (h–l) Two-Tile Independent Sections and Autocorrelation Functions. Panels (h), (j), and (l) are two-tile images in the same order as in the previous panels. The dimensions of the edges of these square panels are 889, 748 and 1209 nm, respectively. Panels (i) and (k) are the autocorrelation functions of the images in panels (h) and (j), respectively. Their edges are of length 430 and 415 nm, respectively.

The design of successful DNA motifs that self-assemble into a 3D array of high resolution has proved to be difficult.¹³ There are many factors that can affect the success of the self-assembly. One of these is simply errors in structural design. We felt that it would be useful to establish the proper design of 3-space-spanning motifs by determining whether double cohesion in two directions produced a well-patterned 2D array, as examined by AFM. If all three directions were flanked by sticky-ends, a three dimensional periodic array would result. To form 2D arrays, we put blunt ends in one of the linearly independent propagation directions, and then repeated the experiment for the other two directions. The resulting lattices are rhomboidal sections of a rhombohedral lattice. Thus, examination of each motif consists of three experiments, inspecting the three different sections formed from each pair of directions in each motif.

The 3D-DX triangle was initially designed with only even separations of half-turns between crossovers, both in the motif and in the final lattice. In this design, there are 73 nucleotides per repeat unit, or 7 double helical turns (24.8 nm). Between the triangle vertices, there are 27 nucleotide pairs, and the sticky-end length is 4 nucleotides on each overhang. Strictly even numbers of half-turns between junction arrays may tend to form bends over a long range due to errors in twist. To combat this effect, a variation of this motif with alternating even and odd separations was designed and built. This system also has 27 nucleotide pairs between triangle vertices and 4-nucleotide sticky-ends. The repeat distance between tiles is 84 nucleotide pairs, or 8 helical turns (28.6 nm).

Figures 3b-d show the atomic force micrographs produced by the self-assembly of the 3D DX triangle containing crossover separations with even numbers of half turns between all junctions; a different direction of propagation has been blunted in each image. There is evidence of curling in the arrays, possibly due to the even-repeat repetition. The repeat distance (~25 nm) is in good agreement with the expected value (24.8 nm). Figures 3e–g show that 2D arrays built by alternating even and odd separations do not experience the same the twisting effects that the even-separation lattices exhibit. The repeat distance (~28 nm) is also within agreement with the expected (28.6 nm). It is possible to build this array from two different tiles, which is shown in Figures 3h, 3j and 3l. Figures 3i and 3k contain the autocorrelation functions for the images in panels h and j, respectively.

The 6-Helix Bundle

The second motif we examined is also constructed from a series of DX molecules. However, instead of combining them in a tensegrity triangle, they are laid out parallel to each other; unlike the TX molecule, ⁶ they have not been assembled so as to be roughly planar, but rather each DX molecule is separated from the next by an angle of 120, to make the motif a 6-helix bundle¹⁴ (6HB). The 10.5-fold helicity of DNA means that 7-and 14-nucleotide separations between crossovers rotate them by 120°. We have utilized this feature to produce a bundle where 6 helices are interconnected in the same way as the DX molecule. This structure is visible in the top part of Figure 4a, which shows a 6HB motif both end-on and laterally. Note the helical repeat after two turns in the lateral image.

Figure 4. Two Dimensional Arrays of Six-Helix Bundle Motifs. (a) Schematics of the Motif.

The top of the panel contains a cross-section and a lateral view of the motif. Note the crossovers visible in the lateral view are separated by two helical turns. The bottom of the panel shows how the motif can form a 2D array. The corners of the hexagons correspond to the positions of the helix axes in the motif. The red hexagons are closer to the viewer than the blue hexagons. (b–d) Three Independent Sections of a Two-Tile Six-Helix Bundle Motif 2D Lattice. The edge-lengths of the images are 566, 342 and 480 nm, respectively. (e) Autocorrelation Function of the Array in (b). The edge length of this image is 324 nm. This is the best-ordered of the three autocorrelation functions; it is taken from an image different from the one shown.

This motif also can span 3-space, using double cohesion. Referring to the end-on image of the 6HB in Figure 4a, one could imagine using sticky ends to join the top two helical domains in front to the bottom two domains at the rear. Likewise one could imagine joining the bottom right domains in front to the upper left domains in the rear, as well as joining the bottom left domains in front to the upper right domains in the rear. The vectors to the centroids of each of these DX component ends span 3-space. Similarly to the 3D-DX triangle, if all three DX domains were equipped with appropriate sticky-ends, a 3D structure could assemble. Any pair of these vectors produce a planar arrangement that is held together by only four of the six sticky-end pairs. An example of such an array is shown in the lower part of Figure 4a, where the top and bottom DX pairs are indicated as being blunt. Note that there are two ways to phase the selection of these DX units within the 6HB molecule. Each unit of the 6HB is 6 turns in length (21.4 nm), with sticky-end lengths of 4 nucleotides. Both a single tile and two tile system using this motif were assembled, but the single-tile system was not as successful as the two-tile system. AFM images of the 6HB with each of the three directions of propagation blunted are shown in Figures 4b-d. Figure 4e shows the autocorrelation function corresponding to the first direction. The measured repeat distance along the helix axis is ~20 nm, in good agreement with the 21.4 nm distance calculated from the components.

The Skewed TX Triangle

Another motif that inherently fills 3-space is the skewed TX triangle, shown in three views in Figure 5a. The left side of Figure 5a illustrates the basic component of this array, and the two images on the right show the complete motif containing three TX motifs. Also based on the tensegrity triangle, this design replaces the double helix edge with TX molecules, which are connected by bulged three-arm junctions¹⁵ at the vertices. The helices of the TX molecules are extended pair-wise on either side, so that the pair of DX units forming the TX share the middle helical domain. These pairs of DX units cohere with other tiles. The design uses the TX motif with an odd number of half turns between both crossovers; there is an even number of half turns in the region between tiles. Again, if all three DX helical domains were assigned sticky-ends, a 3D lattice would form. Similarly, one direction was blunted in order to form 2D arrays. All three directions were examined. There are 45 nucleotide pairs between vertices, and a repeat of 8 turns (28.6 nm) in the lattice that uses a sticky-end length of 6 nucleotides.

Figure 5. Images of the Skewed TX Triangle. (a) Schematics of the Motif.

The left drawing is the skewed TX structure, and the middle drawing shows a view that emphasizes one of the three sides of the motif. The right view is a 3-fold symmetric picture of the motif. (b–d) The Three Independent Sections Built from Self-Assembly of the Motif. The edges of the three sections are 760, 1700 and 1200 nm, respectively.

Figures 5b–d show AFM images that illustrate the results of three different directions of two-dimensional assembly of this motif. It is evident that the 2D arrays also have a pseudo-rhombic pattern, similar to the 3D-DX triangles. The average value for distances in the three images is ~29 nm, which is in good agreement with the designed distance of 28.6 nm. There is a certain amount of variability in the pattern seen in the different projections, but less in the autocorrelation functions (not shown). Nevertheless, it is clear that the motif is sufficiently robust to form well-ordered two-dimensional arrays.

Double Cohesion in a PX Context

Another way to assemble large objects into 2D arrays is to use paranemic (PX) cohesion. PX-DNA is a four-stranded coaxial complex in which two adjacent parallel DNA double helices form crossovers at every point possible.¹⁷ This produces two inter-wrapped double helices in which the strands of either double helix are completely unlinked to those of the other double helix. Hence, the motif can be formed by two DNA dumbbells or by any other pair of topologically-closed molecules tailed in dumbbells. For example, two large topologically-closed DNA triangles have been successfully combined using PX cohesion.¹⁸ Intramolecular PX cohesion has also been central in the formation of a replicable DNA octahedron.¹⁹ Initially, we attempted to form hexagonal 2D arrays via simple PX cohesion.

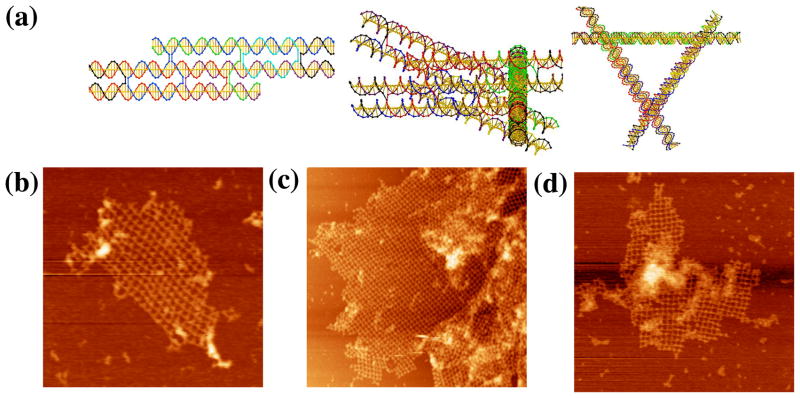
In the design, each triangle edge is made up of three DX molecules, all of whose helix axes are coplanar (Figure 6a). The inner double helices of the three sides are connected to form the triangle. The outer double helixes are involved in inter-triangle cohesion. At one end, the double helical domain extends to form a half PX, while the other end is terminated by a loop extending to the next side of the triangle. The PX overhang end is one and a half PX turns of PX DNA. The resulting lattice is designed to be planar, with pseudo-trigonal symmetry. There are four kinds of hexagons (I, II, III, and IV) that consist of six triangles each. The PX sequences on the six triangles are distinct so that the association between triangles is highly specific. Therefore, eight different triangles are required for this design. Only minimal success (Figure 6b) has been obtained with this approach, leading merely to small or ill-formed arrays. The most successful image, shown in Figure 6c, is the only one found that features a six-triangle arrangement flanking an open center.

Figure 6. PX Cohesion of a Trigonal Array. (a) A Schematic of the Designed Array.

The motif is a triangle whose edges are all DX molecules, and all helix axes are coplanar. There are eight different triangles (numbered in Arabic numerals) with twelve different cohesive PX ends (A-K). They are designed to assemble into four different hexagons (labeled with Roman numerals) with trigonal symmetry. (b–c) AFM Images of Self-Assembly Produced by Single PX-Cohesion. The edges of the two images are 1409 and 113 nm, respectively. Individual triangles can be discerned, but the image seen in (c) is the only example of six triangles flanking an cavity. (d–e) Images of Self-Assembly Produced by Double PX-Cohesion. The edges of the images are 2947 and 1829 nm, respectively. Although this motif was successful at producing trigonal pseudohexagonal arrays when assembled with sticky ends, double PX-Cohesion fails to produce the same result.

We attempted to see whether it was possible to obtain better results by using double PX cohesion, analogous to double sticky-ended cohesion. To try first in a best-case scenario, we used the DX-triangle motif used previously.⁹ PX cohesive motifs were attached to each of the three directions of planar propagation. The results, shown in Figures 6d and 6e are not encouraging; we see the same types of bent intermolecular structures in these images that we seen in Figure 6b. The DX-triangles are known to be robust, so the flexibility must arise in the extra-triangular segments involving the double PX cohesion. Further attempts to employ double PX cohesion with this motif were abandoned.

Discussion

We have expanded the applications of sticky-ended double cohesion, showing that it is a successful tool for producing large arrays in several contexts. Motifs, such as the parallelogram, had reached their maximum propagation size with single sticky-ends, as seen in Figure 6b. Replacing single helices with DX molecules creates more rigid motifs, which then can assemble with stronger intermolecular interactions. Individual units of arrays can be made larger since the connections between them are more robust. This allows for the increase in the size of periodic units. The ability to control features of arrays, including cavity size and patterns, is essential for success in nanotechnology.

PX cohesion has been shown to be a promising way to assemble intramolecular and small specific intermolecular DNA species, if highly specific associations are used.^18,19 However, neither single PX cohesion nor double PX cohesion proved to be a useful means of producing 2D arrangements that entailed triangular motifs. Despite the nominal rigidity that such arrays would be thought to have, the sections connected by PX or double PX cohesive termini are seen repeatedly to be bent, and target structures only result upon rare occasions.

Double sticky-ended cohesion may prove to be a useful tool for the construction of 3D lattices. Self-assembly of 3D crystals has been a central goal of nanotechnology since its origination.¹ Three of the motifs described here have the capacity to span 3-space. AFM examination of 2D arrays resulting from all three directions of a blunted 3-space spanning motif is a sensitive method to determine where the assumption of uniformity in helical motif structures breaks down. For example, the three different 2D sections of the 6HB motif consistently display autocorrelation patterns of different quality. Thus, 2D sections of 3D motifs allows for troubleshooting and tuning motifs to enable better designs.

Experimental

Molecular Design, Synthesis, and Purification

All of the DNA motifs in this paper were designed using the program SEQUIN.²⁰ The sequences are shown in the supplementary information for all motifs, except the DX triangles used in the PX cohesion experiments; those triangles are identical to those reported earlier.⁹ The strands were synthesized either on an Applied Biosystems 394 or on an Expedite 8909, removed from the support, and deprotected using routine phosphoramidite procedures.²¹ Some additional strands were purchased from IDT (Coralville, IA). All strands have been purified by denaturing gel electrophoresis; bands were cut out of 12–20% denaturing gels and eluted in a solution containing 500 mM ammonium acetate, 10 mM magnesium acetate, and 1 mM EDTA.

Formation of Hydrogen-Bonded Complexes and Arrays

Complexes were formed by mixing a stoichiometric quantity of each strand as estimated by OD₂₆₀. Concentration of DNA and buffer conditions varied. For the 3D DX triangle, DAE-E and DAE-O versions, the DNA concentration was 2 μM and 0.25 μM respectively, in 50 mM HEPES, 200 mM ammonium acetate, 150 mM magnesium acetate, 1mM EDTA, pH 7.0 or 10 mM HEPES, 11 mM MgCl₂, 1 mM EDTA, pH 7.8. The final DNA concentration for the 6-helix bundle was 0.5 μM in 10 mM HEPES, 26 mM MgCl₂, 1 mM EDTA, pH 7.8. The DNA concentration for the skewed TX triangle was 0.2 μM, in 10 mM HEPES, 11 mM MgCl₂, 1 mM EDTA, pH 7.8. The DX parallelogram concentration was 50 nM in 5 mM HEPES, 52 mM MgCl₂, 2 mM EDTA, pH 7.8. With the exception of the DX parallelogram, single tile mixtures were annealed from 90°C to room temperature during 40 h in a 2-litre water bath insulated in a styrofoam box. For systems using 2-tiles, each tile was annealed separately, mixed at room temperature, and then raised to 45 °C (for DX-3D triangle) or 37 ° C (for 6HB) in a 2-litre water bath, then cooled to room temperature in a Styrofoam box. The parallelogram was assembled using a temperature-controlled programmable incubator. The first part of the protocol involved cooling from 80 °C to 42 °C at a rate of 1 °C per hour. A thermocycling procedure ensued which went as follows: 42 to 34 to 40 to 34 to 39 to 34 to 37.5 to 34 to 22 °C at a rate of 0.5 °C per hour.

The hexagon PX cohesive arrays were formed in two steps. First, the eight individual triangle molecules were annealed separately in 40 mM Tris, 40 mM Acetic Acid, 12.5 mM Mg Acetate, and 2 mM EDTA using a step anneal (90 °C for 5 min, 65 °C for 30 min, 45 °C for 30 min, and 37 °C for 30 min). Triangles were combined one at a time at 37°C, and left at 37 °C for 30 min before the addition of subsequent triangles. The complete mixture is then left at 23 °C for 1 hour, and then 4 °C for 12 hours. The final DNA concentration was 0.125 μM. Similar procedures were used for the PX double cohesion arrays.

AFM Imaging

A 5–7 μL of the sample was spotted on freshly cleaved mica (Ted Pella, Inc.). For arrays imaged in contact mode, the sample was left to adsorb from 2–20 min. To remove buffer salts, 15–20 drops of doubly distilled water was placed on the mica, the drop was shaken off, and the sample was dried with compressed air. Imaging was performed under 2-propanol in a fluid cell. For arrays imaged in tapping mode in buffer, the sample was deposited and an additional 25 μL of fresh buffer was added to both the mica and to the liquid cell. All AFM imaging was performed on a NanoScope IV (Digital Instruments) instrument, using commercial cantilevers with Si₃N₄ tips.