Results on Differential and Dependent Measurement Error of the Exposure and the Outcome Using Signed Directed Acyclic Graphs

Abstract

Measurement error in both the exposure and the outcome is a common problem in epidemiologic studies. Measurement errors in the exposure and the outcome are said to be independent of each other if the measured exposure and the measured outcome are statistically independent conditional on the true exposure and true outcome (and dependent otherwise). Measurement error is said to be nondifferential if measurement of the exposure does not depend on the true outcome conditional on the true exposure and vice versa; otherwise it is said to be differential. Few results on differential and dependent measurement error are available in the literature. Here the authors use formal rules governing associations on signed directed acyclic graphs (DAGs) to draw conclusions about the presence and sign of causal effects under differential and dependent measurement error. The authors apply these rules to 4 forms of measurement error: independent nondifferential, dependent nondifferential, independent differential, and dependent differential. For a binary exposure and outcome, the authors generalize Weinberg et al.’s (Am J Epidemiol. 1994;140(6):565–571) result for nondifferential measurement error on preserving the direction of a trend to settings which also allow measurement error in the outcome and to cases involving dependent and/or differential error.

In an important paper that laid the foundation for a number of further studies on measurement error, Bross (1) showed that for a binary exposure and outcome, independent nondifferential measurement error in the outcome or, by symmetry, in the exposure could only bias tests for an effect towards the null. Subsequent work (2, 3) showed that this was not the case if the exposure were polytomous and that moreover, in this case, a trend in the effects of an exposure can change direction. In another important result, Weinberg et al. (4) gave monotonicity conditions under which the association between the measured exposure and the outcome would point in the same direction as that between the true exposure and the outcome. This result, however, was restricted to the setting of independent nondifferential measurement error and assumed that the outcome was correctly measured. In this paper, we first review theory concerning causal diagrams with signed edges (5–7) and then use this theory to generalize Weinberg et al.’s monotonicity result to a number of settings with dependent and differential measurement error. The results in this paper, like those of Weinberg et al. (4), assume correctly measured confounders; additional results on mismeasured confounders might make for interesting future work.

Causal diagrams (8, 9) or causal directed acyclic graphs (DAGs) have been useful for reasoning about confounding (8–14), selection bias (15, 16), and measurement error (17, 18). In prior work, it has been shown that DAGs with signed edges are useful in reasoning about confounding (5–7) and, to a certain extent, about selection (19, 20). Here we show how DAGs with signed edges can be useful in reasoning about measurement error.

SIGNED DAGS

In this section, we review results on DAGs and signed DAGs. The reader can refer to Glymour and Greenland (14) for a more thorough introduction to DAGs and to VanderWeele et al. (5) for information on signed DAGs. A DAG is composed of variables (nodes) and arrows between nodes (directed edges) such that the graph is acyclic—that is, there is no sequence of arrows from a node back to itself. A causal DAG is one in which the arrows can be interpreted as causal relations and in which all common causes of any pair of variables on the graph are also included on the graph. If there is a directed edge from X to Y, then X is said to be a parent of Y and Y is said to be a child of X. A path is a sequence of nodes connected by edges regardless of arrowhead direction; a directed path is a path that follows the edges in the direction indicated by the graph’s arrows.

Signs might be given to edges to indicate a variety of relations. For example, a sign might be given to an edge to indicate that an increase in the value of the parent variable increases or leaves unchanged the child variable, on average; we could call this an average monotonic effect. However, using this relatively weak notion of monotonicity, one can construct examples in which V₁ is a parent of V₂ and V₂ is a parent of V₃ and in which V₁ increases V₂ on average and V₂ increases V₃ on average but V₁ decreases V₃ on average (5). That is to say, transitivity of monotonic effects or “signed edges” fails when one uses “monotonicity on average.” We will consequently also make use of a somewhat stronger notion, “distributional monotonicity.” We will say that a parent X has a positive distributional monotonic effect on a child Y if, for each value y, an increase in X renders the event Y > y at least as likely or more likely conditional on the other parents of Y. Transitivity of signed edges holds with distributional monotonic effects (6, 7). Distributional monotonicity is stronger in that it implies average monotonicity, but the converse is not true. In some contexts, average monotonic effects will suffice; some contexts will require distributional monotonic effects. An example in which average monotonicity is satisfied but distributional monotonicity is not is given in Appendix 1 (see also Chen et al. (21)).

More formally, if X is a parent of Y and Q denotes the parents of Y other than X, then we say that X has a positive average monotonic effect on Y if E[Y|X, Q] is nondecreasing in X for all values of Q. Similarly, X has a negative average monotonic effect on Y if E[Y|X, Q] is nonincreasing in X for all values of Q. Note that if E[Y|X, Q] is constant in X, then X has positive and negative average monotonic effects on Y trivially. We will say that X has a positive distributional monotonic effect on Y if, for all x₀ and x₁ with x₁ ≥ x₀, we have P(Y > y|X = x₁, Q = q) ≥ P(Y > y|X = x₀, Q = q) for all y and all q. This essentially requires that as X increases, the cumulative distribution functions for Y are monotonically ordered (no two of them ever crossing). Likewise, X is said to have a negative distributional monotonic effect on Y if, for all x₀ and x₁ with x₁ ≥ x₀, we have P(Y > y|X = x₁, Q = q) ≤ P(Y > y|X = x₀, Q = q) for all y and all q. Distributional monotonicity is retained under monotonic transformations of the outcome (e.g., taking logs), but this is not necessarily the case with average monotonicity, for which the presence or absence of a monotonic effect (or its direction) may depend on the scale (e.g., log-transformed or not). However, if Y is binary, then the definitions of a distributional monotonic effect and an average monotonic effect coincide. Moreover, if X and Y are both binary, then positive/negative covariance is equivalent to a positive/negative distributional monotonic effect.

When a parent X has a positive (distributional or average) monotonic effect on child Y, we will say that the X → Y edge is of positive sign. When X has a negative (distributional or average) monotonic effect on Y, we will say that the edge is of negative sign. If X has neither a positive nor a negative monotonic effect on Y, then the edge is said to be without sign. The sign of a path is then defined to be the product of the signs of the edges that constitute that path (6, 7). If one of the edges on a path is without sign, then the sign of the path is said to be undefined. In each specific context, we will indicate whether distributional or average monotonic effects are being considered. A signed DAG is a DAG with signs on those edges that allow them.

Throughout our exposition, we will use one important result of VanderWeele and Robins (7) governing the covariance among variables on causal DAGs with signed edges.

Result 1 (VanderWeele and Robins (7)): If signs on the graph indicate distributional monotonic effects, then for 2 variables X and Y, if all directed paths between X and Y are of positive sign and for each common cause C_i of X and Y all directed paths from C_i to X are of the same sign as all directed paths from C_i to Y, then Cov(X, Y) ≥ 0. Likewise, if all directed paths between X and Y are of negative sign and those from C_i to X are of opposite sign to those of C_i to Y, then Cov(X, Y) ≤ 0.

The result implies that if the correlation induced by the paths from X to Y aligns with that induced by the common causes of X and Y, then the correlation between X and Y is in the direction that one would expect. However, there may be settings in which, even if all edges have signs, the various signs do not all align and one cannot use result 1 to draw conclusions about the sign of the covariance; we give an example below. In result 1, if the set of common causes or the set of directed paths in question is empty, then the corresponding assumption holds by default. Note that result 1 concerns population covariances/correlations; sample correlations may differ because of random variation. If the sample correlation happens by chance to be in the wrong direction, the inferences drawn using the results presented below could also be wrong.

There are 2 important extensions of this result that follow directly from the proof given by VanderWeele and Robins (7). First, the same result holds if we condition on a set of covariates L that have no parents on the graph; more specifically, we could conclude Cov(X, Y|L = l) ≥ 0 or Cov(X, Y|L = l) ≤ 0 if the conditions of the result hold, with the exception that the set of common causes C_i considered in result 1 does not need to include the set of variables that is being conditioned on, L. Second, the result above makes reference to paths and requires that the signs on edges correspond to distributional monotonic effects. In fact, the result also holds under slightly weaker conditions, in that if an edge is such that on all directed paths referenced in result 1 to which the edge belongs, the edge is the final edge on the path, then only an average monotonic effect (rather than a distributional monotonic effect) for that edge is required for the result to hold. Thus, any directed path consisting of a single edge only requires average monotonic effects. We only need distributional monotonic effects when directed paths have 2 or more edges, and we only need the distributional monotonicity for edges that are not final edges on the directed paths for conclusions based on result 1 to hold. Note that whether an edge is “final” is relative to the particular graph; we can always expand a graph to include additional intermediate variables or we can collapse the diagram over such intermediate variables; the result on the sign of the covariance holds if there is any graph representing the causal structure such that the conditions described above hold. When constructing DAGs, we can collapse over variables that are not common causes, and, as will be seen below, it will be convenient to do so in applying this generalization of result 1.

MEASUREMENT ERROR ON DAGS

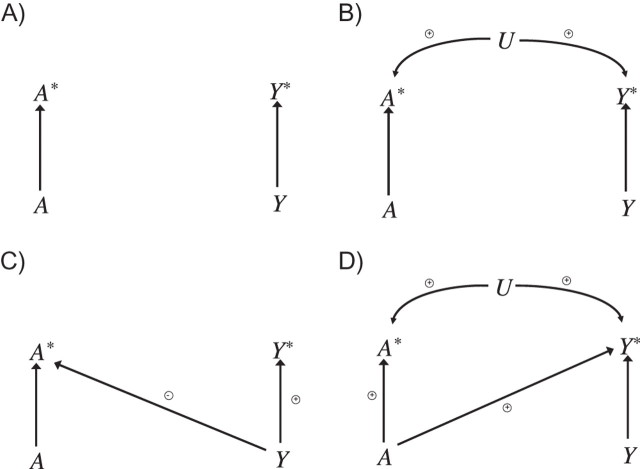
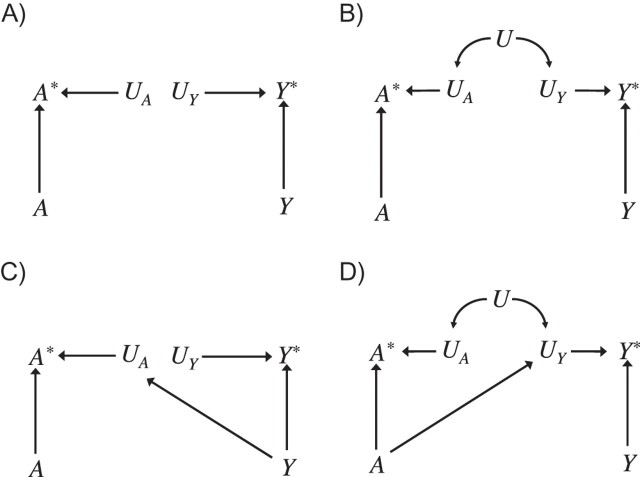
Hernán and Cole (18) gave causal DAGs that illustrated 4 types of measurement error: independent nondifferential, dependent nondifferential, independent differential, and dependent differential. The 4 types of measurement error described by Hernán and Cole are illustrated in the 4 parts of Figure 1.

Figure 1.

Signed directed acyclic graphs illustrating tests for a causal effect in the presence of measurement error. A) Independent nondifferential measurement error; B) dependent nondifferential measurement error; C) independent differential measurement error; D) dependent differential measurement error. A represents true exposure; A^*, measured exposure; Y, the true outcome; Y^*, the measured outcome; and U, a variable leading to correlated/dependent measurement errors. Data are available only on A^* and Y^*. In part A, if there is any association between A^* and Y^*, there must be a causal effect of A on Y. In parts B and D, if there is a negative association between A^* and Y^*, there must be a causal effect of A on Y. In part C, if there is a positive association between A^* and Y^*, there must be a causal effect of A on Y.

If both the exposure A and the outcome Y are measured with error, with values A^* and Y^*, respectively, then the measurement errors are said to be independent if the measured exposure and the measured outcome are statistically independent of one another conditional on the true exposure and the true outcome; otherwise the measurement errors are said to be dependent. The measurement errors are independent in parts A and C of Figure 1; the measurement errors are dependent in parts B and D.

We say that measurement errors are nondifferential if 1) the measured exposure is independent of the true outcome conditional on the true exposure and 2) the measured outcome is independent of the true exposure conditional on the true outcome; otherwise the measurement errors are differential. The measurement errors are nondifferential in parts A and B of Figure 1. If the true outcome affects the measured exposure as in Figure 1C or if the true exposure affects the measured outcome as in Figure 1D, then the measurement errors are differential. Thus, Figure 1A represents independent nondifferential measurement error, Figure 1B dependent nondifferential, Figure 1C independent differential, and Figure 1D dependent differential.

Note that on the diagrams in Figure 1, unlike those in the article by Hernán and Cole (18), we have not represented the factors responsible for measurement error. We have collapsed the diagram over these factors. We do this so that to apply the results on signed DAGs, we only need to specify the net sign of, for example, the A → A^* arrow and the Y → Y^* arrow. We could represent the factors responsible for measurement error, or the measurement errors themselves, on the causal diagram, but this would require specifying the sign of more arrows; further discussion of DAGs representing the factors responsible for measurement error, or the measurement errors themselves, is given in Appendix 2. As in the article by Weinberg et al. (4), the diagrams in Figure 1 allow for measurement errors that may be affected by the true value of the variables; further, the measurement errors are not required to follow any particular distribution, may have nonzero mean values, and may follow different distributions for different values of the true exposure or outcome.

REASONING ABOUT THE PRESENCE OF AN EFFECT FROM SIGNED DAGS UNDER MEASUREMENT ERROR

We now consider how signed edges can be useful in drawing conclusions about the presence of an effect of A on Y under these different forms of measurement error. We will consider a setting without control for possible confounders L, but all of the remarks below would also hold conditional on L. Consider first Figure 1A. Suppose we are interested in testing whether A has any effect on Y. We see from Figure 1A under independent nondifferential measurement error that if there is no effect of A on Y, then measured A^* and Y^* should be uncorrelated. If we believed that Figure 1A correctly represented the causal diagram under the null hypothesis of no exposure effect (with independent and nondifferential measurement errors) and found in the data that A^* and Y^* were correlated, then, if the true correlation between A^* and Y^* were indeed nonzero, we could conclude that there must be some effect of A on Y. In Figure 1A, we did not need to make use of signed edges at all (1, 18).

Consider now Figure 1B and suppose that A^* and Y^* were self-reported exposure and outcome, respectively. Suppose that in a retrospective study, the likelihood of misclassified exposure status is positively correlated with the likelihood of misclassified outcome status due to potential memory failure of the study participants. Suppose that this results in correlation between measurements through memory capacity (U on the diagram). Suppose U had a positive (average) monotonic effect on both A^* and Y^*, as indicated by the signed edges in Figure 1B. By result 1, we could conclude that, under the null hypothesis that A has no effect on Y, we should find that A^* and Y^* are positively correlated. This is because there are no directed paths from A^* to Y^* in Figure 1B and the only common cause of A^* and Y^* is U, and all directed paths from U to A^*, namely U → A^*, are positive and thus of the same sign as all directed paths from U to Y^*, namely U → Y^*. If A^* and Y^* were negatively correlated (i.e., the exposure appeared to prevent the outcome), then, if the true correlation between A^* and Y^* were indeed negative, we could conclude that there must be some true effect of A on Y.

Suppose now in Figure 1C that A denoted alcohol use, A^* self-reported alcohol use, Y dementia, and Y^* self-reported dementia. If alcohol use is underreported for persons with dementia, so that Y has a negative (average) monotonic effect on A^*, and if diagnosis of dementia is sufficiently accurate that actual dementia Y has a positive (average) monotonic effect on diagnosed dementia Y^*, then under the null hypothesis of no effect of A on Y, we would have by result 1 that A^* and Y^* should be negatively correlated. If, with the data, we found that A^* and Y^* were positively correlated (i.e., alcohol appeared to increase dementia), then if the true correlation between A^* and Y^* were indeed positive, we could conclude that there must be some effect of A on Y.

Finally, consider the causal diagram in Figure 1D and suppose that A denoted the use of a potentially protective drug for some outcome Y and that A^* and Y^* denoted self-reported drug use and self-reported outcome in a retrospective study. Suppose that because of possible memory failure, there is a common cause U of measured A^* and Y^* such that U has a positive (average) monotonic effect on both A^* and Y^*. Suppose also that the drug has a side effect which renders diagnosis (and consequently self-report) of the outcome more likely, so that drug use A has a positive (average) monotonic effect on self-reported Y^*, such that in Figure 1D we have both dependent and differential measurement error. Finally, suppose that the information on the self-report of exposure is sufficiently accurate that true exposure A has a positive (average) monotonic effect on self-reported exposure A^*. In Figure 1D, there are 2 common causes of A^* and Y^*, namely A and U. Now all of the directed paths from A to Y^*, namely A → Y^*, are positive and of the same sign as all directed paths from A to A^*, namely, A → A^*. Likewise, all directed paths from U to Y^*, namely U → Y^*, are positive and thus of the same sign as all directed paths from U to A^*, namely U → A^*. By result 1, we would have Cov(A^*, Y^*) ≥ 0 in Figure 1D—that is, under the null hypothesis of no effect of A on Y, we would have a positive association between A^* and Y^*. If, with the data, we found that A^* and Y^* were negatively correlated (i.e., the drug appeared to prevent the outcome), then, if the true correlation between A^* and Y^* were indeed negative, we could conclude that there must be some effect of A on Y.

In each of these 4 cases, our conclusions required that the various signed edges align in the correct manner; in other cases, this will not be the case and result 1 will be inapplicable. For example, if the edge from A to Y^* in Figure 1D had been negative, then result 1 would have been inapplicable for reasoning about the sign of the covariance between A^* and Y^* because, while U, as a common cause of A^* and Y^*, would induce positive correlation between A^* and Y^*, the variable A, as a common cause of A^* and Y^*, would oppose that by inducing negative correlation between A^* and Y^*, and thus the overall sign of the covariance between A^* and Y^* could not be inferred.

Note that none of the results we described in this section required that any of the variables A, Y, A^*, and Y^* be binary. In the next 2 sections, we will consider the assumptions under which we can draw conclusions not only about the presence of an effect of the true exposure on the true outcome but also about the sign of this effect. We first consider the classic result of Weinberg et al. (4).

DIRECTION-OF-EFFECT RESULT OF WEINBERG ET AL.

As we noted in the Introduction, when the exposure is in fact polytomous or continuous rather than binary, nondifferential measurement error can produce a bias away from the null (2, 3). Weinberg et al. (4) considered the settings in which nondifferential misclassification of the exposure would preserve the direction of a trend. In their setting, only the exposure A was potentially mismeasured; the outcome is measured without error and can be either discrete or continuous. They gave the following result.

Result 2 (Weinberg et al. (4)): Under nondifferential measurement error, if E[A^*|A] is nondecreasing in A and if E[Y|A] is monotonic (nondecreasing or nonincreasing) in A, then sign(Cov(Y, A^*)) = sign(Cov(Y, A)).

The result of Weinberg et al. states that provided that the true exposure has a positive average monotonic effect on the measured exposure and provided that the true exposure has a (positive or negative) average monotonic effect on the outcome, the sign of the association between the outcome and the measured exposure will be the same as that between the outcome and the true exposure. Weinberg et al.’s result gives conditions under which the trend reversal described by Dosemeci et al. (2) and Wacholder (3) will not arise.

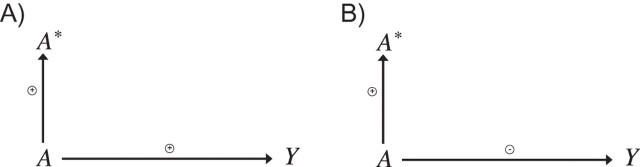
In fact, the result of Weinberg et al. (4) also follows quite simply from the theory of signed DAGs. Consider the diagrams in Figure 2. If E[A^*|A] is nondecreasing in A, then A has a positive average monotonic effect on A^*, as indicated in parts A and B of Figure 2. If E[Y|A] is nondecreasing in A, then A has a positive average monotonic effect on Y, as in Figure 2A, and, by result 1 and its extension allowing for final edges to be monotonic on average, we have that Cov(Y, A^*) ≥ 0 and Cov(Y, A) ≥ 0. If E[Y|A] is nonincreasing in A, then A has a negative average monotonic effect on Y, as in Figure 2B, and, by result 1, we have that Cov(Y, A^*) ≤ 0 and Cov(Y, A) ≤ 0. From this the result of Weinberg et al. (4) follows.

Figure 2.

Signed directed acyclic graphs illustrating the nondifferential measurement error result obtained by Weinberg et al. (4). A represents true exposure; A^*, measured exposure; and Y, the true outcome. Data are available only on A^* and Y. In part A, if there is a positive association between A^* and Y, there must be a positive association between A and Y. In part B, if there is a negative association between A^* and Y, there must be a negative association between A and Y.

EXTENSIONS OF THE DIRECTION-OF-EFFECT RESULT TO SETTINGS WITH DEPENDENT AND DIFFERENTIAL MEASUREMENT ERROR OF THE EXPOSURE AND THE OUTCOME

In this section, we will use signed DAGs to generalize the result of Weinberg et al. to settings with measurement error in the outcome as well as the exposure and to settings with dependent and/or differential measurement error. As will be seen below, the results here are generalizations of the Weinberg et al. (4) result only for the case of binary exposure and binary outcome; for nonbinary exposures or outcomes, the results in this section require stronger assumptions than that of Weinberg et al. (4). Our analysis will follow that of Figure 1, but we will now consider not simply the conclusions that would follow under the null hypothesis but also those that would follow even if there were an effect of the true exposure on the outcome. The analysis also applies conditional on a set of common causes of (true and/or measured) exposure and outcome; if L suffices to control for confounding for the effect of A on Y, then in those cases the sign of the association between A and Y conditional on L will also give the sign of the actual conditional causal effect of A on Y. As we discussed above, when paths with multiple signed edges are considered, assumptions about distributional (rather than simply average) monotonic effects will be needed for all but final edges on the paths.

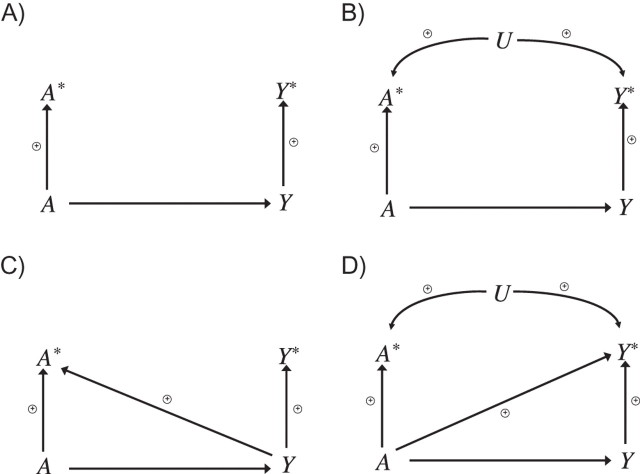
Consider first the case of independent nondifferential measurement error, as in Figure 3A. Suppose that A had a distributional monotonic effect on Y but the sign of the effect was not known. Note that the assumption that A has a distributional monotonic effect on Y is satisfied automatically if A and Y are both binary, because in settings where A and Y are binary, positive/negative covariance is equivalent to a positive/negative distributional monotonic effect. Suppose further that A^* measures A sufficiently well that A has a positive average monotonic effect on A^* and that Y^* measures Y sufficiently well that Y has a positive average monotonic effect on Y^*, as indicated by the signs in Figure 3A. Suppose also first that Cov(Y, A) ≥ 0 so that A has a positive distributional monotonic effect on Y. Here A is the only common cause of A^* and Y^* and all directed paths from A to A^*, namely A → A^*, are positive and thus of the same sign as all paths from A to Y^*, namely A → Y → Y^*. Note that because the directed path A → Y → Y^* has 2 edges, the first of these, A → Y, must have a distributional monotonic effect to apply result 1 but the final edge, Y → Y^*, need only have an average monotonic effect. From result 1, we would have that Cov(Y^*, A^*) ≥ 0. Likewise, if Cov(Y, A) ≤ 0, then it follows that A has a negative distributional monotonic effect of A on Y, and from result 1 it follows that Cov(Y^*, A^*) ≤ 0. Thus, irrespective of whether Cov(Y, A) ≥ 0 or Cov(Y, A) ≤ 0, we have that sign(Cov(Y^*, A^*)) = sign(Cov(Y, A)), extending the result of Weinberg et al. (4) to the setting in which there is independent nondifferential measurement error of a binary outcome as well as a binary exposure.

Figure 3.

Signed directed acyclic graphs illustrating generalizations of the direction-of-effect result to dependent and differential measurement error. A represents true exposure; A^*, measured exposure; Y, the true outcome; Y^*, the measured outcome; and U, a variable leading to correlated/dependent measurement errors. Data are available only on A^* and Y^*. Assuming distributional monotonicity (or binary exposure and outcome), in part A, if there is a positive association between A^* and Y^*, there must be a positive association between A and Y; and if there is a negative association between A^* and Y^*, there must be a negative association between A and Y. In parts B–D, if there is a negative association between A^* and Y^*, there must be a negative association between A and Y.

We will now consider the other 3 forms of measurement error. Consider the case of dependent nondifferential measurement error in Figure 3B. Suppose that A had a distributional monotonic effect on Y (again, this would be satisfied automatically if A and Y were both binary). Suppose that A^* measures A sufficiently well that A has a positive average monotonic effect on A^* and that Y^* measures Y sufficiently well that Y has a positive average monotonic effect on Y^*, as indicated by the signs in Figure 3B. Suppose further that U has positive average monotonic effects on both A^* and Y^*. If Cov(Y, A) ≥ 0, then A has a positive distributional monotonic effect on Y, so that result 1 implies Cov(Y^*, A^*) ≥ 0. If the estimated Cov(Y^*, A^*) < 0, this would give evidence (subject to random variation in sample correlation) that the true association between A and Y is negative.

Similarly, consider the independent differential measurement error in Figure 3C. Suppose that A had a distributional monotonic effect on Y (satisfied automatically if A and Y were both binary). Suppose further that A^* measures A sufficiently well that A has a positive average monotonic effect on A^* and that Y^* measures Y sufficiently well that Y has a positive average monotonic effect on Y^* and the differential measurement error is such that Y has a positive average monotonic effect on A^*. If Cov(Y, A) ≥ 0, then A has a positive distributional monotonic effect on Y, so that result 1 implies Cov(Y^*, A^*) ≥ 0. If the estimated Cov(Y^*, A^*) < 0, this would give evidence that the true association between A and Y is negative.

Finally, consider the dependent differential measurement error in Figure 3D. Suppose that A had a distributional monotonic effect on Y (satisfied automatically if A and Y were both binary). Suppose further that A^* measures A sufficiently well that A has a positive average monotonic effect on A^* and that Y^* measures Y sufficiently well that Y has a positive average monotonic effect on Y^*, that U has positive average monotonic effects on both A^* and Y^*, and the differential measurement error is such that A has a positive average monotonic effect on Y^*. If Cov(Y, A) ≥ 0, then A has a positive distributional monotonic effect on Y, so that result 1 implies Cov(Y^*, A^*) ≥ 0. If the estimated Cov(Y^*, A^*) < 0, this would give evidence that the true association between A and Y is negative.

DISCUSSION

The approach we have described here has a number of strengths. First, by making use of DAGs, our results are very general insofar as we do not make any assumptions about the distributions of the variables or of measurement error or about the functional form relating the variables on the diagram beyond the monotonicity assumptions indicated by the signed edges. Second, our approach is very general in that result 1, which governs the sign of associations among variables on a signed DAG, can be used to draw similar conclusions about the presence and direction of an effect based on numerous other diagrams using the same principles (e.g., we could add arrows from A to Y^* in Figure 3C or from Y to A^* in Figure 3D). Finally, this approach to measurement error using signed DAGs can be used to address numerous types of measurement error, including that which is dependent and/or differential. At least for a binary exposure and outcome (or in cases in which we are willing to assume distributional monotonicity), theory concerning signed DAGs has allowed us to extend Weinberg et al.’s (4) result on the nonreversal of a trend to settings involving dependent and/or differential measurement error.

The signed DAG approach is subject to some limitations. First, drawing conclusions strictly from the sign of associations of the measured variables requires that the sources of association due to measurement error all align in the same direction; when signs do not align, the conclusions will be indeterminate. Second, in settings in which we want to draw conclusions about the direction of an effect of an exposure on the outcome, not merely the presence of an effect, we essentially need either to assume that the true exposure has a distributional monotonic effect on the outcome or to restrict the analysis to settings in which the exposure and/or the outcome are binary (so that this assumption is satisfied automatically). Our results about inferring the presence of an effect were not limited in this way, but in most settings we will also want to draw conclusions about the direction of the effect. Finally, even when we can use signed DAGs to draw conclusions about whether the exposure has a positive or negative effect on the outcome, the results we have given in this paper do not indicate whether the expected estimated effect obtained from the measured exposure and measured outcome is smaller or larger than the actual effect (i.e., the direction of the bias); the signed DAGs only give us conclusions about the direction of the effect, not its magnitude. In future work, investigators could attempt to characterize settings in which the various forms of measurement error produce estimates towards or away from the null and could consider mismeasured confounders (22, 23).

Glossary

Abbreviation

DAG

directed acyclic graph

APPENDIX 1. An Example Comparing Average Monotonicity With Distributional Monotonicity

Let the child Y be an ordered variable with 3 levels, and suppose the only parent of Y is a variable X with 2 levels. Suppose that the probability distribution of Y given X = 0 is P(Y = 0|X = 0) = 0.3, P(Y = 1|X = 0) = 0.5, and P(Y = 2|X = 0) = 0.2, so that the mean of Y conditional on X = 0 is E(Y|X = 0) = 0.9. The cumulative distribution function for Y conditional on X = 0 is then given by P(Y ≤ 0|X = 0) = 0.3, P(Y ≤ 1|X = 0) = 0.8, and P(Y ≤ 2|X = 0) = 1, and the survivor function conditional on X = 0 is given by P(Y > 0|X = 0) = 0.7, P(Y > 1|X = 0) = 0.2, and P(Y > 2|X = 0) = 0. Suppose also that the probability distribution of Y given X = 1 is P(Y = 0|X = 1) = 0.1, P(Y = 1|X = 1) = 0.5, and P(Y = 2|X = 1) = 0.4, so that the mean of Y conditional on X = 1 is E(Y|X = 1) = 1.3. The cumulative distribution function for Y conditional on X = 1 is then given by P(Y ≤ 0|X = 1) = 0.1, P(Y ≤ 1|X = 1) = 0.6, and P(Y ≤ 2|X = 1) = 1, and the survivor function conditional on X = 1 is given by P(Y > 0|X = 1) = 0.9, P(Y > 1|X = 1) = 0.4, and P(Y > 2|X = 1) = 0. Because the mean values are ordered, E(Y|X = 0) = 0.9 ≤ 1.3 = E(Y|X = 1), average monotonicity is satisfied. In addition, because the survivor functions (equivalently, cumulative distribution functions) are ordered as P(Y > 0|X = 0) = 0.7 ≤ 0.9 = P(Y > 0|X = 1), P(Y > 1|X = 0) = 0.2 ≤ 0.4 = P(Y > 1|X = 1), and P(Y > 2|X = 0) = 1 ≤ 1 = P(Y > 2|X = 1), distributional monotonicity is satisfied.

Suppose now instead that the probability distribution of Y conditional on X = 0 were P(Y = 0|X = 0) = 0.3, P(Y = 1|X = 0) = 0.2, and P(Y = 2|X = 0) = 0.5, so that the mean of Y conditional on X = 0 is E(Y|X = 0) = 1.2. The cumulative distribution function for Y conditional on X = 0 would then be given by P(Y ≤ 0|X = 0) = 0.3, P(Y ≤ 1|X = 0) = 0.5, and P(Y ≤ 2|X = 0) = 1, and the survivor function conditional on X = 0 would then be P(Y > 0|X = 0) = 0.7, P(Y > 1|X = 0) = 0.5, and P(Y > 2|X = 0) = 0. Average monotonicity would still be satisfied, since E(Y|X = 0) = 1.2 ≤ 1.3 = E(Y|X = 1), but distributional monotonicity would be lost, because P(Y > 1|X = 0) = 0.5 > 0.4 = P(Y > 1|X = 1).

APPENDIX 2. Causal Diagrams Representing the Measurement Errors Themselves or the Factors Responsible for Them

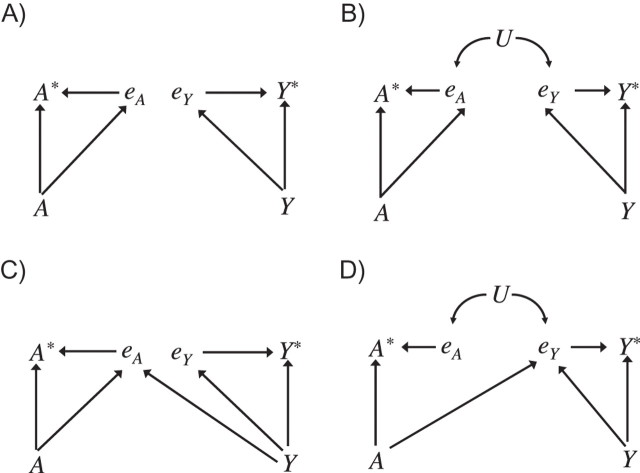
The causal diagrams for measurement error in Figure 1 (see text) could be expanded to also represent the measurement error terms themselves or the factors responsible for measurement error. For example, in Appendix Figure 1, we have expanded Figure 1 to also represent the measurement error terms e_A and e_Y, defined by e_A = A^* − A and e_Y = Y^* − Y. Note that in the diagrams in Appendix Figure 1, as is also implicitly the case in Figure 1, the measurement errors, e_A and e_Y, may be affected by the true values of A and Y, respectively, so that the true variables are correlated with the error term for the measured variables. This would generally be the case whenever dealing with binary exposures and outcomes. The DAGs in Figure 1 also allow for the measurement errors to be affected by the true variables, but the measurement error terms themselves are simply not explicitly represented on the diagrams. On DAGs, we can collapse the diagram over variables that are not common causes; parts A–D of Figure 1 represent the same structures as parts A–D of Appendix Figure 1, but collapsed over the measurement error terms e_A and e_Y. When using signed DAGs to reason about measurement error, it is convenient to collapse over the measurement error variables so that we do not need to specify the sign of all arrows, just the net sign. For example, in Figure 1C, we would only need to specify the sign of the Y → A^* arrow rather than that of both the Y → e_A and e_A → A^* arrows as in Appendix Figure 1C. We note that the diagrams in Figure 1 and Appendix Figure 1 are somewhat different from those in the paper by Hernán and Cole (18). Hernán and Cole do not represent on their diagrams the measurement errors themselves, e_A = A^* − A and e_Y = Y^* − Y, but rather the factors other than A and Y that are responsible for measurement error. In Appendix Figure 1, we might conceive of the measurement error terms e_A and e_Y as being affected by A and Y, respectively, as well as by other factors, such as U_A and U_Y. Hernán and Cole (18) represent on their diagrams the measured variables A^* and Y^*, along with the factors responsible for measurement error, U_A and U_Y, other than the true values of the variables A and Y. These diagrams are given in Appendix Figure 2. Again these represent the same structures as on Figure 1, but they explicitly represent the factors responsible for measurement error other than A and Y, though not the measurement errors themselves.

Appendix Figure 1.

Diagrams representing measurement error terms themselves. A) Independent nondifferential measurement error; B) dependent nondifferential measurement error; C) independent differential measurement error; D) dependent differential measurement error. A represents true exposure; A^*, measured exposure; Y, the true outcome; Y^*, the measured outcome; e_A and e_Y, measurement errors for A and Y, respectively; and U, a variable leading to correlated errors.

Appendix Figure 2.

Diagrams representing factors responsible for measurement error other than the true variables, as in the paper by Hernán and Cole (18). A represents true exposure; A^*, measured exposure; Y, the true outcome; Y^*, the measured outcome; U_A, and U_Y, factors responsible for measurement errors other than the true exposure and outcome, respectively; and U, a variable leading to correlated errors.