Subject-Specific Models of Susceptibility-Induced B₀ Field Variations in Breast MRI

Abstract

PURPOSE

To rapidly calculate and validate subject-specific field maps based on the 3D shape of the bilateral breast volume.

MATERIALS AND METHODS

Ten healthy female volunteers were scanned at 3T using a multi-echo sequence that provides water, fat, in-phase, out-of-phase and field map images. A shape-specific binary mask was automatically generated to calculate a computed field map using a dipole field model. The measured and computed field maps were compared by visualizing the spatial distribution of the difference field map, the mean absolute error, and the 80% distribution widths of frequency histograms.

RESULTS

The ten computed field maps had a mean absolute error of 38 Hz (0.29 ppm) compared to the measured field maps. The average 80% distribution widths for the histograms of all of the computed, measured and difference field maps are 205 Hz, 233 Hz, and 120 Hz, respectively.

CONCLUSION

The computed field maps had substantial overall agreement with the measured field maps, indicating that breast MRI field maps can be computed based on the air-tissue interfaces. These estimates may provide a predictive model for field variations and thus have the potential to improve applications in breast MRI.

INTRODUCTION

Magnetic resonance imaging (MRI) is an important tool for detecting and staging breast cancer, so attaining accurate images is highly desirable (1–3). Certain limitations of breast MRI originate from the magnetic field inhomogeneities within and around the breast (4). These magnetic field inhomogeneities can generate artifacts such as blurring, signal loss, distortion or unreliable fat suppression. Such artifacts may limit the use of certain pulse sequences which are sensitive to magnetic field inhomogeneities, such as fat suppression sequences, echo planar imaging (EPI), diffusion-weighted EPI (DWI), balanced steady-state free precession (bSSFP), and spiral imaging (5–8). Typically, field maps are not obtained in breast MRI, shimming is challenging, and the water/fat content of the breast makes field mapping difficult. Rapidly obtaining an accurate field map for a specific patient could predict these individually unique magnetic field inhomogeneities and could be used to calculate optimal shims for breast MRI or to guide Dixon-based imaging methods as an initial estimate in reconstruction.

Magnetic field inhomogeneities are caused by the irregular shape of the breast and the air-tissue boundaries. These boundaries between the breast and the outside air or the lungs have been shown to contribute to magnetic field perturbations within the breast tissue (9–12). The susceptibility difference at air-tissue boundaries induces field inhomogeneities, which increase with increasing magnetic field strength, and therefore may introduce more challenges when imaging at 3T and higher field strengths. The geometry of the breast may contribute to artifacts, particularly in the area where the breast connects to the chest wall at the inferior base and superior pole of the breast. Furthermore, it is difficult to optimize field uniformity across subjects because of different body fat compositions, possible breast mastectomies or implants, compression from the coil, or other physical distortions. Imperfect shimming has clinical implications, sometimes requiring repeat patient scans in order to achieve diagnostic image quality. Accurately shimming to obtain a uniform B₀ magnetic field in the breast can be difficult. This technique has been applied previously in the brain, and not yet in the breast (13). A number of methods have been developed that calculate the main B₀ static magnetic field map in the brain, such as a least squares approach, in addition to other methods (14,15). The breast presents different challenges for imaging, such as the curvature of the breast, the sharp edges where the breast meets the chest wall and respiratory motion.

The purpose of this study was to determine if the main B₀ magnetic field inhomogeneities could be accurately simulated, based only on a patient-specific bilateral breast shape in three-dimensional image datasets, and to validate this method (13). We estimated the B₀ magnetic field inhomogeneities within the breast at 3T using an efficient computational method, and removed any linear background variations. Subsequently, we compared these computed field maps with measured field maps that were acquired with the IDEAL method (13,16). Modeling the field maps may verify the source of magnetic field inhomogeneity and may help to correct the previously described artifacts in breast MRI (13).

MATERIALS AND METHODS

Initially, the shape of the subject and the corresponding unshimmed measured field map were acquired. Separately, the linear background field inhomogeneities were computed on two spherical phantoms in the breast coil just once, and then were subtracted from every subject’s unshimmed measured field map. The model-based field map was computed based on the shape of the object, and then compared with the measured field map by calculating the mean absolute error and the 80% distribution widths of the histograms of frequencies.

Data Acquisition

A single sequence, 3D iterative decomposition of water and fat with echo asymmetry and least squares acquisition (IDEAL), was used to obtain the in-phase, out-of-phase, water, fat, and field map images of the subject. IDEAL is a three-point chemical species separation method, similar to the Dixon method, that utilizes three images with a different relative phase between the water and fat signals, allowing water-fat separation (16). IDEAL was used because it has the ability to reliably measure the field map in the presence of both water and fat, since accurate field mapping in the presence of multiple spectral peaks requires separation of the species. We measured these reference-standard field maps from the same sequence, using multiple repetitions with echo times (TE) of 2.2 ms, 3.0 ms, and 3.8 ms.

Since MRI scanners have background magnetic field inhomogeneities in the main magnetic field, the MRI scanner applies linear shims automatically in order to compensate for these variations (4,13). Table 1 describes the sources of magnetic field inhomogeneity, showing that there are linear and higher order magnetic field variations due to the background magnetic field and the subject. The difference column demonstrates that the higher order background variations were not computed.

Table 1.

Sources of magnetic field inhomogeneity include linear and higher order terms of the background magnetic field and subject-specific induced variations.

Field Map Variations	Computed In Vivo	Measured In Vivo	Reference Ball Phantom	Difference
Linear Background Magnet Field		X	X
Higher Order Background Magnet Field		X	X	X
Linear + Higher Order Subject Specific	X	X
Residual Subject Specific	X	X

We scanned two spherical ball phantoms in order to compute the subject-independent background magnetic field inhomogeneity just once, as these variations are expected to remain consistent over time, as described in previous work (4). These variations can be computed on a spherical phantom by allowing the scanner to automatically prescan a sphere, which is expected to have a uniform magnetic field inside. These compensating shims were then modeled in MATLAB (MathWorks, Natick, MA, USA) and subtracted from every unshimmed measured field map so that the field variation would be solely due to the subject, instead of adding scanner-specific variations to the theoretical field map (13).

An eight-channel receive-only GE breast coil was used on a 3T GE Excite whole body scanner (General Electric Medical Systems, Waukesha, WI, USA). In vivo bilateral breast imaging was conducted with sagittal or axial scan planes and a large FOV specific for each volunteer, typically 32×32 cm. No breath-holding was applied. The 3D IDEAL acquisition had a flip angle of 12° and a bandwidth of 62.5 kHz. The multi-echo images were acquired using a spoiled gradient recalled echo (SPGR) sequence over 60 – 86 slices of thickness 3.5 – 6 mm with usually a 192×192 matrix, and a TR of 4.8 ms, for a typical scan time of 5 minutes.

Field Map Calculation

The field map was modeled in MATLAB based on magnetic susceptibility using the equation,

$$\mathrm{\Delta }{B}_0(r)=B_0{\mathcal{F}}^{-1}\left\{\left[\frac{1}{3}-\frac{k_z^2}{k_x^2+k_y^2+k_z^2}\right]\mathcal{F}\{\chi (r)\}\right\}$$ (1)

where ΔB₀ (r) is the distribution of the magnetic field perturbation, B₀ is the static magnetic field strength, k_x, k_y and k_z compose the 3D Fourier space coordinate system, χ(r) is the three-dimensional relative magnetic susceptibility difference, and 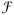represents the three-dimensional Fourier transform (13,17–19). This model can be intuitively understood as a convolution of the magnetic susceptibility distribution with a dipole pattern, and the fast Fourier transform (FFT) convolution is an efficient way to compute the convolution.

For each dataset, the in-phase images were used to obtain the shape of the breasts by first filtering out noise using a 3x3 median filter. Second, the in-phase images were thresholded to create a binary mask of tissue where any voxel with a value initially greater than the mean value in the image is assigned a value of 1, and any voxel with a value initially less than the mean has a value of 0 in the binary tissue mask. The median noise thresholding for all coils was based on the same principle: the threshold value was chosen based on a mean value from the entire image. The boundaries of the breast tissue were modeled with respect to the outside air or lung wall, based on the signal-to-noise ratio (SNR) of the in-phase image. This mask creation process was fully automated, and the images were acquired with a large field-of-view (FOV) to avoid any unnatural edges near the breast, since air-tissue boundaries significantly affect the model.

Air has a magnetic susceptibility value of 0.36 ppm, and water at 37°C has a magnetic susceptibility value of −9.05 ppm, so this large difference in values will result in significant inhomogeneities. We use these values for our computational model of breast tissue (4). The binary mask was then multiplied by −9.41*10⁻⁶, the theoretical relative susceptibility difference between tissue and air. Before the mask was input into the Fourier computation, the image FOV dimensions were zero-padded by a factor of 2 to allow the field perturbations induced by the breast to decay sufficiently at the edges of the computational field (13).

After the computation, the FOV was cropped back to the original image size, and restricted comparative analysis to the breast tissue. The restricted region was eroded by removing two pixels around the entire perimeter in order to avoid discretization effects at boundary. An experimentally determined global B₀ frequency offset was calculated by measuring the mean value of the frequencies in each field map, and then subtracting the mean from the computed field map in order to correct for any variations in the center frequency (13). The center frequency was derived from the measured field map, and the global offset subtraction could account for any field drift. Given a reference image, the simulation time was approximately 30 seconds.

Phantom Validation

We first calculated a computed and measured field map on a single 16cm agar Quality Assurance spherical phantom in a single channel GE head coil. We then compared the difference field map, as well as the absolute error between the two, and the 80% distribution widths of the histograms of the measured, computed, and difference field maps.

The method was validated using a cylindrical water phantom with large susceptibility effects. This phantom has a diameter of 12 cm and a height of 14 cm, with an vial of air (diameter of 3 cm) placed inside a cylinder of water, and scanned in a single channel GE head coil as shown inside Fig. 1. We then measured the absolute error between the computed and measured field map, as well as the 80% distribution widths of the histograms of the measured and computed field maps.

Figure 1.

This phantom with large susceptibility variations demonstrates the dipole shaped inhomogeneity and the accuracy of the model. a: Coronal IDEAL-SPGR MRI in-phase image. b: Binary mask showing water (white) and air (black). c: Computed field map. d: Measured field map. e: Difference map between measured and computed field maps. f: Histogram of ΔB₀ values within the tissue of the measured, computed and difference field maps. g: Horizontal (x) field map traces and vertical (y) field map traces showing substantial agreement between the computed and measured field maps. The absolute error between the computed and measured field map is 16 Hz. The 80% distribution widths of the histograms of the computed, measured, and difference field map histograms inside the mask are 230 Hz, 222 Hz, and 52 Hz, respectively.

Subjects

Ten healthy female volunteers were scanned at 3T to obtain the subject-specific shape of the bilateral breast shape and the corresponding field map. IRB approval and informed consent were obtained after the procedure had been fully explained, and the studies were conducted in accordance with the human ethics committee.

Data Analysis

We used the measured field map from IDEAL to assess the accuracy of the computed field maps by subtracting the two to look at the difference field map. We manually segmented an ROI around the breast tissue so that the breast tissue was separated from sternum bone and lung (18). We compared the field maps qualitatively by noting the visual agreement of the line traces and examining the field maps. The 80% distribution widths of the histograms of the computed, measured, and difference field maps were calculated, and then compared side-by-side for each dataset. The mean absolute error was calculated between the two field maps on a pixel-by-pixel basis by finding the average absolute value of the difference field map. We analyzed the entire dataset from the multiple volunteers by averaging the mean absolute errors and the 80% distribution widths of the histograms of the measured, computed and difference field maps.

RESULTS

Phantom Results

When the scanner automatically applies linear shims to correct for the background inhomogeneity on a 16 cm spherical phantom, the 80% distribution width of the histogram of the values inside the spherical ball phantom measured field map is 18 Hz, demonstrating background magnet field inhomogeneities that the scanner cannot correct with shimming. The 80% distribution width of the computed spherical ball phantom was lower, only 9 Hz. The average absolute error between the computed and measured field map is 7 Hz.

For the air-vial phantom shown in Fig. 1, the absolute error between the computed and measured field map is 16 Hz. The 80% distribution widths of the histograms of the computed, measured, and difference field map histograms inside this mask are 230 Hz, 222 Hz, and 52 Hz, respectively.

In Vivo Results

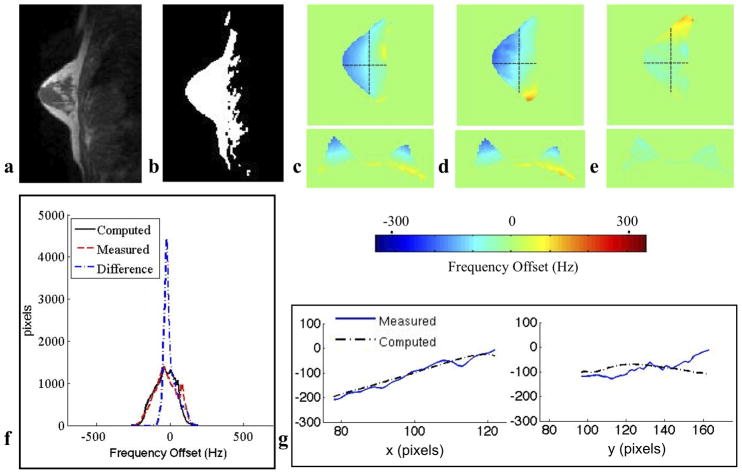
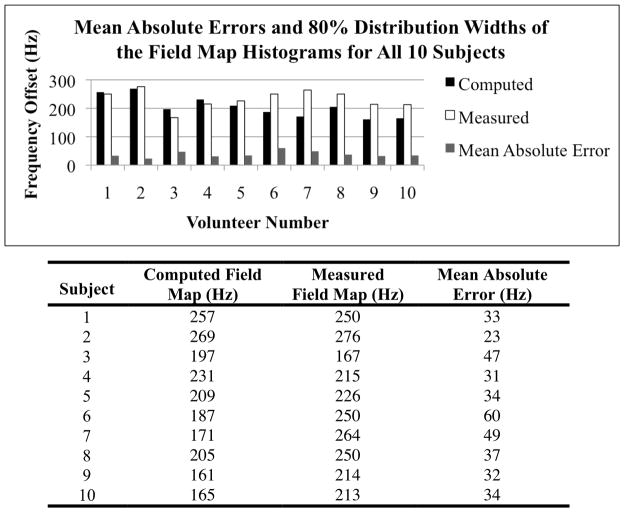
Line traces were drawn along the modeled and measured field maps to demonstrate the visual agreement between the two field traces. Within the tissue, the ten computed field maps closely modeled the inhomogeneities of the ten measured field maps. For all ten subjects, the average absolute error was 38 Hz (0.29ppm). The average 80% distribution widths of the histograms of the computed, measured, and difference field maps for the ten subjects were 205 Hz, 233 Hz, and 120 Hz, respectively. An example of an average in vivo case is shown in Fig. 2 by visualizing a sagittal image of an individual breast. In this individual case, the mean absolute error is 33 Hz, and the 80% distribution widths of the histograms of the computed, measured and difference field maps are 257 Hz, 250 Hz and 113 Hz. The 80% distribution widths of the histograms for the measured and difference field maps for all ten subjects are shown in Fig. 3.

Figure 2.

This in vivo bilateral breast study demonstrates an example of the magnetic field inhomogeneities in vivo and the accuracy of the model. a: Sagittal IDEAL-SPGR MRI in-phase image b: Susceptibility tissue mask showing breast tissue (white) and air (black) c: Computed field map d: Measured field map e: Difference map between measured and computed field maps. f: Histogram of ΔB₀ values within the tissue of the measured, computed and difference field maps. g: Horizontal (x) field map traces vertical (y) field map traces showing substantial agreement between the computed and measured field maps. For this case, the absolute error is 33 Hz, and the 80% distribution widths of the histograms of the computed, measured and difference field maps are 257 Hz, 250 Hz and 113 Hz.

Figure 3.

Mean absolute errors and the 80% distribution widths of the field map histograms for all ten in vivo subjects. For all ten subjects, the average absolute error was 38 Hz. The average 80% distribution widths of the histograms of the computed and measured field maps for the ten subjects were 205 Hz and 233 Hz, respectively.

DISCUSSION

The phantom and in vivo studies show substantial visual agreement and quantitative agreement based on the average 80% distribution width of the values of the histograms and the average absolute error. The mean absolute errors for each subject are reasonable given the 80% distribution widths. Since the IDEAL field maps are insensitive to B₁ inhomogeneities and the field variations are still present in the maps, these field variations are not due to the B₁ field. The maximally allowed deviation for a computed field map from the measured field map depends on the application, whether improving fat saturation methods or using the field map to correct during image reconstruction.

We found that the main differences between the measured and computed field maps were along the edges of the air-tissue boundaries due to discretization effects, and within the chest wall adjacent to the lungs, as expected by the proximity to the air-tissue boundary of the lungs and chest. The remaining sources of error may include partial volume artifacts, any aliasing artifacts, the exclusion of the boundary of the posterior lungs, higher order background variations, patient movement, and respiration. The computed frequency variations may vary depending on the individual geometry of the patient. The majority of the remaining measured frequency variations may be due to individual respiration effects, making each case unique in whether the computed or measured field map has a larger range of field variations. Although the same scanning sequence was used for the measurement and anatomical mask, this method is preferred for our study because it provides the closest validation. In the future, other datasets could be used as the input.

We assumed the entire breast tissue, including both glandular and adipose tissue, had a magnetic susceptibility value equal to that of water at body temperature, as the chemical fat shift caused by the adipose tissue is a shielding mechanism, not a susceptibility shift. The body induces field perturbations that may not have decayed sufficiently at the edge of the original computational volume; therefore, the edges of the volume are expected to have errors (13). This effect was accounted for by zero-padding the mask matrix by a factor of 2 before undergoing the computation, since a previous study demonstrated that this method had minimal absolute errors (13).

The higher order B₀ inhomogeneities that are intrinsic to the background magnetic field specific scanner are a source of error in our method. There are several dominant components that affect the magnetic field homogeneity: the intrinsic B₀ main field linear and higher order inhomogeneities, and the linear and higher order susceptibility-induced inhomogeneities due to the subject (4,13). When the scanner automatically applies linear shims to correct for the background inhomogeneity on a sphere, the 80% distribution width of the histogram of the values inside the spherical ball phantom measured field map should theoretically be zero for an applied perfectly uniform field. However, the results indicated an 80% distribution width of 18 Hz of the shimmed spherical phantom, showing the non-linear B₀ magnetic field inhomogeneities that the scanner cannot correct, and the lowest bound of error that we can reasonably expect. The physical spherical phantom has small imperfections and bubbles that are not captured in the mask, and therefore cannot be modeled. Only linear shim values were considered in this experiment; higher order shims were not modeled since breast field maps are primarily linear (18).

The remaining variations in the breast are likely due to respiration effects, which are typically around 0.1 ppm, 10 times greater than those in the brain, and the average cardiac motion accounts for less than 0.03 ppm variation in the breast (9,10). These variations are associated with the respiratory motion of the tissues in the chest and abdomen, and not the actual movement of the breast itself (9,10). There are several approaches to correct for respiration induced frequency variations, such as real-time B₀ shimming, respiratory triggering or breath-hold acquisitions. These techniques require longer scan time and can be error-prone (11). The respiratory and motion errors could limit the applications of this method to areas that are not significantly affected by respiratory motion, including the actual breast tissue, and excluding the chest wall and back.

This technique could be especially useful for several applications. Patient movement can be problematic because it may change the B₀ distribution, especially if the air-tissue interface is re-positioned, and then the initial shim setting quality may be reduced and may generate more susceptibility artifacts (13,20). Re-scanning the patient to obtain another field map may take too long for a clinical scan, and so the simulated field maps may prove helpful for their rapid field map estimation. This technique would also be useful for patients with silicone implants, as silicone causes large B₀ inhomogeneities due to its magnetic susceptibility value which is 4.5 ppm upfield of water (21). Since frequency-selective suppression pulses are more susceptible to failure in the presence of B₀ inhomogeneities, a water-silicone separated imaging technique would be beneficial, as recently developed (21). Metal clips in the breast would also affect the field map and cause large susceptibility artifacts, although it may be difficult to know the exact shape of the clip in vivo, prior to simulation. Previous work has modeled metallic implants using this method (22).

In conclusion, we investigated the method of computing a breast B₀ field map based on a subject-specific mask of the in-phase images. We found that the ten in vivo breast subjects show substantial visual agreement as well as quantitative agreement due to the results in the average 80% distribution widths of the histograms and the average absolute error. This rapid geometry-based field map estimation could be used to quickly provide initial estimates of field variations for automated shimming routines, and other field-mapping measurement techniques, potentially improving their ability to rapidly converge on the most accurate estimates of the B₀ field in the breasts. This rapid simulation can estimate B₀ inhomogeneities and could be used in clinical protocols in the future.