Comparison of breast tissue measurements using magnetic resonance imaging, digital mammography and a mathematical algorithm

Abstract

Women with mostly mammographically dense fibroglandular tissue (breast density, BD) have a 4- to 6-fold increased risk for breast cancer compared to women with little BD. BD is most frequently estimated from 2-dimensional (2-D) views of mammograms by a histogram segmentation approach (HSM) and more recently by a mathematical algorithm consisting of mammographic imaging parameters (MATH). Two non-invasive clinical magnetic resonance imaging (MRI) protocols: 3-D gradient-echo (3DGRE) and short tau inversion recovery (STIR) were modified for 3-D volumetric reconstruction of the breast for measuring fatty and fibroglandular tissue volumes by a Gaussian-distribution curve-fitting algorithm. Replicate breast exams (N= 2 to 7 replicates in 6 women) by 3DGRE and STIR were highly reproducible for all tissue-volume estimates (coefficients of variation <5%). Reliability studies compared measurements from four methods, 3DGRE, STIR, HSM, and MATH (N=95 women) by linear regression and intra-class correlation (ICC) analyses. Rsqr, regression slopes, and ICC, respectively, were (I) 0.76–0.86, 0.8–1.1, and 0.87–0.92 for %-gland tissue, (II) 0.72–0.82, 0.64–0.96, and 0.77–0.91, for glandular volume, (III) 0.87–0.98, 0.94–1.07, and 0.89–0.99, for fat volume, and (IV) 0.89–0.98, 0.94–1.00, and 0.89–0.98, for total breast volume. For all values estimated, the correlation was stronger for comparisons between the two MRI than between each MRI vs. mammography, and between each MRI vs. MATH data than between each MRI vs. HSM data. All ICC values were >0.75 indicating that all four methods were reliable for measuring BD and that the mathematical algorithm and the two complimentary non-invasive MRI protocols could objectively and reliably estimate different types of breast tissues.

Introduction

In 2011, an estimated 230,480 new cases of invasive breast cancer and 57,650 new cases of in situ breast cancer will be diagnosed among women in the United States (ACS, 2011). Over 39,520 are expected to die from the disease, making breast cancer the second leading cause of death among women. In the mid-1970’s, landmark research by Wolfe (Wolfe, 1976a, Wolfe, 1976b) demonstrated an association between mammographic parenchymal patterns and breast cancer risk. Many studies using different methods (Boyd et al., 1995, Boyd et al., 2005, Byrne et al., 1995, Byrne et al., 2001) for quantifying breast density have since confirmed Wolfe’s original observation that mammographic (breast) density is a strong risk factor for breast cancer. A recent meta-analysis of published studies (McCormack and dos Santos Silva, 2006) confirmed the prior observations that women with extremely dense breast tissue have a 4- to 6-fold excess risk of developing breast cancer compared to women with predominantly fatty tissue in their breasts. Therefore, breast density has been postulated to be a useful intermediate surrogate marker for preventive or therapeutic interventions.

Historically, the assessment of breast density has been performed using conventional x-ray mammography with either a screen-film detector (screen-film mammography) or, more recently, a digital detector [full-field digital mammography, (FFDM)]. Qualitative, categorical assessment of breast density includes the four categories (N1, P1, P2, and DY) of Wolfe’s method (Wolfe, 1976a, Wolfe, 1976b) with N1 being a breast that is primarily adipose tissue with little glandular tissue; P1 being a breast of mostly adipose tissue with dense glandular tissue under nipples; P2 being a breast with prominent ducts occupying at least ¼ of the breast; and DY being a breast containing mostly dense glandular tissue. Another classification is the five categories (I to V) of Tabar’s method (Gram et al., 2005). More recently the BIRADS (Breast Imaging Reporting and Data System) has been used for breast cancer risk estimates (ACR, 2003), and methods that are more quantitative for estimating breast density have been developed. Byng et al (Byng et al., 1996) developed a semi-automatic interactive thresholding method to segment glandular tissue from fatty tissue using the pixel intensity histogram of a mammogram (histogram segmentation method, HSM). The HSM has been the most widely used approach for estimating breast cancer risk in epidemiologic research. Other methods, such as automatic segmentation based on Kittler’s optimal threshold procedure by Sivaramakrishna et al., (Sivaramakrishna et al., 2001) and a multivariate regression model-derived mathematical equation (MATH) using data recorded in imaging parameters of the FFDM’s DICOM report header by Lu et al. (Lu et al., 2007) have not been tested for risk estimation. The general consensus is that breast cancer risk increases with increasing breast density (Boyd et al., 2007, McCormack and dos Santos Silva, 2006).

However, debates continue regarding the accuracy of breast density measured on mammograms and, in particular, its sensitivity for assessing intervention efficacy. The strength of mammographic breast-density measurement for breast cancer research and risk prediction is the low cost and the wide-spread use of mammograms. The weaknesses include, but are not limited to, a variable compression thickness and a variable projection of the breast in order to convert 3-D breast tissue into a 2-D image. Because the purpose of mammography is to detect breast cancer and not to measure breast density, the radiation dose, duration of exposure, and several other instrument settings of the mammographic instrument are routinely varied according to the density of the breast of the woman being imaged. This is done in order to obtain a mammogram with sharp contrast for detecting breast cancer embedded in the glandular tissue. These necessary variations in instrument settings during mammogram acquisition, based upon the breast density of the woman, while desirable and essential for breast cancer detection, seriously confound and compromise breast density assessment as shown by Lu et al (Lu et al., 2007) and critiqued by Kopans (Kopans, 2008). We are not aware of any epidemiologic studies of breast cancer risk estimates or risk predictors using mammograms that have controlled for the inherent variations of instrument-imaging parameters. Thus, mammography may not be sensitive enough to detect small changes in breast density resulting from interventions, and potential radiation risks prevent mammograms from being used in vulnerable young population. The above points have long been recognized as problems for the field of breast imaging and the use of mammographic density as a surrogate biomarker for breast cancer risk. Breast magnetic resonance imaging (MRI) has been suggested to be an attractive alternative for the measurement of breast density, as discussed below.

MRI increasingly is becoming a recommended imaging modality for the detection and diagnosis of breast cancer (Orel and Schnall, 2001, Berg et al., 2004, Warner et al., 2004, Kriege et al., 2004, Wright et al., 2005, Lehman et al., 2005, Kuhl, 2007). In fact, the American Cancer Society has recently updated their guidelines for breast screening with MRI as an adjunct to mammography for screening in high-risk populations (Saslow et al., 2007). MRI has the potential to quantify fibroglandular tissue with a much higher degree of accuracy and precision than x-ray mammography for the following reasons. First and foremost, MRI provides a 3-D image of the breast without compression. In contrast, the 2-D projection imaging modality of x-ray mammography suffers the problem of overlapping anatomy and the inability to see structures in 3-D. Second, MRI can be easily optimized to improve the differences in contrast (i.e., MRI signal intensity) between the fibroglandular and adipose tissue. Rather than relying on differences in x-ray attenuation, MRI sequences can be tuned to be sensitive to differences in tissue T1 relaxation rates (T1), consequently producing excellent tissue discrimination (Merchant et al., 1993, Graham et al., 1996, Boston et al., 2005). Oftentimes, tuning an MRI sequence is as simple as changing the image acquisition parameters, such as the echo time (TE) and/or the repetition time (TR). On the other hand, signal intensity variations in x-ray mammography are a direct result of variations in x-ray attenuation that correlates with the amount of fibroglandular tissue in a breast. Because of radiation dose and other image-acquisition limitations, it is much more difficult to optimize a mammography system to maximize the image contrast between fibroglandular and adipose tissue. This results in necessary variation in mammography instrument settings specific to a woman’s breast density. The setting variation is a serious confounder in epidemiologic breast density studies. Unlike mammography, MRI criteria for breast imaging can be applied independent of a woman’s breast density. Third, in mammography it is more difficult to ensure that the entire breast under compression is in the image, particularly areas near the chest wall. MRI, on the other hand, can visualize the entire breast without the discomfort of marked compression and without excluding breast tissue near the chest wall. Finally, a clinically important argument in favor of MRI is that MRI does not expose the patient to ionizing radiation. MRI eliminates the likelihood of secondary (radiation-induced) carcinogenesis and allows for earlier screening of vulnerable populations such as pre-pubertal girls and women less than 30 years old.

Efforts, therefore, have been made by several research groups to use MRI of the breast for estimation of the content of fibroglandular tissue, as summarized in Table 1 (Poon et al., 1992, Graham et al., 1996, Lee et al., 1997, Klifa et al., 2004, Klifa et al., 2010, Wei et al., 2004, Boston et al., 2005, Khazen et al., 2008, Thompson et al., 2009, Eng-Wong et al., 2008, Ertas et al., 2009, Nie et al., 2008, Nie et al., 2010b, Nie et al., 2010a). Table 1 shows that T1-weighted MRI is the most widely used protocol. There are three basic conceptual approaches for estimating glandular tissue volume. These are graphical user interactive threshold-based segmentation of glandular tissue from fat tissues, the use of a clustering algorithm, or by a logistic function approach. Some studies have tested the reliability of MRI protocols against results obtained from mammograms. However, large scale application of these methods to epidemiologic studies for estimating breast cancer risk is still limited, due partly to the cost of MRI and the amount of time needed to do the quantification. In this report, we describe a unique method in which breast MRI may be used to accurately, reproducibly, and objectively estimate fibroglandular tissue volume and %-glandular tissue (%-G). In this study, we also validated a unique approach for computing %-G from a mathematical algorithm (MATH) that was developed from a multivariate regression model equation that contains all mammogram imaging parameters that are significant and strong predictors for %-G.

Table 1.

Review of literature reporting breast tissue composition analyses using breast magnetic resonance imaging (MRI).

Studies	MRI Protocol	Method for Gland Measurement from MR Images	Validation with Mammographic Density	General Comments
(Poon et al., 1992)	T1 by Look-Locker technique; T2 by multiple echo sequences; and relative water content by a pair of fat- and water- suppressed images	Relative water content of whole breast; T1 and T2 relaxation time for middle slice of breast only; and fourth moment of T2 pixel histogram	Yes, with 4 categories of Wolfe's classification (n=23 women)	Mean relative water to fat content, mean T1 relaxation time, and fourth moment of T2 relaxation time can distinguish DY and N1 patterns of Wolfe, but not mean T2 relaxation time; not used in epidemiologic studies.
(Graham et al., 1996)	MR spectrum by hybrid Dixon method, conventional frequency encoding to obtain 1D image of fat and water; T2 decay from breast volume of interest only by a CPMG sequence of hard pulse	Relative water and fat content estimated from MR spectrum peak area, and first moment of continuous distribution of T2 decay curve by a software	Yes, r>0.60 with semi-automatic interactive thresholding segmentation in n=42 mammograms	Water to fat content associated with sociodemographic risk factors for breast cancer, mean T2 decay associated only with family hitory of breast cancer and BMI.
(Lee et al., 1997)	T1 weighted spoiled gradient echo fast low-angle shot sequence	Manual segmentation of each slice; semi- automatic, assuming a two compartment model by solving two equations (mean MR intensity of the breast × total breast volume = fat volume × fat MR intensity + gland volume × gland MR intensity; and total breast volume=fat volume + gland volume)	Yes, r=0.63 with visual scoring in steps of 5% from 5%–95% in n=40 women	%-Glandular tissue associated with age change
(Klifa et al., 2004) (Klifa et al., 2010)	3D fat suppressed spoiled gradient echo pulse sequences, non-contrast imaging	Semi-automatic identification of breast ROI (Bezier splines and Lapalacian of Gaussian Filter); quantification of gland tissue by unsupervised fuzzy c-means clustering, manual delineation, and/or segmentation of signal intensity histogram by interactive thresholding algorithm.	Yes, r>0.75 with visual 4 categorical scoring (n=30), semi-automatic thresholding segmentation (n=10) and manual delineation of dense area and automatic pixel counting (n=35) of film- screen mammograms	Good reproducibility on replicate images; not validated for studying breast cancer risk factors
(Wei et al., 2004)	Coronal 3D SPGR (spoiled gradient recalled echo) pre- contrast T1-weighted	Semi-automatic isolation of breast ROI, interactive thresholding segmentation of gland from fat in MR images slice-by-slice	Yes, r=0.91 using an in-house software Mammogram Density ESTmator based on interactive thresholding segmentation and with visual scoring by radiologist	Not used for studying risk factors of breast cancer
(Boston et al., 2005)	3D spoiled gradient echo inversion recovery sequence for T1 map construction	Segmentation of T1 histogram into gland and fat using a logistic function that described the probability of a voxel containing glandular tissue to be a function of T1 of the voxel, mean T1 times of fat and gland peaks, respectively, and maximum slope of the logistic curve.	No, concpetual approach developed with phantom and tested in human cases	Empirical logistic model allowed for accurate segmentation of fat and parenchyma in breast phantoms
(Khazen et al., 2008) (Thompson et al., 2009)	Pre-contrast T1 weighted MR	Interactive thresholding segmentation, corrected for non-uniformity using proton density map (MRIBview software)	Yes, r>0.75, visual scoring using 21 point-scale and segmentation by an interactive thresholding algorithm using Cumulus software (n=138 in 2008 study and n=513 in 2009 MARIB study with matched MRI and film-screen mammogram)	Mammograms overestimate breast density, protocol time consuming (n=138), applied to MARIBS study (n=513) that validated the association of breast density with several known risk factors for breast cancer (in 2009 study)
(Eng-Wong et al., 2008)	T1-weighted spoiled gradient- echo with fat suppression per protocol by Yao et al., 2005	User interface software to automatically segment breast region of interest from the rest of body organs, fuzzy c-means based on pixel distance to edge and pixel MR signal intensity to classify tissues into three types, gland, fat and skin (Yao et al., 2005)	Yes, r>0.7 by a semi-automatic interactive thresholding segmentation of pixel intensity histogram of film-screen mammograms (n=20 women)	Raloxifene treatment for 1–2 yrs did not affect mammographic density (n=20), but decreased glandular tissue volume measured by MRI in 27 women (not a randomized trial)
(Ertas et al., 2009)	Proton density weighted and pre- and post-contrast T1 weighted images acquired using 3D spoiled gradient echo pulase sequences, a modification of Khazan et al 2008	Segmentation by Interactive thresholding based on signal intensity uniformity corrected pre- contrast T1 weighted image using a software MRIBView; automated fuzzy c-means clustering based on dual phase T1 estimate histograms, i.e., mean T1 estimate of pre-contrast histogram and the post-initial enhancement changes (n=20)	No	Compostions of breast tissue correlated well between results from interactive thresholding histogram segmentation method and two points fuzzy c-means clustering algorithm on pre-contrast signal intensity histogram and post-initial enhancement changes; not validated for breast cancer risk factors in epidemiologic studies
(Nie et al., 2008) (Nie et al., 2010a) (Nie et al., 2010b)	Non-fat saturated T1-weighted, fast 3D SPGR pulse sequence	Semi-automatic isolation of breast ROI (n=11) and skin removal (n=50), fuzzy c-mean classification to exclude air/lung, B-spline curve- fitting to exclude chest wall muscle; adaptive FCM to isolate dense tissue	No	In 2010 study (n=321), age and race were found to be strong predictors of gland tissue content.

Materials and Methods

Study Design

Samples for this method-development study were from women who enrolled in past clinical trials and clinical research projects at the University of Texas Medical Branch (UTMB). The baseline screening mammograms and breast MR images for this study were obtained from subjects enrolled between 2002 and 2004. Digital mammograms and breast MR images were acquired less than two months apart from a total of 98 pre-menopausal and 3 post-menopausal women, none of whom had apparent mammographic abnormalities. These subjects had varying mammographic density during baseline observation periods. Because mammographic density is known to vary with the menstrual cycle, all premenopausal women were imaged during the luteal phase of their cycles. Digital mammograms were acquired using a GE Senographe 2000D FFDM unit (General Electric Healthcare Institute, Waukesha, WI). Breast MRI was performed using a GE Signa LX 1.5-Tesla MRI system (GE Healthcare Institute, Waukesha, WI). All imaging protocols and examinations were approved by the Institutional Review Board of UTMB and by the Human Research Protection Office of the US Army Medical Research and Materiel Command. All image acquisitions, transfers, manipulation, and processing were compliant with HIPAA regulations. Written informed consent was obtained from each participant.

Full-field Digital Mammography (FFDM) Imaging Protocol

The digital mammography protocol consisted of two standard projections [cranio-caudal (CC) and medio-lateral-oblique (MLO) views for each breast]. Left CC views were quantified for total breast area (T_Area), fibroglandular area (G_Area), adipose area (F_Area), and %-G (=G_Area/ T_Area) using a modification of the histogram-segmentation method (HSM) of Byng et al (Byng et al., 1996) as described in detail by Lu et al., (Lu et al., 2007). Alternatively, %-G also was computed using a mathematical algorithm (MATH) (Lu et al., 2007) omitting the HSM step. The MATH algorithm is from a multivariate regression model equation containing all mammogram imaging parameters that are significant and strong predictors for %-G.

Breast Magnetic Resonance Imaging (MRI) Protocol

Several breast MRI protocols were evaluated for sufficient contrast differentiation between the fibroglandular and adipose tissues in the breast and for signal uniformity. When the project began in late 2002, two clinically-used pulse sequences for breast MRI, the 3-D T1-weighted gradient-echo (3DGRE) and the short tau inversion recovery pulse sequences (STIR) were selected and modified (Table 2). Because signal uniformity was absolutely essential for measuring breast density, a dedicated breast MRI coil was used only to support and position the breasts in the 3DGRE protocol, but signal was acquired only from the body coil to produce uniform images. The breast coil, however, was used in the STIR protocol to improve MR signal. These protocols were applied initially to a small group of 3 pre-menopausal and 3 post-menopausal women by conducting 2 to 7 MRI exams for each woman on separate occasions. Then later, these two MRI protocols were applied once to another group of 95 pre-menopausal women for a reproducibility and validity study.

Table 2.

Image acquisition parameters for the two breast MR imaging protocols.

Scan Parameter	3DGRE	STIR
Acquisition Type	3-D	2-D
Pulse Sequence	Gradient Echo	Inversion Recovery
Slice Thickness (mm)	1.5 (interpolated)	2.0
Interspace Gap (mm)	0	0 (interleaved ×3)
TR (ms)	5.9	6050
TE (ms)	1.4	12.9
Inversion Time (ms)	N/A	150
Receiver Bandwidth (kHz)	31.2	15.6
Signal Averages (NEX)	2	1
Echo Train Length	0	4
FOV (mm × mm)	320 × 320	320 × 320
Matrix Size	256×256 (Recon: 512×512)	256×192 (Recon:256×256)
Phase Encode Direction	ROW	ROW
Flip Angle (°)	10	90
Scan Time (min)	3.0	14.5

Each protocol was designed to ensure that the MRI phase encoding artifacts, caused mainly by cardiac motion, would not appear in the field of view (FOV) of the breast. Table 2 shows the relevant scan parameters for the two pulse sequences. The FOV of 320 mm and matrix size of 256 × 256 were applied most often, but adjustments were made for some women to accommodate different breast sizes. However, the reconstructed matrix size was 512 × 512 for 3DGRE and 256 × 256 for STIR. Slice thickness was kept constant, but the number of slices varied with breast size.

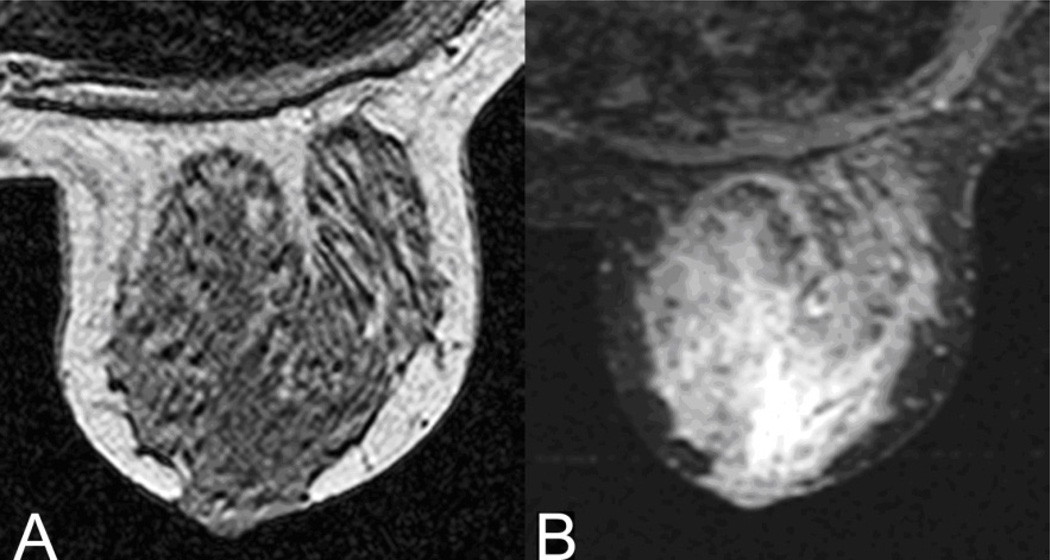
The 3DGRE, a standard gradient-echo pulse sequence routinely used for clinical imaging, was optimized for best contrast and uniformity of adipose and fibroglandular tissues (Table 2). Figure 1A illustrates a typical image generated by the 3DGRE and the image contrast between adipose and fibroglandular tissue. Adipose tissue appears brighter than the fibroglandular tissue, largely due to its greater hydrogen content relative to fibroglandular tissue. The difference in voxel brightness (signal intensity) was sufficient to permit tissue segmentation of fibroglandular tissue from fatty tissue and for computing the %-G. The time to complete the 3DGRE pulse sequence on each subject was about 3 min.

Figure 1.

Central axial slice of a volunteer’s left breast using A) 3DGRE and B) STIR MR pulse sequences. For pulse sequences, consult Table 2.

STIR, an inversion recovery MRI protocol used clinically for the suppression of signal from adipose tissue, was initially chosen for this study because it was the most suitable fat-suppression technique available in 2002. [The IDEAL protocol (Yu et al., 2006) for fat-suppression was not available when the enrollment of study subjects began in 2002.] With STIR (Table 2), the inversion time, TI = 150 ms, effectively neutralized the signal from adipose tissue, as shown in Figure 1B where adipose tissue is dark and fibroglandular tissue is bright. Other similar fat-suppression sequences have been successfully applied to clinical breast MRI scenarios and applications (Merchant et al., 1992, Holden et al., 1996, Niitsu et al., 2003).These were tested but were found to be unsatisfactory for reproducible signal uniformity. Because STIR was a 2-D image acquisition, it acquired 3 interleaved slices in order to provide adequate contrast and also signal uniformity for the entire breast. Thus, STIR was the longer of the two MRI protocols. It took approximately 15 min to complete. The total scan time for the entire breast MRI exam was about 20 min.

3-D Volume-rendered Model Generation from MR images

The breast MR images were transferred across a secure PACS network to a GE 3-D Advantage Windows Workstation (ADW), software version 4.1, for post-processing and 3-D volume-rendered model generation. The 3-D ADW is a dedicated system designed specifically for reconstructing image data collected from MRI. Using 3DGRE as an example, a graphical display of the steps taken to generate the 3-D breast model is shown in Figure 2.

Figure 2.

Steps taken to generate a 3-D volume-rendered breast model. 2A, Entire scan field of view consisting of both breasts and torso anatomy; 2B, A coarse segmentation to isolate the breast region of interest; 2C, More precise trimming to remove the chest wall and other non-breast tissue from each individual slice; 2D, Surrounding air image removed from the previous image; 2E, View of the breast slice image after subtracting air image in 2D from image in 2C. A final trimming is performed to complete the breast segmentation from the rest of the patient’s anatomy. 2F, the final 3-D view of the breast model completed for volume measurement analysis.

Anatomical data were acquired for the entire torso using a large anatomical FOV and the body coil for imaging (Fig. 2A). Figure 2A shows one of the transferred axial 2-D images of the breast. Contiguous axial slices through the breast region were obtained. There were ~112 slices for the 3DGRE pulse and ~60–90 slices for the STIR pulse, depending on the size of the breast. An initial coarse region of interest (ROI) was obtained by isolating the breast from the remaining torso (Fig. 2B). The ROI for 3DGRE showed that the fibroglandular tissue in the breast appeared dark compared to the brighter adipose tissue. The musculature of the chest wall also appeared dark but was removed from the breast ROI so that it would not be included in the summation of the segmented fibroglandular breast tissue.

Under the guidance of an experienced mammographer, the breast ROI was trimmed further, slice-by-slice, to remove the chest wall and other non-breast tissue (Fig. 2C) leaving mostly the breast tissues and the surrounding air which is seen as the faint “salt and pepper” appearance in Figures 2A – C. In order to remove all low MR signal pixels representing air, the higher MR signal pixels of the breast were subtracted from Figure 2C (breast + air) resulting in a difference image representing mainly air. Low MR signal pixels found within the breast boundary were removed to form an “air only” image (Figure 2D). This “air only” image was subtracted from the image in Figure 2C to yield a “breast only” image. A final refined trimming along the visual contour of the breast perimeter (Figure 2F) resulted in image representing only the breast ROI (Fig. 2E). The MR images recorded with each MRI protocol were reconstructed into a 3-D volume image of the breast (Fig. 2F). All of the above image-processing procedures were performed using GE’s proprietary ADW software and have not been automated and required some degree of user interaction. These same steps shown in Figure 2A–D also were applied to STIR images to segment the breast ROI.

Curve-fitting and Estimation of Glandular Tissue from Breast MR Images

The final segmented 3-D volume-rendered breast model (Fig. 2F) was exported to a personal computer for curve-fitting analysis. A program was written to extract the MRI voxel signal intensities, but not the voxel location information, from the 3-D model and generate the corresponding voxel signal intensity histograms. The curve-fitting process for the histograms generated for 3DGRE and STIR models was performed using a commercially available peak-fitting program, PeakFit 4.0 (SyStat Software Inc., San Jose, CA), as described below.

In curve analyses, a two-compartment model of breast tissue composition was assumed. However, voxels containing a varying mixture of fat and gland, the partial volume effect, are well-known and unavoidable phenomena in imaging (Laidlaw et al., 1998, Ruan et al., 2000, Santago and Gage, 1995). For the 3DGRE pulse sequence, the observed histogram of MRI signal intensities usually showed two major peaks with a valley between the two peaks (the histograms in the middle column, Fig. 3) in which the right peak was classified as adipose tissue while the peak that was the most to the left and the intermediate peak were classified as “non-adipose” and voxels were summed to represent fibroglandular tissue (for more details, see Results). The curve fitting algorithm attempted to minimize the residual errors, assuming a Gaussian distribution for all peaks. Because the fat peak is usually the larger of the peaks and also the more symmetrical peak, its shape more easily fits a Gaussian distribution, regardless of its peak size. The fat peak area was isolated first from the higher MRI intensities during curve-fitting. After subtracting (i.e., the ‘lock function’ in the PeakFit software) the area of the fat peak from the complete histogram, two additional Gaussian peaks were optimally fit over the remaining fat-subtracted peak area. The “Fast Peak Fit with Numeric Update” option of the Peakfit program was used to achieve the final fits. The area under the two left curves represents the relative abundance of glandular tissue.

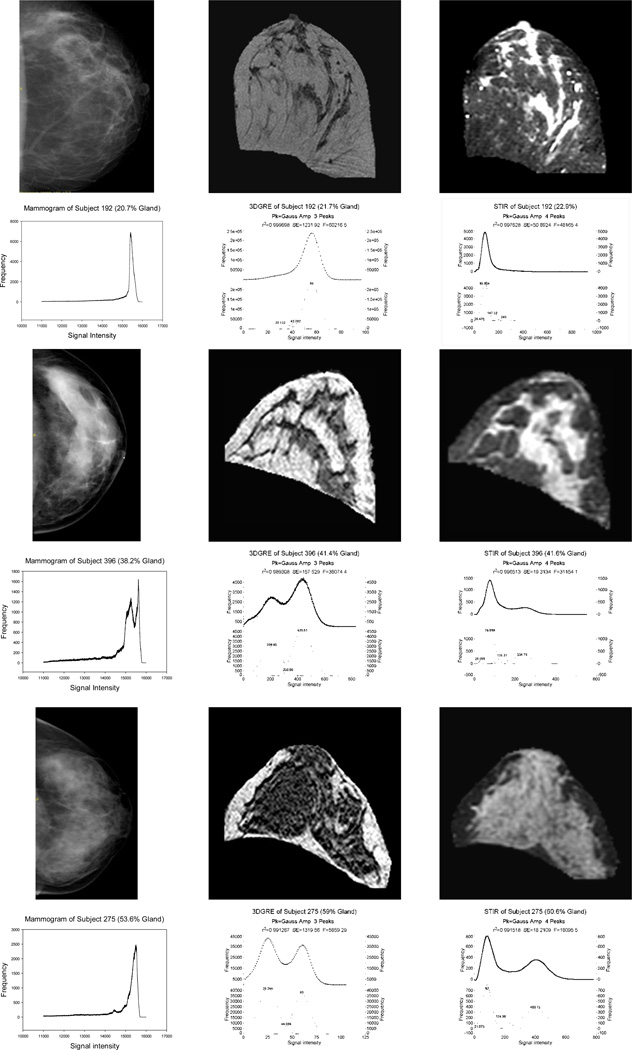
Figure 3.

Mammogram (first column), 3DGRE pulse sequence (second column), and STIR pulse sequence (third column) breast images and, beneath each image, the corresponding signal intensity histograms from 3 women with ~20% G (first two rows for subject 192), ~40% G (third-fourth rows for subject 396), and 60% G (fifth-sixth rows for subject 275). Histograms for 3DGRE and STIR have 2 curves, the upper curve representing unfitted (dots) and fitted (line) curves and the bottom curve representing segmented peaks.

The Smoothing function of the Peakfit program was used to reduce the noise associated with the STIR pulse sequence of the breast. For STIR, the observed histograms of MRI signal intensities typically show one major peak (adipose) at lower voxel signal intensities and a much broader peak with long tails at intensities higher than those from adipose tissue (third column in Fig. 3). Curve fitting analysis demonstrated a minimal residual error when four curves were fitted to the MR signal histograms rather than three curves assumed for 3DGRE models. First, the adipose peak, often the most symmetrical peak, was optimally fitted with a Gaussian distribution (the largest low-signal peak). After subtracting the fat peak area from the entire histogram, a smaller Gaussian distribution peak, representing possibly the residual air in the 3-D model, was fitted to an area left of the adipose peak. The air peak area was excluded in the final calculation of the two breast-tissue types. Finally, two Gaussian peaks were optimally fitted to the remaining brighter peak area to the right of the adipose peak, and the two peak areas were considered to represent the fibroglandular tissue. The ADW software has a function that performed volume analysis for the resampled/reconstructed 3-D model. The reconstructed voxel size (voxel size_rec) is the size of voxel in mm in both x and y directions. The voxel ratio is the ratio between the size of the voxels in the z-direction and in the x-direction. The voxel size and the voxel ratio of the reconstructed 3-D model were recorded in the model DICOM header report, and were retrieved for calculating voxel volume (mm³) and breast tissue composition according to the following equations.

$$\mathit{\text{Voxel volume}}(k_1)={\mathit{\text{FOV}}}_x/{\mathit{(}\mathit{\text{matrix size}}\mathit{)}}_x•{\mathit{\text{FOV}}}_y/{\mathit{(}\mathit{\text{matrix size}}\mathit{)}}_y•\mathit{\text{slice thickness}}={\mathit{(}{\text{voxel size}}_{\text{rec}}\mathit{)}}^3•\mathit{\text{voxel ratio}}$$ (Equation 1.1)

[where: voxel ratio= slice thickness/(voxel size_rec)]

$$\mathit{\text{Fat volume}}\mathit{(}{F}_{\mathit{\text{Vol}}}\mathit{)}=k_1•\mathit{\text{total voxels under fat peak}}$$ (Equation 1.2)

$$\mathit{\text{Gland volume}}\mathit{(}{G}_{\mathit{\text{Vol}}}\mathit{)}=k_1•\mathit{\text{total voxels under two gland peaks}}$$ (Equation 1.3)

$$\mathit{\text{Total breast volume}}(T_{\mathit{\text{Vol}}})=F_{\mathit{\text{Vol}}}+G_{\mathit{\text{Vol}}}$$ (Equation 1.4)

$$\%-\mathit{\text{Gland}}\mathit{(}\%-G\mathit{)}=G_{\mathit{\text{Vol}}}/T_{\mathit{\text{Vol}}}$$ (Equation 1.5)

Mammographic Density (Breast Density) from Mammograms

Total breast area (T_Area), dense breast area (G_Area), fatty tissue area (F_Area), and %-G for each mammogram were estimated by two different approaches, as previously detailed (Lu et al., 2007). One was by a manual labor-intensive HSM algorithm and the other by direct computation from mammogram imaging parameters retrieved from the DICOM report header of each imaged breast using a MATH algorithm derived from a multivariate regression model.

Briefly, for the HSM method, x-ray signal intensity data from the FFDM DICOM header were exported to generate a pixel signal intensity histogram of the imaged breast (first column, Fig. 3). A graphical user interactive-intensity threshold-based segmentation of glandular tissue from fat tissue was performed to obtain the %-G (%-G_HSM), the gland area (dense breast area, G_AreaHSM,), fat area (F_AreaHSM), and total breast area (T_AreaHSM)). We hypothesized that volumes from the glandular area, fat area, or total breast area from a 2-D mammogram can approximate the product of the respective tissue areas from the mammogram and the compression thickness as follows.

$$\mathit{\text{Gland volume}}(G_{\mathit{\text{VolHSM}}})=k_2•G_{\mathit{\text{AreaHSM}}}•\mathit{\text{Compression thickness}}$$ (Equation 2.1)

$$\mathit{\text{Fat volume}}(F_{\mathit{\text{VolHSM}}})=k_2•F_{\mathit{\text{AreaHSM}}}•\mathit{\text{Compression thickness}}$$ (Equation 2.2)

$$\mathit{\text{Total volume}}(T_{\mathit{\text{VolHSM}}})=k_2•T_{\mathit{\text{AreaHSM}}}•\mathit{\text{Compression thickness}}=G_{\mathit{\text{VolHSM}}}+F_{\mathit{\text{VolHSM}}}$$ (Equation 2.3)

Compression thickness was retrieved from the FFDM DICOM header and k₂ represents a normalization factor of 9.96 × 10⁻⁶ cm²/pixel for converting a mammogram pixel area to a metric area.

The second approach, a MATH algorithm, involves no manual segmentation of breast tissues (Lu et al., 2007). The %-G (%-G_MATH) was computed according to Equation 2.4 shown below. The MATH algorithm consisted of individualized mammogram acquisition parameters that were statistically the most significant predictors of %-G by multivariate regression model analysis. The most significant imaging parameters that are predictors of %-G are pre-exposure dose, pre-exposure thickness, radiation dose, pre-exposure kvp, anatomical mean intensity, threshold (‘Thresh’), final exposure thickness, compression force, sensitivity, filter material, and anode material. The coefficients in the equation were determined from multiple regression analysis. Note that Equation 2.4 represents an updated model derived from additional mammograms added to those used in Lu et al., (Lu et al., 2007).

$$\%-G_{\mathit{\text{MATH}}}=\mathit{481.33}-\mathit{0.0057}•\mathit{\text{pre-exposure dose}}+\mathit{1.2305}•\mathit{\text{pre-exposure thickness}}-\mathit{0.094}•\mathit{\text{radiation dose}}+\mathit{5.2056}•\mathit{\text{pre-exposure kvp}}-\mathit{0.0599}•\mathit{\text{anatomical mean intensity}}-\mathit{0.0192}•\mathit{\text{Thresh}}-\mathit{2.0223}•\mathit{\text{final exposure thickness}}-\mathit{0.049}•\mathit{\text{compression force}}-\mathit{37220}•\mathit{\text{sensitivity}}-\mathit{1.9863}•\mathit{\text{filter material}}+\mathit{25.314}•\mathit{\text{anode material}}$$ (Equation 2.4)

For the definition of predictor variables and their corresponding DICOM tag, see Lu et al., (Lu et al., 2007). The material for the variables ‘filter material’ and ‘anode material’ is either molybdenum or rhodium. The molybdenum and rhodium were coded 0 and 1, respectively, when using equation 2.4 to calculate %-G. Glandular volume (G_VolMATH) and fat volume (F_VolMATH) were derived using the following equations. For total breast volume T_VolHSM of Equation 2.3 was used.

$$G_{\mathit{\text{VolMATH}}}=\%-G_{\mathit{\text{MATH}}}•T_{\mathit{\text{VolHSM}}}$$ (Equation 2.5)

$$F_{\mathit{\text{VolMATH}}}=(1-\%-G_{\mathit{\text{MATH}}})•T_{\mathit{\text{VolHSM}}}=T_{\mathit{\text{VolHSM}}}-G_{\mathit{\text{VolMATH}}}$$ (Equation 2.6)

Statistical Analyses

The main outcomes of interest in this study were volumes of fibroglandular (gv), adipose (fv), and total breast tissues (tv), and %-G (also referred to as %-breast density). All outcomes were calculated using four different methods, two from MRI protocols (3DGRE and STIR) and two from mammography protocols (HSM and MATH). The means and standard deviations (SD) were obtained for all outcomes of interest estimated by the four different methods. The reproducibility of within-image values analyzed by different persons, repeated analyses by the same person, and between-replicate images (replicate imaging by an instrument) for measurements of all outcomes of interest by the four methods were assessed by linear regression analyses (Rsqr and regression slope) and intra-class correlation coefficients (ICC). The statistical analysis was performed using the SAS statistical software package version 9.2 (SAS Institute Cary, NC).

The MIXED procedure in SAS^® was used to estimate ICC values. ICC, a ratio of intra-method (σ_b) to intra- and inter-method variations (σ_w²) [ICC = σ_b² / (σ_w² + σ_b²)], is routinely used to assess the reproducibility of laboratory assays or diagnostics tests when the analysis on the same study subject is repeated randomly. The higher the ICC for a method when compared to a reference method, the more in agreement and reliable it is, when compared to a gold standard or, in our case, a reference method. SigmaPlot version 12 (Systat, Richmond, CA) was used to plot all regression curves between any two different methods for measuring %-G, gv, fv, or tv and for generating regression coefficients (Rsqr), regression slopes, and 95% confidence interval bands (CI).

Results

Several MRI protocols were evaluated, but only the two listed in Table 2 were selected for further reproducibility and reliability analyses. Figure 1 shows the intensity contrast between 3DGRE (Fig. 1A) and STIR (Fig. 1B). Glandular tissue appears dark in 3DGRE and bright in STIR. Using the steps described in Figure 2A–F, 3-D breast models were constructed requiring about 30 min to complete. Figure 3 shows corresponding representative mammograms (data in the first/left column) with representative middle MR slices of 3-D models made from 3DGRE (data in the middle column) and STIR (data in the third/right column) for three women with varying %-G. Each row of images is from the same woman, and it has the corresponding pixel /voxel signal intensity histograms beneath each of the mammogram, 3DGRE, and STIR images. As shown, the signal intensity histograms for mammograms tended to exhibit many more peaks with irregular shapes compared to the two dominant peaks amendable for Gaussian distribution curve fits for 3DGRE and STIR. 3DGRE histograms tend to have two distinct peaks when compared to STIR. The glandular peak areas from STIR tended to be broader than those from 3DGRE. Each curve-fitting took about 2–5 min to complete.

Curve-Fitting and Spatial Location of the Fitted Curves

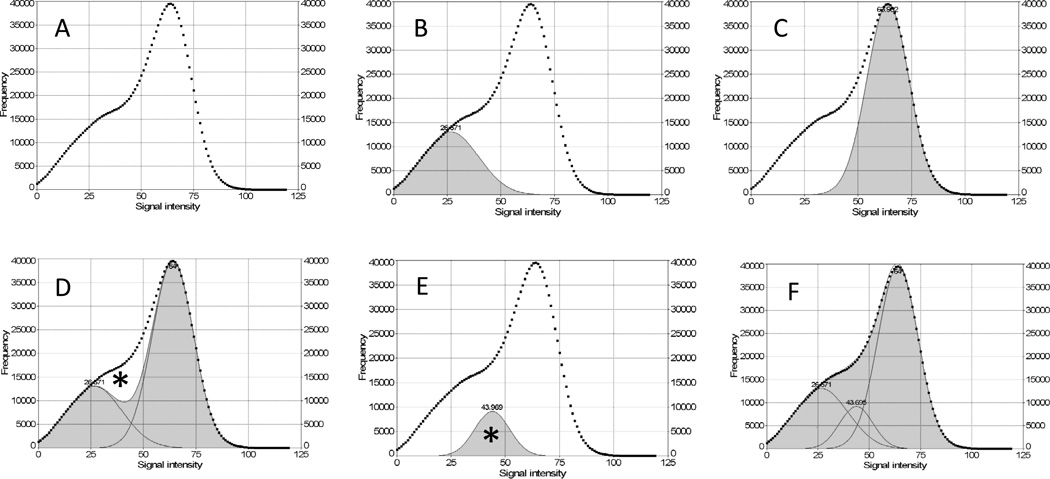
Figure 4 illustrates the steps taken to separate the voxel peak area of glandular breast tissue from that of fatty breast tissue using a 3DGRE model as an example. In curve analyses, a two-compartment model of breast tissue composition was assumed. Figure 4A represents the retrieved unfitted MRI signal intensity histogram of a 3DGRE model. Figure 4B shows a Gaussian-distributed glandular tissue peak (shaded gray), while Figure 4C shows a Gaussian-distributed fatty tissue peak (shaded gray). The summation (shaded gray) of the two peaks from panels B and C is shown in Figure 4D with a curve-fitting Rsqr of 0.92 leaving an unfitted white area (marked *) between the curve in panel A (square symbols) and the shaded sum peak area. The addition of a third Gaussian peak (marked *), as shown in Figure 4E, to the sum peak in Figure 4D was necessary to achieve a nearly perfect curve fit Rsqr of 0.999, as shown in Figure 4F.

Figure 4.

Gaussian curve-fitting analysis of the MRI signal intensity histogram to estimate fibroglandular and fatty breast tissues. (A) histogram from a representative 3DGRE breast model; (B) Gaussian curve fit for fibroglandular breast tissue type (shaded); (C) Gaussian curve fit for fatty tissue type (shaded); (D) sum of the Gaussian curve fit for B and C (shaded) with an Rsqr of 0.92 and an unfitted area (*) representing a region of MRI signal intensities between fibroglandular and fatty tissue types; (E) Gaussian curve fit corresponding to the unfitted area (*) in (D); (F) the sum of the Gaussian curve fit (B+C+E) achieving curve fitting Rsqr of 0.999.

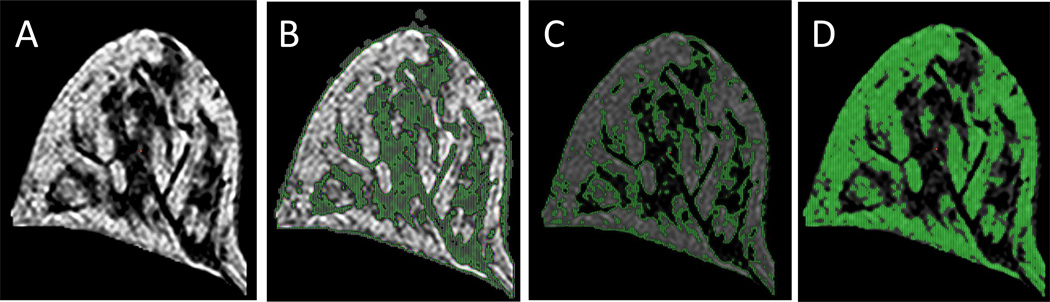
To understand the nature of the three fitted Gaussian curves in Figs. 4B, 4C and 4E, we used the mean ±1 SD MRI signal intensity of the middle/3rd peak (Fig. 4E) provided by the PeakFit report as a guide to map the location for all three Gaussian peaks using the interactive thresholding function of GE’s ADW software for segmenting gland and fat tissues. The spatial location of all voxels with MRI signal intensities ≤ mean -1 SD of the third peak appeared co-localized with glandular tissue, see green highlights in Figure 5B. The mean ±1 SD MRI signal intensities of the middle peak mapped to the boundaries of glands and fat tissue are highlighted green in Figure 5C. All signal intensities ≥ mean + 1 SD of the middle peak appeared in the fat tissue area as the green highlights shown in Fig. 5D. Thus, the middle peak between the gland and adipose tissue contains voxels with a mixture of fat and gland tissues with varying proportions, i.e., partial volume.

Figure 5.

Tissue segmentation based on MRI signal intensity extracted from Gaussian curve fitting analysis. (A) Central slice of a representative breast model; (B) segmented fibroglandular tissue type (green) determined by the Gaussian curve fit (Fig. 4B); (C) segmented tissues (green) representing the Gaussian curve fit to the unfitted area (*) (Fig. 4E); (D) segmented fatty tissue type (green) determined by the Gaussian curve fit (Fig. 4C).

Reproducibility of MRI Protocols

The reproducibility of the MRI protocols was tested in six women (3 pre-menopausal and 3-post-menopausal), who had breasts with varying mammographic density. These women provided one screening mammogram and also were imaged two to seven times on separate occasions within a 2-month period using 3DGRE and STIR protocols for breast tissue amount (area and volume) and composition measurements. Table 3 shows the results (mean and SD) of measures of %-G, gland volume, fat volume, and total breast volume of the left breast. At the present time, there is no known standardized method for measurement of breast tissue composition, and mammographic density is currently the most widely used measure. Thus, values from mammograms were used as references for reproducibility and validity studies described herein. Mammograms provide breast tissue area (a 2-D measure), while MRI provides breast tissue volume (a 3-D measure). To properly compare values from these two radiologic methods, breast tissue volumes from mammograms were estimated by an approximation approach (for more details, see below) using a product of a breast area multiplied by the compression thickness (in mm), while adjusting for a factor (k₂) to normalize pixel area to a cm² unit. The compression thickness is routinely recorded in each digital mammogram DICOM header. As shown in Table 3, the CVs (SD/mean) are usually <5% for repeat MRI exams across a wide range of mammographic density, with some having a 10% to 15% CV. Those with higher CVs tended to be associated with differences in breast positioning. The thickness of a compressed breast is likely to exhibit a gradient with the center of the breast being thicker than the edge of the breast. Moreover, when a 3-D breast is compressed into a 2-D object, the projected 2-D area will undoubtedly give a larger surface area than the projection of a 3-D object into a 2-D area without compression. These two factors, together, contributed to overestimation of breast volume using the approximation approach taken by us to calculate breast volume. As shown, volumes estimated from mammograms tend to be higher than MRI volumes. The CVs for replicate analyses of the same image by a rater were within 5% (Results not shown).

Table 3.

The reproducibility of breast tissue composition from replicate MR exams (mean±SD) of patients’ breasts (N=6) by 3-D gradient echo pulse (3DGRE) and inversion recovery pulse (STIR) compared with mammogram (mammo) results.

		Gland, %-Total Breast			Gland Volume, cc			Fat Volume, cc			Total Volume, cc
Subject ID	No of Images for: mammo, 3DGRE, STIR	mammo	3DGRE	STIR	mammo*	3DGRE	STIR	mammo*	3DGRE	STIR	mammo*	3DGRE	STIR
1	1, 7, 5	52.6	51.9±1.6	54.5±3.5	427.3	334.0±14.5	342.7±18.4	473.2	309.3±8.5	286.2±26.5	900.5	643.3±10.9	628.9±16.1
2	1, 4, 2	11.9	9.3±0.9	7.5±0.5	64.2	45.9±3.6	37.5±2.4	476	451.4±17.6	463.8±2.6	540.2	497.3±15.5	501.4±0.2
3	1, 2, 2	28.2	26.6±1.0	30.4±1.4	367.2	283.8±45.7	325.8±23.9	932.1	779.2±87.2	747.5±103.6	1299.3	1063.0±132.9	1073.3±127.5
4	1, 3, 3	38.5	34.1±0.6	43.4±2.7	455.1	383.2±10.2	458.5±24.0	727.1	739.5±16.5	594.8±40.5	1182.2	1122.7±22.4	1053.3±31.7
5	1, 3, 2	28	32.1±1.7	34±0.6	105.5	87.0±1.8	103.2±1.6	270.8	184.2±15.7	200.1±1.9	376.2	271.1±16.5	303.3±0.3
6	1, 3, 3	31	31.9±1.9	30.7±1.1	321.7	261.4±41.5	254.6±9.9	714.9	555.7±42.0	575.6±7.9	1036.6	817.1±82.4	830.2±4.4

^*volume = tissue area from mammogram × breast compression thickness × 9.96 × 10⁻⁶ cm²/pixel

Validity and Reproducibility of MR Pulse Sequences

The validity and reproducibility of the two MRI protocols for measuring volumes and the glandularity of breast tissues were investigated further on a multiethnic cohort of 95 women. This cohort was 58% Caucasian, 22% Hispanic, 17% African American, 2% of unknown ethnicity, and 1 Asian, age = 35.8 ± 2.5 yr, weight = 74.6 ± 14.8 kg, and height = 162.7± 6.2 cm. For the validity study, the slope, regression equation, and Rsqr of the ordinary least square regression analyses, and the ICC values were estimated for each breast density index of interest (i.e., %-G, gv, fv, and tv) between measurements by any two of the four modalities used. The four modalities are 3DGRE, STIR, HSM, and MATH. The graphic results of these analyses displayed in table-like format are graphically shown in Figure 6. A slope of 1.0 indicates an equivalent relationship between measures. A deviation from 1.0 indicates the extent to which one measure (y-axis) under-estimates or overestimates the values relative to the other reference measure (x-axis). ICC is an index of agreement and reliability. ICC values were greater than 0.75, generally indicating a moderate to high level of agreement between two comparison groups (Laude et al., 2004).

Figure 6.

Reliability and reproducibility relationship between any two of the four different methods of measuring %-glandular tissue (panels A1–A6), glandular volume (panels B1–B6), fat volume (panels C1–C6), and total breast volume (panels D1–D3) in 95 women. Linear regression (Rsqr, regression equation and slope with 95% confidence interval and prediction lines) and intra-class correlation (ICC) analyses are shown. Four methods of measurements for (x, y) paired comparison are 3DGRE, STIR, mammogram by histogram segmentation (HSM), and mammogram from a multivariate regression equation (‘mathematical model’, MATH). Volume from each mammogram is taken from the product of mammogram area and breast compression thickness.

For %-glandular tissue (all panels in column A, Fig. 6), all slopes approximate 1 for comparison between the two MRI protocols (~0.9 in Fig. 6A1), between each MRI vs. the HSM mammogram (~1.0, Figs. 6A2–3), and between each MRI vs. the MATH algorithm (~1.1, Figs. 6A4–5) and between the MATH and the HSM (~0.8, Fig. 6A6). Because the compressed thickness of the breast during mammography varied with the breast density of the woman being imaged, the volume of the breast from a mammogram was estimated by a simple arithmetic approach, i.e. taking the product of the mammogram’s breast area and compression thickness. For glandular tissue volume comparisons (the column B panels, Fig. 6), the two MRI protocols gave the same measurement amounts (slope=0.96, Fig. 6B1) but gave 30%– 40% smaller volumes than those measured by mammograms (slope=0.64–0.74, Figs. 6B2–5). The gland volume measurement from the MATH was 13% less than HSM data (slope=0.87, Fig. 6B6). Fat volumes (all panels in column C in Fig. 6), however, were about the same, e.g., slopes=0.94–1.1, independent of the methods used for measurement. Similarly, total volumes (column D in Fig. 6) measured between the two MRI protocols (Fig. 6D1) and between each type of MRI and the mammogram (Figs. 6D2–3) were also the same (slopes=0.94–1.0). Note that there is only one mammogram for each woman, i.e. an identical total breast area/volume estimate for MATH and HSM, therefore, correlation between these two methods is omitted. The correlation graph between 3DGRE and MATH is the same as in Fig. 6D2, and the correlation graph between STIR and MATH is the same as in Fig. 6D3.

The ICCs are all greater than 0.75 (Fig. 6A–D), a cut-off value for being considered as a reliable and reproducible measure (Laude et al., 2004), and they were 0.86–0.92 for %-glandular tissues (panels in column A), 0.77–0.91 for glandular volumes (panels in column B), 0.89–0.99 for fat volumes (column C), and 0.89–0.98 for total volume (column D), indicating strong measurement reliability of all methods. The mammograms and MR images from these 95 women were analyzed for the amount of different breast tissues by two different analysts to test for inter-rater variability. The slopes, Rsqr, and ICC were all greater than 0.95 (Results not shown) indicating little inter-operator variability and excellent reproducibility between various raters.

Discussion

Two robust breast MRI protocols were developed for measuring breast tissue glandularity that are comparable with methods for estimating breast density from mammograms (Fig. 6). We showed that replicate breast images can be acquired reproducibly on separate occasions, indicating stability of the MR instrument (Table 3) and reliability and reproducibility of analysis protocols (Fig. 6). The two MRI protocols are complimentary because one, 3DGRE, produces predominantly a low MR signal for fibroglandular tissue (middle column in Fig. 3) while the other protocol, STIR, produces a high MR signal for fibroglandular tissue (right column in Fig. 3). Other fat-suppression MRI protocols were evaluated at the beginning of this research and were found to be unreliable compared to STIR for our purposes because of lack of signal homogeneity that could not be corrected. Imaging time in this study is short, about 20 min, which made it more tolerable for the research subjects and it did not adversely affect the routine MRI clinical schedule. The methods do not require contrast material and can be used repeatedly on all subjects, including the vulnerable population of younger females. Our imaging protocols are similar to that of T1 contrast clinical protocols and are in line with most published breast MRI protocols (reviewed in Table 1) for breast tissue composition analyses. However, our tissue composition analysis protocol, utilizing commercially available software, is simplified.

The necessary tissue compression during mammography produces projected breast images that often contain a variable mix of glandular and fatty tissues, i.e. pixels are neither pure glandular nor pure adipose tissue. The consequence of this tissue overlapping is a pixel signal-intensity histogram with multiple peaks (see the first column, rows 4 and 6, Fig. 3). Due to the multiplicity of peaks, it is difficult to apply the curve-fitting method to quantify glandular and fatty tissues on mammograms. The MR voxel signal is acquired 3-D, which reduces the problem of voxel signal from tissue overlapping. For this reason, the MRI voxel signal-intensity histograms (all histograms in the second and third columns, Fig. 3 and Fig. 4) typically tend to be more symmetrical and often exhibit one major peak (in a fatty breast) or two major peaks (in a breast with more glandular relative to fat tissue). Often, one of the peaks, e.g., for fat tissue, showed a reasonable bell-shaped Gaussian distribution, which greatly facilitated the easy application of commercially available peak-fit software to segment glandular tissue from fat tissue, as shown in this paper (Fig. 4).

The tissue volume measurement by the Gaussian-distributed curve-fitting method (Figs. 3–4) has not been reported previously for segmenting glandular tissue from fat tissue. The two most commonly applied algorithms in MR image analyses for tissue content are either interactive visually-guided tissue segmentation using threshold signal intensity or variations of fuzzy c-means for clustering tissue types (reviewed in Table 1). Both of these have some elements of subjectivity, and automation is still being attempted. In contrast, our curve-fitting procedure utilizes readily available commercial software for spectrum analyses. It is more objective, highly reproducible (Table 3 and Fig. 6), and far less labor-intensive when compared to other approaches reviewed in Table 1. Our curve-fitting protocol, as shown in Figure 4, can be readily adapted to analyze other MR pulse sequences that can generate a homogenous image signal.

For measuring the amount of glandular tissue, we (and others) assume that the breast contains two major tissue types, fibroglandular and adipose, but it also contains other minor tissue types such as blood vessels, connective tissue, and fibroblasts, which may not exhibit a similar signal intensity as the glandular tissue under these two different MRI protocols. This could explain, in part, why the non-fat peak area with higher signal intensity in STIR (third column in Fig. 3) exhibited a much broader peak than the fat peak of STIR at the lower signal intensity. The non-fat peak area in STIR is also much more difficult to approximate by curve-fitting compared to that in 3DGRE. In contrast, the voxel signal intensity of the adipose tissue peak from both 3DGRE and STIR (Figs. 3–4), in general, is easier for curve-fitting. Importantly, the Gaussian approximation technique allowed us to separate all MR voxel signal intensity histograms into three Gaussian-shaped peaks with residuals being minimized to a Rsqr>0.998.

In curve-fitting, we showed that there is a shoulder peak area (marked * in Fig. 4D) with intermediate voxel signal intensity between the two Gaussian shaped fat and gland peaks (Fig. 3–4) that can be fitted into a third Gaussian-distributed peak (* peak, Fig. 4E), which is needed to be considered as part of the completed histogram in order to minimize the residual errors and to achieve a good curve-fitting Rsqr >0.998 (compare Fig. 4F vs. Fig. 4D). The shoulder peak is present in both MRI protocols. Figure 5 shows the spatial location of all three Gaussian curves. It is clear that the spatial location of the third peak (in Fig. 4E) predominantly existed in the boundaries between glandular and fatty tissues, as shown in Figure 5C. This result would strongly suggest that this third Gaussian peak (Fig. 4E) consisted of partial volume voxels with a varying proportion of glandular and fatty breast tissues, while the peak in Fig. 4B consists of pure glandular tissue voxels and the peak in Fig. 4C consists of pure fatty tissue voxels. This partial volume effect is unrelated to the overlapping gland and fat tissue projection in a mammogram. Our results are consistent with the partial volume studies performed by several other groups. Santago and Gage modeled partial volume with Gaussian statistics (Santago and Gage, 1995). Ruan et al. showed that brain with three tissue types generated five possible Gausssian curves, three for each pure tissue, and two for every two mixed tissues (Ruan et al., 2000). Laidaw et al. elegantly demonstrated the presence of a partial volume voxel peak to be found between the signal intensities of the tissue types represented within the mixed tissue voxels (Laidlaw et al., 1998). If the partial volume assumption is true, our approach of summing the intermediate peak area together with the major gland peak area as gland tissue may contain some bias. Because gland is usually the smaller compartment of the two breast tissue types, slight variation of the ‘true gland volume’ in the third peak will contribute to a more variable correlation when gland volumes were compared between two different methods of measurement, as seen in Figure 6B1–6. This may also explain why, when any two methods are compared against each other (panels in the same row, e.g. Figs. 6A1,B1,C1 and D1), correlation (be it regression slope or ICC) was always much better with regard to total breast volume (column D panel, Fig. 6) and total adipose volume (column C panel, Fig. 6) than fibroglandular tissue volume (column B panel, Fig. 6) For example, ICC is 0.86 for gland volume (Fig. 6B1) and >0.98 for fat volume and total breast volume (Figs. 6C1, D1) for a 3DGRE vs. STIR comparison.

The histogram profiles of the MRI voxel signal intensity of our study participants (Fig. 3) were very similar to the histogram profiles of voxel T1 times published by Boston et al. (Boston et al., 2005). This is not surprising, because the different mean signal intensities produced by fat and glandular tissue do correlate with the different inherent T1 times of each tissue. Using a Gaussian-distribution algorithm, we segmented fat from glandular tissue, while Boston et al. (Boston et al., 2005) used an empirical logistic model approach (Table 1) that performed the segmentation based on inherent differences of T1 relaxation times between fat and gland. In spite of the differences in the tissue segmentation methods, the final curve fitting shapes and distributions of the segmented fat and gland peaks are strikingly similar between our approach and those of Boston et al. (Boston et al., 2005). Direct comparison between our approach and other segmentation approaches listed in Table 1 will be of interest for additional validation.

Other studies have compared percentage glandular tissue measured from 2-D mammograms with those from 3-D breast MRI and found the Pearson correlation coefficient to range from 0.75 to 0.90 (Table 1). Our Rsqr values shown in Fig. 6A1–5, ranging from 0.76 to 0.80, are within the reported ranges. This is, however, the first study to report a direct comparison of breast tissue volumes (gland, fat, and total breast) measured from a 2-D mammogram (be it from HSM or MATH) and two 3-D MRI protocols (3DGRE and STIR). We approximated breast tissue volume from mammograms by simply multiplying mammogram area (gland, fat, or total breast) with pre-recorded breast compression thickness available from every digital mammogram’s DICOM header. There are two breast compression thicknesses recorded in the header, one for pre-exposure (pilot exposure) and one for final image exposure. The compression thickness between pre-exposure and final exposure is not necessarily the same. By an empirical approach, we found that pre-exposure compression thickness is a much better compression thickness to use for deriving mammogram volume estimates that correlated better with MRI volume estimates (data shown in Fig. 6). Therefore, our approximation approach should be considered as a feasible and an excellent alternative for volume measurement from a 2-D image. Our approach is supported by the high regression Rsqr (all >0.9), regression slope (all~1.0), and ICC (all>0.9) for total volume (Figs. 6D2–3) and fat volume estimates (Figs. 6C2–C5) when comparing mammogram volumes against MRI. The corresponding statistics for gland volume comparison between mammogram and MRI data also is strong (Figs. 6B2–B5), e.g., all Rsqr >0.7, all ICC>0.75, and slopes ~0.7. Thus, the gland volumes estimated from MRI are about 30% (slope, ~0.7) less than those from mammograms. This can be a consequence of variable overlapping gland and fat tissue compression during mammography.

We reported that %-glandular tissue from mammograms can be estimated using a statistical modeling derived MATH algorithm (Equation 2.4) (Lu et al., 2007). In this study, the validity of such an approach was further assessed by comparing results calculated from the MATH with those obtained from two MRI protocols (Fig. 6A4–5, 6B4–5, and 6C4–5). Rsqr values are between 0.74–0.90 and ICCs between 0.78–0.93. The regression slopes are ~1.0 for fat volume comparison (Figs. 6C4–5), ~1.1 for %-gland comparison (Figs. 6A4–5), and ~0.7 for gland volume comparison (Figs. 6B4–5). These statistics show that the mathematical algorithm is valid for estimating %-gland and breast tissue amount. This procedure can be easily automated and could be applied to future epidemiologic studies.

There are several strengths of this study. All participants had time-matched MR images and mammograms. The tissue composition analysis using commercial peak-fit software is easy to implement for other clinically used pulse sequences that produce sharp tissue contrast and signal uniformity in images. The mathematical equation is an efficient and reliable alternative to current published methodology that applies interactive thresholding segmentation. An area requiring improvement for facile application of breast MRI for research is the isolation of the breast region of interest from MRI. All published protocols (reviewed in Table 1), including those in this study, required considerable time and effort to isolate the breast ROI.

In summary, two highly reproducible, reliable, objective, and robust methods for quantifying fibroglandular tissue were presented that combined the use of customized breast MRI protocols and a curve-fitting routine. We also showed that breast tissue volumes can be easily estimated from the product of mammogram area and breast compression thickness, obtained from the DICOM header of a mammogram report. A mathematical algorithm that can be used to instantly calculate the density of a woman’s breasts as soon as her mammogram is acquired is presented and validated in this study. These methods, together, are expected to facilitate investigations when using breast density as a surrogate biomarker in breast cancer research.

Abbreviation used

2-D

2-dimensional

3-D

3-dimensional

3DGRE

3-D gradient-echo

STIR

short tau inversion recovery

TE

echo time

TR

repetition time

TI

inversion time

FOV

field of view

FFDM

full field digital mammography

MRI

magnetic resonance imaging

ICC

intra-class correlation coefficient

SD

standard deviation

CV

coefficient of variation

ROI

region of interest

T1

T1 relaxation rate

%-G

%-glandular tissue or %-breast density

gv

glandular breast tissue volume

fv

fatty breast tissue volume

tv

total breast tissue volume

DICOM

Digital Imaging and Communications in Medicine

HSM

histogram segmentation method

MATH

mathematical algorithm obtained from a multivariate regression model equation