Abstract
We present a broad-band, continuous-wave spectral approach to quantify the baseline optical properties of tissue and changes in the concentration of a chromophore, which can assist to quantify the regional blood flow from dynamic contrast-enhanced near-infrared spectroscopy data. Experiments were conducted on phantoms and piglets. The baseline optical properties of tissue were determined by a multi-parameter wavelength-dependent data fit of a photon diffusion equation solution for a homogeneous medium. These baseline optical properties were used to find the changes in Indocyanine green concentration time course in the tissue. The changes were obtained by fitting the dynamic data at the peak wavelength of the chromophore absorption, which were used later to estimate the cerebral blood flow using a bolus tracking method.
OCIS codes: (300.6340) Spectroscopy, infrared; (290.5820) Scattering measurements; (290.1990) Diffusion
1. Introduction
Near infrared spectroscopy (NIRS) [1] can be used to measure absolute concentrations and changes of endogenous chromophores such as oxy and de-oxy hemoglobin and exogenous ones such as Indocyanine green (ICG) [2]. ICG is a near infrared light absorbing dye which has many clinical applications. To measure absolute optical properties, frequency domain [3] and time domain [4] systems were proposed. In our recent phantom study [5] we have shown that multichannel broadband NIRS can measure optical properties of a two-layer highly scattering medium with the thickness of the top layer close to the adult skull thickness. This method was a generalization of the second-derivative approach proposed earlier by Matcher et al. in [6]. In the present work we further develop the method of [5] to measure both the baseline optical properties of head tissues and changes in the ICG concentration (in vivo). The main methodological challenge of the in vivo tissue measurement compared to the phantom study was a larger number of chromophores. To demonstrate the clinical potential of our method we use the baseline optical properties to measure the time varying concentration of ICG in the animal brain and then use it to measure cerebral blood flow (CBF) by a bolus tracking technique [7,8]. For validation, the CBF values obtained by NIRS were compared to values obtained with perfusion computed tomography (pCT).
2. Materials and methods
2.1. Animal experiment
The study was approved by the Animal Use Subcommittee of the Canadian Council on Animal Care at the University of Western Ontario. Piglets were tracheotomized and mechanically ventilated while anaesthetized by isoflurane. Cannulas were inserted into each ear for injection of the NIRS and CT contrast agents. An additional cannula was inserted into a femoral artery to allow blood samples to be collected for gas and glucose analysis. Following the surgical procedure, animals were allowed to stabilize for 1 h before BF measurements were collected.
Near-infrared spectroscopy and CT data were collected concomitantly. Cerebral blood flow (CBF) was measured using a bolus-tracking method that requires an intravenous bolus injection of ICG (0.1 mg/kg), followed by continuous measurements of the time-varying concentrations of ICG in arterial blood and brain tissue. Computed tomography images of CBF were acquired using a LightSpeed QXi multislice CT scanner (GE Healthcare, Milwaukee, Wisconsin) upon injection of 1.0 ml/kg of the iodinated contrast agent iohexol (300 mg I/mL; Omnipaque TM, GE Healthcare, Waukesha, Wisconsin).
2.2. Near-infrared spectroscopy
An in-house-developed continuous-wave broadband spectrometry system was used to collect the near-infrared data [8]. The main components of the system included an illumination unit and a spectrometer consisting of a holographic grating and a cooled charge-coupled device (CCD). The illumination unit was 50 Watts quartz, halogen light bulb that was band-pass filtered to remove light outside the 600 to 1000 nm range. The filtered light was coupled to a 2-m fiber optic bundle (emission optode) with a numerical aperture of 0.55 and a 3.5 mm-diam. active area. The opposite end of the emission optode was placed on the scalp of the animal and held in position by a specially designed flexible probe holder. Another optical fiber bundle (detection optode) with the same specifications as the emission optode was positioned at 2.7 cm distance from the emitter to collect light that traveled through the tissue. Light collected by the detection probe was recorded at intervals of 200 ms.
2.3. Algorithm
The light propagation in a turbid medium can be described by radiative transfer theory [9,10] which in the present application can be reduced to the diffusion approximation [11,12]. Since the extra-cerebral tissue layer in newborn piglets was very thin (1-2 mm), we could approximate the head as a homogeneous medium.
There is a solution for semi-infinite homogeneous media which defines the continuous-wave photon flux as the following [13]:
| (1) |
where is the diffusion coefficient and ρ is the source detector distance in the radial coordinate, S is the source strength in photon per second,and are the absorption and reduced scattering coefficients, and are the boundary approximation parameters and defined by the following expressions [14]:
| (2) |
It is assumed that all the incident photons are initially scattered at the same depth and is the negative image source some distance beyond the physical surface so that the fluence rate is set to be zero at that point, this called extrapolated boundary condition [15]. This model depends on the absorption and reduced scattering coefficients of the medium. The absorption coefficient of the medium can be calculated as
| (3) |
where the quantities in square brackets represented the concentration of oxy and deoxy-hemoglobin and represented their molar extinction coefficients respectively. and were the absorption coefficients of water and fat, and (%FC) was their volume fraction.
To model the reduced scattering coefficient spectral dependence, we assumed that as a function of wavelength obeys the power law:
| (4) |
with specific values of M and α. To obtain the baseline optical properties (without ICG) the procedure was to try all possible combinations of the parameters ([HbO2], [HHb], , α, and M) to find the best fit of the experimental data curve, using Eq. (1). Each one of the parameters was varied over a range spanning ±100% of the known values. The first spectral derivative of the experimental absorbance,
| (5) |
were compared with the derivative of theoretical absorbance, calculated as described above and also the second spectral derivative of the absorbance A were compared with the derivative of the theoretical absorbance using the modified Beer Lambert law (MBLL):
| (6) |
| (7) |
where DPF is the differential path length factor [16], L is the physical source detector distance, is the change in concentration, is the change in attenuation, and ε is the extinction coefficient.
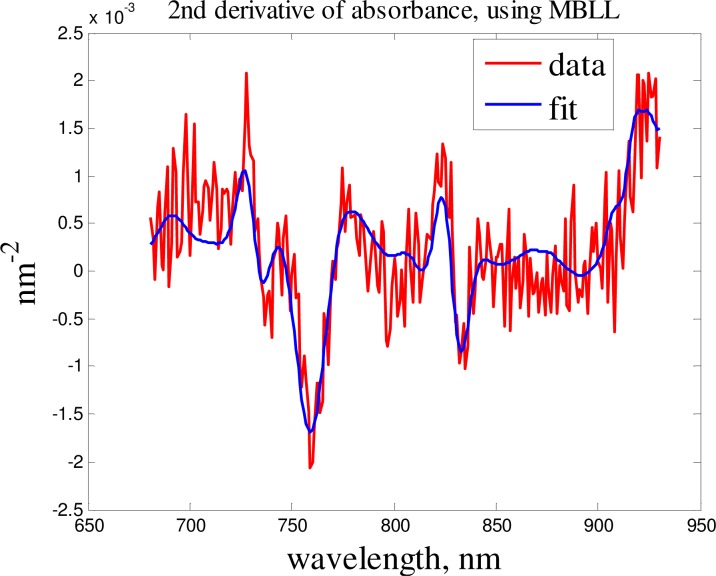
The objective function of the fitting procedure was the norm of residuals for the measured and computed absorbance spectra. The spectral intensity measurements at 2.7 cm source-detector distance were used to obtain the optical properties of the tissue. In this study we used the first and second spectral derivatives of experimental absorbance. The use of the absorbance , which includes the reference signal eliminated instrumental spectral artifacts and the use of first derivative spectra eliminated unknown factors in source-tissue and detector-tissue couplings, also it helped to magnify the spectral features. The initial values of [HHb] and were obtained using the second derivative fit (Fig. 1 .), which removed the crosstalk with [HbO2]. Then these values were used in the first derivative fit to rectify the values of [HHb] and and to obtain the values of [HbO2]. This method helped to obtain more accurate values for water concentration and reduced scattering coefficient.
Fig. 1.
Second derivative data fit.
The tissue ICG concentration time course was estimated assuming that other parameters remain constant and CBF was obtained using the following equation:
| (8) |
where is the arterial ICG concentration measured by a dye densitometer (model DDG-2001 A/K, Nihon Kohden, Tokyo, Japan), is the tissue ICG concentration measured by our optical technique. is the impulse residue function (IRF), and it has the initial value of one, and it decays afterward [17]. By using a deconvolution routine between the two curves of tissue and arterial ICG concentration time course, the IRF curve can be characterized, where the initial height of that corresponds to the CBF and the area under the curve to the CBV [18]. The deconvolution was applied to each set of and curves individually. The algorithm used physiologically derived constraints to stabilize the retrieved flow-scaled function [19].
3. Results
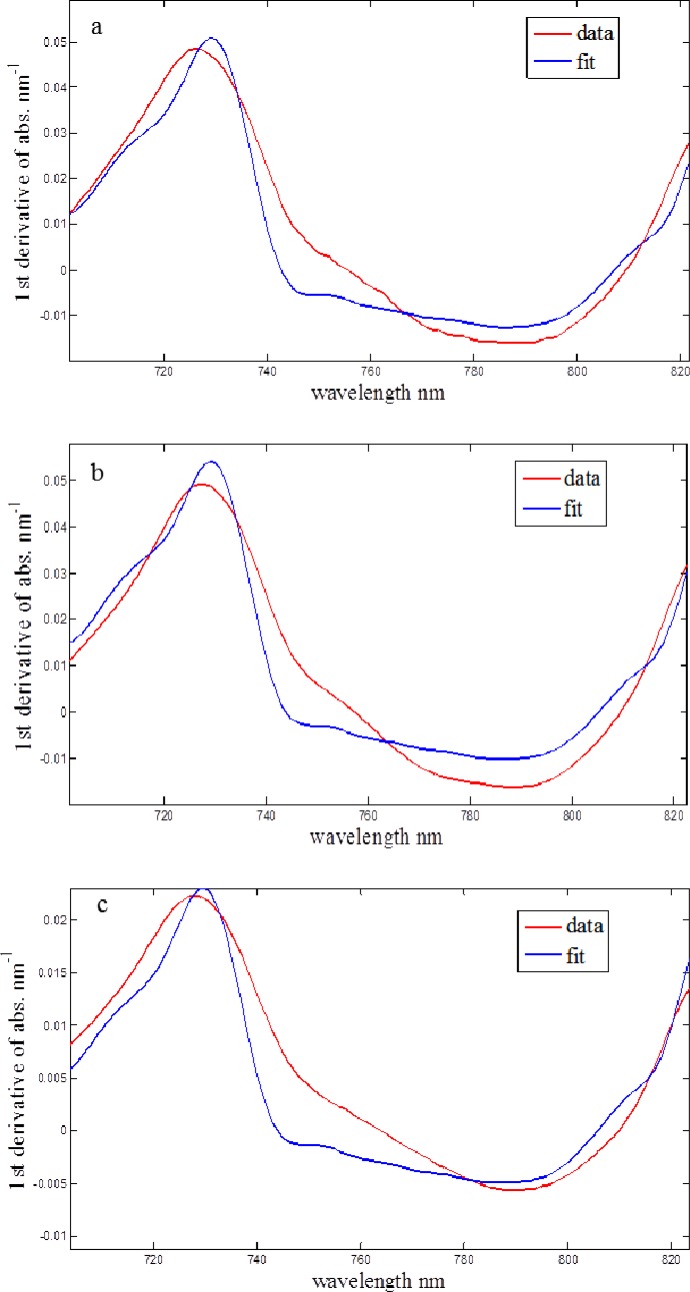
In order to test our setup we performed experiments with 10% milk as a phantom medium, at two different geometries: an infinite medium and semi-infinite medium (with the boundary condition). Since the NIR absorption of fat was much smaller than the absorption of water, we assumed that the absorption in the phantom medium was only due to the water and the role of the fat was purely scattering. The reduced scattering coefficient was measured 3.6 which was the same value for both of the geometries, Fig. 2(a) and Fig. 2(b). After dilution of the milk (5 times with water), the value reduced to 0.9 mm–1 [Fig. 2(c)], which was 4 times less than for the original 10% milk. This showed a good sensitivity of the system to the scattering properties of the medium.
Fig. 2.
First derivative fits for (a) infinite medium,10% milk: = 3.6 mm−1, (%FCH2O) = 86%; (b) semi-infinite medium,10% milk: = 3.6 mm−1, (%FCH2O) = 86%; (c) semi-infinite medium, 2% milk: = 0.9 mm−1, (%FCH2O) = 97%
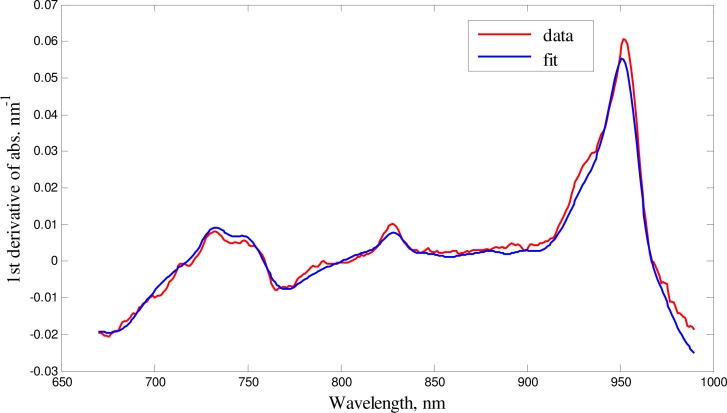
In order to obtain the baseline optical properties of head tissue, we measured the reflectance NIR spectra of the piglets’ heads and of the pigs open brain after the craniotomy (the probes were placed on the surface of the brain in vivo). Figure 3 . shows a representative example of first derivative spectrum of the attenuation of the pig’s open brain and the fit obtained using the diffusion equation for the semi-infinite uniform model. The recovered parameters of the fit are shown in Table 1 . Note that the average measured cerebral water concentration was obtained 79% ± 2% which was close to the known value of 80% for juvenile pigs [16].
Fig. 3.
First derivative of absorbance for a set of data from pig’s open brain fit of the model (blue) to the base line data (red)
Table1. Optical properties of the open brain from recovered parameters of the fit.
| Experiment | Oxy Hb (μM) | Deoxy Hb (μM) | Water (%) | μs′ at 800 nm (mm−1) | α |
|---|---|---|---|---|---|
| 1 | 46 | 14 | 80% | 0.50 | 2 |
| 2 | 54 | 22 | 81% | 0.40 | 3 |
| 3 | 56 | 24 | 77% | 0.60 | 2 |
| 4 | 40 | 16 | 78% | 0.50 | 2 |
| 5 | 50 | 18 | 79% | 0.45 | 2 |
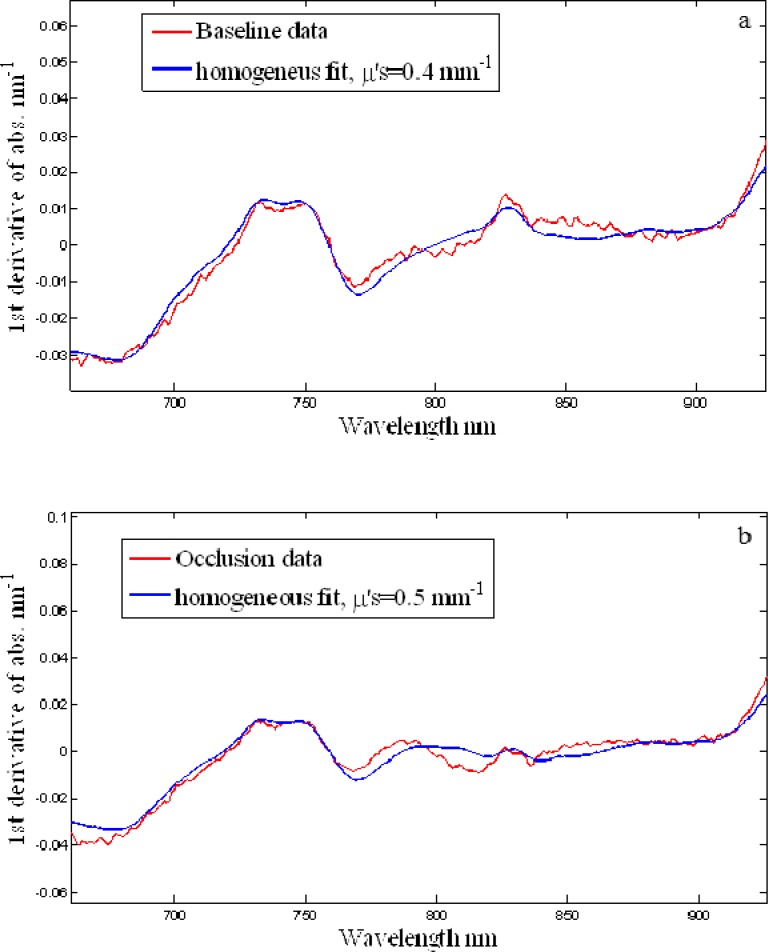
Figure 4 . shows the first derivative spectrum of the attenuation of the brain and the fit obtained using the diffusion equation for semi-infinite uniform model at two conditions (baseline and occlusion). The recovered parameters of the fits are shown in Table 2 .
Fig. 4.
Fit of the model (blue) to the baseline data (red), R2 > 0.90 (a) baseline, (b) occlusion
Table 2. Properties of the piglet brain recovered from the fit, and the cerebral blood flow, blood volume and mean transit time values measured at two different conditions, baseline and occlusion for different animals.
| Subject | Oxy (μM) | Deoxy (μM) | Water (%) | μs′ at 800 nm (mm−1) | α | CBF (ml/min/100gr) | CBV (ml/100gr) | MTT (s) |
|---|---|---|---|---|---|---|---|---|
| Baseline Animal-1 | 83 | 18 | 82 | 0.45 | 1.7 | 69.34 | 8.69 | 7.52 |
| Occlusion Animal-1 | 34 | 20 | 85 | 0.45 | 1.6 | 41.34 | 6.72 | 9.76 |
| Baseline Animal-2 | 50 | 18 | 86 | 0.40 | 1.8 | 44.75 | 6.11 | 8.19 |
| Occlusion Animal-2 | 15 | 37 | 86 | 0.50 | 1.6 | 22.99 | 6.68 | 17.44 |
| Baseline Animal-3 | 50 | 18 | 86 | 0.40 | 1.8 | 44.50 | 5.68 | 7.66 |
The obtained water concentration values were in a good agreement with other studies [6,20], which gives the average value of 85% for water concentration in the newborn brains.
The obtained values of reduced scattering coefficient were also in a reasonable agreement with the values obtained by Fantini et al. [21] for human subjects using frequency domain technique.
In order to validate our results obtained using the first derivative fit of absorbance by the diffusion equation solution, we also used the second derivative fit of absorbance by the modified Beer Lambert law. Considering a semi-infinite geometry, the medium DPF was calculated using the following equation [22].
| (9) |
where ρ is the source detector distance and is the absorption coefficient at the base line, then we can calculate values by using DPF values which we obtained along with deoxy-hemoglobin and water concentration from the second derivative approach. Note that the second derivative approach provides no information about the oxy-hemoglobin concentration value, since the second derivative of the oxy-hemoglobin spectrum does not have any prominent spectral features; hence we used the concentration of oxy-hemoglobin from the first derivative approach to calculate the baseline absorption coefficient. Table 3 shows the results of the comparisons between the two approaches.
Table 3. Comparison of reduced scattering coefficients obtained from two methods (from the fit and by calculation from the DPF formula). The subscripts 1 and 2 refer to the 1st and 2nd derivative of absorbance methods.
| DPF | HHb μM | Water % | |||||
|---|---|---|---|---|---|---|---|
| Baseline | 3.4 | 21 | 85 | 0.021 | 0.022 | 0.40 | 0.46 |
| Occlusion | 3.7 | 20 | 84 | 0.013 | 0.014 | 0.45 | 0.42 |
| Baseline | 3.6 | 22 | 84 | 0.015 | 0.016 | 0.45 | 0.44 |
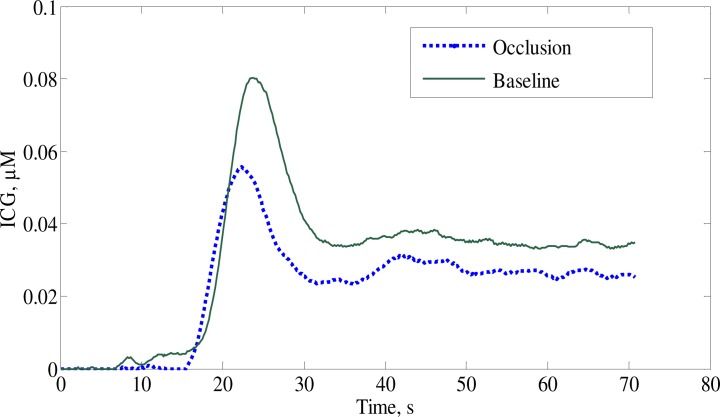
Using measured values of the piglet’s brain optical properties, one can recover the ICG time course curves from the signal changes around 810 nm, which corresponds to ICG’s absorption peak. Figure 5 . shows examples of ICG time traces. These traces were processed with a de-convolution routine to obtain CBF values shown in Table 2 along with the blood volume and the mean transit time.
Fig. 5.
Time traces of the brain ICG concentrations during baseline and occlusion
Table 4 shows the comparison of the average cerebral blood flow over a range of hemodynamic conditions with the computed tomography (CT) results as a gold standard (clinically approved and validated technique to measure CBF [23,24]).
Table 4. Comparison of CBF measurement using continuous-wave NIRS with CT result.
| Hemodynamic conditions | Group mean “CBF” ml/min/(100 g) | Group mean “CBF” ml/min/(100 g) | Mean difference ml/min/(100 g) |
|---|---|---|---|
| NIRS | CT | ||
| Baseline | 52.9 | 48.3 | 4.6 |
| Occlusion | 32.2 | 29.9 | 2.3 |
4. Discussion
Previously we tested our broadband continuous-wave approach in a phantom study [5], in which we were able to reconstruct the concentration of the chromophore (carbon black) of homogenous phantoms with the accuracy better than 4% and the values of reduced scattering coefficient with the accuracy 5-10%. In the present study we applied our method in vivo. We have demonstrated the feasibility of a broadband continuous-wave spectroscopy technique to obtain baseline optical properties of a homogenous tissue (newborn piglets’ brain) in vivo and to reconstruct the ICG concentration changes in the respective tissue with a reasonable accuracy.
The use of spectral derivative was very important for the enhancement of the chromophore spectral features and elimination of the source and detector-surface coupling artefacts, which could cause vertical shifts of the absorbance spectral curves. The advantage of using first derivative of the absorbance was that the concentration of chromophores with less pronounced or broad spectral features, such as oxy-hemoglobin, could be well determined. The required priors for this study were the extinction coefficients spectra of physiologically important chromophores existing in the tissue, as well as ICG’s, as an exogenous chromophore. The focus of this work was to model the wavelength dependent effects of scattering, which let us using both first and second spectral derivatives of absorbance data for the analysis. The differential path length factor (DPF) in the brain tissue was obtained from the second spectral derivative technique, which was in good agreement with the previous reports of DPF values in the piglet’s brain [25]. In addition we obtained an average cerebral water concentration of which was an additional constraint in the first derivative process to obtain more accurate values of reduced scattering. It is evident that water concentrations from both 1st and 2nd derivative technique were in agreement with other studies [16]. We used ICG bolus tracking method to measure CBF which was similar in principle to the contrast-enhanced CT and MRI techniques [26].
The value of the reduced scattering coefficient near 800 nm produced the strongest effect on the recovered values of the ICG concentration. On the other hand, the measurement of the scattering properties could not be separated from the measurement of all chromophore concentrations. We obtained the concentrations of oxy-, and deoxy-hemoglobin and water close to those obtained by the frequency-domain technique [3]. In addition, our values of reduced scattering coefficients of the brain tissue (for 27 mm source detector distance) were in the same range obtained by Fantini et al. using frequency domain technique [23]. Moreover, using the baseline parameters, we obtained relatively accurate ICG concentration values, which resulted in reasonable values of CBF.
5. Conclusions and future work
We obtained reasonable in vivo values of oxy- and deoxy-hemoglobin and water concentrations compared to other studies and techniques. Using our recovered temporal changes of ICG concentrations with a bolus tracking method, we obtained reasonable CBF, CBV and MTT values according to the respective hemodynamic conditions. Both second derivative, using MBLL, and first derivative, using diffusion equation produced similar baseline values of deoxy-hemoglobin concentrations, which indicated that there was no influence of possible artifacts in our reference signal. Obtaining the values of reduced scattering coefficient and water concentration independently from the first derivative was quite difficult but using the second derivative approach to obtain the water concentration made the values of reduced scattering coefficient more reproducible and reasonable. Our phantom experiment showed a good sensitivity of the system to the scattering properties of the medium.
In the future we plan to perform a more detailed analysis of different factors on the accuracy of measured CBF, such as the required accuracy of the extinction spectra, of the baseline optical properties and the actual shape of tissue layers. Moreover, we will apply our broadband fitting technique, which was earlier successfully tested on the two-layer tissue phantoms, to multilayered geometry of the adult pig head with non-negligible extra cerebral layers and ultimately hope to achieve an adaptation to human studies.
Acknowledgments
This work was supported in part by a grant from the Heart and Stroke Foundation of Canada and a discovery grant from the Natural Science and Engineering Research Council, as well as by the Ryerson University Research Fund.
References
- 1.Marin T., Moore J., “Understanding near-infrared spectroscopy,” Adv. Neonatal Care 11(6), 382–388 (2011). [DOI] [PubMed] [Google Scholar]
- 2.Landsman M. L. J., Kwant G., Mook G. A., Zijlstra W. G., “Light-absorbing properties, stability, and spectral stabilization of indocyanine green,” J. Appl. Physiol. 40(4), 575–583 (1976). [DOI] [PubMed] [Google Scholar]
- 3.Choi J., Wolf M., Toronov V., Wolf U., Polzonetti C., Hueber D., Safonova L. P., Gupta R., Michalos A., Mantulin W., Gratton E., “Noninvasive determination of the optical properties of adult brain: near-infrared spectroscopy approach,” J. Biomed. Opt. 9(1), 221–229 (2004). 10.1117/1.1628242 [DOI] [PubMed] [Google Scholar]
- 4.Hunter R. J., Patterson M. S., Farrell T. J., Hayward J. E., “Haemoglobin oxygenation of a two-layer tissue-simulating phantom from time-resolved reflectance: effect of top layer thickness,” Phys. Med. Biol. 47(2), 193–208 (2002). 10.1088/0031-9155/47/2/302 [DOI] [PubMed] [Google Scholar]
- 5.Pucci O., Toronov V., St Lawrence K., “Measurement of the optical properties of a two-layer model of the human head using broadband near-infrared spectroscopy,” Appl. Opt. 49(32), 6324–6332 (2010). 10.1364/AO.49.006324 [DOI] [PubMed] [Google Scholar]
- 6.Matcher S. J., Cope M., Delpy D. T., “Use of the water absorption spectrum to quantify tissue chromophore concentration changes in near-infrared spectroscopy,” Phys. Med. Biol. 39(1), 177–196 (1994). 10.1088/0031-9155/39/1/011 [DOI] [PubMed] [Google Scholar]
- 7.Nabavi D. G., Dittrich R., Kloska S. P., Nam E. M., Klotz E., Heindel W., Ringelstein E. B., “Window narrowing: a new method for standardized assessment of the tissue at risk-maximum of infarction in CT based brain perfusion maps,” Neurol. Res. 29(3), 296–303 (2007). 10.1179/016164107X158956 [DOI] [PubMed] [Google Scholar]
- 8.Diop M., Elliott J. T., Tichauer K. M., Lee T.-Y., St Lawrence K., “A broadband continuous-wave multichannel near-infrared system for measuring regional cerebral blood flow and oxygen consumption in newborn piglets,” Rev. Sci. Instrum. 80(5), 054302 (2009). 10.1063/1.3123347 [DOI] [PubMed] [Google Scholar]
- 9.S. Chandrasekhar, Radiative Transfer (Oxford University Press, New York, 1960). [Google Scholar]
- 10.V. V. Sobolev and A. Treatise, Radiative Transfer (Van Nostrand-Reinhold, Prinston, NJ, 1963). [Google Scholar]
- 11.K. M. Case and P. Z. Zweifel, Linear Transport Theory (Addison-Wesley, Reading, MA, 1967). [Google Scholar]
- 12.A. Ishimaru, Wave Propagation and Scattering in Random Media (Academic, New York 1978). [Google Scholar]
- 13.Fantini S., Franceschini M. A., Gratton E., “Semi-infinite geometry boundary problem for light migration in highly scasttering media: a frequency domain study in the diffusion approximation,” J. Opt. Soc. Am. 11(10), 2128–2138 (1994). 10.1364/JOSAB.11.002128 [DOI] [Google Scholar]
- 14.Patterson M. S., Chance B., Wilson B. C., “Time resolved reflectance and transmittance for the non-invasive measurement of tissue optical properties,” Appl. Opt. 28(12), 2331–2336 (1989). 10.1364/AO.28.002331 [DOI] [PubMed] [Google Scholar]
- 15.Kienle A., Patterson M. S., “Improved solutions of the steady-state and the time-resolved diffusion equations for reflectance from a semi-infinite turbid medium,” J. Opt. Soc. Am. A 14(1), 246–254 (1997). 10.1364/JOSAA.14.000246 [DOI] [PubMed] [Google Scholar]
- 16.Delpy D. T., Cope M., van der Zee P., Arridge S., Wray S., Wyatt J. S., “Estimation of optical pathlength through tissue from direct time of flight measurement,” Phys. Med. Biol. 33(12), 1433–1442 (1988). 10.1088/0031-9155/33/12/008 [DOI] [PubMed] [Google Scholar]
- 17.Elliott J. T., Diop M., Tichauer K. M., Lee T.-Y., St Lawrence K., “Quantitative measurement of cerebral blood flow in a juvenile porcine model by depth-resolved near-infrared spectroscopy,” J. Biomed. Opt. 15(3), 037014 (2010). 10.1117/1.3449579 [DOI] [PubMed] [Google Scholar]
- 18.Brown D. W., Picot P. A., Naeini J. G., Springett R., Delpy D. T., Lee T.-Y., “Quantitative near infrared spectroscopy measurement of cerebral hemodynamics in newborn piglets,” Pediatr. Res. 51(5), 564–570 (2002). 10.1203/00006450-200205000-00004 [DOI] [PubMed] [Google Scholar]
- 19.Elliott J. T., Diop M., Lee T. Y., Lawrence K. S., “Model-independent dynamic constraint to improve the optical reconstruction of regional kinetic parameters,” Opt. Lett. 37(13), 2571–2573 (2012). 10.1364/OL.37.002571 [DOI] [PubMed] [Google Scholar]
- 20.Woodard H. Q., White D. R., “The composition of body tissues,” Br. J. Radiol. 59(708), 1209–1218 (1986). 10.1259/0007-1285-59-708-1209 [DOI] [PubMed] [Google Scholar]
- 21.B. Hallacoglu, A. Sassaroli, M. Wysocki, E. Guerrero-Baruah, M. Beeri, V. Hartounian, M. Shaul, I. Rosenberg, A. M. Troen, and S. Fantini, “Absolute optical measurements of cerebral optical coefficients and hemoglobin concentrations in aging and younger human subjects,” in Biomedical Optics, OSA Technical Digest (Optical Society of America, 2012), paper BTu3A.61. [Google Scholar]
- 22.Fantini S., Hueber D., Franceschini M. A., Gratton E., Rosenfeld W., Stubblefield P. G., Maulik D., Stankovic M. R., “Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy,” Phys. Med. Biol. 44(6), 1543–1563 (1999). 10.1088/0031-9155/44/6/308 [DOI] [PubMed] [Google Scholar]
- 23.Konstas A. A., Goldmakher G. V., Lee T. Y., Lev M. H., “Theoretic basis and technical implementations of CT perfusion in acute ischemic stroke, part 1: Theoretic basis,” AJNR Am. J. Neuroradiol. 30(4), 662–668 (2009). 10.3174/ajnr.A1487 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Konstas A. A., Goldmakher G. V., Lee T. Y., Lev M. H., “Theoretic basis and technical implementations of CT perfusion in acute ischemic stroke, part 2: technical implementations,” AJNR Am. J. Neuroradiol. 30(5), 885–892 (2009). 10.3174/ajnr.A1492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Springett R., Sakata Y., Delpy D. T., “Precise measurement of cerebral blood flow in newborn piglets from the bolus passage of indocyanine green,” Phys. Med. Biol. 46(8), 2209–2225 (2001). 10.1088/0031-9155/46/8/312 [DOI] [PubMed] [Google Scholar]
- 26.Wintermark M., Sesay M., Barbier E., Borbély K., Dillon W. P., Eastwood J. D., Glenn T. C., Grandin C. B., Pedraza S., Soustiel J. F., Nariai T., Zaharchuk G., Caillé J. M., Dousset V., Yonas H., “Comparative overview of brain perfusion imaging techniques,” Stroke 36(9), e83–e99 (2005). 10.1161/01.STR.0000177884.72657.8b [DOI] [PubMed] [Google Scholar]