Tissue dynamics spectroscopy for phenotypic profiling of drug effects in three-dimensional culture

Abstract

Coherence-gated dynamic light scattering captures cellular dynamics through ultra-low-frequency (0.005–5 Hz) speckle fluctuations and Doppler shifts that encode a broad range of cellular and subcellular motions. The dynamic physiological response of tissues to applied drugs is the basis for a new type of phenotypic profiling for drug screening on multicellular tumor spheroids. Volumetrically resolved tissue-response fluctuation spectrograms act as fingerprints that are segmented through feature masks into high-dimensional feature vectors. Drug-response clustering is achieved through multidimensional scaling with simulated annealing to construct phenotypic drug profiles that cluster drugs with similar responses. Hypoxic vs. normoxic tissue responses present two distinct phenotypes with differentiated responses to environmental perturbations and to pharmacological doses.

1. Phenotypic profiling of physiological drug effects

Over the past decade, drug discovery has placed less emphasis on biochemical target-based assays and relied more on live cell-based assays because they more accurately measure how signaling pathways respond to drugs at a systems-biology level [1]. Now, a new evolution is in progress in cell-based assays away from two-dimensional cell monolayer culture to three-dimensional tissue culture because three-dimensional tissue presents a more natural environment to cells [2,3], with contacts to the extracellular matrix and to other cells that affects intercellular signaling that translates to more natural intracellular signaling [4,5] and gene expression [6–8]. The cellular dimensionality and microenvironment exert an essential influence on cancer drug sensitivity [9,10] or resistance [11,12] of 3D cultures relative to 2D monolayers. This impacts false positive selection when drugs are more effective in 2D than in 3D [13,14], resulting in promising early drug leads failing to perform in animal models because most cytotoxic anticancer drugs are less effective in killing tumor cells within multicellular tissues than as grown as monolayer cultures [15]. There is an even more important impact for false negative selection in drug screening, in which drugs are more effective in 3D than in 2D [16–18], but drugs are eliminated at the 2D screening stage that could have been valuable.

Of particular relevance for drug testing is the functional response of cellular tissue to applied drugs. Altered physiological behavior is the result of drug-altered signaling pathways, affecting organelle and vesicle activity, intracellular organization and cytoplasmic streaming, cell division, membrane undulations, cell contacts and cell shape changes. While these dynamic processes can be viewed in two-dimensional monolayer using conventional microscopies, it is more biologically relevant but challenging to extract subcellular motion up to a millimeter deep inside three-dimensional tissue culture. Dynamic images of live tissue are captured by motility contrast imaging (MCI), which measures intracellular motions [19,20]. Motility contrast imaging is an extension of optical coherence imaging (OCI) [21–23] that is an en face version [24–26] of time-domain optical coherence tomography [27,28].

Three-dimensional tissue culture includes multicellular layers (MCL) [29,30], multicellular tumor spheroids (MCT) [31,32], and matrix-based tissue growth [33,34] in which cancer morphogenesis progression and metastasis are strongly dependent on a three-dimensional environment. Thin layers and small nodules can be imaged using conventional techniques, such as confocal fluorescence [35,36], two-photon [37,38], optical projection tomography (OPT) [39] and single-plane illumination projection (SPIM) [40]. However, thicker tissues that can form distinct morphologies like necrotic or hypoxic cores are too thick for these non-invasive imaging techniques. Tumor spheroids can be assayed using conventional invasive techniques [41], but it would be valuable to use non-invasive techniques. High-frequency ultrasound microscopy has been used to probe internal spheroid structure, as well as structural response to applied drugs [42,43]. Here, as an alternative approach, we use laser-ranging and coherence-domain detection with digital holography because it allows for the analysis of temporal fluctuations caused by intracellular motions.

By using low-coherence light and off-axis digital holography to perform as the coherence gate, tissue-scale motional information is obtained with volumetric localization to 30 μm. For instance, motility contrast images of tumor spheroids show strong motion in the outer proliferating shell surrounding a necrotic core. The motility contrast is sensitive to applied drugs and can be used to construct dose-responses. Motility contrast imaging recently has been extended to tissue dynamics spectroscopy (TDS) [44] that is a coherence-gated form of diffusing wave spectroscopy [45,46]. Depth-sectioned dynamic speckle is captured at a high frame rate and analyzed across broad frequencies that correspond to a subcellular velocity range between 2 nm/sec and 2 μm/sec. Spectrograms were cross-correlated previously to highlight similarities and differences among tissue responding to applied drugs [44]. In this paper, we demonstrate the use of tissue dynamics spectroscopy as a new phenotypic screening technology, based on spectrogram feature extraction and dimensionality reduction, and we study the phenotypic drug response of normoxic tissue relative to hypoxic tissue inside multi-cellular tumor spheroids.

2. Experimental samples and methods

To create tumor spheroids, rat osteogenic sarcoma UMR-106 cells were cultured in Dulbecco’s modified Eagles’ medium and then transferred to a rotating bioreactor where they form spheroids in 7-10 days. The spheroids were grown up to 1 mm in diameter. As tumor spheroids are cultured and grow beyond a diameter of approximately 400 μm, nutrient and oxygen transport gradients [47] induce hypoxia and acidosis in the core of the tumor [48] accompanied by a transition to glycolysis [49]. This results in cellular quiescence, apoptosis and eventually necrosis in the spheroid core surrounded by an outer shell with a 100 to 200 μm thickness of proliferating cells [50–52]. The hypoxic core of moderately sized tumor spheroids are important models to study the effect of hypoxia-induced oncological transformations [53,54], as well as chemoresistance to therapy induced by an hypoxic microenvironment [55].

Rat osteogenic tumor spheroids are relatively translucent tumors with strong forward scattering [56,57]. There is a weak tumor size dependence to the extinction coefficient with decreasing extinction with increasing tumor size. The extinction coefficient varies from 15 mm⁻¹ to 8 mm⁻¹ for tumors of diameter 0.3 mm to 1 mm diameter. The anisotropy factor is approximately g = 0.9 for smaller tumors, and decreases to 0.85 for larger tumors [58].

Tissue dynamics imaging is performed using a low-coherence Mach-Zehnder configuration (see [59] for a description of the optical system). The short-coherence light source for these experiments is a 100 fsec Ti:sapphire laser with a center wavelength of 840 nm. The intensity at the tumor is approximately 0.5 W/cm² in a beam diameter of approximately 1 mm. The backscattered light from the tumor spheroid is converted to linear polarization and passes through a polarizing beam splitter (PBS) to the lens that forms an image at the image plane. This image is transformed again by the second lens to a Fourier transform on the CCD chip.

The digital holography is performed in an off-axis configuration. A high acquisition rate of 10 frames per second is followed by a low acquisition rate of 0.5 frames per second. There are 200 frames captured under the high acquisition rate followed by 100 frames captured under the low acquisition rate. Each spatial Fourier-domain hologram frame on the CCD is transformed using a simple 2D FFT which is fast, and requires no extensive characterization of the reference wave. After reconstruction, the field of view is approximately 1 mm, sufficient to image a tumor spheroid, and the depth of focus is 0.5 mm with the focal plane set to the mid-section of the spheroid. The transverse resolution of the image is approximately 15 μm and the longitudinal coherence depth is approximately 20 μm. We perform a temporal frequency analysis of the transformed time-dependent speckle for each pixel and generate a power spectrum with a frequency range from 0.005 Hz to 5 Hz covering 3 orders of magnitude. Each of these data sets is acquired every four minutes for the duration of the experiment, which is typically 6−9 hours, but can extend up to 72 hours.

Tissue dynamics spectroscopy (TDS) analyzes the fluctuating speckle from a series of reconstructed frames. The power spectra are averaged over groups of pixels. For instance, the pixels belonging to the shell and to the core of a multicellular tumor spheroid are averaged separately to provide two low-noise spectra of the shell relative to the core. The shell consists of all pixels within 200 μm of the spheroid surface. The core consists of all other internal pixels. The power spectrum spans three orders of magnitude from the low-frequency plateau to the Nyquist floor. The value of the Nyquist floor at the Nyquist frequency is a combination of system noise plus the power spectrum of intracellular motions integrated between the Nyquist frequency and the detection bandwidth. The detection bandwidth is equal to the inverse of the frame exposure time, which is 10 msec for these data.

3. Tissue dynamics spectroscopy and imaging

To study drug effects on intracellular motions, we measure changes in spectral content as a function of time before and after a drug dose is applied to the sample. The differential relative drug response spectrogram is defined as

$$D\left(\nu ,t\right)=\frac{S\left(\nu ,t\right)-\overline{S}\left(\nu ,t_0\right)}{\overline{S}\left(\nu ,t_0\right)}$$ (1)

where $S\left(\nu ,t\right)$is the power spectrum at time t, and $\overline{S}\left(\nu ,t_0\right)$ is a baseline average power spectrum, taken as the average of 40 baseline spectra acquired every four minutes prior to the application of the drug dose.

The power spectra originate from dynamic light scattering from the moving constituents of the cells and tissues. In a system with a single-exponential speckle decorrelation function, a shift in the decorrelation time τ produces a small-signal tissue-response spectrogram as a function of frequency ν and time t with the form

$$D\left(\nu ,t\right)=\frac{\Delta \nu }{{\nu }_0}\left(\frac{{\nu }^{1+\beta }-{\nu }_0^{1+\beta }}{{\nu }^{1+\beta }+{\nu }_0^{1+\beta }}\right)$$ (2)

where ${\nu }_0=1/2\pi \tau$ is the knee frequency of the power spectrum, and $\Delta \nu =\Delta \tau /2\pi {\tau }^2$ is the shift in the decorrelation time, and β is the anomalous diffusion exponent (usually between 0.7 and 1.3). This simple response function is bounded between ±1 and switches sign at the knee frequency. However, living tissue is much more complicated, with many different contributions across the frequency range, and the decorrelation functions are often stretched exponentials. Furthermore, the small-signal limit of Eq. (2) is often not appropriate for strong drug responses. Therefore, experimental tissue-response spectrograms usually exhibit complicated structure that form the basis of unique drug fingerprints.

We assembled tissue-response spectrograms from 28 environmental conditions and pharmacological concentrations. The multicellular tumor spheroids for this study had diameters that ranged between 500 and 800 μm. The spectrograms were generated for the proliferating shell and the core separately. For spheroids of this size, the core is starved of oxygen and nutrients. In some cases, this leads to necrotic cores, but more commonly it leads to cores that have lower metabolism. The lower metabolism of the core relative to the shell provides an opportunity to look at phenotypic profile differences mediated by the difference in metabolism. The conditions and concentrations in Table 1 correspond to the drug-response spectrograms shown in Fig. 1 . Spectrograms of the shell and core are shown in each case, for a total of 56 spectrograms. The colorscale is between −0.6 and +0.6 on a linear scale.

Table 1. Environmental conditions and pharmacological concentrations.

Nocodazole 0.01 µg/ml	Nocodazole 0.1 µg/ml	Nocodazole 1 µg/ml	Nocodazole 10 µg/ml
Colchicine 1 µg/ml	Colchicine 10 µg/ml	Taxol 1 µg/ml	Taxol 10 µg/ml
Neg Control	Cytochalasin D 1 µg/ml	Cytochal. D 10 µg/ml	Cytochalasin 50 µg/ml
Iodoacetate 1 µg/ml	Iodoacetate 10 µg/ml	Iodoacetate 20 µg/ml	Iodoacetate 40 µg/ml
pH 5	pH 6	pH 8	pH 9
77 Osm	154 Osm	428 Osm	508 Osm
KCN 20 µg/ml	KCN 200 µg/ml	TFN 5 µg/ml	Cyclohex. 10 µg/ml

Fig. 1.

Differential response spectrograms for 28 different drugs, doses and conditions divided into separate responses for the shell (upper) and core (lower). For each spectrogram, frequency is along the vertical axis from 0.005 Hz to 5 Hz, and time is along the horizontal axis for 6 hour durations after the dose or perturbation is applied (vertical line).

The spectrograms show a range of signatures for the different conditions and concentrations. Some drugs, such as Colchicine, were applied at high dose that produced strong differential changes. Other drugs, such as KCN, showed only minor spectral changes even at high doses. Temporal dynamics are observed in some cases, as for Iodoacetate, and temporal drifts are observed for high osmolarity and high pH. The dose dependence is clear in some cases, but in others there can be qualitatively different high-dose behavior relative to low-dose behavior, as for Iodoacetate and cytochalasin. Furthermore, there can be strong differences between the spectrograms of the shell and core for the same drug and concentration, as for cytochalasin at 10 μg/ml. The different patterns observed in this collection of spectrograms provide the opportunity to perform feature identification and extraction as the first step to generate phenotypic profiles for these drugs and conditions.

4. Drug response fingerprinting

The drug-response spectrograms exhibit recognizable features that occur in characteristic frequency ranges at characteristic times after a dose is applied. Our approach to feature recognition and quantification of the drug-response spectrograms is based on projections of the spectrograms onto feature masks. There are many possible choices for feature masks, such as binary masks versus continuous-valued masks, local masks versus global masks, and orthonormal feature masks versus non-orthonormal. The time axis on the spectrograms primarily captures relaxation which is typically exponential. The frequency axis is the Fourier transform of the autocorrelation function, which also is typically exponentially correlated. Therefore, both the time and frequency axes are characterized by Laplace transforms for which there is no orthonormal basis. Therefore, we take the approach of matched filtering [60] in which characteristic regions of the spectrograms can be interpreted mechanistically. For instance, we have shown [59] that low frequencies correspond to large-scale motion like blebbing or the formation of apoptotic bodies, while high frequencies correspond to membrane vesicles or internal organelle motions. These processes and frequencies present natural frequency ranges within our data that are used to generate feature masks to extract these specific features.

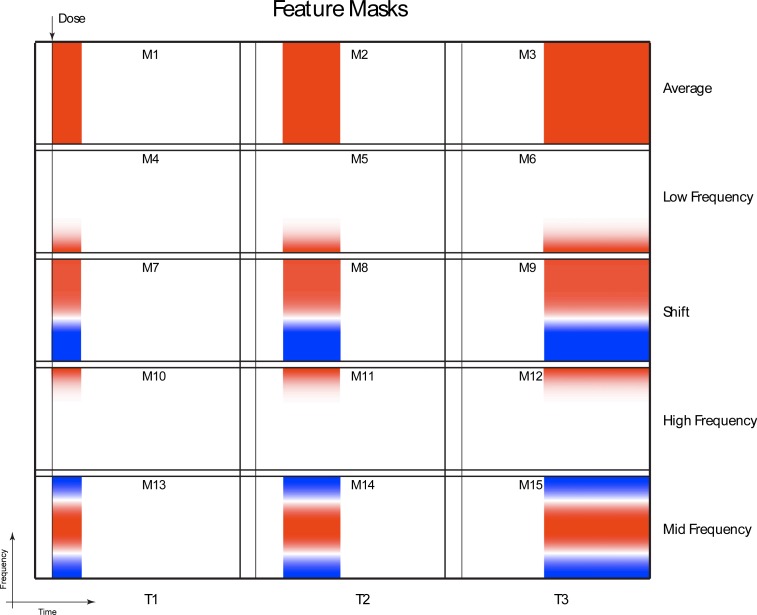
Along the time axis, we apply an increasing sampling for the feature masks, sampling at short times (0 to 50 minutes) for fast response, mid times (50 to 150 minutes) for slower response and long times (150 to 350 minutes) for long-term response. Along the frequency axis, there are several characteristic frequencies that divide the response into natural frequency bands. These occur at 0.01 Hz, 0.1 Hz and 1 Hz. The resulting feature masks are shown in Fig. 2 . The three time frames and 5 frequency signatures generate 15 feature masks. Masks M1-3 capture the average spectral power change, masks M4-6 capture low-frequency, masks M7-9 measure the shift of the spectral weight to higher frequencies, masks M10-12 capture high frequency motions, and masks M13-15 capture enhanced mid frequencies. The cut-off frequencies and times for these masks were chosen based on spectral and time regions that occur with some consistency in the data of Fig. 1.

Fig. 2.

Feature masks for spectrogram feature extraction. The time-frequency space is divided into early time (0 to 50 min), mid-time (50 to 150 min) and late time (150 to 350 min), as well as frequency masks that extract the average, low frequency, frequency shift, high frequency and mid-frequency.

The value of a feature is obtained by the inner product of the kth feature mask $M_k\left(\nu ,t\right)$with the jth differential spectrogram $D^j\left(\nu ,t\right)$

$$V_k^j=\langle D^j\left(\nu ,t\right),M_k\left(\nu ,t\right)\rangle$$ (3)

that produces a k-dimensional vector component $V_k^j$where j is the index for a condition (drug or dose or perturbation), and k is the index for a feature (time-frequency signature). The brackets denote the inner product through

$$\langle D^j\left(\nu ,t\right),M_k\left(\nu ,t\right)\rangle =\frac{1}{N_{norm}}{\displaystyle \sum _{p,q}^{}{D}_{pq}^j{M}_{k,pq}}$$ (4)

where the indexes p, q are along the frequency and time axes, respectively. The normalization N_norm is

$$N_{norm}=\sqrt{{\displaystyle \sum _{p,q}^{}{M}_{pq}{M}_{pq}}{\displaystyle \sum _{i,j}^{}{D}_{pq}{D}_{pq}}}$$ (5)

where D_pq is taken only in the associated time region of the mask. This normalization captures the shape of features, but de-emphasizes the magnitude. This procedure is well suited to recognizing signature features and for clustering drug responses according to their features rather than the strength of their response. Alternatively, the feature vectors can remain unnormalized if dose-response behavior is the focus of interest in the analysis.

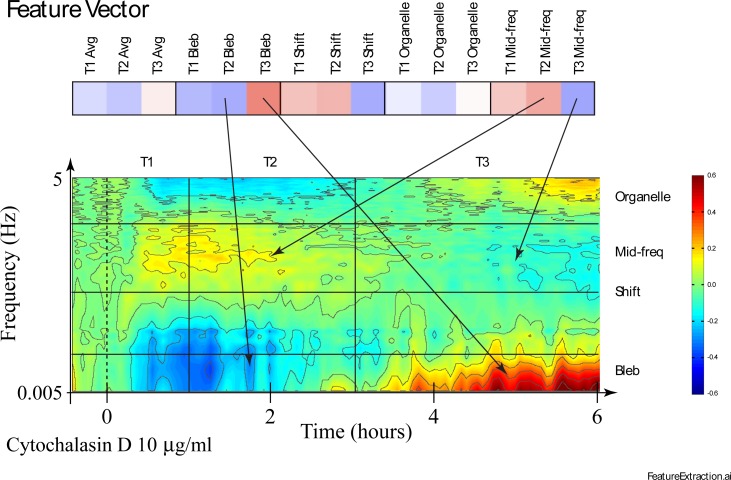
The inner product of each mask with the drug-response spectrogram generates a feature vector that serves as the one-dimensional fingerprint for that drug. An example of a drug-response feature vector is shown in Fig. 3 for 10 μg/ml Cytochalasin D applied to an 800 μm diameter tumor spheroid. The sensitivity of some of the features to the spectrogram is illustrated with arrows. Cytochalasin D weakens the actin cortex which causes enhanced membrane undulations in mid frequencies in the two short time frames T1 and T2. However, approximately 3 hours after applying this high dose, the frequency pattern shifts to high and low-frequency enhancements with mid-frequency suppression. The feature masks capture this change in the feature vector for this drug response.

Fig. 3.

Generation of a feature vector (represented as a pseudo-color row vector) from a drug-response spectrogram using the feature masks of Fig. 2. Characteristic times and frequencies are shown on the spectrogram. The arrows show the dominant contributions for several feature values. Blue-to-Red colorscale is from −0.6 to +0.6.

The stability and noise in the spectrograms are evaluated using negative controls in which growth medium is applied to the tumors using the same protocols as for the drug-response experiments. The noise levels are primarily determined by temperature stability and by low-frequency table vibrations. Typical negative controls exhibit spectral shifts less than 5%, compared to strong drug responses that reach as large as 80%. In our data set, nocodazole at 10 ng/ml and KCN at both 20 μg/ml and 200 μg/ml produced drug-response spectrograms that were not distinguishable from the negative controls. All other drugs, doses and conditions produced statistically significant data. Duplicates and triplicates were performed for some drugs that established the repeatability of the feature vectors to within 10%.

After the feature vectors are generated, they are used to generate a similarity matrix among all the different drugs and conditions. The similarity of the ith and jth spectrogram is defined as the normalized correlation

$$S^{ij}=\frac{{\displaystyle \sum _k^{}{V}_k^i{V}_k^j}}{\sqrt{{\displaystyle \sum _k^{}{V}_k^i{V}_k^i}{\displaystyle \sum _k^{}{V}_k^j{V}_k^j}}}$$ (6)

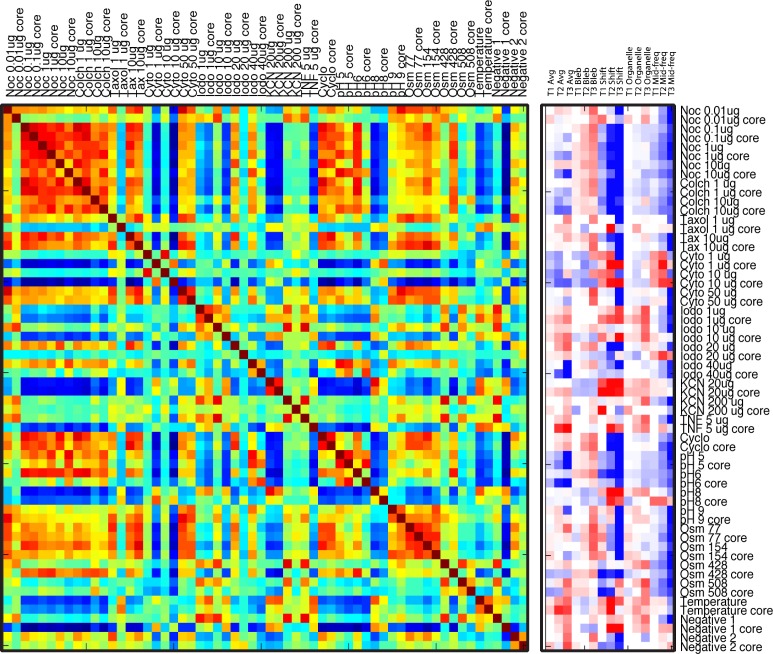
where the similarity is normalized to unity when i = j. The feature vectors $V_k^j$ and the similarity matrix $S^{ij}$ for the 28 doses and conditions of Table 1, plus two negative controls, are shown in Fig. 4 . In this figure, the proliferating shell and the core are treated independently, leading to 60 feature vectors and a 60x60 similarity matrix. The similarity matrix is unity along the main diagonal. The ordering in Fig. 4 is by drug and dose, with the shell alternating with the core. While there is some clustering of similarities, the similarity matrix and feature vectors do not show strong clustering, except for the tubulin destabilizing compounds that share many features in common.

Fig. 4.

Feature vectors and similarity matrix for 60 doses and conditions (treating the proliferating shell and the core independently). The ordering is by drug dose, with the shell alternating with the core.

5. Ordering, clustering and multidimensional scaling

Despite the grouping of increasing doses of some drugs (e.g., nocodazole, iodoacetate, cytochalasin, etc.), there is little structure to the matrix in Fig. 4. One of the goals of phenotypic profiling is to re-order the similarity matrix to group common drug responses together. There is no unique way to order similarity, and there are several common algorithms that lead to similar, but not identical, orderings. One common approach is unsupervised hierarchical clustering [61]. This is an iterative process that sequentially groups pairs of similar responses to produce tree structures. Unsupervised ordering has the advantage that no predefined structures or substructures are defined for the process, leading to an objective grouping of similar responses.

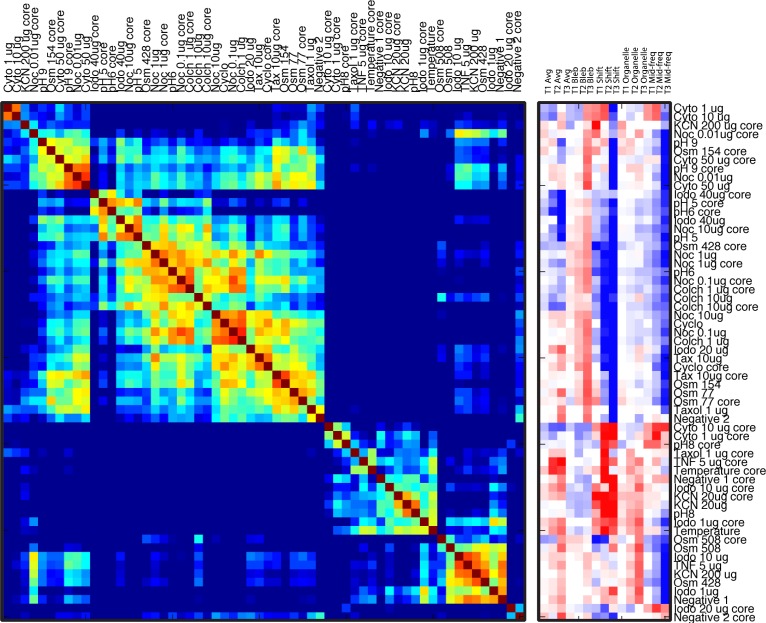
The similarity matrix and feature vectors after hierarchical clustering are shown in Fig. 5 . The similarity matrix is nearly block-diagonal in which similar spectrograms are grouped together, with low cross-talk among the groups. The feature vectors now also are grouped, showing groups of spectrograms that share features in common. Because the features we choose have putative physiological interpretations (blebbing, undulations and organelle motions) [59], the groupings of features also group the physiological responses into a phenotypic profile for these standard compounds and conditions.

Fig. 5.

Feature vectors and similarity matrix after unsupervised hierarchical clustering (treating shell and core independently).

There are several aspects to note in the ordered list. In general, similar compound classes are clustered together, such as the anti-tubulin drugs nocodazole and colchicine. But these cluster separately from taxol that is a tubulin stabilizing drug. In addition, similar environmental conditions cluster together, such as hypotonic osmolarity and low pH separately from hypertonic osmolarity and high pH. One aspect that is striking in its absence is the low correlation between the shell and the core response of the same tumor spheroid to the same compound or condition. This phenotypic difference between the shell and the core of a single spheroid is the topic of a later section.

The disadvantage of hierarchical clustering is that it produces a linear arrangement that does not faithfully represent distance between nodes. In addition, it is an ordering algorithm rather than a clustering algorithm [62]. To test the results of hierarchical clustering, we have also applied k-means clustering and level-set clustering on the raw similarity matrix in Fig. 4. The resulting ordering of the drugs and conditions change in detail, but the overall groupings and block-diagonal structure of the reordered similarity matrix remain nearly the same. However, none of these ordering or clustering algorithms faithfully represent the distance relationships that are contained within the similarity matrix. As subclusters are combined into larger clusters, especially in hierarchical clustering, it is possible to have two adjacent nodes that have low similarity and hence should be far apart. The final ordering is linear, and distance relationships are not represented.

A solution to this “distance” problem is provided by multidimensional scaling (MDS) [61]. In multidimensional scaling, a low-dimensional representation is sought in which similar response nodes are placed close to one another and dissimilar response nodes are placed far apart. The spatial near-far relationships in the low-dimensional graph preserve the high-dimensional near-far relationships of the original feature vectors. Multidimensional scaling is not a “projection” to a lower dimensional plane, but is instead a one-to-one mapping that retains ordering of distances. Although the actual metric distances are lost in the process, as with all data compression, the general relationships of nearness or similarity are preserved.

To apply multidimensional scaling to the similarity matrix, a distance matrix is defined as$d^{ij}=1-S^{ij}$. The MDS algorithm assigns a cost function that is to be minimized. The cost function is the difference between the distance of the two-dimensional location of nodes and the distance defined from the similarity matrix. The cost function is

$$C={\displaystyle \sum _{j>i}^{}{\left(\left|r_i-r_j\right|-d_{ij}\right)}^2}$$ (7)

where r_i is a vector in the low-dimensional target space. We use a simple Euclidean distance norm in the target space. This cost function is minimized using simulated annealing [63] starting from a set of initial positions in two dimensions determined by the first two principal components from principal component analysis [61]. The simulated annealing proceeds through 1000 iterations, with a 0.1% decrease in effective temperature at each iteration. The final positions that emerge from the MDS algorithm appear in the low-dimensional space in a pattern that preserves the trend of distances d_ij from the high-dimensional space spanned by the feature vectors.

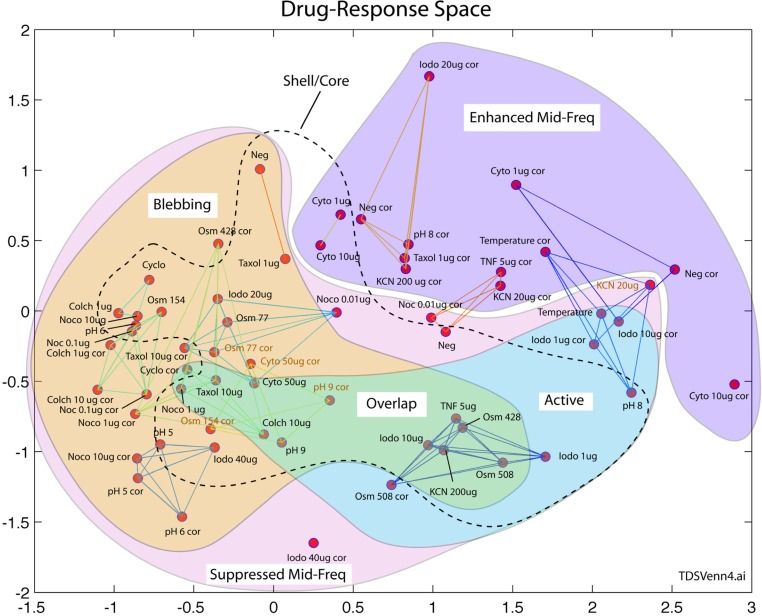
The results of multidimensional scaling of the data in Fig. 4 are shown in Fig. 6 . This low-dimensional phenotypic space has two dimensions. The axes do not have direct physical meaning, but the distribution of nodes retains the ordering of distances that occur in the similarity matrix of Fig. 4. Similar drug responses are grouped closely, and far from other unrelated drug responses. Because of this spatial grouping and separation, it is possible to draw a Venn diagram based on the physiological features in the feature vectors. The Venn diagram shows the drug responses with enhanced mid-frequency, blebbing (enhanced low-frequency) and active (enhanced high frequency). The network connections drawn on the figure are from k-means clustering and show local clusters. The dashed line shows a separation between core response (outside the line) and shell response (inside the line). There are exceptions in this shell-core separation for hypotonic osmolarity, high pH and high-dosage cytochalasin, but in general the shell responses lie closer together near the center of the phenotypic space than the outlying core responses.

Fig. 6.

Multidimensional scaling of the data from Fig. 4 displayed in a two-dimensional phenotypic space. The grouping of the drug responses preserves the overall ordering of distances from the similarity matrix of Fig. 5. Physiological responses are overlain in a Venn diagram based on shared features.

An interesting region is the overlap between blebbing and active organelle/vesicle transport. Taken together, these may be expected if there is apoptosis during which apoptotic bodies are separated from the main cell, and active organelle transport drives the cellular decomposition. There are no drug responses in this overlap region from the hypoxic core which is ATP depleted and cannot support apoptosis. This shell-core separation of putative apoptosis is discussed in the next section.

6. Proliferating shell and hypoxic core phenotypes

As an example of phenotypic profiling based on hypoxic phenotypes, multicellular tumor spheroids provide a natural format to study phenotypic differences in the drug response between normoxic and hypoxic tissue. When tumor spheroids have a diameter larger than approximately 400 μm, the transport of oxygen into the core of the spheroid is impeded, resulting in hypoxic tissue and a band of quiescent cells inside the outer shell of proliferating cells [48]. There is evidence that the phenomenon of multicellular resistance to anticancer drugs displayed by avascular solid tumors is caused, in part, by the population of quiescent cells [64,65]. In addition, hypoxia is a factor in oncogenic progression [53,54] and may participate in the epithelial to mesenchymal transition that ultimately leads to metastasis [66–69]. For these reasons, comparing the effect of anticancer drugs on the hypoxic core relative to the quiescent or proliferating shells may shed light on multicellular resistance.

An understanding of the shell-core differences can be gained by analyzing the shell and core spectrograms responding to cytochalasin D at 50 µg/ml, shown in Fig. 7 . The core spectrogram shows an initially strong mid-frequency enhancement. After 2 hours, there is a strong onset of low-frequency enhancement for both the shell and the core. However, the shell shows a strong enhancement of the high-frequencies associated with vesicle and organelle transport that is missing in the core spectrogram response. This represents a significant physiological difference in the role of the drug for normoxic vs. hypoxic tissue. Because of our knowledge of the physiological processes of apoptosis (active transport requiring ATP and hence normal oxygen levels) relative to necrosis (passive degradation of the cell without need for ATP), we tentatively assign this phenotypic difference to apoptosis in the shell vs. necrosis in the core. This assignment of high-frequency fluctuations associated with apoptosis is consistent with decorrelation times measured using OCT in vitro [70,71], and is also supported by our confocal two-photon microscopy of these drugs on spheroids of these cell types to be discussed below.

Fig. 7.

Shell and core response spectrograms for cytochalasin D at 50 µg/ml. The spectrograms share similar features except for the high-frequency enhancement in the shell that is missing in the core. The colorscale is between −0.7 and +0.7.

The active transport that is present in the shell but missing in the core, combined with the presence of low-frequency enhancement that is common to both, suggests a metric that is the logical AND of both of the features to create an “apoptotic” index that quantitatively captures this feature. This index is constructed from the feature masks appropriate to the low- and high-frequency features, which are masks M6 and M12 of Fig. 3. We define the apoptotic index of the ith drug or condition, Aⁱ, by

$$\begin{array}{c}{A}^i=\mathrm{Re}\left\{M^i\right\}-\mathrm{Im}\left\{M^i\right\}\\ M^i=sqrt\left(V_6^i\right)sqrt\left(V_{12}^i\right)\end{array}$$ (10)

in which $V_6^i$ and $V_{12}^i$ are the feature vector values for masks M6 and M12. The difference between the real and the imaginary parts generates the logical AND with positive apoptotic indexes only for features that themselves are both positive.

The apoptotic index was calculated for the shell and the core spectrograms of Fig. 1 and ranked in decreasing order by the shell. The apoptotic index of the shell response for the top eight apoptotic indexes is shown in Fig. 8 . The strongest apoptotic index is for the shell responding to cytochalasin at 50 µg/ml. Also shown in Fig. 8 are the corresponding apoptotic indexes for the core responses in each case. For this set of 8 drug doses, that produced the strongest positive apoptotic indexes in the shell, the apoptotic index of the cores are all negative. In the cases when the shell has strong active transport in addition to strong low-frequency enhancements, the core is missing one or the other of these features. Upon closer inspection, the missing feature is the active transport band at high frequency in all cases. The key physiological aspect of the core is the lack of ATP to drive active processes, such as the formation of sequestering vesicles and apoptotic bodies. The negative apoptotic indexes of the core region for each of these drugs reflects the quiescent/hypoxic resistance of solid tumors to anti-cancer drugs. For instance, the anti-actin anti-mitotic drug cytochalsin D shows the strongest apoptotic index for the shell, but the strongest negative mitotic index for the core. Taxol and colchicine also show strong differences in the apoptotic index between the shell and the core. On the other hand, there is overlap in the low-frequency feature of the signatures between apoptosis and necrosis, and some necrosis also may be occurring in the shell in tandem with apoptosis.

Fig. 8.

Apoptotic index vs. shell rank for the top 8 apoptosis-inducing drug doses. The apoptotic index is negative for the core drug response in each case because of the absence of active transport in the hypoxic core.

The independent validation for apoptotic processes to confirm their participation in the drug response was obtained through a series of multiphoton confocal microscopy experiments carried out using the UMR-106 spheroids. Spheroids were cultured at 37 °C in the presence of 10 µg/mL cytochalasin D, paclitaxel, and colchicine for 4 hours and iodoacetate for 3 hours. The live, apoptotic, and dead cells in the spheroid outer shell were visualized by optical section using a 20X water immersion objective up to a depth of 100 µm using Hoechst 33342 (live), Yo-Pro-1 (apoptotic), and propidium iodide (dead) (Invitrogen, Grand Island, NY) vital dyes on a Nikon A1R multiphoton microscope with Mai Tai DeepSee tunable IR laser at 750 nm. The percentage of live, apoptotic, and dead cells in the spheroid outer shell was determined for six different spheroids for each drug. One μm optical sections through the outer shell of the spheroid were obtained up to a depth of 100 µm and the number of live/apoptotic/dead cells determined. Apoptotic or dead cells are rare on the outer rim of a control spheroid, but several cell layers deep begins to pick up apoptotic or dead cells. Smaller spheroids have better “live” numbers than older larger spheroids.The results for colchicine, paclitaxel, cytochalasin D, nodocazole and iodoacetate are shown in Table 2 for six replicates. These data show that paclitaxel, nocodazole, cytochalasin and iodoacetate all induce an apoptotic response in the tumor spheroids, with cytochalasin having the largest apoptotic fraction with nocodazole and colchicine having the smallest. These confocal rankings are consistent with the apoptotic index shown in Fig. 8 from TDS.

Table 2. Percentage of live/apoptotic/dead cells in 100 µm optical section of 300-600 µm diameter UMR-106 tumor spheroids.

10 µg/mL	Percent of cells after a 3 hr* or 4 hr** incubation (±S.E.M)
	Live	Apoptotic	Dead
**Control	89.6 ± 2.2	8.3 ± 1.7	1.7 ± 0.68
**Colchicine	65.9 ± 2.7	28.2 ± 2.3	5.7 ± 1.5
**Paclitaxel	63.1 ± 2.4	27.6 ± 1.4	9.1 ± 1.8
**CytochalasinD	56.5 ± 4.6	33.1 ± 3.3	10.2 ± 1.6
*Nocodazole	71.6 ± 2.4	23.8 ± 2.4	4.3 ± 0.33
*Iodoacetate	57.4 ± 2.8	31.8 ± 2.8	10.9 ± 2.3

7. Conclusions

The dynamical consequence of function is motion. As cells and tissues respond to their environment, and respond to applied drugs, the way that they carry out their functions is affected. Coherence-gated dynamic light scattering collects these changes in motion, which are separated out by fluctuation spectroscopy. Changes in different types of motion become biomarkers that are related to mechanism of action. These motional biomarkers are sensitive and subtle, but are not one-to-one with mechanism. Therefore, bioinformatics approaches are needed to distinguish among the many on-target and off-target drug effects.

In this paper, we used feature recognition to segment the information in the time-frequency tissue-response spectrograms to construct N-dimensional feature vectors. These feature vectors were used to generate a correlation matrix among 60 different drugs, doses and conditions. Several ordering or clustering algorithms were applied to the correlation matrix, generating block-diagonal structure that demonstrates the ability to identify distinct groups of drugs and environmental responses. However, one-dimensional ordering cannot represent the high-dimensional relationships among the feature vectors. Therefore, we applied multi-dimensional scaling with simulated annealing to form a two-dimensional map of response relationships that retains rank distances from the higher-dimensionality feature space. This two-dimensional phenotypic profile space displays compact regions such as regions of enhanced active transport and membrane undulations and blebbing. There is a clear separation of core responses from shell responses, and the overlap of active transport with blebbing is consistent with a high apoptotic index constructed by a logical AND of the relevant spectrogram features that correspond to blebbing and active transport.

The use of intracellular motion as an imaging contrast agent, together with its label-free and non-invasive character, provides an opportunity to develop a new three-dimensional tissue screen for many types of drugs in early drug discovery. The technique can be extended into a high-throughput format in the future that would be able to screen compound libraries in three-dimensional tissue prior to the transition to animal models. These fingerprinting and phenotypic profiling applications have been demonstrated here for the first time. Extension of motility contrast imaging to in vivo studies faces challenges related to the motion of living test animals, such as involuntary muscle movement, breathing and heart pumping. The low-frequency bands are probably precluded by these movements. However, the high-frequency regime of organelle transport (greater than 1 Hz) may still be accessible, especially if the data acquisition times are gated to the animal movement.