Abstract
As an integrated step towards a coherent polarizable force field for biomolecular modeling, we analyzed four polarizable water models to evaluate their consistencies with the Thole polarization screening schemes utilized in our latest Amber polarizable force field. Specifically, we studied the performance of both the Thole linear and exponential schemes in these water models to assess their abilities to reproduce experimental water properties. The analysis shows that the tested water models reproduce most of the room-temperature properties of liquid water reasonably well, but fall short of reproducing the dynamic properties and temperature-dependent properties. This study demonstrates the necessity to further fine-tune water polarizable potentials for more robust polarizable force fields for biomolecular simulations.
Introduction
Hydration interactions are crucial for stabilizing biomolecular structures and regulating functions. The interactions with water molecules are also important for facilitating biochemical reactions and enzyme activities. Accurate modeling of water interactions with itself and with biomolecules is therefore critical for computational studies of biomolecular dynamics and functions. A significant number of water models were developed in the last four decades. For computational efficiency, the commonly used water models in biomolecular simulations are characterized by rigid geometries and employ fixed partial charges. In the two widely used models proposed in 1980s, SPC1 and TIP3P,2 fixed partial charges are placed on the three atom centers along with a Lennard-Jones potential describing interactions between the water oxygen atom and other atoms in a simulation system. In the TIP4P model,2 Jorgensen et al. added a pseudo atom located at the bisection of the H-O-H angle carrying the negative partial charge of the water oxygen atom. In the TIP5P model,3 a five-site model, two pseudo atoms were added in a tetrahedral configuration. Reoptimization efforts for these models were also reported when the Ewald summation was incorporated into molecular simulation programs.4,5 It was reported that TIP5P agrees well with experiment in regard to several physical properties of water, such as density, enthalpy of vaporization, diffusion constant, and dielectric constant.3 Moreover, the radial distribution function of TIP5P model exhibits remarkable agreement with the experimental observations.6 A common approach in the development of these models was the adjustment of atomic partial charges to include the polarization effect implicitly in order to reproduce isotropic properties of bulk water. As a consequence, these models may not describe the electrostatic interactions in anisotropic environments, such as the vicinity of large biomolecules or water-membrane interface. Therefore, new-generation of force fields aiming at modeling anisotropic environments require water models that explicitly take the polarization effect into account.
Induced-dipole models, Drude-oscillator models, and fluctuating-charge models are three commonly-used approaches to describe the polarization effect explicitly in the polarizable force fields.7–20 In the induced-dipole models, point inducible dipoles are placed on specified atoms to mimic atomic polarization. This is the strategy employed in the Amber POL317 polarizable water model where point inducible dipoles are placed on all three atoms. In the four-site TTM2-R11 water model, point inducible dipoles are also put on the three atoms but not on the pseudo atom. An alternative approach in the four-site models is to place an inducible dipole only on the pseudo atom as suggested by Dang and Chang.8 In the Amoeba water model,13 polarization is represented by induced dipoles, while permanent multipoles up to quadrupoles are used to model electrostatic interaction, instead of solely relying on partial charges. In addition, Amoeba developers also utilized a flexible water structure to better capture various water properties. In the Drude-oscillator models, Drude particles are harmonically restrained to oscillate around heavy atoms to approximate polarization. The Drude-oscillator models are energetically equivalent to the induced-dipole models, though their dynamic properties can be different due to different simulation protocols that often have to be used.12,14–16,20 SWM4-DP12 and SWM4-NDP15 in the CHARMM force field were developed following this framework. In addition, the COS (charge-on-spring) models14,16,20 in the GROMOS force field can also be classified as Drude-oscillator models. In the fluctuating charge model proposed by Rick et al19 and Zhu et al,18 the partial atomic charges on polarizable atoms are environment-dependent. Thus the polarization effect is captured by the change of partial charges. More complicated water models combine two methods to model polarization. For example, POL5/TZ, POL5/QZ, and TTM2-F models combine fluctuating charge and induced dipole models.9,10
Our latest Amber polarizable force field utilizes the induced-dipole framework.21,22 In the induced-dipole models, the Applequist interaction scheme was first proposed.23 However, when the inter-atomic distance is smaller than a certain threshold, the strongly favorable electrostatic interaction may lead to the so-called “polarization catastrophe”. To overcome the drawback, Thole suggested to screen the polarization interactions when two atoms are too close to each other.24 Various functional forms have been proposed and several of them have been adopted by polarizable water models, for example, in AMOEBA and TTM2-R waters.10,11 An alternative strategy to overcome the “polarization catastrophe” is to damp the linear dependence between the polarization and the electrostatic field. For example, in the COS/D model the polarizabilities of atoms are field dependent:16 the polarizabilities are damped when the electrostatic field has higher magnitude than a predefined threshold to prevent the unlimited polarization.
In this study we analyzed four induced-dipole water models. Among these models, POL317 and Dang and Chang8 model are both induced-dipole models and were developed originally using the Applequist polarization scheme. The remaining two models are converted from the Drude-oscillator models SWM4-DP12 and SWM4-NDP15 from the CHARMM force field. We studied these models within both the Applequist and Thole schemes to evaluate their consistencies with our latest Amber polarizable force field development efforts.21,22 Their performances in reproducing bulk experimental water properties, both room-temperature and temperature-dependent, are discussed in detail below.
Methods
Model specifications
All the polarizable water models evaluated in this work are induced-dipole models in which the induced dipole moment on a polarizable site p(μp) is calculated by
| (1) |
Here αp is the atomic polarizability on site p, Ep is the electric field due to permanent atomic charges, and Tpq is the dipole field tensor:
| (2) |
where I is the unit matrix; fe and ft are distance-dependent screening functions. In the Applequist model,23 fe and ft are both equal to one. The distance-dependent screening functions fe and ft were introduced by Thole to avoid the “polarization catastrophe” where infinite polarization may occur when polarizable sites are too close to each other.24 Thole introduced both linear and several exponential screening function forms in his original study.24
In our previous efforts, we carefully analyzed four different screening schemes and found that both the linear form and an exponential form performed the best in reproducing molecular polarizability for a large set of training and test molecules.21,22 In the linear Thole model, the functions fe and ft are defined as
| (3) |
In the exponential Thole model, the functions fe and ft are given as
| (4) |
It should be pointed out that the above exponential form is different from what is used in the Amoeba force field. However, it is equivalent to the AMOEBA formulation13 if we set . The damping factor a in Eqs. (3) and (4) controls the degree of the screening of electrostatic interactions.
In this study, both three-site and four-site water models were evaluated. The three-site POL3 model17 adopts a tetrahedral geometry and 1.0-Å OH bond length, as in SPC model.1 The original POL3 model is an Applequist model and it is adapted for both the linear and exponential Thole schemes denoted as POL3-LT and POL3-ET, respectively. The point polarizabilities are placed on all three atoms. The four-site Dang and Chang (DC) model adopts the geometry of the TIP4P model where the virtual particle is placed on the bisection of the angle H-O-H (104.5 degrees).2 DA and NDA models are the induced-dipole analogs of SWM4-DP12 and SWM4-NDP models,15 respectively. The SWM4-DP and SWM4-NDP are both Drude-oscillator models, both with a Drude particle connected to the oxygen atom to mimic the polarization of the water molecules. In the induced-dipole analogs of the two models the polarizabilities of the oxygen atom is assigned according to the charge and the force constant of the corresponding Drude particles. It should be noted that the hydrogen atoms and the virtual particle have no assigned polarization in these two models. This is different from the DC model described above that places the point polarizability only on the virtual particle.8 In the following we use DC/DA/NDA-LT/ET to denote their corresponding linear and exponential Thole models, respectively. Note that the geometries and parameters of these Thole models are kept the same as their corresponding Applequist models, and no optimization of these parameters was attempted in this study. Table 1 summarizes the geometries and parameters of all tested models.
Table 1.
Parameters of tested polarizable water models.
| POL3 | DA | NDA | DC | |
|---|---|---|---|---|
| dO–H (Å) | 1.000 | 0.9572 | 0.9572 | 0.9572 |
| θH–O–H(°) | 109.47 | 104.52 | 104.52 | 104.52 |
| dO–M (Å) | NA | 0.23808 | 0.24034 | 0.2150 |
| εOO (kcal/mol/Å2) | 0.156 | 0.1521 | 0.20568 | 0.1825 |
| σOO (Å) | 3.20367 | 3.1506 | 3.18030 | 3.2340 |
| qO (e) | −0.73000 | 0.0000 | 0.0000 | 0.0000 |
| qH (e) | 0.36500 | 0.55370 | 0.55733 | 0.5190 |
| qM (e) | NA | −1.10740 | −1.11466 | −1.03800 |
| αO (Å) | 0.5280 | 1.0430 | 0.9783 | 0.0000 |
| αH (Å) | 0.1700 | 0.0000 | 0.0000 | 0.0000 |
| αM (Å) | NA | 0.0000 | 0.0000 | 1.4440 |
| a (Linear Thole) | 2.441 | 1.8500 | 1.8500 | 1.8500 |
| a (Exponential Thole) | 1.3305 | 1.2600 | 1.2600 | 1.2600 |
Calculation of liquid water properties
Several properties of liquid and vapor water were evaluated and compared with experimental values. These include: density, enthalpy of vaporization, self-diffusion coefficient, rotation correlation time, the Debye relaxation time, dielectric constant, and thermal expansion coefficient. In addition we calculated the second virial coefficient as a function of temperature that characterizes dimer interactions in the gas phase. These properties have been calculated using the following formula and approaches.
- The density of water was calculated by
where N is the number of water molecules taken into the cubic box for molecular dynamics simulations, M is the mass of water molecule, NA is the Avogadro number, and V is the volume of the simulation box.(5) - The enthalpy of vaporization was determined by
where E is the total potential energy of the liquid water, R is the ideal gas constant and T is the temperature.(6) - Self-diffusion coefficient was estimated from the Einstein relation25
where r(t) is the position of the oxygen atom of water molecules at time t. The linear fitting of with respect to t with the fixed intercept of zero was carried out and the slope is the self-diffusion coefficient. The uncertainties of the fitted coefficients are estimated by using different simulation trajectories.(7) - To derive rotational correlation time , with α representing the HH or OH rotation axis, one needs to calculate orientational correlation function that is defined by the following formula:
where Pl is a Legendre polynomial of order l and is a unit vector along the α rotation axis of the molecule. Since follows the exponential decay, the rotational correlation time was determined by fitting the following exponential function(8) (9) - The Debye relaxation time τD was obtained in a similar way to the rotational correlation time by calculating first the normalized autocorrelation function Φ(t)of the total dipole moment of the system M. Function Φ(t) was calculated from:
then τD was obtained by fitting an exponential decay function(10) (11) The isobaric heat capacity is defined as and was obtained by calculating the numerical derivative of the cubic-spline fit of simulated enthalpy 〈H(T)〉p.
The thermal expansion coefficient is defined as , and was obtained from the cubic-spline fit of simulated density 〈ρ(T)〉.
- The classical value of the second virial coefficient, B2, is defined as
where kB is the Boltzmann constant, R is the vector connecting the centers of mass of two water monomers, Ω1 and Ω2 are two sets of Euler angles in a laboratory frame, describing orientations of the two monomers, and V describes the dimer interaction energy. The bracket notation means angular averaging. The actual calculation of B2 was obtained by fixing the position of one water molecule and considering the molecular symmetry. This leads to numerical integration of Eq (15) over the set of angular variables for every fixed value of R vector:(14)
NA is Avogadro’s number and f is a Mayer’s function:(15) (16)
The calculation of the B2(T) was performed in a procedure similar to that used by Reimers, Watts and Klein29 and by Lybrand et al.30,31 The integral was evaluated using a nonproduct numerical integration formula that requires n+2 function evaluation in an n-dimensional unit cube.32 Integration over distance variable has been performed by considering 12 ranges of R value. For each range 5-point Gauss quadrature has been used.
To assess the precision of second virial integration we repeated calculations of the virial coefficient for POL3-LT model using 3- and 7-points Gauss quadratures. The results of these calculations are presented in Table S1. The results for 5 and 7 point quadratures are identical up to five digits or the first digit after the decimal point. This demonstrates that the precision of integration is already achieved at the 5-points quadrature level, which is used across for calculations for all other water models.
Simulation details
For each water model, a cubic box filled with ~500 water molecules (488 for three-site models and 499 for four-site models) is generated by the LEaP module of the AMBER 11 package.33 The molecular dynamics simulations were performed in the isothermal-isobaric (NPT) ensemble at 298 K and 1 atm using a weak-coupling Berendsen scheme34 to a thermostat and barostat with the relaxation time of 1.0 ps. The scaling factor of the velocities λ is computed as
| (17) |
where Δt is the time step, τ is the relaxation time, kB is the Boltzmann constant, Tref is the thermostat temperature, m is the atom masses, vn is the on-step velocities, vn−1/2 and vn+1/2 are the previous and current half-step velocities.35 The equations of motion were integrated by the leap frog algorithm36 with the time step of 1 fs. The geometry of water molecules were constrained by the SHAKE algorithm37 with the relative geometrical tolerance of 10−6. Particle Mesh Ewald method38,39 was used to calculate the electrostatic energy with the cutoff of 9.0 Å to limit direct space sum. The van der Waals interactions were truncated at 9.0 Å and a continuum correction was added to compensate the truncation error in the total van der Waals energy.25 For each models, five independent 5-ns production runs following a 50-ps equilibrium run were performed for the analyses of the liquid water properties. The system configurations were saved every 0.5 ps. All simulations were performed by the SANDER program from the Amber 11 package.33
To study the size effect of the simulation box, a larger box with 2031 water molecules with a longer cutoff of 15.0 Å was also tested for the POL3 water model. Table S2 indicates that differences of simulated density and enthalpy of vaporization are both less than 0.1% and that of dielectric constant is less than 1%. These are well within the statistical uncertainties. Figure S1 shows that the radial distribution functions from both simulations are superposed very well. Therefore the smaller system-size and cutoff are sufficient for determining most of the reported water properties. The 4% difference in self-diffusion coefficient between two different sizes, though also within one standard deviation, raises the concern that the diffusivity might be more sensitive to system size as noted by Yeh and Hummer.40 For this, we caution that our reported values are valid for the reported system sizes only.
Results and discussion
Determination of damping factors in Thole models
In the Thole models the damping factors defined in Eqs. (3) and (4) are introduced to control the magnitude of screening electrostatic interactions to enhance the model’s numerical stability. Apparently, use of the damping factors in general changes the numerical properties of tested water models originally developed in the Applequist model. Thus the damping factors were first optimized to reproduce the properties of original polarizable water models as much as possible before we can assess how well these water models can be incorporated into the proposed Amber polarizable force field.21,22
In the linear Thole (LT) model, the damping factor can be determined analytically without numerical optimization. Specifically, it can be calculated by
| (18) |
where, is the minimum distance between atoms of type p and q, and αp and αq are the polarizabilities of atoms of type p and q. Indeed, our calculations show that the LT scheme reproduces the results of the Applequist model very well for the tested models when the damping factor is less than 1.85 because interactions within that range occurred rarely.
The exponential Thole (ET) model cannot reproduce the Applequist model exactly. To determine the damping factors in the ET water models, a series of 500-ps molecular dynamics simulations were conducted using a range of different damping factors. The simulation length of 500 ps was found to be sufficient to obtain converged values for density and enthalpy of vaporization that were used to prescreen the optimal damping factor in this study. The cumulative average of density values for POL3 water model was calculated at every 100 ps and plotted in Figure S2. The differences of the density and Hvap using 500-ps or 5-ns trajectories are both less than 0.01%. Therefore it is appropriate to prescreen the damping factor using 500-ps trajectories. Apparently, these short simulations are not sufficient enough to achieve convergence for some other properties such as dielectric constant (data not shown).
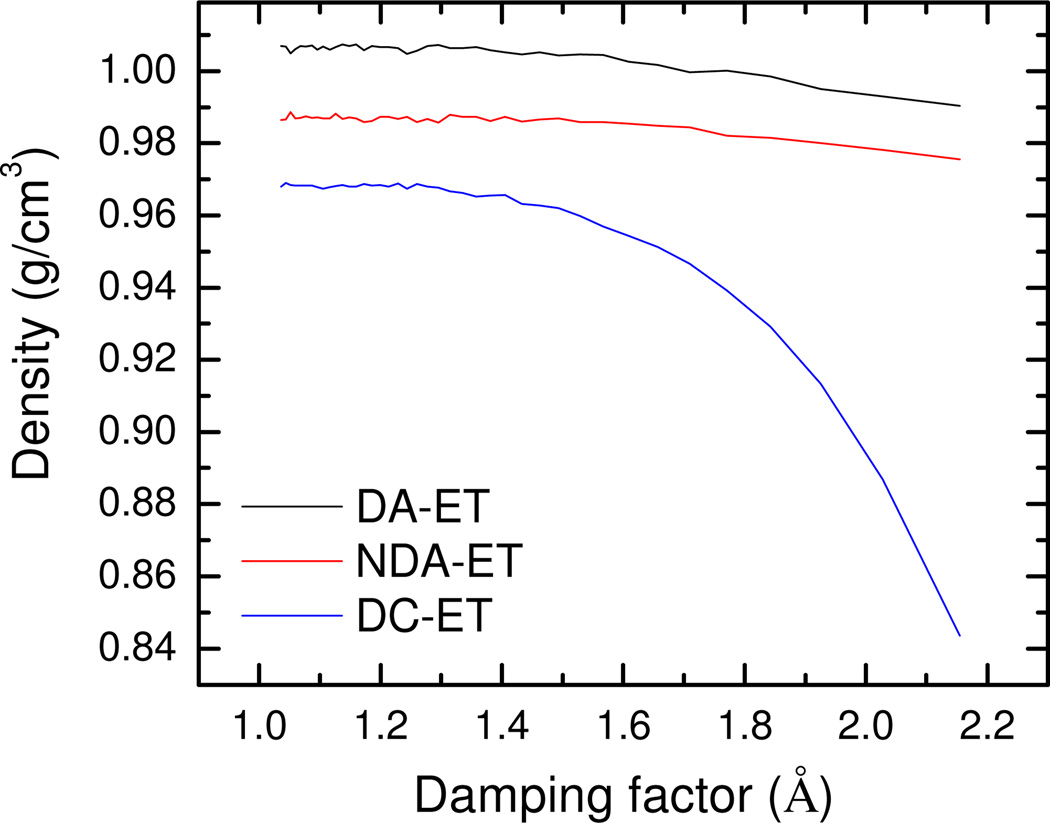
Figure 1 demonstrates the dependence of the simulated liquid water densities as a function of damping factor values for the ET models. It shows that when the damping factor is less than 1.26, the deviation of the densities generated by ET models from those generated by the corresponding Applequist models are about 0.1% (Table 2). Thus, 1.26 was set as the generic damping factor in three of the four tested water models except POL3 with the goal of reproducing the numerical behaviors of these published water models as much as possible within the ET damping scheme.
Figure 1.
Scanning of damping factor for the exponential Thole (ET) damping scheme for the three tested water models, DA, NDA, and DC. See text and Table 1 for more detail on the tested models. Note that the damping factor for POL-ET was scanned to reproduce the experimental value so that it is not shown here.
Table 2.
Physical properties calculated from the models.
| Model | ρa | ΔHvapb | Dc | ε0d | τDg | 〈μ〉h | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| POL3 | 1.002 | 10.46 | 2.4(0.1) | 125(2) | 2.6(0.2) | 2.7(0.2) | 14.9(0.9) | 2.61 | ||
| POL3-LT | 0.999 | 10.43 | 2.5(0.1) | 126(5) | 2.4(0.3) | 2.6(0.3) | 15.1(1.4) | 2.60 | ||
| POL3-ET | 1.000 | 10.43 | 2.6(0.1) | 127(7) | 2.2(0.1) | 2.4(0.3) | 15.0(1.5) | 2.60 | ||
| DA/DA-LT | 1.008 | 10.83 | 1.8(0.0) | 86(2) | 3.0(0.3) | 3.2(0.3) | 13.0(1.6) | 2.50 | ||
| DA-ET | 1.008 | 10.83 | 1.9(0.1) | 83(4) | 3.3(0.3) | 3.4(0.4) | 13.0(2.7) | 2.50 | ||
| NDA/NDA-LT | 0.988 | 10.31 | 2.7(0.0) | 72(2) | 2.1(0.1) | 2.3(0.2) | 8.5(0.6) | 2.41 | ||
| NDA-ET | 0.988 | 10.31 | 2.7(0.0) | 72(2) | 2.3(0.2) | 2.3(0.1) | 8.4(0.6) | 2.41 | ||
| DC/DC-LT | 0.970 | 10.10 | 2.3(0.1) | 122(5) | 2.4(0.2) | 2.6(0.3) | 15.4(1.8) | 2.70 | ||
| DC-ET | 0.969 | 10.08 | 2.4(0.1) | 123(5) | 2.3(0.2) | 2.5(0.2) | 13.9(2.0) | 2.70 | ||
| SWM4-DP12 | 0.997 | 10.52 | 2.3 | 79 | NA | NA | 11.1 | 2.46 | ||
| SWM4-NDP15 | 0.998 | 10.52 | 2.3 | 79 | NA | NA | 11.0 | 2.46 | ||
| AMOEBA13 | 1.000 | 10.48 | 2.0 | 81 | NA | NA | NA | 2.78 | ||
| POL5/TZ9 | 0.997 | 10.51 | 1.8 | 98 | NA | NA | NA | 2.71 | ||
| TIP4P/FQ19 | 0.997 | 10.50 | 1.9 | 79 | NA | NA | 8 | 2.62 | ||
| COS/D16 | 0.997 | 10.52 | 2.5 | 70 | 3.3 | 3.1 | 14.1 | 2.43 | ||
| EXP | 0.997 | 10.51 | 2.3 | 78 | 1.95 | 2.0 | 8.3 | NA | ||
Densities (ρ’ g/cm3), enthalpies of vaporization (ΔHvap, kcal/mol), diffusion constants (D, 10−9 m2/s), dielectric constants (ε0), rotational correlation time (ps) of OH and HH , Debye relaxation time (τD, ps), and average dipole moments (〈μ〉, debye) for the water models at 298 K and 1 atm compared with experiment (EXP). The numbers in parentheses are the standard deviations.
For the POL3 model chosen to be the primary water model for the proposed Amber polarizable force field,21,22 we utilized additional molecular dynamics simulations to optimize the damping factors in the context of both LT and ET damping schemes. In each case the damping factor was optimized, using systematic scanning, to yield the best agreement with experimental density and heat of vaporization. The resultant optimal damping factors are 2.4410 and 1.3305 for POL3-LT and POL3-ET, respectively. It is noted that the damping factor of 1.3305 in POL3-ET models is equivalent to 0.4246 in the equation of Ren and Ponder,13 which is close to the damping factor of 0.39 used for the AMOEBA water model.13 However, it is worth noticing that no additional parameterization was conducted to achieve further agreement with experiment, which is beyond the scope of this study.
It should be pointed out that the damping factors in the linear and exponential Thole models have the same physical meaning but they have different values. Taking the damping factors to reproduce the corresponding Applequist models as an example, the damping factor in the LT model can be calculated by Eq (18). The ET model cannot reproduce Applequist model exactly, but the damping factor in the ET model can be derived from fe as shown below. If fe = 1−10−k, the damping factor can be derived from Eq (4) as follows:
| (19) |
Comparing Eqs (18) and (19), the term (k ln10)1/3 is the difference of the damping factors in LT and ET models.
Room-temperature water properties
Table 2 lists the properties of all tested water models and those of several selected water models reported in literature. The data in the first nine rows were obtained from 5-ns NPT simulations in this study. The average water density in the POL3 simulations are 1.002 g/cm3, which is slightly higher than the experimental density of 0.997 g/cm3 by 0.5%. Its adapted Thole variants, POL3-LT and POL3-ET models, are slightly better due to our additional optimization of the damping factors with 0.2% and 0.3% errors, respectively. The densities of the DA/DA-LT models are ~1% higher than experiment, while the densities of the NDA/NDA-LT models are ~1% lower than experiment. Note that the densities of their theoretical equivalent models, SWM4-DP and SWM4-NDP that use Drude particles, are quite close to the experimental density, as listed in Table 2. Worth noting is the density of the DC model which is 0.970 g/cm3 in our study, ~2.5% smaller than that reported by Dang and Chang,8 0.995 g/cm3, and by Mahoney and Jorgensen,41 0.996 g/cm3. This is probably due to the use of electrostatic cutoff in Dang and Chang’s original simulations.8 The densities of other polarizable water models are overall in good agreement with the experimental density as summarized in Table 2.
The enthalpies of vaporization of DA models are 3% higher than the experimental value, while those of DC models are 4% lower. The deviations from the experimental value for other tested models are all less than 0.5%. However, these deviations are all slightly higher than those of the existing polarizable water models reported by others as listed in Table 2 including SWM4-DP, SWM4-NDP, AMOEBA, POL5/TZ, IP4P/FQ, and COS/D models. This is partially related to the fact that only single damping factor parameter was adjusted in this work since the primary focus is on evaluating the existing polarizable water models and the damping factor parameter was not adjusted to better reproduce experiment, but to better reproduce the original Applequist models.
Diffusion coefficients show some notable deviations from experimental values. The largest differences come from DA (17% lower) and NDA (17% higher) models. This was surprising since both SWM4-DP and SWM4-NDP, from which DA and NDA were derived, were reported to produce excellent agreement with experiment. We speculate that this may be attributed to the subtle difference between the representations of the dipoles since DA and NDA models use the induced point dipoles whereas SWM4-DP and SWM4-NDP use Drude oscillators. Thus, further adjustment of the parameters may improve the DA and NDA models. In comparison, the POL3 models are notably better than DA and NDA models and their diffusion coefficients have only 4–8% deviations from the experiment. DC models have the best agreement with the experiment value. In terms of diffusion coefficients, POL3 and DC models are also better than AMOEBA, POL5/TZ, TIP4P/FQ models.
The rotational relaxations in all of the tested models are 8–70% slower than the experimental values. This is somewhat surprising given the lack of van der Waals interactions on hydrogen atoms which, intuitively, would allow the water models to rotate faster. On the other hand, the lack of van der Waals on hydrogen may require stronger attractive forces between oxygen and hydrogen atoms, giving rise to slower rotation. Thus we think it may be necessary to reduce the O:H attractive force by, perhaps, reducing the polarization effect. Nevertheless, this clearly calls for further optimization.
The DA/NDA models yield reasonable dielectric constant, ranging from 72 to 86. The dielectric constants of the POL3 models and the DC models are both notably higher than the experimental value. The dielectric constant is closely related to the average molecular dipole moment,42 which can be decomposed into the permanent dipole moment and the induced dipole moment. The permanent dipole moment of the POL3 model is 2.02 D, which is higher than those of the other models, 1.85D. The DC model has the larger molecular polarizability of 1.444 Å3 than other tested models. Therefore the high dielectric constant of the POL3 model results from the permanent dipole moment while those of DC models result from the large induced dipole moment. Our data also show that the optimum molecular dipole moment of 2.4D predicted by Guillot42 produces a lower dielectric constant than the experimental value. Thus it is not necessary the optimum value for the polarizable water force field, at least in the induced dipole frameworks. The least-square linear interpolation of our data further shows that the optimum molecular dipole moment for the induced-dipole water models is in the range of 2.45D ~2.46D.
The Debye dielectric relaxation time gives an approximation for the relaxation time of the hydrogen bond network. In POL3, DA, and DC models, the relaxations of the hydrogen bond network are 57–86% slower than that observed experimentally. In contrast, the NDA models have only 1% deviations from the experimental value. This is consistent with the fact that NDA models have the smallest average dipole moment of all the tested models.
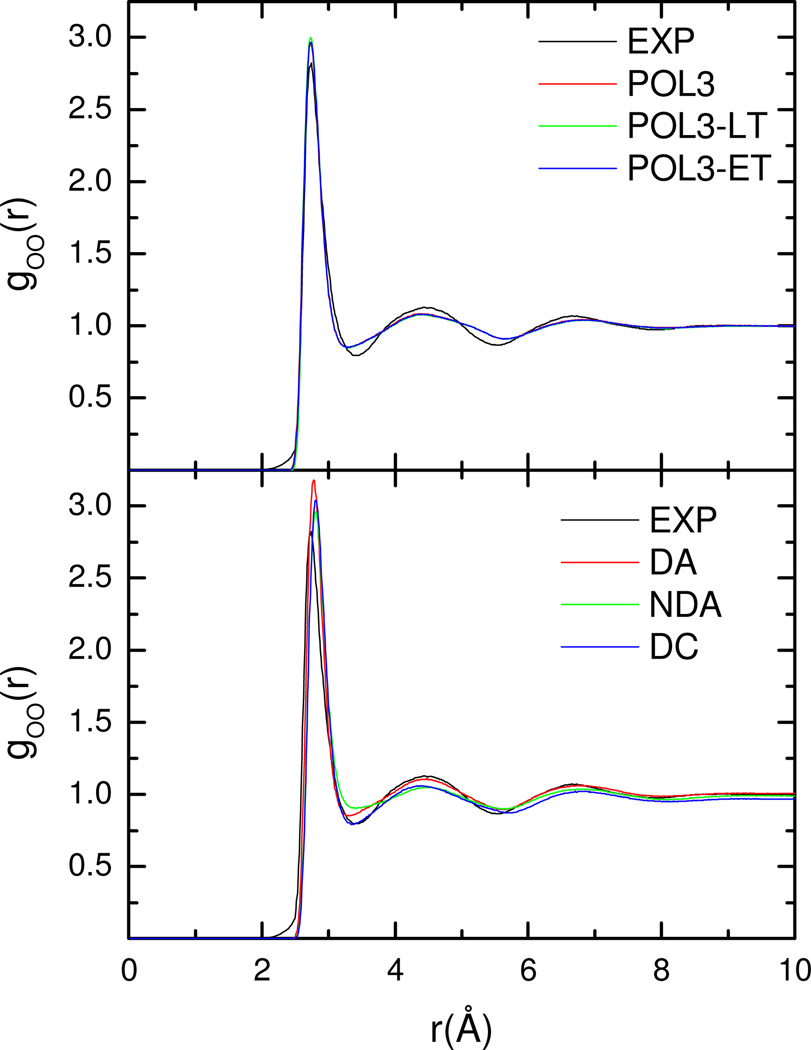
Finally the radial distribution function of O-O, H-H, and O-H are plotted in Figures 2, Figure S3, and Figure S4. The corresponding summary is in Table 3. The positions of the first peaks of gOO for POL3/POL3-LT/POL3-ET water models coincide with the experimental position of 2.8Å, but the heights of the first peaks are slightly overestimated. The positions of the first peaks of other models are located at longer distances (~2.9Å). Their heights are also overestimated compared to the experimental value. The position of the first peak is mainly attributed to the repulsive term of Lennard-Jones potential. The POL3 van der Waals parameters need to be adjusted slightly to decrease the height of the first peak in the future work. The position of the first minimum is correct only in the NDA models at 3.4 Å, but those of other models are located at shorter distances (~3.3Å). All water models have shallower first minima than observed experimentally. The positions and heights of the second peaks are reproduced well by all models except the DC model with a position of 4.2Å and a height of 1.0. The radial distribution functions for the POL3 water model are acceptable since the goal of this study is not to optimize the interaction parameters.
Figure 2.
Comparison of simulated and experimental radial distribution function of water: gOO(r) of tested polarizable water models. Here data for the LT and ET versions of the DA/NDA/DC water models are omitted for clarity since they are virtually identical to their corresponding Applequist models as shown in Table 2.
Table 3.
Comparison of simulated and experimental gOO(r) parameters for various polarizable water models. In each table cell, the first value is the position (Å), and the second value is the height/depth.
| 1st peak | 1st minimum | 2nd peak | 2nd minimum | 3rd peak | |
|---|---|---|---|---|---|
| EXP | 2.73, 2.83 | 3.41, 0.79 | 4.44, 1.13 | 5.51, 0.86 | 6.66, 1.07 |
| POL3 | 2.73, 2.96 | 3.30, 0.85 | 4.40, 1.08 | 5.62, 0.91 | 6.80, 1.04 |
| POL3-LT | 2.73, 3.00 | 3.29, 0.85 | 4.41, 1.08 | 5.65, 0.91 | 6.79, 1.04 |
| POL3-ET | 2.74, 2.97 | 3.30, 0.85 | 4.40, 1.08 | 5.62, 0.91 | 6.81, 1.04 |
| DA | 2.78, 3.19 | 3.31, 0.85 | 4.43, 1.11 | 5.60, 0.90 | 6.72, 1.06 |
| NDA | 2.79, 2.95 | 3.42, 0.90 | 4.43, 1.05 | 5.63, 0.90 | 6.77, 1.04 |
| DC | 2.81, 3.04 | 3.35, 0.79 | 4.36, 1.06 | 5.68, 0.87 | 6.83, 1.02 |
Temperature-dependent water properties
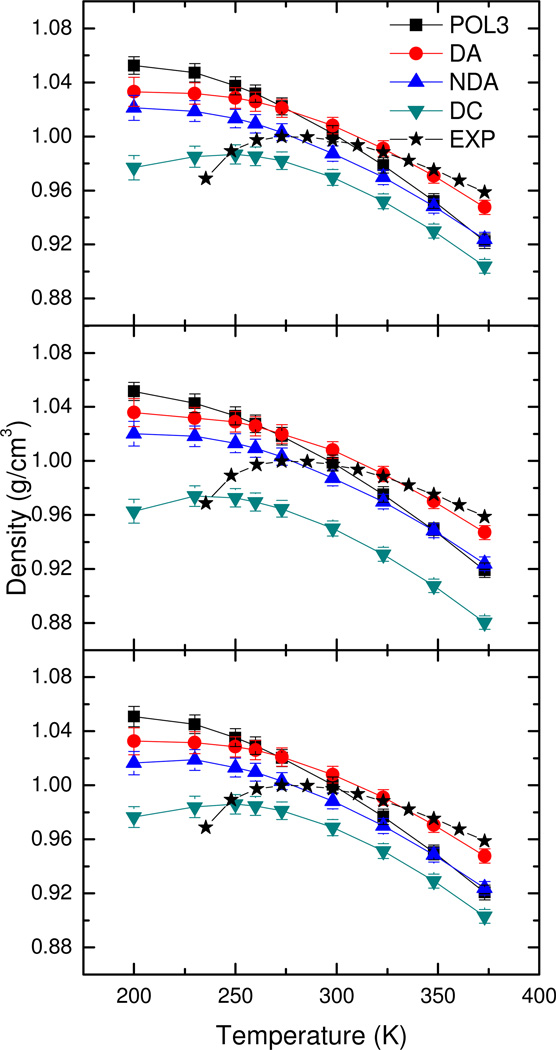
We further derived temperature-dependent properties for the tested water models and compared them to experimental data. Other than the work of Kunz 2009,16 this is probably the first time that temperature-dependent properties of polarizable water models have been thoroughly analyzed and reported. The same simulation protocol was also used to reproduce the temperature-dependent properties of the TIP4P-Ew nonpolarizable water model (data not shown). In general our simulation protocol is consistent with that utilized in the original publication of the TIP4P-Ew water model,4 with the deviation of density within 0.01 g/cm3 and the deviation of enthalpy of vaporization within 0.07 kcal/mol of the published values.4 Previous analyses show that most of the simple water models do not solidify at the melting temperature or lower (≤273K). However an interesting observation from this study is that all tested polarizable water models solidify at the lowest simulation temperatures (200K and 230K). This can be demonstrated by a preliminary self-diffusion coefficient analysis as shown in Table S3, and also by more detailed analyses to be discussed below. Of course these water models still remain as liquid at temperature not too low from the melting point. To streamline the presentation, we have compared simulated properties with experimental measurements of the super-cooled liquid water at all low temperatures (≤273K).
Figure 3 compares the densities of different polarizable water models and experimental data. Experimental data show that the maximum of density occurs at around 277K. Interestingly, only the DC model exhibits a maximum of density at around 250K. Nevertheless, all polarizable models produce densities similar to experimental data: with deviations ranging from 3% to 6% for temperatures from 273K to 323K and with deviations up to 9% for temperatures lower than 273K or higher than 323K.
Figure 3.
Temperature-dependent density of polarizable water models. Top to bottom: Applequist, LT, and ET, respectively. The experimental data exhibit a maximum around 277K while only the DC model has a similar maximum around 250K.
The simulated water densities increase monotonically with reducing temperature, though the values at the lowest simulation temperature (200K) do not show dramatic change as evidenced by the smooth curves in Figure 3. Further analysis of radial distribution functions and diffusion constants at temperatures at and below 298K (Figure S5 and Table S3 for POL3 at selected temperatures) shows increased structural order and solidification as temperature is reduced below 230K. The radial distribution function and density also indicate that despite the increased ordering at 200K, the average distance between the neighboring water molecules does not change appreciably since the first peak of the radial distribution function remains at approximately the same position as that at 298K (see Figure S5) and the density also remains at the same level as that at 298K.
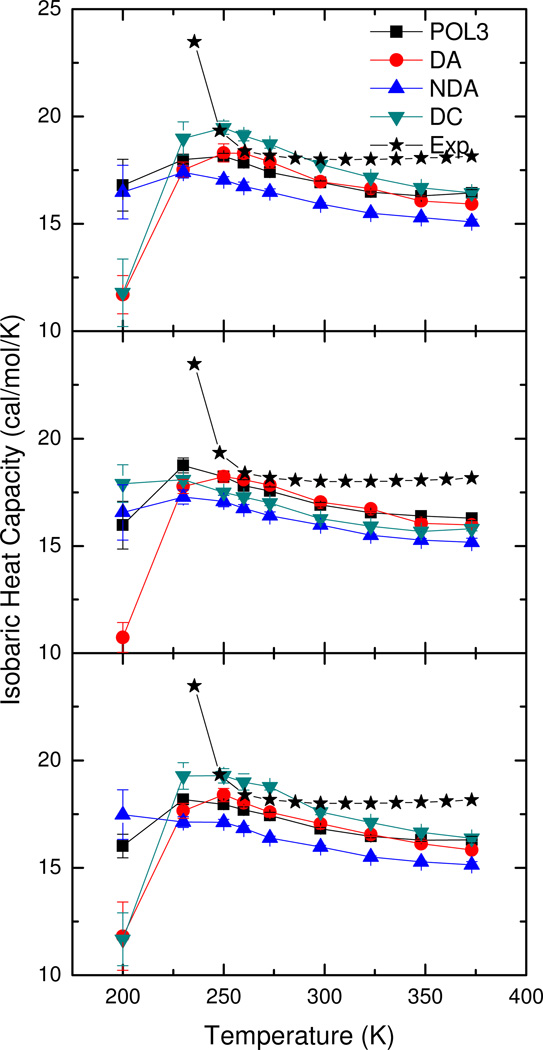
Figure 4 shows the temperature-dependent heat capacities of all tested polarizable water models in this study. Similar to what is observed in the density analysis, all polarizable water models perform quite well at temperature close to its calibrated temperature, i.e. at temperatures higher than 250K. Worth noting is the trend of all tested models are different from experiment at temperatures lower than 250K: all models produce a similar downtrend in contrast to the uptrend in experiment when temperature is reduced. This is consistent with the increased structural order as pointed in the density analysis. Thus the downtrend in the heat capacity temperature-dependent curve, combined with the increased ordering as indicated by radial distribution functions, indicates the existence of phase-transition in our simulations. Note too that the experiment data was collected for super-cooled liquid water. Thus the large discrepancy is not a surprise. However, it should also be pointed out that none of the solid forms observed is ice, whose formation is clearly a very interesting question but is apparently beyond the scope of the simple water models tested here.
Figure 4.
Temperature-dependent heat capacity of polarizable water models. Top to bottom: Applequist, LT, and ET, respectively. All polarizable water models behave similarly to experiment at temperatures between 270K and 300K but dramatically disagree with experiment at temperatures lower than 270K.
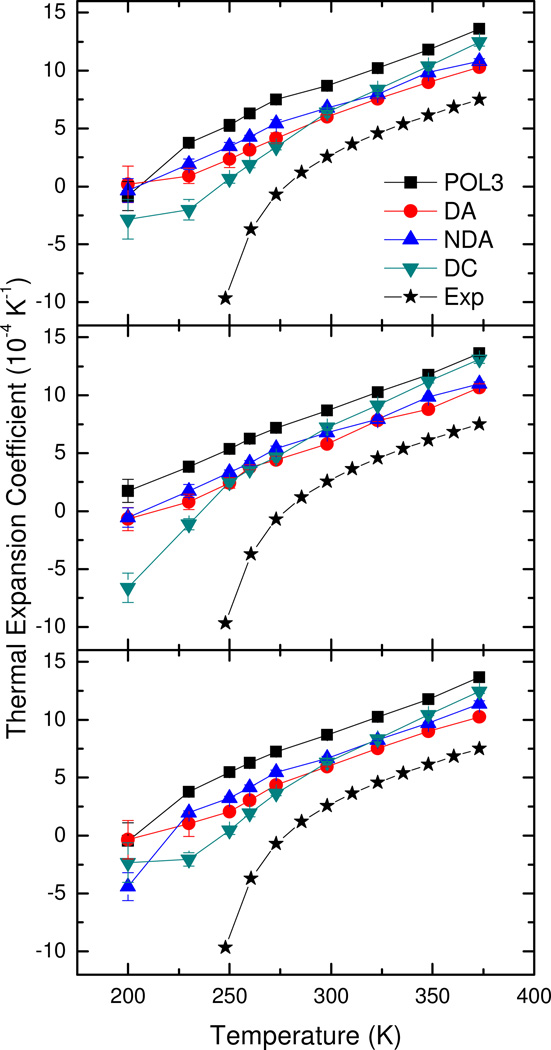
Thermal expansion coefficient for water is an interesting property below 277K: it is negative, i.e., liquid water contracts when it is heated up. The estimates of the expansion coefficients for the tested polarizable water models are presented in Figure 5. It is worth noting that none of the water models in this study exhibits a zero or negative value for the thermal expansion coefficient at 277K. This is because all models produce thermal expansion coefficients that are too high when compared with experiment throughout the tested temperature range. Nevertheless, at the lowest temperature tested (200K), all tested models except DA and POL3-LT exhibit negative thermal expansion coefficient. Furthermore, it is apparent that the temperature-dependent trend in experiment can be observed in POL3, DC-LT and NDA-ET models. Finally, the existence of solid at the lowest temperatures apparently complicates the comparison with experimental values collected for super-cooled liquid water.
Figure 5.
Temperature-dependent thermal expansion coefficient of polarizable water model models. Top to bottom: Applequist, LT, and ET, respectively. Simulated thermal expansion coefficients are all too high when compared with experiment. However the temperature-dependent trend in experiment can be observed in POL3, DC-LT and NDA-ET models.
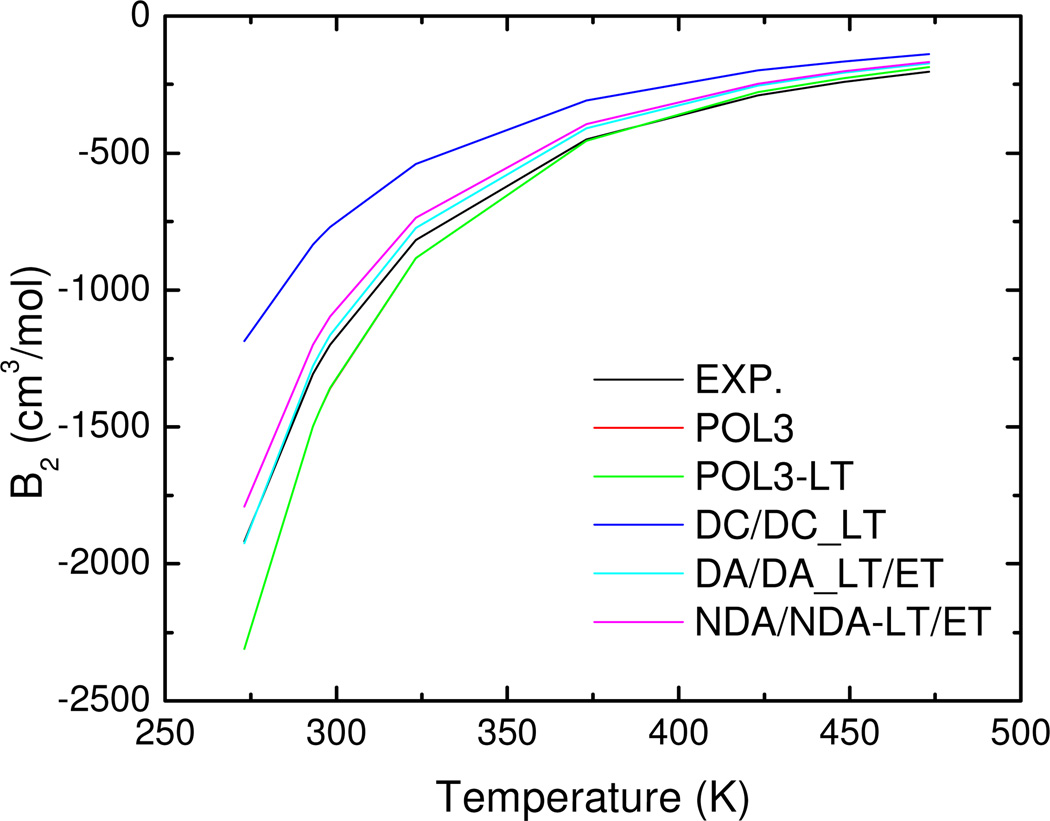
Second virial coefficients for various water models are presented in Figure 6 and Table S4, and are compared with experimental values at a wide range of temperature values. The second virial coefficient is a two-body property that depends only on the dimer interaction potential, thus reflecting the quality of dimer interactions. To assess how well a given water potential reproduces experimental virial coefficient we calculated the χ2 value, defined as sum of errors of calculated values with respect to experimental data: . As can be seen from Figure 6 and Table S4 POL3-LT water model reproduces well experimental data as a function of temperature, with χ2 value 216, which is substantially better than the value of 288 obtained for high quality quantum mechanically derived polarizable CC-pol43 water potential as a function of temperature (see Table S4 and Figure S6). The lowest χ2 values are obtained for DA/DA-LT/ET (87.9) and NDA/NDA-LT/ET (143) water potentials. The DA and NDA polarizable water models have their B2 coefficients slightly higher than the experimental values. At lower temperatures the DA and NDA models follow the experimental temperature dependency better than POL3 water models. The largest discrepancies are exhibited for DC polarizable water models, characterized by too positive B2 values compared to the experiment. This demonstrates that although these models work well in liquid simulations due to many-body polarization contribution, their two-body part is underestimated. In Table S4 we also included popular non-polarizable TIP4P-Ew water model, which was developed to reproduce effectively liquid water. The pairwise interactions for the TIP4P-Ew water model are exaggerated and consequently B2 for every temperature is too low (Table S4 and Figure S6) and χ2 is very large.
Figure 6.
Second virial coefficients of polarizable water models compared with experiment.
Conclusion
In this study, we evaluated four polarizable water models that conform to both the linear and exponential Thole’s polarization schemes, including the POL3, DA, NDA, and DC models. To investigate these polarizable water models, we performed multiple 5-ns NPT simulations, followed by calculations of various bulk water properties for comparison with experimental data.
All tested models are able to yield room-temperature density and enthalpy of vaporization with slight deviations from the experimental values. Among them, the POL3-LT has the best performance in reproducing these two properties. However, none of them can simultaneously yield reliable diffusion coefficient, rotational relaxations, and dielectric constant, indicating further optimizations are needed to improve the dynamic water properties. Overall, the dynamics properties of the NDA/NDA-LT models agree best with experimental data. The second virial coefficient is also reproduced well for these models.
In addition to the room-temperature properties, we also evaluated temperature dependent properties, including density, enthalpy of vaporization, and thermal expansion, with the temperature ranging from that corresponding to the super-cooled states to the boiling point. All tested polarizable water models perform better at high temperatures than at low temperatures, especially below melting point. For examples, none of the tested polarizable model reproduces the maximum in density at around 277K or the negative thermal expansion coefficients right below 277K. Finally, the second virial coefficients were calculated at a number of temperatures to evaluate the quality of dimer interactions. Our data shows that the POL3-LT model generally performs among the best of all tested models/combinations in reproducing the experimental data.
Supplementary Material
Acknowledgment
We are grateful to acknowledge the research support from NIH (R01GM093040, R. Luo, P.I. and R01GM79383, Y. Duan, P.I.) and the TeraGrid for the computational time (TG-CHE090098, J.M. Wang, P.I. and TG-CHE090135, P. Cieplak, P.I.).
Footnotes
Supporting Information
Additional figures tables and figures include: second virial coefficients for the POL3-LT water model calculated using 3-, 5- and 7- point Gauss quadratures; simulation results with different number of water molecules and cutoff; self-diffusion coefficients of water models at 200K, 230K, and 298K; second virial coefficient for all the polarizable water models studied in this work; radial distribution functions of the POL3 water model generated by different simulations with different number of water molecules and cutoff; cumulative averages of density and enthalpy of vaporization of the POL3 model; simulated radial distribution functions gHH(r) and gOH(r) for tested polarizable water models; simulated radial distribution functions gOO(r) at three simulated temperatures for the POL3 water model; the second virial coefficients as a function of temperature for the POL3-LT, TIP3P, TIP4P and CC-pol models. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Berendsen HJC, Postma JPM, van Gunsteren WF, Hermans J. Intermolecular Forces. 1981 [Google Scholar]
- 2.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 3.Mahoney MW, Jorgensen WL. J. Chem. Phys. 2000;112:8910. [Google Scholar]
- 4.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. J. Chem. Phys. 2004;120:9665. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 5.Rick SW. J. Chem. Phys. 2004;120:6085. doi: 10.1063/1.1652434. [DOI] [PubMed] [Google Scholar]
- 6.Sorenson JM, Hura G, Glaeser RM, Head-Gordon T. J. Chem. Phys. 2000;113:9149. [Google Scholar]
- 7.Cieplak P, Dupradeau F-Y, Duan Y, Wang J. Journal of Physics-Condensed Matter. 2009;21 doi: 10.1088/0953-8984/21/33/333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dang LX, Chang TM. J. Chem. Phys. 1997;106:8149. [Google Scholar]
- 9.Stern HA, Rittner F, Berne BJ, Friesner RA. J. Chem. Phys. 2001;115:2237. [Google Scholar]
- 10.Burnham CJ, Xantheas SS. J. Chem. Phys. 2002;116:5115. [Google Scholar]
- 11.Burnham CJ, Xantheas SS. J. Chem. Phys. 2002;116:1500. [Google Scholar]
- 12.Lamoureux G, MacKerell AD, Roux B. J. Chem. Phys. 2003;119:5185. doi: 10.1063/5.0019987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ren PY, Ponder JW. J Phys Chem B. 2003;107:5933. [Google Scholar]
- 14.Yu HB, van Gunsteren WF. J. Chem. Phys. 2004;121:9549. doi: 10.1063/1.1805516. [DOI] [PubMed] [Google Scholar]
- 15.Lamoureux G, Harder E, Vorobyov IV, Roux B, MacKerell AD. Chemical Physics Letters. 2006;418:245. [Google Scholar]
- 16.Kunz APE, van Gunsteren WF. J. Phys. Chem. A. 2009;113:11570. doi: 10.1021/jp903164s. [DOI] [PubMed] [Google Scholar]
- 17.Caldwell JW, Kollman PA. J. Phys. Chem. 1995;99:6208. [Google Scholar]
- 18.Zhu SB, Singh S, Robinson GW. J. Chem. Phys. 1991;95:2791. [Google Scholar]
- 19.Rick SW, Stuart SJ, Berne BJ. J. Chem. Phys. 1994;101:6141. [Google Scholar]
- 20.Yu HB, Hansson T, van Gunsteren WF. J. Chem. Phys. 2003;118:221. [Google Scholar]
- 21.Wang J, Cieplak P, Li J, Hou T, Luo R, Duan Y. Journal of Physical Chemistry B. 2011;115:3091. doi: 10.1021/jp112133g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang J, Cieplak P, Li J, Wang J, Cai Q, Hsieh M, Lei H, Luo R, Duan Y. Journal of Physical Chemistry B. 2011;115:3100. doi: 10.1021/jp1121382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Applequist J, Carl JR, Fung KK. Journal of the American Chemical Society. 1972;94:2952. [Google Scholar]
- 24.Thole BT. Chemical Physics. 1981;59:341. [Google Scholar]
- 25.Allen MP, Tildesley DJ. Computer simulation of liquids. Oxford [England]; New York: Clarendon Press; Oxford University Press; 1987. [Google Scholar]
- 26.Neumann M, Steinhauser O. Chemical Physics Letters. 1984;106:563. [Google Scholar]
- 27.Gereben O, Pusztai L. Chemical Physics Letters. 2011;507:80. doi: 10.1063/1.3624839. [DOI] [PubMed] [Google Scholar]
- 28.Buckingham AD. Proceedings of the Royal Society of London Series a-Mathematical and Physical Sciences. 1956;238:235. [Google Scholar]
- 29.Reimers JR, Watts RO, Klein ML. Chemical Physics. 1982;64:95. [Google Scholar]
- 30.Lybrand TP, Kollman PA. J. Chem. Phys. 1985;83:2923. [Google Scholar]
- 31.Cieplak P, Kollman P, Lybrand T. J. Chem. Phys. 1990;92:6755. [Google Scholar]
- 32.Evans DJ, Watts RO. Molecular Physics. 1974;28:1233. [Google Scholar]
- 33.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Crowley M, Walker RC, Zhang W, Merz KM, Wang B, Hayik A, Roitberg A, Seabra G, Kolossvary I, Wong KF, Paesani F, Vanicek JXW, Brozell SR, Steinbrecher T, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Mathews DH, Seetin MG, Sagui C, Babin V, Kollman PA. Amber. Vol. 10. San Francisco: University of California; 2008. [Google Scholar]
- 34.Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. Journal of Chemical Physics. 1984;81:3684. [Google Scholar]
- 35.Cheatham TE, Brooks BR. Theoretical Chemistry Accounts. 1998;99:279. [Google Scholar]
- 36.Swope WC, Andersen HC, Berens PH, Wilson KR. J. Chem. Phys. 1982;76:637. [Google Scholar]
- 37.Ryckaert JP, Ciccotti G, Berendsen HJC. Journal of Computational Physics. 1977;23:327. [Google Scholar]
- 38.Toukmaji A, Sagui C, Board J, Darden T. J. Chem. Phys. 2000;113:10913. [Google Scholar]
- 39.Sagui C, Pedersen LG, Darden TA. J. Chem. Phys. 2004;120:73. doi: 10.1063/1.1630791. [DOI] [PubMed] [Google Scholar]
- 40.Yeh IC, Hummer G. J Phys Chem B. 2004;108:15873. [Google Scholar]
- 41.Mahoney MW, Jorgensen WL. J. Chem. Phys. 2001;115:10758. [Google Scholar]
- 42.Guillot B. Journal of Molecular Liquids. 2002;101:219. [Google Scholar]
- 43.Bukowski R, Szalewicz K, Groenenboom GC, van der Avoird A. J. Chem. Phys. 2008;128 doi: 10.1063/1.2832746. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.