Topograph, a Software Platform for Precursor Enrichment Corrected Global Protein Turnover Measurements

Abstract

Defects in protein turnover have been implicated in a broad range of diseases, but current proteomics methods of measuring protein turnover are limited by the software tools available. Conventional methods require indirect approaches to differentiate newly synthesized protein when synthesized from partially labeled precursor pools. To address this, we have developed Topograph, a software platform which calculates the fraction of peptides that are from newly synthesized proteins and their turnover rates. A unique feature of Topograph is the ability to calculate amino acid precursor pool enrichment levels which allows for accurate calculations when the precursor pool is not fully labeled, and the approach used by Topograph is applicable regardless of the stable isotope label used. We validate the Topograph algorithms using data acquired from a mouse labeling experiment and demonstrate the influence that precursor pool corrections can have on protein turnover measurements.

Methods of measuring protein synthesis and degradation using stable or radioactive isotope labels have existed for decades. The isotope label is introduced in the form of a labeled amino acid or amino acid precursor, and the incorporation or removal of that label from protein is used to estimate average protein turnover rates (1, 2). Historically, the amount of stable isotope label incorporated into a protein is measured by enriching for the protein (e.g. affinity chromatography, gel electrophoresis, and other biochemical methods), hydrolyzing the protein to amino acids, derivatizing the amino acids, and measuring the labeled amino acid by gas chromatography-mass spectrometry or gas chromatography-combustion-isotope ratio mass spectrometry (3, 4). More recently, proteomics methods have been developed that measure the labeled amino acid on the peptide level, eliminating the need for a protein enrichment step and enabling the monitoring of many proteins in a single experiment (5).

Proteomics approaches to measuring protein turnover rates in mice have been accomplished by the introduction of a ¹⁵N stable isotope label. The labeled diets were created by supplementing a protein-free diet with a ¹⁵N enriched protein source. Price et al. (6) generated ¹⁵N-labeled protein from the alga, Spirulina platensis and Zhang et al. (7) introduced ¹⁵N-label in the form of lysate from the bacterium, Ralstonia eutropha. An advantage of using complete ¹⁵N labeling is the rapid incorporation of ¹⁵N and separation of isotope distributions between labeled and natural isotope abundance peptides, which reduces the need to deconvolute the two distributions. However, current methods require that the dietary protein content be derived from bacterial or alga lysate, a diet that is not normally fed to laboratory mice. As a result, measurements of protein turnover may not reflect conventional mouse model systems because of effects of diet on protein and amino acid metabolism. A more recent work by Claydon et al. (8) demonstrated a stable isotope labeling method by supplementing labeled valine into a standard mouse diet.

The complex data generated from these analyses creates a data processing and analysis challenge; exemplified by recent software platforms that have been developed. Guan et al. (9) and Hoopmann et al. (10) demonstrated data analysis pipelines for ¹⁵N labeled SILAM and SILAC experiments. Here we describe the software platform, Topograph, we have developed for the analysis of liquid chromatography-tandem MS (LC-MS/MS) data from samples with isotopic labels. Topograph is able to deconvolute the complex spectra that may result from overlapping isotope distributions, regardless of the isotope label used. More uniquely, Topograph is able to calculate the relative isotope abundance (RIA)¹ of the amino acid precursor pool, which is necessary to correctly determine the amount of newly synthesized peptide and to subsequently calculate peptide and protein turnover rates.

EXPERIMENTAL PROCEDURES

Mouse Stable Isotope Labeling

All animal experiments were approved by the University of Washington Institutional Animal Care and Use Committee. Mice of C57Bl6/J background were housed in a barrier specific-pathogen-free facility maintained at 70–74 °F, 45–55% humidity, with 28 air changes/hour and 12/12-h light/dark cycle, as described (11). Twelve mice at 3–4 months of age were fed ad libitum leucine-deficient synthetic diet (TD.09846, Harlan Teklad, Madison, WI) supplemented with 7 g/kg of regular leucine for 1 week, then the diet was switched to leucine-deficient diet supplemented with 7 g/kg of deuterated [5,5,5-²H₃]-l-leucine (Cambridge Isotope Laboratory, Andover, MA). The change to a synthetic diet was accompanied by an initial drop in body weight, however, growth rates quickly returned to a rate comparable to mice kept on a regular diet (supplemental Fig. S4). Three mice were euthanized for tissue collection at each of the 3, 10, and 17 day time points after switching to the ²H₃-leucine diet, and two mice were euthanized at the day 6 time point.

Mitochondria Sample Preparation

Mitochondrial isolation was performed as previously described (12). Briefly, cardiac ventricular and liver tissues were homogenized in mitochondrial isolation buffer (250 mm sucrose, 1 mm EGTA, 10 mm HEPES, 10 mm Tris-HCl pH7.4). Lysates were centrifuged at 800 × g for 10 min. The resulting supernatants were centrifuged at 4000 × g for 30 min at 4 °C. The crude mitochondrial pellets were then resuspended in 19% Percoll solution in isolation buffer, and slowly layered on top of a preformed Percoll step gradient, 30 and 60% (v/v), respectively. After centrifugation at 10,000 × g for 20 min, purified mitochondria were retrieved at the interface between two layers. All procedures were performed at 4 °C. The purity of mitochondrial extract was examined using a citrate synthase activity assay and Western blots for mitochondrial protein Prohibitin (Biomeda Corp, 1:1000) and cytosolic protein GAPDH (Millipore, 1:10,000), as previously described (13).

Mitochondrial fractions were solubilized with Rapigest (Waters Corporation, Milford, MA) at a final concentration of 0.1% and boiled for 5 min. The samples were treated with 5 mm dithiothreitol at 60 °C for 30 min to reduce disulfide bonds. The free sulfhydryls were alkylated with treatment of 15 mm iodoacetamide at room temperature, in the dark, for 30 min. Trypsin was added to a final concentration of 1:100 (μg trypsin/μg protein) and the sample digested at 37 °C for 2 h. The trypsin activity was halted and rapigest was hydrolyzed with the addition of HCl to a final concentration of 200 mm and incubation at 37 °C for 30 min. The samples were centrifuged for 10 min at 20,000 × g and the supernatant saved.

LC-MS/MS and Peptide Database Search

LC-MS/MS analysis of the digested samples was performed with a Waters nanoAcquity UPLC and a Thermo Scientific LTQ-FT Ultra. A 1–2 μg peptide sample was loaded onto a 4 cm long (100 μm inner diameter) trapping column then separated over a 35 cm long (75 μm inner diameter) homemade fused silica capillary column, packed with Jupiter Proteo C-12 resin (Phenomenex), at a flow rate of 250 nl/min. The mobile phase gradient used consisted of buffer A (100% water, 0.1% formic acid) and buffer B (100% acetonitrile, 0.1% formic acid). A linear gradient (2% to 32% buffer B in buffer A) was performed from 0 to 180 min, followed by 5 min at 80% buffer B and a re-equilibration step of 15 min at 2% buffer B. The LTQ-FT Ultra was operated with a scan cycle of one MS scan in the ICR cell (50,000 resolving power FWHM at 400 m/z, 1 × 10⁶ target ions) followed by five data-dependent MS/MS scans in the ion trap (2000 target ions, dynamic exclusion was set to 30 s with a repeat count of 1).

Prior to the peptide database search, the MS data was processed with the Bullseye algorithm (14) to optimize precursor mass measurements. MS/MS spectra were searched with the SEQUEST algorithm (version 27) (15) against a mouse IPI protein database (v3.57). A dynamic modification of 3.0188325 for leucine was set to account for [5,5,5-²H₃]-leucine. A static modification of 57.021461 for cysteine was set for carbamidomethyl modifications. The precursor monoisotopic mass tolerance was set to ± 10 ppm and the fragment mass tolerance window was set to 0.36 m/z. No enzyme digestion specificity was set. The false discovery rate for peptide-spectrum matches was determined by the Percolator algorithm (16). For the decoy peptide database file, protein sequences from the target database were reversed.

Topograph Software Program

The software program, Topograph (http://proteome.gs.washington.edu/software/topograph/), was developed in-house for the deconvolution and measurement of peptide isotopolog abundances from LC-MS chromatograms, and the calculation of peptide turnover rates. Peptides analyzed were limited to those with a false discovery rate less than 0.01. For each peptide, from 300 MS scans prior to the first observed MS/MS scan of the peptide to 300 MS scans following the last observed MS/MS scan, the peptide's isotope distribution at each MS spectrum was deconvoluted.

The peptide isotope distribution deconvolution was performed as follows. The isotope distribution for each possible labeled form of the peptide was computed using the method described by Kubinyi (17). A list of m/z windows was generated for all isotope peaks, in all charge states detected, that are predicted to contribute at least 1% of the total signal for an isotopolog's distribution. Using these m/z windows, the amount of each isotopolog in an MS spectrum was determined by calculating the fractional amount of each theoretical isotopolog distribution that best fits the observed signal using a least squares analysis as described by Brauman (18). The total abundance of each isotopolog was determined by integrating over time, across its chromatographic peak. A score was determined for each scan by calculating a dot product of the observed isotope distribution and the predicted isotope distribution, and normalizing to the observed isotope distribution. The scores were intensity weighted and summed across the chromatographic peak to give a deconvolution score. Detection of lower abundance isotopolog peaks was determined by identifying the nearest, most similarly shaped peak to the most abundant isotopolog (19).

Once the isotopolog abundances were determined, the relative isotope abundance (RIA) of the amino acid precursor pool, the amount of pre-existing unlabeled peptide and the amount of newly synthesized peptide were calculated. For peptides containing two or more labeled amino acids, Topograph generated the expected distribution of unlabeled, partially and fully labeled peptides for pre-existing peptides at the start of the labeling experiment. The expected distribution of unlabeled, partially and fully labeled peptides was then generated for newly synthesized peptides, at all percentages of the amino acid precursor pool RIA, in 1% increments. For every RIA increment, the ratio of pre-existing peptide and newly synthesized peptide that best fits the observed isotopolog distribution was determined by least squares analysis. The RIA percentage that best fits the observed isotopolog distribution, again by least squares analysis, was accepted as the RIA of the precursor pool for that peptide. The median of the calculated RIAs for all peptides was used to recalculate the ratio of pre-existing and newly synthesized peptides for all peptides, including those with only a single labeled amino acid.

Peptide Turnover Calculation

For peptide turnover calculations, the peptide population is represented by pre-existing, unlabeled peptides present prior to introducing the label in the diet; and peptides newly synthesized after the introduction of the labeled diet. The dilution of pre-existing, unlabeled peptides by newly synthesized peptides can be described by the equation for exponential decay:

where p₀ is the amount of the pre-existing, unlabeled peptide, at the start of the labeling experiment and p_t is the amount of the pre-existing, unlabeled peptide, at time t. The first order rate constant is λ. t_o is the time delay from the introduction of the tracer in the diet to the appearance of the tracer in the peptide.

We assume a steady state level of peptides during the course of the experiment, which we believe to be a reasonable approximation for the slowly or nonproliferating adult mouse tissues examined. Thus,

where p_n is the amount of peptide that is newly synthesized since the start of the experiment. The fraction of the peptide that is newly synthesized, n, can be written as:

Substituting in equation 2 and 3, equation 1 can be written

Applying the natural log to equation 4 results in equation 5

Equation 5 can be rewritten in terms of n to obtain the curve for newly synthesized peptide

RESULTS

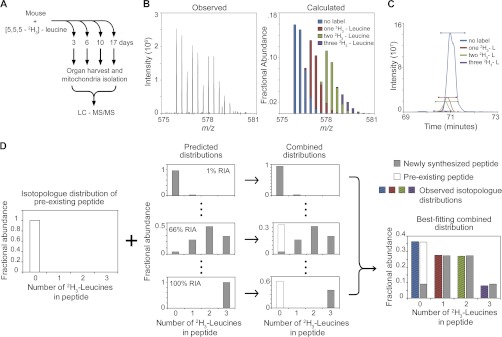
We used data obtained from the mitochondria of mice fed a Harlan synthetic leucine-free diet supplemented with [5,5,5-²H₃] leucine to validate our approach. Mice were fed the isotope enriched diet for up to 17 days. The mice were euthanized at four time points, with three biological replicates at each time point. Mitochondria were enriched from the liver and heart tissues and analyzed by LC-MS/MS as described in Methods (Fig. 1A).

Fig. 1.

Overview of experimental design and analysis by Topograph. A, Mice were fed a diet containing [5,5,5-²H₃]-leucine. At 3, 6, 10, and 17 days, the mice were euthanized, liver, and heart tissues were harvested and mitochondria were isolated. The isolated mitochondria were digested with trypsin and then analyzed by LC-MS/MS. B, An example of an observed peptide isotope distribution and its predicted isotopolog deconvolution by Topograph. The deconvolution was done for every MS scan of an identified peptide isotope distribution. C, A plot of the summed ion signal for each isotopolog over time. The horizontal bars above each peak indicate the time range used to calculate the integrated ion signal for each isotopolog. Peptides containing deuterated leucines are more hydrophilic and elute in the lower organic mobile phase portion of the gradient (24). D, Overview of process used to determine the amino acid precursor pool relative isotope abundance (RIA) initial estimation and the ratio of pre-existing/newly synthesized peptide. The isotopolog distribution of pre-existing peptides is combined with the predicted distributions of newly synthesized peptides at each RIA from 1% to 100%. A least squares comparison determines the optimum pre-existing:newly synthesized peptide ratio. A second least squares comparison determines the combined distribution that best fits the observed isotopolog distribution.

Peptide turnover rates were calculated using a formula for exponential decay and the fractional abundance of pre-existing and newly synthesized peptides. The initial step of Topograph was to deconvolute the isotope distribution of all peptides identified by MS/MS to determine the abundance of each of the peptide's isotopolog (Fig. 1B). The fractional abundance of each peptide isotopolog was calculated by integrating the area of the chromatographic peak (Fig. 1C). The individual peptide isotopolog ratios were used to distinguish between pre-existing and newly synthesized protein, as described further below.

We used two assumptions in our protein turnover model. First, the steady state level of proteins in mitochondria was assumed not to change significantly over time. That is, as proteins were degraded they were replaced with newly synthesized proteins at the same rate. We believe that this assumption is reasonable because all samples were collected from fully developed adult mice interrogated over a small fraction of their lifespan. Second, we assumed that the amino acids incorporated into proteins during synthesis all originated from a single homogeneous tRNA pool for the tissue studied. This second assumption simplifies turnover calculations by eliminating the need to calculate the isotope abundances of multiple amino acid precursor pools, and the equilibrium rates between them.

For turnover rate calculations, proteins were treated as belonging to one of two populations. The first was pre-existing proteins that were present in the mouse before introducing the labeled diet. The second protein population was newly synthesized proteins, synthesized after introduction of label. The fractional abundance of the two populations directly applies to the turnover calculations. The mouse diet before the introduction of the fully labeled leucine diet contained only amino acids in natural isotope abundances, meaning that pre-existing peptides existed only in the form of the unlabeled isotopolog. Newly synthesized proteins, however, could not be assumed to consist of only labeled isotopologs. On entry to the cell, the labeled amino acid tracer was diluted by unlabeled amino acids that already existed as free amino acids or were released from the breakdown of proteins. As a result, proteins newly synthesized from this amino acid pool consisted of a mixture of unlabeled and labeled isotopologs in a ratio directly related to the RIA. Knowledge of the precursor pool RIA can therefore be used to calculate the ratio of newly synthesized protein present, which is an essential element in the method described here.

The approach used to solving the precursor pool RIA has been described by Doherty et al. (20) and was used to investigate protein turnover rates in chickens. The basis of the method is similar to mass isotopomer distribution analysis, originally developed by Hellerstein and Neese (21) for measuring the biosynthesis of fatty acids and cholesterol. Mass isotopomer distribution analysis uses the combinatorial probability of the incorporation of individual monomers into a biopolymer to distinguish between pre-existing and newly synthesized molecular species. Similarly, the initial RIA estimation generated in Topograph could only be calculated for peptides with two or more possible labeled amino acids. For peptides that contain only a single possible label, there exist multiple combinations of RIA and newly synthesized/pre-existing peptide ratios that result in identical isotopolog distributions, making it impossible to identify the correct RIA. For multiple-labeled peptides, however, each RIA generates a unique isotopolog distribution (supplemental Fig. S1). Once the precursor pool RIA was identified from multiple-labeled peptides, it was then applied to the analysis of peptides that contained only a single possible label.

The precursor pool RIA was solved for each multiple-leucine containing peptide by generating a series of predicted isotopolog distributions, for all precursor pool RIA values from 1% to 100% in 1% increments. For each of these predicted distributions, Topograph combined it with the pre-existing peptide isotopolog distribution. The series of combined distributions was compared with the observed distribution and the best-fitting one determined by least squares analysis (Fig. 1D). The best-fitting distribution provided an initial amino acid RIA estimate for that peptide and time point. Fig. 2A illustrates a histogram of amino acid RIA measurements for a mouse liver mitochondria sample at the day 10 time point. The mean RIA measurement was 51% with a standard deviation of 10.5%, a standard error of the mean of 0.36% and a median of 50%. A separate experiment analyzing labeled yeast lysate was also performed which further validated the precursor pool RIA calculation method (supplemental Fig. S2).

Fig. 2.

Amino acid precursor pool measurements and peptide turnover curves. A, An example histogram of the initial precursor pool RIA measurements for a mouse mitochondria liver harvested after 10 days of a labeled leucine diet. The RIA can only be determined from peptides with two or more leucines. B, A plot of the median precursor pool RIA measurements for liver and heart mitochondria samples over time. The median value is used re-calculate pre-existing/newly synthesized peptide ratios. The higher RIA in liver mitochondria indicates the liver incorporates labeled leucine more rapidly than the heart. The high level of labeled leucine in heart at 3 days is caused by imprecision in measurement from low protein turnover in heart proteins. C, The natural log of the degradation of the pre-existing peptide (100%– % newly synthesized peptide) over time is plotted for the peptide LEDTLWAGLTDQHVK. The decay rate of the peptide is equal to the slope of the linear regression of these data points. D, For the example peptide, LEDTLWAGLTDQHVK, the percentage of the peptide that was newly synthesized is plotted over time. A synthesis curve was plotted based on the decay rate determined from the linear regression in panel (C). E, Synthesis curves for the peptide, FNGGGHINHTIFWTNLSPK, were calculated with and without correcting for the amino acid precursor pool relative isotope abundance. With precursor pool correction the calculated decay rate was 0.116 day⁻¹ (half-life of 6.0 days). Without precursor pool correction the calculated decay rate was 0.054 day⁻¹ (half-life of 12.9 days.

An overall precursor pool RIA value for each sample was calculated by taking the median of the initial RIA values from the sample. The fractional abundances of pre-existing and newly synthesized peptide populations were then re-calculated by applying the median RIA measurement to all peptides including those with only one possible label. Shown in Fig. 2B are the median RIA values plotted for each mouse mitochondrial sample over time. The overall trend was an increase in the RIA over time, indicative of the gradual incorporation of labeled leucine into newly synthesized proteins. RIA measurements at the earliest time point (day 3) had the greatest degree of variation. In the liver mitochondria samples, RIA measurements at day 3 had an average coefficient of variation (CV) of 54%, compared with days 6, 10, and 17, which had average CVs of 41%, 22%, and 17%, respectively. The greater imprecision at the earlier time points was in part because of the low fraction of labeled isotopologs; in this condition small variations in the isotopolog measurements resulted in large differences in precursor RIA estimations (supplemental Fig. S3). This error is apparent in the day 3 time point of Fig. 2B. However, these resulting differences did not significantly affect peptide turnover calculations (e.g. see Fig. 2C) because large differences in the median RIA estimation have a lesser effect on the calculated fraction of newly synthesized peptide when the amount of labeled isotopolog is low.

The rate of synthesis of new proteins (which in steady state is the same as the rate of degradation of the pre-existing population of proteins) can be described by an equation for a first-order exponential decay and the fractional abundances of pre-existing and newly synthesized peptides, as calculated by Topograph. These were used to solve for the rate constant (see Methods). Plotted in Fig. 2C is an example of the pre-existing peptide ratios for the acetyl-coenzyme A acyltransferase 2 (ACAA2) peptide, LEDTLWAGLTDQHVK, plotted over time. Following the equation for exponential decay, the slope of the linear regression of these data points is the decay constant. Plotted in Fig. 2D is the synthesis curve, determined using the decay constant, for this peptide. The x-intercept of the synthesis curve is at approximately day 1 and is indicative of the time from introduction of label to appearance of the label in synthesized protein. This delay may be caused by a number of factors, such as the lag in the time from introduction of the label to the time of ingestion, the time required for digestion and distribution of the label to the organ of interest, and the time required for the label to enter the amino acid precursor pool of the cells.

Application of the precursor RIA to turnover calculations can have dramatic effects on the calculated turnover estimates (Fig. 2E). Without knowledge of the precursor pool RIA, all labeled forms of the peptide were treated as newly synthesized and all unlabeled forms were considered pre-existing. In experiments with low label incorporation rates, this results in an underestimation of the amount of newly synthesized peptide. For the peptide shown in Fig. 2E, the uncorrected decay rate was calculated to be 0.054 day⁻¹ (half-life of 12.9 days). Using the precursor RIA values calculated by Topograph, the portion of the unlabeled peptide that is newly synthesized can be accurately determined, resulting in a corrected decay rate of 0.116 day⁻¹ (half-life of 6 days).

In addition to peptide turnover rates, turnover values may be calculated for proteins. A protein group is comprised of proteins which are defined by a set of unique peptide sequences. Protein groups are limited to unique peptide sets because the contribution of a nonunique peptide to the turnover rate of a protein group is ambiguous and cannot be determined. Although assigning peptides and protein groups in this manner limits the number of data points, it also removes the need to determine a nonunique peptide's contribution. In Fig. 3A, the synthesis curves for peptides unique to superoxide dismutase 2 (SOD2) is plotted. There were nine and 13 peptides unique to SOD2 detected in the liver and heart mitochondria, respectively. The decay rate of SOD2 was 0.158 and 0.026 day⁻¹ (half-life of 4.4 and 26.7 days) with 95% confidence intervals of ±0.016 and ±0.003 day⁻¹, in liver and heart, respectively.

Fig. 3.

Peptides in heart mitochondria turn over more slowly than in liver mitochondria. A, The percentage of newly synthesized peptide is plotted over time for all peptides of superoxide dismutase 2 (SOD2, Swiss-Prot P09671) that were detected in the mice liver and heart mitochondria samples. The solid lines indicate the calculated synthesis curves. The dotted lines indicate the 95% confidence interval. Thirteen peptides unique to SOD2 were detected from the heart samples and nine unique peptides were detected from the liver samples. There were 39 and 76 data points with a unique peptide and time point in liver and heart samples, respectively. The decay rate of SOD2 was 0.158 day⁻¹ in liver mitochondria and 0.026 day⁻¹ in heart mitochondria. B, A histogram is plotted of the log₂ of the ratio of the first-order rate constants for proteins detected in both the liver and heart mitochondria samples. Proteins were filtered to those with a minimum of seven time points.

In total, turnover rates were calculated for 337 and 244 proteins in liver and heart mitochondria samples (minimum of seven data points were used for each protein). One hundred and sixty-one proteins were common in both data sets. The median decay rate of proteins in the liver mitochondria was 0.176 day⁻¹ (half-life of 3.9 days) compared with 0.0295 days⁻¹ (half-life of 23.4 days) in heart mitochondria. Comparing the 161 proteins in common between both data sets, nearly all heart mitochondrial proteins have a slower turnover rate than the corresponding liver mitochondrial protein (Fig. 3B), an observation consistent with data previously published on average protein turnover rates of various tissues in mice (8) and rats (22).

DISCUSSION

Disruptions in protein homeostasis are a consequence of disease, and a number of disease treatments that focus on restoring homeostasis have been suggested (23). The ability of mass spectrometry based methods to measure protein turnover on a global scale is valuable in understanding the changes in the interacting network of pathways that occur in diseased states. Our software platform, Topograph, was developed to aid in the analysis of the vast amounts of data acquired from such experiments. The features available in Topograph enable the proteomics based study of protein turnover in a manner previously made difficult because of limitations in available software tools. Topograph provides a graphical user interface for data analysis and a novel implementation of existing algorithms to calculate the amino acid precursor pool enrichment level, resulting in more direct and accurate turnover rate calculations. In the data reported here, we analyzed mitochondrial proteins from heart and liver tissue of mice labeled with [5,5,5-²H₃] leucine; however, the algorithms would be applicable to the use of other stable isotope labels, such as ¹⁵N. The flexibility in labeling methods allows for the use of synthetic diets, which can be formulated to closely approximate the composition of conventional diets. We envision this approach as being widely applicable to studies of aging and metabolism and diseases of altered protein homeostasis, including those of protein aggregation and misfolding.