Sample Size Tables for Computer-Aided Detection Studies

Abstract

OBJECTIVE

Calculating the sample size for a multireader, multicase study of readers’ diagnostic accuracy is complicated. Studies in which patients can have multiple findings, as is common in many computer-aided detection (CAD) studies, are particularly challenging to design.

MATERIALS AND METHODS

We modified existing methods for sample size estimation for multireader, multicase studies to accommodate multiple findings on the same case. We use data from two large multireader, multicase CAD studies as ballpark estimates of parameter values.

RESULTS

Sample size tables are presented to provide an estimate of the number of patients and readers required for a multireader, multicase study with multiple findings per case; these estimates may be conservative for many CAD studies. Two figures can be used to adjust the number of readers when there is some data on the between-reader variability.

CONCLUSION

The sample size tables are useful in determining whether a proposed study is feasible with the available resources; however, it is important that investigators compute sample size for their particular study using any available pilot data.

Multiple-reader, multiple-case studies are common and important tools used to estimate and compare diagnostic and screening tests’ accuracy, but they are challenging to design. There are many possible sampling strategies for study patients and readers, a variety of reading formats and confidence scales, various endpoints, and many factors to consider in determining the number of patients and readers required for the study.

For diagnostic and screening tests used to detect and locate lesions, sample size determination must take into account the possibility that multiple lesions can occur in the same patient (e.g., multiple colon polyps, multiple lung nodules). Multiple lesions are common in the types of conditions evaluated by computer-aided detection (CAD) devices. In these studies, it is important that the reader not only determine that an image depicts the condition, but also correctly locate the abnormalities. In a typical CAD study, readers are asked to find and mark all suspicious lesions, grade their suspicion level, and recommend appropriate follow-up for the patient. A single interpretation of an image can include multiple true- and false-positive findings of various suspicion levels.

There have been several excellent articles about the design of multireader, multicase CAD studies [1–4]. In this article, we focus on sample size estimation for multireader, multicase CAD studies. We illustrate how to modify sample size calculations for multireader, multicase studies to account for multiple true lesions in the same patient and for both true- and false-positive findings in the same patient. We generate sample size tables that can be used as starting values or rough estimates for planning CAD studies.

Materials and Methods

Two Computer-Aided Detection

Study Examples

Two large completed CAD trials are used to illustrate common designs for CAD studies and to provide ballpark estimates of several parameters needed for sample size calculation.

The first trial is a study of high-risk patients with either symptoms of lung disease or a suspicious finding on a prior chest radiograph who underwent CT of the lung (Nadich D et al., presented at the 2005 annual meeting of the Radiological Society of North America). Two hundred patients were recruited consecutively; thus, the final ratio of patients with lung nodules versus those without lung nodules was unknown at the start of the study. Seventeen study readers participated in blinded two-step sequential readings in which they first interpreted a CT image without CAD and stored their results and then were shown the CAD marks and asked to reinterpret the same image. The reference standard for the study was the majority opinion of a five-member panel of expert chest radiologists. In this study, 85% of the patients with nodules had more than one nodule.

The second study used a retrospective design to evaluate asymptomatic patients who had undergone CT colonography [5]. Fifty-two patients with colon polyps and 48 patients without polyps were selected for the study on the basis of the results of optical colonoscopy or review by a three-member panel of expert radiologists; 25% of the patients with polyps had more than one polyp. Nineteen study readers participated in a crossover design in which all of the study readers interpreted the images twice: first, during a reading session without CAD; and, second, 4 weeks later during a two-step sequential session. During the latter, readers first interpreted an image without CAD (step 1) and then immediately were shown the CAD marks and asked to interpret the image again (step 2).

In both studies readers were asked to mark all suspicious lesions and score each according to their confidence that the lesion represented a lung nodule or colon polyp, respectively. In the lung CAD trial, a confidence scale of 1–10 was used, where 1 indicated that the lesion was definitely not a nodule and 10 indicated that the lesion was definitely a nodule. In the colon CAD trial, a confidence scale of 1–100 was used, where a score of 1 indicated that the lesion was definitely not a polyp and 100 indicated that the lesion was definitely a polyp. For estimating sensitivity and specificity, cutpoints of 6 and 51, respectively, were used to define a positive test result.

The primary measure of test accuracy for both studies was the area under the receiver operating characteristic (ROC) curve, but both sensitivity (lesion-level) and specificity (patient-level) were also estimated. There are several possible statistical methods available for analyzing ROC data where both detection and correct localization of the suspicious lesion are required for the lesion to be considered a true-positive [6–10]. For the two studies discussed here, a region-of-interest (ROI) approach was used [9, 10]. In the lung CAD study, the lung was divided a priori into five lung lobes (i.e., five ROIs per patient); in the colon CAD study, the colon was divided a priori into six colonic segments (i.e., six ROIs per patient).

The statistical analysis was based on the findings from the multiple ROIs per patient. This approach was used for two reasons: First, it characterizes a reader’s ability both to detect and to correctly locate the abnormality; and, second, sample size computations, based on conjectured parameter values, that account for within-ROI or within-lesion correlation can be derived using previously established statistical results.

Sample Size Estimation for Multireader, Multicase Studies With Multiple Findings

We used the general approach to multireader, multicase sample size estimation outlined by Hillis et al. [11]. Hillis et al. described sample size estimation for multireader, multicase studies in two general situations: when there is a pilot study and we want to scale it up for a pivotal trial, and when there are no pilot study data. In this article, we assume that there was no pilot study, which is the more common scenario and is the most difficult to compute sample size for.

For a specified total number of study patients, N_total, and a specified number of study readers, Hillis et al. [11] outlined four steps to computing the power for a multireader, multicase study: First, specify the effect size; second, conjecture parameter values; third, compute the noncentrality parameter and denominator degrees of freedom; and, fourth, compute the power. The four steps are further detailed in Appendix 1.

For estimating the ROI-level area under the ROC curve and lesion-level sensitivity, the correlation between lung lobes or colonic segments or between true lesions from the same patient must be accounted for in the sample size calculation. We refer to these data as “clustered data.” Clustered data affect the calculation of σ²_ε (step 2) in the sample size calculation. Formulae for estimating σ²_c are given in Appendix 1 (equations 1–3); these formulae need to be modified for clustered data. The modifications to these formulae, as well as the estimation of parameter values from the two CAD studies, are described in Appendix 2.

The two most popular reading formats for multireader, multicase CAD studies are sequential and crossover readings. In the sequential format, a reader interprets an image without CAD and records his or her result, then immediately is shown the CAD marks for that image and asked to reinterpret and record the result again. In contrast, in the crossover design, a reader interprets images without CAD in a session where CAD is not available. At another reading session, often separated from the first reading by at least 1 month, readers interpret the same image with CAD. Sample size calculation is similar for these two reading formats (see Appendix 2). In the sample size tables we present results for both of these reading formats.

Results

Tables 1 and 2 provide sample size estimates for CAD studies using either a crossover or sequential design. For both tables, we used the ballpark values for various parameters; however, we note that when investigators have reliable parameter estimates available from pilot work, then those data should be used in the formulae in Appendix 2 instead of the ballpark estimates provided here.

TABLE 1.

Sample Size Requirements for Study With Sensitivity as Endpoint

			No. of Readers (R) and No. of Patients With Lesions (ND)
Sensitivity	Effect Size	No. of Lesions per Patient (fD)	Crossover Design	Sequential Design
0.5	0.04	All patients have 1 lesion (1.0)	None	21 and 100; 24 and 60
		25% of patients have 2 lesions (1.25)	25 and 100	21 and 90; 25 and 50
		50% of patients have 2 lesions (1.5)	25 and 90	20 and 100; 24 and 50
0.5	0.06	All patients have 1 lesion (1.0)	13 and 100; 20 and 40	11 and 80; 16 and 30
		25% of patients have 2 lesions (1.25)	13 and 90; 18 and 40	11 and 70; 15 and 30
		50% of patients have 2 lesions (1.5)	12 and 100; 18 and 40	11 and 70; 15 and 30
0.7	0.04	All patients have 1 lesion (1.0)	24 and 100; 25 and 90	20 and 100; 24 and 50
		25% of patients have 2 lesions (1.25)	24 and 100; 25 and 80	20 and 90; 25 and 40
		50% of patients have 2 lesions (1.5)	24 and 90; 25 and 80	20 and 90; 25 and 40
0.7	0.06	All patients have 1 lesion (1.0)	13 and 80; 18 and 40	11 and 70; 15 and 30
		25% of patients have 2 lesions (1.25)	12 and 90; 20 and 30	10 and 100; 14 and 30
		50% of patients have 2 lesions (1.5)	12 and 80; 19 and 30	10 and 90; 14 and 30
0.9	0.04	All patients have 1 lesion (1.0)	20 and 90	18 and 80; 14 and 30
		25% of patients have 2 lesions (1.25)	19 and 100; 20 and 80	18 and 70; 20 and 40
		50% of patients have 2 lesions (1.5)	19 and 100; 20 and 70	18 and 70; 19 and 50
0.9	0.06	All patients have 1 lesion (1.0)	11 and 60; 14 and 30	9 and 100; 11 and 30
		25% of patients have 2 lesions (1.25)	11 and 60; 12 and 40	9 and 90; 10 and 40
		50% of patients have 2 lesions (1.5)	11 and 50; 13 and 30	9 and 90; 10 and 40

Note—Sample sizes are for a study with at least 80% power, 5% type 1 error rate (two-tailed test), and assuming that r₁ = 0.6 for the crossover design and 0.8 for the sequential design, RHO_DD = 0.5, RHO_NN = 0.2, (r₂ − r₃) = 0, and σ²_{τ × R} = 0.0014.

TABLE 2.

Sample Size Requirements for Study With the Area Under the Receiver Operating Characteristic Curve as Endpoint

				No. of Readers (R) and No. of Patients With Lesions (ND)
AUC	Effect Size	No. of Subunits per Patient	No. of Lesions per Patient (fD)	Crossover Design	Sequential Design
0.5	0.04	2	All patients have 1 lesion (1.0)	20 and 100; 24 and 60	18 and 100; 21 and 50
			25% of patients have 2 lesions (1.25)	20 and 100; 24 and 50	19 and 70; 21 and 40
			50% of patients have 2 lesions (1.5)	20 and 100; 24 and 50	18 and 90; 20 and 50
0.5	0.04	4	All patients have 1 lesion (1.0)	20 and 90; 24 and 50	18 and 90; 20 and 50
			25% of patients have 2 lesions (1.25)	20 and 90; 24 and 50	18 and 80; 20 and 50
			50% of patients have 2 lesions (1.5)	20 and 80; 24 and 40	18 and 80; 20 and 40
0.5	0.04	6	All patients have 1 lesion (1.0)	20 and 90; 24 and 50	19 and 60; 21 and 40
			25% of patients have 2 lesions (1.25)	20 and 80; 24 and 50	18 and 80; 20 and 40
			50% of patients have 2 lesions (1.5)	19 and 100; 24 and 40	18 and 70; 20 and 40
0.5	0.06	2	All patients have 1 lesion (1.0)	11 and 70; 13 and 40	10 and 60; 11 and 40
			25% of patients have 2 lesions (1.25)	10 and 100; 12 and 50	10 and 50; 11 and 40
			50% of patients have 2 lesions (1.5)	10 and 100; 12 and 50	10 and 50; 11 and 40
0.5	0.06	4	All patients have 1 lesion (1.0)	10 and 100; 12 and 50	10 and 50; 11 and 30
			25% of patients have 2 lesions (1.25)	10 and 90; 12 and 50	9 and 100; 11 and 30
			50% of patients have 2 lesions (1.5)	10 and 90; 12 and 40	9 and 100; 11 and 30
0.5	0.06	6	All patients have 1 lesion (1.0)	10 and 90; 12 and 50	10 and 50; 11 and 30
			25% of patients have 2 lesions (1.25)	10 and 90; 12 and 40	9 and 100; 11 and 30
			50% of patients have 2 lesions (1.5)	10 and 80; 12 and 40	9 an 90; 11 and 30
0.7	0.04	2	All patients have 1 lesion (1.0)	20 and 100; 24 and 50	18 and 100; 22 and 40
			25% of patients have 2 lesions (1.25)	20 and 100; 24 and 50	18 and 90; 21 and 40
			50% of patients have 2 lesions (1.5)	20 and 90; 24 and 50	18 and 90; 22 and 30
0.7	0.04	4	All patients have 1 lesion (1.0)	20 and 90; 24 and 50	18 and 90; 22 and 30
			25% of patients have 2 lesions (1.25)	20 and 80; 24 and 50	18 and 80; 22 and 30
			50% of patients have 2 lesions (1.5)	19 and 100; 23 and 50	18 and 80; 22 and 30
0.7	0.04	6	All patients have 1 lesion (1.0)	20 and 90; 24 and 50	18 and 90; 22 and 30
			25% of patients have 2 lesions (1.25)	20 and 80; 24 and 40	19 and 60; 22 and 30
			50% of patients have 2 lesions (1.5)	20 and 80; 24 and 40	18 and 70; 20 and 40
0.7	0.06	2	All patients have 1 lesion (1.0)	11 and 70; 13 and 40	10 and 60; 11 and 40
			25% of patients have 2 lesions (1.25)	10 and 100; 12 and 50	10 and 50; 11 and 40
			50% of patients have 2 lesions (1.5)	10 and 100; 11 and 60	10 and 50; 11 and 30
0.7	0.06	4	All patients have 1 lesion (1.0)	10 and 100; 11 and 60	10 and 50; 11 and 30
			25% of patients have 2 lesions (1.25)	10 and 90; 12 and 40	9 and 100; 11 and 30
			50% of patients have 2 lesions (1.5)	10 and 80; 12 and 40	9 and 100; 10 and 40
0.7	0.06	6	All patients have 1 lesion (1.0)	10 and 90; 12 and 50	10 and 50; 11 and 30
			25% of patients have 2 lesions (1.25)	10 and 90; 12 and 40	9 and 100; 11 and 30
			50% of patients have 2 lesions (1.5)	10 and 80; 12 and 40	9 and 90; 11 and 30
0.9	0.04	2	All patients have 1 lesion (1.0)	18 and 100; 22 and 40	18 and 50; 20 and 30
			25% of patients have 2 lesions (1.25)	18 and 90; 20 and 50	17 and 80; 19 and 40
			50% of patients have 2 lesions (1.5)	18 and 90; 22 and 40	18 and 50; 20 and 30
0.9	0.04	4	All patients have 1 lesion (1.0)	18 and 90; 20 and 50	18 and 50; 20 and 30
			25% of patients have 2 lesions (1.25)	18 and 90; 22 and 30	17 and 80; 19 and 30
			50% of patients have 2 lesions (1.5)	18 and 90; 20 and 50	17 and 70; 19 and 30
0.9	0.04	6	All patients have 1 lesion (1.0)	18 and 90; 22 and 40	17 and 80; 19 and 40
			25% of patients have 2 lesions (1.25)	18 and 90; 22 and 30	17 and 80; 19 and 30
			50% of patients have 2 lesions (1.5)	18 and 80; 22 and 30	17 and 70; 19 and 30
0.9	0.06	2	All patients have 1 lesion (1.0)	10 and 60; 12 and 30	9 and 70; 10 and 30
			25% of patients have 2 lesions (1.25)	10 and 50; 12 and 30	9 and 60; 10 and 30
			50% of patients have 2 lesions (1.5)	10 and 50; 11 and 30	9 and 60; 10 and 30
0.9	0.06	4	All patients have 1 lesion (1.0)	10 and 50; 11 and 40	9 and 60; 10 and 30
			25% of patients have 2 lesions (1.25)	10 and 50; 11 and 30	9 and 60; 10 and 30
			50% of patients have 2 lesions (1.5)	9 and 100; 11 and 30	9 and 50; 10 and 30
0.9	0.06	6	All patients have 1 lesion (1.0)	10 and 50; 11 and 40	9 and 60; 10 and 30
			25% of patients have 2 lesions (1.25)	10 and 50; 11 and 30	9 and 60; 10 and 30
			50% of patients have 2 lesions (1.5)	9 and 100; 11 and 30	9 and 50; 10 and 30

Note—Total patient sample size is 2 × N_D. Sample sizes are for a balanced study (i.e., N_D = N_N) with at least 80% power, 5% type 1 error rate (two-tailed test), and assuming that r₁ = 0.6 for the crossover design and 0.8 for the sequential design, RHO_DD = 0.5, RHO_NN = 0.2, (r₂ − r₃) = 0, and σ²_{τ × R} = 0.0014.

In Table 1, for a given estimate of readers’ average lesion-level sensitivity without CAD (first column), an estimate of the improvement in sensitivity with CAD (second column), and an estimate of the number of true lesions per patient among patients with lesions (column 3), the table provides several combinations of reader size and number of patients with true lesions needed for a crossover study (column 4) and sequential study (column 5).

Similarly, in Table 2, for a given estimate of readers’ average ROI-level area under the ROC curve without CAD (first column), an estimate of the improvement in ROC area with CAD (second column), the number of segments per patient (e.g., six colonic segments, two breasts) to be used in the analysis (third column), and an estimate of the number of true lesions per patient among patients with lesions (column 4), the table provides several combinations of reader size and the total number of patients with true lesions needed for a crossover study (column 5) and sequential study (column 6). Note that in the sample size calculations for Table 2, we considered a design with equal numbers of patients with and without true lesions. Thus, the total patient sample size from Table 2 is twice the number of patients listed in the table.

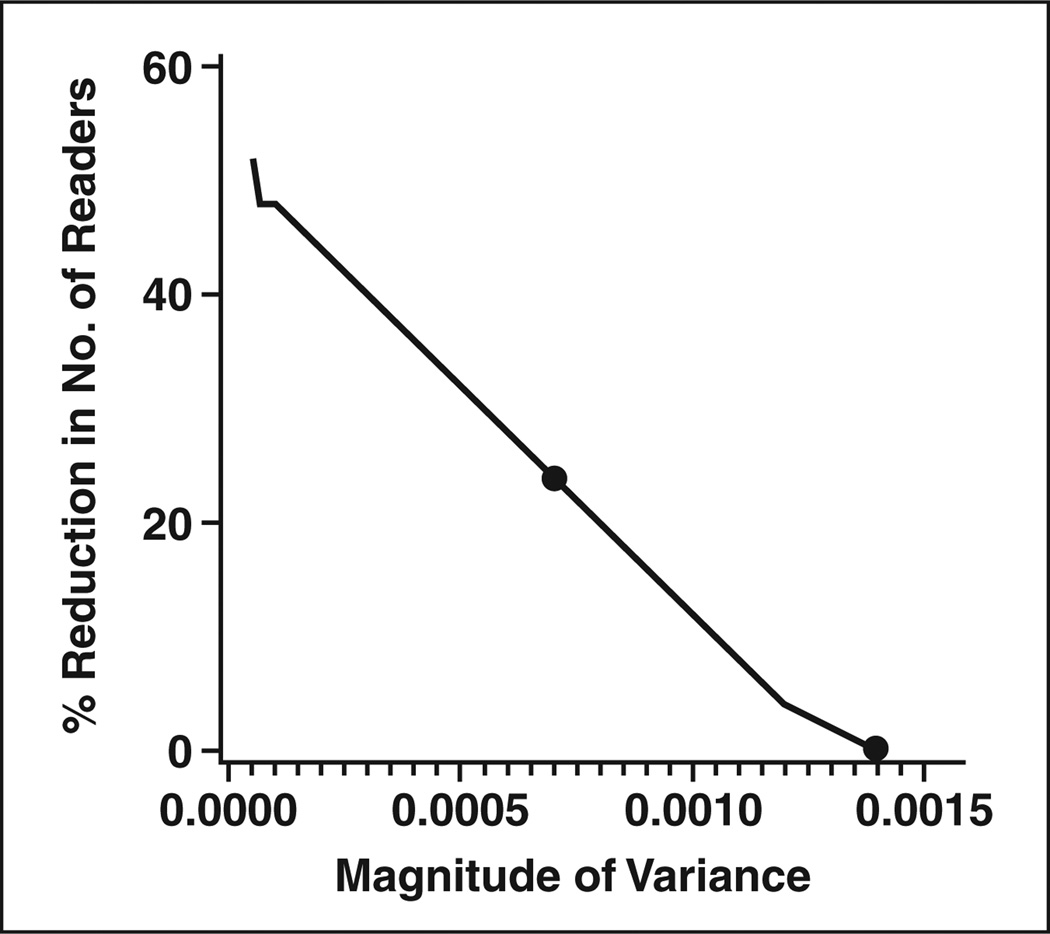
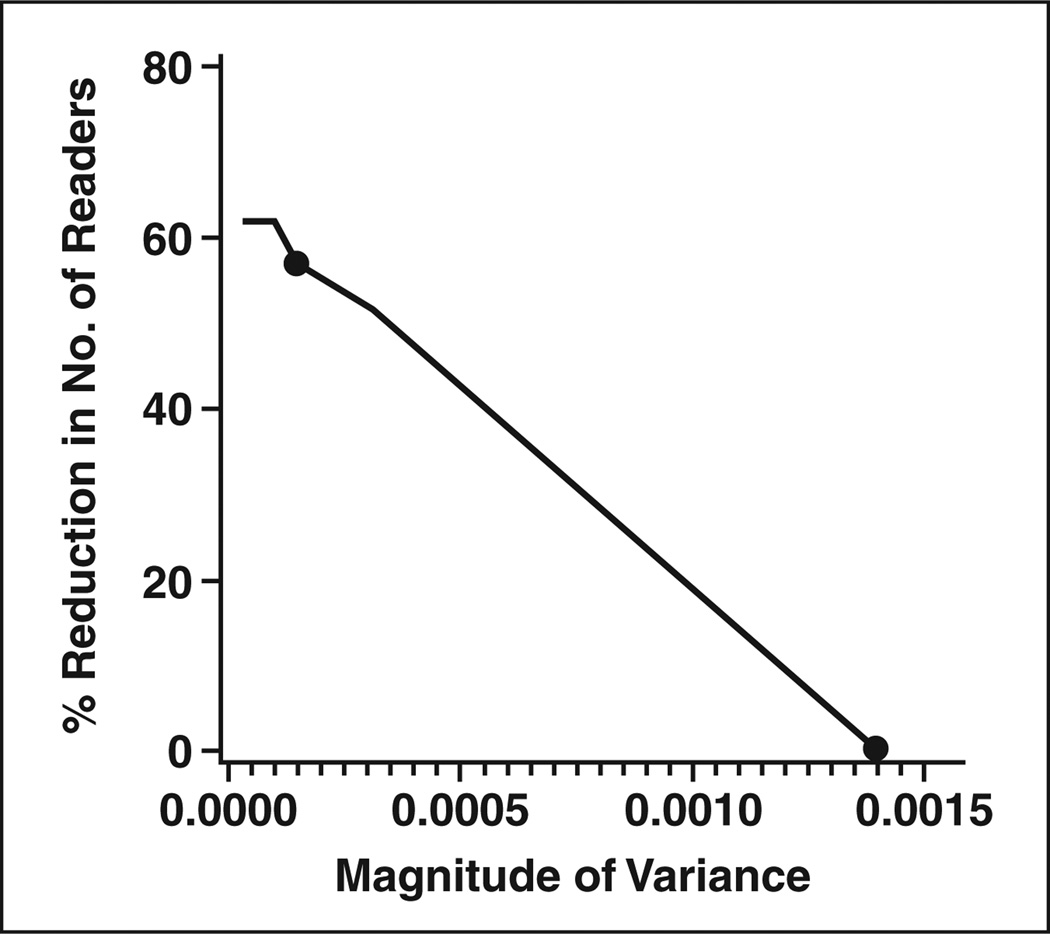
The sample size tables are based on the ballpark estimates of the parameter values derived from the two CAD studies. They may not be applicable for all CAD studies. The estimates can be affected by the disease, the technology, the relevant reader population, the accuracy endpoint, and the study design. For example, we found that the estimated correlation between lesions or between ROIs (i.e., RHO_DD and RHO_NN; see Appendix 2) differed between the two studies, often larger in the colon study. Fortunately, the values of these correlations used in the sample size formulae have very little effect on sample size. In contrast, the value of the variance for the interaction between readers and modality has a large effect on sample size. For the two CAD studies analyzed here, the estimate of this variance ranged from values near zero to values of 0.0014. We used a ballpark estimate of 0.0014 for Tables 1 and 2; thus, we might consider the sample size estimates in these tables to be conservative (i.e., larger than necessary) for many CAD studies. For studies in which the value of the variance of the interaction is expected to be smaller than 0.0014 (i.e., based on previous studies or pilot work), we have generated figures that provide an estimate of the percentage reduction in the number of readers required. Figures 1 and 2 illustrate the estimated percent reduction in the required reader sample size for endpoints of sensitivity (Fig. 1) and ROC area (Fig. 2) for different values of the variance of the interaction term. The figures also show the maximum, as well as median, value of the variance observed in the two CAD studies. At the median variance value for the sensitivity endpoint, 19 readers would be needed instead of the 25 required with the maximum value observed; for the ROC area endpoint, nine readers would be needed instead of the 21 required with the maximum value.

Fig. 1.

Estimated percentage reduction in required reader sample size as function of variance of interaction between reader and test for studies using sensitivity as endpoint. Two points represent maximum (0.0014) and median (0.000704) values of variance observed over two studies described in text.

Fig. 2.

Estimated percentage reduction in required reader sample size as function of variance of interaction between reader and test for studies using area of receiver operating characteristic curve as endpoint. Two points represent maximum (0.0014) and median (0.000145) values of variance observed over two studies described in text.

For illustration of the use of the tables and figures, consider a study in which the primary endpoint is sensitivity. Suppose that readers’ average sensitivity without CAD is 0.5 and we expect an improvement in sensitivity with CAD of 0.04. If 50% of patients have two lesions, then a conservative estimate of sample size (from Table 1) would include 25 readers and 90 patients with the disease with a crossover design or 20 readers and 100 patients with disease with a sequential design. Now suppose that we conjecture that readers’ sensitivities might range from 0.4 to 0.6, and we roughly estimate that this range represents 4 SDs; thus, our best estimate of the between-reader variance (σ_b²) is 0.0025. With an estimate of the between-reader variability, we can then estimate the variance for the interaction between reader and test [12]. An estimate of the variance of the interaction between reader and test is

$${{\mathrm{\sigma }}^{\mathit{2}}}_{\mathrm{\tau }\times R}=({{\mathrm{\sigma }}_b}^2)\times (1-r_b),$$

where r_b is the correlation between the accuracies when the same readers evaluate patients using different tests [12]. Rockette et al. [13] have recommended a value of 0.8 for r_b by estimating this correlation over many studies. Our estimate of the variance of the interaction between reader and test is then 0.0005. Using Figure 1, we estimate that we need about 30% fewer readers with σ²_{τ × R} = 0.0005 than with the ballpark estimate of 0.0014 used in the tables. So, a rough estimate of the sample size required for this study is 90 patients with disease and 18 readers for a crossover design or 100 patients with disease and 14 readers with a sequential design.

Discussion

We have generated tables that allow an investigator to determine a rough estimate, and in many cases an upper bound, for the number of readers and patients needed for a CAD study. The tables provide several combinations of reader sample size and patient sample size to consider. We also provide two figures that can be used to estimate the reader sample size for different values of variance for the interaction between reader and test. The tables and figures are particularly useful in determining whether a proposed study is feasible with available resources.

In calculating sample size for any study, when there is uncertainty about a parameter’s value, it is important to be conservative in choosing values so that the study is not underpowered. For example, if the area under the ROC curve is unknown, a conservative approach would be to use a low value for the area, with 0.5 being the most conservative value. Similarly, it is important not to overestimate the average number of true lesions that each patient with lesions may have. A conservative approach is to assume one lesion per patient; this might be appropriate for some studies in which the prevalence of disease is very low, as in screening mammography. For colonoscopy studies, however, this assumption is probably too conservative because asymptomatic patients often have more than one polyp. Clearly, choosing values for parameters in sample size estimation requires some balance; conservative values yield larger studies with greater expense, more resources, and often a lengthier study. On the other hand, overly optimistic values can lead to underpowered studies with wasted costs, resources, and time and misleading conclusions.

In deciding on a reasonable combination of reader sample size and patient sample size for a study, it is important to consider planned secondary analyses. For example, if we plan to estimate the sensitivity of CAD for different lesion types (e.g., by pathology, morphology, size, or location), then having a representative sample of patients is important and one might choose a sample size combination with a larger number of patients and fewer readers. If the study plans to investigate the effect of CAD on readers with different experience levels, then having a representative sample of readers is important and one might choose a sample size combination with more readers and fewer patients.

Once a multireader, multicase CAD study is completed, several statistical methods are available to analyze the clustered data from a single reader [14–20], and there are several statistical approaches to multireader, multicase studies that handle clustered data or can be modified to handle clustered data [7–12, 21–28].

Last, we note that our study has several limitations. First, we estimated several study parameters on the basis of values from only two large CAD studies. A larger number of CAD studies would have provided more reliable estimates and a broader range for the values of these study parameters. This is of particular importance because some parameters have large effects on sample size. Although the estimated correlation between lesions or between ROIs has a small effect on sample size, the variance associated with the interaction between readers and test has a large effect on sample size. Second, we considered just two values for the effect size; actual studies may conjecture effect sizes smaller than 0.04 or between 0.04 and 0.06. For these reasons, it is important that investigators compute sample size for their particular study using any available pilot data and not rely on the tables presented here.

APPENDIX 1

Steps in Determining Sample Size for Multireader, Multicase Studies [11] Based on Multireader, Multicase Statistical Methods [21–23]

Step 1: Specify the Effect Size, d

Specify the absolute difference (d) in performance with computer-aided detection (CAD) versus without CAD that you want to detect with sufficient power.

Step 2: Conjecture Parameter Values

There are four parameters that must be conjectured:

• the correlation between modalities for the same reader (r₁);

• the difference between the correlations of different readers for the same and different modalities (r₂ − r₃) (See Appendix 2);

• an estimate of σ²_{τ × R}, which is the variance of the interaction between modality and reader; and

• an estimate of σ²_ε, which is the variance of a reader’s estimated accuracy due to both intrareader variability (σ²_w) and patient sample variability (σ²_c). Note that σ²_ε = σ²_w + σ²_c.

When there are no pilot data, σ²_c for the receiver operating characteristic (ROC) curve area measure is often estimated from the following formula, which assumes that the underlying test scores follow a normal distribution [29]:

$${{\mathrm{\sigma }}^2}_c=(0.0099\times e^{-A\times A/\mathit{2}})\times [(5A^2+8)+(A^2+8)/k]/N_D$$ (equation 1)

where A = Ф⁻¹ (AUC) × 1.414. AUC is the conjectured area under the ROC curve, Ф⁻¹ is the inverse of the cumulative normal distribution function, N_D is the number of patients with true lesions, and k is the ratio of the number of patients without lesions (N_N) to the number of patients with lesions (N_D).

Alternatively, Blume [30] recommends the estimate of σ²_c in equation 2, which does not make any assumptions about the distribution of the test results, for the ROC area measure:

$${{\mathrm{\sigma }}^2}_c=\mathit{\text{AUC}}\times (1-\mathit{\text{AUC}})/N$$ (equation 2)

where the denominator, N, is the smaller of N_N and N_D.

For sensitivity, σ²_c is often estimated as follows:

$${{\mathrm{\sigma }}^2}_c=p\times (1-p)/N_D$$ (equation 3)

where p is the conjectured sensitivity and N_D is the number of patients with true lesions in the study sample. For specificity, equation 3 can be used with p defined as the conjectured specificity and with N_D replaced by N_N, the number of patients without lesions.

The intrareader variability, σ²_w, is often conjectured or estimated from other studies.

Step 3: Estimate the Noncentrality Parameter and Denominator Degrees of Freedom

An estimate of the noncentrality parameter, Δ, is

$$\{(R/2)d^2\}/\{{{\mathrm{\sigma }}^2}_{\mathrm{\tau }\times R}+{{\mathrm{\sigma }}^2}_{\mathrm{\epsilon }}(1-r_1+[R-1][r_2-r_3])\}$$ (equation 4)

where R is the number of readers.

An estimate of the denominator degrees of freedom is

$$(R-1)\times {\{{{\mathrm{\sigma }}^2}_{\mathrm{\tau }\times R}+{{\mathrm{\sigma }}^2}_{\mathrm{\epsilon }}(1-r_1+[R-1][r_2-r_3])\}}^2/{\{{{\mathrm{\sigma }}^2}_{\mathrm{\tau }\times R}+{{\mathrm{\sigma }}^2}_{\mathrm{\epsilon }}(1-r_1-[r_2-r_3])\}}^2$$ (equation 5)

Step 4: Compute the Power for R Readers

$$\text{Power}=\text{Prob}(F1,\mathit{\text{df}}2;\mathrm{\Delta }>F1-\mathrm{\alpha };1,\mathit{\text{df}}2)$$ (equation 6)

where Prob indicates probability, F1,df2;Δ denotes a random variable having a noncentral F distribution with 1 and df2 degrees of freedom (1,df2) and noncentrality parameter Δ, and F1 − α; 1,df2 denotes the 100(1 − α) percentile of a central F distribution with 1 and df2 degrees of freedom.

APPENDIX 2

Formulae for Computing the Power for a Multireader, Multicase Study Modified for Clustered Data and Estimation of Parameter Values From the Two Computer-Aided Detection Studies Described in the Text

For both the area under the receiver operating characteristic (ROC) curve and sensitivity, the correlation between lung lobes or colonic segments and the correlation between true lesions from the same patient is accounted for by the correlated analysis-of-variance model proposed by Obuchowski and Rockette [22]. This model is specified by the following equation:

$${\mathrm{\theta ̂}}_{\mathit{\text{ij}}}=\mu +{\mathrm{\tau }}_i+R_j+{(\mathrm{\tau }R)}_{\mathit{\text{ij}}}+{\mathrm{\epsilon }}_{\mathit{\text{ij}}}$$

where θ̂_ij is the outcome for the ith test and jth reader, μ is the mean, τ_i is the fixed effect of the ith test, R_j is the random reader effect, (τR)_ij is the random test-by-reader interaction, and ε_ij is the error term. The random effects are assumed to be normally distributed with zero means and respective variances σ²_R, σ²_τR, and σ²_ε. The error terms are correlated, with r₁, r₂, and r₃ denoting correlations between errors corresponding to different tests and one reader, one test and different readers, and different tests and readers, respectively.

For sample size estimation, we let N_D and N_N denote the number of patients with at least one true lesion and the number of patients without any lesions, respectively. We denote the total number of patients in the study as N_total (N_total = N_D + N_N). Patients with true lesions may have more than one true lesion, so the total number of true lesions will often exceed N_D.

Obuchowski and McClish [29] recommended that to estimate σ²_ε, one should first estimate σ²_c using equation 1, 2, or 3, and then add an estimate of σ²_w; however, no data were presented to assess the validity of this estimate of σ²_ε. Using the data from the two CAD examples, we compared the observed values of σ²_ε with the estimate of σ²_c from equations 1–3. In all scenarios, the estimate of σ²_c from equations 1–3 was greater than the observed value of σ²_ε. The estimate of σ²_c from equation 1 overestimated the observed value of σ²_ε by an average of 26%, the estimate from equation 2 overestimated by 83%, and the estimate from equation 3 overestimated by 5%. These results suggest that, when available, pilot data should be used to estimate σ²_ε.

The denominators of formulae 1–3 (i.e., N_D and N) need modification to account for clustered data. First, we consider lesion-level sensitivity. To modify equation 3, we need to estimate the average number of true lesions among patients with true lesions (we denote this f_D) and the average intraclass correlation—that is, the correlation of lesion-level assessments between lesions in the same patient (we denote this RHO_DD). Formula 3 can then be modified as follows:

$${\mathrm{\sigma }}_{\mathrm{c}}=\mathrm{p}\times (1-\mathrm{p})/{\mathrm{M}}_{\mathrm{D}}$$ (equation 3′)

where p is the conjectured sensitivity, M_D = N_D × f_D / DEFF; DEFF is the design effect [31]; and M_D is the effective number of lesions in the sample. By “effective” we mean the number of lesions after accounting for the fact that lesions from the same patient are correlated.

The design effect is defined as the variance when the clustered data are appropriately accounted for divided by the variance when it is incorrectly assumed that multiple observations from the same patient are independent [31]:

$$\mathit{\text{DEFF}}={\mathit{\text{Var}}}_{\mathit{\text{clustered}}}/{\mathit{\text{Var}}}_{\mathit{\text{independent}}}.$$

Kish [31] and Obuchowski [14] show that under some simplifying assumptions, the design effect can be rewritten for sample size calculations as follows:

$$\mathit{\text{DEFF}}=1+(f_D-1)\times {\mathit{\text{RHO}}}_{\mathit{\text{DD}}}.$$

When there is no correlation between lesions from the same patient (i.e., RHO_DD = 0), then M_D = f_D × N_D; when there is perfect correlation between lesions from the same patient (i.e., RHO_DD = 1), then M_D = N_D. If we do not expect many study patients to have multiple true lesions, then setting M_D = N_D is a reasonable approach; however, even when f_D is only slightly greater than 1, the power of the study can be improved by using equation 3′ instead of equation 3.

The value of f_D depends on the clinical setting and the patient inclusion and exclusion criteria. For example, in the lung CAD study there was an average of 7.3 nodules per patient; in the colon CAD study there was an average of 1.4 polyps per patient. The numbers differ greatly because the lung CAD study involved high-risk patients undergoing diagnostic or follow-up testing, whereas the colon CAD study involved asymptomatic patients.

The correlation RHO_DD can be more difficult to conjecture. In the colon CAD study, the value of RHO_DD was 0.53 (intraclass correlation coefficient [17]); in the lung CAD study, RHO_DD equaled 0.27. For sample size estimation it is important not to underestimate RHO_DD; a ballpark estimate of 0.5 was used in the sample size tables.

The modification required when the ROI-level ROC area is the endpoint is similar but involves both patients with and those without true lesions [14]. We first need to define the subunits, or ROIs, from which the ROC area will be estimated. These subunits might be colon segments, lung lobes, or breasts. Next, we conjecture the correlation of subunit-level confidence scores between the subunits in the same patient. Let RHO_DD denote the intraclass correlation between subunits from the same patient where each subunit has a true lesion; let RHO_NN denote the intraclass correlation between subunits from the same patient where each subunit does not have a true lesion; and let RHO_ND denote the intraclass correlation between subunits from the same patient where one subunit does not have a true lesion and one does have a true lesion. In the lung CAD study, the estimated value of RHO_DD was 0.22 [17], and in the colon CAD study, the estimated value of RHO_DD was 0.51. (Note that these intraclass correlations are computed from the confidence scores.) A ballpark estimate of 0.5 for RHO_DD was used in the sample size tables.

In the lung CAD study, the estimated value of RHO_NN was 0.14 and in the colon CAD study it was 0.04. So, in both studies RHO_NN was much smaller than RHO_DD. A ballpark estimate of 0.2 for RHO_NN was used in the sample size tables. In both studies the estimated value of RHO_ND was near zero. For the sample size tables, a ballpark estimate of zero was used for RHO_ND.

Using a similar strategy as derived and evaluated by Obuchowski [14], we propose the following modification to equation 1:

$$\sigma {\mathit{2}}_c=(\mathit{0.0099}\times e^{-A\times A/\mathit{2}})\times [\mathit{5}{A}^{\mathit{2}}+\mathit{8})+(A^{\mathit{2}}+\mathit{8})/k\prime ]/M_D$$ (equation 1′)

where k′ is the ratio of the number of effective subunits without lesions (M_N) to the effective number of subunits with lesions (M_D). M_D = N_D × f_D / DEFF_D, with f_D being the average number of subunits with lesions among patients with lesions and DEFF_D = 1 + (f_D − 1) × RHO_DD. Similarly, M_N = (H) × f_N / DEFF_N, with f_N being the average number of subunits without lesions among patients with at least one subunit without a lesion, H is the number of study patients that have at least one subunit without a true lesion, and DEFF_N = 1 + (f_N − 1) × RHO_NN. Note that H is often all the patients in the study (i.e., N_N + N_D). (Equation 1′ assumes that RHO_ND is negligible.)

Similarly, equation 2 can be modified as follows:

$${{\sigma }^{\mathit{2}}}_c=\text{AUC}\times (1-\text{AUC})/M$$ (equation 2′)

where M is the smaller of M_N and M_D, which are defined in equation 1′.

Determining sample size for sequential and crossover designs is similar except that the correlation, r₁ (i.e., the correlation between two reader-level outcomes [e.g., AUC or sensitivity] for the same reader), is usually greater in a sequential design than a crossover design [32–35]. Rockette et al. [13] reported an average value of 0.47 for r₁ over multiple studies completed at their institution where a crossover design was used and the area under the ROC curve was the measure of accuracy. In the colon CAD study, the average value of r₁ from the crossover design was 0.62 for the ROC area and 0.65 for sensitivity. The larger value of r₁ observed in the colon CAD study is perhaps not surprising because the two “modalities” in a CAD study are the same images, differing only by the presence of CAD marks. One might expect higher correlation between readers’ estimated accuracies with and without CAD as compared with the correlation between readers’ estimated accuracies for two modalities that provide very different images. For the sample size tables, we use a ballpark estimate for r₁ of 0.60 for a CAD crossover study with sensitivity or the ROC area as the measure of accuracy. (We note that lower values of r₁ result in more conservative sample size estimates.)

The average value of r₁ for specificity in the colon CAD study was 0.27. Note that Rockette et al. [13] did not report on the value of r₁ for specificity.

In a sequential design, several studies have reported strong correlation between readers’ findings without CAD versus with CAD [32–35]. In our two CAD examples, the observed values of r₁ ranged from 0.756 to 0.928 for the ROC area, 0.822–0.939 for sensitivity, and 0.533–0.860 for specificity. We note that in the lung CAD study, the estimate of 0.533 is based on only a small number of observations. For the sample size tables, we use a ballpark estimate of 0.80 for r₁ for sequential designs.