4D cone beam CT via spatiotemporal tensor framelet

Abstract

Purpose: On-board 4D cone beam CT (4DCBCT) offers respiratory phase-resolved volumetric imaging, and improves the accuracy of target localization in image guided radiation therapy. However, the clinical utility of this technique has been greatly impeded by its degraded image quality, prolonged imaging time, and increased imaging dose. The purpose of this letter is to develop a novel iterative 4DCBCT reconstruction method for improved image quality, increased imaging speed, and reduced imaging dose.

Methods: The essence of this work is to introduce the spatiotemporal tensor framelet (STF), a high-dimensional tensor generalization of the 1D framelet for 4DCBCT, to effectively take into account of highly correlated and redundant features of the patient anatomy during respiration, in a multilevel fashion with multibasis sparsifying transform. The STF-based algorithm is implemented on a GPU platform for improved computational efficiency. To evaluate the method, 4DCBCT full-fan scans were acquired within 30 s, with a gantry rotation of 200°; STF is also compared with a state-of-art reconstruction method via spatiotemporal total variation regularization.

Results: Both the simulation and experimental results demonstrate that STF-based reconstruction achieved superior image quality. The reconstruction of 20 respiratory phases took less than 10 min on an NVIDIA Tesla C2070 GPU card. The STF codes are available at https://sites.google.com/site/spatiotemporaltensorframelet.

Conclusions: By effectively utilizing the spatiotemporal coherence of the patient anatomy among different respiratory phases in a multilevel fashion with multibasis sparsifying transform, the proposed STF method potentially enables fast and low-dose 4DCBCT with improved image quality.

INTRODUCTION

On-board 4D cone beam CT (4DCBCT) offers respiratory phase-resolved volumetric imaging,^{1, 2, 3, 4} and improves the accuracy of target localization in image guided radiation therapy.⁵ However, the clinical utility of 4DCBCT has been greatly impeded by its degraded image quality, prolonged imaging time, and increased imaging dose. Conventional approaches for respiration-correlated or 4DCBCT imaging reconstruct each respiratory phase independently, and thus often have a very limited amount of projection data available for image reconstruction. Although some progress has been made to improve the 4DCBCT image quality,^{6, 7, 8} there is clearly an unmet need for improving the current 4DCBCT imaging technique.

Considering the fact that the patient anatomy during respiration is highly correlated and redundant, the efficient 4DCBCT reconstruction should utilize the spatiotemporal coherence of the patient anatomy among different respiratory phases,^{9, 10, 11, 12, 13} which is inherently superior to the conventional phase-independent reconstructions. In this letter, we present a novel method that effectively utilizes such spatiotemporal coherence in a multilevel fashion with multibasis sparsifying transform, with the attempt for fast and low-dose 4DCBCT with improved image quality.

METHODS

Specifically, a new sparse representation method–the spatiotemporal tensor framelet (STF)—is proposed to characterize the spatiotemporal coherence of the 4D images. This new method goes as follows. Let us consider a 4D image as a tensor X = {x_ijkm, i ≤ N_x, j ≤ N_y, k ≤ N_z, m ≤ N_t} and define X^x, X^y, X^z, X^t as the unfolded matrices of X along x, y, z, t dimension, respectively. For example, X^y is a N_y by N_x×N_z×N_t matrix with each column X^y_ikm = {x_ikm, j ≤ N_y}. Let W₁ be the standard 1D framelet transform (see the Appendix). Then the STF transform W and its adjoint W^T are defined by

$$\begin{array}{ccc}\hfill Y=WX& =& \{W_1{X}_{jkm}^x,W_1{X}_{ikm}^y,W_1{X}_{ijm}^z,W_1{X}_{ijk}^t,i\le N_x,\hfill \\ & & j\le N_y,k\le N_z,m\le N_t\},\hfill \end{array}$$ (1)

$$\begin{array}{ccc}\hfill W^{T}Y& =& (\sum _{jkm}{W}_1^T{Y}_{jkm}^x+\sum _{ikm}{W}_1^T{Y}_{ikm}^y+\sum _{ijm}{W}_1^T{Y}_{ijm}^z\hfill \\ & & +\sum _{ijk}{W}_1^T{Y}_{ijk}^t)/4.\hfill \end{array}$$ (2)

The STF via Eqs. 1, 2 is a natural generalization of 1D framelet to the high-dimensional space through the tensor approach and it is easy to verify that many nice features of the framelet are kept, such as W^T(WX) = X. STF has mainly two advantages: STF takes into account the temporal similarity of the 4D images by the 1D framelet operator along the temporal dimension (e.g., W₁X^t) in addition to the spatial sparsity (e.g., W₁X^x); in terms of the required memory, STF (e.g., ∼4 nN) is more feasible for high-dimensional problems (e.g., 4DCBCT) than the framelet (e.g., ∼n⁴N). Here n is the number of framelet bases (refinement masks) and N = N_x × N_y × N_z × N_t.

With STF, 4DCBCT is formulated as a L1 minimization problem

$$X=\underset{X}{\arg \min }{\Vert AX-Y\Vert }_2^2+\lambda {\Vert WX\Vert }_1.$$ (3)

In Eq. 3, AX is the x-ray transform of X with the scan geometry specified later, Y represents the 4DCBCT data, and ∥WX∥₁ is the L1 norm of the STF of X, i.e.,

$$\begin{array}{ccc}\hfill {\Vert WX\Vert }_1& =& \sum _{j,k,m}\Vert W_1{X}_{jkm}^x{\Vert }_1+\sum _{i,k,m}\Vert W_1{X}_{ikm}^y{\Vert }_1\hfill \\ & & +\sum _{i,j,m}\Vert W_1{X}_{ijm}^z{\Vert }_1+\sum _{i,j,k}\Vert W_1{X}_{ijk}^t{\Vert }_1.\hfill \end{array}$$ (4)

The detail of ∥W₁·∥₁ is in the Appendix, which clearly indicates that STF is a generalization of the first-order differencing operator, i.e., spatiotemporal total variation (STV),^{12, 13} which will be compared with STF next as a state-of-art reconstruction method.

This typical nondifferentiable L1 problem 3 can be solved through the split Bregman method.^{14, 15} Here, we implement a GPU-based parallel solver based on our prior algorithms^{10, 11} for both STF and STV, in which the recently proposed fast and highly parallelizable algorithms¹⁶ are used to accelerate the x-ray transform AX and its adjoint A^TX that are two most time-consuming components. Here l is scaled with the L1 norm of A and the data are scaled so that the image intensity is roughly between 0 and 1, for which l = 0.1 serves as a good choice for image reconstruction. Please note that STF is slightly faster than STV due to the left-inverse property W^TW = 1, since otherwise W^TW needs to be computed repeatedly for STV.

MATERIALS

The 4DCBCT reconstruction was evaluated first using a digital NCAT phantom,¹⁷ and then with experimental data. To generate the 30-s simulation data for the NCAT phantom, 40 respiratory phases were utilized, which corresponded to the maximal temporal resolution (100 ms) that was allowed by the simulation setting. For physical experiments, the CIRS dynamic thorax phantom was used, which provides known, accurate (<0.1 mm), and reproducible target motion inside a tissue equivalent phantom.¹⁸ The phantom body represents an average human thorax in shape, proportion, and composition. A lung equivalent rod containing a spherical target was inserted into the phantom. The TrueBeam^TM LINAC (Varian Medical Systems, Palo Alto, CA) equipped with an on-board kV imaging system was used to scan the phantom. The kV detector has a physical size of 39.7 × 29.8 cm². The kV imaging parameters were set to be 100 kVp, 80 mA, and 10 ms pulse width.

In both cases, the distance from source to the isocenter was 100 cm, the distance from the isocenter to the detector plane was 50 cm. The projection dataset was a 256 × 64 array (central slices of the measurement data) with the pixel size 0.16 × 0.16 cm². The respiratory signal during scanning was a sinusoidal curve with a period of 4 s. The full-fan scan was performed with a single 200° gantry rotation that takes ∼30 s. The total number of projections was 400 and 372 for the digital and physical phantom, respectively.

For reconstruction, the field of view was 33 × 33 × 8 cm³. The reconstructed image had the spatial dimension 256 × 256 × 64 with the spatial resolution 0.13 × 0.13 × 0.13 cm³. A total of 20 respiratory phases were reconstructed to provide a temporal resolution of ∼200 ms. The stopping criterions for both STF and STV were based on the minimal data fidelity discrepancy. There were 18–20 projections of data corresponding to each reconstructed phase.

RESULTS

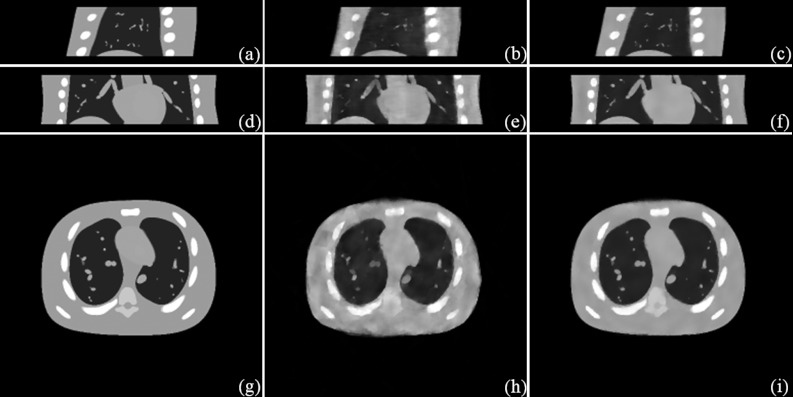
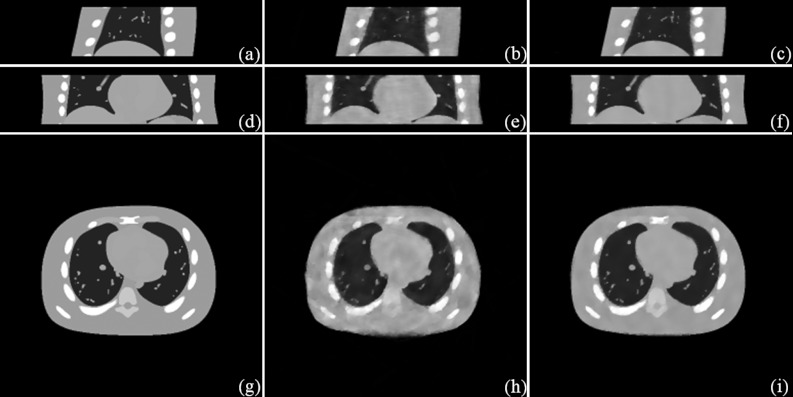
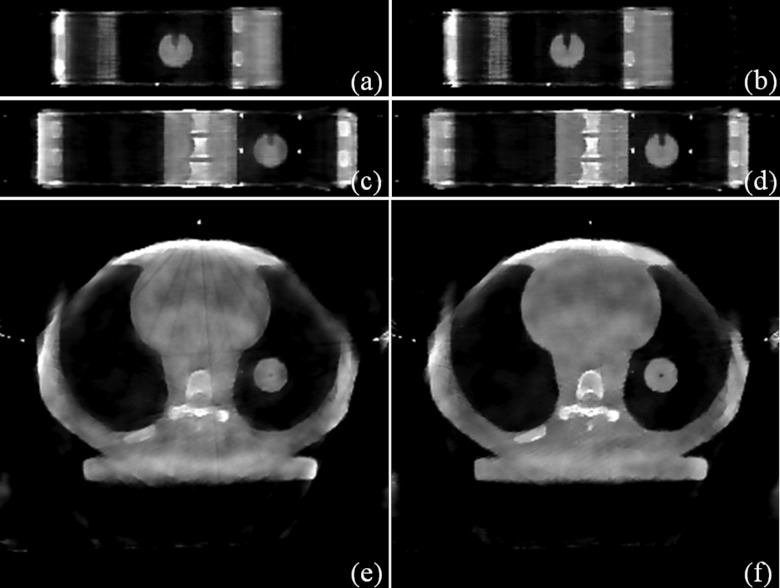
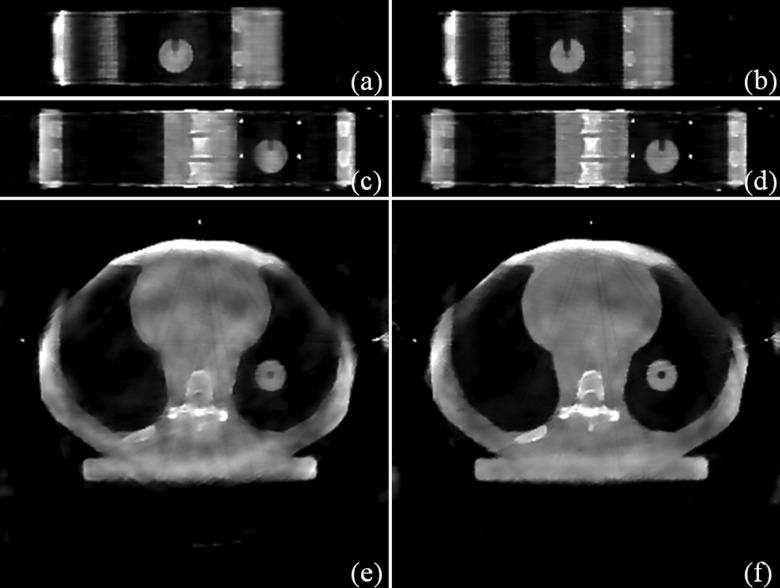
With the simulation data, the phantom images, the STV results, and the STF results are displayed in Fig. 1 (the exhale phase) and Fig. 2 (the inhale phase). The relative differences between the reconstructed image X and the phantom image X₀ through ∑_ijkm|X-X₀|/∑_ijkm|X₀|, were 8.0% for STV and 3.5% for STF. With the experimental data, the STV results and the STF results are displayed in Fig. 3 (Phase 8) and Fig. 4 (Phase 16). Both the simulation and experimental results (Fig. 1234) suggest that STF enables the 30-s 200° full-fan 4DCBCT scan, and it offers the superior image quality than STV.

Figure 1.

Simulation results (the exhale phase). Sagittal view: (a) Phantom; (b) STV; (c) STF. Coronal view: (d) Phantom; (e) STV; (f) STF. Transverse view: (g) Phantom; (h) STV; (i) STF.

Figure 2.

Simulation results (the inhale phase). Sagittal view: (a) Phantom; (b) STV; (c) STF. Coronal view: (d) Phantom; (e) STV; (f) STF. Transverse view: (g) Phantom; (h) STV; (i) STF.

Figure 3.

Experimental results (Phase 8). Sagittal view: (a) STV; (b) STF. Coronal view: (c) STV; (d) STF. Transverse view: (e) STV; (f) STF.

Figure 4.

Experimental results (Phase 16). Sagittal view: (a) STV; (b) STF. Coronal view: (c) STV; (d) STF. Transverse view: (e) STV; (f) STF.

In terms of the temporal resolution, the reconstructed 4D images had 20 phases, while the maximally allowed phases for the setting were roughly 40. On the other hand, the conventional 4DCBCT reconstruction often has roughly ten phases. In this sense, STF is able to improve the temporal resolution of the reconstructed 4D image, or equivalently reduce the number of projections for the same temporal resolution. The further improvement of the 4D reconstruction with the maximal phases or the minimal number of projections will be explored.

The GPU-based reconstruction was implemented with a NVIDIA Tesla C2070 GPU card (448 cores and 5.25 GB device memory). The required device memory was less than 1 GB, while the total computer memory was roughly 5 GB (mainly due to STF). Two most time-consuming components are the x-ray transform (∼2 s each) and its adjoint (∼13 s each). Since the image reconstruction takes roughly 30 iterations and each iteration involves one pair of the x-ray transform and its adjoint, the total computational time for a 4D reconstruction via STF is currently less than 10 min. Further acceleration is possible with the GPU card with more cores or the multi-GPU parallelization, since the computational cost of the used x-ray transform and its adjoint per parallel thread is O(1).¹⁶

CONCLUSION

We have proposed a novel 4DCBCT image reconstruction technique based on STF, a high-dimensional tensor generalization of the 1D framelet that effectively utilizes the spatiotemporal coherence of 4DCBCT images in a multilevel and fashion with multibasis sparsifying transform. The proposed STF method potentially enables fast- and low-dose 4DCBCT with improved image quality. The STF codes are available online.¹⁹

APPENDIX: 1D FRAMELET TRANSFORM AND ITS ADJOINT

In this study, W₁ is the 1D piecewise-linear framelet or tight frame transform (TF) constructed by three following refinement masks:

$$\begin{array}{c}\hfill w_0=\frac{1}{4}\left[\begin{array}{ccc}1& 2& 1\end{array}\right],w_1=\frac{\sqrt{2}}{4}\left[\begin{array}{ccc}1& 0& -1\end{array}\right],w_2=\frac{1}{4}\left[-\begin{array}{ccc}1& 2& -1\end{array}\right].\end{array}$$ (A1)

Please note that w₀, w₁, and w₂ correspond to the averaging operator, the first-order differencing operator, and the second-order differencing operator, respectively. Therefore, the TF transform contains the total variation (TV) transform on multilevels.

Let x be a 1D vector. The multilevel 1D TF transform of x up to L levels is

$$\begin{array}{ccc}\hfill W_{1}x& =& \left[\underset{\mathrm{Level}:1}{\underbrace{\begin{array}{ccc}{\left[W_{1}x\right]}_0^1& {\left[W_{1}x\right]}_1^1& {\left[W_{1}x\right]}_2^1\end{array}}}\cdots \underset{\mathrm{Level}:l}{\underbrace{\begin{array}{ccc}{\left[W_{1}x\right]}_0^l& {\left[W_{1}x\right]}_1^l& {\left[W_{1}x\right]}_2^l\end{array}}}\right.\hfill \\ & & \left.\cdots \underset{\mathrm{Level}:L}{\underbrace{\begin{array}{ccc}{\left[W_{1}x\right]}_0^L& {\left[W_{1}x\right]}_1^L& {\left[W_{1}x\right]}_2^L\end{array}}}\begin{array}{c}{x}^L\end{array}\right],\hfill \end{array}$$ (A2)

where the fine-to-coarse convolutions are defined by the following with x⁰ = x:

$$\begin{array}{ccc}& & x^l=w_0^l*x^{l-1},{\left[W_{1}x\right]}_0^l=w_0^l*x^l,{\left[W_{1}x\right]}_1^l=w_1^l*x^l,\hfill \\ & & {\left[W_{1}x\right]}_2^l=w_2^l*x^l,1\le l\le L.\hfill \end{array}$$ (A3)

Here for the efficient multilevel decomposition, instead of downsampling x^l, we dilute the masks A1 to w^l_i, e.g.,

$$w_0^l=\frac{1}{4}\left[\begin{array}{c}1\end{array}\underset{2^l-1}{\underbrace{\begin{array}{ccc}0& \cdots & 0\end{array}}}2\underset{2^l-1}{\underbrace{\begin{array}{ccc}0& \cdots & 0\end{array}}}1\right].$$ (A4)

And its transpose W₁^T is defined as

$$W_1^T\left(W_{1}x\right)=x^L+\sum _{l=1}^L\left({\left[W_{1}x\right]}_0^l+{\left[W_{1}x\right]}_1^l+{\left[W_{1}x\right]}_2^l\right).$$ (A5)

Consequently, the 1D TF norm is the sum of the L1 norm of the TF terms at multilevels with multifilters, i.e.,

$$\begin{array}{c}\hfill \Vert W_1{x\Vert }_1={\Vert x^L\Vert }_1+\sum _{l=1}^L\{\Vert {\left[W_{1}x\right]}_0^l{\Vert }_1+{\left[W_{1}x\right]}_1^l{\Vert }_1+\Vert {\left[W_{1}x\right]}_2^l{\Vert }_1\},\end{array}$$ (A6)

Also, it is worthy to mention that, in terms of the computation speed, the algorithm with TF regularization is in general faster than using the transform without left inverse, such as TV, since it would require additional computation of W^TW otherwise.