Abstract
The thinning dynamics of a liquid neck before break-up, as may happen when a drop detaches from a faucet or a capillary, follows different rules and dynamic scaling laws depending on the importance of inertia, viscous stresses, or capillary forces. If now the thinning neck reaches dimensions comparable to the thermally excited interfacial fluctuations, as for nanojet break-up or the fragmentation of thermally annealed nanowires, these fluctuations should play a dominant role according to recent theory and observations. Using near-critical interfaces, we here fully characterize the universal dynamics of this thermal fluctuation-dominated regime and demonstrate that the cross-over from the classical two-fluid pinch-off scenario of a liquid thread to the fluctuation-dominated regime occurs at a well-defined neck radius proportional to the thermal length scale. Investigating satellite drop formation, we also show that at the level of the cross-over between these two regimes it is more probable to produce monodisperse droplets because fluctuation-dominated pinch-off may allow the unique situation where satellite drop formation can be inhibited. Nonetheless, the interplay between the evolution of the neck profiles from the classical to the fluctuation-dominated regime and the satellites’ production remains to be clarified.
Keywords: critical fluids, singularity formation
For a drop to detach from a capillary or a faucet, the liquid thread connecting them must thin and break. This break-up, or pinch-off, is an example of a singularity with well-established scaling laws and similarity solutions (1–5). Different regimes and scaling laws have been predicted and observed. For small liquid viscosities, the balance between inertia and capillarity leads to the so-called inertial thinning regime, with the thread radius vanishing as time to pinch-off to the power 2/3. When the radius of the thinning thread becomes smaller than the so-called viscous length scale 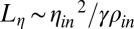 (where
(where 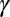 ,
, 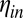 , and
, and 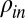 are respectively the surface tension, the shear viscosity, and the density of the fluid), viscous forces become important and the neck radius decreases linearly vs. time (1) as
are respectively the surface tension, the shear viscosity, and the density of the fluid), viscous forces become important and the neck radius decreases linearly vs. time (1) as 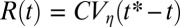 , where
, where 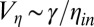 is a capillary velocity,
is a capillary velocity, 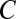 is a constant, and
is a constant, and 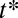 is the break-up time at neck pinch-off; a viscous time scale can be defined as
is the break-up time at neck pinch-off; a viscous time scale can be defined as 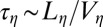 . Two thinning regimes have been predicted and observed in this case: the so-called viscocapillary regime at low Reynolds numbers exhibiting symmetric necks with
. Two thinning regimes have been predicted and observed in this case: the so-called viscocapillary regime at low Reynolds numbers exhibiting symmetric necks with 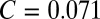 (6) and the viscocapillary-inertial regime emerging when further thinning significantly increases the inner fluid velocity and thus inertia (7). In this latter case, the constant is
(6) and the viscocapillary-inertial regime emerging when further thinning significantly increases the inner fluid velocity and thus inertia (7). In this latter case, the constant is 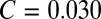 and the neck profiles are asymmetric. Note that more recently, other symmetric break-up dynamics have been found for a class of non-Newtonian fluids for which thinning is dictated by the rheological properties of the fluids (8, 9).
and the neck profiles are asymmetric. Note that more recently, other symmetric break-up dynamics have been found for a class of non-Newtonian fluids for which thinning is dictated by the rheological properties of the fluids (8, 9).
When the viscosity of the outer fluid is no more negligible, as in the present investigation, the thinning dynamics is dominated by viscocapillary stresses when the radius of the rupturing neck 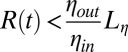 (1), where
(1), where 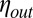 is the shear viscosity of the fluid outside the thread. The variation of the radius again obeys a linear scaling law
is the shear viscosity of the fluid outside the thread. The variation of the radius again obeys a linear scaling law 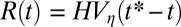 , where
, where 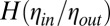 is a function that was experimentally (2) and theoretically evaluated (10, 11). In this two-fluid viscocapillary regime, the thinning neck is asymmetrical, eventually leading to the formation of satellite droplets.
is a function that was experimentally (2) and theoretically evaluated (10, 11). In this two-fluid viscocapillary regime, the thinning neck is asymmetrical, eventually leading to the formation of satellite droplets.
Though these different regimes consider the interface as smooth even at the smallest scales examined, recent simulations of nanojet break-up (12, 13), as well as theoretical (14) and experimental work (15), revealed that the interface roughness due to the interfacial thermal fluctuations may play a dominant role in liquid column break-up when 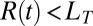 , where
, where 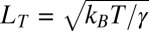 is the so-called thermal length scale estimated by comparing the thermal energy
is the so-called thermal length scale estimated by comparing the thermal energy 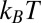 to the surface tension
to the surface tension 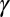 . In this case, the thinning neck is predicted to be symmetrical with respect to the break-up location, thus minimizing the formation of satellite drops at pinch-off (13, 14). Moreover, the thinning of the neck is predicted to follow the scaling law
. In this case, the thinning neck is predicted to be symmetrical with respect to the break-up location, thus minimizing the formation of satellite drops at pinch-off (13, 14). Moreover, the thinning of the neck is predicted to follow the scaling law 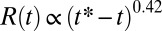 (14), where the proportionality factor remains to be determined theoretically and experimentally (14, 15). Because the thermal length is classically in the range of a few molecules, observation of this thinning regime in a laboratory-scale experiment requires a significant increase of
(14), where the proportionality factor remains to be determined theoretically and experimentally (14, 15). Because the thermal length is classically in the range of a few molecules, observation of this thinning regime in a laboratory-scale experiment requires a significant increase of 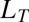 . A route for fulfilling this condition is the use of near-critical binary fluids with strongly fluctuating interfaces (16), which offer the unique opportunity of reaching strongly fluctuating hydrodynamic regimes.
. A route for fulfilling this condition is the use of near-critical binary fluids with strongly fluctuating interfaces (16), which offer the unique opportunity of reaching strongly fluctuating hydrodynamic regimes.
Results
The experiment is performed in a near-critical phase-separated water-in-oil micellar phase of a microemulsion whose mass composition is adjusted to be critical at a temperature 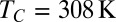 . The fluid preparation and properties are detailed in SI Text. For a temperature
. The fluid preparation and properties are detailed in SI Text. For a temperature 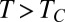 , the mixture separates in two coexisting phases of different micellar concentrations separated by an interface that has large thermally induced interfacial fluctuations near
, the mixture separates in two coexisting phases of different micellar concentrations separated by an interface that has large thermally induced interfacial fluctuations near 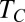 . Two main reasons motivated this choice of system. (i) Due to the supramolecular nature of the micelles, the bulk correlation length of density fluctuations
. Two main reasons motivated this choice of system. (i) Due to the supramolecular nature of the micelles, the bulk correlation length of density fluctuations 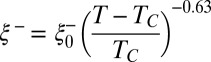 is intrinsically large, allowing interfacial fluctuations to be observable optically. (ii) It follows from the universal ratio
is intrinsically large, allowing interfacial fluctuations to be observable optically. (ii) It follows from the universal ratio 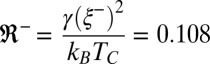 (17) that the interfacial tension
(17) that the interfacial tension 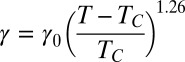 is extremely weak compared with that of usual liquid mixtures. For
is extremely weak compared with that of usual liquid mixtures. For 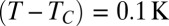 , one finds
, one finds 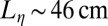 and
and 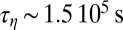 on the one hand, and
on the one hand, and 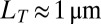 as
as 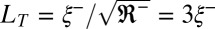 on the other. Moreover, considering
on the other. Moreover, considering 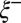 as the relevant length scale, the corresponding relaxation time scale
as the relevant length scale, the corresponding relaxation time scale 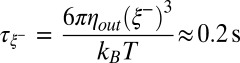 is orders of magnitude larger than in usual molecular liquids. Neck thinning driven by thermal fluctuations thus becomes experimentally accessible.
is orders of magnitude larger than in usual molecular liquids. Neck thinning driven by thermal fluctuations thus becomes experimentally accessible.
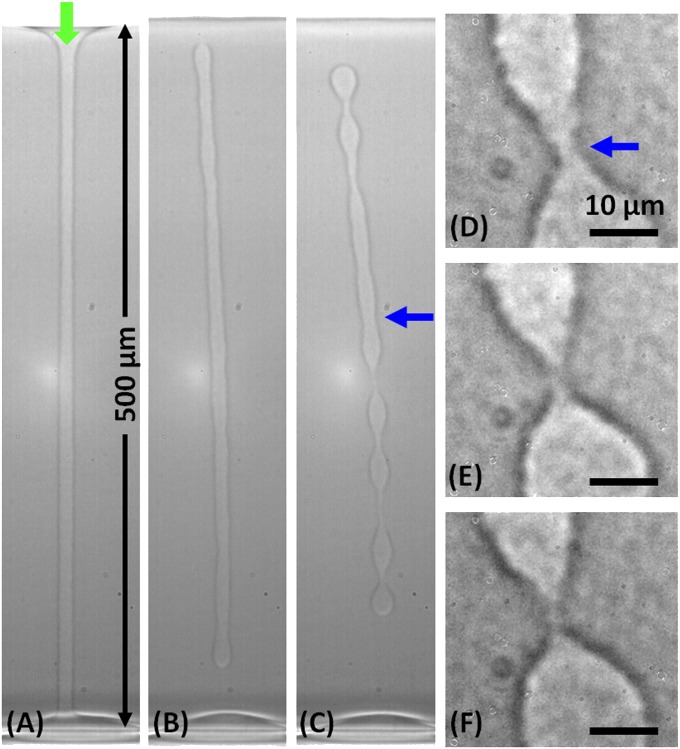
The second key point of the experiment requires starting with an initially stable and well-controlled liquid column to properly fix initial conditions and boundary effects before further destabilization. Though large-aspect-ratio liquid columns are known to be unstable due to the Rayleigh–Plateau instability (3), it is briefly shown in SI Text that this fundamental limitation can be circumvented using the radiation pressure of a continuous laser beam to deform the meniscus separating the coexisting phases (18), which is located in the middle of the sample due to near criticality. For a sufficient beam power, the surface deformation ends up connected to the bottom glass face of the cell, thus forming a large-aspect-ratio liquid column whose diameter is controlled by the incident beam power. Hydrodynamic stabilization is provided through the radiation pressure exerted by the beam propagation inside the column (19). Fig. 1A illustrates the regularity of such a laser-sustained liquid column.
Fig. 1.
(A) Initial large-aspect-ratio column (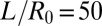 ) formed in a 1-mm-thick cell at
) formed in a 1-mm-thick cell at 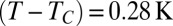 and stabilized optically between the near-critical meniscus on the top and bottom face of the cell. The vertical arrow indicates incidence of the frequency-doubled
and stabilized optically between the near-critical meniscus on the top and bottom face of the cell. The vertical arrow indicates incidence of the frequency-doubled 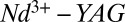 continuous-wave laser beam (wavelength in vacuum
continuous-wave laser beam (wavelength in vacuum 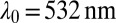 ) of waist
) of waist 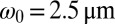 and power
and power 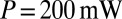 used to produce the column. The picture is captured just before laser interruption. (B) Column destabilization 4 s after laser interruption; note the fast pinch-off at the boundaries. (C) Column 8 s after laser interruption; the horizontal arrow indicates the neck under study taken near the middle of the liquid column. (D–F) Close-up view of the neck thinning 2 s, 0.2 s, and 0.02 s before break-up. Note the roughness of the interface, which is a direct signature of the thermal fluctuations close to a critical point.
used to produce the column. The picture is captured just before laser interruption. (B) Column destabilization 4 s after laser interruption; note the fast pinch-off at the boundaries. (C) Column 8 s after laser interruption; the horizontal arrow indicates the neck under study taken near the middle of the liquid column. (D–F) Close-up view of the neck thinning 2 s, 0.2 s, and 0.02 s before break-up. Note the roughness of the interface, which is a direct signature of the thermal fluctuations close to a critical point.
Once formed, the column is left to relax after turning off the laser beam, as illustrated in Fig. 1 B and C. To avoid boundary effects, we focus on a midcolumn rupture event, as that indicated by the horizontal arrow in Fig. 1C. We record the neck-thinning dynamics with a 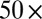 Olympus microscope objective (N.A. = 0.45) coupled to a video camera (
Olympus microscope objective (N.A. = 0.45) coupled to a video camera (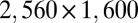 pixels) operating at variable frame rates. Fig. 1 D–F illustrates a typical thinning morphology with particular emphasis on the observed neck symmetry and the inhibition of satellite drop formation in this case. Note, however, the occurrence of a more-elongated neck below the one selected for a close-up; such a neck may lead to satellite drop formation because it may break at more than one location. Fig. 2 presents the thinning dynamics of a column for
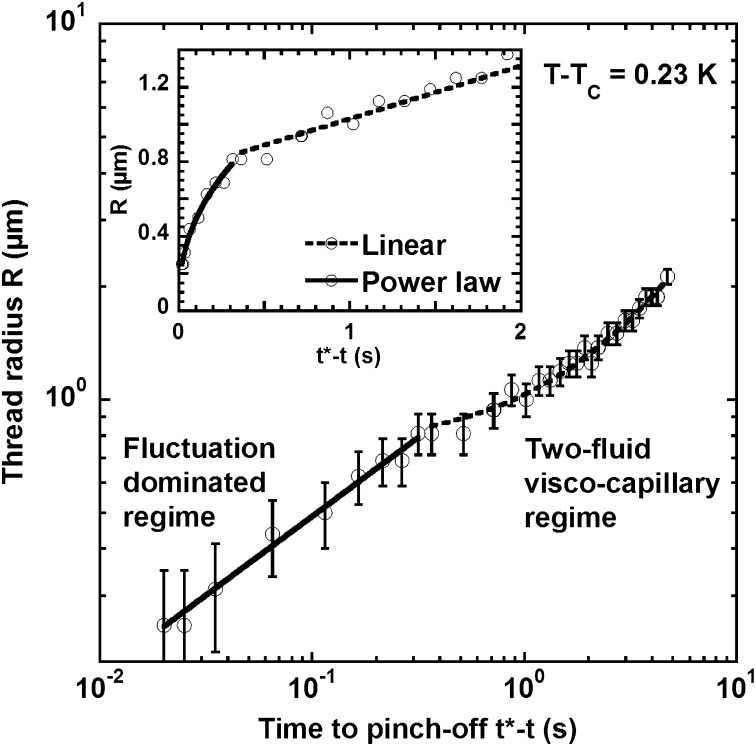
pixels) operating at variable frame rates. Fig. 1 D–F illustrates a typical thinning morphology with particular emphasis on the observed neck symmetry and the inhibition of satellite drop formation in this case. Note, however, the occurrence of a more-elongated neck below the one selected for a close-up; such a neck may lead to satellite drop formation because it may break at more than one location. Fig. 2 presents the thinning dynamics of a column for 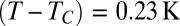 . The determination of the neck radius is detailed in Materials and Methods. After the first stages of the Rayleigh–Plateau instability, the neck radius
. The determination of the neck radius is detailed in Materials and Methods. After the first stages of the Rayleigh–Plateau instability, the neck radius 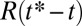 starts to decrease linearly in time, as expected for two-fluid viscocapillary thinning (Fig. 2, Inset). Beyond a cross-over at
starts to decrease linearly in time, as expected for two-fluid viscocapillary thinning (Fig. 2, Inset). Beyond a cross-over at 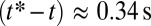 and
and 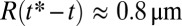 , i.e.,
, i.e., 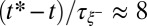 and
and 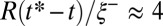 , the thinning dynamics switches to a power law behavior, well approximated by
, the thinning dynamics switches to a power law behavior, well approximated by 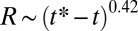 , up to break-up; a power law fit gives
, up to break-up; a power law fit gives 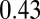 .
.
Fig. 2.
Log-log plot of the time variation of the neck thinning up to break-up at 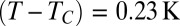 . (Inset) A linear plot with duration of the linear regime, which has been deliberately reduced to highlight the transition toward a power law behavior. The viscocapillary and the fluctuation-dominated regimes are fit respectively to a linear function and a power law with exponent forced at 0.42. The error bars correspond to a measurement error of
. (Inset) A linear plot with duration of the linear regime, which has been deliberately reduced to highlight the transition toward a power law behavior. The viscocapillary and the fluctuation-dominated regimes are fit respectively to a linear function and a power law with exponent forced at 0.42. The error bars correspond to a measurement error of 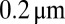 on the diameter.
on the diameter.
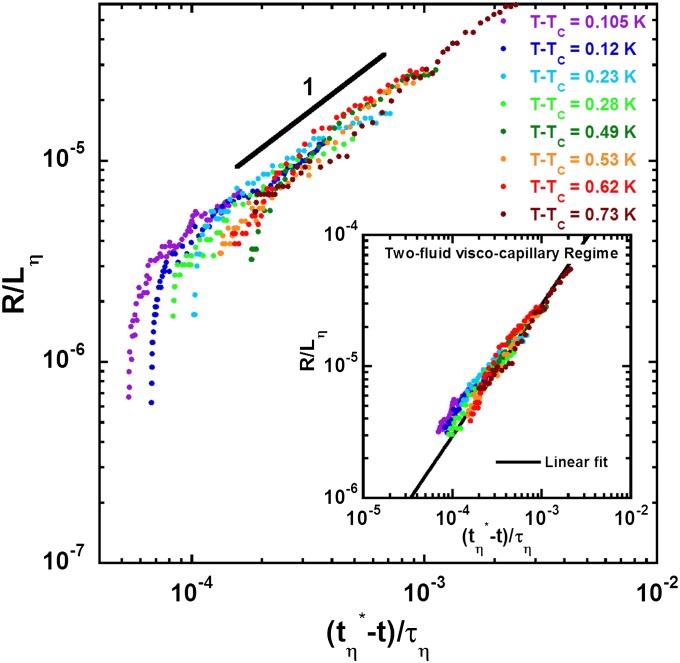
To confirm the robustness of the observed thinning dynamics, we first investigate the two-fluid viscocapillary behavior. The variation of 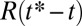 measured for each
measured for each 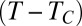 is fit linearly to extract the break-up time
is fit linearly to extract the break-up time 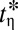 expected for pure two-fluid viscocapillary thinning. Data are then reanalyzed in terms of reduced length and time scales, respectively
expected for pure two-fluid viscocapillary thinning. Data are then reanalyzed in terms of reduced length and time scales, respectively 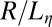 and
and 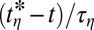 , to focus on this regime. Note that we should have used the length scale
, to focus on this regime. Note that we should have used the length scale 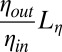 , but close to the critical point
, but close to the critical point 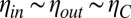 , the viscosity at criticality. As shown in Fig. 3, the measurements all fall onto a single master straight line over more than one order of magnitude in rescaled length and time scales. We extract
, the viscosity at criticality. As shown in Fig. 3, the measurements all fall onto a single master straight line over more than one order of magnitude in rescaled length and time scales. We extract 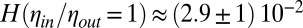 from the fit of the whole data set exhibiting a linear regime, illustrated in Fig. 3
Inset, which is in agreement with previous measurements
from the fit of the whole data set exhibiting a linear regime, illustrated in Fig. 3
Inset, which is in agreement with previous measurements 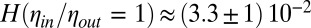 (2). Note that this rescaling requires confidence in the value of the interfacial tension
(2). Note that this rescaling requires confidence in the value of the interfacial tension 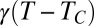 , which is here deduced from
, which is here deduced from 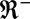 and the set value of
and the set value of 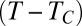 . However, weak temperature variations around the set point as well as minor deviations from the set composition of the sample can produce large relative variations of
. However, weak temperature variations around the set point as well as minor deviations from the set composition of the sample can produce large relative variations of 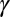 for temperatures close to
for temperatures close to 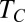 . Consequently, some experiments were preceded by in situ contactless measurements of the interfacial tension from the meniscus deformation by the optical radiation pressure at a very low beam power. As briefly discussed in SI Text, this method leads to a relative uncertainty
. Consequently, some experiments were preceded by in situ contactless measurements of the interfacial tension from the meniscus deformation by the optical radiation pressure at a very low beam power. As briefly discussed in SI Text, this method leads to a relative uncertainty 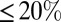 for
for 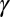 , which de facto has an incidence on the determination of
, which de facto has an incidence on the determination of 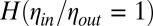 from the linear slope
from the linear slope 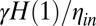 expected for the viscocapillary regime.
expected for the viscocapillary regime.
Fig. 3.
Universal thinning dynamics in the viscocapillary regime. The measured breakup time 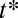 is replaced by the breakup time
is replaced by the breakup time 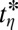 that would be expected for pure viscocapillary break-up, and the dynamics is presented in radius and time reduced with the viscous length
that would be expected for pure viscocapillary break-up, and the dynamics is presented in radius and time reduced with the viscous length 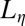 and characteristic time
and characteristic time 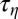 over a sevenfold variation in
over a sevenfold variation in 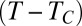 . (Inset) Fit of the whole set of data belonging to the viscocapillary regime.
. (Inset) Fit of the whole set of data belonging to the viscocapillary regime.
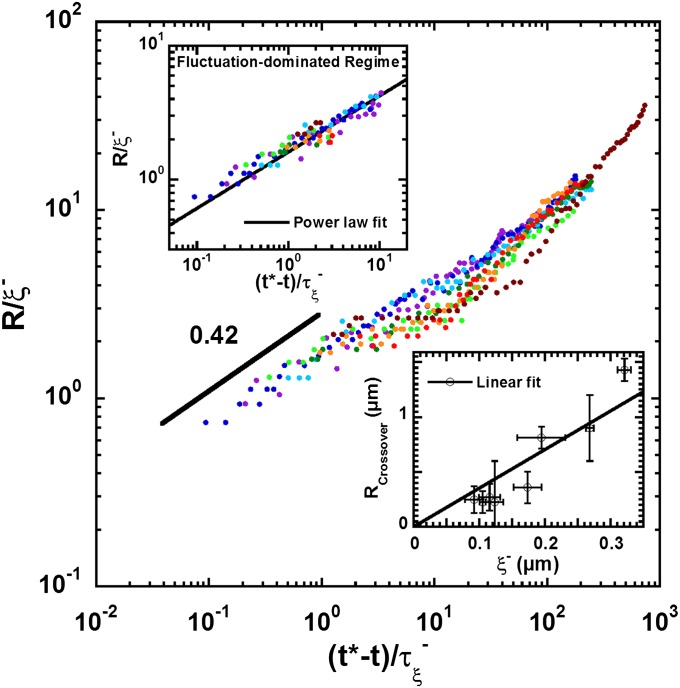
Eventually, the neck thinning deviates from the linear viscocapillary behavior and accelerates during the last instants, indicating the presence of an additional more-efficient mechanism operating at small length scales and expected when interfacial fluctuations play a role. Although small scales may be difficult to determine (Materials and Methods), the fact that this deviation appears systematically for a wide range of conditions signals the onset of a different rupture regime. To further investigate this regime, the data set for all 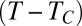 examined is now rescaled with the correlation length and time scales
examined is now rescaled with the correlation length and time scales 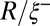 and
and 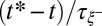 . Fig. 4 shows that data rescaling leads to a single behavior up to the cross-over with the viscocapillary dynamics. The fit of the whole data set belonging to this regime is illustrated in Fig. 4
Upper Inset and gives
. Fig. 4 shows that data rescaling leads to a single behavior up to the cross-over with the viscocapillary dynamics. The fit of the whole data set belonging to this regime is illustrated in Fig. 4
Upper Inset and gives 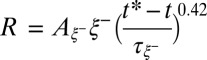 , with
, with 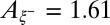 , when forcing the exponent to its predicted value
, when forcing the exponent to its predicted value 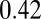 . A free-parameter nonlinear fit leads to
. A free-parameter nonlinear fit leads to 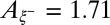 and an exponent 0.37. The existence of a universal thermal fluctuation-dominated regime is thus firmly demonstrated by finding, over two orders of magnitude in rescaled time, a robust exponent close to the numerically calculated one, 0.42. Our data also allow a measurement of the amplitude
and an exponent 0.37. The existence of a universal thermal fluctuation-dominated regime is thus firmly demonstrated by finding, over two orders of magnitude in rescaled time, a robust exponent close to the numerically calculated one, 0.42. Our data also allow a measurement of the amplitude 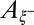 over a wide range of conditions, and show that the relevant length and time scales for this pinching regime are indeed the correlation length and its relaxation time.
over a wide range of conditions, and show that the relevant length and time scales for this pinching regime are indeed the correlation length and its relaxation time.
Fig. 4.
Universal thinning dynamics in the thermal fluctuation-dominated regime (same color convention as in Fig. 3). The dynamics is presented in radius and time reduced with the correlation length 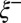 and relaxation time
and relaxation time 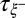 . (Upper Inset) Power law fit, with exponent forced to 0.42, of the whole set of data belonging to the thermal fluctuation regime. (Lower Inset) Variation of the neck radius at the thinning regime cross-over
. (Upper Inset) Power law fit, with exponent forced to 0.42, of the whole set of data belonging to the thermal fluctuation regime. (Lower Inset) Variation of the neck radius at the thinning regime cross-over 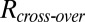 vs.
vs. 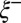 ; the error bars add the statistical determination by different methods (best fits around the cross-over and largest temporal window) and the measurement error.
; the error bars add the statistical determination by different methods (best fits around the cross-over and largest temporal window) and the measurement error.
Fig. 4 also shows that the cross-over from the viscocapillary to the thermal fluctuation-dominated regime appears as an inflection point at a well-defined range in rescaled time and radius, centered around 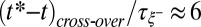 and
and 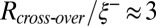 , i.e.,
, i.e., 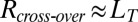 . The cross-over to the fluctuation-dominated regime therefore occurs at scales comparable to the height fluctuations of the interface, which in this case are simply proportional to the bulk correlation length
. The cross-over to the fluctuation-dominated regime therefore occurs at scales comparable to the height fluctuations of the interface, which in this case are simply proportional to the bulk correlation length 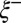 . Again and despite the difficulty of extracting such small values of the neck radii, a systematic variation in
. Again and despite the difficulty of extracting such small values of the neck radii, a systematic variation in 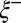 of the cross-over radius is observed. One may argue that this cross-over originates from a balance between the driving capillary pressure and the additional pressure in the neck due to the fluctuating interface. Neglecting the axial curvature, the Laplace pressure inside the neck is
of the cross-over radius is observed. One may argue that this cross-over originates from a balance between the driving capillary pressure and the additional pressure in the neck due to the fluctuating interface. Neglecting the axial curvature, the Laplace pressure inside the neck is 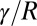 . Besides, the thermal energy density in an elementary cylinder of radius
. Besides, the thermal energy density in an elementary cylinder of radius 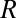 and length
and length 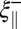 is given by
is given by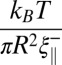 , where
, where 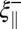 represents the axial correlation length of the interface fluctuations, which is proportional to
represents the axial correlation length of the interface fluctuations, which is proportional to 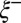 (20). Because
(20). Because 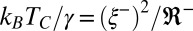 (17), this balance occurs for
(17), this balance occurs for 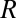 proportional to
proportional to 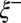 . We identify this radius as the cross-over between the two regimes. Fig. 4
Lower Inset shows that
. We identify this radius as the cross-over between the two regimes. Fig. 4
Lower Inset shows that 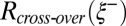 is indeed consistent with a linear variation
is indeed consistent with a linear variation 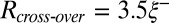 .
.
Discussion
Besides being of importance as it tackles the difficult problem of hydrodynamics of strongly fluctuating media (21), the thermal fluctuation-dominated pinch-off regime is supposed to have clear repercussions on the formation of satellite drops. To shed light on this issue, we considered different 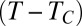 , to tune the amplitude of fluctuations, and different beam powers and waists to modify the mean radius
, to tune the amplitude of fluctuations, and different beam powers and waists to modify the mean radius 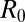 of the initial light-sustained liquid column. This column ends up breaking into a number of main drops due to the Rayleigh–Plateau instability (4) when light is turned off. Besides these main drops, smaller droplets may appear in between, which are referred to as satellite drops. Fig. 5 A–C shows that the number of satellites depends on the ratio between the initial radius
of the initial light-sustained liquid column. This column ends up breaking into a number of main drops due to the Rayleigh–Plateau instability (4) when light is turned off. Besides these main drops, smaller droplets may appear in between, which are referred to as satellite drops. Fig. 5 A–C shows that the number of satellites depends on the ratio between the initial radius 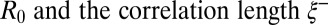 : the smaller this ratio the smaller the number of satellites. Satellite droplets are basically absent in Fig. 5A, where only the main drops are present, whereas farther away in temperature from the critical point, they are systematically present. To quantify this observation, we present in Fig. 5D the fraction of satellite drops, defined as the ratio of the number of satellite drops to the number of necks between main drops, vs.
: the smaller this ratio the smaller the number of satellites. Satellite droplets are basically absent in Fig. 5A, where only the main drops are present, whereas farther away in temperature from the critical point, they are systematically present. To quantify this observation, we present in Fig. 5D the fraction of satellite drops, defined as the ratio of the number of satellite drops to the number of necks between main drops, vs. 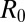 . This figure shows that the mean satellite fraction is roughly unity for
. This figure shows that the mean satellite fraction is roughly unity for 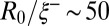 (an example of an almost bidisperse situation can be seen in Fig. 5B), and strongly fluctuates in the range
(an example of an almost bidisperse situation can be seen in Fig. 5B), and strongly fluctuates in the range 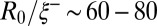 from one experiment to another, and along the same liquid thread as illustrated in Fig. 5C, where zero, one-, and two-satellite events are present in the same snapshot.
from one experiment to another, and along the same liquid thread as illustrated in Fig. 5C, where zero, one-, and two-satellite events are present in the same snapshot.
Fig. 5.
(A–C) Typical liquid thread before and after destabilization for different 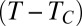 . (A)
. (A) 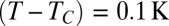 , and a laser beam of waist
, and a laser beam of waist 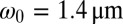 and power
and power 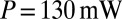 to produce a liquid column of rescaled radius
to produce a liquid column of rescaled radius 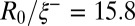 ; note the absence of satellite drops. (B)
; note the absence of satellite drops. (B) 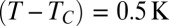 ,
, 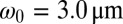 , and
, and 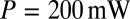 , leading to
, leading to 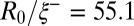 ; note the production of an almost bidisperse drop distribution. (C)
; note the production of an almost bidisperse drop distribution. (C) 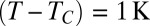 ,
, 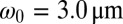 , and
, and  , leading to
, leading to 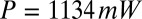 ; note the simultaneous presence of zero, one-, and two-satellite events keeping a satellite fraction close to 1. The interface roughness increase due to the interfacial thermal fluctuations can also be noticed from C to A when the critical point is neared. (Scale bars: A–C, 20 μm.) (D) Variation of the satellite fraction vs. rescaled radius of the initially optically stabilized liquid column
; note the simultaneous presence of zero, one-, and two-satellite events keeping a satellite fraction close to 1. The interface roughness increase due to the interfacial thermal fluctuations can also be noticed from C to A when the critical point is neared. (Scale bars: A–C, 20 μm.) (D) Variation of the satellite fraction vs. rescaled radius of the initially optically stabilized liquid column 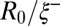 ; the dashed linear fit is a guide to the eye.
; the dashed linear fit is a guide to the eye.
Most important is that this satellite fraction is a decreasing function of 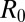 and goes to zero when
and goes to zero when 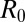 becomes smaller than a cutoff value
becomes smaller than a cutoff value 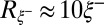 (a linear fit leads to
(a linear fit leads to  ). This decrease and the fact that
). This decrease and the fact that 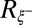 is close to
is close to  both point to the major role of thermal fluctuations in preventing satellite drop formation. Nonetheless, the exact details of the evolution of the neck profile from asymmetric in the two-fluid viscocapillary regime to symmetric in the fluctuation-dominated regime and its link to the decrease of the satellite fraction in Fig. 5D remains to be elucidated. In addition, as noted in Fig. 1C, elongated necks may coexist with symmetric ones in the fluctuation-dominated regime, leading to the presence of a small number of satellite drops [as for
both point to the major role of thermal fluctuations in preventing satellite drop formation. Nonetheless, the exact details of the evolution of the neck profile from asymmetric in the two-fluid viscocapillary regime to symmetric in the fluctuation-dominated regime and its link to the decrease of the satellite fraction in Fig. 5D remains to be elucidated. In addition, as noted in Fig. 1C, elongated necks may coexist with symmetric ones in the fluctuation-dominated regime, leading to the presence of a small number of satellite drops [as for 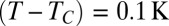 in Fig. 5D]. Though the fluctuation-dominated regime does inhibit satellite drop formation, the subtle interplay between the temporal evolution of the neck shape and the production of these satellites in the presence of fluctuations calls for additional theoretical and experimental work.
in Fig. 5D]. Though the fluctuation-dominated regime does inhibit satellite drop formation, the subtle interplay between the temporal evolution of the neck shape and the production of these satellites in the presence of fluctuations calls for additional theoretical and experimental work.
In conclusion, we have demonstrated the robustness of the signature of thermal fluctuations on the thinning dynamics of liquid necks, as well as the existence of a well-defined cross-over to this regime. Our measurements bring a quantitative description of this regime in a near-critical fluid. Because the existence of this regime requires self-similar solutions, our results bring support to their relevance even in strongly fluctuating systems. We have also shown that the consequences of such fluctuation-dominated thinning can be quite important for the production of satellite drops, as predicted (12, 14), even though how this works precisely remains to be addressed. This property may be useful to produce monodisperse drops at very small scales, with examples ranging from nanojet devices such as carbon nanotube channels (22) to the fragmentation of nanowires by thermal annealing (23) for creating chains (24) or patterns (25) of monodisperse nanoparticles.
Materials and Methods
The minimum neck radius measurement is carried out using movies of the break-up of the chosen liquid neck taken at frame rates between 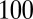 and
and 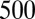 frames per second. An example is given in Fig. 6 for
frames per second. An example is given in Fig. 6 for 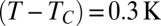 . First, and as depicted by the rectangular window in Fig. 6A, the images are inspected to visually delimit the region of minimal neck diameter. The intensity profile in the direction perpendicular to the neck is then measured and averaged over the few pixels of the depicted window along the direction of the neck. This intensity profile is fit to a Gaussian up to the black stripes associated with the interface. By translating the window along the neck over which the intensity profile is measured and averaged, different Gaussian widths can be measured, and we select the minimum width at half-maximum as the minimum neck diameter. The resulting intensity profile corresponding to Fig. 6A is reported vs. distance in pixels in Fig. 6F, row a. At the used magnification, each pixel corresponds to
. First, and as depicted by the rectangular window in Fig. 6A, the images are inspected to visually delimit the region of minimal neck diameter. The intensity profile in the direction perpendicular to the neck is then measured and averaged over the few pixels of the depicted window along the direction of the neck. This intensity profile is fit to a Gaussian up to the black stripes associated with the interface. By translating the window along the neck over which the intensity profile is measured and averaged, different Gaussian widths can be measured, and we select the minimum width at half-maximum as the minimum neck diameter. The resulting intensity profile corresponding to Fig. 6A is reported vs. distance in pixels in Fig. 6F, row a. At the used magnification, each pixel corresponds to 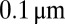 . Intensity profiles are then measured at successive times. Several images as well as their associated profiles are shown in Fig. 6 at different times before rupture; rows a–e in Fig. 6F correspond to snapshots A–E. As the diameter becomes smaller and smaller, this determination becomes more and more difficult because the profiles become less well-defined. Still, such a procedure remains quite reasonable down to at least
. Intensity profiles are then measured at successive times. Several images as well as their associated profiles are shown in Fig. 6 at different times before rupture; rows a–e in Fig. 6F correspond to snapshots A–E. As the diameter becomes smaller and smaller, this determination becomes more and more difficult because the profiles become less well-defined. Still, such a procedure remains quite reasonable down to at least 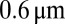 in diameter, as shown in Fig. 6E. Diameters below
in diameter, as shown in Fig. 6E. Diameters below 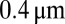 become very difficult to measure, because the contrast between the neck and the outer medium becomes very small. Further inspection of the rupture region, nevertheless, allows estimating the final rupture time.
become very difficult to measure, because the contrast between the neck and the outer medium becomes very small. Further inspection of the rupture region, nevertheless, allows estimating the final rupture time.
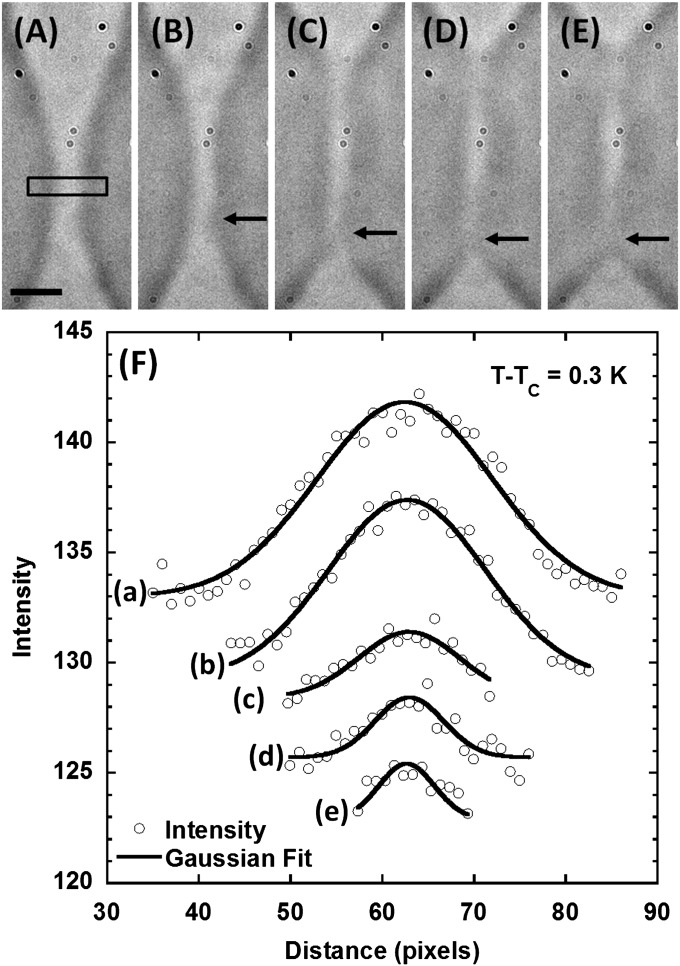
Fig. 6.
(A–E) Photographs extracted from an experiment performed at 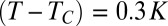 show a close-up of the neck region to be analyzed to measure the minimum neck diameter and therefore the minimum neck radius used in this study. (Scale bar: A, 5 μm.) The images correspond to (A) 0.86 s, (B) 0.56 s, (C) 0.17 s, (D) 0.08 s, and (E) 0.02 s before estimated rupture time. The associated intensity profiles are obtained by averaging along the direction perpendicular to the symmetry axis of the neck over the few pixels of the window indicated in A. These profiles are fit to a Gaussian whose minimum width is obtained by moving the window up and down. (F) Illustration of fits, respectively, denoted a–e in correspondence to A–E and arbitrarily shifted in intensity; the corresponding widths are (a) 19 pixels, (b) 17 pixels, (c) 11 pixels, (d) 7.5 pixels, and (e) 6 pixels. The minimum diameter, from which the minimum neck radius is obtained to plot the thinning dynamics of the neck vs. time, is taken to be the width at half-maximum of the Gaussian fit, i.e., the minimum width of the Gaussian is multiplied by
show a close-up of the neck region to be analyzed to measure the minimum neck diameter and therefore the minimum neck radius used in this study. (Scale bar: A, 5 μm.) The images correspond to (A) 0.86 s, (B) 0.56 s, (C) 0.17 s, (D) 0.08 s, and (E) 0.02 s before estimated rupture time. The associated intensity profiles are obtained by averaging along the direction perpendicular to the symmetry axis of the neck over the few pixels of the window indicated in A. These profiles are fit to a Gaussian whose minimum width is obtained by moving the window up and down. (F) Illustration of fits, respectively, denoted a–e in correspondence to A–E and arbitrarily shifted in intensity; the corresponding widths are (a) 19 pixels, (b) 17 pixels, (c) 11 pixels, (d) 7.5 pixels, and (e) 6 pixels. The minimum diameter, from which the minimum neck radius is obtained to plot the thinning dynamics of the neck vs. time, is taken to be the width at half-maximum of the Gaussian fit, i.e., the minimum width of the Gaussian is multiplied by 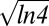 .
.
Supplementary Material
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1207634109/-/DCSupplemental.
References
- 1.Lister JR, Stone HA. Capillary breakup of a viscous thread surrounded by another viscous fluid. Phys Fluids. 1998;10(11):2758–2764. [Google Scholar]
- 2.Cohen I, Nagel SR. Testing for scaling behavior dependence on geometrical and fluid parameters in the two fluid drop snap-off problem. Phys Fluids. 2001;13(12):3533–3541. [Google Scholar]
- 3.Eggers J. Nonlinear dynamics and breakup of free-surface flows. Rev Mod Phys. 1997;69(3):865–929. [Google Scholar]
- 4.Eggers J, Villermaux E. Physics of liquid jets. Rep Prog Phys. 2008;71(3) 036601. [Google Scholar]
- 5.Basaran OA. Small-scale free surface flows with breakup: Drop formation and emerging applications. AIChE J. 2002;48(9):1842–1848. [Google Scholar]
- 6.Papageorgiou DT. On the breakup of viscous liquid threads. Phys Fluids. 1995;7(7):1529–1544. [Google Scholar]
- 7.Eggers J. Universal pinching of 3D axisymmetric free-surface flow. Phys Rev Lett. 1993;71(21):3458–3460. doi: 10.1103/PhysRevLett.71.3458. [DOI] [PubMed] [Google Scholar]
- 8.Suryo R, Basaran OA. Local dynamics during pinch-off of liquid threads of power law fluids: Scaling analysis and self-similarity. J Nonnewton Fluid Mech. 2006;138(2-3):134–160. [Google Scholar]
- 9.Savage JR, Caggioni M, Spicer PT, Cohen I. Partial universality: Pinch-off dynamics in fluids with smectic liquid crystalline order. Soft Matter. 2010;6(5):892–895. [Google Scholar]
- 10.Cohen I, Brenner MP, Eggers J, Nagel SR. Two fluid drop snap-off problem: Experiments and theory. Phys Rev Lett. 1999;83(6):1147–1150. [Google Scholar]
- 11.Zhang WW, Lister JR. Similarity solutions for capillary pinch-off in fluids of differing viscosity. Phys Rev Lett. 1999;83(6):1151–1154. [Google Scholar]
- 12.Moseler M, Landman U. Formation, stability, and breakup of nanojets. Science. 2000;289(5482):1165–1170. doi: 10.1126/science.289.5482.1165. [DOI] [PubMed] [Google Scholar]
- 13.Landman U. Materials by numbers: Computations as tools of discovery. Proc Natl Acad Sci USA. 2005;102(19):6671–6678. doi: 10.1073/pnas.0408038102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Eggers J. Dynamics of liquid nanojets. Phys Rev Lett. 2002;89(8) doi: 10.1103/PhysRevLett.89.084502. 084502. [DOI] [PubMed] [Google Scholar]
- 15.Hennequin Y, et al. Drop formation by thermal fluctuations at an ultralow surface tension. Phys Rev Lett. 2006;97(24) doi: 10.1103/PhysRevLett.97.244502. 244502. [DOI] [PubMed] [Google Scholar]
- 16.Aarts DG, Schmidt M, Lekkerkerker HN. Direct visual observation of thermal capillary waves. Science. 2004;304(5672):847–850. doi: 10.1126/science.1097116. [DOI] [PubMed] [Google Scholar]
- 17.Moldover MR. Interfacial tension of fluids near critical points and two-scale-factor universality. Phys Rev A. 1985;31(2):1022–1033. doi: 10.1103/physreva.31.1022. [DOI] [PubMed] [Google Scholar]
- 18.Wunenburger R, Casner A, Delville JP. Light-induced deformation and instability of a liquid interface. I. Statics. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73(3 Pt 2) doi: 10.1103/PhysRevE.73.036314. 036314. [DOI] [PubMed] [Google Scholar]
- 19.Brasselet E, Wunenburger R, Delville JP. Liquid optical fibers with a multistable core actuated by light radiation pressure. Phys Rev Lett. 2008;101(1) doi: 10.1103/PhysRevLett.101.014501. 014501. [DOI] [PubMed] [Google Scholar]
- 20.Indekeu JO, Aarts DG, Lekkerkerker HN, Hennequin Y, Bonn D. Thermal fluctuation forces and wetting layers in colloid-polymer mixtures: Derivation of an interface potential. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;81(4 Pt 1) doi: 10.1103/PhysRevE.81.041604. 041604. [DOI] [PubMed] [Google Scholar]
- 21.Assenheimer M, Steinberg V. Transition between spiral and target states in Rayleigh–Bénard convection. Nature. 1994;367(6461):345–347. [Google Scholar]
- 22.Mattia D, Gogotsi Y. Review: Static and dynamic behavior of liquids inside carbon nanotubes. Microfluid Nanofluid. 2008;5(3):89–305. [Google Scholar]
- 23.Toimil Molares ME, Balogh AG, Cornelius TW, Neumann R, Trautmann C. Fragmentation of nanowires driven by Rayleigh instability. Appl Phys Lett. 2004;85(22):5337–5339. [Google Scholar]
- 24.Chen JT, Zhang M, Russell TP. Instabilities in nanoporous media. Nano Lett. 2007;7(1):183–187. doi: 10.1021/nl0621241. [DOI] [PubMed] [Google Scholar]
- 25.Park H, Russell TP, Park S. Spatial control of dewetting: Highly ordered Teflon nanospheres. J Colloid Interface Sci. 2010;348(2):416–423. doi: 10.1016/j.jcis.2010.05.011. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.