Phase competition in trisected superconducting dome

Abstract

A detailed phenomenology of low energy excitations is a crucial starting point for microscopic understanding of complex materials, such as the cuprate high-temperature superconductors. Because of its unique momentum-space discrimination, angle-resolved photoemission spectroscopy (ARPES) is ideally suited for this task in the cuprates, where emergent phases, particularly superconductivity and the pseudogap, have anisotropic gap structure in momentum space. We present a comprehensive doping- and temperature-dependence ARPES study of spectral gaps in Bi₂Sr₂CaCu₂O_8+δ, covering much of the superconducting portion of the phase diagram. In the ground state, abrupt changes in near-nodal gap phenomenology give spectroscopic evidence for two potential quantum critical points, p = 0.19 for the pseudogap phase and p = 0.076 for another competing phase. Temperature dependence reveals that the pseudogap is not static below T_c and exists p > 0.19 at higher temperatures. Our data imply a revised phase diagram that reconciles conflicting reports about the endpoint of the pseudogap in the literature, incorporates phase competition between the superconducting gap and pseudogap, and highlights distinct physics at the edge of the superconducting dome.

The momentum-resolved nature of angle-resolved photoemission spectroscopy (ARPES) makes it a key probe of the cuprates, the interesting phases of which have anisotropic momentum-space structure (1–4): both the d-wave superconducting gap and the pseudogap above T_c have a maximum at the antinode [AN, near (π, 0)] and are ungapped at the node, although the latter phase also exhibits an extended ungapped arc (5–8). Ordering phenomena often result in gapping of the quasiparticle spectrum, and distinct quantum states produce spectral gaps with characteristic temperature, doping, and momentum dependence. These phenomena were demonstrated by recent ARPES experiments that argued that the pseudogap is a distinct phase from superconductivity based on their unique phenomenology (8–15): the pseudogap dominates near the AN (8, 11), and its magnitude increases with underdoping (11, 12), whereas near-nodal (NN) gaps have a different doping dependence and can be attributed to superconductivity because they close at T_c (8, 12). Previous measurements focused on AN or intermediate (IM) momenta, but laser-ARPES, with its superior resolution and enhanced statistics, allows for precise gap measurements near the node where the gap is smallest. Our work is unique in its attention to NN momenta using laser-ARPES, and we demonstrate, via a single technique, that three distinct quantum phases manifest in different NN phenomenology as a function of doping.

Results

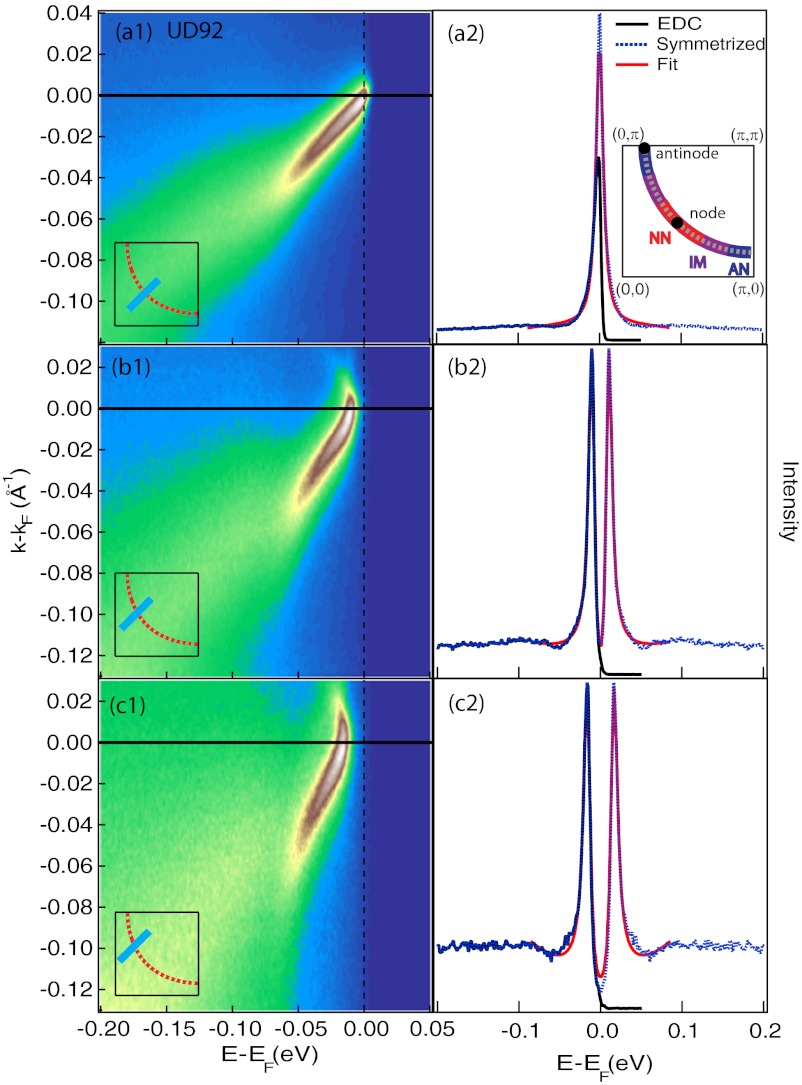
Gaps at parallel cuts were determined by fitting symmetrized energy distribution curves (EDCs) at k_F to a minimal model (16). The Fermi wavevector, k_F, is defined by the minimum gap locus. Example spectra, raw and symmetrized EDCs at k_F, and fits are shown for UD92 (underdoped, T_c = 92) in Fig. 1.

Fig. 1.

Raw data, EDCs, and fitting. (A1, B1, C1) Spectra for UD92 at the node (A1) and away from the node (B1 and C1), with cut geometry and position shown in insets. Horizontal lines are k_F. (A2, B2, C2) Raw (black) and symmetrized (blue) EDCs at k_F. EDCs are fit to a minimal model (16) (red) to extract gap. (A2, Inset) A quarter of the cuprate Brillouin zone and the FS (dotted line). The node and antinode points are identified with black dots. Locations of NN (red), IM (purple), and AN (blue) momenta are shown.

Low Temperature.

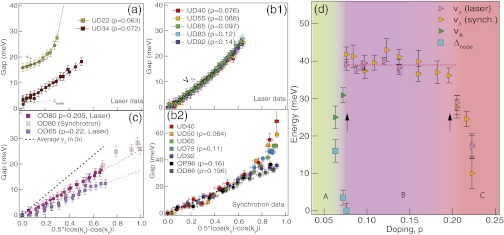
Fig. 2 A–C shows gaps around the Fermi surface (FS) in terms of the simple d-wave form, 0.5|cos(k_x) − cos(k_y)|, measured T∼10K for the samples in our study (see SI Appendix for more details). These data are quantified by the gap slope, v_Δ, which measures how fast the d-wave gap increases as a function of momentum away from the node. We find that the low-temperature v_Δ changes suddenly at two dopings, p = 0.076 and p = 0.19, which are marked in the energy-doping phase diagram in Fig. 2D, dividing the superconducting dome into three regions, labeled A, B, and C. In a d-wave superconductor, v_Δ is expected to scale with T_c, and in region C (p > 0.19) (Fig. 2C), v_Δ and T_c indeed decrease together. Region B (0.076 ≤ p ≤ 0.19), exhibits a markedly different behavior: NN gaps are almost coincident over a large portion of the FS for all samples shown in Fig. 2B, indicating a doping-independent v_Δ, despite T_c varying more than twofold. The laser-ARPES gap functions show a slight curvature, nearly identical for all dopings, which is not visible in synchrotron-ARPES data because of poorer resolution and a sparser sampling of momenta. We note that the crossover between regions B and C is very abrupt, as v_Δ decreases by almost 25% for a change in doping Δp = 0.01, after having been constant within error bars for Δp = 0.12. There is also a very abrupt transition between regions A and B at p = 0.076 (Fig. 2A), as region A is marked by a FS which is gapped at every momentum. The gap minimum (Δ_node) is at the nodal momentum [along (0, 0) − (π, π)] and increases with underdoping. Although v_Δ is no longer defined, the gap is still anisotropic around the FS. We define a gap anisotropy parameter in region A, v_A, from the momentum dependence of the gap in Fig. 2A, and v_A decreases with underdoping. The low-temperature NN energy scales that characterize each of the three phase regions are summarized in Fig. 2D. These findings are an important refinement to previous results, which indicated that the NN region is dominated by superconductivity. These results demonstrate more conventional d-wave superconductivity in region C, unconventional doping-independent d-wave superconductivity in region B, and a nodeless unconventional superconductivity in region A.

Fig. 2.

Three distinct phase regions at low temperature. Label UD/OP/OD denotes underdoped/optimal/overdoped sample with T_c given by the number which follows. Gaps plotted in terms of the simple d-wave form. v_Δ (v_A) is from a fit over the linear portion of the gap function, as shown by a solid or dotted line in A or B1, respectively. (A) In region A, FS is fully gapped with gap minimum, Δ_node, at nodal momentum. Gap anisotropy v_A decreases with underdoping. (B) Region B has doping-independent v_Δ. (C) In region C, v_Δ decreases as T_c decreases. Dashed line is guide-to-the-eye for average v_Δ observed in region B. Error bars in laser-ARPES reflect 3σ error in fitting procedure and an additional 100% margin. Error bars in synchrotron data reflect uncertainty of determining E_F (±0.5 meV), error from fitting procedure, and an additional 100% margin. (D) Summary of low-temperature NN energy scales. Arrows mark critical dopings defining three phase regions.

Temperature Dependence.

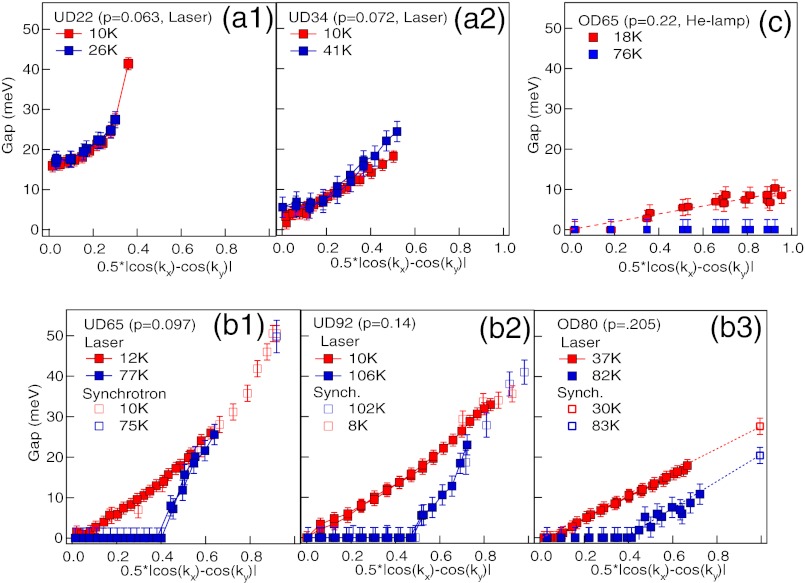
In Fig. 3 we compare low-temperature gaps with gaps just above T_c in each of the three phase regions. For samples that are in region A at low temperature, the NN gaps are temperature-independent across T_c, and the FS remains fully gapped above T_c. This finding indicates that the gap at the nodal momentum does not have a purely superconducting origin and that the onset doping for region A is the same at low temperature and T_c. In region B, gaps close or diminish near the node at T_c but AN gaps remain above T_c. This observation of Fermi arcs near the node, defined as momenta where the symmetrized EDCs at k_F are peaked at E_F (7), and gaps near the antinode are the usual ARPES signature of the pseudogap above T_c. All of the samples that exhibit characteristic doping-independent NN gaps of region B at low temperature also display a Fermi arc and antinodal gap above T_c. Additionally, OD80 (p∼0.205) has an AN gap persisting T>T_c, demonstrating a pseudogap above T_c at this doping. Thus, we classify the temperature dependence of OD80 with region B in Fig. 3 even though it exhibits region C phenomenology at low temperature. This finding suggests that the doping separating regions B and C may be different at low temperature and at T_c and that the pseudogap may exist at higher temperature for p > 0.19. The most overdoped sample in our study, OD65, is the only one to exhibit an ungapped FS T>T_c, demonstrating that the normal state pseudogap persists until p∼0.22, in agreement with other recent ARPES results (17).

Fig. 3.

Distinct temperature dependence of gap in each of three phase regions. Red: low temperature gap. Blue: gap T>T_c. (A) In region A, NN gaps do not close across T_c. (B) In region B, NN gaps partially close at T_c, with AN pseudogap remaining T>T_c. OD80 is in phase region C at low temperature, but behaves like phase region B T>T_c. (C) He-lamp data. For p ≥ 0.22, gap closes everywhere on FS T>T_c.

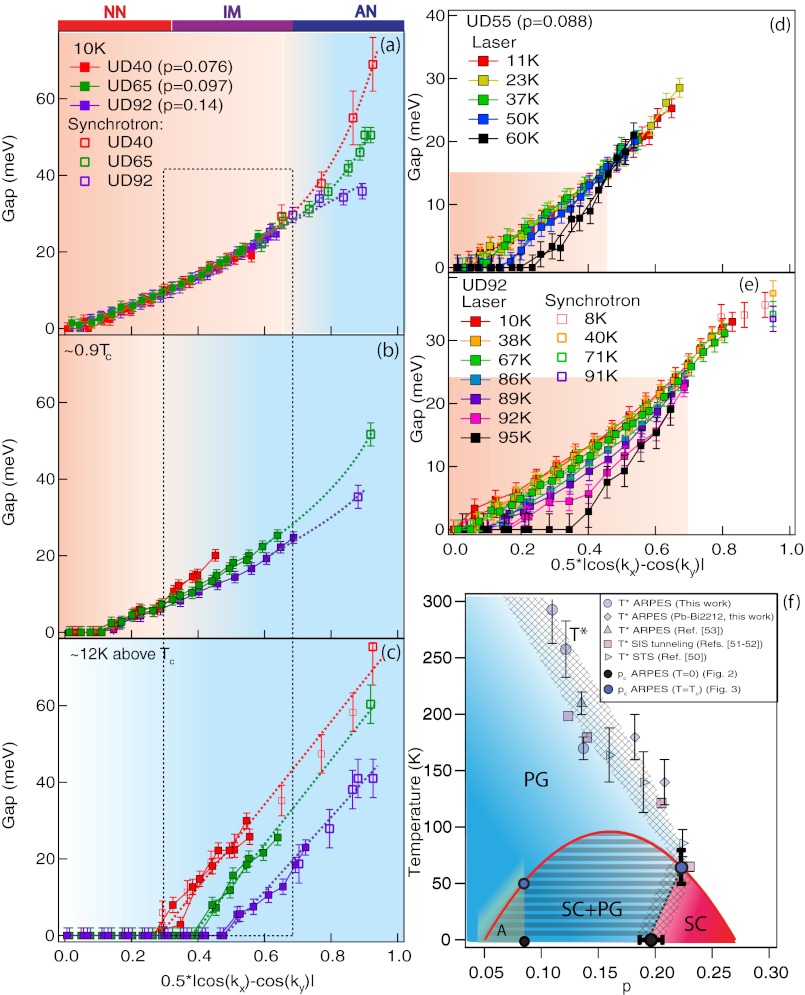
We study temperature-and-doping dependence of gaps in two ways: doping dependence at comparable temperature and temperature dependence at varied dopings. The former is shown in Fig. 4 A–C, where three dopings (UD40, UD65, and UD92) are compared at three temperatures. These dopings are chosen to be in a regime where the superconductivity and pseudogap energy scales are well separated in Bi-2212 (SI Appendix). Two distinct doping dependencies are observed in different regions of the FS: doping-independent gaps and gaps which increase with underdoping. At 10K, doping-independent gaps are observed at NN and IM momenta, and gaps that increase with underdoping are observed at the AN. Just below T_c, however, doping-dependent gaps extend into the IM region. Above T_c, gaps increase with underdoping everywhere except the Fermi arc. Notably, a region of the FS (marked with a dashed box in Fig. 4 A–C) is home to doping-independent gaps at low temperatures but doping-dependent gaps near or above T_c. Fig. 4 D and E shows a full temperature dependence of gaps from low temperature to T_c for UD55 and UD92. Temperature dependence near the node occurs in a limited temperature range within 25% of T_c, and the momentum region where gaps decrease near T_c becomes larger with increasing doping.

Fig. 4.

Phase competition in region B (A–C) Gaps in UD40, UD65, and UD92 at 10K, 0.9 T_c, and 12 K above T_c. Synchrotron and laser data shown with open and filled symbols, respectively. Dashed lines are guides to the eye. Doping-independent or dependent gaps indicated by pink or blue shading, respectively. Dashed box marks momenta where gaps are doping-dependent in B and C but doping-independent in A. (D and E) Gap functions at various temperatures below and across T_c for UD55 and UD92 (see SI Appendix for additional dopings). Shaded regions denotes momenta where the gap T>T_c is smaller than the low temperature gap. Filled and open symbols are laser and synchrotron-ARPES data, respectively. (F) Proposed phase diagram. T* is determined from ARPES measurements at antinode (SI Appendix and ref. 53), STS (50), and superconductor-insulator-superconductor tunneling (51, 52).

Discussion

Phase Region A.

Whereas some ARPES experiments suggest a smooth evolution of phenomenology from the moderately underdoped regime to the edge of the superconducting dome (7, 18, 19), our data indicate an emergent phase in region A (p < 0.076) that coexists with superconductivity, characterized in ARPES by a gap at every FS momentum. These results are supported by similar data in other cuprates. A fully gapped state at the underdoped edge of the superconducting dome has been shown in Ca_2−xNa_xCuO₂Cl₂ (Na-CCOC) (20) and Bi₂Sr_2−xLa_xCuO_6+δ (La-Bi2201) (21), and our study demonstrates a fully gapped FS, both above and below T_c, in Bi-2212 at superconducting dopings. It is possible that region A represents an extension of pseudogap physics, but multiple spectroscopic changes p < 0.076 together with reports of a distinct order at the underdoped edge of the superconducting dome in other compounds points to distinct physics. There are three abrupt changes in NN gap phenomenology at p = 0.076: a fully gapped FS appears, the gap anisotropy away from the nodal momentum starts to decrease, and the NN gaps become temperature-independent across T_c, such that Fermi arcs are not observed. The latter result connects to in-plane transport in deeply underdoped cuprates, which shows negative dρ_ab/dT before the superconducting transition (22). Notably, EDCs in region A remain sufficiently sharp near the nodal momentum (SI Appendix), such that it is unlikely that this behavior is primarily disorder driven. There have been recent reports of a similar critical doping p∼0.07–0.10 in YBa₂Cu₃O_y (YBCO), varyingly attributed to a metal-insulator quantum critical point (23), a Lifshitz transition (24), or spin density wave order (SDW) (25). Although a similar onset doping might suggest a common origin of phenomena observed in YBCO and Bi-2212, there are some inconsistencies—such as thermal conductivity data—that do not support a fully gapped FS at low dopings in YBCO (26). This discrepancy may be materials-dependent, reflecting differences in disorder and Fermiology. Alternately, the ground state in region A may exhibit intrinsic time or spatial variation such that different techniques are sensitive to different aspects, which is supported by neutron scattering and muon spin-relaxation measurements in YBCO, indicating slowly fluctuating spin order at the edge of the superconducting dome (27). It has been shown that SDW order can gap nodal quasiparticles (28), so this may be common to both compounds.

Phase Regions B and C.

Although superconductivity has been shown to dominate at NN momenta (8, 9), Fig. 2B indicates that NN gaps are remarkably insensitive to T_c in a broad doping range constituting region B, highlighting that NN gaps in region B do not reflect the bare superconducting order parameter. This doping-independent v_Δ is supported by specific heat measurements in YBCO (29) and from scanning tunneling spectroscopy (STS) data in Bi-based cuprates (30, 31). Our data are the most complete ARPES demonstration of this behavior, crucially revealing p = 0.076 and p = 0.19 as dopings where region B abruptly ends. The sudden change in v_Δ at p = 0.19 is interpreted as the T = 0 endpoint of the pseudogap. This assignment has a precedent from low-temperature experiments, which indicated that both the superfluid density and the Cu-site impurity-doping needed to suppress superconductivity are maximum at p = 0.19 (29, 32, 33). Additionally, earlier ARPES data showed a maximum in the antinodal quasiparticle spectral weight, one measure of the strength of superconductivity relative to other spectral features, at p = 0.19 (34). In the interpretation that p = 0.19 is the T = 0 endpoint of the pseudogap, the more conventional relation between T_c and v_Δ in region C reflects a pure superconducting ground state at low temperature, and region B is identified as a coexistence regime of superconductivity and the pseudogap. Coexistence of superconductivity and pseudogap in region B has support both from other experiments and from independent ARPES data in our study. STS experiments show symmetry-breaking order associated with the pseudogap throughout this doping range (35), and intrinsic tunneling spectroscopy shows distinct superconducting and pseudogap features below T_c (36). In the present study, for all of region B, coexistence of pseudogap and superconductivity in Bi-2212 manifests via distinct temperature dependence of gaps near the node and further away from the node (8). For the most underdoped portion of region B (p < 0.12), coexistence also manifests in a gap function that deviates strongly from a simple d-wave form at the AN, such that v_Δ < Δ_AN, where Δ_AN is the AN gap (SI Appendix). The doping where Δ_AN first surpasses v_Δ is not significant, and simply indicates the doping where the superconducting gap (NN) energy scale is sufficiently smaller than the pseudogap (AN) energy scale. For some lower T_c cuprates, gaps already deviate from a simple d-wave form at optimal doping and show stronger deviation than Bi-2212 in the underdoped regime (9, 12, 37). Although the pseudogap is considered to be primarily an AN phenomenon, our results demonstrate that it also manifests at NN momenta in region B via the doping-independent v_Δ. Similarly, the absence of the pseudogap in the ground state p > 0.19 is also apparent at NN momenta, via a doping-dependent v_Δ. The remarkable doping-independent v_Δ in region B remains unexplained, but it may indicate a superconducting gap whose magnitude is renormalized by coexistence with the pseudogap.

The temperature dependence of spectral gaps provides microscopic information about the dynamics of the superconductivity/pseudogap coexistence in region B. Fig 4 A–C demonstrates that at IM momenta, gaps have characteristic doping dependence of T*—increasing with underdoping (38, 39)—when superconductivity is weak just below T_c or absent above T_c, but are doping-independent at low temperatures. This finding shows that the pseudogap is not static below T_c, but rather, it is suppressed by superconductivity at low temperatures. This nuance within the “two-gap” picture indicates that the temperature dependence of the pseudogap must also be considered for quantitative understanding of the superconducting state. Fig. 4 A–C shows that the Fermi arc just above T_c does not represent the only momenta where superconductivity emerges, because the doping-independent gap region at T = 10K extends beyond the Fermi arc measured T>T_c. A better way to define momenta with superconducting character is by temperature dependence near T_c, and the superconductivity-dominated momentum region defined in this manner expands with doping. Although a pure superconducting gap closes entirely at T_c, we use a more lenient definition—a gap which diminishes approaching T_c—to define momenta with superconducting character. We note that superconductivity exists over the entire FS in Bi-2212, as sharp quasiparticles are observed at the AN for p > 0.08 (34, 40, 41), but our definition of the “superconducting region” selects the portion of the FS where the temperature dependence of gaps indicates significant spectral contributions from superconductivity. This definition also permits for coexistence of pseudogap and superconductivity at some momenta, accounts for the observation that the pseudogap itself has temperature dependence, and is not hindered by difficulties in defining the Fermi arc length because of its temperature dependence (7). The temperature-dependence data in Fig. 4 A–E provides a phase-competition picture of superconductivity/pseudogap interaction in momentum space: the pseudogap is suppressed by superconductivity at low temperatures and larger dopings, and it surrenders a portion of the FS where it once existed.

Proposed Phase Diagram.

The starting point of the phase diagram proposed in Fig. 4F is the observation of three distinct phase regions at low temperature as a function of doping, separated by two potential quantum critical points inside the superconducting dome at p = 0.076 and p = 0.019. The former marks the onset of region A, possibly related to SDW order, and the latter is interpreted as the T = 0 endpoint of the pseudogap. Both critical points have support from other experiments in numerous cuprates (20, 23, 25, 29, 32, 33, 42), and some theoretical proposals also favor a ground state with multiple critical points (43). Our data demonstrate how these potential critical points manifest in the phenomenology of NN spectral gaps measured by ARPES. The phase diagram in Fig. 4F also features conjectured reentrant behavior of the pseudogap inside the superconducting dome, as a direct consequence of phase competition between superconductivity and the pseudogap (44–46). The phase boundary between regions B (SC+PG) and C (SC) is anchored by ARPES data at T = 0 and T = T_c, which show a sudden change in v_Δ and an absence of pseudogap T>T_c, respectively. These data are supported by OD80, data which obey region C phenomenology at low temperature, but region B phenomenology at higher temperature, with the pseudogap persisting above T_c. It has been shown that the T = 0 endpoint of a competing order is expected to shift under the superconducting dome (47), such that high-temperature measurements of the pseudogap phase boundary do not extrapolate to the T = 0 endpoint seen inside the superconducting dome. This result manifests clearly in the BaFe₂As₂ family of iron pnictide compounds where both magnetic and structural phases have been shown to coexist with and be suppressed by superconductivity (48, 49), and a phase diagram with reentrant behavior has been demonstrated (49). A phase diagram with a reentrant pseudogap resolves conflicting reports about the fate of the pseudogap transition temperature, T*, inside the superconducting dome. Some experiments suggest that the T* line intersects the superconducting dome and reaches T = 0 at p = 0.19 (29, 38), whereas others, particularly spectroscopies, including our ARPES measurements of T* shown in Fig. 4F, indicate that T* and T_c merge on the strongly overdoped side (17, 50–53). Although variations between different experiments are expected, our data uniquely demonstrate both behaviors using a single technique.

Conclusions

We have performed a thorough doping-and-temperature dependence study of spectral gaps in superconducting Bi-2212. At low temperature, we report three distinct phase regions with different characteristic phenomenology of NN gaps. In phase region B (0.076 < p < 0.19), which is identified as a regime where superconductivity coexists with the pseudogap in the ground state, gaps at NN and IM momenta are independent of doping. In region C (p > 0.19), identified as a pure superconducting ground state, the d-wave superconducting gap decreases as T_c decreases. Region A (p < 0.076) is identified as an emergent phase characterized by a fully gapped FS and a gap anisotropy that decreases with underdoping. Temperature dependence of gaps reveals phase competition between the pseudogap and superconductivity, where pseudogap physics dominate a smaller region of the FS at low temperatures and larger dopings. From these doping- and temperature-dependence data we propose a unique phase diagram featuring a trisected superconducting dome and reentrant behavior of the pseudogap.

Materials and Methods

Laboratory-based experiments were done with 7 eV laser or monochromated He-I light (21.2 eV) (Gammadata He lamp) and a Scienta SES2002 analyzer. The 7 eV photons were produced by second harmonic generation from a 355-nm laser (Paladin; Coherent) using a nonlinear crystal KBe₂BO₃F₂. Laser energy and momentum resolution were 3 meV and better than 0.005 Å⁻¹, respectively. Synchrotron data were taken at the Stanford Synchrotron Radiation Lightsource with a Scienta R4000 analyzer and energy resolution ∼8 meV. Samples were cleaved at 10–30K in situ at a pressure <4 × 10⁻¹¹ torr to obtain a clean surface. Doping was determined from T_c via an empirical curve, T_c = T_c,max*[1-82.6(p − 0.16)²], taking 96K as the optimum T_c for Bi-2212 (54).

During the review process, following the submission of this manuscript, related papers appeared in support of charge density wave order, possibly related to the pseudogap, which competes with superconductivity (55, 56). In addition, another paper reported a gap at the nodal momentum in La_2−xSr_xCuO₄ (57).