Size and complexity in model financial systems

Abstract

The global financial crisis has precipitated an increasing appreciation of the need for a systemic perspective toward financial stability. For example: What role do large banks play in systemic risk? How should capital adequacy standards recognize this role? How is stability shaped by concentration and diversification in the financial system? We explore these questions using a deliberately simplified, dynamic model of a banking system that combines three different channels for direct transmission of contagion from one bank to another: liquidity hoarding, asset price contagion, and the propagation of defaults via counterparty credit risk. Importantly, we also introduce a mechanism for capturing how swings in “confidence” in the system may contribute to instability. Our results highlight that the importance of relatively large, well-connected banks in system stability scales more than proportionately with their size: the impact of their collapse arises not only from their connectivity, but also from their effect on confidence in the system. Imposing tougher capital requirements on larger banks than smaller ones can thus enhance the resilience of the system. Moreover, these effects are more pronounced in more concentrated systems, and continue to apply, even when allowing for potential diversification benefits that may be realized by larger banks. We discuss some tentative implications for policy, as well as conceptual analogies in ecosystem stability and in the control of infectious diseases.

Although global financial systems have seen considerable growth in size, concentration, and complexity over the past few decades (1), our understanding of the dynamic behavior of such systems has not necessarily kept pace. Indeed, the current financial crisis has presented a stark demonstration of the potential for modern financial systems to amplify and disseminate financial distress on a global scale. From a regulatory perspective, these events have prompted fresh interest in understanding financial stability from a system level. In particular, although precrisis regulation (as typified by the Basel II accords) sought to minimize the risk of failure of individual banks irrespective of systemic importance, new regulation will seek to target the systemic consequences of bank collapse as well. To quote Haldane and May (2), “What matters is not a bank’s closeness to the edge of the cliff; it is the extent of the fall.”

In this context, a clear feature of interest is the presence of large, highly connected banks. These banks have conceptual parallels in biology: simple models have been influential in underlining the importance of “superspreaders” in the spread and control of infectious diseases (3, 4), and “keystone” species are thought to serve a valuable role in ecosystem stability (5, 6). Here we develop dynamic models to apply and extend these lessons to financial systems. Our approach is theoretical, and our models necessarily oversimplified. Nonetheless, by considering transmission mechanisms specific to modern financial systems, our approach recognizes some important differences between these and other complex systems. We show how, even with such distinctions, the basic insights deriving from our model allow us to draw certain parallels with other situations where size and complexity are important.

If financial crises may be compared with forest fires, causes for the initiating sparks pose important questions in their own right: for example, the role of excessive leverage and credit growth (7) or the pricing for complex financial instruments (8, 9). Here, however, our focus is on the role of large banks in the “flammability” of the system, or its capacity for amplification and propagation of an initiating shock. We ask the following questions: How does the impact of a bank’s collapse scale with its size? How might capital adequacy standards seek to mitigate this impact? More broadly, what is the effect of concentration and diversification on system stability?

Network approaches (10–14) are well-suited for such questions, particularly in modeling contagion that is transmitted through linkages in the financial system. Here we adopt such an approach to bring together three important transmission channels into a unified framework: (i) liquidity hoarding, where banks cut lending to each other as a defensive measure (1, 15); (ii) asset price contagion linked to market illiquidity (16–18); and (iii) the propagation of defaults via counterparty credit risk (19–21).

Although the network effects listed above act on defined webs of connectivity, confidence effects can operate more broadly, with the overall state of the system potentially influencing an individual bank’s actions, and vice versa. This motivates a special feature of our model, which explicitly integrates network dynamics with confidence effects.

The interaction of such network and confidence effects arguably played a major role in the collapse of the interbank market (a network of lending exposures among banks) and global liquidity “freeze” that occurred during the crisis (22). Interbank loans have a range of maturities, from overnight to a matter of years, and may often be renewed, or rolled over, at the point of maturity. A pronounced feature of the 2007/2008 crisis was that, as the system deteriorated, banks stopped lending to each other at all but the shortest maturities (7, 29). The bankruptcy of Lehman Brothers in September 2008 transmitted distress further across the financial network, and signaled that there was no guarantee of government support for institutions in distress. The effects extended well beyond those institutions directly exposed to Lehman Brothers, with banks throughout the system withdrawing interbank lending outright and propagating distress to the real economy by sharply contracting household and corporate lending (23). At the time of writing, ongoing events illustrate the potential for similar dynamics in the context of sovereign and banking sector distress in some Eurozone countries.

Several specific motivating factors have been proposed to explain “liquidity hoarding” (the maturity-shortening and ultimate withdrawal of interbank lending): precautionary measures by lending banks in anticipation of future liquidity shortfalls, counterparty concerns over specific borrowing banks, or collapses in overall system confidence (24, 25). Our framework parsimoniously incorporates all of these mechanisms, but also captures the idea that a bank’s distress may affect not just those directly exposed or linked to it, but also confidence in the market at large.

In what follows we summarize essential features of the model structure, with details provided in Materials and Methods, and a summary of model parameters and their default values given in Table S1. We use this model to explore the impact of an initiating shock, with particular reference to the nonlinearities arising from each of the contagion channels modeled, the effects of size disparity among banks and system concentration, and the effects of diversification. We then outline tentative implications for regulatory capital requirements before discussing important caveats to our work. Throughout the paper, we abstract from extraordinary policy intervention in crisis, so that liquidity cannot be obtained more easily from the central bank than from the market, and failing institutions are not bailed out.

Model Overview

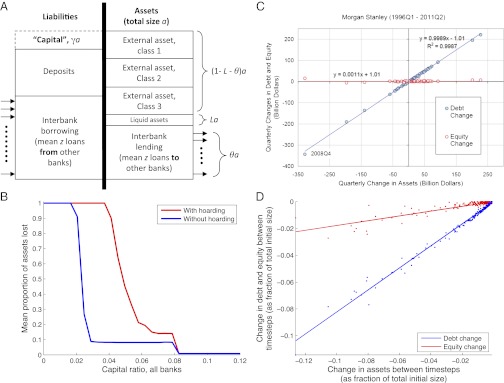
Fig. 1A shows a minimal balance-sheet representation of an individual bank or node in the system. On the asset side of Fig. 1A, this bank lends to other banks in the system and holds a small proportion l of assets as “liquid assets” (e.g., cash, central bank reserves, and high-quality government bonds). The remainder of the asset side consists of holdings in (and thus exposures to) a range of distinct “external” asset classes held against the real economy, such as mortgages, corporate lending, and commercial real estate lending. The liability side is even simpler, consisting of retail deposits (taken to be external to the system) and interbank borrowing. The “capital buffer” is the excess of assets over (debt) liabilities and if this falls below zero, the bank is insolvent (“capital default”). In our treatment, we think of capital in simple terms, consisting only of common equity, thus excluding any form of unsecured term debt (e.g., subordinated debt) or contingent capital. Given that we also abstract from risk-weighting of assets, the capital-to-assets ratio can be thought of as a simple leverage ratio, with our baseline choice of 4% conservatively reflecting typical leverage ratios seen before the crisis (7).

Fig. 1.

The basic model and its behavior. (A) Schematic, balance-sheet representation of a single bank. See Fig. S1 for a schematic of how this bank interacts with others in the network. (B) Effect of liquidity hoarding. Although intended as a defensive action (increasing h_i), hoarding imposes negative externalities on other banks in the system. (C) Empirical findings (30), illustrating that the dynamics of a bank’s total assets (x axis) arise predominantly from changes in debt (blue line) rather than equity (red line). Although shown for the example of Morgan Stanley, qualitatively similar behavior applies for other banks. [Reproduced with permission from Hyun Shin.] (D) Simulation results corresponding to the lower left quadrant of C. Plotted points are accumulated by following the evolution of a random bank’s balance sheet through a simulation, repeating, and superimposing all results over 50 simulations. Note that both axes are negative because we simulate here only the postshock, contractionary phase.

We take a system of 200 banks, interconnected in two distinct ways: (i) the interbank market, represented by a directed network with “nodes” being individual banks and each “edge” being a loan from one bank to another; and (ii) a system of shared exposures to a set of external assets, such that two different banks may hold some external asset classes in common, but not necessarily all (see Fig. S1 for an illustration of this overall scheme). For the interbank network we label half of loans, at random, as initially having long-term maturity, and the remainder as being short-term: in our discrete time simulations we assume that long-term loans can be made short-term from one time step to the next, but only short-term loans can be withdrawn in the same interval.

We assume for simplicity that there are two sizes of banks, where “big” banks are λ-times larger on average than “small” ones, but are λ-times fewer. Thus, big banks issue and receive λ-times as many loans, and—by holding the same number of external asset classes as small banks in our baseline set-up—they hold λ-times as much of each single asset class, including interbank assets. We subsequently allow large banks to be more diversified (holding more asset classes) than smaller ones. In both set-ups, bank size and interconnectivity are correlated, in agreement with data (26). This formulation also yields “heavy-tailed” bank size and connectivity distributions, consistent with available evidence (27, 28). Note also that λ can be interpreted as a concentration parameter, as the proportion of assets in the system held by big banks, divided by the proportion of banks that are big, is easily shown to be 1/2 (1+ λ). Although this framework lends itself to a straightforward comparison of big and small banks, we explore an alternative bank-size distribution in the SI Text.

So far we have described the structure of the system and its interconnectedness. To describe its dynamics, we now explicitly link confidence effects to fundamental balance sheet characteristics such as capital and liquidity strength. We define the “system confidence” C and the “individual health” h_i of bank i as follows:

where, at a given time, A is the total value of all remaining assets in the system (at the current market price) as a proportion of its initial level (reflecting confidence in terms of solvency); E is the fraction of interbank loans not withdrawn (reflecting confidence in terms of liquidity); c_i is the capital of bank i as a proportion of its initial value, and m_i reflects the bank’s liquidity position, the fraction of its short-term liabilities that it can settle immediately, through its liquid and short-term assets (see Materials and Methods for details of how c_i and m_i are calculated). Note that C denotes the condition of the system, equally felt by all participants, given that A and E are taken to be common knowledge. For simplicity, Eq. 1 neglects the effect of maturity shortening on system confidence C. Results of an alternative formulation, aiming to incorporate this effect, are presented in the SI Text (see Fig. S2 A and B). In principle, this framework could also be extended to incorporate exogenous confidence shocks driven by a deterioration in market conditions or heightened volatility, perhaps as might be embodied in the CBOE Volatility Index (VIX); or uncertainty over A and E in Eq. 1.

We discussed above how liquidity hoarding could arise from a combination of factors, including a bank’s own health, that of its counterparties, and more broadly, confidence in the system as a whole. Terms in Eq. 1 can be used to capture all three factors. Specifically, we suppose simply that a long-term link from bank i to bank j (these being lender and borrower, respectively) is made short-term whenever

As described in Materials and Methods, this behavior raises m_i, thus allowing an individual bank to improve its own health. We also suppose that a short-term loan is withdrawn altogether (i.e., the corresponding “link” is removed from the network) whenever

Withdrawals can also propagate through the interbank network if borrowers need to recall their own interbank lending to meet their obligations, with banks experiencing liquidity default if they have insufficient liquidity to do so, as described in Materials and Methods.

The intuitive basis for the rules embodied in Eqs. 2 and 3 is as follows: when C = 1, there is no hoarding. With a perturbation to C, however, hoarding may potentially be triggered anywhere in the system either because of precautionary motives (driven by the bank’s own health, h_i, or counterparty concerns (driven by h_j), both causing and exacerbated by further deterioration in C. In Eq. 3, the exponent on the right-hand side ensures that withdrawals—being a last resort—happen only under more extreme stress than shortening of loan maturities. Although clearly stylized, these rules are broadly consistent both with notions of optimizing balance-sheet management by individual banks and with observed behavior during the crisis (24, 29) though as will become evident below, such behavior has clear adverse spillovers for other banks in the system. As illustrated in the simulations below, Eqs. 2 and 3 can also drive large fluctuations in balance sheets operating through changes in debt rather than equity, thus allowing the model to generate the procylicality in leverage that many financial institutions are seen to exhibit in the data (30).

Although liquidity hoarding acts on the interbank network, we also incorporate shocks transmitted through the system of external assets. As a bank fails, the sale of its assets to outside investors has the potential to drive down the price of those assets in the market, adversely affecting the capital position of other banks also holding these assets. Previous work (17, 19, 20, 31) has illustrated the potential for this process to push these additional banks to default, thus reinforcing the downward pressure on asset prices. The intensity of this process is related to market liquidity, or the ability of assets to be sold without significant price movements. In our framework, we directly link market liquidity to system confidence C, as detailed in Materials and Methods. This captures the idea that confidence effects—for example, as driven by social contagion (32)—are likely to cause market liquidity to deteriorate in times of crisis. Overall, then, asset price contagion is determined both by the amount of assets liquidated and by overall market conditions at that time.

Finally, we include the potential for cascades of capital default through the interbank network, as explored by other authors (19, 20, 31): should bank i undergo capital default, it cannot settle its debt in its entirety, and thus its creditors, in turn, lose value on their interbank lending, eroding their own assets and thus their own capital. Further details are given in Materials and Methods. In summary, our model combines channels for direct transmission between banks (that is, of asset contagion and counterparty default) with the indirect, system-wide effects represented by Eqs. 1–3. It also captures how the interplay of market and funding illiquidity can generate a downward spiral during crises (33).

Results

For our baseline simulations, we take λ = 24, giving a system with 8 large banks and 192 small ones. We assume that all banks have the same capital and liquidity ratios [broadly in line with observed median pre-crisis ratios (7)], with parameters given in Table S1. Clearly the results presented here are dependent on the type of shock and initial parameters chosen, so should be interpreted as an illustration of systemic effects only. To demonstrate the significance of liquidity hoarding and confidence effects, we apply a shock to the capital buffer of a randomly chosen, large “index bank” by setting the value of one of its external assets, also selected at random, to zero (other banks holding this asset are unaffected). As a measure of impact, we then record the loss in total assets across the system as a fraction of its initial value, thus counting large banks in proportion to their size. Fig. 1B shows mean results, both with and without liquidity hoarding. Counterparty credit risk and asset price contagion generate losses in both cases, but hoarding has a clear negative externality on the system: although representing defensive behavior on the part of individual banks to improve their own liquidity position, it leads to a decrease in E and thus C in Eq. 1. The effects of hoarding are also amplified by an adverse feedback with asset price contagion.

Considering the evolution of bank balance sheets is a useful approach for unpicking the relative contributions of different contagion channels illustrated in Fig. 1B, and comparing this to data. Fig. 1C illustrates recent empirical findings (30) that contractions in balance sheets tend to be associated primarily with debt (linked to the withdrawal of interbank lending), rather than with diminishing equity (e.g., from asset contagion or counterparty credit risk). Fig. 1D shows corresponding model results, illustrating behavior qualitatively consistent with Fig. 1C, because of the inclusion of confidence effects and liquidity hoarding. (Omitting hoarding, and withdrawal of lending in particular, yields the converse outcome in which the blue line has zero gradient, and the red accounts for all changes in bank assets.)

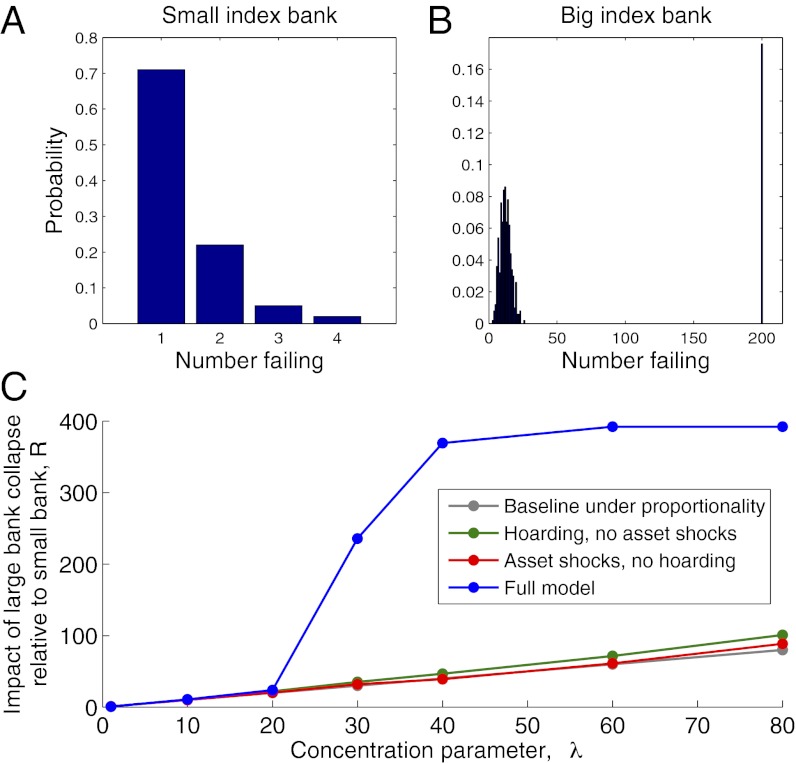
Next, we explore connections between idiosyncratic and systemic risk, in particular how the systemic importance of a given bank depends on its size. Here, we measure the importance of a given bank as the overall impact to the system, arising from its idiosyncratic failure: we choose an index bank of given size at random, and force it to default by setting its capital buffer to zero.* Without affecting any other part of the balance sheet, this initial condition ensures that, beyond the system’s exposures to the failing bank (through shared assets and counterparty links), there is no exogenous difference between the collapse of a small bank and a big one: in particular, although the initial capital loss is greater when a big index bank fails, this does not affect simulation outcomes because (for example) system confidence, C, depends on asset, and not capital, positions. Fig. 2 A and B shows frequency distributions for the resulting number of failed banks, comparing the cases of small and big index banks. The figure demonstrates that, although the failure of a small bank affects a relatively small group of other banks, the impact of a large bank’s collapse scales more than proportionately with size, entailing a nonzero probability of whole-system collapse.

Fig. 2.

Frequency distributions for numbers of banks failing in the baseline set-up (λ = 24), following the failure of a single index bank of given size. Comparing distributions from: (A) small index bank collapse and (B) big index bank collapse. (C) Comparing the effects of large bank collapse, relative to those of small bank collapse, as a function of λ. The upper (blue) curve reaches a plateau at the maximum possible value for a finite system with 200 banks. See main text for details.

To explore this systematically, as a measure of impact we write f_S for the mean fraction of total assets lost following collapse of a small index bank, and correspondingly f_B in the case of a large index bank. The ratio R = f_B/f_S thus gives some measure of the disparity between the impact of big and small bank collapse, and Fig. 2C plots this ratio for a range of λ. If the impact of bank collapse scales in proportion with bank size, we would expect R = λ, as represented by the bottom, gray line in Fig. 2C. In agreement with Fig. 2 A and B, however, the upper (blue) curve in Fig. 2C illustrates that R consistently exceeds proportional scaling. Intermediate curves show corresponding results in reduced models where either liquidity hoarding or asset price contagion are excluded: for the parameter ranges considered here and when the initiating shock is only a single bank failure, these channels in isolation are relatively limited in their capacity to precipitate system-wide collapse following the failure of a large index bank. (The strength of asset contagion, for example, grows too slowly here with declining C, to spread significantly beyond the index bank, whether big or small.) However, these results illustrate how, in combination, these channels mutually reinforce each other in a nonlinear way: for example, liquidity hoarding has a negative externality realized in a reduction in C, which in turn can exacerbate market illiquidity to intensify asset shocks, further pushing remaining banks nearer to collapse.

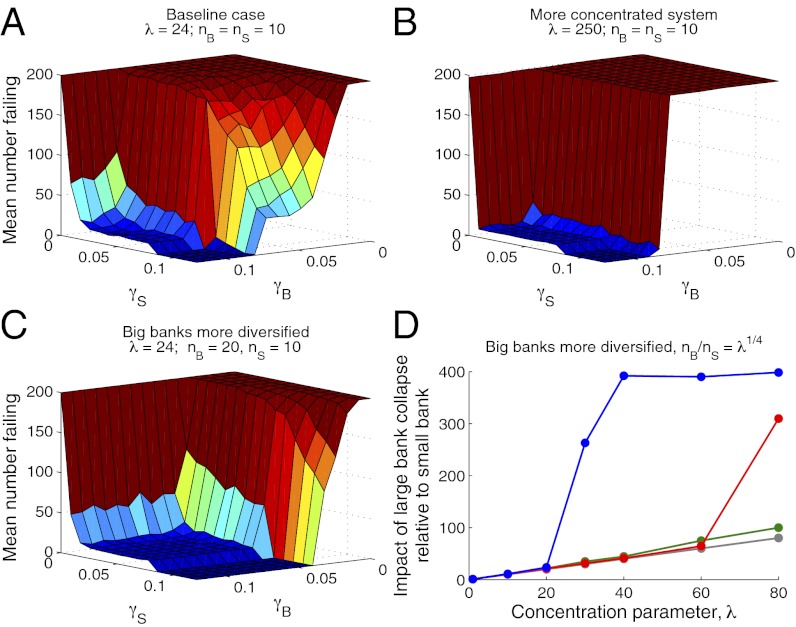
Next, how can loss-absorbing capital serve to mitigate the systemic effects of an asset shock? Taking λ = 24 once again, we now consider a scenario in which banks suffer losses because the value of a specific asset class, taken at random subject to being held by nine small banks and one large one, falls to zero. Fig. 3A illustrates results, exploring different capital ratios for small and big banks. Higher levels of capital promote system stability in general, but there is an asymmetry with respect to bank size. In particular, the diagonal in the x-y plane running from the foreground [at (0.15, 0.15)] to the hidden origin [at (0,0)] represents the case where all banks have the same capital ratio irrespective of size. Along this line, contagion may be contained as long as capital is sufficiently high. If not, however, there is a sharp transition in which much of the system collapses. A system in which larger banks have higher capital ratios (i.e., where the absolute size of the capital buffer scales more than proportionately with size) lies in the region to the left of this line, and conversely for the region to the right. A comparison of these regions illustrates the essential result that contagion is better mitigated by well-capitalized big banks than by well-capitalized small ones: arguably the converse of the pattern of capital ratios before the current financial crisis.

Fig. 3.

Exploring the relative importance of big and small bank capital ratios under different scenarios. Here, γ_B, γ_S represent capital ratios of big and small banks respectively. (A) λ = 24, giving 8 big banks and 192 small ones. (B) Big banks are 250-times the size of small ones, but 70-times less numerous, giving 3 big banks and 197 small ones. (C) λ = 24, with big banks having more diversified assets. Here n_B, n_S denote the number of asset classes held by big and small banks, respectively. (D) Repeating Fig. 2C, in the case where relative diversification (n_B/n_S) scales with λ as indicated. (See Materials and Methods for details.)

The differences between these regions, although broadly illustrative, will of course depend on concentration, λ, in the system. Recent data (34) indicate that in the first quarter of 2011, 79% of United States banking system assets were held by the largest 1.4% of banks. Translated into our simple framework, these percentages roughly correspond to a highly concentrated scenario in which the big banks are 250-times the size of small ones, while numbering 3 in a system of 200. Fig. 3B shows results of simulations adopting these parameters; although highly stylized, these illustrate nonetheless how increasing concentration serves to widen the disparity between the two regions described above. Fig. S3 presents results from an alternative model that seeks more faithfully to reproduce the actual distribution of United States bank sizes.

So far these results take big banks as simply proportionately scaled versions of small ones, and thus neglect the potential for larger banks to mitigate their own risk by having more diversified asset portfolios. Could such behavior also serve to limit the systemic importance of big banks? Returning to the case λ = 24, Fig. 3C allows big banks to hold twice as many asset classes as small banks, under the same asset-specific initiating shock as in Fig. 3A. This figure illustrates the risk-mitigating effects of diversification on the part of individual banks: large banks remain solvent with lower levels of capital than in Fig. 3A because they are less vulnerable to losses on any individual asset class. Importantly, however, the steepness of the surface is not mitigated by increasing diversification, and is in fact increased. This result arises because greater diversification increases the overall number of exposures through shared assets, exacerbating the role of asset contagion in system collapse. This effect is underscored by Fig. 3D, which repeats Fig. 2C but incorporates diversification (see Materials and Methods for details). For sufficiently concentrated systems, this illustrates the potential for asset contagion by itself (Fig. 3D, red curve) to cause system collapse following the failure of a large index bank, an outcome not apparent in Fig. 2C. Indeed, in the limit, perfectly diversified banks holding an equal fraction of all available assets will also be perfectly correlated (see also ref. 35). In addition, it is clear from these results that the systemic consequences of large bank collapse continue to scale more than proportionately with size.

Discussion

The systemic importance of large, well-connected banks has gained recognition in policy discussion, most notably in proposals from the Financial Stability Board and Bank for International Settlements (36) and the United Kingdom Independent Commission on Banking (ICB) (37), and in the so-called “Swiss finish” (38). However, policy recommendations for requirements concomitant with systemic importance (as reflected in metrics such as bank size and interconnectedness) have drawn some contention from the financial industry.

Our work aims to contribute to this discussion from a dynamic perspective, drawing together different channels of contagion into a unified framework, and incorporating system-level confidence effects. We demonstrate a key consequence of the resulting nonlinearities: the disproportionate importance of large, well-connected banks for system stability. Moreover, we show that although asset portfolio diversification may serve to limit the risk of failure of an individual bank, it does not mitigate the importance of that bank to systemic risk, and may indeed exacerbate it. Overall, these results illustrate the different approaches needed for regulation focused on idiosyncratic risk and that focused on a systemic level. While sound macroprudential regulation remains important for the former, the latter, relating to the so-called structural dimension of macroprudential policy (39), supports the notion of regulatory requirements concomitant with bank size, interconnectedness, or (more generally) systemic importance. Furthermore, such requirements may also have the beneficial side-effect of providing much-needed disincentives for financial institutions to become “too big to fail.”

Our findings echo familiar concepts in other complex systems. Like keystone species in ecosystems (5, 6), large banks can perform a stabilizing function as long as they remain healthy (Fig. 3). Conversely, their failure can adversely affect the entire system (Fig. 2). In the context of infectious diseases, the largest banks—by their connectivity—are comparable with “superspreaders” of infection (3, 4). There too, targeted intervention pays dividends: concentrating vaccination in the most well-connected or the most infectious individuals achieves disease elimination with lower coverage than is required in the case of random vaccination (3, 4). As we have explored here, however, balance-sheet linkages and pervasive confidence effects can play a distinctive role in financial systems, intensifying these dynamics (Fig. 2C).

As with any theoretical approach, there are important caveats to our model. First, our representation of confidence dynamics is a necessarily phenomenological approach for an important, yet poorly understood mechanism. A key empirical challenge for future work is to quantify these confidence processes, for example the relative weights of the different factors in Eqs. 1–3. Second, we assume individual and system fundamentals are fully transparent to all in the system. We thus potentially neglect the effects of uncertainty, for example over the actual health of counterparties or the extent of system-wide liquidity hoarding. Nonetheless, given that such uncertainty would intensify with deteriorating fundamentals and confidence, we would expect these effects to accentuate the dynamics we have explored. Third, although this work has concentrated on capital ratios, liquidity requirements are potentially also an important policy response. Future work may seek to treat these more systematically, for example by considering the impact of “haircut shocks,” which can exogenously generate liquidity shortfalls (1, 22). Similarly, effective resolution mechanisms could also enhance the resilience of the system to the risks posed by systemically important institutions. Finally, our work contributes toward the identification of indicators for the systemic importance of institutions by exploring the role of size and interconnectedness as correlated attributes. Future refinements of this approach may seek to examine more closely the separate effects of these two important factors.

To conclude, market confidence and unprecedented interconnectivity make for far-reaching, complex dynamics in modern financial systems. Any attempt at regulating on a systemic scale can, therefore, only benefit from a deeper understanding of these dynamics. Simple dynamic models, for all their limitations, can offer a valuable starting point for guiding such essential insights.

Materials and Methods

Network Details.

We represent the lending network as a directed graph, taking each individual loan to be the same size; we allow multiple loans in both directions between any given pair of banks, which are then aggregated to give the total bilateral exposure between pairs of banks. Small banks have an in- and out-degree (equivalently, numbers of interbank borrowing and lending links) drawn from a Poisson distribution with mean z_s (we typically take z_S = 5), and big banks have mean λz_S (to begin we take λ = 24). Thus, big banks have systematically higher levels of interbank exposure than small banks. Herein we assume a purely random structure for the interbank lending network; in the SI Text, however, we show results allowing for preferential lending between banks of different sizes (see Fig. S2 C and D).

For external assets, we define a sharing scheme by assuming that there exists a fixed number Γ of distinct asset classes. Of these classes, big banks hold n_B distinct asset classes each, in equal value, and small banks hold n_S asset classes each. In the baseline set-up we assume simply that n_B = n_S = 10. Moreover, every asset class is held in common by g banks (typically 10). This setup implies that Γ = (N_Bn_B + N_Sn_S)/g, where N_B, N_S are the number of big and small banks, respectively.

Developing the baseline set-up to allow for diversification (Fig. 3 C and D), we write: n_B = n_S λ^x, such that x = 0 recovers the baseline scenario (all banks being equally diversified), and x > 0 yields n_B > n_S so that larger banks are diversified over a wider range of asset classes than small banks (this also allows for the possibility that some asset classes are only held by large banks.). Note that, with other parameters fixed, specifying x fixes n_B and n_S. In particular, n_B, n_S are, respectively, increasing and decreasing functions of x. Where any of these calculations imply noninteger values for n_B, n_S, and so forth, we adopt the nearest noninteger value.

Health Expressions.

Hoarding is driven by health and confidence effects, as outlined above, with an alternative formulation presented in the SI Text. In particular, to calculate an individual bank’s liquidity position m_i in Eq. 1, we assume that both short-term interbank loans and liquid assets l_i are available on demand to meet funding outflows. An expression for m_i is thus:

where L_i^ST is the total value of the bank’s short-term interbank liabilities, A_i^ST is the total value of the bank’s short-term interbank assets, and l_i is the amount of liquid assets held by the bank.

Initiating Shocks.

With the system thus constructed, we initiate contagion by either: (i) an idiosyncratic capital shock applied to a single, randomly selected bank (Figs. 1 and 2), or (ii) an aggregate shock, simultaneously affecting the capital positions of all g banks holding a randomly selected (distressed) asset (Fig. 3). We then calculate the system-level confidence and individual healths, C and h_i, to propagate shocks in discrete time, as follows in the next section.

Shock Propagation and Bank Failure.

A bank fails for solvency reasons if shocks to its assets erode its capital buffer to zero. A bank may also fail for liquidity reasons: that is, having insufficient cash to meet immediate obligations. We describe here how both of these may occur with reference to the propagation of: (i) lending withdrawals (liquidity hoarding), (ii) asset price contagion, and (iii) counterparty defaults.

Lending withdrawals.

Banks may cut lending in the interbank market as a result of effects acting through C and h_i. When a bank withdraws lending from a debtor bank j, this amounts to the loss of short-term borrowing on the liability side of bank j. In such an event, bank j must settle these claims immediately and—if liquid assets l are insufficient—will raise cash by withdrawing a necessary and sufficient amount of its own, short-term lending, A_j^ST (asset side; Fig. 1A). If, however, even these measures are insufficient, bank j is assumed to undergo liquidity default, given the difficulty in realizing the full value of external assets quickly. Thus, for example, if m_j < 1 in Eq. 1, bank j is vulnerable to liquidity default if all of its interbank creditors withdraw funding simultaneously (a wholesale “bank run,” which would be prompted as h_j → 0 in Eq. 3).

Asset price contagion.

We assume that, by liquidating its external assets, a failing bank may depress the price of those assets in the market. This process causes the capital position of other banks holding these same assets to be eroded. Previous work (17, 19, 20, 31) has modeled this process by assuming that the price of asset i is diminished to a fraction exp(–αx_i) of its original value, where x_i is the proportion of that asset being sold by the failing bank, and α > 0 is a constant denoting systemic market illiquidity. Market illiquidity is also linked directly to confidence effects, writing α = 1 – C. Thus, confidence effects on asset prices are mild or negligible when C = 1, but become more severe as C declines. Note that for simplicity, we make the conservative assumption that the prices of different assets are uncorrelated, aside from their common dependence on C, and also suppose that assets are sold to outside investors rather than to other banks in the network.

Counterparty defaults.

Counterparty defaults propagate through the interbank network in the opposite direction to liquidity hoarding: that is, from borrower to lender. Suppose that a bank i suffers a shock of size S exceeding its capital γ_i, causing insolvency. Its z creditors will then suffer a loss on their lending to this bank: in particular, neglecting bankruptcy costs, we assume that they each receive an asset-side shock of size (S – γ_i)/z, bounded above by the total size of their exposure to the failing bank. This process erodes their own capital position and can cause cascades of capital defaults (31).