Abstract
Interaction between integral membrane proteins and the lipid-bilayer component of biological membranes is expected to mutually influence the proteins and the membrane. We present quantitative evidence of a manifestation of the lipid–protein interactions in liposomal membranes, reconstituted with actively pumping Na+,K+-ATPase, in terms of nonequilibrium shape fluctuations that contain a relaxation time, τ, which is robust and independent of the specific fluctuation modes of the membrane. In the case of pumping Na+-ions, analysis of the flicker-noise temporal correlation spectrum of the liposomes leads to τ ≃ 0.5 s, comparing favorably with an intrinsic reaction-cycle time of about 0.4 s from enzymology.
Keywords: sodium pump reconstituted in giant vesicles, vesicle fluctuation analysis, membrane dynamics
The interaction between integral proteins and lipids in biological membranes is a key to unraveling the molecular organization and the biological functioning of cell membranes (1, 2). Quantitative studies of lipid–protein interactions in membranes proceed most conveniently by means of well-defined biophysical model systems (3). Fundamental questions involve how lipids influence protein function, on the one hand, and how proteins and protein function impact on the properties of the lipids and membrane organization, on the other hand. Generally, biophysical model studies are performed under some kind of equilibrium conditions, and it is difficult to quantitatively read out membrane properties under the conditions of fully functional proteins. We present here a model study of a lipid–protein reconstitution in giant unilamellar vesicles (GUVs) from which it is possible not only to read out a well-defined nonequilibrium property, the dynamic flicker spectrum, of an active membrane but also to analyze this property in terms of a molecular time scale of an active protein, Na+,K+-ATPase, while pumping sodium ions.
It has been known for a long time that thermal noise establishes itself in equilibrium bending fluctuations and the characteristic flickering motion of erythrocytes (4), and it has been proposed that protein activity contributes to an enhancement of the flickering in erythrocytes (5–8) and lymphocytes (9). The physical picture is that protein activity, in particular the pumping of ions across the membrane, couples to the lipid-bilayer component of the membrane or the cytoskeleton and hence renormalizes the effective bending rigidity. Quantitative interpretation of experimental data for complex real biological membranes is, however, difficult and questionable (10). For this reason, model studies of so-called active membranes, being lipid bilayers with reconstituted active proteins, such as bacteriorhodopsin (11) and Ca2+-ATPase (12), have been advanced, showing, by use of micropipette aspiration techniques, that the membranes become softer when the proteins were active, an observation that was interpreted as due to enhanced bending fluctuations and flickering. We demonstrate here, in the case of active membranes with Na+,K+-ATPase, that this is indeed the case and that analysis of the flicker spectrum furthermore shows that this enhancement leads to a quantitative measure of the intrinsic reaction-cycle time scale of the enzyme. Hence we can relate a macroscopic membrane property out of thermal equilibrium to a microscopic molecular property of an enzymatic ion pump of crucial importance for membrane function.
Results
GUVs Reconstituted with Nonactive and Active Na+,K+-ATPase.
GUVs of diameters in the range of 17–50 μm, reconstituted with Na+,K+-ATPase, were formed from submicron-size proteoliposomes using a modified electroswelling technique applicable in a buffer under high salt conditions (13). The proteoliposomes were produced from small liposomes (∼100 nm) that were composed by either 1,2-dioleyl-sn-glycero-3-phosphocholine (DOPC)/cholesterol (Chol):60/40 (mol/mol) or DOPC/1,2-dioleyl-sn-glycero-3-phosphoserine (DOPS)/Chol:40/20/40 (molar ratio) with 3.4 mg/mL of lipids and 0.31 mg/mL or 0.39 mg/mL of enzyme. The Na+,K+-ATPase, prepared from the rectal gland of the shark Squalus acanthias (14), was functionally reconstituted into the liposomes as described earlier (15), and they were characterized with respect to protein density, symmetry of insertion, as well as hydrolytic activity. The turnover number in the absence of potassium ions (16) was determined for Na+-ATPase to be 221 ± 15 min−1 at 23 °C. We have estimated the molar lipid–protein ratio in the two types of GUVs to be 2,698 and 2,128, respectively. In the following we will restrict ourselves to the case of only sodium-ion pumping in which Na+ replaces extracellular K+ (17). The activity of the reconstituted enzymes can be controlled by the absence or presence of ATP in the buffer medium containing 30 mM NaCl, 200 mM sucrose, 30 mM histidine, and 2 mM MgCl2.
Shape Fluctuations and Flickering.
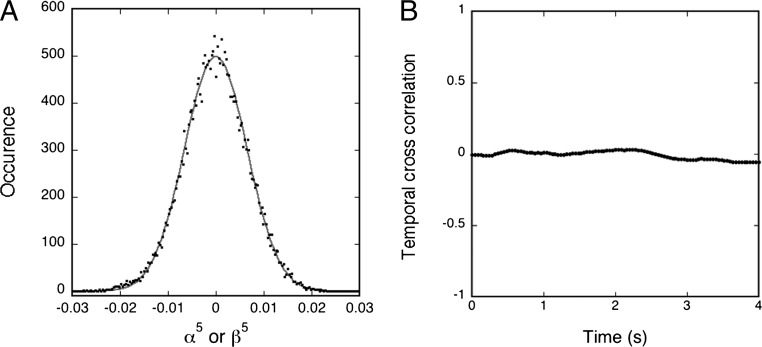
The GUVs were observed in a phase-contrast microscope at 20 °C, their 2D contour was recorded at 25 frames per second with a video integration time of 4 ms, and the flickering was analyzed by statistical methods involving both Fourier and Legendre polynomial decompositions of the angular correlation function developed for equilibrium fluctuating liposomes (18). This analysis takes into account that the mechanical properties of the actual liposome monitored will depend on its composition and tension. The time-dependent angular autocorrelation function is decomposed into a cosine representation, and the amplitudes of the corresponding modes can be correlated with the Fourier amplitudes of the contour fluctuations (18). For each set of conditions, a number of independent liposomes, 7–22, were analyzed and the same procedures were applied for both nonactive membranes (without ATP) and active membranes (with ATP). Somewhat surprisingly it turns out that the distributions of the fluctuations in the active case are effectively Gaussian with no mode correlation (as in the nonactive case) as shown in Fig. 1. However, the amplitudes are markedly enhanced. The analysis shows that upon activation, the bending modulus diminished in an amount of 7–8 kBT compared with the nonactive case (Table 1, systems 1 and 2). This is consistent with the softening found previously from micropipette aspiration techniques applied to active membranes reconstituted with bacteriorhodopsin (11) and Ca2+-ATPase (12). For control it has been verified that the presence of ATP in nonactive membranes has only a marginal influence on the bending modulus (Table 1, system 3).
Fig. 1.
For a proteoGUV of DOPC/DOPS/Chol/ATPase, a radius of 12.97 μm in the presence of 1 mM of ATP is shown: (A) Experimental distribution of the Fourier amplitudes of the contour fluctuations; α5 or β5. (B) Plot of the normalized temporal cross-correlation function between modes 5 and 6. Mode 5 has been chosen randomly among the midrange modes (4–10), which have good statistics and are not limited by the video integration time. The solid curve in A is the best fit of the data to a Gaussian.
Table 1.
Influence of the presence of ATP (1 mM) on the bending rigidities for three different systems
| System | ATP | Bending rigidity (kBT) |
| (1) DOPC/Chol/ATPase | No | 26.40 ± 0.75 (16) |
| Yes | 19.45 ± 1.02 (8) | |
| (2) DOPC/DOPS/Chol/ATPase | No | 28.88 ± 0.97 (10) |
| Yes | 20.40 ± 0.60 (17) | |
| (3) DOPC/Chol | No | 22.93 ± 0.60 (22) |
| Yes | 23.80 ± 0.63 (10) |
The number of vesicles recorded for each system is indicated in parentheses and the error represents the SD among the population of vesicles.
The mode decomposition of the angular correlation function filters out the contributions from the lateral length scales πR/n. Our analysis in Fig. 1A shows that the average of the amplitudes of these modes are well described by Gaussian fluctuations of Helfrich’s functional around a spherical configuration for active as well as nonactive membranes, although the bending rigidity κ is varying. Therefore, we expect the spatial correlation function to have the same form in the two cases, with an effective κ for the active membrane. Although the spatial correlations are similar for the active and nonactive membrane, the temporal correlations are vastly different in the two cases, so we focus on these in the following section.
Temporal Correlations and Their Time Scales.
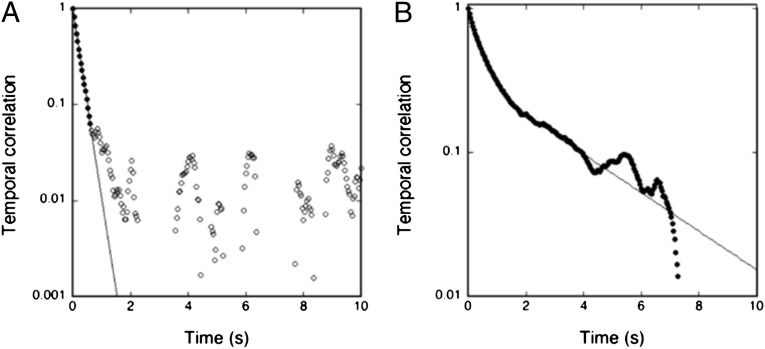
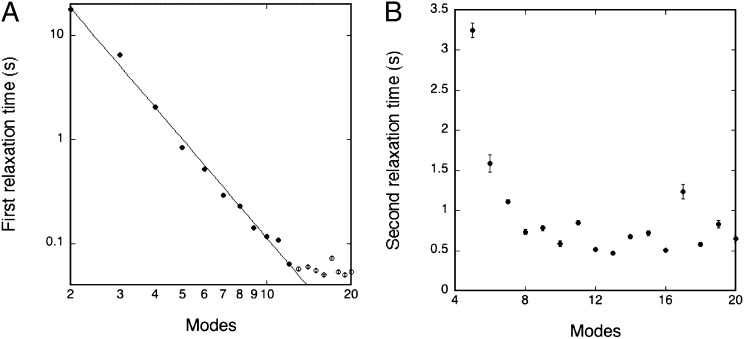
In equilibrium, the temporal autocorrelation function of the amplitudes for a given mode n is predicted to exhibit a monoexponential decay (19) characterized by a relaxation time τ1. This is indeed found to be the case, as illustrated in Fig. 2A, at early times (≲ 1 s). At later times, the instrumental limitations prevent the observation of a relaxation time. The relaxation time τ1 for the nonactive case is found, as expected, to depend on the mode number and to scale as τ1 ∼ n–3 (19). Turning then to the active case (compare with Fig. 2B), it is found that the temporal autocorrelations are considerably stronger than in equilibrium and they can be observed at much later times than in the nonactive case. However, the decay function is more complex but rather well described by a double exponential, as illustrated in Fig. 2B—i.e., by two relaxation times τ1 and τ2. Similar to the nonactive case, the first relaxation time is strongly dependent on mode number, and it is found that in the early-time regime it is effectively described by τ1 ∼ n–3, as shown in Fig. 3A, for modes in the range of 2–12 (higher modes are unresolved due to instrumental limitations)—i.e., the very same power-law decay as in the nonactive case. In contrast, the second relaxation time is after an initial decay found to be independent of mode number beyond n ≳ 8 (for lower modes, τ2 is too close to τ1 to be resolved). Hence, we have found that the system of active membranes is characterized by a specific time constant that is robust and independent of mode number. Furthermore we have found that this time constant is independent of vesicle size and vesicle tension (Table 2). As shown in Fig. 3B, the corresponding time scale is τ2 ≃ 0.5 s. The robustness of this number suggests that it is related to an intrinsic property of the functioning enzyme, as we shall discuss below.
Fig. 2.
Normalized temporal correlation function for mode n = 5 for proteoGUVs of DOPC/DOPS/Chol/ATPase of similar reduced membrane tension. (A) Nonactive membranes in the absence of ATP conforming to a monoexponential form of the short-time decay (solid line). (B) Active membranes in the presence of ATP (1 mM) conforming to a double-exponential form for the full duration of the experiment. The double-exponential fit is illustrated by the solid line. The corresponding decay constants (relaxation times) for the first and second exponentials are depicted in Fig. 3.
Fig. 3.
Relaxation time as a function of mode number, n, for active membranes consisting of a proteoGUV of DOPC/DOPS/Chol/ATPase in the presence of ATP, (compare with Fig. 2B). (A) The initial relaxation time scales as τ1 ∼ n–3.1 for modes in the range of 2–12. (B) Second relaxation time, τ2, is found to be independent of mode number for n ≳ 8. The error bars are calculated from the double-exponential fit for each exponential parameter and subsequently converted to an error bar for each relaxation time.
Table 2.
Influence of the vesicle size and vesicle tension on the relaxation time τ2 for system 1 (DOPC/Chol/ATPase) and system 2 (DOPC/DOPS/Chol/ATPase)
| System | τ2 (s) | Reduced tension | Radius R (μm) | Modes |
| (1) | 0.39 ± 0.09 | −9.12 | 14.23 | 4–20 |
| 0.63 ± 0.05 | −3.62 | 10.63 | 7–15 | |
| 0.50 ± 0.07 | −2.84 | 17.28 | 8–20 | |
| 0.66 ± 0.05 | 2.84 | 10.02 | 9–18 | |
| 0.95 ± 0.08 | 7.92 | 17.76 | 7–16 | |
| (2) | 0.70 ± 0.06 | −4.64 | 12.97 | 8–20 |
| 0.46 ± 0.04 | −3.26 | 8.13 | 6–19 | |
| 0.43 ± 0.05 | 2.74 | 12.46 | 6–20 | |
| 0.43 ± 0.07 | 7.71 | 11.52 | 6–20 |
The values of τ2 given in this table are averages of τ2 data extracted from the temporal correlation function fit for the modes indicated in the fifth column. The reduced tension is defined as σred = σR2/κ, where R is the vesicle radius and σ is a small effective tension set by the entrapped volume of the vesicle. σred is a measure of how deflated the vesicle is.
Discussion
In this article we have demonstrated that the flickering of active membranes reconstituted with functional proteins, viz. Na+,K+-ATPase, can be analyzed by techniques well known from equilibrium systems. In particular we have found that the temporal autocorrelations of the shape fluctuations are strongly correlated and can be observed on much longer times than is the case for equilibrium, nonactive membranes. The relaxation behavior is well described by a double exponential. The short-time decay is effectively described by τ1 ∼ n–3 for modes in the range of 2–12—i.e., the very same power-law decay as in the nonactive case and as predicted by the classical Milner-Safran theory (19). This observation is in accordance with our finding that it is possible to obtain the bending modulus for the fluctuating GUVs in the case of active membranes in the same way as for the nonactive, equilibrium case, and that a Gaussian distribution effectively describes the modes in both cases. We have also found that there is no correlation of crossing modes for neither the nonactive nor the active membranes (Fig. 1B).
The most conspicuous finding of our work on active membranes is a robust relaxation time, τ2 ≃ 0.5 s, describing the long-time behavior in a way that is independent of mode number and details of the individual GUVs. This finding strongly suggests that this time scale is a characteristics of the active protein—i.e., the sodium-pumping Na+,K+-ATPase. Enzymatic studies of Na+-ATPase activity (16) have shown that the maximum turnover number of this pump activity (the inverse intrinsic reaction-cycle time scale) is about 0.9 s−1 at 10 °C and 3.7 s−1 at 23 °C, leading by interpolation to an estimate of about 3 s−1 at 20 °C, corresponding to a characteristic time scale of 0.3–0.4 s The good correspondence between this number and our finding of 0.5 s from analysis of the flicker spectrum suggests that not only does the actively functioning protein manifest the lipid-protein interactions in a perturbation in the membrane physical properties but also the quantitation of this perturbation allows a readout of a fundamental intrinsic property of the enzyme. The relaxation time, corresponding to the turnover number (also know as the molecular activity), reflects the slowest step in the enzymatic reaction cycle, which for Na+-ATPase is the E2P dephosphorylation step (20). It is possible that this step is accompanied by conformational and shape changes that directly couple to the lipid bilayer matrix (21).
The finding in the present study, that the intense structural rearrangements in the enzyme taking place during Na+,K+-ATPase turnover as shown by structural studies of ion-pumps (22) are transmitted to the lipid-membrane matrix by a mechanical coupling, may open up possibilities for studying directly lipid–protein interactions associated with important regulatory and signaling properties of ion-pumps. Examples of discovered properties of Na+,K+-ATPase regulation, where the application of such direct lipid–protein interaction studies may also prove useful, include (i) the putative role of Na+,K+-ATPase in cell signaling (23, 24) and (ii) oxidative regulation and signaling by Na+,K+-ATPase activity (25–27). Furthermore, because our work has demonstrated a route between measurement of a macroscopic membrane property, viz. the flicker spectrum, on the one hand and a microscopic, molecular property, viz. the molecular activity or reaction-cycle turnover number, on the other hand, it now becomes possible to test and identify potent anticancer agents directed toward the Na+,K+-ATPase (28). Furthemore, our findings hold a promise for the application of a similar approach to other membrane proteins for which catalytic reaction cycle times have not yet been determined.
Materials and Methods
Materials.
DOPC (1,2-dioleyl-sn-glycero-3-phosphocholine), DOPS (1,2-dioleyl-sn-glycero-3-phosphoserine), and cholesterol were purchased from Avanti Polar Lipids and used without further purification. NaCl (sodium chloride, purity > 99.5%) and sucrose (purity > 98%) were from Fluka, whereas l-Histidine (purity > 99%) and MgCl2 (magnesium dichloride, purity > 99%) were from Sigma-Aldrich. Ultra pure MilliQ water (18.3 MΩcm) was used in all steps involving water.
Preparation of Proteoliposomes.
Membrane-bound Na+,K+-ATPase from rectal glands of the shark Squalus acanthias was prepared essentially as described in (14). This involved isolation of well-defined membrane fragments by differential centrifugation, following treatment of microsomes with low concentrations of deoxycholic acid (∼0.15%), which permeabilized the microsomes and removed loosely attached proteins. The specific hydrolytic activity was 30–33 U/mg of protein (1 U = 1 μmol Pi/min) at 37 °C at standard conditions according to Ottolenghi (29). The protein content was determined according to Lowry et al. (30) using bovine serum albumin as the standard.
Functional reconstitution of shark Na+,K+-ATPase was achieved as described in (15, 31). Cosolubilization of shark Na+,K+-ATPase membranes and the lipids of choice in 130 mM NaCl, 4 mM MgCl2, and 30 mM histidine, pH 7.0, at a lipid–protein weight ratio estimated to give a final lipid-to-protein ratio of 10 was obtained using the nonionic detergent C12E8 (ethylene glycol dodecyl monoether, at 4 mg/mg protein). The detergent was subsequently removed by addition of hydrophobic Bio-Beads, and liposomes containing reconstituted Na+,K+-ATPase spontaneously formed. Careful control during enzyme solubilization ensured that reconstitution took place without loss of catalytic activity or ion-transport capacity. The reconstitution of Na+,K+-ATPase by cosolubilization of protein and lipids in the detergent C12E8 followed by detergent elimination using Bio-Beads led to an asymmetric incorporation of fully active Na+,K+-ATPase (15).
The proteoliposomes were characterized morphologically and functionally. This included the determination of (i) the pump density through protein determination of reconstituted ATPase performed according to Peterson modification (32) of the Lowry method; (ii) the symmetry of protein insertion—i.e., rightside-out (r/o), inside-out (i/o), or nonoriented (n-o), where the fraction of enzyme reconstituted as i/o was determined using functional tests as described in detail in (15, 31); and (iii) the maximum hydrolytic activity of reconstituted i/o-oriented Na+,K+-ATPase measured using [32P]-ATP as described in (33). The protein orientation after reconstitution was determined taking advantage of the sidedness of the Na,K-ATPase including a high cytoplasmic Na+-affinity, a high extracellular K+-affinity, and an extracellular ouabain binding site. Essentially, the maximum hydrolytic Na,K-ATPase activity of i/o-oriented enzyme was measured by first equilibrating the proteoliposomes with 20 mM KCl using the K+-ionophore nigericin (7 μM) to ensure optimal K+ concentration at the extracellular face (inside) of i/o enzyme. Then, the proteoliposomes were incubated with 5 mM Mg2+, 1 mM Pi, and 1 mM ouabain to inhibit enzyme with the extracellular side exposed, as the hydrophilic ouabain cannot penetrate the proteoliposome. Finally, the hydrolytic activity was determined in a test solution of 130 mM NaCl, 20 mM KCl, 4 mM MgCl2, and 3 mM ATP. If the same measurement is performed but now without ouabain, the nonoriented enzyme is activated too. The measured activities are then compared with the maximum activity of the total amount of reconstituted enzyme measured in proteoliposomes reopened by addition of 0.35 mg C12E8/mg lipid, giving the relative amount of i/o-oriented enzyme (activity in the presence of ouabain) and of i/o plus n-o-oriented enzyme (activity in the absence of ouabain). The reconstitution described results in an asymmetric incorporation with about 15% of the enzyme oriented inside-out.
The proteoliposomes were composed by either DOPC/Chol:60/40 (molar ratio) or DOPC/DOPS/Chol:40/20/20 (molar ratio) with 3.4 mg/mL of lipids and 0.31 or 0.39 mg/mL of enzymes. These proteoliposomes were unilamellar and large with a diameter of about 100 nm, as determined from freeze-fracture electron microscopy pictures and quasi-elastic laser light-scattering (34). Functional analysis showed that about 45% of the enzymes were incorporated with an orientation as in the cell (r/o), whereas only around 15% had the opposite orientation (i/o). The rest was incorporated in a way, where it was accessible to both ATP (intracellular side) and ouabain (extracellular side). The Na+,K+-ATPase activity at 23 °C of Na+,K+-ATPase reconstituted in liposomes was estimated to be 564 ± 21 μmol/mg/h, whereas the Na+-ATPase activity, where Na+ substitutes for extracellular K+ (17, 35), was 92 ± 9.7 μmol/mg/h (16). The turnover number for Na+-ATPase was thus found to be equal to 221 ± 15 min−1, knowing that the number of phosphorylation sites was 6.9 ± 0.6 nmols/mg of protein (16).
Preparation of GUVs.
The proteoGUVs were formed by the electroswelling technique, which has been presented in (13) with some modifications, here to obtain a functional insertion of the sodium pump in the lipid bilayer. The preformed proteoliposomes were diluted to 1.1 mg/mL of lipids, and droplets of 2 μL of this suspension were carefully deposited on platinum electrodes. The mixed lipid film was then partially dried overnight in a desiccator under saturated vapor pressure of a saturated NaCl solution, as suggested in (36). This step was crucial, as a complete drying of the mixed lipid film would denature the enzyme. The electroswelling of the mixed film was done in a buffer composed of 30 mM NaCl, 2 mM MgCl2, 200 mM sucrose, and 30 mM histidine at pH 7. The parameters of the electric field were adjusted to the conditions of the particular system, specifically the presence of Na+,K+-ATPase and the complex composition of the buffer solution. It was necessary to apply a high electric amplitude field of about 1,000 V/m for the swelling period that lasted longer than for simple GUVs, namely up to 2–3 h, to obtain vesicles of proper sizes, whereas the frequency of the electric field was fixed at 50 Hz and 5 Hz for the so-called “swelling period” and “rebounding period,” respectively (13).
If we assume that the ratio lipid–pump measured in the proteoliposomes was maintained in the proteoGUVs, we obtained for DOPC/Chol and DOPC/DOPS/Chol lipid–pump weight ratios equal to 10.97 and 8.72, respectively—i.e., lipid–pump molar ratios of 2,698 and 2,128.
Video Recordings.
Vesicles, after having been detached from the electrodes at the end of the electroformation protocol, were observed either directly in the electroformation cuvettete where no ATP was added or in an ATP-containing chamber (1 mM of ATP) to which the GUV suspension was transferred. In both cases, a temperature-controlled chamber holder (T = 20 °C) was used to maintain constant temperature. The giant vesicles were visualized using a phase contrast microscope (Axiovert S100 Zeiss), equipped with a 40/0.60× objective (440865 LD Achroplan). The vesicle 2D contour in the focal plane of the objective was thus obtained, and a CCD Camera (SONY SSC-DC50AP) was used to record a series of 10,000–45,000 pictures at a rate of 25 frames per second with a video integration time of 4 ms.
Numerical Analysis of the Flicker Spectrum.
The video image sequences of the GUV thermal fluctuations were analyzed using custom-made software to perform contour extraction, contour cleaning, and the fluctuation-analysis procedures presented in (18, 37). Because a complex dependence of the membrane properties on the vesicle composition was expected, a precise analysis of the statistical distribution of vesicle contours based on a mode decomposition of the angular correlation function introduced in (18) was performed. Static analysis of the flicker spectrum led to the determination of the bending modulus by analysis of the distributions of the amplitudes of decomposition of the angular correlation function in the cosine basis. For a given system, the bending elastic modulus represented an average of measurements among a population of 7–22 vesicles, whose diameters were between 17 and 50 μm. We wish to stress that the same standard procedure presented in (18) has been applied to obtain bending moduli for both passive and active membranes. Dynamic analysis of the flicker spectrum of the amplitudes of decomposition in the Legendre polynomial basis enabled us to determine the temporal correlation functions for a given mode (19). Relaxation times were extracted from the fitting of these temporal correlation functions.
Acknowledgments
MEMPHYS–Center for Biomembrane Physics is supported by the Danish National Research Foundation. This work was supported in part by a grant from the Danish Research Councils (11-107269), the Danish Medical Research Foundation, and the Danish Agency for Science Technology and Innovation.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
References
- 1.Engelman DM. Membranes are more mosaic than fluid. Nature. 2005;438(7068):578–580. doi: 10.1038/nature04394. [DOI] [PubMed] [Google Scholar]
- 2.Lingwood D, Simons K. Lipid rafts as a membrane-organizing principle. Science. 2010;327(5961):46–50. doi: 10.1126/science.1174621. [DOI] [PubMed] [Google Scholar]
- 3.Mouritsen OG. Model answers to lipid membrane questions. Cold Spring Harb Perspect Biol. 2011;3(9):a004622. doi: 10.1101/cshperspect.a004622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brochard F, Lennon J. Frequency spectrum of the flicker phenomenon in erythrocytes. J Phys. 1975;36:1035–1047. [Google Scholar]
- 5.Sheetz MP, Singer SJ. On the mechanism of ATP-induced shape changes in human erythrocyte membranes. I. The role of the spectrin complex. J Cell Biol. 1977;73(3):638–646. doi: 10.1083/jcb.73.3.638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levin S, Korenstein R. Membrane fluctuations in erythrocytes are linked to MgATP-dependent dynamic assembly of the membrane skeleton. Biophys J. 1991;60(3):733–737. doi: 10.1016/S0006-3495(91)82104-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tuvia S, Levin S, Bitler A, Korenstein R. Mechanical fluctuations of the membrane-skeleton are dependent on F-actin ATPase in human erythrocytes. J Cell Biol. 1998;141(7):1551–1561. doi: 10.1083/jcb.141.7.1551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Park Y, et al. Metabolic remodeling of the human red blood cell membrane. Proc Natl Acad Sci USA. 2010;107(4):1289–1294. doi: 10.1073/pnas.0910785107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mittelman L, Levin S, Korenstein R. Fast cell membrane displacements in B lymphocytes. Modulation by dihydrocytochalasin B and colchicine. FEBS Lett. 1991;293(1–2):207–210. doi: 10.1016/0014-5793(91)81188-e. [DOI] [PubMed] [Google Scholar]
- 10.Evans J, Gratzer W, Mohandas N, Parker K, Sleep J. Fluctuations of the red blood cell membrane: Relation to mechanical properties and lack of ATP dependence. Biophys J. 2008;94(10):4134–4144. doi: 10.1529/biophysj.107.117952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Manneville J, Bassereau P, Levy D, Prost J. Activity of transmembrane proteins induces magnification of shape fluctuations of lipid membranes. Phys Rev Lett. 1999;82:4356–4359. [Google Scholar]
- 12.Girard P, Prost J, Bassereau P. Passive or active fluctuations in membranes containing proteins. Phys Rev Lett. 2005;94(8):088102. doi: 10.1103/PhysRevLett.94.088102. [DOI] [PubMed] [Google Scholar]
- 13.Pott T, Bouvrais H, Méléard P. Giant unilamellar vesicle formation under physiologically relevant conditions. Chem Phys Lipids. 2008;154(2):115–119. doi: 10.1016/j.chemphyslip.2008.03.008. [DOI] [PubMed] [Google Scholar]
- 14.Skou JC, Esmann M. Preparation of membrane Na+,K+-ATPase from rectal glands of Squalus acanthias. Methods Enzymol. 1988;156:43–46. doi: 10.1016/0076-6879(88)56006-8. [DOI] [PubMed] [Google Scholar]
- 15.Cornelius F. Incorporation of C12E8-solubilized Na+,K+-ATPase into liposomes: Determination of sidedness and orientation. Methods Enzymol. 1988;156:156–167. doi: 10.1016/0076-6879(88)56018-4. [DOI] [PubMed] [Google Scholar]
- 16.Cornelius F. Phosphorylation/dephosphorylation of reconstituted shark Na+,K(+)-ATPase: One phosphorylation site per α β protomer. Biochim Biophys Acta. 1995;1235(2):197–204. doi: 10.1016/0005-2736(95)80005-z. [DOI] [PubMed] [Google Scholar]
- 17.Cornelius F, Skou JC. Na+-Na+ exchange mediated by (Na+ + K+)-ATPase reconstituted into liposomes. Evaluation of pump stoichiometry and response to ATP and ADP. Biochim Biophys Acta. 1985;818(2):211–221. doi: 10.1016/0005-2736(85)90572-3. [DOI] [PubMed] [Google Scholar]
- 18.Méléard P, Pott T, Bouvrais H, Ipsen JH. Advantages of statistical analysis of giant vesicle flickering for bending elasticity measurements. Eur Phys J E Soft Matter. 2011;34(10):116. doi: 10.1140/epje/i2011-11116-6. [DOI] [PubMed] [Google Scholar]
- 19.Milner ST, Safran SA. Dynamical fluctuations of droplet microemulsions and vesicles. Phys Rev A. 1987;36(9):4371–4379. doi: 10.1103/physreva.36.4371. [DOI] [PubMed] [Google Scholar]
- 20.Cornelius F, Fedosova NU, Klodos I. E2P phosphoforms of Na,K-ATPase. II. Interaction of substrate and cation-binding sites in Pi phosphorylation of Na,K-ATPase. Biochemistry. 1998;37(47):16686–16696. doi: 10.1021/bi981571v. [DOI] [PubMed] [Google Scholar]
- 21.Thøgersen L, Nissen P. Flexible P-type ATPases interacting with the membrane. Curr Opin Struct Biol. 2012;22(4):491–499. doi: 10.1016/j.sbi.2012.05.009. [DOI] [PubMed] [Google Scholar]
- 22.Toyoshima C. Structural aspects of ion pumping by Ca2+-ATPase of sarcoplasmic reticulum. Arch Biochem Biophys. 2008;476(1):3–11. doi: 10.1016/j.abb.2008.04.017. [DOI] [PubMed] [Google Scholar]
- 23.Xie Z, Askari A. Na(+)/K(+)-ATPase as a signal transducer. Eur J Biochem. 2002;269(10):2434–2439. doi: 10.1046/j.1432-1033.2002.02910.x. [DOI] [PubMed] [Google Scholar]
- 24.Mijatovic T, Ingrassia L, Facchini V, Kiss R. Na+/K+-ATPase alpha subunits as new targets in anticancer therapy. Expert Opin Ther Targets. 2008;12(11):1403–1417. doi: 10.1517/14728222.12.11.1403. [DOI] [PubMed] [Google Scholar]
- 25.Figtree GA, et al. Reversible oxidative modification: A key mechanism of Na+-K+ pump regulation. Circ Res. 2009;105(2):185–193. doi: 10.1161/CIRCRESAHA.109.199547. [DOI] [PubMed] [Google Scholar]
- 26.Shinoda T, Ogawa H, Cornelius F, Toyoshima C. Crystal structure of the sodium-potassium pump at 2.4 A resolution. Nature. 2009;459(7245):446–450. doi: 10.1038/nature07939. [DOI] [PubMed] [Google Scholar]
- 27.Liu CC, et al. Susceptibility of β1 Na+-K+ pump subunit to glutathionylation and oxidative inhibition depends on conformational state of pump. J Biol Chem. 2012;287(15):12353–12364. doi: 10.1074/jbc.M112.340893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mijatovic T, Dufrasne F, Kiss R. Cardiotonic steroids-mediated targeting of the Na(+)/K(+)-ATPase to combat chemoresistant cancers. Curr Med Chem. 2012;19(5):627–646. doi: 10.2174/092986712798992075. [DOI] [PubMed] [Google Scholar]
- 29.Ottolenghi P. The reversible delipidation of a solubilized sodium-plus-potassium ion-dependent adenosine triphosphatase from the salt gland of the spiny dogfish. Biochem J. 1975;151(1):61–66. doi: 10.1042/bj1510061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lowry OH, Rosebrough NJ, Farr AL, Randall RJ. Protein measurement with the Folin phenol reagent. J Biol Chem. 1951;193(1):265–275. [PubMed] [Google Scholar]
- 31.Cornelius F, Skou JC. Reconstitution of (Na+ + K+)-ATPase into phospholipid vesicles with full recovery of its specific activity. Biochim Biophys Acta. 1984;772(3):357–373. doi: 10.1016/0005-2736(84)90153-6. [DOI] [PubMed] [Google Scholar]
- 32.Peterson GL. A simplification of the protein assay method of Lowry et al. which is more generally applicable. Anal Biochem. 1977;83(2):346–356. doi: 10.1016/0003-2697(77)90043-4. [DOI] [PubMed] [Google Scholar]
- 33.Ernster L, Lindberg O. Determination of organic phosphorus compounds by phosphate analysis. Methods Biochem Anal. 1956;3:1–22. doi: 10.1002/9780470110195.ch1. [DOI] [PubMed] [Google Scholar]
- 34.Cornelius F, Møller JV. 1995. Liposomes in reconstitution of ion-pumps. Handbook of Non-medical Applications of Liposomes, Vol II, eds Lasic D.D. and Barenholz Y. (CRC Press, Boca Raton, FL), pp 219–243.
- 35.Lee KH, Blostein R. Red cell sodium fluxes catalysed by the sodium pump in the absence of K+ and ADP. Nature. 1980;285(5763):338–339. doi: 10.1038/285338a0. [DOI] [PubMed] [Google Scholar]
- 36.Girard P, et al. A new method for the reconstitution of membrane proteins into giant unilamellar vesicles. Biophys J. 2004;87(1):419–429. doi: 10.1529/biophysj.104.040360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mitov MD, Faucon JF, Méléard P, Bothorel P. Thermal fluctuations of membranes. Adv Supramol Chem. 1992;2:93–139. [Google Scholar]