Skip to main content
PMC home page
British Journal of Clinical Pharmacology logoLink to British Journal of Clinical Pharmacology
. 2012 Mar 1;74(5):815–823. doi: 10.1111/j.1365-2125.2012.04260.x

Population PK/PD analysis of metformin using the signal transduction model

Jung-woo Chae 1, In-hwan Baek 2, Byung-yo Lee 1, Seong-kwon Cho 3, Kwang-il Kwon 1
PMCID: PMC3495146  PMID: 22380769

Abstract

AIMS

To develop a population pharmacokinetic (PK) and pharmacodynamic (PD) model for metformin (500 mg) using the signal transduction model in healthy humans and to predict the PK/PD profile in patients with type 2 diabetes.

METHODS

Following the oral administration of 500 mg metformin to healthy humans, plasma concentrations of metformin were measured using LC-MS/MS. A sequential modelling approach using NONMEM VI was used to facilitate data analysis. Monte Carlo simulation was performed to predict the antihyperglycaemic effect in patients with type 2 diabetes.

RESULTS

Forty-two healthy humans were included in the study. Population mean estimates (relative standard error, RSE) of apparent clearance, apparent volume of distribution and the absorption rate constant were 52.6 l h−1 (4.18%), 113 l (56.6%) and 0.41 h−1, respectively. Covariate analyses revealed that creatinine clearance (CLCR) significantly influenced metformin: CL/F= 52.6 × (CLcr/106.5)0.782. The signal transduction model was applied to describe the antihyperglycaemic effect of metformin. The population means for efficacy, potency, transit time and the Hill coefficient were estimated to be 19.8 (3.17%), 3.68 µg ml−1 (3.89%), 0.5 h (2.89%) and 0.547 (9.05%), respectively. The developed model was used to predict the antihyperglycaemic effect in patients with type 2 diabetes. The predicted plasma glucose concentration value was similar to previous values.

CONCLUSIONS

The population signal transduction model was developed and evaluated for metformin use in healthy volunteers. Model evaluation by non-parametric bootstrap analysis suggested that the proposed model was robust and parameter values were estimated with good precision.

Keywords: antihyperglycaemic effect, metformin, PK/PD, signal transduction model, simulation

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

  • Metformin, a biguanide glucose lowering agent, is commonly used to manage type 2 diabetes.

  • The molecular mechanisms of metformin have not been fully identified, but turnover of biomarkers such as glucose and signalling pathways or translocation of glucose transporters are closely related to the glucose-lowering effects of metformin.

  • The PK/PD of metformin have been investigated in healthy humans and patients with type 2 diabetes mellitus and modelling has been performed using an indirect response model.

WHAT THIS STUDY ADDS

  • The purpose of this investigation was to develop a population PK/PD model for metformin using a signal transduction model in healthy humans and predict the PK/PD profile in patients with type 2 diabetes.

  • The aim was to compare a previous model (a biophase model) with the signal transduction model, and use a more appropriate model to follow the actions of metformin.

  • Additionally, our developed model was appropriate to predict the time course of plasma metformin and fasting plasma glucose (FPG) concentrations in patients with type 2 diabetes.

  • To our knowledge, this is the first published population PK/PD analysis using the signal transduction model for metformin.

Introduction

Metformin, a biguanide glucose lowering agent, is commonly used to manage type 2 diabetes [1]. Metformin is used as monotherapy, as an adjunct to diet for managing type 2 diabetes mellitus in patients whose hyperglycaemia cannot be controlled by diet alone [2]. Metformin may also be used in combination with other antidiabetic agents in patients with type 2 diabetes who do not achieve adequate glycaemic control with a sulfonylurea agent alone [3]. The glucose lowering effect of metformin is primarily the result of reduced hepatic glucose output through inhibition of gluconeogenesis and glycogenolysis [4]. The glucose lowering effect of metformin vs. the plasma concentration curve shows a counter clock-wise hysteresis loop [5].

Biophase models are most appropriate when delay in drug action occurs from the distribution site to the site of action [6]. However, this modelling approach is often applied inappropriately when the most relevant underlying process that causes the delay is not drug distribution. Other reasons, such as glucose turnover, signalling pathways or translocation of glucose transporters, may be more relevant to the action of antidiabetic drugs [7]. Moreover, the turnover and homeostasis of glucose and insulin is not accounted for by biophase models. Signal transduction models describe a drug mechanism that immediately alters the production or loss of endogenous substances, and, therefore, are the most useful when turnover (glucose concentration) can be measured directly [8].

The pharmacokinetics (PK) and pharmacodynamics (PD) of metformin have been investigated in healthy humans and patients with type 2 diabetes mellitus [5, 9–11], and modelling has been performed using an indirect response model [5]. However, the indirect response model is insufficient to explain the PK/PD relationship and describe the visual inspection of metformin. No reported study clearly describes the glucose lowering effect and the plasma concentrations of metformin in healthy humans using the NONMEM program and the signal transduction model method.

The objectives of this study were to examine the relationship between the plasma concentration of metformin and its antihyperglycaemic effect in healthy humans following administration of a single 500 mg metformin tablet. A Monte Carlo simulation was performed using the ADAPT 5 program (Biomedical Simulation Resource, Los Angeles, CA, USA) to predict plasma glucose concentrations in patients with diabetes. The model was used to predict the antihyperglycaemic effect in patients with type 2 diabetes. The predicted plasma glucose concentration value was similar to that of previous studies [12, 13] in patients with diabetes. Thus, the proposed model was able to predict the antihyperglycaemic effect.

Methods

Subjects

In total, 1008 observations were available for the PK/PD analysis of metformin, consisting of 504 metformin plasma concentrations and 504 glucose concentrations. The study enrolled 42 healthy male subjects, 25.58 ± 3.55 years of age, weighing 68.63 ± 8.14 kg. The healthy volunteer characteristics upon entry into the study are summarized in Table 1. All subjects were selected after completing a thorough history and physical examination, and a normal laboratory examination in which haematology, serum chemistry and urinalysis were conducted. No subject had taken any drug for at least 10 days. Exclusion criteria included health problems, drug or alcohol abuse, and abnormalities in laboratory screening.

Table 1.

Summary of demographic and data characteristics

Mean (SD) Median Range
Number of healthy humans 42
Number of observations (PK/PD) 1008 (504/504)
Age (years) 26 (4) 27 21–31
Weight (kg) 69 (8) 69 61–78
Height (m) 1.8 (0.1) 1.7 1.6–1.8
FPG (mg dl−1) 98 (7) 98 92–105
CLcr (ml min−1) 107 (16) 106 90–123
TBIL (mg dl−1) 1.1 (0.3) 1.1 0.8–1.6
Hb (g dl−1) 16 (0.8) 16 15–17
Open in a new tab

CLcr, creatinine clearance; FPG, fasting blood glucose; Hb, haemoglobin; TBIL, total bilirubin.

Subjects were educated as to the risks and benefits of the study before enrolment and submitted written informed consent. The study protocol was approved by the ethics committee of the Institute of Drug Research and Development at Chungnam National University (Daejeon, Korea) and all subjects gave written informed consent. Data were collected at Sun Obstetrics and Gynecology Hospital (Daejeon, Korea).

Study design

All subjects fasted for at least 12 h prior to dosing. At time zero, an intravenous cannula was inserted into a forearm vein and blank blood samples were collected. After baseline blood sampling, the metformin tablet (Diabex 500 mg, Daewoong) was orally administered with 200 ml water. All volunteers consumed 12 g of sugar 20 min after drug administration. Blood samples to determine plasma metformin were taken at 0.5, 1, 1.5, 2, 2.5, 3, 4, 6, 8, 10 and 12 h after drug administration. In addition, plasma glucose concentration was measured at the same time after drug administration. All subjects abstained from food until 4 h after drug administration. The blood samples were collected in heparinized tubes, immediately centrifuged (10 min, 3000 rev min−1), and stored at −20°C until LC-MS/MS analysis. An identical study was performed without metformin administration 1 week later to determine the glucose concentration without metformin (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Time course of the percent change in plasma glucose concentration from baseline (mean ± SE, n= 42). Black circles are the control group (Inline graphic), and white circles are the metformin group (Inline graphic). All volunteers consumed 12 g of sugar 20 min after drug administration and abstained from food until 4 h after the administration

Metformin and glucose assay

Plasma concentrations of metformin were quantified by LC-MS/MS using the PE SCIEX API 2000 (triple-quadrupole) system (Applied Biosystems, Foster City, CA, USA) equipped with an electrospray ionization interface. Briefly, 800 µl of plasma was spiked with the internal standard (metoprolol) and was extracted by protein precipitation. Metformin and metoprolol (Sigma Chemical, St Louis, MO, USA) were detected by mass spectrometry, operating under positive selected reaction monitoring MS/MS conditions at the following mass transitions: 130.0 → 60.0 m/z for metformin and 268.0 → 116.0 m/z for metoprolol [14]. The assay lower limit of quantification was 0.05 µg ml−1. The intra-assay precision ranged from 2.77 to 12.68% and the mean percentage accuracy ranged from 93.99 to 104.17%.

Plasma glucose concentrations were determined with the glucose-oxidase/UV method (Stanbio Laboratory, Boerne, TX, USA). The calibration curve was linear (r2 > 0.99) over the range of 0–500 mg dl−1. The intra-day coefficients of variation were 1.57% and the inter-day coefficients of variation were less than 2.94% for the plasma assays. The glucose lowering effect of metformin (% effect) was calculated as percentage change at each collection time from the control group glucose concentrations [5].

Population PK/PD analysis

Pooled data from the healthy volunteers were analyzed with NONMEM VI (ICON Development Solutions, Ellicott City, MD, USA) [15] with a G77 FORTRAN compiler. Analysis and post processing were performed with the aid of the PsN toolkit [16] and Xpose (ver. 4) [17], programmed in the statistics package R.

A sequential modelling approach was used to facilitate the data analysis. The population PK analysis was performed in the first step. Using the individual PK parameter estimates as part of the input, population PD analysis was performed. An exploratory two-stage PK analysis was performed to identify the optimal structure model, using a one compartment body model with first order absorption and elimination. The differential equations used to describe the PK model were as follows:

graphic file with name bcp0074-0815-mu1.jpg
graphic file with name bcp0074-0815-mu2.jpg

where X is the mass of the compound in each compartment (1: absorption, 2: central), Ka is the absorption rate constant (units of inverse time), V2 is the apparent volume of the central compartment, and CL is the elimination clearance (units of volume per time).

The between-subject variability for the PK parameters was developed as an exponential error model as follows:

graphic file with name bcp0074-0815-mu3.jpg

where Pi is the parameter for the ith subject, θ is the typical population value of the parameter, and ηi is the random intersubject effect with a mean of 0 and variance ω2. The within-subject variability was developed as an additive error model, as follows:

graphic file with name bcp0074-0815-mu4.jpg

where Yij and Y pij present the ith subject's jth observed and predicted concentration, respectively, and ε is the random residual error, which is normally distributed with a mean of 0 and variance σ2. A first order conditional estimation method applying an additive error model was used to estimate the parameters. Individual subject PK parameters were calculated using the NONMEM posterior conditional estimation technique. In general, the additive error model is applied when the variance is assumed to have a constant absolute magnitude and independent for all measurements. In the case of PK concentrations, where a wide range of concentrations is measured, the error in measurement based on the analytical method is usually a combination of additive and proportional error. However, when we compared the additive, proportional and combination error model, the additive model was the most appropriate for the PK of metformin.

The model that was previously suggested to describe signal transduction processes [18, 19] was used to model the delayed antihyperglycaemic effect of metformin (Figure 2). Drug concentration in the central compartment (Cp= X2/V2), derived from the PK model, was linked to mean response vs. time data using the follow set of equations:

Figure 2.

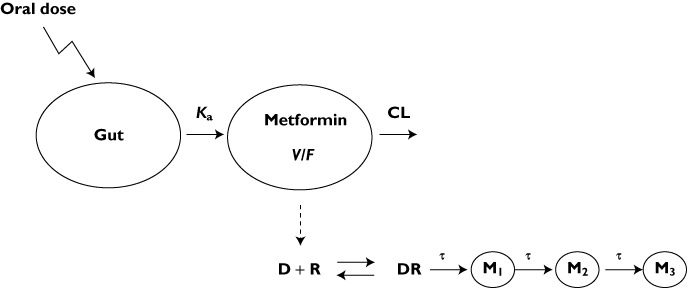
Figure 2

Open in a new tab

Pharmacokinetic/pharmacodynamic (PK/PD) model of metformin. The PK are described by a one compartment model in which concentration in the central compartment (Cp) is linked to the PD model. The drug (D) interacts with the receptor (R) and produces a drug−receptor complex (DR) that initiates a series of signal transduction processes. τ is the mean production time for second messengers (M1–M3)

graphic file with name bcp0074-0815-mu5.jpg
graphic file with name bcp0074-0815-mu6.jpg
graphic file with name bcp0074-0815-mu7.jpg
graphic file with name bcp0074-0815-mu8.jpg

where DR represents a hypothetical drug–receptor complex that produces M1, a secondary messenger, Emax is maximal M1 production and EC50 is the drug concentration that produces 50% of Emax. This model represents a cascade process in which M1 is transformed into another secondary messenger M2 and M2 is further transformed into M3. The most parsimonious three-step signal transduction model was applied, assuming that the mean transit time (τ) of the biosignal through all transit compartments, M1, M2, and M3, was identical [20].

M3 represents the change in the antihyperglycaemic effect. The measured response is:

graphic file with name bcp0074-0815-mu9.jpg

The proportional error was used for pharmacodynamics part of the model.

Model evaluation

The performance and precision of the final PK/PD model were investigated by an internal validation method, which consisted of a non-parametric bootstrap analysis [21–23]. A new randomly sampled replicate of the original data set was obtained in the bootstrap analysis (that is, a bootstrap sample) with replacement. The final population PK/PD model was re-fitted to each of the bootstrap replicates one at a time and this process was repeated 1000 times with different random draws. Bootstrap runs with unsuccessful minimization were excluded from further analysis [24]. The median and 95% confidence interval (CI) for the population parameters were obtained.

The predictive properties of final model were evaluated using a visual predictive check (VPC) assessment obtained after 1000 simulations of the data set. The VPC was used to evaluate the adequacy of the model by comparing the distribution of observed PK/PD data with the distribution of simulated PK/PD data based on the final PK/PD parameter estimates [25]. The percentage of observed data outside the 5th and 95th percentiles of simulated concentrations was calculated to assess the final models. The observed concentration vs. time data were graphically overlaid with the median values along with the 5th and 95th percentiles from the simulated concentration–time profiles. The model was deemed adequate if the observed concentration data were appropriately distributed within the 5th and 95th percentiles of the simulated data.

Results

PK/PD

The individual posterior Bayesian estimates of the PK parameters (CL/F and V/F) generated from the base model were plotted against the characteristics of healthy volunteers (gender, age, height, weight, CLcr, total bilirubin, and haemoglobin). CLcr was highly correlated with CL/F and the incorporation of CLcr into the base model produced a significant decrease in the objective function value (Δ OFV =−9.22, P < 0.01). Comparing base model estimates with final model estimates, the η shrinkage for CL/F was relatively small (26.22%). It was considered appropriate to use the plots of the random effects (η) of PK parameters vs. covariates for screening potential covariates [26]. The structure of the final PK model was:

graphic file with name bcp0074-0815-mu10.jpg
graphic file with name bcp0074-0815-mu11.jpg
graphic file with name bcp0074-0815-mu12.jpg

PK parameter estimates obtained from this model and the 95% CIs from the bootstrap analysis are shown in Table 2[27, 28]. The mean apparent volume of distribution (V/F) was 113 l (RSE, 4.18%). Ka and apparent clearance (CL/F) were estimated as 0.41 h−1 (2.43%) and 52.6 l h−1 (4.18%). Most parameters showed a reasonable amount of inter-individual variability (≤41%). The observed bootstrap means were generally consistent with the population mean estimates. The coefficient of variation for the random residual constant was reasonable (23%). The incorporation of CLcr into the base model explained part of the inter-individual variability of CL/F, with its value decreasing, from 47% to 41%.

Table 2.

Pharmacokinetic and pharmacodynamic parameters and estimates of variability

Parameter, unit Definition Population mean (% RSE) Bootstrap median (95% CI*) Interindividual variability (IIV) CV% Bootstrap IIV CV% (95% CI*)
Pharmacokinetic
 CL (l h−1) Apparent clearance 52.6 (4.18) 52.9 (48.5, 56.7) 29.7 27.9 (26.5, 29.1)
 V (l) Apparent volume of distribution 113 (56.6) 113 (100, 126) 22.1 22.2 (20.2, 24.1)
 Ka (h−1) Absorption rate constant 0.41 (2.43) 0.41 (0.39, 0.43) –† –†
 Residual error (ng ml−1) 23.0 (11.7) 23.1 (21.7, 25.2)
Pharmacodynamic
 τ Mean transit time 0.50 (2.97) 0.48 (0.48, 0.51) –† –†
 Emax Maximum simulation 19.8 (3.17) 20.3 (19.2, 20.4) –† –†
 EC50 Simulation constant 3.68 (3.89) 3.68 (3.49, 3.81) –† –†
 r Hill coefficient 0.55 (9.05) 0.59 (0.50, 0.60) 4.05 4.07 (3.86, 4.22)
 Residual error, % 40.4 (1.52) 40.4 (38.2, 42.9)
Open in a new tab
*

CI, confidence interval calculated from 1000 bootstrap resamplings.

†

Not estimated. % RSE, relative standard error for estimate; CV, coefficient of variation.

Goodness of fit plots for the final PK/PD model are shown in Figures 3 and 4. The plots of observed concentration vs. population predicted concentrations (A) and individual predicted concentrations (B) showed the better visual agreement between predicted and observed data. These plots show an improvement in fit with the latter (B) including covariates, observed as tighter and more random scatter about the identity line and good concordance. The diagnostic plots of the final population PK/PD model revealed no systemic bias. The conditional weighted predictions for the final population PK/PD model were generally distributed around zero and were relatively symmetrical.

Figure 3.

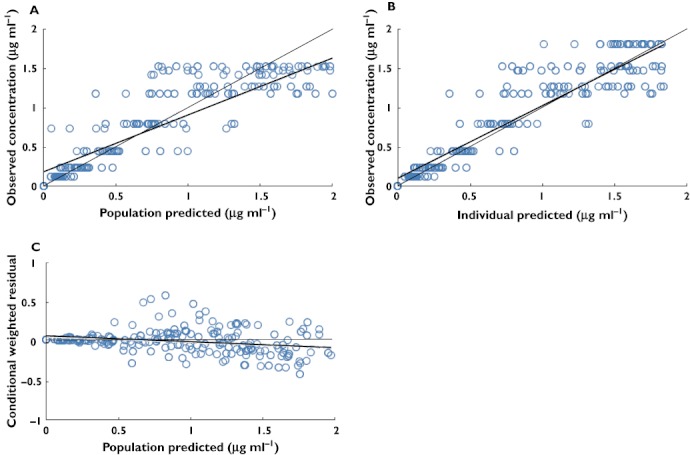
Figure 3

Open in a new tab

Goodness of fit plots for final covariate pharmacokinetic model. The thin solid line is the line of identity and the thick solid line is the trend line. (A) Typical predicted (PRED) vs. observed metformin concentrations, (B) Bayesian predicted vs. observed metformin concentrations and (C) conditional weighted residuals vs. PRED

Figure 4.

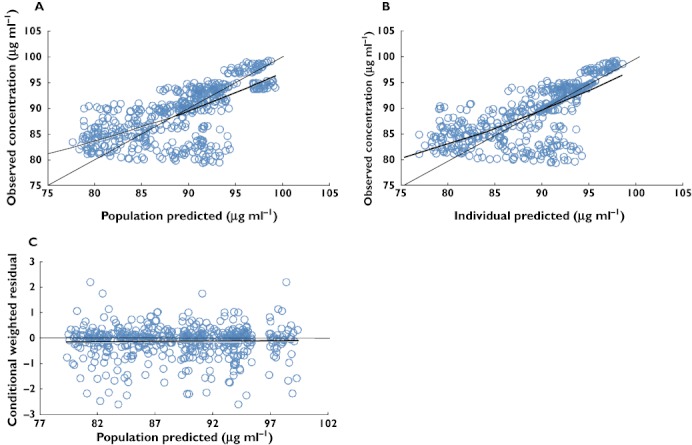
Figure 4

Open in a new tab

Goodness of fit plots for the final covariate pharmacodynamic model. The thin solid line is the line of identity and the thick solid line is the trend line. (A) Typical predicted (PRED) vs. observed fasting plasma glucose concentrations, (B) Bayesian predicted vs. observed fasting plasma glucose concentrations and (C) conditional weighted residuals vs. PRED

The signal transduction model was sequentially fitted to metformin concentrations and the antihyperglycaemic effect. A population PD analysis was performed using the individual PK parameter estimates as part of the input. The summary of the population PD parameters obtained from the final PK/PD model is listed in Table 2. The population means for efficacy (Emax) and potency (EC50) were estimated to be 19.8 and 3.68 µg ml−1. The estimated transit time (τ) was about 0.5 h. The Hill coefficient (r) was estimated to be 0.55 and between-subject variability was 4.05%. Bootstrap CIs for PD parameters were obtained (Table 2). The coefficient of variation for the random residual constant was 40.4%.

Monte Carlo simulations were performed with the final covariate model to compare the distribution of simulated metformin concentrations and fasting plasma glucose (FPG) cconcentrations with that of the observed data following administration of metformin 500 mg in healthy humans (Figure 5). With the exception of some metformin and FPG concentrations, most of the observed data fell into the range between the 5th to 95th percentiles of the simulated values. Overall, the final model was able to describe the observed metformin and FPG concentrations reasonably well.

Figure 5.

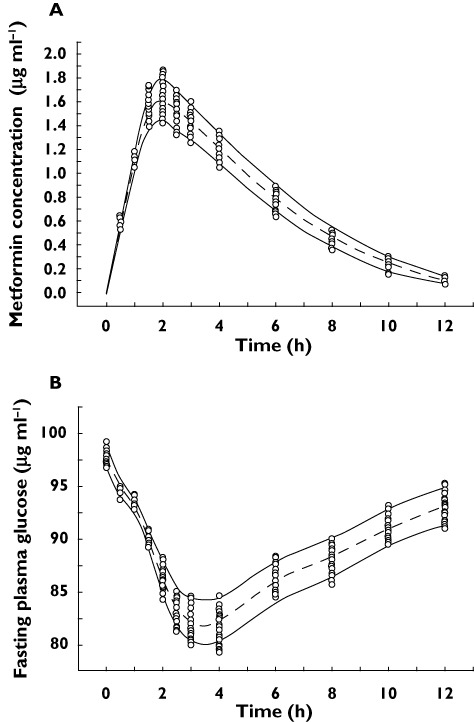
Figure 5

Open in a new tab

Visual predictive check: Observed and model predicted metformin concentrations (A) and observed and model predicted fasting plasma glucose levels (B) following administration of metformin 500 mg to healthy humans. Inline graphic 5th and 95th percentile, simulated, Inline graphic median, simulated and Inline graphic observed concentrations

Discussion

The molecular mechanisms of metformin have not been fully identified, but turnover of biomarkers such as glucose and signalling pathways or translocation of glucose transporters are closely related to the glucose-lowering effects of metformin. Furthermore, the counterclockwise hysteresis loops observed in the metformin plasma concentration−glucose concentration changes indicate the presence of a time delay between the change in plasma concentration and the effect of the drug. Compared with the indirect response model, the signal transduction model had better goodness of fitness and lower objective function value (Δ OFV =−14.21). Thus, in this study, the population PK/PD analysis using a signal transduction model in healthy humans was developed and used. Moreover, the simulation was performed to predict metformin plasma concentrations and the glucose lowering effects in patients with diabetes using a Monte Carlo simulation.

The PK of metformin were best described by a one compartment model with first order absorption and elimination. CLcr was an influential covariate explaining part of the variability in the CL/F of metformin. This is because, in accordance with clinical observations, metformin is not metabolized and is primarily eliminated unchanged, through renal excretion [12, 13, 29, 30].

Despite the limited dose range and interindividual variability, the estimated EC50 (3.68 µg ml−1) was comparable with values reported in previous studies (2.26 µg ml−1[5], 4.23 µg ml−1[11]), in which the plasma glucose time course was obtained and the glucose-lowering effect of metformin was investigated after administering metformin to healthy volunteers and patients with type 2 diabetes mellitus.

To predict a patient's FPG values following metformin administration as defined by the final structure signal transduction model, Monte Carlo simulations were performed (n= 1000) for the regimen of 500 mg metformin orally administered twice daily for 2 weeks. Monte Carlo methods were generated using the final model based on the central tendency and dispersion of each PK and PD parameter. The simulated PK and PD of the drug represent the wide spectrum of subjects with better predictive capabilities for the PK/PD of drugs. Due to this benefit, Monte Carlo simulations are being used increasingly to predict the PK/PD variability of diabetic agents in a population [11, 31]. In a Monte Carlo simulation, the distribution of the model parameter values must be known and used as inputs. Diabetes mellitus diagnostic criteria values were used to simulate the glucose concentration in patients with diabetes. The FPG of a patient with diabetes is >126 mg dl−1 and the 2 h postprandial glucose is >200 mg dl−1, so the initial FPG value for patients was set between 126 mg dl−1 and 200 mg dl−1. In a previous study, patients with type 2 diabetes (n= 182) received 500 mg metformin twice daily for 104 weeks and changes in glucose plasma were observed [32]. The FPG value was initially 178.1 mg dl−1. After 104 weeks, the glucose concentration was 141.3 mg dl−1. In another study, patients with type 2 diabetes (n= 435) received 500 mg metformin twice daily for 24 weeks and changes in plasma glucose were observed [33]. The FPG value was initially 142.1 mg dl−1. After 24 weeks, the glucose value was 122.8 mg dl−1. The mean values and SDs of the parameters (n= 42) obtained from our final signal transduction model were used as inputs for a Monte Carlo simulation, and the baseline plasma glucose concentration from a previous study (plasma glucose = 142.1 mg dl−1, 178.1 mg dl−1) was set as the initial plasma glucose value, and reasonable PK/PD predictions (n= 1000) for 500 mg metformin orally administered twice daily for 2 weeks were simulated. The steady-state predicted FPG concentrations were compared with those reported in a previous study. Simulated FPG concentrations (initial FPG baseline, 178.1 mg dl−1, 142.1 mg dl−1) decreased by about Δ 30.2 mg dl−1 (95% CI 22.8, 38.1) and Δ 24.0 mg dl−1 (95% CI 16.7, 31.3), respectively. Both values were similar to the values of a previous study of Δ 36.8 mg dl−1 (95% CI 28.3, 43.5) [32] and Δ 19.3 mg dl−1 (95% CI 12.5, 26.1), respectively [33]. Thus, the model we developed for PK/PD of patients with diabetes seemed reliable.

In conclusion, a population signal transduction model was developed and evaluated using metformin in healthy volunteers. Model evaluation using nonparametric bootstrap analysis suggested that the proposed model was robust, and that the values were estimated with good precision. Although the model was developed initially in healthy volunteers with normal renal function, the simulation results revealed that the model was useful to predict FPG concentrations in patients with type 2 diabetes. The model was appropriate to predict the time course of plasma metformin and of FPG concentrations in patients with type 2 diabetes and may be useful in the design and analysis of future studies evaluating metformin in combination with other drugs for treating type 2 diabetes mellitus.

Acknowledgments

This work was supported by Samnam Pharmaceuticals, Geumsan, Chungcheongnam-do, Korea.

Competing Interests

There are no competing interests to declare.

REFERENCES

  • 1.McEvoy GK, Livak KG. AHFS drug information. 2002. pp. 3052–61. ASPH.
  • 2.Moses R, Slobodnjuk R, Boyages S, Colagiuri S, Kidson W, Carter J, Donnelly T, Moffitt P, Hopkins H. Effect of repaglinide addition to metformin monotherapy on glycemic control in patients with type 2 diabetes. Diabetes Care. 1999;22:119–24. doi: 10.2337/diacare.22.1.119. [DOI] [PubMed] [Google Scholar]
  • 3.Kwon KI. Clinical Drug Therapy of Disease. 2nd edn. Seoul, South Korea: Shinil; 2003. pp. 433–7. [Google Scholar]
  • 4.DeFronzo RA, Goodman AM. Efficacy of metformin in patients with non-insulin-dependent diabetes mellitus. The Multicenter Metformin Study Group. N Engl J Med. 1995;333:541–9. doi: 10.1056/NEJM199508313330902. [DOI] [PubMed] [Google Scholar]
  • 5.Lee SH, Kwon KI. Pharmacokinetic-pharmacodynamic modeling for the relationship between glucose-lowering effect and plasma concentration of metformin in volunteers. Arch Pharm Res. 2004;27:806–10. doi: 10.1007/BF02980152. [DOI] [PubMed] [Google Scholar]
  • 6.Groenendaal D, Freijer J, Roiser A, de Mik D, Nicholls G, Hersey A, Ayton AD, Danhof M, de Lange EC. Pharmacokinetic/pharmacodynamic modeling of the EEG effects of opioids: the role of complex biophase distribution kinetics. Eur J Pharm Sci. 2008;34:149–63. doi: 10.1016/j.ejps.2008.03.003. [DOI] [PubMed] [Google Scholar]
  • 7.Foti D, Chiefari E, Iuliano R, Brunetti L, Paonessa F, Manfioletti G, Barbetti F, Brunetti A, Croce CM, Fusco A. Lack of the architectural factor HMGA1 causes insulin resistance and diabetes in humans and mice. Nat Med. 2005;11:765–73. doi: 10.1038/nm1254. [DOI] [PubMed] [Google Scholar]
  • 8.Landersdorfer CB, Jusko WJ. Pharmacokinetic/pharmacodynamic modeling in diabetes mellitus. Clin Pharmacokinet. 2009;47:417–48. doi: 10.2165/00003088-200847070-00001. [DOI] [PubMed] [Google Scholar]
  • 9.Dunn CJ, Peters DH. Metformin: a review of its pharmacological properties and therapeutic use in non-insulin-dependent diabetes mellitus. Drugs. 1995;49:721–49. doi: 10.2165/00003495-199549050-00007. [DOI] [PubMed] [Google Scholar]
  • 10.Sambol NC, Chiang J, O'Conner M, Liu CY, Lin ET, Goodman AM, Benet LZ, Karam JH. Pharmacokinetics and pharmacodynamics of metformin in healthy subjects and patients with noninsulin-dependent diabetes mellitus. J Clin Pharmacol. 1996;36:1012–21. doi: 10.1177/009127009603601105. [DOI] [PubMed] [Google Scholar]
  • 11.Hong Y, Rohatagi S, Habtemariam B, Walker JR, Schwartz SL, Mager DE. Population exposure-response modeling of metformin in patients with type 2 diabetes mellitus. J Clin Pharmacol. 2008;48:696–707. doi: 10.1177/0091270008316884. [DOI] [PubMed] [Google Scholar]
  • 12.Krentz AJ, Bailey CJ. Oral antidiabetic agents: current role in type 2 diabetes mellitus. Drugs. 2005;65:385–411. doi: 10.2165/00003495-200565030-00005. [DOI] [PubMed] [Google Scholar]
  • 13.Bailey CJ, Turner RC. Metformin. N Engl J Med. 1996;334:574–9. doi: 10.1056/NEJM199602293340906. [DOI] [PubMed] [Google Scholar]
  • 14.Wang Y, Tang Y, Gu J, Fawcett JP, Bai X. Rapid and sensitive liquid chromatography–tandem mass spectrometric method for the quantification in human plasma. J Chromatogr B Analyt Technol Biomed Life Sci. 2004;808:215–9. doi: 10.1016/j.jchromb.2004.05.006. [DOI] [PubMed] [Google Scholar]
  • 15.Beal SL, Sheiner LB, Boekmann AJ. NONMEM User Guides. Ellicott City, MD: Icon Development Solutions; 2006. [Google Scholar]
  • 16.Lindblom L, Pihlgren P, Jonsson EN. PsN toolkit – a collection of computer intensive statistical methods for non-linear mixed effect modeling using NONMEM. Comput Methods Programs Biomed. 2005;79:241–57. doi: 10.1016/j.cmpb.2005.04.005. [DOI] [PubMed] [Google Scholar]
  • 17.Jonsson N, Karlsson MO. Xpose – an S-PLUS based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Comput Methods Programs Biomed. 1999;58:51–64. doi: 10.1016/s0169-2607(98)00067-4. [DOI] [PubMed] [Google Scholar]
  • 18.Sun YN, Jusko WJ. Transit compartments versus gamma distribution function to model signal transduction processes in pharmacodynamics. J Pharm Sci. 1998;87:732–7. doi: 10.1021/js970414z. [DOI] [PubMed] [Google Scholar]
  • 19.Mager DE, Jusko WJ. Pharmcodynamic modeling of time dependent transduction systems. Clin Pharmacol Ther. 2001;70:210–6. doi: 10.1067/mcp.2001.118244. [DOI] [PubMed] [Google Scholar]
  • 20.Perlstein I, Stepensky D, Krzyzanski W, Hoffman A. A signal transduction pharmacodynamic model of the kinetic of the parasympathomimetic activity of low dose scopolamine and atropine in rats. J Pharm Sci. 2002;91:2500–10. doi: 10.1002/jps.10243. [DOI] [PubMed] [Google Scholar]
  • 21.Iwi G, Millard RK, Palmer AM, Preece AW, Saunders M. Bootstrap resampling: a powerful method of assessing confidence intervals for doses form experimental data. Phys Med Biol. 1999;44:55–62. doi: 10.1088/0031-9155/44/4/021. [DOI] [PubMed] [Google Scholar]
  • 22.Yano Y, Beal SL, Sheiner LB. Evaluating pharmacokinetic/pharmacodynamic models using the posterior predictive check. J Pharmacokinet Pharmacodyn. 2001;28:171–92. doi: 10.1023/a:1011555016423. [DOI] [PubMed] [Google Scholar]
  • 23.Ette EI, Williams PJ, Kim YH, Lane JR, Liu MJ, Capparelli EV. Model appropriateness and population pharmacokinetic modeling. J Clin Pharmacol. 2003;43:610–23. [PubMed] [Google Scholar]
  • 24.Parke J, Holford NH, Charles BG. A procedure for generating bootstrap samples for the validation of nonlinear mixed effects population models. Comput Methods Programs Biomed. 1999;59:19–29. doi: 10.1016/s0169-2607(98)00098-4. [DOI] [PubMed] [Google Scholar]
  • 25.Post TM, Freijer JI, Ploeger BA, Danhof M. Extensions to the visual predictive check to facilitate model performance evaluation. J Pharmacokinet Pharmacodyn. 2008;35:185–202. doi: 10.1007/s10928-007-9081-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Xu Z, Vu T, Lee H, Hu C, Ling J, Yan H, Baker D, Beutler A, Pendley C, Wagner C, Davis HM, Zhou H. Population pharmacokinetics of golimumab, an anti-tumor necrosis factor-alpha human monoclonal antibody, in patients with psoriatic arthritis. J Clin Pharmacol. 2009;49:1056–70. doi: 10.1177/0091270009339192. [DOI] [PubMed] [Google Scholar]
  • 27.Xu Z, Seitz K, Fasanmade A, Ford J, Williamson P, Xu W, Davis HM, Zhou H. Population pharmacokinetics of infliximab in patients with ankylosing spondylitis. J Clin Pharmacol. 2008;48:681–95. doi: 10.1177/0091270008316886. [DOI] [PubMed] [Google Scholar]
  • 28.Royer B, Yin W, Pegram M, Ibrahim N, Villanueva C, Mir D, Erlandsson F, Pivot X. Population pharmacokinetics of the humanised monoclonal antibody, HuHMFG1 (AS1402), derived from a phase I study on breast cancer. Br J Cancer. 2010;102:827–32. doi: 10.1038/sj.bjc.6605560. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Vitaly R, Igor NT. Rx drug information. 2007. Available at http://www.druglib.com/druginfo/metformin/description_pharmacology/ (last accessed 12 April 2012)
  • 30.Scheen AJ. Clinical pharmacokinetics of metformin. Clin Pharmacokinet. 1996;30:359–71. doi: 10.2165/00003088-199630050-00003. [DOI] [PubMed] [Google Scholar]
  • 31.Watanalumlerd P, Christensen JM, Ayres JW. Pharmacokinetic modeling and Simulation of gastrointestinal transit effects on plasma concentrations of drugs from mixed immediate-release and enteric-coated pellet formulations. Pharm Dev Technol. 2007;12:193–202. doi: 10.1080/10837450701212750. [DOI] [PubMed] [Google Scholar]
  • 32.Williams-Herman D, Johnson J, Teng R, Golm G, Kaufman KD, Goldstein BJ, Amatruda JM. Efficacy and safety of sitagliptin and metformin as initial combination therapy and as monotherapy over 2 years in patients with type 2 diabetes. Diabetes Obes Metab. 2010;12:442–51. doi: 10.1111/j.1463-1326.2010.01204.x. [DOI] [PubMed] [Google Scholar]
  • 33.Aschner P, Katzeff HL, Guo H, Williams-Herman D, Kaufman KD, Goldstein BJ. Efficacy and safety of monotherapy of sitagliptin compared with metformin in patients with type 2 diabetes. Diabetes Obes Metab. 2010;12:252–61. doi: 10.1111/j.1463-1326.2009.01187.x. [DOI] [PubMed] [Google Scholar]

Articles from British Journal of Clinical Pharmacology are provided here courtesy of British Pharmacological Society

RESOURCES