Rapid three-dimensional MAS NMR spectroscopy at critical sensitivity

Solid-state magic angle spinning nuclear magnetic resonance (MAS NMR) is maturing rapidly. Progress is highlighted by recent examples that demonstrate its capability to yield site-specific assignments and atomic resolution structural information on fibrillar,^[1–3] membrane-associated,^[4–6] and non-crystalline proteins.^[7–9] Furthermore, applications to systems of ever-increasing molecular size are limited only by the signal-to-noise ratio (S/N) in the multidimensional spectra required for adequate resolution,, rather than by more fundamental limitations from spin relaxation. Therefore, the most pressing need in MAS NMR is arguably for more efficient data acquisition methods.

Acquisition problems in MAS NMR, relative to solution NMR, are two-fold. First, ¹³C-detection is necessary to obtain the narrow linewidths required for site-specific assignments and structure determination; however, ¹³C detection is inherently less sensitive than ¹H detection. Second, slower relaxation and the need for high-power ¹H-decoupling in solids necessitate longer recycle delays. For these reasons employing three or more dimensions in MAS NMR experiments has not yet become a common practice.^{[7, 10–14]}

In solution NMR, more efficient acquisition has relied on non-uniform sampling (NUS), which has been successfully applied to multidimensional experiments on larger systems.^[15–19] Although extending NUS to MAS NMR would be of enormous practical importance, the application of conventional NUS methods to MAS NMR has been limited by the specific problem of accurately modeling weak signals in noisy spectra,^[20–22] in addition to the general problems of quantitative spectral reconstruction and slow computation.^[23] The lower sensitivity in MAS NMR experiments requires an unprecedented robustness of any NUS scheme in order to minimize artefacts.

Here, we address these challenges with SIFT (Spectroscopy by Integration of Frequency and Time domain information), a rapid and model-free method for computing a NMR spectrum from a NUS time domain dataset.^[24] SIFT works by replacing missing information in the time domain with a priori knowledge of “dark” regions in the frequency domain, i.e. those regions known to contain no NMR signals. The frequency domain information, assimilated by a very rapid computational process, obviates some time-domain sampling with no sacrifice in resolution and no modeling bias.

We previously used SIFT to process 2D NUS ¹⁵N-HSQC solution data, where dark regions created by over-sampling were utilized to replace up to 75% of the uniform time domain data points.^[24] Here we demonstrate the effectiveness of the SIFT method in solids, using dark regions resulting from the need for rotor-synchronized sampling in the indirect dimensions. Unlike other NUS data processing methods that actively model signals to reconstruct a spectrum, SIFT suppresses the sampling noise by using only definitive information from the dark spectral areas. Thus, SIFT avoids bias from subjective discrimination between weak signals and noise, and reconstructs missing time data points with high fidelity, as if they had been actually recorded. These favorable properties make SIFT uniquely suited for processing NUS data in the sensitivity-limited regime.

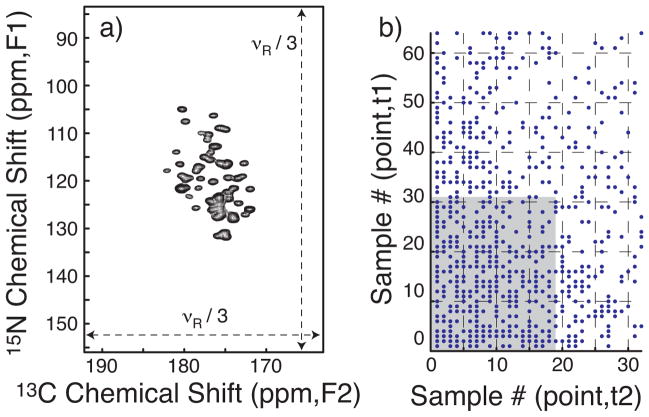
To demonstrate the application of SIFT to NUS MAS NMR, we recorded a 3D NCOCX spectrum (Fig. 1a) of a microcrystalline, uniformly [¹⁵N,¹³C]-labeled sample of the β1 domain of protein G (GB1) at high digital resolution (1.1 ppm for F1, 0.7 ppm for F2, before zero filling). For both t1 and t2, the dwell time was synchronized to three-times the rotor period, 3/ν_R (bandwidth equal to ν_R/3 Hz), in order to fold the spinning sidebands onto the corresponding centerbands. The spinning frequency ν_R was chosen to avoid rotational resonance due to overlap of the sidebands of carbonyl ¹³C signals with the aromatic and aliphatic signals in the acquisition dimension (F3). Due to these constraints, the bandwidth in the indirect acquisition dimensions (F1, F2) left spectral regions known to be devoid of signals. Whereas those “dark” regions are conventionally neglected, SIFT actively uses them.

Figure 1.

(a) The projection down the direct acquisition axis (F3) of the NCOCX spectrum of GB1. The full spectral range is shown for both the ¹⁵N (F1) and ¹³C (F2) dimensions. (b) The dots represent the NUS schedule comprising 608 quasi-random on-grid points with exponentially decaying probability density. The shaded area corresponds to a truncated set of 608 (32×19) uniform points. A full dataset with 2048 (64×32) samples was acquired as a reference and time samples were omitted according to the schedule to form the NUS dataset. Forty scans were averaged per t1/t2-sample. The NUS schedule was generated by the sampling scheduler available at http://sbtools.uchc.edu/nmr/sample_scheduler/. The dwell time was 270 μs for t1 and t2 at a MAS frequency of 11.1 kHz.

To model critical sensitivity, we intentionally under-packed the sample rotor such that only ~50% of the active volume was filled. With a molecular weight of ~6.4 kDa for GB1, the NMR sensitivity for this half-packed sample would correspond to that of a fully packed ~13 kDa microcrystalline protein at the same density. Signal averaging took ~7 min per t1/t2-sample for an acceptable S/N ratio, while extended signal evolution was also required for suitable linewidths.

The NUS schedule employed (Fig. 1b) omits more than 70% of the time domain samples in the full, uniform grid of 64(t1) × 32(t2) time points. The input for SIFT processing comprises the NUS schedule, the acquired time-domain data, and specification of the dark spectral regions. The processing, which involves no user intervention or parameter tuning, took ~2 min on a single processor. The SIFTed time domain data may be transformed and phased as though directly acquired.

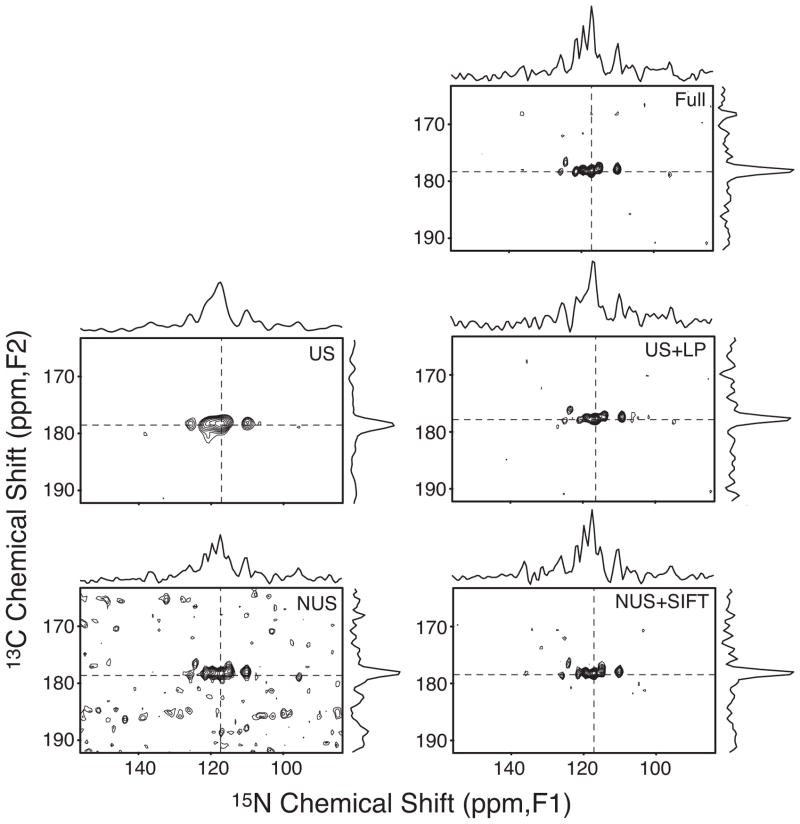
Figure 2 shows that the S/N degradation due to NUS (bottom, left) is almost perfectly reversed after SIFT-processing (bottom, right), leading to S/N that is nearly the same as that of the fully acquired spectrum with more than three times as many acquired points (top). This is significantly better than the sqrt(608/2048) = 0.54 relative S/N that is expected for the shortened acquisition time and obtained with other major processing methods, such as Multidimensional Decomposition (MDD)^[19], that rely almost exclusively on information in the time domain. The nearly identical S/N achieved in < 1/3 of the acquisition time means that the SIFTed spectrum is >1.7-fold more sensitive per unit time relative to the conventionally acquired spectrum.

Figure 2.

A two-dimensional slice taken at F3=178.4 ppm from the NCOCX spectrum using: the full, uniform 2048 t1/t2-samples (top); the truncated 608 uniform samples corresponding to the shaded area in Figure 1b with zero-filling (middle, left); the same with linear prediction (middle, right); the 608 NUS samples corresponding to the dots in Figure 1b without SIFT processing (bottom, left); the last with SIFT processing (bottom, right). The spectrum without SIFT processing (bottom left, where FFT was used after the missing time points were filled with zeroes) corresponds to the classical discrete Fourier transform (DFT) of the NUS data^[17]. The minimum contour line is at 18% of the tallest peak in each panel. 1D traces at dashed lines are also shown, for which the vertical scales are the same for all panels. The shown slice contains signals with about 1–2 times the median peak intensity and S/N ranging between 8.4 and 15.6. Slices with weaker signals are shown in Figure S1 of the Supporting Information.

The improved S/N provided by SIFT processing reduced the number of lost signals ~10-fold compared with the NUS spectrum not processed by SIFT. Of the 123 correlation signals observed in the fully sampled data, the weaker 62 had S/N ratios ranging from 3.1 to 7.7. At this critical sensitivity, classical discrete Fourier transform of the NUS data (Fig. 2; bottom, left) resulted in 18 (29%) of the 62 weaker peaks being lost (i.e., intensity below the threshold of 3σ, where σ is the average noise standard deviation measured in each spectrum). On the other hand, the SIFTed spectrum lost only 2 (3.2%) of the peaks (see Supporting Information).

With NUS and SIFT combined, we recorded a 3D NCOCX spectrum at ~1-ppm digital resolution in 2.8-days, instead of 9.5 days with the standard method. A sample with twice the molecular weight (or a fully-packed ~26-kDa protein), would require ~7 × 2² ~ 28 min per t1/t2-sample for the same sensitivity. This translates into an 11-day experiment with NUS, versus a 38-day conventional ¹³C detected experiment.

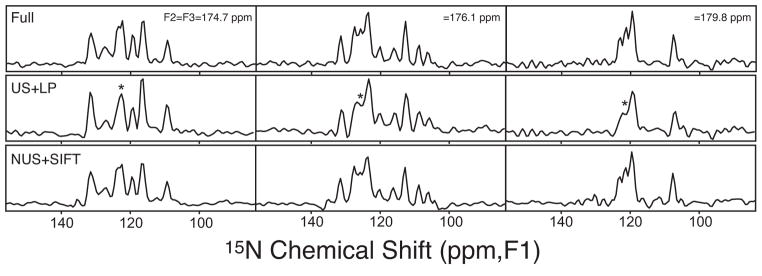
In addition to excellent S/N, SIFT offers high fidelity. Line-shape distortion of the type seen in MaxEnt-processed spectra^{[21, 22]} is not observed in the SIFTed spectrum, despite the much lower intrinsic S/N of the present data. We also found that SIFT yields more accurate peak intensities and positions than those obtained by linear prediction (LP) of a truncated uniformly sampled (US) dataset. For example, Figure 2, middle right, shows that LP does not accurately restore crowded spectral regions even with a reasonable number of coefficients (8). This is especially clear in the F1 slice. Further instances are illustrated by the additional F1 slices in Figure 3. In all the spectral regions where LP failed, the SIFT spectrum reproduced the full data very well. Overall, SIFT rendered peak frequencies with RMS errors of 0.13, 0.11 and 0.09 ppm in F1, F2, and F3, respectively (see Figure S2 in the Supporting Information).

Figure 3.

Representative F1-slices through crowded spectral regions. Each column compares the spectrum of the full data (top), LP of truncated US data (middle), and SIFT-processed NUS data (bottom). From the left to right, slices were taken at F2=F3=174.7, 176.1, and 179.8 ppm, respectively. The vertical scale is the same throughout each column. The asterisks mark the unresolved peaks in the LP spectra.

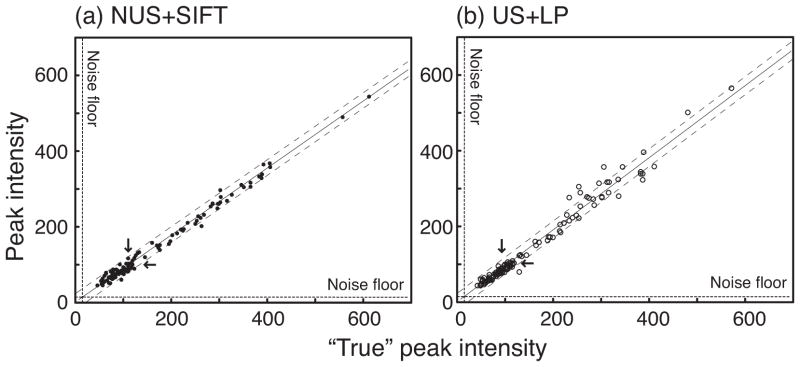
To assess the accuracies of peak intensities, Figure 4 plots the intensities in the SIFTed spectrum and the linear predicted spectrum vs. the “true” peak intensities obtained from the fully acquired dataset. The excellent linearity obtained with SIFT (Figure 4a) demonstrates accurate relative peak intensities. The correlation coefficient was 0.995 overall and 0.877 for the “weak” signals. The dynamic range was ~13 in this example, but the superb linearity of SIFT signal intensities over a dynamic range of ~100 has been shown previously^[24]. The variation of the observed peak intensities was mostly within the intrinsic noise-width of the dataset (~±25), which is indicated by the dashed lines flanking the regression line. This indicates the absence of intensity bias in SIFT-processing. The accuracy remained high for the weakest signals, certifying the robustness of the SIFT process in the presence of formidable noise. In contrast, LP tends to reproduce large signals with less accuracy (see Figure 4b)

Figure 4.

Signal intensities observed in the spectrum of (a) SIFT-processed NUS data and (b) LP-processed US data vs. the fully sampled reference data. The linear regression shown with a solid line is slightly different between (a) and (b). Dashed lines flanking the regression line show the intrinsic noise width in the reference spectrum. Dashed lines along the x- and y-axes show the floor of noise standard deviation. The medians of all the observed signal intensities in the reference, SIFT-processed and linear-predicted spectra (marked by arrows) were about 110, 100 and 95 respectively.

In conclusion, by using the noise-tolerant SIFT process^[24], we have extended the applicability of high-dimensional NUS-NMR methodology to data with the marginal sensitivity typical of MAS NMR of biological macromolecules. Quick SIFT processing (~ 2 min) of NUS data yielded a high-quality 3D spectrum without any calibration or parameter optimization. After SIFT processing, the reduced number of time samples in NUS did not appreciably decrease the S/N relative to that for uniformly acquired reference data. Meanwhile the measurement time was reduced by a factor of ~3.4. These results suggest that a 3D NCOCX-type MAS experiment can be recorded at sufficient sensitivity to resolve single nuclear sites for ~25-kDa proteins in a reasonable period of time. The approach demonstrated herein requires no special hardware and will expedite experiments similarly on all FT spectrometers. For example, if a 10-fold sensitivity gain were available via dynamic nuclear polarization (DNP)^[25], the above high-resolution 3D experiment would be possible for 250 kDa proteins. Moreover, the exquisite accuracy of SIFT signal frequencies and intensities paves the way for quantitative structural and dynamical investigations in noisy systems that have frustrated all other reported NUS processing methods. Thus, SIFT will significantly expand opportunities for high-dimensional MAS NMR experiments in studies of large molecules and molecular assemblies of biological and medical importance.

Experimental Section

Sample Preparation

Uniformly ¹³C and ¹⁵N labeled GB1 was prepared according to previously published protocols,^{[26, 27]} as described in the Supporting Information.

NMR Measurements

The experiment was performed on a custom-built 500 MHz (¹H frequency) spectrometer equipped with a solenoid-coil 3.2mm MAS system (Revolution NMR, Fort Collins, CO). The sampling schedule is converted to a text-based list that is read by the pulse program and control macro to set respective delays (courtesy of Dr. P. van der Wel, University of Pittsburgh). Details on the NMR parameters are given in the Supporting Information.

SIFT processing

MATLAB scripts for SIFT processing are available at http://www.brandeis.edu/~herzfeld/SIFT. The signal-containing “bright” region was 102.5 – 133.2 ppm (F1, ¹⁵N) and 169.3 – 183.9 ppm (F2, ¹³C′), known from 1D “scouting” experiments for the corresponding nuclei. The number of SIFT cycles was 10, which took ~ 2 min. Further details on processing parameters and spectral analysis are given in the Supporting Information