Abstract
Many educated adults possess exact mathematical abilities in addition to an approximate, intuitive sense of number, often referred to as the Approximate Number System (ANS). Here we investigate the link between ANS precision and mathematics performance in adults by testing participants on an ANS-precision test and collecting their scores on the Scholastic Aptitude Test (SAT), a standardized college-entrance exam in the USA. In two correlational studies, we found that ANS precision correlated with SAT-Quantitative (i.e., mathematics) scores. This relationship remained robust even when controlling for SAT-Verbal scores, suggesting a small but specific relationship between our primitive sense for number and formal mathematical abilities.
Keywords: Approximate Number System, math ability, Weber fraction, number comparison
Imagine you see a collection of marbles and are asked how many marbles there are. As educated human adults from a numerate culture we have access to two different ways of answering this question: We can either count the marbles and give a precise answer (e.g., “There are exactly 23 marbles.”) or we can estimate the number of marbles without having to count (e.g., “There are about 20 marbles.”). The ability to give a precise answer relies on the ability to count and apply the correct linguistic labels (Gelman & Gallistel, 1978). Counting and other formal mathematical abilities such as performing exact arithmetic operations are culturally learned and rely on the ability to understand and manipulate symbols such as number words and Arabic numerals (e.g., Pica, Lemer, Izard, & Dehaene, 2004). The development of these skills often takes years of explicit instruction and children and adults differ greatly in their mastery of these formal mathematical abilities (e.g., Geary, 1994).
In contrast, the ability to quickly estimate numbers of objects such as the number of marbles on the floor is a basic skill that we share with many animals, and it is deeply rooted in our evolutionary and ontogenetic history (see e.g., Brannon, Jordan, & Jones, 2010; Libertus & Brannon, 2009, for reviews). While infants, animals and humans in some cultures may have no exact number words to describe the numerical estimates they habitually make, laboratory experiments as well as spontaneous decisions in everyday life (e.g., whether to fight or to flee) show that they are capable of performing such estimations (Agrillo, Dadda, Serena, & Bisazza, 2008; Libertus & Brannon, 2010; Pica et al., 2004; Xu & Spelke, 2000). These findings support the conclusion that these estimation skills are not tied to language or other symbolic representations. Adults, infants, and non-human animals are able to determine approximately how many items are in a collection often in less than a second (Cantlon & Brannon, 2006; Halberda, Sires, & Feigenson, 2006; Hyde & Spelke, 2009; Libertus, Pruitt, Woldorff, & Brannon, 2009; Libertus, Woldorff, & Brannon, 2007; Nieder & Dehaene, 2009). These rapid estimation skills are thought to rely on the Approximate Number System (ANS), part of our broader Number Sense (Berch, 2005), which allows us to rapidly estimate the number of objects in real-world settings (“How many cups do I have?”). This same system also supports our ability to compare these numerical estimates (“Are there more people than cups?”) and perform basic arithmetic operations over these gut-sense representations (e.g., subtraction: “Approximately how many more cups do I need?”) (Barth, La Mont, Lipton, & Spelke, 2005; Gilmore, McCarthy, & Spelke, 2007; McCrink & Spelke, 2010).
The ANS allows us to rapidly determine e.g., if there are more blue or yellow dots in a brief flash (Dehaene, 1992; Halberda & Feigenson, 2008; Halberda, Mazzocco, & Feigenson, 2008). For all people, these numerical discriminations are ratio-dependent – i.e., the imprecision of the numerical representations in the ANS increases with larger numbers (Dehaene & Changeux, 1993; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004) and discriminating numbers that are far apart is easier than discriminating numbers that are closer together (e.g., it is easier to see that 16 is more than 10 than it is to see that 8 is more than 6; Buckley & Gilman, 1974). There are large individual differences in people’s abilities to make accurate discriminations using the ANS, and these differences in performance allow us to estimate the precision of each individual’s ANS (Halberda, Ly, Willmer, Naiman, & Germine, 2012; Halberda et al., 2008) (assessment software has been made freely available at www.Panamath.org). Studies suggest that the precision of the ANS improves greatly during the infant years (Libertus & Brannon, 2010; Lipton & Spelke, 2003; Xu & Spelke, 2000) and throughout early childhood (Halberda & Feigenson, 2008; Odic, Libertus, Feigenson, & Halberda, in press; Piazza et al., 2010) while individuals of the same age can vary quite widely in their ANS precision (Halberda et al., 2012; Halberda et al., 2008).
It remains controversial whether the ANS affects performance in school mathematics. School mathematics performance and the more primitive ANS estimation performance engage both overlapping and distinct brain regions (e.g., Dehaene, Molko, Cohen, & Wilson, 2004). It has been suggested that they may be related because estimation abilities could serve as a foundation for early school mathematics understanding (De Smedt, Verschaffel, & Ghesquiere, 2009; Holloway & Ansari, 2009; Libertus, Feigenson, & Halberda, 2011). Halberda, Mazzocco, and Feigenson (2008) assessed students’ math abilities longitudinally from kindergarten through sixth grade and, at 14 years of age, participants’ ANS precision. ANS precision measured at 14 years of age was found to significantly correlate with school mathematics performance all the way back to kindergarten and at every school year in between. Importantly, this relationship remained robust even when controlling for other factors such as general intelligence, spatial abilities, and working memory suggesting a fairly specific relationship between the ANS and school mathematics abilities. In a recent study, Libertus and colleagues (2011) expanded this finding by showing that the link between ANS precision and math ability is already present in preschool-aged children, before formal math instruction begins. Additional evidence for a link between ANS precision and school mathematics ability during childhood comes from evidence that decreased precision of the ANS may be related to developmental dyscalculia - a severe math learning disability that is not tied to general cognitive deficits (Desoete, Ceulemans, De Weerdt, & Pieters, 2010; Mazzocco, Feigenson, & Halberda, 2011; Piazza et al., 2010).
Debate in this area continues, and determining the mechanisms that may support a link between ANS precision and school mathematics abilities during childhood remains an active area for theorizing. If this link exists, it may reside in children’s intuitive arithmetic operations (Gilmore et al., 2007; Gilmore, McCarthy, & Spelke, 2010), a mapping between the ordinal relations of the ANS and ordinal relations among number symbols (Lyons & Beilock, 2011), or more directly in the acquisition of number symbol meanings and online access to those meanings (De Smedt et al., 2009; Holloway & Ansari, 2009; Rousselle & Noel, 2007; Sasanguie, De Smedt, Defever, & Reynvoet, 2011).
The question of whether the ANS remains relevant during later school mathematics performance in adults remains more controversial still. For example, DeWind and Brannon (2012) and Lyons and Beilock (2011) found a significant correlation between ANS precision and formal mathematics performance in adults. However, Inglis and colleagues (2011), Price and colleagues (2012), and Castronovo and Göbel (2012) all found that ANS precision does not correlate with performance on formal math tests in adults. For example, Castronovo and Göbel (2012) found that school mathematics ability was significantly related to the error in adults’ mappings between the ANS and the number words, but that no such relationship held for simpler ANS discrimination tasks. The importance of the mapping accuracy between the ANS and the number symbols for predicting mathematics performance has been highlighted by their paper and several others (Booth & Siegler, 2006; Holloway & Ansari, 2009; Lyons & Beilock, 2011; Mundy & Gilmore, 2009).
The interpretation of these previous results is made more difficult by differences in experimental methods between these studies. Price and colleagues (2012) highlighted that different experimental parameters return different estimates of ANS precision, and while none of the versions of the ANS tasks they used returned a significant correlation between ANS precision and school mathematics performance in adults, all of these correlations showed poorer ANS precision relating to poorer school mathematics performance. The magnitude of the relationships found by Price and colleagues (e.g., r = −0.28) is similar to previous significant results (e.g., Halberda et al., 2008) and correcting for the low reliability of their ANS precision estimates (r = 0.44) via an attenuation correction (Schmidt & Hunter, 1996) returns a significant correlation between ANS precision and school mathematics performance (r = −0.35). Our impression is that the current state of the literature suggests relatively high confidence that a relationship between ANS precision and school mathematics performance can be seen in children and that this relationship may be most consistently observed when tasks require accessing the meaning of number symbols. There is lower confidence that such a relationship obtains in adults and continued work is required.
The goal of the present study was to investigate the link between ANS precision and mathematics ability in college students. To this end, we tested students enrolled at Johns Hopkins University on an ANS precision test, i.e., a non-symbolic number comparison task similar to the one employed by Halberda and colleagues (2008). In Experiment 1, students were tested in a group-setting; in Experiment 2, students were tested individually. Additionally, in both experiments we collected official transcripts of participants’ scores on the Scholastic Aptitude Test (SAT), a standardized test of quantitative and verbal abilities required for college admission in the United States of America. We hypothesized that quantitative but not verbal abilities as measured by the SAT would correlate with participants’ performance on the ANS precision test.
2. Experiment 1
2.1 Method
2.1.1 Participants
Participants were students from two undergraduate courses at Johns Hopkins University: an introductory cognition course (N = 93) and a course on conceptual development (N = 27), both within the Psychology Department. Students in both classes were predominantly in their second or third year of undergraduate study. All participants provided informed written consent prior to their participation in the experiment. Student records ensured that no student was included twice in our sample resulting in 120 unique participants. We were primarily interested in the relationship between ANS precision and SAT performance and did not seek to investigate differences among these variables as a function of major, class enrollment, or sex in this sample and this information was not collected. Preliminary analyses revealed that there were neither differences in SAT scores nor in performance on the ANS precision test between the two classrooms and so scores were combined into a single sample for all analyses.
2.1.2 Materials
2.1.2.1 ANS precision test
To measure the precision of each student’s Approximate Number System (ANS), we administered a standard number discrimination task modeled after Halberda and colleagues (2008; see also Pica et al., 2004; Cantlon & Brannon, 2006). Participants were told that they would briefly see displays of blue and yellow dots on the large projector screen in the front-center of the classroom. Their task was to write down, on each trial, whether there were more blue or more yellow dots. Each stimulus array was presented for 500 milliseconds, controlled by the computer. Participants received four practice trials, during which the whole class was asked to shout out their answer. Subsequently, there were 60 trials during which participants were instructed to quietly write down their answer on a provided answer sheet. Each trial began 2 seconds after the previous trial and the entire assessment lasted approximately 5 minutes.
To vary the difficulty of the task, the ratio between the blue and yellow dots was manipulated across trials. Ratios varied from an easy 2.0 ratio (24:12 dots) to the very hard 1.05 (18:17 dots). The full set of ratios used was: 2.0, 1.50, 1.33, 1.25, 1.16, 1.14, 1.1, 1.09, 1.07 and 1.05 with 6 trials for each ratio, and ratio varied from trial to trial. On half of the trials, the correct answer was yellow; on the other half, the correct answer was blue. The two sets of dots were separated on either side of the screen (Figure 1). Materials and instructions for duplicating this experiment are available for download and free use at www.panamath.org under Educators & Giving the Test.
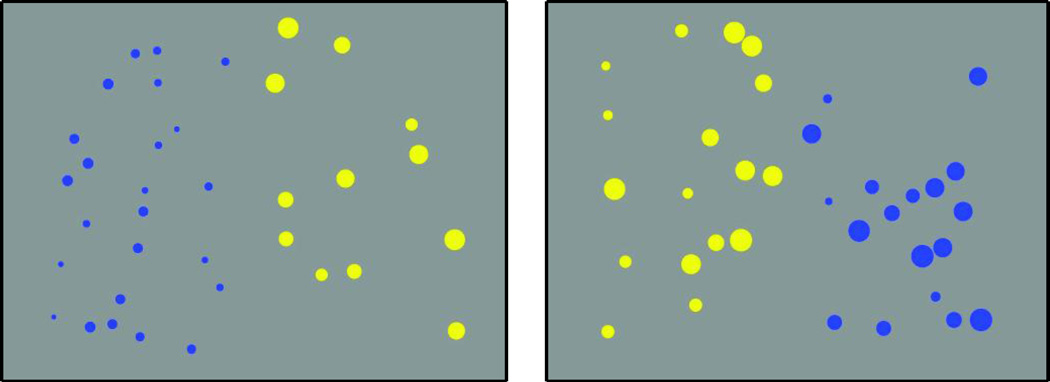
Figure 1.
Sample stimuli of the ANS precision test. On the left is an easy ratio of 2.0 (24 blue dots and 12 yellow dots), and on the right is the difficult ratio of 1.05 (17 yellow dots and 18 blue dots).
To control for perceptual aspects of the stimuli that could co-vary with the number of dots, on half of the trials the numerically larger set was also larger in cumulative surface area (correlated trials). Thus, if there were twice as many yellow dots, there were twice as many yellow pixels as well, and students might have been able to base their answer on the amount of yellow or blue pixels rather than the number of yellow or blue dots. On the other half of the trials the numerically larger set was smaller in cumulative surface area (anti-correlated trials). Thus, if there were twice as many yellow dots, there were twice as many blue pixels (i.e., bigger blue dots). On these trials, answering based on the amount of pixels would give the wrong answer. This method ensures that only an answer based on the number of dots can consistently give the right answer on every trial encouraging students to base their answers only on number.
2.1.3 Procedure
All tasks were administered in the classroom during a regularly scheduled lecture without prior notification to the students. On the day of the experiment, students were told that they could participate in a brief study and were told that their participation was entirely voluntary. Interested students received a booklet that included a consent form that had them explicitly agree to having their Scholastic Aptitude Test (SAT) scores provided to the experimenters by the school’s registrar’s office. The booklet also included a sheet on which they recorded their responses to the task. After the task was completed, the participants received debriefing sheets. Their consent forms were submitted to the registrar, who provided the experimenters with the students’ official SAT scores. Only those students who agreed to having their SAT scores provided were included in the present study (approximately 73% of students present in each classroom yielding a total of 120 students). There were no differences in ANS precision between the students who agreed to having their SAT scores provided and those who did not.
2.2 Results and Discussion
Scholastic Aptitude Test (SAT) scores were separated by their Verbal (SAT-V) and Quantitative (SAT-Q) components; each section was out of 800 points. All students had taken the SAT during the years 2007–2009. The average SAT-V score was 681.58 (SE = 6.48), and the average SAT-Q score was 697.25 (SE = 6.07). There was a significant correlation between SAT-V and SAT-Q (r = 0.35; p < .01). The national averages for SAT-V and SAT-Q scores around this time were 502 and 515 respectively (College Board, 2009).
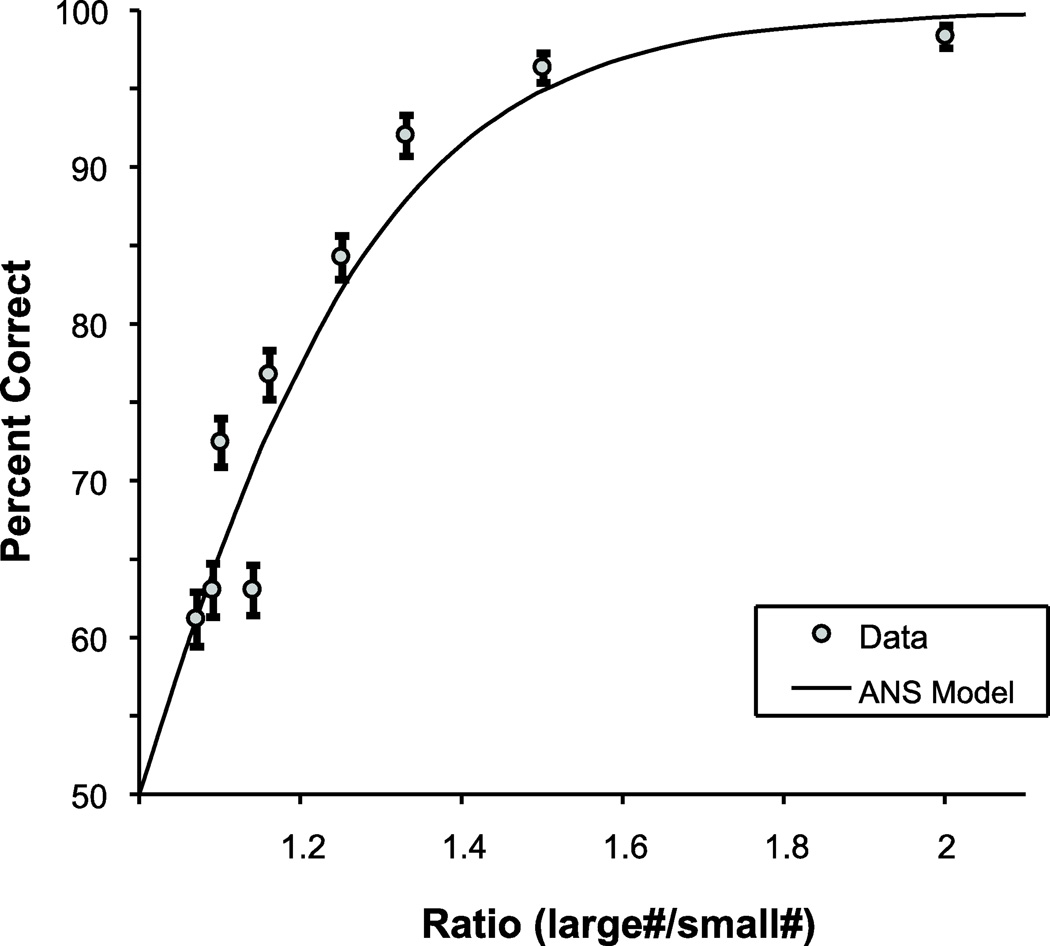
On the ANS precision test, participants responded correctly on 75.9% of all trials (SE = 0.4%). As predicted by Weber’s law, participants’ accuracy decreased as the numerical ratio approached equality (i.e., a ratio of 1 occurs when the number of blue and yellow dots are equal; see Figure 2). To find each individual participant’s Weber fraction (w), an estimate of their ANS precision, we fit each participant’s responses over all 60 trials with a commonly-used psychophysical model (1) (cf., Green & Swets, 1966; Halberda & Feigenson, 2008; Halberda et al., 2008; Pica et al., 2004).
| (1) |
Figure 2.
Percentage of correct responses on the ANS precision test in Exp. 1 as a function of ratio between the numbers of dots in each set. Bars indicate standard error of the mean.
The model assumes that the underlying representations are distributed along a continuum of Gaussian random variables. An important implication of this model is that the two different numbers on each trial will often have similar and overlapping representations. In other words, as the ratio of two quantities becomes increasingly similar (i.e., closer to a ratio of 1.0), their Gaussian representations should tend to overlap more and participants should have greater difficulty in determining which color has more dots resulting in decreased accuracy as the ratio becomes more difficult.
This model has only a single free parameter – w – which indexes the amount of imprecision in the underlying Gaussian representations (i.e., the standard deviation of the Gaussian number representations such that SDn = n * w). Larger w values indicate larger standard deviations and thereby poorer discrimination of the system across all ratios and numerosities. The best fitting w value was determined for each subject using the least-squares method, and the model successfully fit each participant’s data (for further details on fitting procedures see Halberda et al., 2008).
The average w was 0.17 (SE = 0.004), indicating that, on average, the most difficult ratio participants could reliably discriminate was 7:6 (e.g., 7 versus 6 dots, or 14 versus 12 dots, etc). There were, however, large individual differences, with some participants having a w as low as 0.06 (i.e., 18:17 dots) and some as high as 0.27 (i.e., 5:4 dots). These results are consistent with previous reports in the literature (Halberda & Feigenson, 2008; Piazza et al., 2010; Pica et al., 2004).
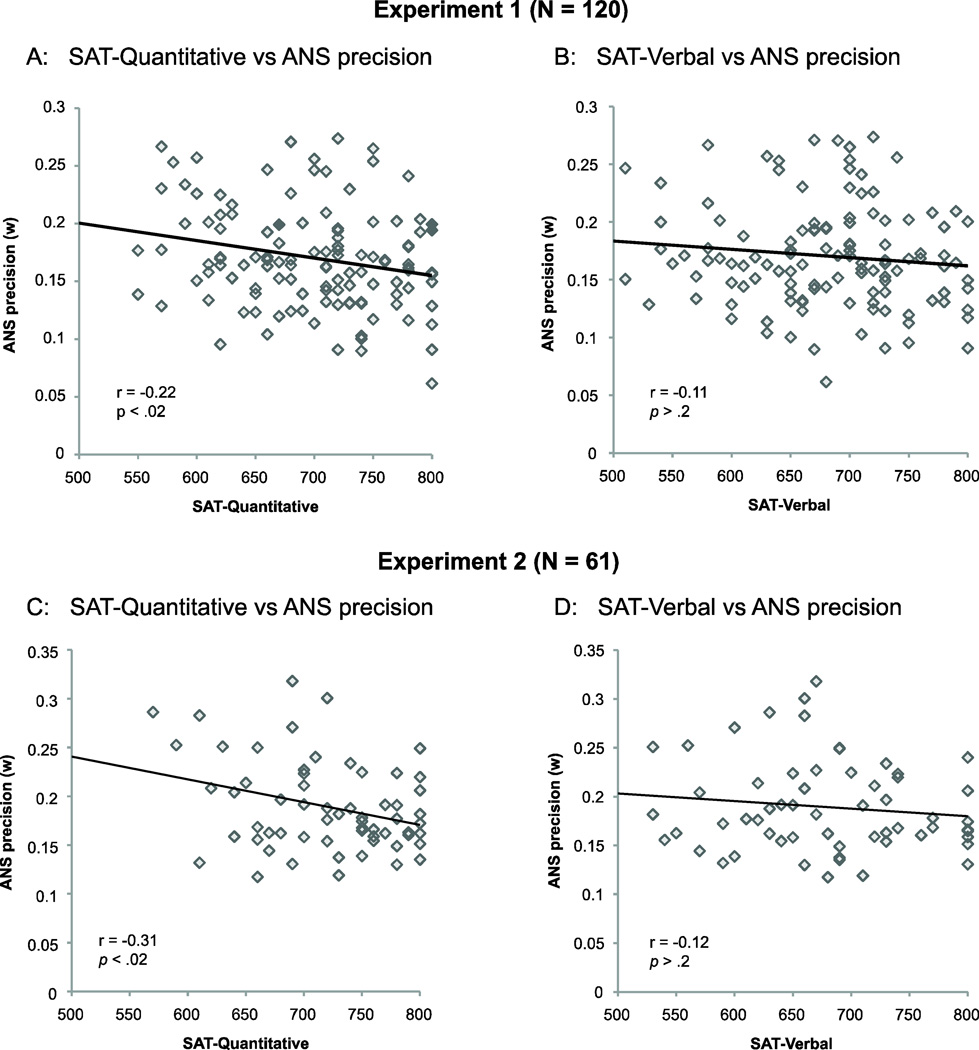
A linear regression of w with SAT-Q scores revealed that w significantly correlated with SAT-Q (r = −0.22; p < .02; Figure 3a); a separate regression revealed that w did not significantly correlate with SAT-V (r = −0.11; p = .22; Figure 3b). The correlation between w and SAT-Q remained significant even when SAT-V was controlled for (r = −0.19; p < .05). We found that having more precise representations in the Approximate Number System, i.e., a smaller w, was associated with scoring better on the quantitative section of the SAT, even when controlling for verbal SAT performance.
Figure 3.
Relationship between ANS precision and quantitative (Exp. 1: A, Exp. 2: C) and verbal (Exp. 1: B, Exp. 2: D) SAT scores respectively.
One issue with correlational measures is that they are limited by the measurement error inherent in each task. To correct for the measurement error in each, many researchers correct correlations via the attenuation correction (Schmidt & Hunter, 1996; Wilmer, 2008), which computes the proportion between the given r coefficient and the geometric mean of the reliabilities of the two variables. SAT-Q and SAT-V reliabilities were estimated at 0.91 and 0.90, respectively (Ewing, Huff, Andrews, & King, 2005). The ANS task reliability was estimated at 0.94 via a Spearman-Brown-corrected split-half correlation (Wilmer, 2008). The corrected correlation between SAT-Q and w was −0.24 (p < .01), and the corrected correlation between SAT-V and w was −0.12 (p = .18).
We found a significant correlation between college-aged students’ performance on the SAT-Q and the precision of their Approximate Number System (ANS) as assessed in a group-setting in the classroom. One concern, however, may be that testing students in the classroom may have biased our results (e.g., perhaps only the good students attended class, or sat in the front of the room where they could properly see the task, etc.). In previous research examining the ANS, participants were typically tested individually in a laboratory setting (e.g., Piazza et al., 2004). Thus, to replicate our result in a different test setting, we tested a new group of students’ in the laboratory. As in Experiment 1, we also obtained official transcripts of participants’ scores on the Scholastic Aptitude Test (SAT).
3. Experiment 2
3.1 Method
3.1.1 Participants
Participants were 61 undergraduate students who participated for course credit. All participants provided informed written consent prior to their participation in the experiment. None of the participants had previously participated in Experiment 1. Each participant completed two sessions of the ANS precision test (average delay = 76.39 days, SD = 5.23). This separation was included to ascertain the reliability of the ANS precision estimates and to assess the longitudinal stability of w scores during adulthood.
3.1.2 Materials and Procedures
3.1.2.1 ANS precision test
Each participant was individually tested in a dimly lit room. The experiment was presented on a Macintosh Pro with a 22” LCD screen and participants were seated about 42 cm away from the monitor.
Similar to Experiment 1, participants were told that they would briefly see displays of blue and yellow dots on the computer screen (see Figure 1). Each stimulus array was presented for 600 milliseconds, controlled by the computer, and participants had to indicate, by pressing either the F or J buttons, whether more of the dots were blue or yellow. In each of the two visits, participants received two practice trials, and then did 264 trials; the entire assessment lasted approximately 10 minutes.
The full set of ratios used were: 2.47, 1.43, 1.28, and 1.18, with 66 trials for each ratio. On half of the trials, the correct answer was yellow; on the other half of the trials, the correct answer was blue. The two sets of dots were separated on either side of the screen (Figure 1). Same as in Experiment 1, on half of the trials the numerically larger set was also larger in cumulative surface area (correlated trials), and on the other half the numerically larger set was smaller in cumulative surface area (anti-correlated trials).
3.2 Results and Discussion
Scholastic Aptitude Test (SAT) scores were separated by their Verbal (SAT-V) and Quantitative (SAT-Q) components; each section was out of 800 points. All students had taken the SAT during the years 2007–2009. The average SAT-V score was 678.20 (SE = 9.68), and the average SAT-Q score was 720.16 (SE = 7.78). There was a significant correlation between SAT-V and SAT-Q (r = 0.31; p < .02).
To calculate w, we used the same method as in Experiment 1. The average w at Time 1 was 0.20 (SE = 0.008) and at Time 2 was 0.19 (SE = 0.008). There were no significant differences between w at the two time points (t(60) = 0.95, p = .35) suggesting that there were no practice effects over time. A more detailed analysis of the reliabilities within and between each time point is discussed related to relationships with SAT scores below.
To have maximal power for estimating ANS abilities, we collapsed performance from the two sessions into one dataset and then modeled to find the best-fitting w for each subject. The average combined w in this sample was 0.19 (SE = 0.005), indicating that – similar to Experiment 1 – the most difficult ratio participants could reliably discriminate was 7:6 (e.g., 7 versus 6 dots, or 14 versus 12 dots, etc).
A linear regression of this combined w score with SAT scores revealed that w significantly correlated with SAT-Q (r = −0.31; p < .02; Figure 3c), and did not with SAT-V (r = −0.12; p = .33; Figure 3d). The correlation between w and SAT-Q remained significant even when SAT-V was controlled for (r = −0.29; p < .05). As in Experiment 1, we performed an attenuation correction on the scores. The Spearman-Brown-corrected split-half reliability for the ANS task was 0.74 (Time 1 = 0.69, Time 2 = 0.72). The corrected correlation between SAT-Q and w was −0.37 (p < .01), and the corrected correlation between SAT-V and w was −0.15 (p = 0.23).
Linear regressions of w at each time point with SAT scores revealed similar but slightly weaker results. At Time 1, w did not correlate with SAT-Q (r = −0.19, p = .13) or SAT-V scores (r = −0.19, p = .14). However, when an attenuation correction was applied, there was a marginal correlation between w and SAT-Q (r = −0.24, p = .06) as well as w and SAT-V (r = −0.24, p = .06). At Time 2, w significantly correlated with SAT-Q (r = −0.31, p = .01) but not with SAT-V (r = −0.04, p = .79). The attenuation-corrected correlation between w and SAT-Q at Time 2 was −0.39 (p < .01) and −0.04 (p = .73) for w and SAT-V.
Interestingly, we found a surprisingly low correlation between Time 1 and Time 2 (r = 0.22, p = .08), although the attenuation-correction reliabilities showed a stronger effect (r = 0.32, p = .01). Part of the reason for the small test-retest reliability may be that some students showed more variability in w scores between the two sessions than others. To test this, we calculated w-change scores for each participant by taking the absolute change between the two time points. The average w-change score was 0.05 (SE = 0.01). This score correlated significantly with SAT-Q (r = −0.30, p < .05) but not SAT-V scores (r = −0.13, p = .33). Thus, it appears that students who have low SAT-Q scores also showed more variability between the two testing sessions. To probe this further, we took the average w scores and divided our sample into a high-w (M = 0.22; SE = 0.006) and a low-w group (M = 0.15; SE = 0.002), and examined their w-change scores. We found that the high-w group showed significantly higher amounts of w-change (M = 0.07; SE = 0.01) than the low-w group (M = 0.03, SE = 0.005; t(29) = 2.31; p < .03). This suggests that poorer performing students may be particularly important for observing a significant relationship between ANS precision and school mathematics performance; these students in particular may have more highly variable ANS scores and may require repeated testing to gather sufficient evidence for their true ANS abilities.
Overall, we found that having a more precise ANS, i.e., a smaller w, was associated with scoring better on the quantitative section of the SAT, even when controlling for verbal SAT performance replicating our results from Experiment 1. W estimates from each testing session separately showed a similar pattern, but the effect at Time 1 did not reach statistical significance. Moreover, changes in w between the two time points were correlated with SAT-Q but not SAT-V performance. These findings suggest that the relationship between ANS and SAT-Q performance is small, specific to mathematics, and stable and that w estimates are more labile in participants who have low SAT-Q scores and high w scores. The variability in estimates of w across time, especially in poorer performing subjects, highlights the importance of assessing reliability and perhaps sampling ANS precision from multiple time points.
4. General Discussion
We found a significant correlation between performance on the quantitative subtest of the Scholastic Aptitude Test (SAT) and precision of the Approximate Number System (ANS) in college-aged students in two correlational studies. This relationship remained robust even when controlling for performance on the verbal subtest of the SAT, which controls for verbal abilities, general intelligence or effort, and additional factors as mediating this relationship. Additionally, this association was found both when students’ ANS precision was assessed in a group-setting in the classroom as well as in individual testing sessions in the laboratory. These findings suggest a specific link between formally taught mathematical abilities and an intuitive sense of number that is enduring and observable even in college entrance exams.
Previous research has shown a link between mathematical ability and ANS precision in children starting as young as three years of age and continuing through adolescence (Halberda et al., 2008; Libertus et al., 2011; Mazzocco et al., 2011; Piazza et al., 2010). The present study demonstrates this link in college students consistent with some previous reports (DeWind & Brannon, 2012; Lyons & Beilock, 2011). Our findings, however, contradict recent results by Inglis and colleagues (2011), Price and colleagues (2012), and Castronovo and Göbel (2012) who found that ANS precision does not correlate with performance on formal math tests in adults. There are several factors that might underlie these seemingly disparate results. First, Inglis and colleagues had to exclude about 25% of the participants for using non-numeric cues to perform the ANS precision test and another 10% because they didn’t perform above chance in the ANS precision test, whereas all of the participants in our study performed the ANS precision test accurately enough to yield ANS precision estimates. In spite of this higher drop rate, the w estimates derived by Inglis and colleagues were much higher (0.39) than the ones found in our experiments (Exp. 1: 0.17, Exp. 2: 0.19) and in other studies (Cordes, Gelman, Gallistel, & Whalen, 2001; Halberda & Feigenson, 2008; Pica et al., 2004; Whalen, Gallistel, & Gelman, 1999). A w estimate of 0.39 in adults is markedly different than that predicted for the ANS in adults. More generally, the present results suggest that it may be critical to account for fluctuations in participants’ ANS precision either via attenuation correction or multiple testing sessions, particularly for the lowest performing subjects. In Experiment 2, these subjects had the most labile ANS scores across sessions, and previous work on math learning disability suggests the possibility that lower achieving children may be responsible for driving much of the observed correlation between ANS precision and school mathematics performance (Desoete et al., 2010; Mazzocco et al., 2011), though continued testing across ages and ability levels is certainly required before firm conclusions can be drawn about which ages and which ability levels will show this relationship most robustly. The current results and previous papers suggest a small but consistent and specific relationship between ANS precision and school mathematics performance in adulthood.
4.1 Possible reasons for a link between the Approximate Number System and school math abilities
It remains unknown exactly when and how ANS representations integrate with formal math abilities. One hypothesis is that the ANS is instrumental in the acquisition of symbolic numerical skills such as counting and arithmetic (Dehaene, Dehaene-Lambertz, & Cohen, 1998; Gallistel & Gelman, 2000; Gilmore et al., 2007), (but see Butterworth, 2010; Carey, 2000). Greater precision in the ANS may allow children to acquire the counting sequence and other subsequent symbolic numerical skills more easily, possibly also leading to a heightened robustness of their symbolic number representations. As such, the ANS may be of particular importance at the onset of formal math learning. Under such a view, our demonstration of a robust relationship between ANS precision and performance on a college entrance exam late in life might be quite unexpected.
A second hypothesis is that poorer precision in students’ ANS representations may lead to difficulties in performing and evaluating arithmetic operations and understanding the ordinal relationship between Arabic numerals (Gilmore et al., 2007, 2010; Lyons & Beilock, 2011). Students with good estimation abilities may be able to verify and reject outcomes of arithmetic operations with greater ease, whereas students with less precise estimation abilities may rely heavily on rote-learned arithmetic strategies and may not notice errors in their execution of such strategies. Furthermore, a more precise ANS may help students understand the ordinal relationship between numbers more reliably. In this case, an imprecise ANS may be especially detrimental for understanding the relationship between numerical symbols and arithmetic performance when children first learn arithmetic strategies or when people struggle with the correct execution of arithmetic strategies. Under this view, it is perhaps surprising that performance on a college entrance exam – which does not rely heavily on basic arithmetic to differentiate young adults – would correlate well with ANS precision.
A third hypothesis is that poorer precision of the ANS representations may lead to decreased engagement in number-related activities, which may lead to an increase in math anxiety and a decrease in math ability (Maloney, Ansari, & Fugelsang, 2011; Maloney, Risko, Ansari, & Fugelsang, 2010).
We believe the links between the ANS and formal math abilities are most likely reciprocal. Future studies are needed to elucidate which of the hypotheses mentioned above, in isolation or combination, are correct and what the nature of the reciprocity between the ANS and school math abilities is. Our favored hypothesis is that the heart of the ANS is its ordinal character and that it is this sense of ordinality – as opposed to a sense of fuzzy cardinalites – that underlies the relationship between the ANS and school mathematics (Lyons & Beilock, 2011). For example, the ANS may be central to providing an intuitive understanding of arithmetic transformations (e.g., that ‘+’ means ‘getting bigger’ in number), and a student’s confidence in these foundational concepts may have a lasting impact on current and later math learning. That is, the ANS may be critical for developing a sense of confidence and understanding of transformations within numerical space as opposed to being relied on to solve any particular math problem on an exam like the SAT. At the same time, engagement in number-related activities, and estimation activities in cluttered real-world environments, might positively impact ANS precision and improve student outcomes.
In summary, we found that the acuity of college students’ Approximate Number System correlates with their math scores on a college-entrance examination even when controlling for verbal abilities. The results of the present study reveal a link between an intuitive sense of number and formal math abilities. Together with previous work these findings suggest that this association emerges in early childhood and continues throughout adolescence all the way into adulthood.
Supplementary Material
Highlights.
Investigated Approximate Number System (ANS) acuity and math ability in college.
Two correlational studies using scores on a college-entrance exam (the SAT).
ANS acuity correlates with math but not verbal skills on college-entrance exam.
Link between ANS acuity and math abilities continues into college-years.
Acknowledgements
We thank Jonathan Flombaum and Lisa Feigenson for taking time from their lectures to allow us to assess their students, and the students for their participation. This research was supported by NICHD grant R01 HD057258 to JH and development of the Panamath software was supported by NSF grant DRL0937675 to JH.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Agrillo C, Dadda M, Serena G, Bisazza A. Do fish count? Spontaneous discrimination of quantity in female mosquitofish. Anim Cogn. 2008;11(3):495–503. doi: 10.1007/s10071-008-0140-9. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke ES. Abstract number and arithmetic in preschool children. Proc Natl Acad Sci U S A. 2005;102(39):14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berch DB. Making sense of number sense: implications for children with mathematical disabilities. J Learn Disabil. 2005;38(4):333–339. doi: 10.1177/00222194050380040901. [DOI] [PubMed] [Google Scholar]
- Booth JL, Siegler RS. Developmental and individual differences in pure numerical estimation. Dev Psychol. 2006;42(1):189–201. doi: 10.1037/0012-1649.41.6.189. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Jordan KE, Jones SM. Behavioral Signatures of Numerical Discrimination. In: Platt ML, Ghazanfar AA, editors. Primate Neuroethology. Oxford: Oxford University Press; 2010. [Google Scholar]
- Buckley PB, Gilman CB. Comparison of Digits and Dot Patterns. Journal of Experimental Psychology. 1974;103(6):1131–1136. doi: 10.1037/h0037361. [DOI] [PubMed] [Google Scholar]
- Butterworth B. Foundational numerical capacities and the origins of dyscalculia. Trends Cogn Sci. 2010;14(12):534–541. doi: 10.1016/j.tics.2010.09.007. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science. 2006;17(5):401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Carey S. The origin of concepts. Journal of Cognition and Development. 2000;1:37–41. [Google Scholar]
- Castronovo J, Göbel SM. Impact of High Mathematics Education on the Number Sense. PLoS One. 2012;7(4):e33832. doi: 10.1371/journal.pone.0033832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- College Board. 2009 College-Bound Seniors - Total Group Profile Report: The College Board. 2009 [Google Scholar]
- Cordes S, Gelman R, Gallistel CR, Whalen J. Variability signatures distinguish verbal from nonverbal counting for both large and small numbers. Psychonomic Bulletin & Review. 2001;8(4):698–707. doi: 10.3758/bf03196206. [DOI] [PubMed] [Google Scholar]
- De Smedt B, Verschaffel L, Ghesquiere P. The predictive value of numerical magnitude comparison for individual differences in mathematics achievement. Journal of Experimental Child Psychology. 2009;103(4):469–479. doi: 10.1016/j.jecp.2009.01.010. [DOI] [PubMed] [Google Scholar]
- Dehaene S. Varieties of numerical abilities. Cognition. 1992;44(1–2):1–42. doi: 10.1016/0010-0277(92)90049-n. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Changeux J-P. Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience. 1993;5(4):390–407. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Dehaene-Lambertz G, Cohen L. Abstract representations of numbers in the animal and human brain. Trends Neurosci. 1998;21(8):355–361. doi: 10.1016/s0166-2236(98)01263-6. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Molko N, Cohen L, Wilson AJ. Arithmetic and the brain. Current Opinition in Neurobiology. 2004;14(2):218–224. doi: 10.1016/j.conb.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Desoete A, Ceulemans A, De Weerdt F, Pieters S. Can we predict mathematical learning disabilities from symbolic and non-symbolic comparison tasks in kindergarten? Findings from a longitudinal study. Br J Educ Psychol. 2010 doi: 10.1348/2044-8279.002002. [DOI] [PubMed] [Google Scholar]
- DeWind NK, Brannon EM. Malleability of the approximate number system: effects of feedback and training. Frontiers in Human Neuroscience. 2012;6(68) doi: 10.3389/fnhum.2012.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewing M, Huff K, Andrews M, King K. Assessing the Reliability of Skills Measured by the SAT. New York: The College Board; 2005. [Google Scholar]
- Gallistel CR, Gelman II. Non-verbal numerical cognition: from reals to integers. Trends in Cognitive Sciences. 2000;4(2):59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Geary DC. Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association; 1994. [Google Scholar]
- Gelman R, Gallistel CR. The child's understanding of number. Cambridge: Harvard University Press; 1978. [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Symbolic arithmetic knowledge without instruction. Nature. 2007;447(7144):589–591. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Non-symbolic arithmetic abilities and mathematics achievement in the first year of formal schooling. Cognition. 2010;115(3):394–406. doi: 10.1016/j.cognition.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green D, Swets JA. Signal detection theory and psychophysics. New York: John Wiley & Sons, Inc.; 1966. [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the 'number sense': The approximate number system in 3-4-5-, and 6-year-olds and adults. Developmental Psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Halberda J, Ly R, Willmer J, Naiman D, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences. 2012 doi: 10.1073/pnas.1200196109. www.pnas.org/cgi/doi/10.1073/pnas.1200196109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455(7213):665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Halberda J, Sires SF, Feigenson L. Multiple spatially overlapping sets can be enumerated in parallel. Psychol Sci. 2006;17(7):572–576. doi: 10.1111/j.1467-9280.2006.01746.x. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children's mathematics achievement. Journal of Experimental Child Psychology. 2009;103(1):17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Hyde DC, Spelke ES. All numbers are not equal: an electrophysiological investigation of small and large number representations. J Cogn Neurosci. 2009;21(6):1039–1053. doi: 10.1162/jocn.2009.21090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inglis M, Attridge N, Batchelor S, Gilmore C. Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin & Review. 2011 doi: 10.3758/s13423-011-0154-1. [DOI] [PubMed] [Google Scholar]
- Libertus ME, Brannon EM. Behavioral and Neural Basis of Number Sense in Infancy. Current Directions in Psychological Science. 2009;18(6):346–351. doi: 10.1111/j.1467-8721.2009.01665.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Brannon EM. Stable individual differences in number discrimination in infancy. Developmental Science. 2010;13(6):900–906. doi: 10.1111/j.1467-7687.2009.00948.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Preschool Acuity of the Approximate Number System Correlates with School Math Ability. Developmental Science. 2011;14(6):1292–1300. doi: 10.1111/j.1467-7687.2011.01080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Pruitt LB, Woldorff MG, Brannon EM. Induced Alpha-band Oscillations Reflect Ratio-dependent Number Discrimination in the Infant Brain. Journal of Cognitive Neuroscience. 2009;21(12):2398–2406. doi: 10.1162/jocn.2008.21162. [DOI] [PubMed] [Google Scholar]
- Libertus ME, Woldorff MG, Brannon EM. Electrophysiological evidence for notation independence in numerical processing. Behavioral and Brain Functions. 2007;3:1. doi: 10.1186/1744-9081-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense. Large-number discrimination in human infants. Psychological Science. 2003;14(5):396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lyons IM, Beilock SL. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 2011;121(2):256–261. doi: 10.1016/j.cognition.2011.07.009. [DOI] [PubMed] [Google Scholar]
- Maloney EA, Ansari D, Fugelsang JA. The effect of mathematics anxiety on the processing of numerical magnitude. Quarterly Journal of Experimental Psychology. 2011;64(1):10–16. doi: 10.1080/17470218.2010.533278. [DOI] [PubMed] [Google Scholar]
- Maloney EA, Risko EF, Ansari D, Fugelsang J. Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition. 2010;114(2):293–297. doi: 10.1016/j.cognition.2009.09.013. [DOI] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability. Child Development. 2011;82(4):1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrink K, Spelke ES. Core multiplication in childhood. Cognition. 2010;116(2):204–216. doi: 10.1016/j.cognition.2010.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mundy E, Gilmore CK. Children's mapping between symbolic and nonsymbolic representations of number. J Exp Child Psychol. 2009;103(4):490–502. doi: 10.1016/j.jecp.2009.02.003. [DOI] [PubMed] [Google Scholar]
- Nieder A, Dehaene S. Representation of number in the brain. Annu Rev Neurosci. 2009;32:185–208. doi: 10.1146/annurev.neuro.051508.135550. [DOI] [PubMed] [Google Scholar]
- Odic D, Libertus ME, Feigenson L, Halberda J. Developmental Change in the Acuity of Approximate Number and Area Representations. Developmental Psychology. doi: 10.1037/a0029472. (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, et al. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116(1):33–41. doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron. 2004;44(3):547–555. doi: 10.1016/j.neuron.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Price GR, Palmer D, Battista C, Ansari D. Nonsymbolic numerical magnitude comparison: Reliability and validity of different task variants and outcome measures, and their relationship to arithmetic achievement in adults. Acta Psychologica. 2012;140:50–57. doi: 10.1016/j.actpsy.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Noel MP. Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition. 2007;102(3):361–395. doi: 10.1016/j.cognition.2006.01.005. [DOI] [PubMed] [Google Scholar]
- Sasanguie D, De Smedt B, Defever E, Reynvoet B. Association between basic numerical abilities and mathematics achievement. Brit Jour Dev Psych. 2011 doi: 10.1111/j.2044-835X.2011.02048.x. [DOI] [PubMed] [Google Scholar]
- Schmidt FL, Hunter JE. Measurement Error in Psychological Research: Lessons From 26 Research Scenarios. Psychological Methods. 1996;1(2):199–223. [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: The psychophysics of number representation. Psychological Science. 1999;10(2):130–137. [Google Scholar]
- Wilmer JB. How to use individual differences to isolate functional organization, biology, and utility of visual functions; with illustrative proposals for stereopsis. Spat Vis. 2008;21(6):561–579. doi: 10.1163/156856808786451408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.