Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Nov 12;2:835. doi: 10.1038/srep00835

Comparing the performance of FA, DFA and DMA using different synthetic long-range correlated time series

Ying-Hui Shao 1,2, Gao-Feng Gu 1,2, Zhi-Qiang Jiang 1,2, Wei-Xing Zhou 1,2,3,a, Didier Sornette 4,5,b
PMCID: PMC3495288  PMID: 23150785

Abstract

Notwithstanding the significant efforts to develop estimators of long-range correlations (LRC) and to compare their performance, no clear consensus exists on what is the best method and under which conditions. In addition, synthetic tests suggest that the performance of LRC estimators varies when using different generators of LRC time series. Here, we compare the performances of four estimators [Fluctuation Analysis (FA), Detrended Fluctuation Analysis (DFA), Backward Detrending Moving Average (BDMA), and Centred Detrending Moving Average (CDMA)]. We use three different generators [Fractional Gaussian Noises, and two ways of generating Fractional Brownian Motions]. We find that CDMA has the best performance and DFA is only slightly worse in some situations, while FA performs the worst. In addition, CDMA and DFA are less sensitive to the scaling range than FA. Hence, CDMA and DFA remain “The Methods of Choice” in determining the Hurst index of time series.

A complex system, be it ecological, biological, technological, social, economic or financial, is usually embedded in a complex network, which is composed of a large number of interacting heterogeneous constituents linked via interwoven nonlinear heterogenous ties1. The observed signals of the physical quantities characterizing a complex system often exhibit long-range correlations2. It is of crucial importance and significance to quantify such long-range correlations to have a deep understanding of the dynamics of the underlying complex systems. More than ten techniques have been invented to detect long-range correlations in time series3,4,5, such as the rescaled range (R/S) analysis6, the wavelet transform module maxima (WTMM) approach7,8,9,10,11, the fluctuation analysis (FA)12, the detrended fluctuation analysis (DFA)13, the detrending moving average analysis (DMA)14, and so on.

Our work focuses on three methods (FA, DFA and DMA) that are very popular especially in the econophysics community. Consider a time series {x(t) : t = 1, 2, …, N} with zero mean and its profile y(t) constructed as the cumulative sum of x(t). The three methods proceed to obtain fluctuation functions F(s) specific to a timescale s. For long-range correlated time series, we have

graphic file with name srep00835-m1.jpg

where α is a scaling exponent. In FA, the fluctuation function is computed as follows12

graphic file with name srep00835-m2.jpg

which is actually a special case of the structure function in turbulence15. In contrast, both DFA and DMA adopt detrending techniques. The time series y(t) is covered by Ns disjoint boxes of size s. When the whole time series y(t) cannot be completely covered by Ns boxes, we can utilize 2Ns boxes to cover the time series by starting from both ends of the time series. In each box, a trend function g(t) of the sub-series is determined. The residuals are calculated by

graphic file with name srep00835-m3.jpg

where the trend g(t) is a polynomial function in the DFA algorithm13 and a moving average function over s data points in the DMA method14. The fluctuation function F(s) is then obtained as the r.m.s. of the residual time series:

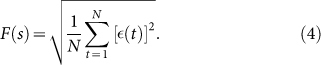graphic file with name srep00835-m4.jpg

Note that all these methods have a multifractal version16,17,18,19,20 and can be generalized to handle high-dimensional fractals and multifractals20,21,22. When y(t) is a fractional Brownian motion (FBM), the scaling exponent α is identical to the Hurst index H23,24,25,26.

Several groups have attempted to assess the performance and relative merits of these techniques. Xu et al.27 compare the performances of DFA and DMA on long-range power-law correlated time series synthesized using the modified Fourier filtering method28, and find that DFA is superior to different DMA variants. Bashan et al.29 observe that the centred DMA performs as well as DFA for long time series with weak trends and slightly outperforms DFA for short data with weak trends. They conclude that DFA “remains the method of choice” when the trend is not a priori known. Serinaldi30 uses the Davies-Harte algorithm to generate fractional Gaussian noises (FGNs) and FBMs by summing the FGNs31, and find that DFA and DMA have comparable performances. Jiang and Zhou32 report that DFA and the centred DMA perform similarly and both of them outperform the backward and forward DMA methods, when the FBMs are generated using the Fourier-based Wood-Chan algorithm33. Huang et al.34 find comparative performances of FA and DFA for FBMs with H = 1/3, which are generated with the Wood-Chan algorithm33. In contrast, Bryce and Sprague35 argue that FA outperforms DFA, for FGNs with H = 0.3 that are generated using the Davies-Harte algorithm31.

We notice that these studies concentrate on DFA versus DMA or DFA versus FA and report what appears to be contradictory results when considered together. A careful reading unveils that these studies cannot be directly compared because they have adopted different synthesis algorithms (or generators) for the long-range correlated time series to be tested. Indeed, comparing the performances of long-range correlation detection methods is not an easy task for the following reasons. Firstly, there are many algorithms to generate FGNs and FBMs36, and one should be careful not to draw too rapid conclusions on the relative performance of long-range correlation detection methods that may be sensitive to the micro-structure of the generated time series that depend on the specific synthesis algorithm. Secondly, real time series may contain a priori unknown nontrivial trends37,38,39,40, which complicates significantly the detection of long-range correlations, because trends and long-range correlations often lead to similar signals. Thirdly, there is no consensus on an objective determination approach of the scaling range, which plays a crucial role in the estimation of the scaling exponents. Often, studies use quite short scaling ranges (a decade or less), which is an hindrance for determining the genuine presence of long-range correlations41,42,43.

In this work, we focus on comparing FA, DFA and two versions of DMA, where a linear detrending is adopted in DFA and the backward and centred versions of DMA (denoted BDMA and CDMA respectively) are investigated since the forward DMA performs the worst according to the literature. The comparison between FA, DFA and two versions of DMA is conducted on time series generated using three different algorithms, thus generating a 3 × 4 matrix of comparisons: (1) FGNs using the Davies-Harte algorithm (FGN-DH)31 so that we can compare with the analysis by Bryce and Sprague35, (2) FBMs using a wavelet-based generator (WFBM)44, which input Hurst indexes are very close to the estimated DFA exponents even when H < 0.545, and (3) FBMs using the random midpoint displacement algorithm (FBM-RMD)46, because the numerical results of the generated time series are in excellent agreement with the analytical results for DMA26. Besides, we do not consider trends or other hidden nonlinear structures.

Results

Fluctuation functions

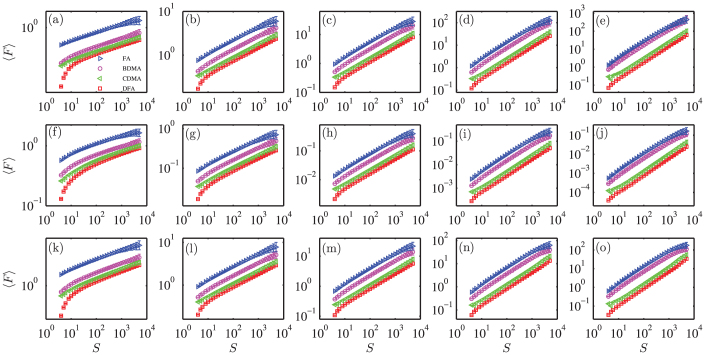
Figure 1 compares the fluctuation functions calculated with four different scaling analysis methods (FA, BDMA, CDMA, DFA) on time series generated using three different generators (FGN-DH, FBM-RMD and WFBM). We notice that panel (b) confirms the results in Ref.[35], which compares the performances of FA and DFA on FGNs with Hin. One can also notice that the error bar increases with s for each curve.

Figure 1. Scaling plots of 〈F〉 against s.

Figure 1

Open in a new tab

Each plot contains four curves obtained from four different analysis methods (FA, BDMA, CDMA and DFA) and each curve represents a fluctuation function averaged over 100 repeated simulated time series with the error bars showing the standard deviations. The three rows correspond to three generators (FGN-DH, FBM-RMD and WFBM from top to bottom). Each column corresponds to a fixed Hurst index (Hin = 0.1, 0.3, 0.5, 0.7, and 0.9 from left to right). The curves have been shifted vertically for better visibility.

When the scale s is small and the Hurst index Hin is small, the curvature of the fluctuation function for DFA is remarkable, while the FA curve looks quite straight. In addition, the DMA curves also exhibit some mild curvature. With the increase of the Hurst index Hin of the analysed time series, the curvature of the DFA and DMA curves decreases. We thus confirm that FA performs best in most cases and DFA performs worst at small scales.

However, the conclusions are very different at large scales. The DFA curves have the smallest error bars, the centred DMA curves show the second smallest error bars, and the FA curves exhibit the largest error bars. More significantly, the DFA and CDMA curves are very straight, while the FA and BDMA curves exhibit some clear curvature with the magnitude of the curvature becomes larger with the increase of the Hurst index Hin.

These observations are qualitatively the same for different time series generators.

Local slopes

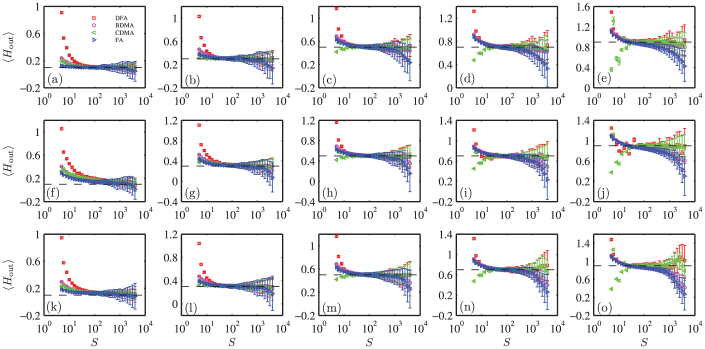
Figure 2 compares the local slopes, which are the estimates of the Hurst exponent, calculated with four different scaling analysis methods on the time series generated using three different generators. Comparing the three plots of each column, it is found that the relative performances are qualitatively the same for the three time series generators. For each scaling analysis method, the error bars become larger with the increase of the scale for each fixed Hurst index Hin or with the increase of the Hurst index Hin at fixed scale. Again, the error bars of the DFA curve are the largest in each plot.

Figure 2. Local slopes of the fluctuation functions.

Figure 2

Open in a new tab

Each plot contains four curves obtained from four different scaling analysis methods (FA, BDMA, CDMA and DFA) and each curve represents a slope function averaged over 100 repeated simulated time series with the error bars showing the standard deviations. The three rows correspond to three generators (FGN-DH, FBM-RMD and WFBM from top to bottom). Each column corresponds to a fixed Hurst index (Hin = 0.1, 0.3, 0.5, 0.7, and 0.9 from left to right). The horizontal dashed lines indicates the exact value of the Hurst index used to generate the synthetic time series.

At large scales, we find that FA is the worst in the sense that the FA curves have the largest error bars and deviate the most from the theoretical line 〈Hout〉 = Hin. In contrast, DFA and CDMA have comparable performances and perform best.

At small scales, the order of performance, as measured by the proximity of the estimates of the scaling exponents to the true Hurst values and by the size of the error bars, is 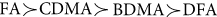Inline graphic for Hin = 0.1 in the first column, 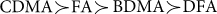Inline graphic for Hin = 0.3 in the second column, 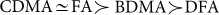Inline graphic for Hin = 0.5 in the third column, 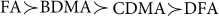Inline graphic for Hin = 0.7 in the fourth column, and 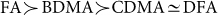Inline graphic for Hin = 0.9 in the fifth column, where 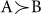Inline graphic means that A is superior to B.

Effect of scaling range

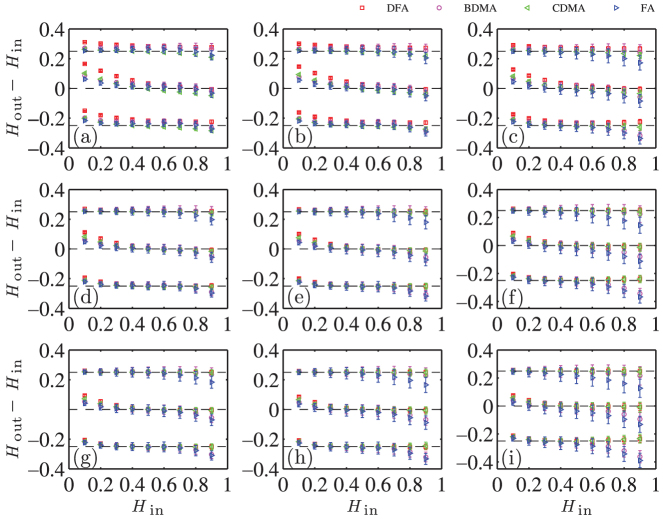
In order to perform the scaling analysis onto real systems using any of the above methods, it is of crucial importance to determine the scaling range. This is because the estimate of the scaling exponent may vary dramatically if one changes the scaling range. We now investigate the effect of the scaling range on the estimation accuracy of the Hurst index performed with the four scaling analysis methods applied to time series synthesized by the three different generators.

Let us first consider the FGNs. We find that the FA gives accurate estimates when Hin < 0.5, while the estimated indexes deviate more and more from the theoretical values when Hin increases in the persistent time series range, for all nine scaling ranges. The DFA estimates are not accurate only when sright = 999 (first row) and Hin < 0.5 and DFA outperforms FA for all the other cases. More intriguingly, CDMA gives very accurate estimates of the Hurst indexes and performs the best almost in all situations. Overall, DFA outperforms BDMA and FA is the worst estimator.

For the time series generated with FBM-RMD and WFBM, the relative performances of the four scaling analysis methods are qualitatively the same. When 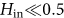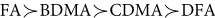Inline graphic, Inline graphic. For other situations, DFA and CDMA give very accurate estimates of the Hurst indexes and perform the best, while FA performs the worst.

Taking all these observations together, we conclude that CDMA has the best performance and DFA is slightly worse. When the scaling range is properly determined, DFA and CDMA have similar performances. In contrast, FA has the worst performance, especially in the sense that it cannot provide accurate estimations of the Hurst index for persistent time series.

Discussion

We have investigated the performances of four estimators (FA, DFA, BDMA, and CDMA) for the characterization of long-range power-law correlated time series synthesized with three different generators (FGN-DH, FBM-RMD and WFBM). We have illustrated that, overall, CDMA and DFA are the best and exhibit comparable performances, while FA performs the worst. In particular, CDMA and DFA are less sensitive than FA to the choice of the scaling range. We depart significantly from the conclusion of Ref.[35] that FA is superior to DFA, by showing that this statement holds only for very special cases (FGNs with Hin = 0.3) that cannot be extended to other situations.

An important issue is the effect of the length of time series on the results and conclusions, especially for short time series4. We repeated the analysis by generating time series of length 500 and 2000, respectively. A time series of length 2000 corresponds to time windows of 8 years of trading at the daily scale, or less than a week of data sampled at the minute time scale. The analysis comparing the results for windows of 500 and 2000 time steps to those for windows of 20000 time steps is presented in Supplementary Information and confirms that the conclusions remain unchanged, because the corresponding plots for the two cases with different time series lengths are almost indistinguishable, except that the results for shorter time series have larger fluctuations as expected29.

When analysing real world data, one might confront many complicating factors. The behaviors of many factors have been studied for synthetic time series and real-world data, such as strong trends38,47, nonstationarity39, nonlinearity40, and Hurst exponent being larger than 129,48,49. There are also a lot of efforts to improve the estimators making them more suitable for real data50,51,52,53,54,55,56. These topics are however out of the scope of the current work.

Methods

Description and preprocessing of the data

For each generator (FGN-DH, FBM-RMD or WFBM), we synthesize 100 time series of length 20000 for a given Hurst index Hin. These time series are used in all the analyses. The discrete values of the fluctuation function F(s) of each time series for each scaling analysis method are calculated at 32 s-values logarithmically sampled in the interval [4, 5000].

Figure 1 details

Each point (〈F(s)〉, s) shows the average of 100 F(s) values over the 100 time series for each Hin at scale s for a given generator and a given estimator.

Figure 2 details

For each time series, we calculate the local slope of ln F(s), which is the centred difference using two adjacent data points. Each point shows the average and the standard deviation estimated over the corresponding 100 local slopes.

Figure 3 details

For each time series, we calculate the slope of ln F(s) using the data points within the chosen scaling range. Each point shows the average and the standard deviation over the corresponding 100 slopes.

Figure 3. Impacts of the scaling range on the Hurst index estimates.

Figure 3

Open in a new tab

Each plot has a different scaling range [sleft, sright], where sleft = 4, 10, 20 from left column to right column and sright = 999, 1992, 5000 from top row to bottom row. In each plot, there are three clusters of curves. Each cluster corresponds to the three generators (FGN-DH, FBM-RMD and WFBM from top to bottom). The top and bottom clusters have been shifted vertically by +0.25 and −0.25 respectively for better visibility. In each clusters, there are four sets of points with their error bars that are obtained from four different analysis methods (FA, BDMA, CDMA and DFA). Each point shows the average slope of the Hurst index estimates over 100 simulated time series. The error bars show the standard deviations.

Author Contributions

ZQJ, WXZ and DS conceived the study, YHS, WXZ and DS designed the study, and YHS, GFG, ZQJ, WXZ and DS performed the study. WXZ and DS wrote the paper and reviewed the manuscript.

Supplementary Material

Supplementary Information

Effect of time series size on the results

srep00835-s1.pdf (1.5MB, pdf)

Acknowledgments

This work was partially supported by the Natural Science Foundation of China (11075054), the Shanghai (Follow-up) Rising Star Program (11QH1400800), and the Fundamental Research Funds for the Central Universities.

References

  1. Albert R. & Barabási A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002). [Google Scholar]
  2. Sornette D. Critical Phenomena in Natural Sciences (Springer, Berlin, 2004), 2 edn. [Google Scholar]
  3. Taqqu M. S., Teverovsky V. & Willinger W. Estimators for long-range dependence: An empirical study. Fractals 3, 785–798 (1995). [Google Scholar]
  4. Delignieres D. et al. Fractal analyses for ‘short’ time series: A re-assessment of classical methods. J. Math. Psychol. 50, 525–544 (2006). [Google Scholar]
  5. Kantelhardt J. W. Fractal and multifractal time series. In Meyers, R. A. (ed.) Encyclopedia of Complexity and Systems Science vol. LXXX, 3754–3778 (Springer, Berlin, 2009). [Google Scholar]
  6. Hurst H. E. Long-term storage capacity of reservoirs. Trans. Amer. Soc. Civil Eng. 116, 770–808 (1951). [Google Scholar]
  7. Holschneider M. On the wavelet transformation of fractal objects. J. Stat. Phys. 50, 963–993 (1988). [Google Scholar]
  8. Muzy J. F., Bacry E. & Arnéodo A. Wavelets and multifractal formalism for singular signals: Application to turbulence data. Phys. Rev. Lett. 67, 3515–3518 (1991). [DOI] [PubMed] [Google Scholar]
  9. Bacry E., Muzy J. F. & Arnéodo A. Singularity spectrum of fractal signals from wavelet analysis: Exact results. J. Stat. Phys. 70, 635–674 (1993). [Google Scholar]
  10. Muzy J. F., Bacry E. & Arnéodo A. Multifractal formalism for fractal signals: The structure-function approach versus the wavelet-transform modulus-maxima method. Phys. Rev. E 47, 875–884 (1993). [DOI] [PubMed] [Google Scholar]
  11. Muzy J. F., Bacry E. & Arnéodo A. The multifractal formalism revisited with wavelets. Int. J. Bifurcat. Chaos 4, 245–302 (1994). [Google Scholar]
  12. Peng C.-K. et al. Long-range correlations in nucleotide sequences. Nature 356, 168–170 (1992). [DOI] [PubMed] [Google Scholar]
  13. Peng C.-K. et al. Mosaic organization of DNA nucleotides. Phys. Rev. E 49, 1685–1689 (1994). [DOI] [PubMed] [Google Scholar]
  14. Alessio E., Carbone A., Castelli G. & Frappietro V. Second-order moving average and scaling of stochastic time series. Eur. Phys. J. B 27, 197–200 (2002). [Google Scholar]
  15. Kolmogorov A. N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85 (1962). [Google Scholar]
  16. Ghashghaie S., Breymann W., Peinke J., Talkner P. & Dodge Y. Turbulent cascades in foreign exchange markets. Nature 381, 767–770 (1996). [Google Scholar]
  17. Castro e Silva A. & Moreira J. G. Roughness exponents to calculate multi-affine fractal exponents. Physica A 235, 327–333 (1997). [Google Scholar]
  18. Weber R. O. & Talkner P. Spectra and correlations of climate data from days to decades. J. Geophys. Res. 106, 20131–20144 (2001). [Google Scholar]
  19. Kantelhardt J. W. et al. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 316, 87–114 (2002). [Google Scholar]
  20. Gu G.-F. & Zhou W.-X. Detrending moving average algorithm for multifractals. Phys. Rev. E 82, 011136 (2010). [DOI] [PubMed] [Google Scholar]
  21. Gu G.-F. & Zhou W.-X. Detrended fluctuation analysis for fractals and multifractals in higher dimensions. Phys. Rev. E 74, 061104 (2006). [DOI] [PubMed] [Google Scholar]
  22. Carbone A. Algorithm to estimate the Hurst exponent of high-dimensional fractals. Phys. Rev. E 76, 056703 (2007). [DOI] [PubMed] [Google Scholar]
  23. Talkner P. & Weber R. O. Power spectrum and detrended fluctuation analysis: Application to daily temperatures. Phys. Rev. E 62, 150–160 (2000). [DOI] [PubMed] [Google Scholar]
  24. Heneghan C. & McDarby G. Establishing the relation between detrended fluctuation analysis and power spectral density analysis for stochastic processes. Phys. Rev. E 62, 6103–6110 (2000). [DOI] [PubMed] [Google Scholar]
  25. Kantelhardt J. W., Koscielny-Bunde E., Rego H. H. A., Havlin S. & Bunde A. Detecting long-range correlations with detrended fluctuation analysis. Physica A 295, 441–454 (2001). [Google Scholar]
  26. Arianos S. & Carbone A. Detrending moving average algorithm: A closed-form approximation of the scaling law. Physica A 382, 9–15 (2007). [Google Scholar]
  27. Xu L. M. et al. Quantifying signals with power-law correlations: A comparative study of detrended fluctuation analysis and detrended moving average techniques. Phys. Rev. E 71, 051101 (2005). [DOI] [PubMed] [Google Scholar]
  28. Makse H. A., Havlin S., Schwartz M. & Stanley H. E. Method for generating long-range correlations for large systems. Phys. Rev. E 53, 5445–5449 (1996). [DOI] [PubMed] [Google Scholar]
  29. Bashan A., Bartsch R., Kantelhardt J. W. & Havlin S. Comparison of detrending methods for fluctuation analysis. Physica A 387, 5080–5090 (2008). [Google Scholar]
  30. Serinaldi F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Physica A 389, 2770–2781 (2010). [Google Scholar]
  31. Davis R. B. & Harte D. S. Tests for the Hurst effect. Biometrika 74, 95–102 (1987). [Google Scholar]
  32. Jiang Z.-Q. & Zhou W.-X. Multifractal detrending moving-average cross-correlation analysis. Phys. Rev. E 84, 016106 (2011). [DOI] [PubMed] [Google Scholar]
  33. Wood A. T. A. & Chan G. Simulation of stationary Gaussian processes in [0, 1]d. J. Comput. Graph. Stat. 3, 409–432 (1994). [Google Scholar]
  34. Huang Y.-X. et al. Arbitrary-order Hilbert spectral analysis for time series possessing scaling statistics: Comparison study with detrended fluctuation analysis and wavelet leaders. Phys. Rev. E 84, 016208 (2011). [DOI] [PubMed] [Google Scholar]
  35. Bryce R. M. & Sprague K. B. Revisiting detrended fluctuation analysis. Sci. Rep. 2, 315 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Zhou W.-X. & Sornette D. Statistical significance of periodicity and log-periodicity with heavy-tailed correlated noise. Int. J. Mod. Phys. C 13, 137–170 (2002). [Google Scholar]
  37. Montanari A., Taqqu M. S. & Teverovsky V. Estimating long-range dependence in the presence of periodicity: An empirical study. Math. Comput. Model. 29, 217–228 (1999). [Google Scholar]
  38. Hu K., Ivanov P. C., Chen Z., Carpena P. & Stanley H. E. Effect of trends on detrended fluctuation analysis. Phys. Rev. E 64, 011114 (2001). [DOI] [PubMed] [Google Scholar]
  39. Chen Z., Ivanov P. C., Hu K. & Stanley H. E. Effect of nonstationarities on detrended fluctuation analysis. Phys. Rev. E 65, 041107 (2002). [DOI] [PubMed] [Google Scholar]
  40. Chen Z. et al. Effect of nonlinear filters on detrended fluctuation analysis. Phys. Rev. E 71, 011104 (2005). [DOI] [PubMed] [Google Scholar]
  41. Malcai O., Lidar D. A., Biham O. & Avnir D. Scaling range and cutoffs in empirical fractals. Phys. Rev. E 56, 2817–2828 (1997). [Google Scholar]
  42. Mandelbrot B. B. Is nature fractal? Science 279, 783–785 (1998). [Google Scholar]
  43. Avnir D., Biham O., Lidar D. & Malcai O. Is the geometry of nature fractal? Science 279, 39–40 (1998). [Google Scholar]
  44. Abry P. & Sellan F. The wavelet-based synthesis for the fractional Brownian motion proposed by F. Sellan and Y. Meyer: Remarks and fast implementation. Appl. Comp. Harmonic Anal. 3, 377–383 (1996). [Google Scholar]
  45. Ni X.-H., Jiang Z.-Q. & Zhou W.-X. Degree distributions of the visibility graphs mapped from fractional Brownian motions and multifractal random walks. Phys. Lett. A 373, 3822–3826 (2009). [Google Scholar]
  46. Mandelbrot B. B. The Fractal Geometry of Nature (W. H. Freeman, New York, 1983). [Google Scholar]
  47. Horvatic D., Stanley H. E. & Podobnik B. Detrended cross-correlation analysis for non-stationary time series with periodic trends. EPL (Europhys. Lett.) 94, 18007 (2011). [Google Scholar]
  48. Telesca L. & Lovallo M. Long-range dependence in tree-ring width time series of Austrocedrus Chilensis revealed by means of the detrended fluctuation analysis. Physica A 389, 4096–4104 (2010). [Google Scholar]
  49. Gao J. B., Hu J., Mao X. & Perc M. Culturomics meets random fractal theory: Insights into long-range correlations of social and natural phenomena over the past two centuries. J. R. Soc. Interface 9, 1956–1964 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Nagarajan R. & Kavasseri R. G. Minimizing the effect of periodic and quasi-periodic trends in detrended fluctuation analysis. Chaos, Solitons & Fractals 26, 777–784 (2005). [Google Scholar]
  51. Nagarajan R. & Kavasseri R. G. Minimizing the effect of sinusoidal trends in detrended fluctuation analysis. Int. J. Bifurcat. Chaos 15, 1767–1773 (2005). [Google Scholar]
  52. Nagarajan R. & Kavasseri R. G. Minimizing the effect of trends on detrended fluctuation analysis of long-range correlated noise. Physica A 354, 182–198 (2005). [Google Scholar]
  53. Xu N., Shang P.-J. & Kamae S. Minimizing the effect of exponential trends in detrended fluctuation analysis. Chaos, Solitons & Fractals 41, 311–316 (2009). [Google Scholar]
  54. Shang P.-J., Lin A.-J. & Liu L. Chaotic SVD method for minimizing the effect of exponential trends in detrended fluctuation analysis. Physica A 388, 720–726 (2009). [Google Scholar]
  55. Qian X.-Y., Gu G.-F. & Zhou W.-X. Modified detrended fluctuation analysis based on empirical mode decomposition for the characterization of anti-persistent processes. Physica A 390, 4388–4395 (2011). [Google Scholar]
  56. Gao J. B., Hu J. & Tung W. W. Facilitating joint chaos and fractal analysis of biosignals through nonlinear adaptive filtering. PLoS One 6, e24331 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Effect of time series size on the results

srep00835-s1.pdf (1.5MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES