Kinetic Parameter Estimation Using a Closed-Form Expression via Integration-by-Parts

Abstract

Dynamic emission computed tomographic imaging with compartment modeling can quantify in vivo physiologic processes, eliciting more information regarding underlying molecular disease processes than is obtained from static imaging. However, estimation of kinetic rate parameters for multi-compartment models can be computationally demanding and problematic due to local minima. A number of techniques for kinetic parameter estimation have been studied and are in use today, generally offering a tradeoff between computation time, robustness of fit, and flexibility with differing sets of assumptions. This paper presents a means to eliminate all differential operations by using the integration-by-parts method to provide closed-form formulas, so that the mathematical model is less sensitive to data sampling and noise. A family of closed-form formulas can be obtained. Computer simulations show that the proposed method is robust without having to specify the initial condition.

1. Introduction

Dynamic emission computed tomographic imaging can measure the kinetics of the tracer’s distribution and exchange between body tissues. Using quantitative analysis techniques such as compartment modeling (Cherry et al 2003, Phelps 2004, Watabe et al 2006, Gullberg et al 2010), dynamic imaging can quantify in vivo physiologic and metabolic processes, providing information regarding underlying molecular disease processes that cannot be obtained from static imaging. However, the fitting of compartment models to dynamic imaging data may be computationally demanding and can have issues with convergence due to local minima.

A number of techniques for kinetic parameter estimation have been studied and are in use today, generally offering a tradeoff between computation time, robustness of fit, and flexibility with differing sets of assumptions. Perhaps the most robust—but also most computationally demanding—approach for estimating individual rate parameters for multi-compartment models is classic nonlinear least-squares estimation (Press et al 1988). Here, a least-squares or weighted least-squares objective function is iteratively minimized to obtain best-fit kinetic parameter estimates. Numerous curve-fitting algorithms have been investigated for this application, including derivative-based or downhill simplex methods (Press et al 1988), ridge-regression (Byrtek et al 2003, Byrtek et al 2005, O’Sullivan and Saha 1999, Yun et al 2001, Zhou et al 2002, Zhou et al 2003), simulated annealing (Wong 2002), and even discretized exhaustive search paradigms. The best results are obtained when accurate weighting is applied, though determination of the best weights is itself a challenging problem that depends on many variables including the reconstruction algorithm used (Yaqub 2006).

Unfortunately, the least-squares objective function for multi-compartment models with noisy data is ill-formed, containing broad shallow valleys and (potentially) local minima. As such, careful implementation of the curve-fitting algorithm with extensive iteration and handling of local minima is required to confidently find the global minimum. This results in computational-demands that, while reasonable for fitting individual time-activity curves, may become impractical for voxelwise parametric imaging where millions of fits need to be performed.

Much of the difficulty in the curve-fitting approaches is due to the presence of nonlinear terms in the solution to the compartment modeling equations. Significant efforts have been made to “linearize” the problem. Graphic methods that use the slope and intercept to estimate the macro kinetic parameters have found a wide range of applications. The most popular methods for two compartment models are the Patlak method (Patlak et al 1983, Zhou et al 2010) for an irreversible model and Logan method for a reversible model (Logan et al 1990). The slope in the Patlak plot provides the overall uptake rate and the slope in the Logan plot provides a measure of the total radiotracer distribution volume. The graphic methods are stable, but may not be able to estimate all kinetic parameters. Other linearization methods include the weighted integration method (Carson et al 1986, Yokoi et al 1991), linear least-squares (LLS) and generalized linear least-squares (GLLS) methods (Chen et al 1998, Feng et al 1999, Ho and Feng 1999, Wen et al 2009). Such methods are based on integrating the compartment modeling equations to obtain linear systems of equations relating the rate parameters (or combinations thereof) to integrals of the time-activity curves and blood input functions.

More recently, approaches employing temporal basis functions to reduce noise and improve parameter estimation have also been studied (Boellaard et al 2005, Gunn et al 2002, Hong and Fryer 2010, Reader et al 2006, Verhaeghe et al 2008, Watabe et al 2005). Performance comparisons of these methods have been made by Feng et al (1995) and more recently Dai et al (2011). Overall, the nonlinear least-squares method was found to provide the most robust parameter estimates when properly implemented, though this approach is also the most computationally intensive and initial condition dependent. Of the fast approaches, GLLS performed well for lower noise data, but may exhibit large bias and poor precisions when the noise level is high. Certain basis function approaches appear promising, though they are currently slower than GLLS and less thoroughly investigated.

This work offers a weighted integration method that converts the linear differential equation into an equation that does not contain any derivatives. In a sense, this approach can be viewed as transforming the time curves and their first and second order derivatives into a “wavelet” domain. Different sets of wavelets can result in different closed-form formulas. The selection of the “wavelets” or weighting functions is discussed. The proposed method is applied to microPET rat FDG data. The performance is compared with that of the traditional non-linear least-squares fitting method.

2. Derivation of closed-form formulas

2.1. The method using inner product and integration by parts

Without loss of generality, we use a generic two-compartment to illustrate the development of the closed-form methodology. The model is shown in Figure 1 and can be described by two first-order differential equations:

$$\frac{{dC}_1(t)}{dt}=(-k_2-k_3)C_1(t)+k_4{C}_2(t)+K_{1}B(t),$$ (1)

$$\frac{{dC}_2(t)}{dt}=k_3{C}_1(t)-k_4{C}_2(t).$$ (2)

Figure 1.

A general two-tissue-compartment-model.

The above two equations are referred to as the state equations in system theory. The compartment time-activities C₁(t) and C₂(t) are not individually accessible from the imaging measurement; however, the sum of them, C(t) defined as

$$C(t)=C_1(t)+C_2(t)$$ (3)

can be measured. Equation (3) is called the output equation in system theory. Combining (1)~(3) yields a linear second-order differential equation:

$$\frac{d^{2}C(t)}{{dt}^2}+(k_2+k_3+k_4)\frac{dC(t)}{dt}+k_2{k}_{4}C(t)=K_1\frac{dB(t)}{dt}+K_1(k_2+k_4)B(t),$$ (4)

where the kinetic parameters K₁, k₂, k₃, and k₄ are to be estimated from the measurements C(t) and B(t). Since C(t) and B(t) are usually measured at a set of non-uniformly distributed points and the sampling intervals are large, it is not a good idea to estimate the kinetic parameters directly from the relationship in (4), because the approximations of the first- and second-order derivatives contain large errors.

The traditional approach is to solve (4) and obtain an expression that is a nonlinear relationship between the measurements and the kinetic parameters:

$$C(t)={\alpha }_1\underset{0}{\overset{t}{\int }}{e}^{-s_1(t-\tau )}B(\tau )d\tau +{\alpha }_2\underset{0}{\overset{t}{\int }}{e}^{-s_2(t-\tau )}B(\tau )d\tau ,$$ (5)

where

$$\{\begin{array}{l}{s}_1=\frac{(k_2+k_3+k_4)-\sqrt{{(k_2+k_3+k_4)}^2-4k_2{k}_4}}{2}\hfill \\ s_2=\frac{(k_2+k_3+k_4)+\sqrt{{(k_2+k_3+k_4)}^2-4k_2{k}_4}}{2}\hfill \\ {\alpha }_1=K_1\frac{k_3+k_4-s_1}{s_2-s_1}\hfill \\ {\alpha }_2=K_1\frac{k_3+k_4-s_2}{s_1-s_2}\hfill \end{array}.$$ (6)

The traditional approach is to fit the nonlinear relationship (5) to obtain the kinetic parameters K₁, k₂, k₃, and k₄.

This paper proposes an approach that finds the inner product of each term in (4) with a “wavelet” function, g(t, T_n), and the resultant relationship is still linear:

$$\begin{array}{l}<\frac{d^{2}C(t)}{{dt}^2},g(t,T_n)>+(k_2+k_3+k_4)<\frac{dC(t)}{dt},g(t,T_n)>+k_2{k}_4<C(t),g(t,T_n)>\\ =K_1<\frac{dB(t)}{dt},g(t,T_n)>+K_1(k_2+k_4)<B(t),g(t,T_n)>.\end{array}$$ (7)

The wavelet function, g(t, T_n), is determined by two variables. The first variable t is a regular continuous variable of a one-dimensional time function, while the second variable T_n is a discrete variable representing the width of the support of the wavelet and 1/ T_n is the discrete “frequency.” The inner product in (7) is defined as

$$<f(t),g(t,T_n)>=\underset{-\infty }{\overset{\infty }{\int }}f(t)g(t,T_n)dt.$$ (8)

Since in our applications, f(t) = 0 when t < 0, and g(t, T_n) has support of [0, T_n], (8) becomes (noticing the upper and lower limits)

$$<f(t),g(t,T_n)>=\underset{0}{\overset{T_n}{\int }}f(t)g(t,T_n)dt.$$ (9)

The method of integration-by-parts is able to improve the accuracy of the mathematical model when it is implemented numerically with sampled data. This goal is achieved by replacing differentiation operations by inner-product integrals. Using the integration-by-parts method, an integral of the first or second order derivatives of the sampled data is an integral of the first or second order derivatives of the wavelet function. After the sampled data are expressed by a piece-wise constant continuous function, the inner-products are evaluated analytically, instead of numerically. In order to achieve this goal, the wavelets g(t, T_n) are required to satisfy the following conditions: (i) The span T_n cannot be longer than the data acquisition time frame; (ii) The combination of all wavelets should cover the entire data acquisition time frame; (iii) Analytical expressions of the indefinite integral of P(t) g(t, T_n), P(t) g′(t, T_n), and P(t) g″(t, T_n) exist, where P(t) is any polynomial. (iv) g(T_n, T_n) = 0. This last requirement (iv) guarantees that derivatives of f(t), which can be C(t) or B(t) in our applications, are never used except at t = 0. We can always assume that the derivatives of C(t) or B(t) are zero. This point can be better understood by looking at the integration-by-parts formula:

$$\underset{0}{\overset{T_n}{\int }}{f}^{″}(t)g(t)dt=f^{\prime }(t)g(t){\mid }_0^{T_n}-\underset{0}{\overset{T_n}{\int }}{f}^{\prime }(t)g^{\prime }(t)dt=f^{\prime }(t)g(t){\mid }_0^{T_n}-f(t)g^{\prime }(t){\mid }_0^{T_n}+\underset{0}{\overset{T_n}{\int }}f(t)g^{″}(t)dt$$

If g(T_n) = 0, f′(T_n) is not required.

With these restrictions, (7) becomes

$$\begin{array}{l}<C(t),g^{″}(t,T_n)>+(k_2+k_3+k_4)<C(t),-g^{\prime }(t,T_n)>+k_2{k}_4<C(t),g(t,T_n)>\\ =K_1<B(t),-g^{\prime }(t,T_n)>+K_1(k_2+k_4)<B(t),g(t,T_n)>.\end{array}$$ (10)

Expression (10) is a linear relation and does not contain any derivatives. One can use (10) to formulate a closed-form solution for the kinetic parameters.

The motivation of using finite-time-duration “wavelets,” instead of Fourier bases (Zeng et al 2011), is that the blood input function and the time-activity curve are only measured for a short time duration. An accurate Fourier transform would require the data to be available for the entire time axis or require the data to be periodic.

2.2. Considering contamination

In our PET applications, the measured tissue activity C(t) is contaminated by the blood input function B(t). In other words, C(t) is not measured; the measurement is V(t) as given by

$$V(t)=C(t)+\beta B(t),$$ (11)

where β is the contamination factor. The differential equation (4) is replaced by

$$\begin{array}{l}\frac{d^{2}V(t)}{{dt}^2}+(k_2+k_3+k_4)\frac{dV(t)}{dt}+k_2{k}_{4}V(t)\\ =\beta \frac{d^{2}B(t)}{{dt}^2}+[K_1+\beta (k_2+k_3+k_4)]\frac{dB(t)}{dt}+[K_1(k_3+k_4)+\beta k_2{k}_4]B(t).\end{array}$$ (12)

Let

$$\{\begin{array}{l}{x}_1=k_2+k_3+k_4\hfill \\ x_2=k_2{k}_4\hfill \\ x_3=\beta \hfill \\ x_4=K_1+\beta (k_3+k_4)\hfill \\ x_5=K_1(k_3+k_4)+\beta k_2{k}_4\hfill \end{array}.$$ (13)

Evaluating the inner product similar to that performed in (10), we have

$$\begin{array}{l}<V(t),g^{″}(t,T_n)>+x_1<V(t),-g^{\prime }(t,T_n)>+x_2<V(t),g(t,T_n)>\\ =x_3<B(t),g^{″}(t,T_n)>+x_4<B(t),-g^{\prime }(t,T_n)>+x_5<B(t),g(t,T_n)>.\end{array}$$ (14)

Let us introduce some shorthand notations:

$$\{\begin{array}{l}{A}_0(T_n)=<V(t),g^{″}(t,T_n)>\hfill \\ A_1(T_n)=<V(t),g^{\prime }(t,T_n)>\hfill \\ A_2(T_n)=<V(t),-g(t,T_n)>\hfill \\ A_3(T_n)=<B(t),g^{″}(t,T_n)>\hfill \\ A_4(T_n)=<B(t),-g^{\prime }(t,T_n)>\hfill \\ A_5(T_n)=<B(t),g(t,T_n)>\hfill \end{array},$$ (15)

where A₀,…, A₅ are functions of T_n. Then (14) is expressed as

$$A_0(T_n)=x_1{A}_1(T_n)+x_2{A}_2(T_n)+x_3{A}_3(T_n)+x_4{A}_4(T_n)+x_5{A}_5(T_n).$$ (16)

To estimate the unknowns x₁, …, x₅, an objective function is set up as

$${\chi }^2={\left|\right|A_0(T_n)-x_1{A}_1(T_n)-x_2{A}_2(T_n)-x_3{A}_3(T_n)-x_4{A}_4(T_n)-x_5{A}_5(T_n)\left|\right|}^2.$$ (17)

To find the closed-form solution, we take the partial derivatives of the objective function (17) with respect to x₁, …, x₅, respectively, and set the derivatives to zero. This results in a system of linear equations:

$$\begin{array}{l}<A_0,A_1>=x_1<A_1,A_1>+x_2<A_2,A_1>+x_3<A_3,A_1>+x_4<A_4,A_1>+x_5<A_5,A_1>\\ <A_0,A_2>=x_1<A_1,A_2>+x_2<A_2,A_2>+x_3<A_3,A_2>+x_4<A_4,A_2>+x_5<A_5,A_2>\\ <A_0,A_3>=x_1<A_1,A_3>+x_2<A_2,A_3>+x_3<A_3,A_3>+x_4<A_4,A_3>+x_5<A_5,A_3>\\ <A_0,A_4>=x_1<A_1,A_4>+x_2<A_2,A_4>+x_3<A_3,A_4>+x_4<A_4,A_4>+x_5<A_5,A_4>\\ <A_0,A_5>=x_1<A_1,A_5>+x_2<A_2,A_5>+x_3<A_3,A_5>+x_4<A_4,A_5>+x_5<A_5,A_5>.\end{array}$$ (18)

In (18), $<A_i(T_n),A_j(T_n)>={\displaystyle \sum _n}{A}_i(T_n)A_j(T_n)$ defines the dot product operation, and T_n is a discrete sampling time, which is usually non-uniformly distributed. The closed-form solution of x₁, …, x₅ is:

$$\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]={\left[\begin{array}{ccccc}<A_1,A_1>& <A_2,A_1>& <A_3,A_1>& <A_4,A_1>& <A_5,A_1>\\ <A_1,A_2>& <A_2,A_2>& <A_3,A_2>& <A_4,A_2>& <A_5,A_2>\\ <A_1,A_3>& <A_2,A_3>& <A_3,A_3>& <A_4,A_3>& <A_5,A_3>\\ <A_1,A_4>& <A_2,A_4>& <A_3,A_4>& <A_4,A_4>& <A_5,A_4>\\ <A_1,A_5>& <A_2,A_5>& <A_3,A_5>& <A_4,A_5>& <A_5,A_5>\end{array}\right]}^{-1}\left[\begin{array}{c}<A_0,A_1>\\ <A_0,A_2>\\ <A_0,A_3>\\ <A_0,A_4>\\ <A_0,A_5>\end{array}\right].$$ (19)

Finally, the estimated kinetic parameters are obtained by inverting (13):

$$\{\begin{array}{l}\beta =x_3\hfill \\ K_1=x_4-x_1{x}_3\hfill \\ k_2=x_1-\frac{x_5-x_2{x}_3}{x_4-x_1{x}_3}\hfill \\ k_3=\frac{x_5-x_2{x}_3}{x_4-x_1{x}_3}-\frac{x_2(x_4-x_1{x}_3)}{x_1(x_4-x_1{x}_3)-(x_5-x_2{x}_3)}\hfill \\ k_4=\frac{x_2(x_4-x_1{x}_3)}{x_1(x_4-x_1{x}_3)-(x_5-x_2{x}_3)}\hfill \end{array}.$$ (20)

Using the procedure presented above, one can readily obtain closed-form solutions for special cases such as (i) k₄ = 0, (ii) k₃ = 0 and k₄ = 0, (iii) β = 0, and so on.

3. Methods

3.1. The weighting of the wavelet functions

In the objective function (17), a weighting factor, W(T_n), can be assigned for each sampling time instance T_n. The weighted objective function is

$${\chi }^2={\left|\right|W(T_n)\times [A_0(T_n)-x_1{A}_1(T_n)-x_2{A}_2(T_n)-x_3{A}_3(T_n)-x_4{A}_4(T_n)-x_5{A}_5(T_n)]\left|\right|}^2.$$ (21)

It is an art to select the weighting factor W(T_n). As demonstrated in PET rat data studies, larger weighting factors are suggested for larger sampling times, T_n, that is, at lower “frequencies” 1/T_n of the wavelets. The weighting factor W(T_n) can be combined with the wavelet function g(t, T_n). Some examples of wavelet functions and their weights are given below.

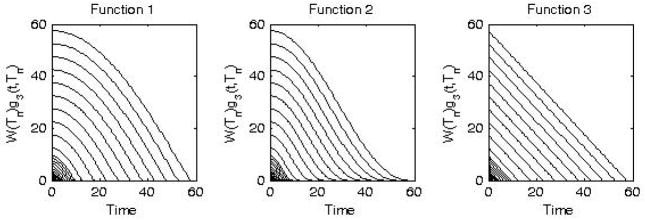
• Function 1.

  $$g_1(t,T_n)=\{\begin{array}{ll}cos\frac{\pi t}{2T_n},\hfill & 0\le t\le T_n\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\text{and}{W}_1(T_n)=T_n.$$ (22)
• Function 2.

  $$g_2(t,T_n)=\{\begin{array}{ll}0.5+0.5cos\frac{\pi t}{T_n},\hfill & 0\le t\le T_n\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\text{and}{W}_2(T_n)=T_n.$$ (23)
• Function 3.

  $$g_3(t,T_n)=\{\begin{array}{ll}1-t/T_n,\hfill & 0\le t\le T_n\hfill \\ 0,\hfill & \mathit{otherwise}\hfill \end{array}\text{and}{W}_3(T_n)=T_n.$$ (24)

These three examples of weighted wavelets W(T_n)g(t, T_n) are shown in Figure 2. The authors believe that Function #3 (24) is essentially the LLS (linear least squares) method (Chen et al 1998, Feng et al 1999). As a side-note, we believe that the original presentation of the LLS method included a typographical mistake and used the expressions of $\underset{0}{\overset{T_n}{\int }}\underset{0}{\overset{T_n}{\int }}C(t)\mathit{dtdt}$ and $\underset{0}{\overset{T_n}{\int }}\underset{0}{\overset{T_n}{\int }}B(t)\mathit{dtdt}$, respectively, for $\underset{0}{\overset{T_n}{\int }}\underset{0}{\overset{t}{\int }}C(\tau )d\tau dt$ and $\underset{0}{\overset{T_n}{\int }}\underset{0}{\overset{t}{\int }}B(\tau )d\tau dt$.

Figure 2.

Examples of three weighted wavelets defined in (22), (23), and (24), respectively.

The weighting used in the proposed algorithm is not noise related weighting, but a time related weighting. For example, one weighting scheme may emphasize a better fit at the initial time, while another weighting scheme may emphasize a better fit at the tail time region, and so on. The optimal weighting scheme seems to be data and wavelet function dependent. The default weighting function is W(T_n) = T_n, where T_n is the time-duration of a wavelet function. By altering this weighting function from the default a slightly better fit might be obtained.

3.2. Implementation considerations

The integrand of each inner product integral consists of two parts: one part being the discrete measurements and the other part being an analytical expression (e.g., g(t,T_n)). If a discrete method is used to evaluate the inner product integral, the analytical part (e.g., g(t,T_n)) must be sampled and some accuracy will be lost. On the other hand, if the discrete measurements are expressed in a piecewise analytical form, the inner product has a closed form which can be evaluated analytically, and no discretization errors are introduced. Thus, it is suggested that when implementing (15), the inner products be calculated analytically. There is more than one way to convert the discrete samples into a continuous, piece-wise analytical function. The least computationally expensive approach is to use a straight line segment to connect two adjacent samples. The second computationally economic approach is to connect three adjacent samples using a quadratic function. As the computation cost is allowed to increase, a third order polynomial, which is commonly termed a cubic spline, can be used, and so on. In most data acquisition schemes, the sampling interval is small when the activity changes rapidly, and a piece-wise linear model is adequate. In the proposed method, the discrete samples of V(t) and B(t) are first converted into a quasi-continuous function that has analytical expressions as a piece-wise linear function.

The computer implementation procedure is:

• Step 1Acquire the blood input function B and the contaminated compartment time-activity curve V, at a set of sampling times. Obtain an analytical expression for B(t) and V(t) between all sampling time via linear interpolation or polynomial interpolation so that the resultant B(t) and V(t) are continuous and have analytical expressions.
• Step 2Analytically evaluate the inner products in (15).
• Step 3Use (19) to solve for the unknowns x₁, …, x₅.
• Step 4Use (20) to obtain the kinetic parameters K₁, k₂, k₃, k₄, as well as the contamination factor β.

3.3. Computer Simulations

In computer simulations, the blood input functions were in the form of (Feng et al 1993):

$$\widehat{B}(t)=(A_{1}t-A_2-A_3)e^{-{\lambda }_{1}t}+A_2{e}^{-{\lambda }_{2}t}+A_3{e}^{-{\lambda }_{3}t},t\ge 0,$$ (25)

where A₁ = 21.28, A₂ = 7.71, A₃ = 0.37, λ₁ = 22.24 min⁻¹, λ₂ = 8.36 min⁻¹, and λ₃ = 0.1 min⁻¹. The blood and tissue time activity curves were non-uniformly sampled as 30×5sec., 20×10 sec., 10×30 sec., 10×60 sec., 10×150 sec., and 3×300 sec. At each sampling time, the activity was integrated over a 60-second time window. The total scanning time was about one hour (i.e., 3650 seconds).

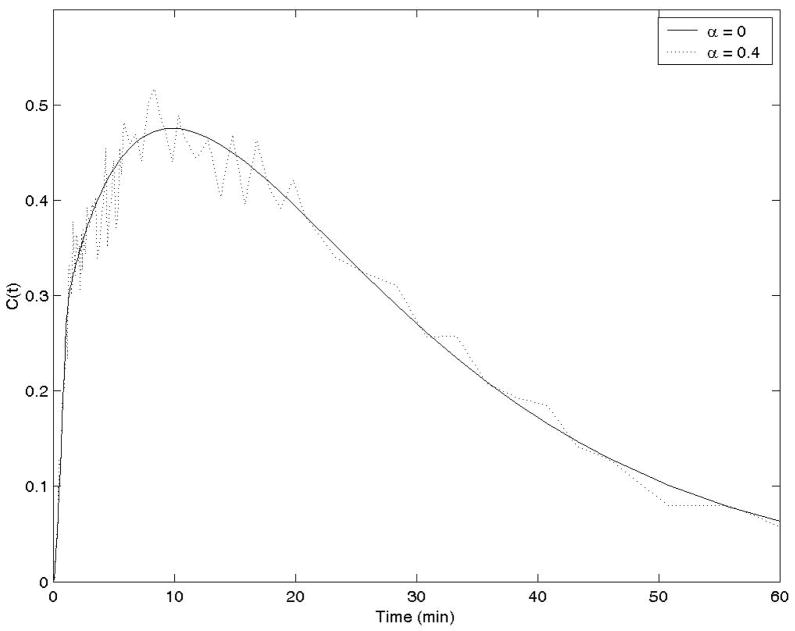
The compartment time-activity-curve Ĉ(t) was generated by using the analytical convolution expression given in (5) with K₁ = 0.4 min⁻¹, k₂ = 0.3 min⁻¹, k₃ = 0.2 min⁻¹ and k₄ = 0.1 min⁻¹. Both of the B̂(t) and Ĉ(t) functions were then integrated over 60 seconds, obtaining B(t) and C(t), respectively. Scaled Gaussian noise, N(0,1) (mean=0, standard deviation=1), was added to the noiseless data C(t), using the noise scaling factor:

$$\alpha \sqrt{\frac{C(t)2^{-t/T_{1/2}}}{T(\mathit{second})}}.$$ (26)

where T_1/2 (=110 min) is the half-life of the isotope, and the proportional constant α was selected as 0.4 for a typical noise level. The noiseless case was implemented by using α = 0. This noise model is suggested in (Feng et al 1993). Typical noisy time activity curves C(t) are shown in Figure 3 for these two α values. In the computer simulations, One hundred runs were used for computer simulations of noisy data. The proposed closed-form method with three different wavelet functions and the traditional iterative nonlinear least squares fitting method with different initial conditions were used to estimate the kinetic parameters.

Figure 3.

Time-integrated time-activity curves C(t) used in the computer simulations with 2 different noise levels.

3.4. PET Imaging Protocol

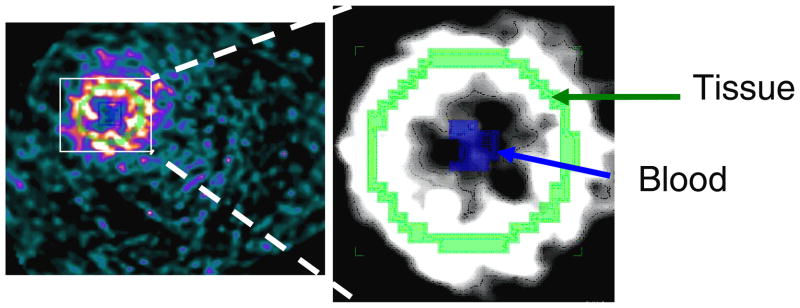
The proposed closed form method for estimation of kinetic model parameters was evaluated with data obtained from a simultaneous PET/MRI study at the University of Tuebingen. A non-fasted Lewis and Sprague Dawley male rat was imaged simultaneously with a 7T Bruker Biospec MRI scanner and PET-insert. The Siemens Inveon PET insert consisted of 10 LSO-APD block detectors having a 19 mm axial FOV (Judenhofer et al 2007). At time of injection of approximately 1mCi of FDG the acquisition began acquiring dynamic data in listmode with ECG gating for 60 mins. Simultaneous with the PET acquisition, a tagged MRI acquisition was performed. The data were reconstructed with OSEM and MR based attenuation correction as a dynamic sequence of 3D images. These images were then used to obtain time activity curves for blood input sampled from the left ventricular blood pool (~30 mm³) and for the left ventricular myocardium (~200 mm³) via manual region of interest selection. The data were histogramed into 38 time frames over 60 minutes: 12 frames of 5 seconds, 6 frames of 10 seconds, 4 frames of 30 seconds, 6 frames of 60 seconds, and 10 frames of 300 seconds. The image matrix size was 128 × 128 × 89, the pixel size was 0.487 mm × 0.487 mm × 0.8 mm, the number of subsets in the OS-EM reconstruction was 16, and the number of iterations was 4. A slice of the reconstruction is shown in Fig. 4.

Figure 4.

A short axis slice through the rat’s heart, with tissue and blood regions labeled.

FDG is initially rapidly taken up by the myocardium and then continues to accumulate slowly from the blood pool and thus displays trapping in the myocardium tissue, characteristic of irreversible kinetics. For this reason the two compartment model with four rate constants (K₁, k₂, k₃, k₄) can be simplified by assuming that the dephosphyrlatyion rate of FDG is small enough that it can be ignored (k₄ = 0) (Phelps et al 1978). In the rat studies, k₄ was assumed to be zero.

3.5. Iterative nonlinear least squares fitting method

In this paper, the proposed closed-form method is compared with the traditional iterative nonlinear least squares fitting method, in which the Matlab® built-in nonlinear fit routine nlinfit was used to fit the following model (27),

$$V(T_n)=\beta B(T_n)+{\alpha }_1\underset{0}{\overset{T_n}{\int }}{e}^{-s_1(T_n-t)}B(t)dt+{\alpha }_2\underset{0}{\overset{T_n}{\int }}{e}^{-s_2(T_n-t)}B(t)dt,$$ (27)

where T_n is non-uniformly distributed sampling times, the t is a continuous time variable. Two sets of initial conditions were used for the fit, and two different results were obtained for each study.

4. Results

Results are presented for both the traditional iterative nonlinear fitting method and the proposed closed-form method. In both methods, the discrete measurements were converted into piece-wise linear quasi-continuous functions and an analytical integration was calculated whenever an integration was needed.

4.1. Results of the computer simulations

In the noiseless situation (α = 0), the closed-form method and the iterative least squares fitting method both gave the true kinetic parameters: [K₁, k₂, k₃, k₄] = [0.4, 0.3, 0.2, 0.1]. When there was noise (α = 0.4), the proposed closed-form methods gave more accurate results than the iterative nonlinear fitting method. The results of the mean values and the standard deviations for the estimated kinetic parameters were as listed in Table 1 for both methods. The mean values and standard deviations were obtained with 100 noise realizations.

Table 1.

Computer Simulation Results with Noisy Data (α = 0.4, and 100 noise realizations)

Parameters	True Value [Noiseless data results]	Proposed closed-form methods			Iterative nonlinear fitting
		Function 1	Function 2	Function 3	Good Init. Cond. [0.1, 0.1, 0.1, 0.1]	Bad Init. Cond. [0.8, 0.8, 0.8, 0.8]
K1 (min−1)	0.4	0.40±0.020	0.40±0.022	0.38±0.019	0.40±0.024	0.33±0.159
k2 (min−1)	0.3	0.29±0.067	0.31±0.087	0.25±0.047	0.27±0428	−0.24±1.143
k3 (min−1)	0.2	0.18±0.073	0.20±0.098	0.16±0.045	0.10±0.968	−1.25±3.155
k4 (min−1)	0.1	0.09±0.021	0.09±0.025	0.10±0.012	0.10±0.034	−0.44±1.129

4.2. Results for the rat data

In the rat data, the true kinetic parameters are unknown. The fitting error was then used to evaluate the performance of each method. The fitting error is defined as the normalized distance between the measured time-activity-curve and the estimated time-activity-curve:

$$\mathit{error}=\frac{\underset{0}{\overset{\infty }{\int }}{[C_{\mathit{measured}}(t)-C_{\mathit{estimated}}(t)]}^{2}dt}{\underset{0}{\overset{\infty }{\int }}{[C_{\mathit{measured}}(t)]}^{2}dt}.$$ (28)

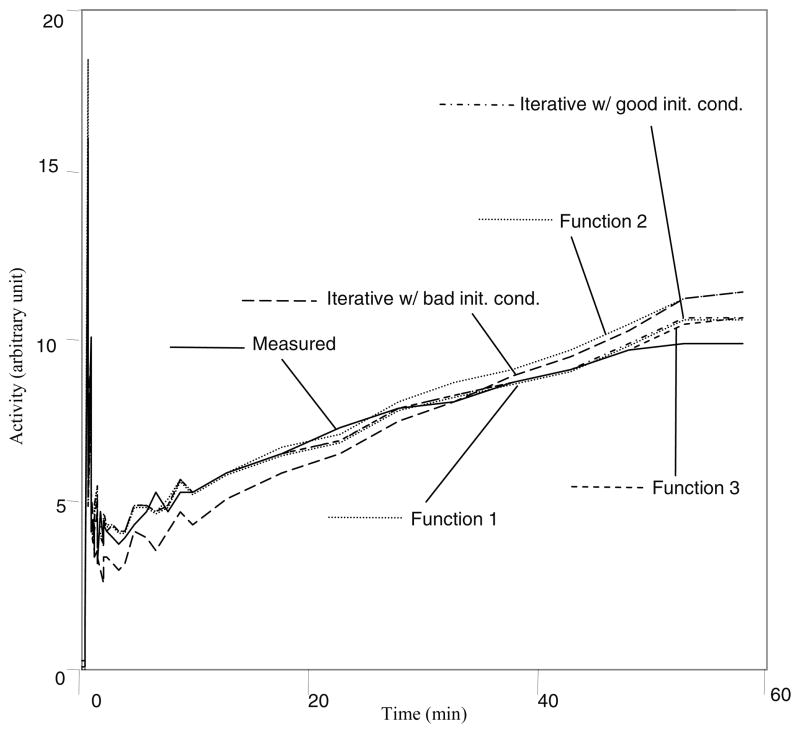
The results are summarized in Table 2. The wavelet functions g(t,T_n) are defined in (22), (23), and (24), respectively. However, the weighting function is defined as $W(T_n)=T_n^p$, where the value of p is given in Table 2. The default value of p is one, as used in the computer simulations in this paper. Changing the value of p can slightly affect the estimation results. In fitting the rat data, the value of p was changed by trial-and-error until the optimal value was found that gave the smallest fitting error (28). Some estimated time-activity-curves are shown in Fig. 5. The proposed closed-form method is computationally efficient. It took 0.0024 seconds to estimate the kinetic parameters for the rat study, using an AMD 270 core processor with the Linux operating system.

Table 2.

Rat data kinetic parameter estimation

Parameters	Proposed closed-form methods			Iterative nonlinear fitting
	Function 1 (p = 0.6)	Function 2 (p = 0.3)	Function 3 (p = 0.7)	Good Init. Cond. [0.1, 0.2, 0.3, 0.3]	Bad Init. Cond. [1, 2, 3, 4]
K1 (min−1)	0.346	0.285	0.323	0.377	2.713
k2 (min−1)	0.516	0.56	0.474	0.619	7.937
k3 (min−1)	0.046	0.062	0.045	0.050	0.107
β	0.373	0.432	0.379	0.371	0.271
error	0.026	0.031	0.026	0.025	0.028

Figure 5.

The time-activity-curve fits using the proposed closed-form method and the traditional iterative least squares fitting method for the experimental rat data.

5. Conclusions

This paper has developed a closed-form solution for the general kinetic parameter estimation problem. The strategy in this method is to use inner products to eliminate the derivatives via the well-known integration by parts technique. The inner products require a set of wavelet functions that have different “pulse widths” T_n. These wavelet functions must have simple closed-form expressions for their derivatives and the integration by parts can be used to simplify the differential equation. This is to ensure that the resultant equation does not contain any derivatives. The proposed closed-form method is an extension of the LLS (linear least squares) method (Chen et al 1998, Feng et al 1999), which is a special case of the proposed method by using the wavelet Function #3 (24).

The mathematical model is continuous, while the data are discrete and are non-uniformly sampled in a short period of time. Accurate approximation of the continuous integrals is necessary; otherwise the resultant discrete model may contain some errors. These errors result from the discretization of an analytical expression (e.g., g(t,T_n)) and can be avoided if analytical evaluation of the inner products is utilized. In other words, using the naïve discrete convolution may give a poor approximation of the continuous convolution. Continuous convolution should be calculated analytically as a continuous integral and the discrete samples must first be converted into a quasi-continuous function by piece-wise linear or piece-wise polynomial interpolation.

The proposed closed-form method has been verified by comparing with the traditional iterative nonlinear least squares fitting method using computer simulations and experimental data obtained by PET imaging of a rat. The requirement of k₄ = 0 was enforced for the rat data.

This closed-form method also has its drawbacks. It is difficult to enforce any constraints (e.g., positivity or range constraints on the kinetic parameters).