Abstract
In this work, we demonstrate a novel and cost-effective approach to implement a disposable microfluidic contactless impedance cytometer. Conventional methods for single cell impedance cytometry use microfabricated electrodes in direct contact with the buffer to measure changes of its electrical impedance when cells pass through the applied electric field. However, this approach requires expensive microfabrication of electrodes, and also, the fabricated electrodes cannot be reused without thorough and time-consuming cleaning process. Here, we introduce a novel approach to allow for single cell impedance cytometry using electrodes that can be reused, without the need for microfabrication of the electrodes. This disposable device can be potentially inserted onto a Printed Circuit board (PCB) which has a non-disposable, yet inexpensive, electronic reading apparatus. This significantly reduces the manufacturing costs, making it suitable for low resource settings, such as point-of-care testing in the developing countries.
Introduction
Over 34 million people in the world today are infected with the HIV virus, of which almost 90% live in the developing world where resources are extremely limited1. Thus the need for ultra-low cost diagnosis, monitoring, and therapy in these settings is of utmost necessity. One of the most commonly used methods for diagnosing and monitoring HIV patients is through obtaining CD4 cell counts2. The conventional method for CD4 cell counting is through the use of flow cytometry3, which is expensive and unaffordable in the developing world. Other diseases in the developing world which are prevalent include tuberculosis and Malaria. An important test for diagnosing tuberculosis involves counting lymphocytes4, while counting of monocytes offers important information for diagnosis of malaria5. Thus, it is absolutely necessary to develop a disposable diagnostic tool which can rapidly and accurately count cells. To this end, in this work we focused on developing a disposable low cost cytometer which uses impedance sensing to count cells. Impedance cytometry is preferable because of the substantially lower cost of the readout and detection circuitry as compared to equally sensitive optical methods. For the various applications mentioned, this sensing technology can be used in conjunction with microfluidic technologies which can pre-isolate cells6,7,8 based on surface antigen. In this work we focus solely on lowering the cost of the impedance sensor.
The earliest cytometer capable of measuring single cell impedance was reported by Coulter more than 50 years ago9. In this system, by applying voltage on a pair of electrodes and creating an electric field across a pore, the changes in the ionic current through the pore can be monitored as micro-particles pass through. Hence, it can be used to detect, count, and characterize cells of various sizes. This work was followed by the analysis of Deblois and Bean10, where they used an adaptation of Maxwell’s approximation to estimate the increase in resistance of the conducting pore as a result of the presence of a finite-sized particle. Hoffman and Britt11 extended Coulter counter’s operation to perform high frequency AC measurements which is more informative of certain cellular properties.
The Coulter principle in a micro-fabricated device was first demonstrated by Larsen et al.12. Thereafter, the advances in microfabrication technology resulted in an increasing trend of the development of microfluidic chip-based Coulter counters that would address the need for analyzing micro-scale (and even nano-scale) particles with high sensitivity. As one of the pioneers of the field, Morgan et al. demonstrated single cell dielectric spectroscopy using a microfabricated flow cytometer13. Saleh and Sohn14 used a fabricated microchip Coulter counter on a quartz substrate to sense colloids as small as 87 nm. Furthermore, over past few years, several groups focused on improving the impedance sensing scheme and throughput of the micro-fabricated Coulter counter15, as well as resolving issues such as clogging. Wu et al.16 used a design of symmetric mirror channels in the sensing scheme of their sensor. This improved the measured signal-to-noise ratio and allowed for detection of 520 nm-diameter particles in a sensing pore of 50×16×20 μm3 (volume ratio of the particle to the sensing channel: 0.0004%). To improve the throughput of the Coulter counter, a design of four apertures was demonstrated17,18 which detects and counts micron-size particles through corresponding sensing channels simultaneously. Moreover, with the use of a tuned radio frequency (RF) probe and measuring the reflected RF power, a high bandwidth counting rate of 30 kHz in a single microfluidic channel was reported19. To resolve the clogging issue, the use of three-dimensional hydrodynamic focusing20 was presented, which creates a narrow sample stream on the floor of the channel for close interaction with sensing electrodes, without the risk of blocking the channel.
With the advances in the design of Coulter sensors and the electronic measurements as mentioned above, these devices have found use in biomedical, clinical, and point-of-care diagnostic applications. Recently, the use of a Coulter-type chip to determine the concentration of spermatozoa in semen was reported21. Kim et al. presented a microfluidic chip with polyelectrolytic gel electrodes (PGEs) to quantify the number of red blood cells (RBCs) in diluted whole blood22. Furthermore, Holmes and Morgan demonstrated an impedance cytometry platform, in which lymphocytes, monocytes, and neutrophils were separately distinguished and counted in human whole blood23.
The recent developments in impedance cytometry have enabled high-speed measurement, detection, and characterization of single cells. However, to our knowledge, none were focused on reducing the cost of the device while preserving the core functionality of the sensor, which would allow for the device to find application in point-of-care diagnostics in limited resource settings. The existing approaches for single cell impedance cytometry use micro-fabricated electrodes in direct contact with the buffer to measure changes of its electrical impedance when cells pass through the applied electric field. However, these methods not only require expensive microfabrication of electrodes, but also, the fabricated electrodes cannot be reused without a thorough and time-consuming cleaning process. Low cost contactless conductivity detection has previously been demonstrated in a capillary electrophoresis setting24,25,26,27,28,29,30. Nonetheless, to the extent of our knowledge, contactless impedance measurement has not been demonstrated for single cell detection. Recently, contactless cell manipulation using Dielectrophoresis was demonstrated31. Similar to this approach, and as conceptually shown in Figure 1(a), we used a contactless measurement method to perform single cell impedance cytometry using electrodes that can be reused, without the need for microfabrication of the electrodes. We implemented a disposable biochip that can be inserted onto a Printed Circuit board (PCB) which has reusable electrodes to perform contactless electrical impedance measurements. This significantly reduces the manufacturing costs, making it suitable for low resource settings, such as point-of-care testing in developing countries.
Figure 1.
(a) Diagram of the device. PDMS channel and glass coverslip containing the sample is disposable, while the biosensor electronic chip is reusable. (b) Simplified equivalent circuit model of the microfluidic device. R refers to the series resistance of channel and pore. ΔR is the change in channel resistance as a result of the passage of beads or cells. Cg is glass coverslip capacitance for each electrode-glass-electrolyte interface, and Cpar is the parasitic capacitance.
Theoretical Analysis
Figure 1(b) represents the simplified equivalent circuit model of the relevant components in the microfluidic device. The conducting medium, i.e. the electrolyte can simply be modeled as resistance. The parasitic capacitance which takes into account the direct coupling between the two electrodes is also incorporated in this model. The interface between the glass-covered electrodes and electrolyte is effectively an insulator (glass) in between two conductors (electrode and electrolyte) and can be modeled as capacitance. In the conventional devices, with metal electrodes in direct contact with the solution, the role of the double layer capacitance in the signal spectrum is mainly apparent at low frequencies21, 32, typically from DC up to 10–100 kHz. However, in our design the glass capacitance influences the signal spectrum for a much broader frequency range, possibly close to or beyond the measurement bandwidth, as the glass capacitance is orders of magnitudes smaller (due to its larger thickness) than the double layer capacitance. Therefore, when performing electrical measurements this dominating capacitance causes only a small fraction of the applied voltage to appear across the conducting medium, which in turn, degrades the measured signal close to the minimum detectable level. As a result, a careful circuit analysis is required to systematically identify the relevant parameters in the design space to ensure that the optimum setting is used to maximize the Signal-to-Noise ratio (SNR).
The first step is to properly define the signal of interest in our context. Here, we intend to measure the increase in impedance as a result of the passage of cells or beads. For the frequency range of interest (mainly limited by the measurement setup’s gain and noise performance), the presence of beads and the cells (e.g. Red Blood Cells32) can simply be modeled as insulators in a conducting channel, resulting in the change of impedance to be mainly resistive. Also, our channel length is longer than its diameter, and therefore, we can use the approximation given by Deblois and Bean10, which provides an upper-bound value for the increase in resistance of a circular cylindrical conducting channel:
| (1) |
where ρ is the resistivity of the electrolyte, d the diameter of the passing spherical particle, Dm the diameter of a slightly bulged cylinder, and L the length of the pore, and
| (2) |
is the correction factor, which in our case corrects the approximation by only ~1%, since the diameter of the sphere is much smaller than that of the channel. In our fabricated design, our channel has a rectangular shape. Therefore, in the equation above, we use an effective value of Dm14, obtained from equating the cross-sectional area of our rectangular pore with that of a circular pore.
The resistance variation ΔR manifests itself in the form of change in the baseline current ΔI, for the applied AC voltage Vin. In our measurement setup, ΔI is amplified through a transimpedance stage with the gain of −Rf, and after down-conversion to base-band, is low-pass filtered and measured in the form of ΔVout, the change in the output baseline voltage. The qualitative description given above can be analytically expressed as following:
| (3) |
Z represents the device’s impedance as shown in Figure 1(b), which is a series combination of channel and pore resistance (R) and glass coverslip capacitance (Cg, for each electrode-glass-electrolyte interface), all in parallel with the parasitic capacitance (Cpar):
| (4) |
where s represents the complex frequency, with angular frequency ω being its imaginary component. The change in baseline current ΔI as a result of the small change in the channel resistance, due to the passage of beads or cells, can be derived as:
| (5) |
| (6) |
| (7) |
Resulting in change in output baseline voltage ΔVout of:
| (8) |
| (9) |
Here, ΔVout is measured at the output of the lock-in amplifier and is the signal that we use in relation with the output-referred voltage noise to study the SNR characteristic of the design. The term in this expression, dictates that signal at low frequency is degraded significantly by the small value of the glass coverslip’s capacitance. Ideally, to improve the signal level, a large coverslip capacitance (higher dielectric material or thinner coverslip) is preferred. However, here we were limited by the commercially available coverslips to facilitate the contactless measurements. To overcome this limitation, we have to increase the frequency of excitation f (where ω = 2πf). The signal in low frequency range ( ) is directly proportional to the square of frequency of excitation. The increase in the signal slows down with frequency, and eventually the signal reaches its saturation value of . This saturation value provides an upper-bound for our measurable signal.
One should keep in mind that the improvement of signal with frequency is practically restricted mainly by the slew-rate limitation of the amplifier, and not by the amplifier gain roll-off. Referring to the equation 9, to increase the measureable signal at the output, high amplitude baseline voltage must be applied at the input of the sensing device. This effectively, makes our measurements slew rate limited when operating at high frequencies, since the electrodes of the sensing device short capacitively (Cpar) in that frequency range and subsequently increase the baseline voltage at the output of the amplifier.
While the increase in signal with frequency is desired, it is only practically useful when it is improved with relation to the noise level in our system. For this purpose an electronic circuit noise model of the device and the measurement setup is developed, which allows to analytically derive and simulate the electrical noise behavior of the circuit. As Gawad et al.33 speculated in a similar measurement setup, to explain the order of magnitude of difference in their expected and measured output voltage noise, other sources of noise, such as heating of the solution, instantaneous bubble formation, and variation in flow speed may also be relevant in our system. However, here, we limit the scope of the discussion to the well-understood noise contribution from the electrical components in the setup. In the frequency range of interest, the major noise contributors are the conducting solution-contained channel (thermal noise) and the lock-in amplifier. The thermal noise of the channel can be represented by the voltage power spectral density of (where k is Boltzmann’s constant, T the temperature in Kelvin). The lock-in amplifier noise can be represented by its equivalent voltage and current noise generators, which in our case had voltage and current noise spectral density of and respectively. By summing up the relevant contributing noise sources we can derive the power spectral density of the total input-referred current as
| (10) |
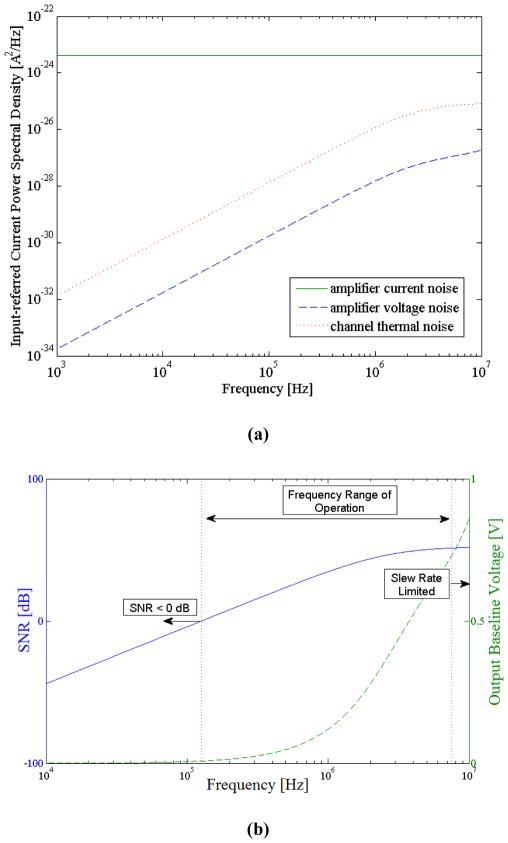
From equation 10 we can observe that the first term (amplifier’s input-referred current noise) is independent of the frequency of operation, while the other terms vary with frequency. To better understand the impact of each term on the overall electronic noise performance, we simulated the noise model of our circuit. Figure 2(a) illustrates the input-referred current power spectral density of the contributing noise sources. This figure shows for the frequency range of interest, the power spectral density of the lock-in amplifier’s current noise is more than an order of magnitude higher than the other contributing terms.
Figure 2.
(a) Input-referred current power spectral density of the contributing noise sources. (b) Simulation results illustrating the frequency range of operation. At low frequencies, signal is below the noise level (SNR < 0 dB) due to the presence of the glass coverslip. At high frequencies, the parasitic capacitance becomes electrically short and hence, the baseline output voltage increases. This makes our measurements slew rate limited.
This results in an overall flat noise power spectral density in our system, while as discussed previously the measureable signal increases with frequency. Therefore, to improve the SNR in our measurements, we need to operate at sufficiently high frequencies to reduce the degrading effect of the relatively thick coverslip which unavoidably must be used to facilitate the contactless measurements. The upper bound on the frequency of operation in this context is determined by the amplifier’s slew-rate. The above discussion can be better illustrated by Figure 2(b), which represents the simulated SNR and the output baseline voltage, based on the measurement settings and the specification of our device and lock-in amplifier (more in the Experimental section). Finally, it’s worth mentioning that the signal and circuit analysis carried out for this device can also be used to model the conventional impedance sensing devices by simply replacing the glass coverslip capacitance Cg in this work, with the double-layer capacitance present at the interface of the electrode-buffer in the conventional methods.
Experimental Section
Channel and PCB Fabrication
We fabricated an 8 μm high micropore with two narrow regions (14 μm) sandwiching a wide region (54 μm) as shown in Figure 3(a). The micropore is connected from either side to a tapered wider and taller channel of width 300 μm and height 20 μm. The use of grated sidewalls in our fabricated pore allows us to measure a coded signal (here, a double-pulse pattern) in our raw and pre-processed measurements. Using this approach and by applying a matched filter to our data, we could achieve a higher SNR compared to applying a low-pass filter alone34, and hence we could better distinguish the signal from the amplitude noise. However, this is not a requirement in our design and we would still be able to measure the desired signal using a simple (non-corrugated) pore of comparable dimensions. The channel including the pore was fabricated in PDMS (polydimethylsiloxane). Using SU-8 photoresist, the master mold for the channel was patterned onto a silicon substrate. PDMS (10:1 prepolymer/curing agent) was poured onto the master mold and allowed to cure at 80 °C overnight. Once the PDMS channel was formed, it was peeled off from the mold. Then, two holes of diameter 3 mm were punched, one at each end, to create the channel’s inlet and outlet ports. The PDMS microchannel was then bonded to a 150 μm-thick coverslip (VWR, USA) after oxygen plasma treatment35.
Figure 3.
(a) The fabricated channel SU-8 mold. Micropore contains two narrow 14 μm wide regions, and one wider 54 μm wide region. Pore is 8 μm in height and is surrounded by two outer electrodes for measuring current across pore. (b,c) The view of the PCB fabricated electrodes without (b) and with (c) the disposable microfluidic chip. Each electrode is connected to an SMA RF connector to interface with the impedance spectroscope.
The pair of electrodes (2 mm in width, 5 mm in length, and 2 mm apart) were fabricated using PCB technology (Sierra Circuits Inc. USA) with FR4 as the insulating material (Figure 3(b,c)). Each electrode was connected to an SMA RF connector (Pomona Electronics, USA) to interface with the impedance spectroscope. The dimensions of the electrodes were chosen sufficiently large, to allow for easy alignment of the disposable channels that were to be placed on top. Furthermore, to ensure a stable and sealed contact of the disposable chip with the electrodes, high vacuum grease was applied at the bottom of the chip before placed on the PCB. In the large scale production of such a device, the pre-alignment can be done when bonding the channel to the glass coverslip. Then, using a slide-and-snap mechanism (a place holder for aligning and clamping down) the disposable chip can be securely inserted onto the PCB board. This will minimize variations in the x, y, and z direction that may affect the sensitivity.
Measurement Setup
We used an impedance spectroscope (Zurich Instruments HF2IS, Switzerland) and a transimpedance amplifier (Zurich Instruments HF2TA, Switzerland) to excite the electrodes and monitor the real-time variation in output signal as a result of passage of particles using lock-in technique. This setup is also used to capture the impedance spectrum of the device in order to validate and characterize the equivalent circuit model of the device.
Experimental Procedure
First, to validate the developed circuit model the impedance between the two electrodes (with the disposable microfluidic chip on top) was measured. Three separate buffers with different conductivities were used. The buffers were deionized (DI) water, PBS (phosphate-buffered saline), and NaCl-concentrated-PBS with measured conductivities of 1.2 mS/m, 1.7 S/m, and 12 S/m respectively. The DI water and NaCl-concentrated-PBS filled channel corresponds to the cases were the channel has high and low resistance respectively. Next, upon validation of the model, with NaCl-concentrated-PBS as the solution buffer and using the same measurement setup, we demonstrated the core functionality of the device, and also, verified the signal analysis that was presented in the previous section. To ensure the reproducibility of results, the above experiments were performed on three different devices.
By directly pipetting into the inlet well, 2.8 μm diameter sample beads were injected into the channel. The heights of the fluid columns in both the inlet and outlet were adjusted to generate and control the fluid flow. In the fully developed system the flow would be controlled with the aid of an inexpensive micro-syringe pump, where negative pressure is applied to the syringe to pull the fluid. A 10 V AC voltage, modulated at four different frequencies (200 kHz, 400 kHz, 600 kHz, and 800 kHz) was applied at one terminal of the device. To measure the change in channel impedance as a result of the passage of beads, the other terminal of the device was connected to the transimpedance amplifier with the gain of 10 kV/A. By demodulating the amplified signal (at the same four modulating frequencies) the signal was down-converted to base-band and recorded for each frequency channel. The results were then postprocessed in MATLAB (R2010b, MathWorks Inc, USA), where we applied a bandpass filter (with the midband range of 10 Hz to 100 Hz), to remove the low frequency drift at the output that is often observed in such measurement setups21, while rejecting all the high frequency components greater than that of our peaks. In parallel to performing electrical detection, the passage of beads through the pore was video-recorded, to verify that each measured peak in our system indeed corresponds to passage of beads through the pore.
Finally, with the established measurement settings from our previous experiments (above), we validated the functionality of our device to detect biological cells in a real biological sample. For this purpose, we used whole blood (sheep). Then, following the same procedure as before and applying 10 V (modulated and demodulated at 900 kHz) we demonstrated single cell detection.
Results and Discussions
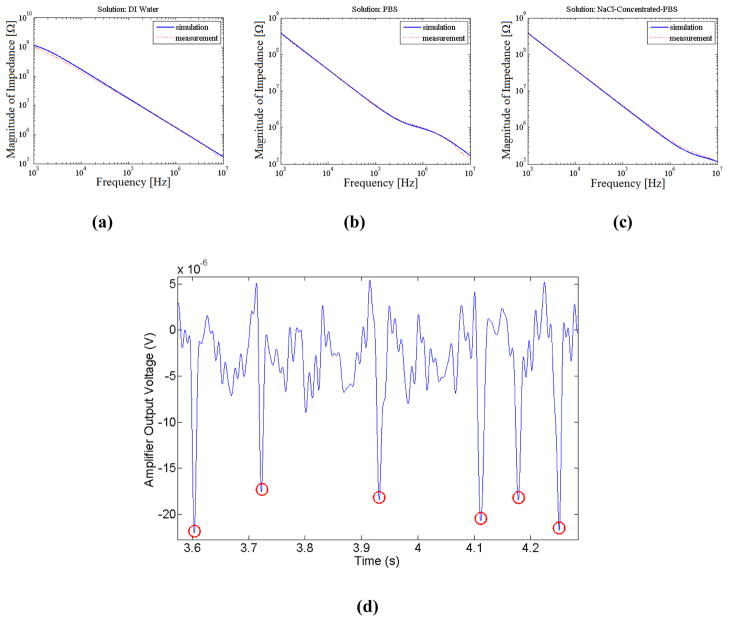
Figure 4(a)–(c) illustrates the measured impedance spectrum of the device for three cases of channel filled with DI water, PBS, and NaCl-concentrated-PBS. For each case the impedance spectrum predicted by the theoretical circuit model is overlaid. The component values in the circuit model were determined through hand analysis and preliminary characterization measurements. The overlaid spectrums show a close agreement between the measured and simulated results which supports our developed circuit model for the device. In the case where the channel is filled with PBS, the effect of buffer resistance can be seen, where a transitional plateau in the spectrum for a short intermediary frequency range is evident. The frequency width for which this plateau is apparent is determined by the ratio of the second pole to the zero in the device impedance expression (equation 4), which can be simplified to and in our case is 4.5 (corresponding to less than half a frequency decade). This resistive plateau is pushed to lower frequencies when the channel is filled with DI water, and to higher frequencies when channel is filled with NaCl-concentrated-PBS due to the lower and higher channel conductivities respectively. When operating above the frequency at which the resistive plateau becomes apparent ( ) the impedance of the glass capacitance becomes negligible in comparison with the resistance of the channel and pore ( ). This in turn shows that beyond this frequency, the degrading effect of the coverslip capacitance on the signal strength is in effect suppressed and maximum signal is effectively achieved, as can be seen from the derived signal expression in equation 7. In all three impedance spectrums, the onset of deviation of measured from theoretical values in high frequencies can be attributed to the slew-rate limitation in our measurements (as explained in ‘Theoretical Analysis’ section).
Figure 4.
(a)–(c) Impedance spectrum between the two electrodes, with the disposable microfluidic chip on top, with sample solution as (a) DI water, (b) PBS, and (c) NaCl-concentrated-PBS. (d) Measured output voltage, indicating the passage of six beads captured at 800 kHz (buffer NaCl-concentrated-PBS).
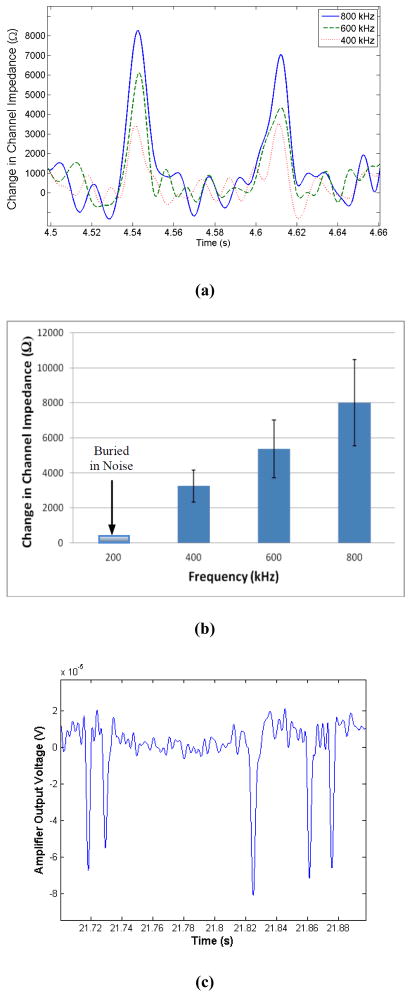
To illustrate the functionality of the device, representative data for the passage of six beads captured at 800 kHz is shown in Figure 4(d). As was verified optically, all the measured peaks corresponded to the passage of beads through the pore. Furthermore, to demonstrate the improvement of signal with frequency, the passage of 60 beads through the pore was captured at 200 kHz, 400 kHz, 600 kHz, and 800 kHz. Based on our results, no peaks could be detected for the measurements at 200 kHz (signal was buried by noise), while the peak signal at other three captured frequencies was evident, and increased with frequency of operation. Figure 5(a) shows the representative data, illustrating the signal in the form of the equivalent change in channel impedance as a result of passage of two beads for different captured frequencies. Furthermore, the overall outcome of our experiment is illustrated in Figure 5(b), which demonstrates the improvement in signal with frequency (for the range of interest).
Figure 5.
(a) Representative data, change in channel impedance, due to the passage of two beads after filter is applied. (b) Experimentally measured change in channel impedance as a result of passage of beads representing 60 distinct peaks. With increase in frequency, the measurable change in impedance increases. The measurement results at 200 kHz were buried in noise. Error-bars indicate one standard deviation of variation in the average. (c) Measured output voltage, indicating the passage of five blood cells in the sheep whole blood as the buffer.
Finally, in our experiment using sheep whole blood as our sample we successfully detected blood cells where the passage of each single cell through the pore resulted in a SNR of at least 2.5 (8 dB). As before, we verified optically that all the measured peaks corresponded to the passage of the cells through the pore. In specific, passage of the blood cells corresponded to the peaks with the magnitudes proportional to that of the cell sizes. As representative data, Figure 5(c) illustrates the measurement output voltage indicating the passage of five blood cells in the sheep whole blood as the buffer. This validates the functionality of our device to detect biological cells in physiological buffer conditions.
In conclusion, we validated the developed circuit model for our disposable device, and we demonstrated the desired impedance sensing functionality of device. Additionally, we showed that for the frequency range of interest, the peak signal improves with frequency, and there is a lower bound on the operating frequency, below which the peak signal will be buried by noise. This minimum frequency of operation requirement is practically imposed by the presence of the small coverslip capacitance (with relatively high thickness). While ideally, we would prefer to use thinner coverslips or coverslips with higher dielectric constant (to increase its capacitance), here we were limited by the commercially available coverslips to facilitate the contactless measurements. Our future work on improving the performance of the device will be focused on revisiting our choice of barrier to isolate the electrodes from the buffer. Here, we used the glass coverslip (as the substrate for PDMS channel) to form the barrier, however, this can be replaced by a thin PDMS membrane which contains the channel, while providing a barrier between the electrode and buffer. In addition, for this work the electrical excitation and signal conditioning were performed off-chip. In our future work, we will package and integrate the electronic circuitry into the PCB board containing the electrodes.
Conclusions
We have designed, fabricated, and experimentally tested a novel microfluidic platform to demonstrate contactless flow through impedance cytometry. The platform contains a disposable biochip that can be inserted onto a PCB with reusable electrodes. This significantly reduces the manufacturing costs, making it suitable for low resource settings, such as point-of-care testing in the developing countries. In this work, we used a glass coverslip as a barrier to isolate the electrodes from the buffer. To resolve the signal degradation issue due to the presence of the coverslip, we operated at sufficiently high frequency to capacitively couple the electrodes to the electrolyte in the channel, while meeting the measurement’s bandwidth and slew-rate limitations.
Acknowledgments
This work was supported by the National Institutes of Health grant PO1HG000205. All authors planned the research and contributed to manuscript preparation. S. Emaminejad and M. Javanmard performed the experiments and data analysis.
References
- 1.Joint United Nations Programme on HIV/AIDS. World Health Organization; Dec, 2005. AIDS Epidemic Update: November 2009. available at http://www.unaids.org/en/media/unaids/contentassets/dataimport/pub/report/2009/jc1700_epi_update_2009_en.pdf. [Google Scholar]
- 2.Guidelines for the Use of Antiretroviral Agents in HIV-1-Infected Adults and Adolescents. Department of Health and Human Services; Oct 6, 2005. [accessed 20th March 2006]. available at http://aidsinfo.nih.gov/ContentFiles/AdultandAdolescentGL.pdf. [Google Scholar]
- 3.Balakrishnan P, Dunne M, Kumarasamy N, Crowe S, Subbulakshmi G, Ganesh AK, Cecelia AJ, Roth P, Mayer KH, Thyagarajan SP, Solomon S. An inexpensive, simple, and manual method of CD4 T-cell quantitation in HIV-infected individuals for use in developing countries. J Acquir Immune Defic Syndr. 2004;36(5):1006–10. doi: 10.1097/00126334-200408150-00002. [DOI] [PubMed] [Google Scholar]
- 4.McKenzie FE, Prudhomme WA, Magill AJ, Forney JR, Permpanich B, Lucas C, Gasser RA, Wongsrichanalai C. White Blood Cell Counts and Malaria. Journal of Infectious Diseases. 2005;192(2):323–330. doi: 10.1086/431152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Martin DJ, Sim JG, Sole GJ, Rymer L, Shalekoff S, van Niekerk AB, Becker P, Weilbach CN, Iwanik J, Keddy K, et al. CD4+ lymphocyte count in African patients co-infected with HIV and tuberculosis. Journal of acquired immune deficiency syndromes and human retrovirology: official publication of the International Retrovirology Association. 1995;8(4):386–91. [PubMed] [Google Scholar]
- 6.Cheng X, Irimia D, Dixon M, Sekine K, Demirci U, Zamir L, Tompkins RG, Rodriguez W, Toner M. A microfluidic device for practical label-free CD4+ T cell counting of HIV-infected subjects. Lab on a Chip. 2007;7(2):170–178. doi: 10.1039/b612966h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cheng X, Irimia D, Dixon M, Ziperstein JC, Demirci U, Zamir L, Tompkins RG, Toner M, Rodriguez WR. A microchip approach for practical label-free CD4+ T-cell counting of HIV-infected subjects in resource-poor settings. J Acquir Immune Defic Syndr. 2007;45(3):257–61. doi: 10.1097/QAI.0b013e3180500303. [DOI] [PubMed] [Google Scholar]
- 8.Watkins NN, Sridhar S, Cheng X, Chen GD, Toner M, Rodriguez W, Bashir R. A microfabricated electrical differential counter for the selective enumeration of CD4+ T lymphocytes. Lab Chip. 2011;11(8):1437–47. doi: 10.1039/c0lc00556h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Coulter W. High Speed Automatic Blood Cell Counter and Cell Size Analyzer. Proceedings of the National Electronics Conference; Chicago. 1956. [Google Scholar]
- 10.DeBlois RW, Bean CP. Counting and Sizing of Submicron Particles by the Resistive Pulse Technique. Review of Scientific Instruments. 1970;41(7):909–916. [Google Scholar]
- 11.Hoffman RA, Britt WB. Flow-system measurement of cell impedance properties. Journal of Histochemistry & Cytochemistry. 1979;27(1):234–240. doi: 10.1177/27.1.374580. [DOI] [PubMed] [Google Scholar]
- 12.Larsen UD, Blankenstein G, Branebjerg J. Microchip Coulter particle counter, Solid State Sensors and Actuators, 1997. TRANSDUCERS ‘97 Chicago. 1997 International Conference on; 16–19 Jun 1997; 1997. pp. 1319–1322. [Google Scholar]
- 13.Morgan H, Sun T, Holmes D, Gawad S, Green NG. Single cell dielectric spectroscopy. Journal of Physics D: Applied Physics. 2007;40(1):61. [Google Scholar]
- 14.Saleh OA, Sohn LL. Quantitative sensing of nanoscale colloids using a microchip Coulter counter. Review of Scientific Instruments. 2001;72(12):4449–4451. [Google Scholar]
- 15.Wang L, Flanagan LA, Jeon NL, Monuki E, Lee AP. Dielectrophoresis switching with vertical sidewall electrodes for microfluidic flow cytometry. Lab on a Chip. 2007;7(9):1114–1120. doi: 10.1039/b705386j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wu X, Kang Y, Wang YN, Xu D, Li D, Li D. Microfluidic differential resistive pulse sensors. ELECTROPHORESIS. 2008;29(13):2754–2759. doi: 10.1002/elps.200700912. [DOI] [PubMed] [Google Scholar]
- 17.Ashish VJ, Jiang Z, Jun H, Joan C. Detection and counting of micro-scale particles and pollen using a multi-aperture Coulter counter. Measurement Science and Technology. 2006;17(7):1706. [Google Scholar]
- 18.Ashish VJ, Rupesh S, Jiang Z. A label-free high throughput resistive-pulse sensor for simultaneous differentiation and measurement of multiple particle-laden analytes. Journal of Micromechanics and Microengineering. 2006;16(8):1530. [Google Scholar]
- 19.Wood DK, Oh SH, Lee SH, Soh HT, Cleland AN. High-bandwidth radio frequency Coulter counter. Applied Physics Letters. 2005;87(18):184106–3. [Google Scholar]
- 20.Scott R, Sethu P, Harnett CK. Three-dimensional hydrodynamic focusing in a microfluidic Coulter counter. Review of Scientific Instruments. 2008;79(4):046104–3. doi: 10.1063/1.2900010. [DOI] [PubMed] [Google Scholar]
- 21.Segerink LI, Sprenkels AJ, ter Braak PM, Vermes I, van den Berg A. On-chip determination of spermatozoa concentration using electrical impedance measurements. Lab on a Chip. 2010;10(8):1018–1024. doi: 10.1039/b923970g. [DOI] [PubMed] [Google Scholar]
- 22.Kim KB, Chun H, Kim HC, Chung TD. Red blood cell quantification microfluidic chip using polyelectrolytic gel electrodes. ELECTROPHORESIS. 2009;30(9):1464–1469. doi: 10.1002/elps.200800448. [DOI] [PubMed] [Google Scholar]
- 23.Holmes D, Morgan H. Single Cell Impedance Cytometry for Identification and Counting of CD4 T-Cells in Human Blood Using Impedance Labels. Analytical Chemistry. 2010;82(4):1455–1461. doi: 10.1021/ac902568p. [DOI] [PubMed] [Google Scholar]
- 24.Lichtenberg J, de Rooij NF, Verpoorte E. A microchip electrophoresis system with integrated in-plane electrodes for contactless conductivity detection. ELECTROPHORESIS. 2002;23(21):3769–3780. doi: 10.1002/1522-2683(200211)23:21<3769::AID-ELPS3769>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 25.Tanyanyiwa J, Hauser PC. High-Voltage Capacitively Coupled Contactless Conductivity Detection for Microchip Capillary Electrophoresis. Analytical Chemistry. 2002;74(24):6378–6382. doi: 10.1021/ac020489+. [DOI] [PubMed] [Google Scholar]
- 26.Pumera M, Wang J, Opekar F, Jelínek I, Feldman J, Löwe H, Hardt S. Contactless Conductivity Detector for Microchip Capillary Electrophoresis. Analytical Chemistry. 2002;74(9):1968–1971. doi: 10.1021/ac011219e. [DOI] [PubMed] [Google Scholar]
- 27.Wang J, Pumera M, Chatrathi MP, Escarpa A, Konrad R, Griebel A, Dörner W, Löwe H. Towards disposable lab-on-a-chip: Poly(methylmethacrylate) microchip electrophoresis device with electrochemical detection. ELECTROPHORESIS. 2002;23(4):596–601. doi: 10.1002/1522-2683(200202)23:4<596::AID-ELPS596>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 28.Wang J, Tian B, Sahlin E. Micromachined Electrophoresis Chips with Thick-Film Electrochemical Detectors. Analytical Chemistry. 1999;71(23):5436–5440. doi: 10.1021/ac990807d. [DOI] [PubMed] [Google Scholar]
- 29.Wang J, Chatrathi MP, Mulchandani A, Chen W. Capillary Electrophoresis Microchips for Separation and Detection of Organophosphate Nerve Agents. Analytical Chemistry. 2001;73(8):1804–1808. doi: 10.1021/ac001424e. [DOI] [PubMed] [Google Scholar]
- 30.Guijt RM, Baltussen E, van der Steen G, Frank H, Billiet H, Schalkhammer T, Laugere F, Vellekoop M, Berthold A, Sarro L, van Dedem GWK. Capillary electrophoresis with on-chip four-electrode capacitively coupled conductivity detection for application in bioanalysis. ELECTROPHORESIS. 2001;22(12):2537–2541. doi: 10.1002/1522-2683(200107)22:12<2537::AID-ELPS2537>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 31.Park K, Suk HJ, Akin D, Bashir R. Dielectrophoresis-based cell manipulation using electrodes on a reusable printed circuit board. Lab on a Chip. 2009;9(15):2224–2229. doi: 10.1039/b904328d. [DOI] [PubMed] [Google Scholar]
- 32.Cheung K, Gawad S, Renaud P. Impedance spectroscopy flow cytometry: On-chip label-free cell differentiation. Cytometry Part A. 2005;65A(2):124–132. doi: 10.1002/cyto.a.20141. [DOI] [PubMed] [Google Scholar]
- 33.Gawad S, Cheung K, Seger U, Bertsch A, Renaud P. Dielectric spectroscopy in a micromachined flow cytometer: theoretical and practical considerations. Lab on a Chip. 2004;4(3):241–251. doi: 10.1039/b313761a. [DOI] [PubMed] [Google Scholar]
- 34.Javanmard M. Pulse Width Modulation Using Coded Corrugated Microfluidic Sidewalls for Low Signal-Noise Ratio Single Cell Impedance Cytometry. 15th International Conference on Miniaturized Systems for Chemistry and Life Sciences; Seattle, Washington. 2011. [Google Scholar]
- 35.McDonald JC, Duffy DC, Anderson JR, Chiu DT, Wu H, Schueller OJA, Whitesides GM. Fabrication of microfluidic systems in poly(dimethylsiloxane) ELECTROPHORESIS. 2000;21(1):27–40. doi: 10.1002/(SICI)1522-2683(20000101)21:1<27::AID-ELPS27>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]