Estimating A Reference Standard Segmentation With Spatially Varying Performance Parameters: Local MAP STAPLE

Abstract

We present a new algorithm, called local MAP STAPLE, to estimate from a set of multi-label segmentations both a reference standard segmentation and spatially varying performance parameters. It is based on a sliding window technique to estimate the segmentation and the segmentation performance parameters for each input segmentation. In order to allow for optimal fusion from the small amount of data in each local region, and to account for the possibility of labels not being observed in a local region of some (or all) input segmentations, we introduce prior probabilities for the local performance parameters through a new Maximum A Posteriori formulation of STAPLE. Further, we propose an expression to compute confidence intervals in the estimated local performance parameters.

We carried out several experiments with local MAP STAPLE to characterize its performance and value for local segmentation evaluation. First, with simulated segmentations with known reference standard segmentation and spatially varying performance, we show that local MAP STAPLE performs better than both STAPLE and majority voting. Then we present evaluations with data sets from clinical applications. These experiments demonstrate that spatial adaptivity in segmentation performance is an important property to capture. We compared the local MAP STAPLE segmentations to STAPLE, and to previously published fusion techniques and demonstrate the superiority of local MAP STAPLE over other state-of-the- art algorithms.

I. Introduction

Label fusion algorithms have attracted considerable interest in recent years. First, they may be used to evaluate inter- and intra-expert manual segmentation variability, for example to help reaching a consensus for the manual delineation of structures [1]. Further, they are also utilized for the evaluation of segmentation or registration algorithms in comparison to several raters. Such algorithms allow for the evaluation of one or several automatic segmentation algorithms against multiple manual reference segmentations, thereby providing robust evaluations of automatic delineation. Popular methods for segmentation evaluation [2], [3] compute global scores over the entire image. However, it has been suggested [4] that evaluating local performance of a segmentation algorithm is better suited in some cases, as in some applications the requirements for accuracy vary across the image: very precise delineations may be needed in crucial areas while a lower precision may be acceptable for other areas. New techniques for local performance estimation are critical for such applications, in order to facilitate the automatic and quantitative assessment of segmentation accuracy while incorporating information from multiple experts.

Label fusion algorithms have also been recently utilized in atlas construction [5] and to fuse multiple atlases for segmentation [6], [7], [8], showing a significant improvement over standard single-template based segmentation techniques. As shown in [9], [10], the label fusion strategy is a crucial aspect of successful multi-template based segmentation. Among recent works on label fusion, several have used majority voting [7], i.e. the segmentation label for a voxel is selected as the most common label from all the aligned template segmentations at that voxel. Template selection and majority voting enable automated segmentation, however they are limited by the use of a global metric for template selection, by considering each voxel independently from the others, and by assuming each template contributes equally to the final segmentation. Majority voting generates locally inconsistent segmentations in regions of high anatomical variability and in regions where poor registration accuracy is achieved, such as in the cortical gray matter which has high inter-individual anatomical variability.

To address these challenges, several groups [10], [11], [12] proposed weighted majority voting, defining weights from intensity differences between the images. In regions of variable registration accuracy, the intensity differences are able to weight those templates that best match (smaller local intensity differences) higher than those that match poorly (larger local intensity differences). However, such intensity-based weights are also prone to local errors, noise or artifacts in the images, and to the strategy used for intensity normalization and image registration. The most appropriate way to define these weights or to incorporate intensity information remains unclear.

A widely used algorithm for label fusion is STAPLE [13], [3]. It has been evaluated for label fusion and found superior to several combination rules, including majority voting [9]. It utilizes the Expectation-Maximization algorithm to compute both a multi-label reference standard and segmentation performance parameters. These quality parameters are used to infer optimal weighting for the estimation of the reference standard segmentation, and provides a mechanism to determine the quality of input segmentations in label fusion. This is useful for segmentation evaluation and segmentation variability evaluation. Further, it may provide an improved multi-atlas based segmentation by better accounting for error, noise and artifacts in aligned segmentations.

Again, one disadvantage of global parameters is that performance may vary from one point to another depending, for example, on the ability of an expert to delineate some part of a structure, or on fatigue involved in a manual delineation task. Further, in the case of template fusion, spatially varying performance may occur due to anatomical variability between templates, and to registration errors, such as boundary mislocalization. This may explain why the STAPLE algorithm has been reported to give mixed results in some previous studies, depending on the region segmented and on the quantitative measure of segmentation accuracy. While Rohlfing et al. [9] found that STAPLE outperforms other approaches, Klein et al. [14] found no significant difference between STAPLE initialized with a prior from voting and majority voting, suggesting that either all input images were equally well aligned to the target and thus equal weighting is appropriate, or that the weight of the prior was so high as to overwhelm the weighting of the input images. Further, both Artaechevarria et al. [10] and Langerak et al. [15] showed that STAPLE performed worse when poorly initialized with a uniform global prior that was not representative of the expected segmentation, a finding previously recognized in [3].

These observations suggest that performance of the STAPLE algorithm could be significantly improved by computing spatially varying performance parameters for each input segmentation. Moreover, such local performance estimates would greatly benefit segmentation evaluation, thereby helping in the development of consensus for manual segmentations and improving our understanding of the expert segmentation process. However, developing a STAPLE algorithm with spatially varying parameters is not trivial and requires that three main questions be answered. First, one needs to define how local computations are performed to ensure that the obtained reference standard and local performance estimates vary appropriately over the image. Secondly, performing local operations may lead to cases where some structures are not present for some experts in a local region. The regular STAPLE algorithm requires observations of each label in order to estimate performance. In the absence of observations for a label, an estimate of performance for that label cannot be computed with STAPLE. This can lead to erroneous fusion results. Thirdly, since the computations are local, the size of the local regions considered for computation is crucial. Too small or too large a region may lead to erroneous performance estimates and reference standard estimation. It is therefore critical to be able to characterize the inferential uncertainty in the estimated performance parameters for each voxel, so as to quantitatively assess the confidence interval for each of the local estimates.

We propose here an algorithm that solves all of the challenges described above. We present a new local Maximum a Posteriori STAPLE algorithm, hereafter denoted local MAP STAPLE, which estimates spatially varying local performance parameters and a reference standard segmentation from a set of input segmentations. The formulation of this algorithm provides three major advances:

• First, we introduce the local MAP STAPLE computation based on a sliding window technique,

• Second, to account for the possibility of unobserved labels, and to model information regarding segmentation performance known ahead of time, we formulate a Maximum A Posteriori estimator by defining a prior probability distribution for the expert performance parameters,

• Third, confidence intervals for the estimated performance parameters are calculated by computation of the observed Information Matrix, enabling the local assessment of the inferential uncertainty in the parameter values.

We describe in Section III several experiments with the local MAP STAPLE algorithm to characterize its performance and its value for the local evaluation of intra- and inter-expert segmentation variability. First, with simulated segmentations with known reference standard segmentation and spatially varying performance, showing that local MAP STAPLE performs better than both STAPLE and majority voting. We then present evaluations with brain MRI. We evaluated brain segmentation by label fusion from inter-subject registration of template segmentations from a commonly used database of brain segmentations. We compared the local MAP STAPLE segmentations to STAPLE, and previously published fusion techniques and found that local MAP STAPLE has superior performance to that of other state-of- the-art fusion and segmentation algorithms.

II. Methods

A. Notations and Regular STAPLE Algorithm

The STAPLE algorithm estimates a hidden reference standard segmentation and rater performance parameters from a collection of delineations. It takes as an input a set of segmentations from J experts (either manual or automatic segmentations). These may be either binary or multi-category segmentations, i.e. several structures are delineated with each structure represented by one specific label [3]. The labeling of each voxel, in an image of I voxels, provided by the segmentation generators is referred to as segmentation decision d_ij, indicating the label given by expert j for voxel i, i ∈ [1 … I]. The goal of STAPLE is then to estimate both a reference standard segmentation T, and performance parameters θ = {θ₁, …, θ_j, …, θ_J} describing the agreement over the whole image between the experts and the reference standard. Each θ_j is represented by an L × L matrix, where L is the number of labels in the segmentation (including the background), and θ_js′s is the probability that expert j gave the label s′ to a voxel i when the reference standard label is s: θ_js′s = P(d_ij = s′|T_i = s).

As the reference standard T is unknown, an Expectation-Maximization approach [16], [17] is used to estimate T and θ through the maximization of the expected value of the complete data log-likelihood Q(θ|θ^(k)):

$$Q(\theta \mid {\theta }^{(k)})=\sum _i\sum _j\sum _s{W}_{si}log({\theta }_{{jd}_{ij}s})$$ (1)

where W_si denotes the posterior probability of T for label s: P(T_i = s|D, θ^(k)). The EM algorithm proceeds to identify the optimal estimate θ̃ by iterating two steps:

• E-Step: Compute Q(θ|θ^(k)), the expected value of the complete data log-likelihood given the estimate of the expert parameters at the preceding iteration: θ^(k). Evaluating this expression requires the posterior probability of T:

  $$\begin{array}{l}P(T=s\mid D,{\theta }^{(k)})=\prod _i{W}_{si}\\ =\prod _i\frac{P(T_i=s){\prod }_j{\theta }_{{jd}_{ij}s}^{(k)}}{{\sum }_{s^{\prime }}P(T_i=s^{\prime }){\prod }_j{\theta }_{j{d}_{ij}{s}^{\prime }}^{(k)}}\end{array}$$ (2)

  which is straightforward to estimate, and is easily extended to account for spatial homogeneity via a Markov Random Field [3].

• M-Step: Estimate new performance parameters at iteration k + 1, θ^(k+1), by maximizing Q(θ|θ^(k)).

B. Algorithm Overview

We describe here our new algorithm that estimates a reference standard with spatially varying expert performance parameters. The new algorithm is a generalization of the STAPLE algorithm [3], and is executed on local regions of the input images. We first need to define the patches from which to compute the reference standard segmentation. Note that some regions will not require any computation: these are the regions for which at every voxel all experts agree on the label. In such regions, all experts are consistent with each other and the most likely true label is undoubtedly the label assigned by the experts. Therefore, the estimation of the reference standard and the local performance parameters is performed only in regions where the experts do not agree.

We shall call the set of voxels in which the experts are not in 100% consensus agreement the undecided region U. In this region U, we have considered several ways of defining subset regions. A solution that split U into a set of independent non-overlapping patches would be computationally efficient, as the number of voxels involved in each computation is then matched to the size of the region U. However, this would restrict changes in performance to specific local regions, with potential discontinuities at region boundaries. We suggest instead to use a sliding window strategy, considering a locally defined regions around each voxel. Our approach is summarized in Algorithm 1.

Algorithm 1.

Overview of the Local MAP STAPLE Algorithm

1:	for all voxels x ∈ U do
2:	Define a block B(x) of a predefined half window size V, centered in x.
3:	Compute a MAP STAPLE estimate of the reference standard and performance parameters for the region B(x) (Section II-C).
4:	Compute confidence intervals of the estimated parameters (Section II-D).
5:	Store performance parameter estimates and reference standard probabilities for the voxel x.

Using this approach, each voxel x is considered in turn to be the center of a local region B(x) in which the estimation is performed. This ensures a smooth transition across the voxels by considering overlapping neighborhoods for each computation. In the following, we describe the main steps of the algorithm (lines 3 and 4 of Algorithm 1). First, we address challenges that may arise when considering small regions of interest (Section II-C). We then present in Section II-D an approach to estimate confidence intervals for the local performance parameters, which allows us to evaluate the inferential uncertainty of the parameter values due to the consideration of a small neighborhood.

C. Accounting for Missing Labels in Local Regions: a Maximum A Posterior Formulation

For each voxel x located in the undecided region U, we define around it a cubic block B(x) of predefined half window size V. For the voxels of this block, the STAPLE EM algorithm is executed to estimate the local reference standard and the local performance parameters. However, when considering small blocks, some labels may be unobserved in some of the segmentations. This can occur in both binary and multi-category segmentations. It has not been possible in previous work [3] to estimate segmentation performance for labels for which no segmentation decisions are observed. This absence of observation of some structures may lead the algorithm into undesirable maxima coupled with poor label fusion, as illustrated in Fig. 1. The absence of some structures must therefore be taken into account in order to have a consistent and accurate estimation of the local reference standard.

Fig. 1. Illustration of Label Fusion with Missing Data.

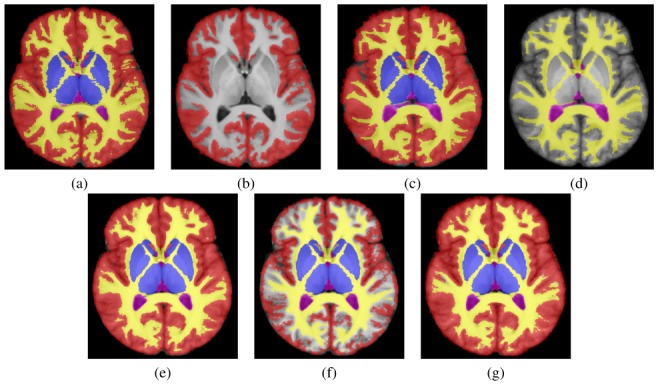
Individual manual segmentations (a,c): original segmentations, (b,d): segmentations with 4 missing structures. Legend: red, blue, green: cortical, sub-cortical and cerebellar grey matter, yellow: white matter, pink: CSF, cyan: cerebellar white matter and brainstem. (e): reference label fusion (all structures used), (f): label fusion without accounting for missing structures, (g): label fusion utilizing prior information with a MAP STAPLE formulation.

We propose to account for missing labels by introducing a prior probability for segmentation performance. This enables computation of the reference standard even in the absence of observed segmentation labels for each input segmentation. This leads to a Maximum A Posteriori (MAP) formulation of the STAPLE algorithm, referred to as MAP STAPLE [18], allowing the algorithm to converge to the correct local optimum, even in the absence of segmentation labels (see Fig. 1.g). The MAP estimate is equivalent to augmenting the expected value of the complete data log-likelihood Q(θ|θ^(k)) with a term log(P(θ)) corresponding to the prior probability of the performance parameters:

$$Q_{\mathit{MAP}}(\theta \mid {\theta }^{(k)})=Q(\theta \mid {\theta }^{(k)})+\gamma log(P(\theta ))$$ (3)

where γ is a parameter that models the relative weight of the data term and of the prior. As the performance parameters for each expert and each label are independent, P(θ) can be expressed as a product of the independent probabilities of each performance parameter: P(θ_js′s). We choose a Beta distribution $B_{\alpha ,\beta }(x)=\frac{1}{Z}{x}^{\alpha -1}{(1-x)}^{\beta -1}$ as the model for the prior probability of each performance parameter. This distribution allows us to model a wide variety of differently shaped performance characteristics, by varying the two shape parameters α and β. Furthermore, a uniform distribution is represented by α = β = 1. This MAP formulation leads to simple update scheme that can be efficiently solved.

1. Solution of the MAP STAPLE Estimator in the Multi-Category Case

In the multi-category case, we define a prior probability distribution for each expert performance parameter θ_js′s, using a Beta distribution with parameters α_js′s and β_js′s. This leads to the following expected value of the complete data log-likelihood function:

$$Q_{\mathit{MAP}}^{\prime }({\theta }_j\mid {\theta }^{(k)})=\gamma \sum _{s^{\prime }}\sum _s\left(({\alpha }_{{js}^{\prime }s}-1)log({\theta }_{{js}^{\prime }s})+({\beta }_{{js}^{\prime }s}-1)log(1-{\theta }_{{js}^{\prime }s})\right)+\sum _i\sum _s{W}_{si}log({\theta }_{{jd}_{ij}s})$$ (4)

By design, this formulation does not modify the expression of the reference standard label probabilities W_si. The E-step indeed only requires the computation of P(T|D, θ^(k)) which depends only on the current estimates θ^(k) and not on the prior on these parameters. W_si is therefore expressed as:

$$W_{si}=\frac{P(T_i=s){\prod }_j{\theta }_{{jd}_{ij}s}}{{\sum }_{s^{\prime }}P(T_i=s^{\prime }){\prod }_j{\theta }_{j{d}_{ij}{s}^{\prime }}}$$ (5)

Further, equating the derivatives of $Q_{\mathit{MAP}}^{\prime }$ to 0 for each expert j leads to the following system of equations in the general case:

$${\theta }_{{js}^{\prime }s}=\frac{\gamma A_{s^{\prime }s}+{\sum }_{i:d_{ij}=s^{\prime }}{W}_{si}}{{\sum }_{n^{\prime }}\left(\gamma A_{n^{\prime }s}+{\sum }_{i:d_{ij}=n^{\prime }}{W}_{si}\right)},$$ (6)

where $A_{n^{\prime }s}={\alpha }_{{jn}^{\prime }s}+{\beta }_{{jn}^{\prime }s}+\frac{{\beta }_{{jn}^{\prime }s}-1}{{\theta }_{{jn}^{\prime }s}-1}-2$

This system is a continuous mapping of the form θ_j = f(θ_j), with f: ]0, 1[^N→]0, 1[^N (where N is the number of parameters to compute for expert j). This system always has a unique solution (called a fixed point). A closed form solution is available when all β_js′s parameters are equal to 1, and also when the prior is a uniform distribution. Furthermore, the fixed point solution can be readily identified through iterative application of the above equation [18]. This scheme consists in applying the f mapping to the current estimate. That is, computing the sequence {x_n}_n≥1 where x_n+1 = f(x_n) until convergence.

2. Exact Solution for Solving the MAP Formulation in the Binary Case

When considering binary segmentations as an input, several simplifications can be made which lead to an analytical closed form solution of the MAP STAPLE formulation. First, the expert parameters can be reduced to only two parameters for each expert: sensitivity p_j = θ_j11, and specificity q_j = θ_j00. To simplify as much as possible the notation for the following equations, we will keep the general notation θ_js′s for the performance parameters, keeping in mind that only p_j and q_j are meaningful parameters (as θ_j01 and θ_j10 are completely determined by θ_j01 = 1 − p_j and θ_j10 = 1 − q_j ). Therefore a prior probability is needed only for the p_j and q_j parameters. This leads to the following expected value of the complete data log-likelihood function:

$$Q_{\mathit{MAP}}^{\prime }({\theta }_j\mid {\theta }^{(k)})=\sum _i\sum _s{W}_{si}log({\theta }_{{jd}_{ij}s})+\gamma \sum _s\left[({\alpha }_{\mathit{jss}}-1)log({\theta }_{\mathit{jss}})+({\beta }_{\mathit{jss}}-1)log(1-{\theta }_{\mathit{jss}})\right]$$ (7)

As for the multi-category case, the form of P(T|θ, D) is not modified by the introduction of priors on the performance parameters. It remains the same as described in [3]. The solution of the optimal θ parameters is altered by the prior, and leads to a closed form analytical solution for p_j (θ_j11) and q_j (θ_j00):

$${\theta }_{\mathit{jss}}=\frac{{\sum }_{i:d_{ij}=s}{W}_{si}+\gamma ({\alpha }_{\mathit{jss}}-1)}{{\sum }_i{W}_{si}+\gamma ({\alpha }_{\mathit{jss}}+{\beta }_{\mathit{jss}}-2)}$$ (8)

D. Estimating Inferential Uncertainty of Local Performance Parameters: Confidence Intervals

Estimation of segmentation performance from local regions may vary in the quality of the estimates, due to changes in the segmentation performance and due to changes in the amount of data for each label in each region. The effect of these changes can be characterized by estimating the inferential uncertainty in the performance parameters. That is, we may estimate the certainty with which each point estimate of performance is known. Reliable estimation of the reference standard occurs when the performance parameters are sufficiently certain.

The inferential uncertainty of the expert performance parameters is computed through the evaluation of the information matrix I(θ). The confidence intervals are then computed from the parameter covariance matrix, which is obtained by inverting the information matrix Σ(θ) = I⁻¹(θ) [19]. If the complete data was known, then the computation of the information matrix would be straightforward (as it is the matrix of the second derivatives of the log-likelihood function). However, for an EM algorithm such as local MAP STAPLE, the complete data is unknown. The hidden variables (the reference standard segmentation) are estimated and the confidence intervals are then computed from the observed information matrix, which accounts for the uncertainty due to the estimates of the hidden variables. The observed information matrix I(θ) is obtained by subtracting the missing-data information matrix from the complete-data information matrix:

$$I(\theta )=I_c(\theta )-I_m(\theta )$$ (9)

The complete-data information matrix I_c(θ) is computed using the expected value of the complete data log-likelihood Q_MAP (θ|θ^(k)). The missing-data information matrix I_m(θ) is readily computed as described below.

We presented in [20] the derivation of the expressions of I_c and I_m for the STAPLE algorithm, both for the multi-category and binary case. Interestingly, the MAP STAPLE formulation leads to a new expression only for the complete-data information matrix, whereas the missing-data information matrix remains the same as derived in [20]. Here, we provide the expressions of I_c for the MAP STAPLE algorithm.

1. The Multi-Category Segmentation Information Matrix

For multi-category segmentations, I_c is computed by the following expression:

$${\mathbf{I}}_{c;{\theta }_{{js}^{\prime }s}}(\theta )=\gamma \left[\frac{{\alpha }_{{js}^{\prime }s}-1}{{\theta }_{{js}^{\prime }s}^2}+\frac{{\beta }_{{js}^{\prime }s}-1}{{(1-{\theta }_{{js}^{\prime }s})}^2}\right]+\sum _{i:d_{ij}=s^{\prime }}\frac{W_{si}^{(k)}}{{\theta }_{{js}^{\prime }s}^2}$$ (10)

This expression incorporates two new terms that depend on the Beta distribution parameters, as compared to Eq. (13) in [20]. The missing-data information matrix remains the same as expressed in Eqs. (14–17) in [20].

2. The Binary Segmentation Information Matrix

In the case of binary segmentations, the off-diagonal performance parameters are completely determined by the on-diagonal performance parameters, and the expression for the information matrix can be simplified. This enables computation of the exact observed information matrix. As for the multi-category case, only the expression of I_c is modified when working with the MAP formulation. I_m is expressed as in Eqs. (9–11) in [20], while I_c is computed as:

$${\mathbf{I}}_{c;{\theta }_{\mathit{jss}}}=\gamma \left[\frac{{\alpha }_{\mathit{jss}}-1}{{\theta }_{\mathit{jss}}^2}+\frac{{\beta }_{\mathit{jss}}-1}{{(1-{\theta }_{\mathit{jss}})}^2}\right]+\sum _i\frac{W_{si}^{(k)}}{{\theta }_{j,d_{ij},s}^2}$$ (11)

III. Results

In order to assess the performance of our new algorithm, we have carried out several experiments. First, we have performed experiments on simulated data, to evaluate label fusion and performance parameters with respect to a known reference standard. In addition, we have applied our algorithm to MRI scans of the brain, and we demonstrate the improvements of local MAP STAPLE compared to STAPLE and other state-of-the art algorithms.

A. Local MAP STAPLE Implementation Details and Computation Times

In the following experiments, the local MAP STAPLE algorithm (as well as the regular STAPLE algorithm) was executed until convergence. The convergence of the estimator is detected when the change of the performance parameters from iteration to iteration is below a user-defined threshold (10⁻⁸ in our experiments) or when a maximum number of iterations is reached (100 in our experiments). In practice, the algorithm converged always before reaching the maximum number of iterations.

We utilized the following MAP STAPLE parameters to model prior information about segmentation performance for each input segmentation and for each label. If an expert did not delineate a given structure on a specific local block, we assume it does not mean that he has a poor segmentation performance in general. In other words, we assume that the probability for an expert to delineate the correct structure is a priori high, i.e. absence of evidence is not evidence of poor estimation. This is done by setting all diagonal parameters for each expert to a beta distribution close to 1 (e.g. α_jss = 5, β_jss = 1.5) and, in the multi-category case, the non-diagonal parameters to a beta distribution close to 0 (e.g. α_js′s = 1.5, β_js′s = 5).

In the following, we ran experiments with varying Half Window Sizes (HWS) for the local blocks, using a multi-threaded implementation for both STAPLE and local MAP STAPLE. Overall, we found that our algorithm runs at least as fast as the original STAPLE algorithm. For example, both algorithms took about 5 minutes to complete for the simulated data. Moreover, on the IBSR dataset experiments described in detail below, the local MAP STAPLE algorithm ran substantially faster: STAPLE ran in about 9 hours while local MAP STAPLE took 7 hours (these running times are longer since many structures are considered for these datasets).

B. Experiments on Simulated Data

To illustrate the capacity of the local MAP STAPLE algorithm to characterize spatially varying expert performance, we generated a synthetic phantom with spatially varying performance parameters. The true segmentation is a square image (200×200) with leftmost 100 columns having value 0 and rightmost columns having value 1. We used random sampling to generate 32 segmentations illustrated in Fig. 2: 12 segmentations with sensitivities and specificities in Fig. 2.a, 6 from those in Fig. 2.b, and 14 from those in Fig. 2.c.

Fig. 2. Illustration of Images Simulated with Spatially Varying Performances.

(a,b,c): Local performance values for the various synthetic images generated (12 generated from (a), 6 from (b), 14 from (c)). (d,e,f): Illustration of the images generated respectively using (a,b,c) performances.

We present in Fig. 3 the results of label fusion of the 32 segmentations using local MAP STAPLE, STAPLE and majority voting. Fig. 3.a shows the majority voting result, 3.b the regular STAPLE fusion, and 3.c–e the local MAP STAPLE results with different HWS: 1,4, and 16, respectively. These results illustrate visually that local MAP STAPLE performs better than regular STAPLE when spatially varying performances are considered. Moreover, local MAP STAPLE with higher HWS values seems to perform better than when small HWS values are used, and both STAPLE and local MAP STAPLE appear better than majority voting.

Fig. 3. Comparison of Fusion Results on Synthetic Segmentations.

Illustration of estimated true segmentations using (a): majority voting, (b): STAPLE, (c,d,e): local MAP STAPLE with HWS of respectively 1, 4, and 16. Ground truth estimated through local MAP STAPLE is more accurate than using regular STAPLE or majority voting.

To further characterize these results, we present in Fig. 4 the average parameter maps estimated by local MAP STAPLE together with the confidence intervals derived from Section II-D averaged for the images of group 1 (Fig. 2.a, 2.d). This figure illustrates why results may be less good for local MAP STAPLE with an HWS of 1. In this case, the estimated parameters are quite different from the real parameters. Moreover, the uncertainty on these estimations is very large (up to 40 % of the estimated value). This may therefore lead to local errors in the estimation of the underlying ground truth. When considering larger HWS values, the parameters maps are more accurate and the uncertainty in the estimation also decreases (similarly to what had been shown in [20]). Overall, these results suggest that both HWS of 4 and 16 are good for this experiment, with a slight preference to an HWS of 4 which provides accurate smoothly varying spatial parameter maps, with relatively tight confidence intervals for the estimated parameters. The range of HWS for which excellent results are obtained suggests the estimator is robust to this parameter.

Fig. 4. Comparison of Parameter Maps for local MAP STAPLE.

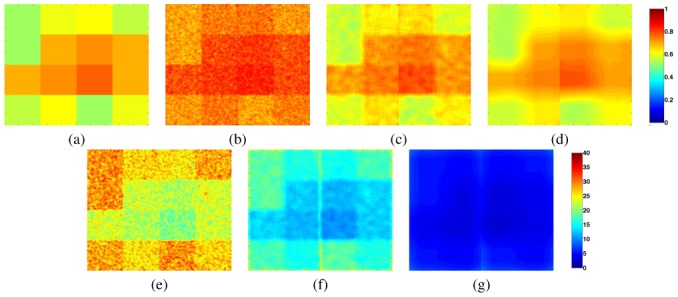
Local parameter maps and their relative uncertainty at the 95 % level, averaged over the first group of 12 images generated from Fig. 3.a. (a): Ground truth parameter map. (b,c,d): local parameter maps for local MAP STAPLE with HWS of 1, 4 and 16. (e,f,g): corresponding uncertainty in the estimated local parameters (in percentage of the estimated value). Color bars show the scale of the parameter maps and relative uncertainty maps.

To further verify these observations, we present in Table I the quantitative error rates for each method. We observe that STAPLE (which is computing global performance parameters) cannot estimate the ground truth accurately and created 123 misclassified voxels, because of the variation of the performance of the experts across the image. However, local MAP STAPLE estimates local performances for each experts and does accurately estimate the ground truth for the HWS of 4 and 16, with 7 and 11 misclassifications respectively over the entire image.

TABLE I. Quantitative Comparison of Label Fusion Methods.

Number of classification errors when estimating the reference standard from experts with spatially varying performances. Comparison of three different methods: majority voting, regular STAPLE and local MAP STAPLE (L-ST) with three different half window sizes (HWS).

Fusion Method	Majority Voting	STAPLE	L-ST (HWS 1)	L-ST (HWS 4)	L-ST (HWS 16)
# Errors	178	123	69	7	11

Furthermore, majority voting cannot estimate the ground truth correctly, despite the use of only local information. Since it treats each expert equally and does not estimate the performance of each expert, it estimates a segmentation with 178 voxels misclassified in the image. The local MAP STAPLE algorithm exhibits improved performance over majority voting, which is based on entirely local information, and STAPLE which estimates global performance parameters. The capacity to compute performance parameters at a spatial scale corresponding to the performance variation observed in the image provides local MAP STAPLE with superior fusion performance.

C. Experiments with Brain MRI Segmentations

We obtained segmentations of 18 brain MRI scans from the Internet Brain Segmentation Repository (IBSR). The repository includes T1-weighted MR images and their corresponding manual segmentation. The MR brain datasets and their manual segmentations were provided by the Center for Morphometric Analysis at Massachusetts General Hospital. The volumetric images have been positioned into the Talairach orientation (rotation only). In addition, bias field correction has been performed on this data. Two sets of manual segmentations (for a total of 128 structures) are available for each subject:

• manual segmentation of the 34 main gray and white matter structures of the brain (3rd Ventricle, 4th Ventricle, Brain Stem, CSF and, Left and Right: Accumbens area, Amygdala, Caudate, Cerebellum Cortex, Cerebral Cortex, Cerebellum White Matter, Cerebral White Matter, Hippocampus, Inf Lat Vent, Lateral Ventricle, Pallidum, Putamen, Thalamus Proper, VentralDC, and vessel)

• parcellation of the left and right cerebral cortex into 96 structures.

With this database, we consider the problem of estimating the best segmentation of a target MRI scan. For each target MRI, we consider the other 17 MRI scans and their manual segmentations as template scans. We use non-rigid registration to project each of the template segmentations onto the target, and then carry out label fusion to estimate the segmentation of the target MRI. Based on a recent evaluation of non-rigid registration [21], we selected SyN [22] for carrying out the non-rigid registration. We therefore utilized this registration software, first finding a global affine transformation, followed by SyN with standard parameters which were selected for this data (greedy SyN algorithm with a gradient step of 0.5, similarity metric: probability mapping, Gaussian regularization with σ = 2). We then compared label fusion algorithms to the manual segmentation provided for each MRI.

Based on this leave-one-out evaluation framework, we present a qualitative evaluation of overall segmentation performance of local MAP STAPLE and show its value in providing comprehensive maps of local performance and confidence in the estimated parameters. Then, we compare local MAP STAPLE quantitatively to other state-of-the-art label fusion methods.

1. Qualitative Evaluation of Local MAP STAPLE

For qualitative evaluation, we carried out label fusion using STAPLE, majority voting and local MAP STAPLE. A HWS of 5 was chosen based on the results from synthetic data described above. Fig. 5 illustrates segmentation results for two representative slices of one IBSR image, generated by expert manual segmentation (first column), STAPLE (second column), local MAP STAPLE (third column) and majority voting (fourth column).

Fig. 5. Illustration of IBSR Label Fusion Segmentation.

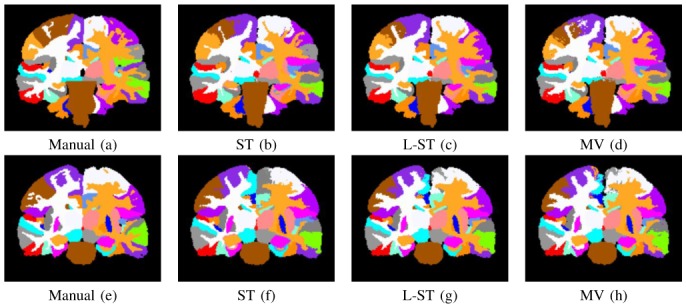
Comparison of segmentations generated by ST: STAPLE (b,f), L-ST: local MAP STAPLE (c,g), MV: majority voting (d,h), and expert manual segmentation (a,e) in a series of coronal images from a representative scan. Local MAP STAPLE is superior to STAPLE and majority voting, especially for structures that have high inter-individual variability.

In this figure, we can observe that STAPLE tends to enlarge cortical structures, while local STAPLE and majority voting do not. This qualitatively demonstrates the value of using local performance estimation when fusing these locally variable structures. In addition, local MAP STAPLE may be utilized to better understand local variations in anatomy or expert segmentation for any structure. For example, for the post-central gyrus, we present in Fig. 6 the performance map for one of the experts and the associated uncertainty in these values (represented as a relative value with respect to the estimated parameter, in percentages), along with the illustration of the reference standard and the corresponding input segmentation.

Fig. 6. Parameter Maps computed with local MAP STAPLE for one IBSR Segmentation.

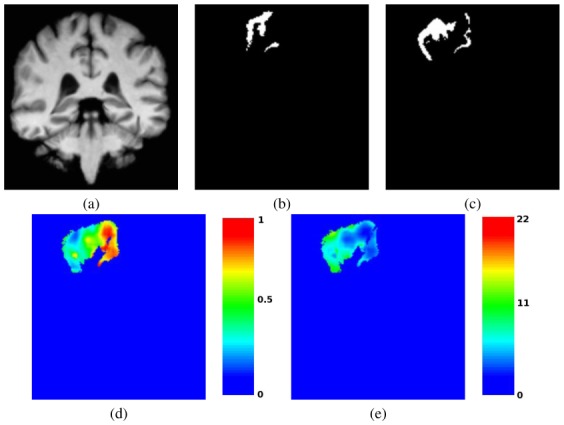
Local parameter map (sensitivity) and its relative uncertainty for the right post-central gyrus of one subject projected on a target subject. (a): Anatomical image of the projected subject, (b): Segmentation of the post-central gyrus for the projected subject, (c): Local MAP STAPLE reference standard obtained from the 17 projected segmentations (including (b)), (d): Local parameter map for local MAP STAPLE. (e): Confidence bounds for the parameters shown in (d) (in percentage of the estimated value). Color bars show respectively the scale of the parameter map and relative uncertainty map (in percentage of the estimated parameter value). The local sensitivity map of this representative input segmentation varies widely across the image. Local variation in segmentation performance is identified by local MAP STAPLE but not by majority voting or STAPLE.

These performance maps illustrate where and how much the expert segmentation differs from the consensus of all segmentations and how confident we are in these values. In particular, these maps show why local MAP STAPLE has the ability to outperform other methods: the sensitivity of the input segmentation is clearly highly variable, which violates the assumptions made both by regular STAPLE and majority voting. Moreover, such parameter and confidence maps may have many potential applications in segmentation evaluation and inter-expert variability estimation. For example, with further processing, future work could develop an algorithm that utilizes these values to drive the registration algorithm to better handle the high variability in these areas and obtain better segmentations. In other settings, these maps may also help to evaluate the local variability in expert segmentation (by illustrating the regions where experts disagree when segmenting a particular structure) and help reaching a consensus in expert segmentation of some structures.

2. Quantitative Evaluation of Binary Segmentation Performance

We carried out a quantitative validation of local MAP STAPLE for the task of label fusion for segmentation, and compared it to state-of-the-art label fusion techniques. We report results for 9 different methods:

• M₁: majority voting

• M₂: SIMPLE [15]

• M₃: COLLATE [23]

• M₄: STAPLE

• M₅: STAPLE with assigned consensus region

• M₆: Local MAP STAPLE

• M₇: STAPLER [24]

• M₈: Sabuncu et al. algorithm [12]

• M₉: Artaechevarria et al. method [10]

In order to enable a fair comparison of these different techniques we have utilized the same preprocessing steps and registration parameters for all of the data leading to the results obtained by each of the 9 label fusion algorithms. For SIMPLE, COLLATE and STAPLER, we utilized the implementations available from the MASI-fusion package. Local MAP STAPLE and STAPLE implementations as well as the evaluation data utilized here are available from the Computational Radiology Laboratory website.

The COLLATE algorithm [23] is an extension of the original STAPLE algorithm, which defines confusion regions based on differences in labelling of aligned images, and leads to different performance estimates depending on the degree of consensus in the initial labelling. We also utilized the global STAPLE algorithm, both with and without the definition of a consensus region [3], [25]. Rohlfing et al. introduced a consensus region to accelerate the STAPLE computation in [25], [9] and noticed that this also leads to improved label fusion performance. STAPLER [24] is an extension of STAPLE, designed to deal with missing and also repeated segmentations. The algorithm uses training data to improve the estimation of the ground truth and performance parameters. SIMPLE [15] is a selective and iterative method which uses a threshold rule to select the best templates at each iteration.

Several recent algorithms have attempted to exploit the local intensity similarity of the target image and template images beyond that achieved by the nonrigid registration. Intensity differences are used a second time after registration to estimate a weight or ranking of the raters for each decision from each voxel of each template. Mean square error based methods and normalized cross correlation have been proposed as the similarity metric in these approaches. Among these approaches, we compared to the algorithms of Sabuncu et al. [12] and Artaechevarria et al. [10], as these are excellent representatives of this class of intensity and label fusion algorithm.

For the COLLATE algorithm, we were unable to obtain whole brain multi-category label fusion results due in part to the challenge of finding parameter settings that lead to good performance. The authors describe the setting of appropriate COLLATE parameters in the following manner [23]:

The optimal number of consensus levels for a given task largely depends upon the difficulty of the labeling task. For a straightforward task where the only confusion about the true label would exist along the boundary between labels, then the binary consensus level case would be appropriate. For a more difficult problem, such as estimating the full brain structure in a multi-atlas multi-label task, more than two consensus levels may be more appropriate and would make for an interesting area of future consideration.

Similarly, the SIMPLE algorithm [15] has been reported only for binary label fusion applications. Therefore, we carried out binary label fusion with each structure independently, and report the results for each structure.

We evaluated 32 structures in 18 subjects, consisting of the following 16 anatomical regions on the left and right side of the brain: inferior frontal 3 gyrus pars triangularis (F3t), inferior frontal 3 gyrus pars opercularis (F3o), precentral gyrus (PRG), middle temporal gyrus anterior (P2a), middle temporal gyrus temporo-occipital (TO2), inferior temporal gyrus temporo-occipital (TO3), post-central gyrus (POG), superior parietal lobule (SPL), supramarginal gyrus posterior (SGp), angular gyrus (AG), juxtaparacentral lobule (supplementary motor cortex) (JPL-SMC), para-hippocampal gyrus posterior (PHp), occipital fusiform gyrus (OF), Heschl’s gyrus (Heschl’s) and the accumbens area. We report in Table II the assessment of segmentation performance of each algorithm in comparison to the manual segmentation, averaged over all 18 subjects and the left and right side. The table reports the relative improvement in performance of each fusion algorithm with respect to the Dice coefficient values obtained by majority voting.

TABLE II. Comparison of Dice similarity coefficients obtained by state-of-the-art fusion techniques.

Dice coefficients are shown for method M₁, majority voting. Other columns show the relative performance improvement with respect to M₁ is then displayed for each fusion technique (in percentages). Local MAP STAPLE has better average performance, better performance range, and better absolute performance for all structures considered.

	M1 (Dice)	M2 (%)	M3 (%)	M4 (%)	M5 (%)	M6 (%)	M7 (%)	M8 (%)	M9 (%)
F3t	0.48	6.72	16.64	−4.30	17.65	18.72	7.82	−2.20	2.98
F3o	0.62	−0.93	5.99	−18.57	5.91	6.04	−8.87	−0.26	1.25
PRG	0.73	−3.19	2.54	−10.00	2.71	3.00	−4.52	0.63	1.53
T2a	0.53	2.06	12.73	−7.17	13.80	14.13	2.18	−1.55	2.12
TO2	0.59	−3.06	9.68	−13.85	8.60	9.07	−3.38	−0.14	2.40
TO3	0.59	−1.38	7.50	−10.56	7.03	7.41	−1.50	0.61	2.81
POG	0.71	−3.29	4.59	−10.03	4.25	4.28	−5.09	0.95	2.10
SPL	0.45	17.98	27.34	4.71	27.43	28.15	17.72	2.56	3.58
SGp	0.51	2.33	16.48	−7.74	16.66	17.09	3.57	0.77	4.87
AG	0.22	60.68	76.14	75.18	94.78	101.38	94.35	−5.13	3.24
JPL-SMC	0.57	2.76	9.08	−8.44	10.20	10.74	0.17	1.37	2.93
PHp	0.65	−3.50	3.75	−14.53	3.08	3.27	−5.95	0.94	1.29
OF	0.28	21.51	61.94	42.39	60.09	62.73	61.65	−4.11	15.68
Heschl’s	0.61	−4.56	5.42	−15.73	6.28	6.34	−5.04	−0.21	1.09
Amygdala	0.78	−1.24	1.12	−12.52	0.83	0.91	−9.14	0.46	0.45
Accumbens	0.75	−2.19	0.86	−15.57	0.98	1.12	−7.83	−0.01	0.11
Min range	0.22	−4.56	0.86	−18.57	0.83	0.91	−9.14	−5.13	0.11
Max range	0.78	60.68	76.14	75.18	94.78	101.38	94.35	2.56	15.68
Average	0.57	2.08	11.12	−7.18	11.58	12.11	1.92	0.03	2.41

We found that local MAP STAPLE outperforms all of the other algorithms, with an average performance improvement over majority voting of 12.1%, with peak improvement of over 100% for a structure with high inter-individual variability.

We observed differences in performance between different forms of the regular STAPLE algorithm. In particular, M₄ (global STAPLE) and M₅ (global STAPLE estimation applied only in the region without consensus) have significantly different performance, simply due to a change in the region over which estimation is carried out. M₅ first identifies a consensus region, defined by that region in which all aligned labels from all inputs are equal [25], [9], [3], and then the voxels in the consensus region are assigned the consensus label value and are ignored in all further calculations.

We executed the COLLATE algorithm M₃ using the parameter settings recommended by the authors [23], which utilizes two consensus levels with weights of 0.99 and 0.01 respectively. The performance of this method is superior to that of M₄ but statistically significantly worse than that of STAPLE with an assigned consensus region, and statistically significantly worse than local MAP STAPLE. Interestingly, it has been observed in [23] that

COLLATE with binary consensus levels is essentially equivalent to performing STAPLE only over the confusion region.

We tested for statistically significant differences in performance between these algorithms using a paired-samples two-tailed t-test, examining the Dice coefficients of segmentations of the 32 structures in the 18 subjects created by each algorithm. We found a significant difference between the performance of local MAP STAPLE and STAPLE with an assigned consensus region (t-score= 4.22, p < 0.0001), and we found a significant difference between the performance of local MAP STAPLE and COLLATE (t-score=5.84, p<0.0001), and between local MAP STAPLE and STAPLE (t-score=26.44, p<0.0001). In addition, we found a significant difference between the performance of COLLATE and STAPLE with an assigned consensus region (t-score=3.28, p<0.001).

These experiments demonstrate further the advantage of accounting for spatially varying performance. Methods utilizing global performance parameters are not able to identify the locally varying positions and shapes of structures that exhibit high inter-individual anatomical variability. In contrast, local MAP STAPLE provides a mechanism to estimate local performance, through the estimation of the segmentation of the target and the comparison of the aligned structures to the segmentation of the target. Intensity differences between the template and target are exploited by nonrigid registration which provides the alignment. This estimate of local performance provides an optimal weighting that in practice outperforms majority voting, as it allows for but does not assume equal weighting between the input structures.

The performance advantage of using a consensus region is especially prominent when binary label comparisons are made for multi-category segmentations. The consideration of a single label versus all others maximizes the number of voxels that may be in consensus. The identification of a final multi-category segmentation from a set of sequential pairwise binary comparisons is not as efficient as a single multi-category segmentation [25], [9], [3]. In multi-category segmentations, there are fewer voxels in complete consensus, the performance parameters vary spatially, and a larger advantage is provided by the local MAP STAPLE estimate.

3. Quantitative Evaluation of Multi-Category Segmentation Performance

We performed a quantitative evaluation of local MAP STAPLE in its multi-category version, to illustrate its value for label fusion on the IBSR datasets. Table III illustrates the segmentation quality achieved by each of three methods with the ability to perform multi-category fusion (majority voting - MV, STAPLE and local MAP STAPLE - L-ST), by comparing the average Dice overlap scores for the 128 structures on the 18 datasets when each structure is simultaneously segmented with the other structures.

TABLE III. Comparison of Overall Segmentation Performance on IBSR Data.

Average Dice scores on the segmentation of the 18 IBSR datasets. These scores are statistically significantly different and demonstrate that local MAP STAPLE (L-ST) has superior performance.

	STAPLE	MV	L-ST
Average Dice Score	0.76	0.81	0.82
Standard Deviation	0.02	0.02	0.02

In this experiment, local MAP STAPLE performance was significantly superior to that of STAPLE (paired t-test, p-value < 10⁻⁶) and majority voting (paired t-test, p-value < 0.001). This demonstrates the advantage of accounting for spatially varying performance. These variations can arise in several ways in this setting. First, the alignment between template and target may cause errors in some areas (such as close to boundaries) and not in others. Further, inter-individual anatomical differences may lead to parts of some structures being well aligned, and others being less well aligned, leading to a spatially varying performance. There are also many structures delineated in the images, and therefore many boundaries between structures. This fact can lead to spatially varying boundary localization differences as the segmentation errors are frequently located in those regions.

IV. DISCUSSION AND CONCLUSION

Label fusion is a powerful strategy for forming a segmentation, as well as for evaluating automatic or manual delineations with respect to each other. Segmentation performance may vary across an image for many reasons. For example, when asked to manually delineate a structure, experts may have responded differently to local intensity features to identify the structure. Fatigue when delineating many structures may also lead to variable error rates in interactive segmentations. For segmentation by registration algorithms, registration errors when aligning template images may lead to local performance variations.

We have described and evaluated a new algorithm, called local MAP STAPLE, to account for spatially varying performance parameters and to compute accurate estimates of the reference standard segmentation. This algorithm estimates simultaneously, from a set of input segmentations, a reference standard segmentation and spatially varying performance parameters. This is achieved through a dense sliding window strategy. To account for the possibility of unobserved labels (such as locally missing or mislabelled structures) in some regions, we formulated a Maximum A Posteriori estimator, providing a prior probability distribution on each performance parameter, which allows effective estimation of a reference standard segmentation when there are no observations of certain labels from which to estimate rater performance. We derived expressions to estimate confidence intervals for the local MAP STAPLE performance estimates, to allow for the characterization of the uncertainty in the performance parameters which may vary with the local quality of the segmentations and the size of the sliding window.

We have demonstrated the excellent performance of local MAP STAPLE for both label fusion and comparison of expert segmentations. First, we showed a clear and substantial improvement of the reference standard estimation with simulated binary segmentation data with spatially varying performance, when compared to regular STAPLE or majority voting. Then, we evaluated label fusion for brain segmentation using the IBSR database. For these datasets, local MAP STAPLE performs quantitatively better than other state-of-the-art label fusion algorithms reported in the literature, including regular STAPLE and majority voting.

Majority voting can be understood as a special case of the local MAP STAPLE algorithm, for which a local window of one voxel is assumed, and in which a uniform prior is assumed, i.e. each template is assumed to be equally effective and no label is prevalent. The same result can be achieved with local MAP STAPLE if we make the same assumption for the prior, initialize each template as equally likely, and run MAP STAPLE for a half-iteration (Expectation step only) with a window of one voxel. Selecting the most likely label at each voxel from this specific setting will then lead to the majority voting result. Furthermore, if any of these assumptions are incorrect for a particular label fusion problem, such as for cortical structures for example, local MAP STAPLE provides a mechanism to provide excellent estimation. If the local MAP STAPLE window size is extended to encompass the entire image, then a global estimate is obtained as for the STAPLE algorithm.

We evaluated local MAP STAPLE in comparison to recently published state-of-the-art fusion algorithms, using a standardized data set and identical nonrigid registration in each case. In intensity and label fusion algorithms, intensity differences are used to define a weight for each decision for each voxel of each template. Mean square error based methods and normalized cross correlation have been proposed as the similarity metric, and these have been used both globally and locally, or template ranking and to exclude certain templates. The most recently introduced approaches utilize local intensity information to weight a majority voting label fusion [12], [10]. By directly using image intensities, these algorithms can become very sensitive to the native signal intensity or to the nature of the intensity normalization that may be carried out, and as demonstrated in the results that we have obtained, an intensity-based weighting cannot compensate effectively for some of the intrinsic weaknesses of the majority voting approach. We demonstrated that local MAP STAPLE achieved superior performance to the intensity and label fusion algorithms of Artaechevarria et al. [10] and Sabuncu et al. [12].

In these intensity and label fusion algorithms, after completing an intensity-based nonrigid registration, intensity differences are used a second time to estimate a weight or ranking of the raters. We note that this implies that after registration there remain unexploited intensity differences that can be used to further increase the accuracy of the correspondence estimation. If there were unexploited residual signal intensity differences that were helpful in identifying true correspondences, it would be natural to design a registration algorithm that sought to exploit these. It may be that intensity and label fusion combination algorithms benefit most from the nonrigid registration algorithms that achieve alignment with a substantial residual registration error, and that the benefit of these approaches is reduced as the residual registration error is reduced. In practice, the regularization approach used by most nonrigid registration algorithms provides a balance between precisely matching intensities, toleration of noise and contrast in the images, and the desired smoothness of the registration transformation. It is not clear how best to infer from these intensity differences what constitutes uncapturable inter-individual anatomical variability, and what constitutes imprecise alignment of anatomical structures that should be brought into closer alignment, and this will be an interesting direction of research in future work.

We compared local MAP STAPLE to the algorithm called SIMPLE [15], which compares the template images to the estimated reference standard, and excludes the worst templates at each iteration. However, convergence to a particular optimum is not guaranteed with SIMPLE, and in practice it is common to observe cycling amongst the volumes that are included and excluded, as the exclusion of some templates leads to a different reference standard estimate, which then causes different volumes to be excluded and the initially excluded volumes to be reintroduced. The authors [15] propose to use an iteration count limit to avoid infinite cycling, and this forces convergence to a particular result that depends on the particular setting of the iteration count limit. We demonstrated that local MAP STAPLE achieved superior performance to SIMPLE.

Our experimental results indicate that accounting for spatial variation in performance is an important characteristic to achieve excellent quality label fusion. Our results demonstrate differences in performance between different forms of the regular STAPLE algorithm. In particular, label fusions with STAPLE achieved significantly different performance with a simple change in the region over which estimation is carried out. STAPLE applied with a consensus region, defined by that region in which all aligned labels from all inputs are equal [25], [9], [3] had superior performance to STAPLE applied globally. The voxels in the consensus region are assigned the consensus label value and are ignored in all further calculations. We observed here that a consequence of this is that the performance estimates are focused on those regions that are not in consensus, and this provides spatial adaptivity in the performance estimates. Those regions in consensus are regions in which local performance is very high, as all input segmentations are in complete agreement, whereas the region where there is no consensus has imperfect performance by some inputs. A global estimate that combines the performance in the consensus regions and the non-consensus regions attempts to approximate these differences in performance with a single parameter, and this approximation leads to worse label fusion in practice as seen in the results for STAPLE applied globally. This difference in region of calculation may explain in part why previous comparisons to STAPLE in the literature have reported inconsistent findings for the relative performance of STAPLE to, for example, majority voting.

We evaluated the COLLATE algorithm in the setting of binary segmentation, with two consensus weights. Experimentally, we observed that performance was decreased the further these weights are from 1.0 and 0.0. The reason for this worse performance is that the COLLATE algorithm does not exploit the available spatial adaptivity. Instead the selection of weights for consensus levels inappropriately combines performance from different regions, the region in complete consensus where performance is high, and the region in confusion where performance varies. In the COLLATE algorithm, performance estimates are combined across these regions with a combination rule that depends on the selected weights. Weights are used to emphasize decisions carried out at certain confusion levels, and to create a balance between the influence of voting and performance weighting. Indeed, if the COLLATE weights are chosen to be 0.5 and 0.5, we obtain a final result weighted towards majority voting, and as the weights become closer and closer to 1.0 and 0.0, the algorithm becomes closer to STAPLE with an assigned consensus region [25], [9], [3]. It is unclear with what principle consensus level weights could be chosen for multi-category segmentations [23]. The model of COLLATE suggests that voxels with different selection rates by different raters should be weighted differently when assessing performance. However, in a local region over which performance of each rater is well modeled as constant, every voxel is helpful in identifying the distinct decisions that separate good raters from bad raters, and in local MAP STAPLE comparison to the estimated reference standard segmentation enables effective assessment of rater performance without regard to whether or not other raters are performing well or poorly in a region. We demonstrated that local MAP STAPLE achieved superior performance to COLLATE.

Asman et al. [26] described a ‘spatial STAPLE’ algorithm that considers sub-regions of the image over which STAPLE is run. This work highlights the importance of accounting for spatially varying performance in expert fusion and segmentation by label fusion. Although very promising, this approach did not overcome the challenges in effectively enabling spatial adaptivity in the performance estimation and label fusion. Two different formulations of a sparse regional confusion matrix model were proposed. In the first model, every region was non-overlapping and sparse performance estimates were obtained with each voxel belonging to only one region, but the use of large nonoverlapping regions was observed to poorly model the desired spatial adaptivity [26]. In a second model, a sparse sliding window region definition was proposed, in which it was possible for a voxel to be associated with more than one region, and where nearest neighbor interpolation was used to associate performance parameters for a region with each voxel. As a consequence, it is possible for a voxel to have a segmentation decision that contributes to a weight estimate, but for that same weight estimate to contribute to updating different performance parameters than were used in estimating the weight. Therefore, in the proposed sparse sliding window configuration, the estimation of the probability of the reference standard segmentation (‘E-step’) and the estimation of the performance parameters (‘M-step’) utilizes different subsets of the observations of the segmentations. The resulting system of equations is not a consistent estimator, and the iterative procedure suggested for solving them is not guaranteed to converge. In contrast, local MAP STAPLE uses a dense sliding window to define the spatial support of the performance estimation, and is guaranteed to converge. In recognizing and addressing the challenges of performance estimation from local information alone, the work of [26] proposed an ad hoc technique for regularization of the performance parameters using a global estimate of the performance parameters, and observed that a problem of ‘label inversion’ could arise in which dramatically incorrect segmentations arise. In this work, we demonstrate the efficacy of the MAP formulation at addressing this challenge. Furthermore, [26] provides only point estimates of performance parameters, whereas we demonstrate how to construct estimates of confidence intervals that characterize the certainty of the performance parameter estimates, providing a quantitative measure of the efficacy of the information available from the input images for providing a label fusion.

Future work may further increase the performance of label fusion. The current algorithm utilizes only label information, but it may be possible to achieve further increases in performance of local MAP STAPLE by incorporating intensity information. A straightforward mechanism to do this would be to extend the prior probability of labels f(T_i = s) to depend on intensity information. We demonstrated that local MAP STAPLE provides similar results for a range of local region sizes, illustrating an insensitivity to region size for these applications. Further work may also develop new approaches for identifying the optimal region size for spatially varying performance estimates. To this end, the inferential uncertainty presented in Section II-D may be a valuable criterion to balance the need to have sufficient data to achieve tight confidence intervals, while being sufficiently local to adapt to the rate of change of performance.