Abstract
Building on our recently introduced library-based Monte Carlo (LBMC) approach, we describe a flexible protocol for mixed coarse-grained (CG)/all-atom (AA) simulation of proteins and ligands. In the present implementation of LBMC, protein side chain configurations are pre-calculated and stored in libraries, while bonded interactions along the backbone are treated explicitly. Because the AA side chain coordinates are maintained at minimal run-time cost, arbitrary sites and interaction terms can be turned on to create mixed-resolution models. For example, an AA region of interest such as a binding site can be coupled to a CG model for the rest of the protein. We have additionally developed a hybrid implementation of the generalized Born/surface area (GBSA) implicit solvent model suitable for mixed-resolution models, which in turn was ported to a graphics processing unit (GPU) for faster calculation. The new software was applied to study two systems: (i) the behavior of spin labels on the B1 domain of protein G (GB1) and (ii) docking of randomly initialized estradiol configurations to the ligand binding domain of the estrogen receptor (ERα). The performance of the GPU version of the code was also benchmarked in a number of additional systems.
1 Introduction
Biomolecular simulation attempts to model the configurational fluctuations in proteins and other biomolecules, but the field remains largely trapped in two unsatisfactory extremes. On the one hand, there are traditional all-atom simulations, which prioritize chemical accuracy at the expense of sampling. Even though specialized modern hardware implementations can generate multi-microsecond all-atom trajectories and beyond for small systems,1,2 many proteins are up to an order of magnitude larger than the reported systems;3 furthermore, protein motions can require seconds or even longer (e.g.,4,5). The other extreme is coarse-grained models, which sacrifice chemical detail in exchange for much better sampling (e.g.,6–11). Coarse models have fundamental limitations in explaining atomistic details of biochemistry.
The middle ground between all-atom and coarse-grained modeling has not received nearly as much attention, but important advances have been made. Several groups have performed mixed-resolution simulations: a model which incorporates all-atom (AA) resolution in an area of interest (e.g., binding site) but a coarse-grained (CG) representation elsewhere.12–16 Also noteworthy are algorithmic efforts to use models at multiple resolutions to accelerate sampling.17–22
Hybrid AA/CG models, we believe, can play a fundamental role in the study of biomolecules by simulation. Hybrid models offer the possibility to perform high-quality statistical sampling (un-like all-atom models) while maintaining atomistic chemical accuracy in an important region such as a binding or active site (unlike coarse-grained models). Hybrid models may thus provide an important class of computational tools to complement existing AA and CG approaches. For instance, although not addressed in the current report, hybrid models should be useful for investigating the often discussed idea that large-scale motions can be allosterically coupled to functional atomistic motions,23–26 which is not universally accepted.27 In more general terms, hybrid models offer a way to construct models which are as detailed as possible but still permit good sampling. Modern statistical analyses permit objective assessment of sampling quality.28–31
Regardless of the chemical accuracy of a model, it is important to perform the best simulation possible given available computing resources. However, software for molecular simulation may not be exploiting modern hardware capacity fully, even when graphics processing units (GPUs) are used.1,32,33 That is, almost all simulation software is structured in what can be termed a “calculation-intensive” way: at each time step, all required interactions are calculated on the fly via repeated floating-point operations. In all-atom MD calculations, this typically means that 99% of random-access memory (RAM) goes unused, with a still larger percentage going unused for coarse-grained systems. Standard simulations employ RAM on a Mbyte scale whereas commodity hardware typically offers GByte RAM capacity.
To exploit modern GByte RAM capacity, our group has developed “library based” approaches in which biomolecules are divided into molecular fragments (e.g., amino acids), which are sampled in advance and stored in RAM.34–40 Because each fragment is represented by configurations distributed according to the Boltzmann factor of a standard all-atom force field, energy terms and subtle correlations internal to the fragment are accounted for in advance. Library approaches can offer tremendous efficiency for small, implicitly solvated peptides,35,38–40 and also great flexibility in constructing and sampling protein models.34,36,37 Memory can also be exploited in molecular simulations by tabulating interactions among molecules or fragments, which can speed up calculations and smooth interactions.41
Here we report the application of memory-intensive library-based computing to construct mixed-resolution models of proteins. The basic strategy is to exploit memory to track the locations of all atoms at every time step, but save computation by including only a subset of the interactions, e.g., atomistic terms within a binding site and alpha-carbons interactions elsewhere in the present report. In the present implementation, all side chain atoms are stored in libraries of atomistic configurations, while backbone atom coordinates are treated as ordinary (continuous) degrees of freedom to permit trial moves that perturb the overall fold of the protein only locally. Sampling is performed with the “library-based Monte Carlo” (LBMC) algorithm34–37 which permits swapping of side chain configurations with library configurations, as well as standard Monte Carlo moves such Cartesian displacements or local rigid-body rotations. We adapt the standard generalized-Born surface-area (GBSA) implicit solvent model42,43 to mixed-resolution models and port the GBSA calculation to GPU to save computing time.
In this report, we describe initial applications of mixed-resolution LBMC in two fairly different contexts: spin-label fluctuations and small-molecule docking. We first study a spin-labeled GB1 domain by simulating spin-label fluctuations and comparing them to experimental measurements made using double electron electron resonance (DEER).44–50 We explore the ability of LBMC simulations to provide detailed ensembles to aid the interpretation of DEER measurements. The spin labels and neighboring residues are modeled atomistically with the remainder of the protein coarse-grained. Second, we assess the potential of mixed-resolution LBMC for mutually adaptive docking — where both the ligand and receptor flexibly adapt to one another. We docked allatom estradiol into the ligand binding domain of the estrogen receptor (ERα) with the binding region modeled atomistically. The LBMC simulations can recover from poor initial configurations including significant steric clashes. Lastly, we report timing results on a range of systems to compare the GPU and CPU implementations.
The remainder of the paper provides full details of our studies. Section 2 reviews the basics of LBMC simulations and describes the current mixed-resolution and hybrid GBSA approaches. Porting of the GBSA calculation to GPU is also described in Sec. 2. Systems and results are given in Section 3, while Sec. 4 discusses limitations of the results along with possible improvements and future applications.
2 Methods
Hybrid coarse/atomistic models are constructed conveniently using library-based Monte Carlo (LBMC).34–37 In LBMC, molecules are divided into fragments for which pre-calculated all-atom (AA) configurations are stored in “libraries”. Because the stored configurations and the LBMC implementation provide correct atomistic geometry (e.g., via bonded interactions), the software maintains the flexibility to include or exclude arbitrary non-bonded interactions. In particular, it is straightforward to use a subset of atomic sites as interaction centers for coarse-grained models.
We briefly review LBMC before describing the hybrid coarse/atomistic model.
2.1 Library-based Monte Carlo
Full details regarding the LBMC methodology have been previously published,34–37 so we review only the essential aspects here. LBMC is a statistically rigorous method for using libraries of pre-calculated molecular fragment configurations to generate ensembles of a full molecule in conformance with the Boltzmann factor for the full forcefield. Not all degrees of freedom need to be included in fragment libraries.34
In the present implementation, only side chain degrees of freedom (from the alpha carbon and beyond) are included in libraries. More precisely, all internal coordinates of the side chain are included in the libraries, although alpha-carbon Cartesian coordinates are not included. Protein backbone coordinates are not included in libraries, but are tracked explicitly. Thus, all protein atomic positions are tracked in the present LBMC implementation, unlike in our previous LBMC protein simulations.34,36
An LBMC simulation divides the full set of atomic coordinates x into a number of non-overlapping subsets for the libraries and for the explicit coordinates not contained in any library:
| (1) |
where is the set of atomic coordinates for fragment i and xexp is set of explicit coordinates. In the present implementation, each side chain is characterized by its own library, while backbone atoms are explicit. Side chain libraries are generated to be consistent with an atomistic force field (here, OPLSAA51–53 and the GBSA implicit solvent model42,43), which amounts to the distribution
| (2) |
| (3) |
where includes all OPLSAA interactions internal to the fragment, both bonded and non-bonded terms, and represents the GBSA solvent model defined below. The total potential energy function for the system, Utot, is of the form
| (4) |
where Urest includes all other terms in the model, which are specified below. Regardless of the choice for Urest, it can be shown34 that the Metropolis criterion for a trial swap move with library i (i.e., exchanging the current configuration for fragment i with one from the library) is given by
| (5) |
where xo and xn are the old and trial configurations for the full system and ΔUrest = Urest(xn) – Urest(xo). The acceptance criterion does not depend on UAAi since the correct distribution of these terms has been built into the library. Note further that it is straightforward to derive an acceptance criterion for the case when swap attempts are restricted to a subset of similar “neighbor” configurations in the library.34
Our hybrid simulations employ other trial moves appropriate to our explicit treatment of backbone atoms. A particularly important category of moves perturbs only local segments of the protein, leaving the remainder unchanged.54 The local moves we employ are single-atom translations and rigid-body rotations. Rigid-body rotations are used for both backbone segments and for sidechains. We also employ “phi-psi” trial moves which twist backbone dihedral angles.
Trial moves for a ligand include the single-atom displacements noted above and an additional move combining center-of-mass translation and full-ligand rotation. For the ligand translation/rotation, a randomly directed trial displacement is generated uniformly with a maximum possible displacement here set equal to 0.1 Å, while uniformly random rotations are generated using unit quaternions.
To summarize, the full set of trial moves employed in the present LBMC implementation is as follows: side chain swaps, side chain rotations, single-atom displacements, rigid body moves, phi-psi moves, and ligand moves (when a ligand is present). The fractions of move types are given below when each system is described. Different choices made for the move-type distribution principally reflect differences in degrees of freedom among systems (e.g., presence or absence of a ligand) rather than systematically optimized choices.
2.2 Hybrid coarse/atomistic models
Hybrid CG/AA models are straightforward to implement in LBMC because all atoms are automatically tracked. CG or hybrid models implemented in LBMC appear to have certain intrinsic advantages. Consider the example of developing a model where side chains are represented by one or a small number of interaction sites or “beads”. Because side chain configurations are stored atomistically, CG sites can be placed with reference to the true molecular geometry already accounted for in the library. Physically reasonable side chain configurations are thus more likely.
Hybrid resolution models in this study are constructed by dividing a protein into two non-overlapping regions: all-atom and coarse-grained (Figure 4). In other words, we divide the full set of coordinates into parts so that x = (xAA;xCG). The subset xCG should be understood to include all atoms in the CG region because atomistic interactions internal to side chains are always retained via pre-calculated libraries in LBMC, as explained above. Note that each of the coordinate sets xAA and xCG is further subdivided into fragments (amino acid sidechains) and explicit atoms (protein backbone). Ligand atoms are always included in the atomistic set xAA in this study.
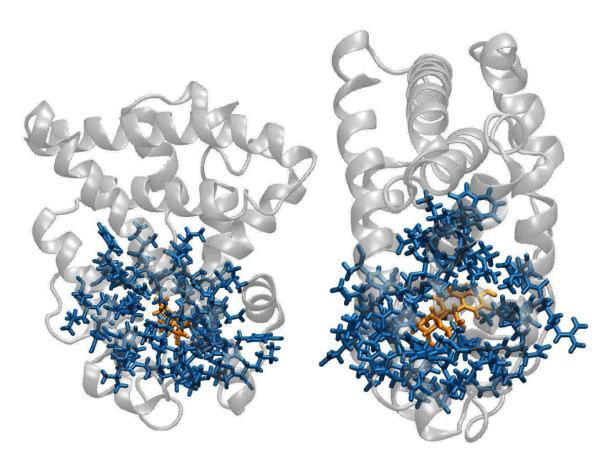
Figure 4.
A mixed-resolution model of the ligand binding domain of the estrogen receptor (ERα). Residues within 5 of the binding pocket have been represented atomistically (blue). The atomistic region contains 764 atoms. The remainder of the protein is modeled with Gō interactions (Sec. 2). The estradiol molecule (orange), is also represented atomistically.
In overview, standard OPLSAA interactions prevail in the AA region, simplified non-bonded interactions are used in the CG region, and cross interactions between AA and CG regions employ CG energetics. The choice of whether to use CG or AA cross interactions is somewhat arbitrary and can be seen, in effect, merely as shifting the CG/AA boundary. In this study, which presents our first use of a hybrid model, we employ a very simple CG model, namely Go̵ or “structure based” interactions among alpha carbons. Nevertheless, the backbone is represented in atomistic detail to improve the physical realism of tertiary configurations. We use a version of the standard GBSA implicit solvent model42,43 which is adapted to a hybrid context. All interactions are specified below.
In further detail, the total potential energy of the system is the sum of four terms:
| (6) |
where UAA, UCG and Ucross are the potential energies of the AA region, the CG region, and of AA-CG interactions, respectively. The Usolv term models solvent effects and depends on both AA and CG coordinates in our GBSA implementation as detailed below. (Note that the U AA term here is not the simple sum of the UAAi terms used previously in Eq. 3 for the libraries.)
All-atom interactions are modeled using the standard OPLSAA forcefield51–53 in the present implementation, so we have simply
| (7) |
The CG region is modeled by an atomistic backbone and Gō interactions among alpha-carbons. We write
| (8) |
where is the set of OPLSAA backbone interactions described below, is the set of backbone atoms in the CG region, UGo is the Gō potential specified below, and is the set of alpha carbons in the CG region. Backbone coordinates are defined to include all backbone Cartesian coordinates plus those internal coordinates which also depend on beta-carbons: this permits establishing correct backbone geometry (e.g., Ramachandran propensities). For pro-line residues all the atoms were explicitly modeled as part of the backbone. To most faithfully reproduce atomistic backbone geometry, we employed
| (9) |
Thus, the backbone is described by the same OPLS-AA bond, angle, and torsion energy functions as the AA region. We also included van der Waals and Coulomb interactions between atoms connected through three and four chemical bonds, i.e., bonded 1-4 and 1-5 interactions. Bonded 1-4 interactions are included because they were part of the OPLS-AA torsion parameterization.51–53 Bonded 1-5 interactions were included to model the correct local backbone geometry, particularly Ramachandran propensities.
2.3 GM potential
GM interactions are modeled with pairwise hard-core square-well potentials, which is suitable for a Monte Carlo implementation. The Gō potential depends on a set of interaction sites x = {r1;r2;…}, which are alpha carbon locations in the present study. It will prove convenient to specify the potential in terms of the difference vectors rij = ri – rj. The potential is given by
| (10) |
where is the total energy for native contacts and is the total energy for non-native contacts. All residues that are separated by a distance less than a cutoff, Rcut, in a reference experimental structure are given native interaction energies defined by a square well
| (11) |
Here rnatij indicates the distance between alpha-carbons of residues i and j in the reference experimental structure. All residues that are separated by more than Rcut in the experimental structure are given non-native interaction energies defined by
| (12) |
where ρi is the hard-core radius of residue i, defined at half the α-carbon distance to the nearest non-covalently bonded residue in the experimental structure, and h determines the strength of the repulsive interactions.
The present study uses parameters Rcut = 8:0 Å δ = 0:2, ε = 1:0. The value of ε is chosen to be as small as possible but large enough so that a protein is stably folded at temperature T = 300K. For all studies, the parameter h = 0.3 was used, therefore the non-native go interactions have a strength equal to 30% of the native go strength. We found this value to be sufficiently strong for our studies.
Regarding reference structures for Gō interactions, for GB1 we used coordinates from Protein Data Bank code 2GI9 and PDB code 1ERE for the estrogen receptor.
Interactions between CG and AA regions are embodied in Ucross, which includes both Gō interactions among alpha carbons and bonded interactions among backbone atoms. Thus, atomistic backbone interactions are consistently used throughout a protein, but other cross-boundary interactions are coarse-grained for simplicity. In terms of quantities defined above, the cross-region interaction potential is thus given by:
| (13) |
where the arguments “xCG : xAA” are a shorthand to indicate interactions between all sites where at least one site is from the CG region and at least one is from the AA region. The subscripts of the arguments indicate whether backbone atoms or alpha carbons are being considered. The function UOPLSAAbb is defined in Eq. (9) and UGo is defined in Eq. (10).
2.4 GBSA solvent model
To model solvent effects, we employed the GBSA implicit approach42,43 but in a modified form suitable for our hybrid scheme. The use of an implicit model of solvation is consistent with our streamlined hybrid modeling. GBSA interactions occur only among atomistic sites, but include the dielectric influence of CG residues in an averaged way, as detailed below. Solvation effects among CG residues are assumed to be accounted for by Gō interactions, which is convenient for this initial hybrid study, but one not required in our approach. Thus, hydrophobic effects are included implicitly for both the AA and CG regions.
GBSA is applied to atoms in the AA region largely following the formalism of Qiu et al.43 except that modified Born radii α ^i (instead of αi) are used, as specified below. Thus, we set
| (14) |
where UGB is the standard form43 and USA is given below. The modified Born radius for atom i is calculated according to
| (15) |
where Rvdw;i is van der Waals radius of atom i, ϕ is the probe radius, P1, P2, P3, P4 are scaling factors, CCF is a scaling function, while Vj is the volume of atom j. Eq. (15) would be precisely the GBSA implementation of Qui et al.43 if represented the distance between atoms i and j instead of the modified definition given below. The first three terms in Eq. (15) are considered constant because bonds and bond angles are relatively stiff and, therefore, do not affect Born radii much. The last summation in Eq. (15) covers all atoms in the system (in both AA and CG regions) not covalently bonded to atom i.
The non-polar surface-area term USA is the same as that used in the TINKER software55 and is given by56,57
| (16) |
where σi is an empirical atomic solvation parameter for atom i. Default TINKER values for the σi parameters were used.
Our modification of the GBSA formalism consists solely of approximating inter-atomic distances required for Eq. (15) between atoms in AA and CG regions by using the alpha-carbon Cα of a CG residue for all atoms in the residue. Specifically, if dist(i; j) represents the distance between atoms i and j, we set
| (17) |
where Cα( j) is the alpha carbon of the residue to which atom j belongs. Procedurally, in the evaluation of Eq. (15), the function r̂ permits the use of residue volumes which are the sum of atomic volumes Vj in the residue. Physically, the r̂ function assumes that all CG atoms are distant enough to be treated in an averaged way at the alpha-carbon distance. Such an approximation is reasonable given the hybrid CG/AA modeling. In several test proteins, the average deviation from the exact Born radii (based on exact atomic positions in the CG region) was found to be less than 5% with a standard deviation of less than 10% in all cases (data not shown). Recall from above that GBSA interactions do not occur among atoms in the CG region.
2.5 GBSA implicit solvent calculation on the GPU
We used a GPU to accelerate the bottleneck calculation in our initial CPU-only implementation of mixed-resolution LBMC. In the CPU implementation, benchmarks (data not shown) indicated that the GBSA calculation, on average, accounted for 95% of the total computational cost in a typical simulation. This is not surprising since a naive GBSA energy calculation scales as N2 – that is, the GBSA energy contributions between all-pairs of atoms needs to be calculated and summed. Note that due to the mixed-resolution nature of the model however, “number of atoms” should be interpreted to be the sum of the number of atoms in residues that are represented in full atomistic detail plus the number of residues which are represented solely by their Cα atoms. In contrast, the cost of a typical Monte Carlo move is much smaller and scales as m(N –m) where m is the number of atoms involved in the move (e.g. m = 1 for single atom moves and N » m > 1 for group moves ). For our set of moves, m « N, further underscoring the high cost of the GBSA calculation.
Therefore, in an effort to reduce the fraction of time spent on the GBSA calculation, a simple GPU “port” was written for the GBSA energy function. That is, the GBSA energy is evaluated on the GPU after every MC trial move. The high N2 “all-pairs” cost of the GBSA calculation made it a very strong candidate for GPU calculation. The GPU port of the GBSA energy calculation was implemented using the CUDA programming language on a nvidia GTX 480 GPU. The general form of the N2 all-pairs calculation algorithm for CUDA has been studied and optimized extensively, but in different contexts, for example in gravitational n-body molecular dynamics simulations.58 Therefore, the algorithm we used is identical to the one implemented in reference,58 where the pairwise GBSA energy terms in our implementation is equivalent to the pairwise force terms used in the corresponding MD simulation.
3 Systems and results
We use the flexibility of mixed-resolution LBMC to examine systems of different size and complexity. At one extreme, we study two relatively simple models of a spin-labeled GB1 domain (B1 domain of protein G) to assess fluctuations in the labels. GB1 is a well-characterized small protein that serves as a model system for structural studies.59–61 The estrogen receptor, on the other hand, is a much larger protein of therapeutic importance that exhibits more complex behavior.62–67 We employ LBMC to constuct a more complex AA/CG model which is used for docking the endogenous ligand, estradiol, with full ligand/receptor flexibility. The initial results described below are promising in both cases.
3.1 Spin label fluctuations in the GB1 domain
Our study of the spin-labeled GB1 domain is motivated by the growing prevalence of double electron-electron resonance (DEER) experiments44–49 for biomolecular systems. DEER experiments report on ensemble properties of the system (e.g., the distribution of distances between spin labels), without resolving individual structures of the underlying molecular ensemble. Furthermore, the spin-label distance distribution is a convolution of backbone and label fluctuations. Molecular simulations provide a natural way to model the molecular details,68–78 but efforts have been hampered by the usual challenges of sampling and force field accuracy. We therefore wish to investigate the potential of LBMC to mitigate sampling issues. The ability to employ a pre-sampled library of spin-label configurations (the spin label is a chemically extended cysteine side chain) makes LBMC a strong candidate for sampling the fluctuations.
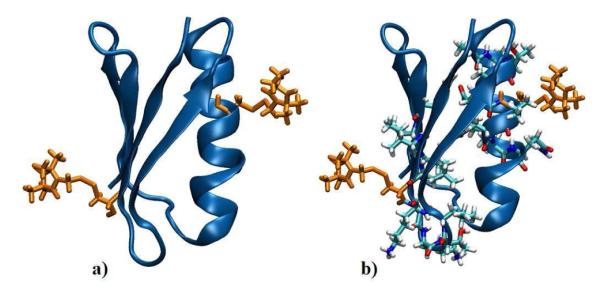
We investigated two relatively simple LBMC models of GB1. See Fig. 1. Consistent with the experimental set-up,50 our model GB1 protein is spin-labeled using the methanethiosulfonate spin label (MTSL) on two opposing sides of the protein and attached to the backbone via disulphide bonds. Sites Asn 8 and Lys 28 were labeled. In the first model (A), only the spin labels are modeled in full atomic detail and no interactions with surrounding residues are present; the backbone is rigid. In the second model (B), ten additional flexible residues surrounding each label were modeled atomistically with the backbone again rigid, for a total of 20 AA residues plus the AA spin labels. The models are shown in Fig. 1. Spin label parameters were taken from.76
Figure 1.
Two mixed-resolution LBMC models for the spin-labeled GB1 system. Model A includes only motion of the all-atom spin label, while model B further includes 20 additional all-atom side chains.
LBMC simulations for both models were run for 108 Monte Carlo steps (MCS) where a MCS is a move randomly selected from the set of possible moves. In particular, for models A and B, the distribution of moves was simply 50% side chain swaps and 50% side chain rotations. However, model B includes a larger set of flexible residues, as described above.
Each simulation was run for three days using GPU-accelerated LBMC, although good sampling was obtained in a small fraction of the time as shown below. Compared to CPU-only simulation, we observed a speed-up of a factor of ~ 5 for both models.
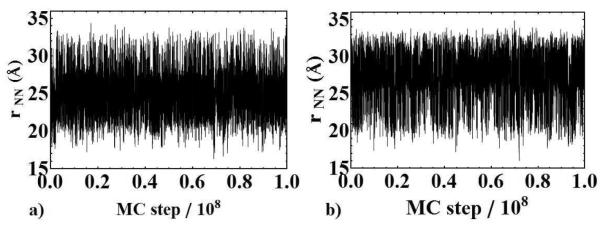
Distances between spin-label nitrogen atoms, rNN, were measured from LBMC trajectories using the nitrogen positions of each respective spin label. The rNN distance trajectories are shown in Fig. 2 a) and b) corresponding to models A and B, respectively. In both cases, the systems exhibit good sampling in this coordinate space, as evidenced by numerous fluctuations about a steady mean value. As seen in Fig. 3 reasonable statistics were obtained within the first 10% of the simulations — representing only a few hours of wallclock time.
Figure 2.
The rNN distance trajectory as obtained from model A (a) and model B (b) plotted vs. MC step, where rNN denotes the distance between spin-label nitrogen atoms.
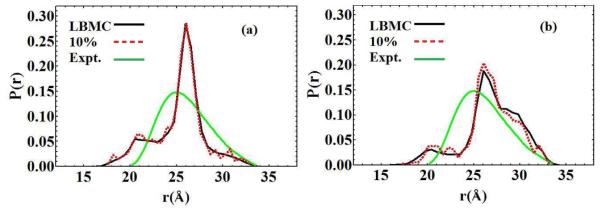
Figure 3.
The corresponding probability distributions obtained from the rNN distance trajectories in model A (a) and model B (b) compared with the experimental spin-label distance distribution (green). Black curves denote the probability distributions using the entire length of the simulation whereas the dashed red curves represent the first 10% of the simulation. Convergence occurs within a few hours of runtime in each simulation.
The comparison of the LBMC rNN distances with the distribution derived from DEER data is reasonable. See Fig. 3. There is significant overlap between the experimental and simulated distributions, with similar spreads in values. In both cases, the predicted most probable distance is within 1.0 Å of the experimental value and also within the experimental uncertainty of ±1.0Å. The LBMC distributions are bimodal, as compared to the unimodal distribution calculated from DEER data, but the more flexible Model 2 is somewhat broader and in better agreement. Some disagreement is to be expected due to the simplicity of our models, force field inaccuracy and experimental error, but the key point is the encouraging ability to sample a model well that can be systematically improved by better parameterization and additional flexibility.
We also examined the rotameric distribution of the spin labels, which are characterized by five dihedral angles and hence reasonably complex. We compared our data with rotamers recently characterized crystallographically for both the alpha helical spin label (residue 28) and the beta-sheet spin label (residue 8).50 The simulated spin-label ensembles included all rotamers found experimentally, judged by the criterion that the root-mean-square deviation per dihedral was < 15°. The simulations also sampled numerous other rotamers, which future work will attempt to validate.
3.2 Fully flexible docking in the estrogen receptor
Our goal in studying the estrogen receptor is to determine whether LBMC might be a useful platform for fully flexible docking, in which both the ligand and receptor can adapt to one another. Because we begin our simulations from poor initial configurations often with significant steric overlaps, and because the receptor “relaxes” initially without the ligand bound properly, our data is suggestive of the potential of LBMC in more practical cross-docking cases.
We study the ligand binding domain of the α isoform of the estrogen receptor (ERα). See Fig. 4. The starting structure consists of ERα with a bound estradiol molecule (PDB ID: 1ERE). All residues within 5 Å of the ligand were represented in full atomistic detail, resulting in a total of 764 atoms (representing 44 residues) and an additional 192 residues represented only by their Cα positions.
The docking simulations employ a procedure that perturbs both the ligand pose and the receptor. Each LBMC run starts with the receptor/ligand complex in the crystal structure. The complex is simulated for 500 MC steps, at which point a perturbation is applied. The perturbation we used is a rotation to a completely random new orientation, independendent of the initial pose, which can lead to significant steric clashes and RMSD values (of the ligand) exceeding 5 Å. The simulations were continued until a total of 104 MCS was completed, requiring about five minutes of wall-clock time on a single CPU; a GPU was not used for these calculations. Additionally, the distribution of LBMC trial moves for this system is as follows: 10% side chain swaps, 10% side chain rotations, 10% single atom moves, 20% rigid body moves, 20% phi-psi moves, and 30% ligand moves.
The receptor structure is fully flexible and the relatively plastic binding pocket can change before or after the perturbation. More than 400 independent simulations were performed to gather reliable statistics. Two sample trajectories are shown in Fig. 5.
Figure 5.
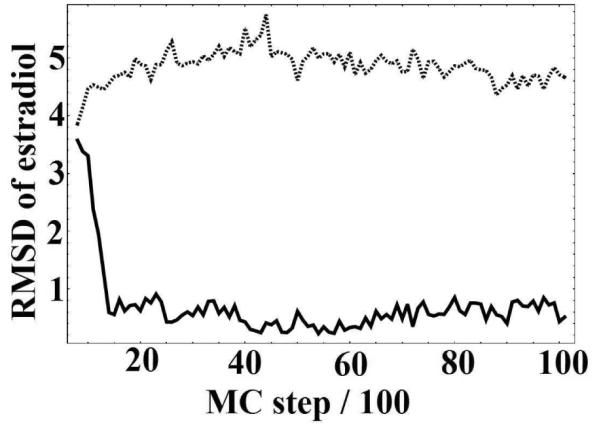
Two representative trajectories from the estradiol/ERα docking simulations. The vertical axis shows the all-atom RMSD of estradiol relative to the 1ERE crystal structure after the receptors have been aligned. The top curve (dashed) is a trajectory where the ligand was not able to dock successfully after the perturbation. The bottom curve (solid) shows a trajectory that successfully returns to the crystal structure pose starting from a perturbation of similar magnitude.
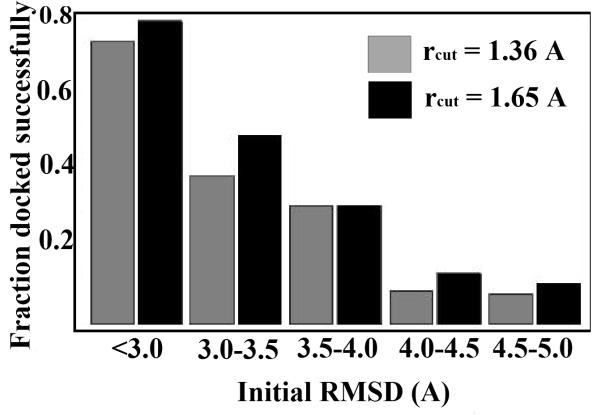
The data were analyzed to determine the magnitude of perturbations from which LBMC simulation could recover the crystal pose. See Fig. 6. Relaxation back to the initial pose was deemed successful if the mean RMSD of the last 10 frames of each trajectory was within a certain cutoff. We employed the all-atom RMSD of estradiol (only) compared to the 1ERE crystal structure following alignment of the receptors. Fig. 6 shows that a large fraction of trajectories with significant perturbations (and significant steric clashes) could recover the crystal pose. The data show that docking success was relatively insensitive to the choice of cutoff: values of rcut = 1:65Å and 1:36Å were used. These values were also validated using independent, long LBMC runs to determine the range of bound-state fluctuations (data not shown).
Figure 6.
Docking statistics for a range of perturbation magnitudes. The histogram shows the fraction of structures that were docked successfully for a range of initial RMSD values of estradiol compared to the crystal structure. Two criteria were used to determine the success or failure of docking runs (see text): rcut = 1:65Å (black) rcut = 1:36Å (gray).
The results suggest that LBMC may prove a valuable tool for flexible docking. We emphasize that, after the perturbation, the receptor structure remains flexible and will change from the initial crystal configuration. In fact, most MC moves are applied to the receptor (see Sec. 2). Thus, successful docking runs involve a mutual adaptation of the perturbed ligand and receptor back to the crystal pose.
3.3 GPU Benchmarks & Precision
LBMC simulations were also performed on a number of additional systems in order to obtain GPU benchmarks and confirm the reliability of the GPU port. The results of these simulations are summarized in Table 1.
Table 1.
The net speed-up of LBMC using GPU calculation of the GBSA solvent energy calculation. Speed-up was measured relative to a single-threaded CPU implementation. For all systems benchmarked below, an equal distribution of trial moves was used unless otherwise specified in the text.
| System | PDB code | No. atoms in atomistic residues |
No. coarse-grained residues |
Speed-up (GPU/CPU) |
|---|---|---|---|---|
| GGBP | 2HPH | 1237 | 226 | 14.5 |
| ERα | 1ERE | 764 | 192 | 13.7 |
| DFHR | 1RX5 | 238 | 144 | 10.1 |
| CaM | 1CFD | 264 | 132 | 9.6 |
| GB1 | 2GI9 | 370 | 36 | 6.0 |
All reported overall speed-ups due to the GPU implementation are given with respect to the CPU-only version of the code. In general, the overall speed-up of the simulation due to the GPU port will depend on several factors – one of the most important being the system size. Larger systems generally exhibit larger speed-ups, roughly to the point where all GPU threads are saturated. For small enough systems, one should expect a speed decrease due to the overhead associated with data transfer to and from the GPU, although such a regime was not explored. The second important factor is the distribution of types of MC move being performed during a simulation. Some MC moves are more expensive than others, so the way they are distributed will also affect the observed speed-up. For a fully-atomistic simulation consisting of ≈ 1800 atoms and a roughly uniform distribution of the MC moves described above, the net speed up was determined to be 11.4. On the other hand, for a fully atomistic system containing 300 atoms (again with a roughly uniform distribution of MC moves), the observed speed-up was a modest factor of 2. All systems we have examined thus far have fallen between these two extremes, as can be seen in the table.
All GPU related functions use floating point precision in our implementation. We found this to be more than sufficient for our purposes. In particular, direct comparisons of the GBSA solvation energy obtained on the GPU vs. the CPU were possible for identical configurations. In all the systems examined, the largest absolute deviation observed between the CPU and GPU computed solvation energies was 0.21 kcal/mol, representing a percent error of < 0.01%. In general however, the size of the discrepancy is directly related to the system size, and in the systems examined in this study, absolute deviations were typically much less than 0.1 kcal/mol.
4 Discussion
On the whole, the results of our study suggest LBMC provides an effective platform for mixed-resolution modeling of proteins. The basic goal, at least for the systems examined, has been met: to provide a reasonable balance between model accuracy and sampling power that typically is not available either from all-atom or coarse-grained simulations. Nevertheless, our current implementation of LBMC has noteworthy limitations and room for improvement.
4.1 Limitations
Several limitations of the present LBMC platform are notable and suggest improvements discussed below. (i) Although we believe our implicit solvent model is a good match to the mixed CG/AA model, no implicit solvent model can capture the specific hydrogen-bonding properties of explicit water. (ii) In the current study, the boundary between CG and AA regions does not prevent side chains at the boundary from occupying unphysical rotamers. (iii) The current CG model is fairly primitive. Finally, (iv) the selection of MC trial moves was not optimized for the mixed-resolution model. Remediation of each of these issues, to an extent, may be quite feasible as described below.
4.2 Future model improvements
Improved treatment of solvent
Our solvent modeling could be improved in two ways: by changing the implicit solvent calculation or by including explicit solvent. GBSA is a well-tested implicit approach, but it is costly and not ideally suited to MC. Approximate treatments optimized for MC may provide performance enhancements.79 The inclusion of some explicit solvent is fully compatible with LBMC, but may require pre-sampled water clusters or a grand-canonical treatment80,81 to limit the size of the solvent region and still allow protein fluctuations.
Improved CG/AA boundary
Technical complications at the boundary between model types are familiar from mixed quantum mechanical/molecular mechanical models.82 In our case, it should be possible to prevent unphysical rotameric side chain conformations at the boundary by a straight-forward modification to our current implementation. To ensure the boundary residues remain in reasonable rotamers, those side chains can simply be “frozen” — that is, no library-swap trial moves will be attempted. Neighboring AA residues will continue to interact atomistically with the initial rotamers.
Better CG Models
Improving CG interactions through better models is perhaps the most obvious single improvement to make. The simple alpha-carbon-based CG model used here does not represent a limitation of the LBMC protocol, but rather of our initial implementation. Although the mixed AA/CG models rely primarily on the AA region to embody necessary specific interactions, the AA region remains allosterically coupled to the CG region throughout our LBMC simulations. Hence, a systematically parameterized CG model10,11 should only improve the LBMC approach without significantly increasing cost. We began to experiment with better side chain interactions in a previous study37 but a more systematic treatment remains to be performed. Of note, a memory-intensive and tunable tabulation strategy appears to be naturally suited to LBMC.41 A high-quality CG model may enable the use of a smaller AA region.
MC “timescale” issues
The mixture of trial moves described above was developed on an ad hoc basis. One potentially important physical issue not addressed is the differing timescales expected for slow and fast motions. Generally, the atomistic region will exhibit motions much faster than the CG region, suggesting that trial moves in the CG region could be much less frequent. Systematically adjusting MC trial moves will be an important avenue for exploration.
4.3 Possible future applications
We foresee a number of ligand-binding applications as suggested by the initial study of the estrogen receptor. While LBMC may prove too expensive for extreme high-throughput screening (> 105 compounds), the data above suggest that it may be useful for screening hundreds or thousands of compounds. Our docking trajectories (Fig. 5) suggest that considerably less simulation time per trial could be used.
Beyond docking, mixed-resolution LBMC may be useful for studying allosteric systems and for estimating binding free energies. For allostery, a protein could be examined with and without a ligand to compare fluctuations. The binding and unbinding processes could also be examined in conjunction with a path-sampling method such as “weighted ensemble”.83,84 A true affinity ΔGbind0 could be calculated using LBMC models with standard free energy methods.85
The ability to tune the resolution of a model within the current LBMC protocol could make it useful for mixed-resolution sampling approaches.17–19 Such approaches typically require the construction of a ladder of models of gradually varying resolution, which has been difficult to achieve in a way that employs true coarse-grained models — i.e., potentials that are both smooth and inexpensive per energy call.
LBMC also appears to have significant potential for future studies of spin-labeled systems. The software can focus computational effort on the spin labels and nearby residues while maintaining flexibility in, and allosteric coupling to, the remainder of the protein.
5 Summary and Conclusions
We describe initial simulations performed with mixed-resolution models implemented in the context of library-based Monte Carlo (LBMC). LBMC, which uses pre-calculated all-atom (AA) libraries of molecular fragments (side chains in this report), is a natural platform for constructing mixed resolution models. Library configurations ensure correct internal geometry while permitting a subset of sites to be used for effective coarse-grained (CG) models. GPU computing was also used to speed the calculations. We studied and benchmarked a number of mixed CG/AA protein models, focusing on a spin-labeled GB1 domain and docking/binding to the estrogen receptor. The data suggest that LBMC is a promising platform for mixed-resolution modeling and that such models could be an important bridge between AA and CG models, providing localized accuracy comparable to AA models with sampling speed comparable to CG models. Nevertheless, key improvements outlined above remain to be implemented.
Acknowledgement
We thank Linda Jen-Jacobson for useful discussions. DMZ acknowledges support from the National Science Foundation (Grants MCB-0643456 and MCB-1119091), as well as the National Institutes of Health (Grant GM076569). SS acknowledges support from the National Science Foundation (Grant MCB-0842956).
References
- (1).Friedrichs MS, Eastman P, Vaidyanathan V, Houston M, Legrand S, Beberg AL, Ensign DL, Bruns CM, Pande VS. J. Comput. Chem. 2009;30:864–872. doi: 10.1002/jcc.21209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, Wriggers W. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
- (3).Berg JM, Tymoczko JL, Stryer L. Biochemistry. 5th ed WH Freeman & Co; New York: 2002. [Google Scholar]
- (4).Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associate; Sunderland, MA: 2001. [Google Scholar]
- (5).Bechinger B. In: Membrane Binding and Pore Formation. Anderluh G, Lakey J, editors. Landes Bioscience; 2010. pp. 24–30. [Google Scholar]
- (6).Levitt M, Warshel A. Nature. 1975;253:694–698. doi: 10.1038/253694a0. [DOI] [PubMed] [Google Scholar]
- (7).Bahar I, Atilgan AR, Erman B. Fold. Design. 1997;2:173–181. doi: 10.1016/S1359-0278(97)00024-2. [DOI] [PubMed] [Google Scholar]
- (8).Liwo A, Oldziej S, Pincus MR, Wawak RJ, Rackovsky S, Scheraga HA. J. Comp. Chem. 1997;18:849–873. [Google Scholar]
- (9).Zuckerman DM. J. Phys. Chem. B. 2004;108:5127–5137. [Google Scholar]
- (10).Izvekov S, Voth GA. J. Phys. Chem. B. 2005;109:2469–2473. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- (11).Monticelli L, Kandasamy SK, Periole X, Larson RG, Tieleman DP, Marrink S-J. J. Chem. Theory Comput. 2008;4:819–834. doi: 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
- (12).Neri M, Anselmi C, Cascella M, Maritan A, Carloni P. Phys. Rev. Lett. 2005;95:218102. doi: 10.1103/PhysRevLett.95.218102. [DOI] [PubMed] [Google Scholar]
- (13).Praprotnik M, Site LD, Kremer K. J. Chem. Phys. 2005;123:224106. doi: 10.1063/1.2132286. [DOI] [PubMed] [Google Scholar]
- (14).Shi Q, Izvekov S, Voth GA. J. Phys. Chem. B. 2006;110:15045–15048. doi: 10.1021/jp062700h. [DOI] [PubMed] [Google Scholar]
- (15).Praprotnik M, Site LD, Kremer K. J. Chem. Phys. 2007;126:134902–134908. doi: 10.1063/1.2714540. [DOI] [PubMed] [Google Scholar]
- (16).Neri M, Baaden M, Carnevale V, Anselmi C, Maritan A, Carloni P. Biophys. J. 2008;94:71–78. doi: 10.1529/biophysj.107.116301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Lyman E, Ytreberg FM, Zuckerman DM. Phys. Rev. Lett. 2006;96:028105. doi: 10.1103/PhysRevLett.96.028105. [DOI] [PubMed] [Google Scholar]
- (18).Lyman E, Zuckerman DM. J. Chem. Theory Comp. 2006;2:656–666. doi: 10.1021/ct050337x. [DOI] [PubMed] [Google Scholar]
- (19).Zuckerman D. Chapter 12. In: Voth GA, editor. Coarse-Graining of Condensed Phase and Biomolecular Systems. Taylor & Francis; Boca Raton, FL: 2009. pp. 171–184. [Google Scholar]
- (20).Christen M, van Gunsteren WF. J. Chem. Phys. 2006;124:154106. doi: 10.1063/1.2187488. [DOI] [PubMed] [Google Scholar]
- (21).Li H, Yang W. J. Chem. Phys. 2007;126:114104. doi: 10.1063/1.2710790. [DOI] [PubMed] [Google Scholar]
- (22).Liu P, Shi Q, Lyman E, Voth GA. J. Chem. Phys. 2008;129:114103. doi: 10.1063/1.2976663. [DOI] [PubMed] [Google Scholar]
- (23).Gunasekaran K, Ma B, Nussinov R. Proteins. 2004;57:433–443. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- (24).Popovych N, Sun S, Ebright RH, Kalodimos CG. Nat. Struct. Mol. Biol. 2006;13:831–838. doi: 10.1038/nsmb1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Bahar I, Chennubhotla C, Tobi D. Curr. Opin. Struct. Biol. 2007;17:633–640. doi: 10.1016/j.sbi.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- (27).Kamerlin SCL, Warshel A. Proteins. 2010;78:1339–1375. doi: 10.1002/prot.22654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Lyman E, Zuckerman DM. Biophys. J. 2006;91:164–172. doi: 10.1529/biophysj.106.082941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Lyman E, Zuckerman DM. J. Phys. Chem. B. 2007;111:12876–12882. doi: 10.1021/jp073061t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Grossfield A, Zuckerman DM. Annu. Rep. Comput. Chem. 2009;5:23–48. doi: 10.1016/S1574-1400(09)00502-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Zhang X, Bhatt D, Zuckerman DM. J. Chem. Theory Comput. 2010;6:3048–3057. doi: 10.1021/ct1002384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Stone JE, Phillips JC, Freddolino PL, Hardy DJ, Trabuco LG, Schulten K. J. Comput. Chem. 2007;28:2618–40. doi: 10.1002/jcc.20829. [DOI] [PubMed] [Google Scholar]
- (33).Dynerman D, Butzlaff E, Mitchell JC. J. Comput. Biol. 2009;16:523–537. doi: 10.1089/cmb.2008.0157. [DOI] [PubMed] [Google Scholar]
- (34).Mamonov AB, Bhatt D, Cashman DJ, Ding Y, Zuckerman DM. J. Phys. Chem. B. 2009;113:10891–10904. doi: 10.1021/jp901322v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Ding Y, Mamonov AB, Zuckerman DM. J. Phys. Chem. B. 2010;114:5870–5877. doi: 10.1021/jp910112d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Cashman DJ, Mamonov AB, Bhatt D, Zuckerman DM. Curr. Top. Med. Chem. 2011;11:211–220. doi: 10.2174/156802611794863607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Bhatt D, Zuckerman DM. J. Chem. Theory Comput. 2010;6:3527–3539. doi: 10.1021/ct100406t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Zhang X, Mamonov AB, Zuckerman DM. J. Comput. Chem. 2009;30:1680–1691. doi: 10.1002/jcc.21337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Mamonov AB, Zhang X, Zuckerman DM. J. Comput. Chem. 2011;32:396–405. doi: 10.1002/jcc.21626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Lettieri S, Mamonov AB, Zuckerman DM. J. Comput. Chem. 2011;32:1135–1143. doi: 10.1002/jcc.21695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (41).Lettieri S, Zuckerman DM. J. Comput. Chem. 2012;33:268–275. doi: 10.1002/jcc.21970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Still WC, Tempczyk A, Hawley RC, Hendrickson TF. J. Am. Chem. Soc. 1990;112:6127–6129. [Google Scholar]
- (43).Qiu D, Shenkin PS, Hollinger FP, Still WC. J. Phys. Chem. A. 1997;101:3005–3014. [Google Scholar]
- (44).Milov A, Salikhov K, Shchirov M. Fiz. Tverd. Tela (Leningrad) 1981;23:975–982. [Google Scholar]
- (45).Larson R, Singel D. J. Chem. Phys. 1993;98:5134–5146. [Google Scholar]
- (46).Milov A, Ponomarev A, Tsvetkov Y. Chem. Phys. Lett. 1984;110:67–72. [Google Scholar]
- (47).Martin RE, Pannier M, Diederich F, Gramlich V, Hubrich M, Spiess HW. Angewandte Chemie International Edition. 1998;37:2833–2837. doi: 10.1002/(SICI)1521-3773(19981102)37:20<2833::AID-ANIE2833>3.0.CO;2-7. [DOI] [PubMed] [Google Scholar]
- (48).Yang Z, Ji M, Saxena S. Appl. Magn. Reson. 2010;39:487–500. [Google Scholar]
- (49).Reginsson GW, Schiemann O. Biochem. J. 2011;434:353–363. doi: 10.1042/BJ20101871. [DOI] [PubMed] [Google Scholar]
- (50).Cunningham TF, McGoff MS, Sengupta I, Jaroniec CP, Horne WS, Saxena S. Submitted for publication. [DOI] [PubMed]
- (51).Jorgensen WL, Maxwell DS, Tirado-Rives J. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- (52).Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. J. Phys. Chem. B. 2001;105:6474–6487. [Google Scholar]
- (53).Banks JL, Beard HS, Cao Y, Cho AE, Damm W, Farid R, Felts AK, Halgren TA, Mainz DT, Maple JR, Murphy R, Philipp DM, Repasky MP, Zhang LY, Berne BJ, Friesner RA, Gallicchio E, Levy RM. J. Comput. Chem. 2005;26:1752–1780. doi: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Betancourt MR. J. Chem. Phys. 2011;134:014104–014113. doi: 10.1063/1.3515960. [DOI] [PubMed] [Google Scholar]
- (55).Ponder JW, Richards FM. J. Comp. Chem. 1987;8:1016–1026. http://dasher.wustl.edu/tinker/ [Google Scholar]
- (56).Schaefer M, Bartels C, Karplus M. J. Mol. Biol. 1998;284:835–848. doi: 10.1006/jmbi.1998.2172. [DOI] [PubMed] [Google Scholar]
- (57).Ponder J. Personal communication.
- (58).Nyland L, Prins J. Simulation. 2007;3:667. [Google Scholar]
- (59).Kuszewski J, Clore GM, Gronenborn AM. Protein Science. 1994;3:1945–1952. doi: 10.1002/pro.5560031106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Ding K, Louis JM, Gronenborn AM. J. Mol. Biol. 2004;335:1299–1307. doi: 10.1016/j.jmb.2003.11.042. [DOI] [PubMed] [Google Scholar]
- (61).Franks WT, Zhou DH, Wylie BJ, Money BG, Graesser DT, Frericks HL, Sahota G, Rienstra CM. J. Am. Chem. Soc. 2005;127:12291–12305. doi: 10.1021/ja044497e. [DOI] [PubMed] [Google Scholar]
- (62).Brzozowski AM, Pike ACW, Dauter Z, Hubbard RE, Bonn T, Engström W, Öhman L, Greene GL, Gustafsson J, Carlquist M. Nature. 1997;389:753–758. doi: 10.1038/39645. [DOI] [PubMed] [Google Scholar]
- (63).Shiau AK, Barstad D, Loria PM, Cheng L, Kushner PJ, Agard DA, Greene GL. Cell. 1998;95:927–937. doi: 10.1016/s0092-8674(00)81717-1. [DOI] [PubMed] [Google Scholar]
- (64).Oostenbrink BC, Pitera JW, van Lipzig MM, Meerman JH, van Gunsteren WF. J. Med. Chem. 2000;43:4594–4605. doi: 10.1021/jm001045d. [DOI] [PubMed] [Google Scholar]
- (65).Pike ACW, Brzozowski AM, Hubbard RE. J. Steroid Biochem. Molec. Biol. 2000;74:261–268. doi: 10.1016/s0960-0760(00)00102-3. [DOI] [PubMed] [Google Scholar]
- (66).Gee AC, Katzenellenbogen JA. Molec. Endocrin. 2001;15:421–428. doi: 10.1210/mend.15.3.0602. [DOI] [PubMed] [Google Scholar]
- (67).Burendahl S, Danciulescu C, Nilsson L. Proteins. 2009;77:842–856. doi: 10.1002/prot.22503. [DOI] [PubMed] [Google Scholar]
- (68).Sale K, Sár C, Sharp K, Hideg K, Fajer P. J. Magn. Reson. 2002;156:104–112. doi: 10.1006/jmre.2002.2529. [DOI] [PubMed] [Google Scholar]
- (69).Beier C, Steinhoff H-J. Biophys. J. 2006;91:2647–2664. doi: 10.1529/biophysj.105.080051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Budil DE, Sale KL, Khairy KA, Fajer PG. J. Phys. Chem. A. 2006;110:3703–3713. doi: 10.1021/jp054738k. [DOI] [PubMed] [Google Scholar]
- (71).Murzyn K, Róg T, Blicharski W, Dutka M, Pyka J, Szytula S, Froncisz W. Proteins. 2006;62:1088–1100. doi: 10.1002/prot.20838. [DOI] [PubMed] [Google Scholar]
- (72).Li H, Fajer M, Yang W. J. Chem. Phys. 2007;126:024106. doi: 10.1063/1.2424700. [DOI] [PubMed] [Google Scholar]
- (73).Fajer MI, Li H, Yang W, Fajer PG. J. Am. Chem. Soc. 2007;129:13840–13846. doi: 10.1021/ja071404v. [DOI] [PubMed] [Google Scholar]
- (74).DeSensi SC, Rangel DP, Beth AH, Lybrand TP, Hustedt EJ. Biophys. J. 2008;94:3798–3809. doi: 10.1529/biophysj.107.125419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Ding F, Layten M, Simmerling C. J. Am. Chem. Soc. 2008;130:7184–7185. doi: 10.1021/ja800893d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Sezer D, Freed JH, Roux B. J. Phys. Chem. B. 2008;112:5755–5767. doi: 10.1021/jp711375x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (77).Sezer D, Freed JH, Roux B. J. Chem. Phys. 2008;128:165106. doi: 10.1063/1.2908075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Sarver J, Towsend JE, Rajapakse G, Jen-Jacobson L, Saxena S. J. Phys. Chem. B. 2012 doi: 10.1021/jp211094n. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Michel J, Taylor RD, Essex JW. J. Chem. Theory Comput. 2006;2:732–739. doi: 10.1021/ct600069r. [DOI] [PubMed] [Google Scholar]
- (80).Beglov D, Roux B. J. Chem. Phys. 1994;100:9050–9063. [Google Scholar]
- (81).Im W, Berneche S, Roux B. J. Chem. Phys. 2001;114:2924–2937. [Google Scholar]
- (82).Senn HM, Thiel W. Angew. Chem. Int. Ed. 2009;48:1198–1229. doi: 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- (83).Huber GA, Kim S. Biophys. J. 1996;70:97–110. doi: 10.1016/S0006-3495(96)79552-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Zhang BW, Jasnow D, Zuckerman DM. J. Chem. Phys. 2010;132:054107. doi: 10.1063/1.3306345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Chipot C, Pohorille A. Free Energy Calculations. Springer; Berlin: 2007. [Google Scholar]