Investigation of the Polymeric Properties of α-Synuclein and Comparison with NMR Experiments: A Replica Exchange Molecular Dynamics Study

Abstract

Intrinsically disordered proteins (IDPs) have been shown to be involved in a number of cellular functions, in addition to their predominance in diseased states. α-synuclein may be described as one such IDP implicated in the pathology of Parkinson’s disease. Understanding the conformational characteristics of the monomeric state of α-synuclein is necessary for understanding the role of the monomer conformation in aggregation. Polymer theories have been applied to investigate the statistical properties of homopolymeric IDPs. Here we use Replica Exchange Molecular Dynamics (REMD) simulations using temperature as a proxy for solvent quality to examine how well these theories developed for homopolymeric chains describe heteropolymeric α-synuclein. Our results indicate that α-synuclein behaves like a homopolymer at the extremes of solvent quality, while in the intermediate solvent regime, the uneven distribution of charged residues along the sequence strongly influences the conformations adopted by the chain. We refine the ensemble extracted from the REMD simulations of α-synuclein, which shows the best qualitative agreement with experiment, by fitting to the experimental NMR Residual Dipolar Couplings (RDCs) and Paramagnetic Relaxation Enhancements (PREs). Our results demonstrate that the detailed shape of the RDC patterns are sensitive to the angular correlations that are local in sequence while longer range anti-correlations which arise from packing constraints affect the RDC magnitudes.

Introduction

Intrinsically Disordered Proteins (IDPs) have gained much attention in light of the finding that over 30% of the proteins encoded by the eukaryotic genome contain unstructured regions over 50 residues long ^1,2. The functional repertoire of IDPs include signal transduction, transcription and translation and protein complex assembly ³. A number of neurodegenerative diseases including Alzheimer’s, Parkinson’s and Huntington’s diseases have been correlated with the aggregation of IDPs ⁴. IDPs are best described as fluctuating ensembles of conformations in solution lacking stable structure under physiological conditions ³ and are typically characterized by their low sequence complexity, high net charge and low hydrophobicity ⁵. Characterizing the conformational states of IDPs under physiological conditions is important for understanding their function, in addition to determining the driving forces that promote aggregation of these proteins in diseased states. Structural analysis of IDPs is challenging due to their highly flexible nature. NMR ⁶ and molecular simulations ^7–10 can provide high-resolution data for the conformational characterization of disordered proteins.

α-synuclein

The monomeric conformation of α-synuclein is described as a 140 residue polypeptide with classic IDP characteristics - low sequence complexity, low overall hydrophobicity with hydrophobic patches and high net charge ⁵. The physiological function of α-synuclein has been attributed to acting as a chaperone to promote assembly of large protein complexes ¹¹, vesicle transportation and neurotransmitter release ¹². The sequence of α-synuclein (Fig. 1A) has an uneven distribution of charged residues along the chain and is divided into 3 regions – the N-terminal domain (residues 1–60) with a balanced distribution of positive and negatively charged residues corresponding to a polyampholyte chain, the Non Amyloid-beta Component of Alzheimer’s disease (NAC, residues 61–95), which forms the hydrophobic core of the protein having minimal charged residues and the highly acidic C-terminal domain (residues 96–140) with a predominance of negative charges characteristic of a polyelectrolyte chain. α-synuclein can adopt different conformations under various conditions. The N-terminal region of α-synuclein has been shown to form amphipathic helices upon binding to lipid membranes and micelles ¹³. A conformational change to the monomeric form of α-synuclein leading to its aggregation into fibrils has been shown to play a key role in the pathology of Parkinson’s disease ^14–16. Characterizing the monomeric form is important for understanding the conformational changes leading to the aggregated state.

Figure 1.

(A) Primary sequence of human α-synuclein. The N, NAC and C-terminal regions are represented in blue, green and red respectively. (B–D) Representative conformations of α-synuclein selected for the low (B), intermediate (C), and high temperature (D) ensembles. The representative structures were chosen based on the top four clusters, determined using the hierarchical clustering method ¹⁰¹. The color scheme used here are the same as that in A.

The monomeric form of α-synuclein, long thought to be the dominant physiological species, has been studied using a variety of experimental and simulation techniques ⁷. NMR experiments have been used extensively to probe the conformational propensities of α-synuclein ^10,17–21. Residual Dipolar Couplings (RDCs) and Paramagnetic Relaxation Enhancements (PREs) are the most commonly used measurements for probing the structural properties of this IDP ^{19,20,22–24}. NMR PRE measurements have been used as constraints in molecular dynamics simulations to generate ensembles consistent with experimental data ²³. A number of simulation studies have also reported the generation of ensembles based on the use of combinations of one or more experimental parameters including RDCs, PREs, chemical shifts, diffusion and SAXS measurements ^{10,20,22–25}.

NMR studies of the monomeric state of α-synuclein suggest the presence of residual structure in solution ^{17,19–21,23}, with the N-terminal region having a propensity to adopt transient helical conformations ^18,21. The average size of α-synuclein is more compact than would be expected for a random coil conformation ^2,26,27, arising as a result of transient long-range contacts between different domains ^19–21,23. The conformational characteristics of α-synuclein leading to its aggregation reported in the literature are disparate, with some studies suggesting the requirement of partially folded intermediate conformations for fibril formation while others hint that release of long-range interactions promotes aggregation ^10,28. A more recent study suggests exposure of the aggregation-prone region of the NAC (residues 8–18 in this region) in a non-negligible fraction of the ensemble could lead to the formation of cross-beta structure ²⁴. The conformational characteristics for the α-synuclein ensemble reported based on fits to PREs are inconsistent, with some studies suggesting conformations involving interactions between the N and C-terminal regions^20,24 and others suggesting predominantly extended conformations for the C-terminal region¹⁰. These studies underscore the underdetermined nature of the problem; structural characteristics of IDPs are not uniquely determined by fitting any given experimental parameter. Addressing this degeneracy is necessary in order to provide a proper representation for the conformational characteristics of α-synuclein.

Polymer properties of IDPs

The conformational characteristics of IDPs have been described in terms of their statistical properties using well-established concepts from polymer physics ^29,30. These statistical properties include chain descriptors such as the ensemble-averaged radius of gyration (R_g) and the persistence length (l_p) ^31–33. The radius of gyration of homopolymer chains scale with chain length N as <R_g>=R_oN^ν, where R_o is a constant and the scaling exponent ν is dependent on the nature of the solvent ^34,35. In good and poor solvents, the scaling factors have been determined to be 0.59 and 0.33 respectively for chains with excluded volume interactions between monomers. Proteins however are heteropolymeric chains composed of amino acids with varying side-chain chemical characteristics. IDPs characterized by their high net charge are more expanded due to charge repulsion ^9,36. How is the scaling affected for the heteropolymeric chain of α-synuclein, with an unbalanced distribution of charged residues resulting in regions with polyampholyte and polyelectrolyte characteristics? This question forms one focus of the current work.

Persistence length describes the average local stiffness of polymer chains, which corresponds to the distance over which the memory of the direction of the chain persists. The characteristics of the monomeric units making up the polypeptide chain can be expected to influence the magnitude of the persistence length. Experimental measurements of persistence lengths of unfolded proteins are reported to be within the range of 4 to 8Å ³⁷ based on atomic force microscopy measurements. A number of approximate procedures are used to calculate the persistence length of polymer chains ³⁸. For NMR residual dipolar couplings arising due to transient alignment of the chain, it has been proposed that these patterns persist over length scales corresponding to the persistence length of the chain ^39,40. We have used REMD simulations to estimate the persistence length of α-synuclein and we discuss the relationship between the persistence length of α-synuclein estimated from the simulations and the length scale over which angular correlations of the polypeptide chain affect the RDCs.

In this study, we focus on the following problems – (1) we compare the polymer theory of homopolymer chains to the statistical properties of heteropolymeric α-synuclein under different solvent conditions using temperature as a proxy for solvent quality. (2) We generate conformational ensembles of α-synuclein that fit the experimental RDC and PRE measurements and (3) We analyze the relationship between the persistence length of α-synuclein and the length of the transiently aligning segments used in the calculation of RDCs from models of the α-synuclein conformational ensemble generated from REMD simulations. Our results demonstrate that at the extremes of solvent quality, α-synuclein scales as expected for a homopolymer chain under poor and good solvent conditions respectively, while at intermediate values, the heterogeneity of the charge distribution and the identity of the monomeric units significantly influence the polymeric characteristics of the chain. We construct α-synuclein conformational ensembles which fit both the experimental RDCs and PREs, which consequently fit both the local and long-range conformational characteristics of the monomeric form of α-synuclein. Our results suggest that RDCs are sensitive to the angular correlations of the chain that are local in sequence while longer-range correlations act as a scaling factor which affects the magnitudes of the RDCs but has little effect on the RDC pattern of positive and negative RDCs.

Results

Polymer chain characteristics of α-synuclein

Scaling behavior of α-synuclein

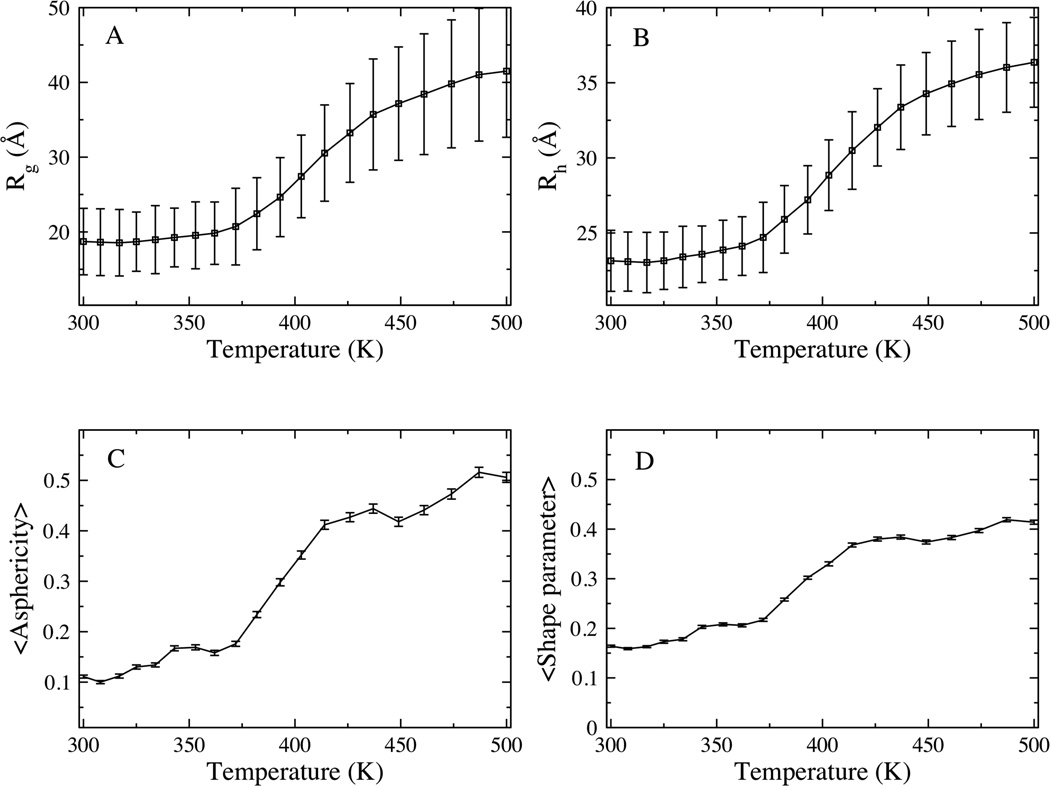
REMD simulations were performed to generate the conformational ensembles of α-synuclein at neutral pH over a range of temperatures between 300K and 500K. Temperature has been used previously ^41,42 to alter the conformational equilibrium of polypeptides in a way that mimics the effects of changing solvent conditions, with low temperature corresponding to poor solvent conditions while higher temperatures correspond to good solvent conditions. In this work, we vary temperature as a surrogate for changing solvent conditions. We note that the temperature scale over which structural changes occur is characteristic of implicit solvent models like that used in this work ^43–45. Fig. 2 shows the global size, represented by the radius of gyration (R_g) and hydrodynamic radius (R_h), and shape descriptors including the asphericity (™) and shape parameter (S) as a function of the simulation temperature. Expansion of the α-synuclein ensemble is observed as the temperature is raised from 300 – 500K. Here, we elaborate on the observations for the low, intermediate and high temperatures represented by the 300K, 414K and 500K ensembles respectively. At low temperature, the ensemble adopts a collapsed conformation, with the average size of 17 Å (and 23.15 Å) for the R_g (and R_h), slightly more expanded than that expected for well folded protein that is 140 residues long (R_g ~15 Å and R_h 20.5 Å respectively) ⁴⁶ with dimensions similar to that of a molten globule ⁴⁷. The asphericity (™) and shape parameter (S) are around 0.1 and 0.15 respectively, values consistent with an approximately spherical chain shape (Fig. 1B). At high temperature, the ensemble adopts an extended conformation, with the average R_g of 41.5 Å (R_h of 36.36 Å), consistent with previous reports for the average size for the random coil conformation of α-synuclein ⁴⁸, and that expected from scaling laws for unfolded conformations ^46,49. The asphericity and shape parameters for the high temperature ensemble are 0.5 and 0.42 respectively, consistent with a prolate ellipsoid or a cigar-shaped conformation. At intermediate temperature, the conformational ensemble consists of a heterogeneous set of structures that span a range of sizes with both the average R_g and R_h of 30.5 Å at the midpoint. The ™ and S values for the intermediate temperature ensemble are 0.41 and 0.37 respectively. We note that while the intermediate temperature ensemble adopts a smaller average size compared to high temperature, the shape characteristics (™ and S) at both temperatures are similar, with both ensembles adopting prolate ellipsoid conformations. Representative conformations for the low, intermediate and high temperature ensembles are presented in Fig. 1 B–D.

Figure 2.

Global shape and size descriptors for α-synuclein. Average radius of gyration, R_g (A) hydrodynamic radius, R_h (B) Asphericity, ™ (C) and shape parameter, S (D) plotted as a function of simulation temperature. Standard deviations within ensembles are represented as error bars.

The scaling of internal distances (R_ij) is another polymer parameter that is used to characterize the polymer chain under different solvent conditions. This parameter, similar to the average size (R_g and R_h), for homopolymeric chains follows the Flory scaling laws under different solvent conditions. R_ij is calculated as follows:

$$\langle {\mathrm{R}}_{\text{ij}}\rangle =\langle \frac{1}{{\mathrm{Z}}_{\text{ij}}}{\displaystyle \sum _{\mathrm{m}\in \mathrm{i}}}{\displaystyle \sum _{\mathrm{n}\in \mathrm{j}}}|{\mathbf{r}}_{\mathrm{m}}^{\mathrm{i}}-{\mathbf{r}}_{\mathrm{n}}^{\mathrm{j}}|\rangle$$ (1)

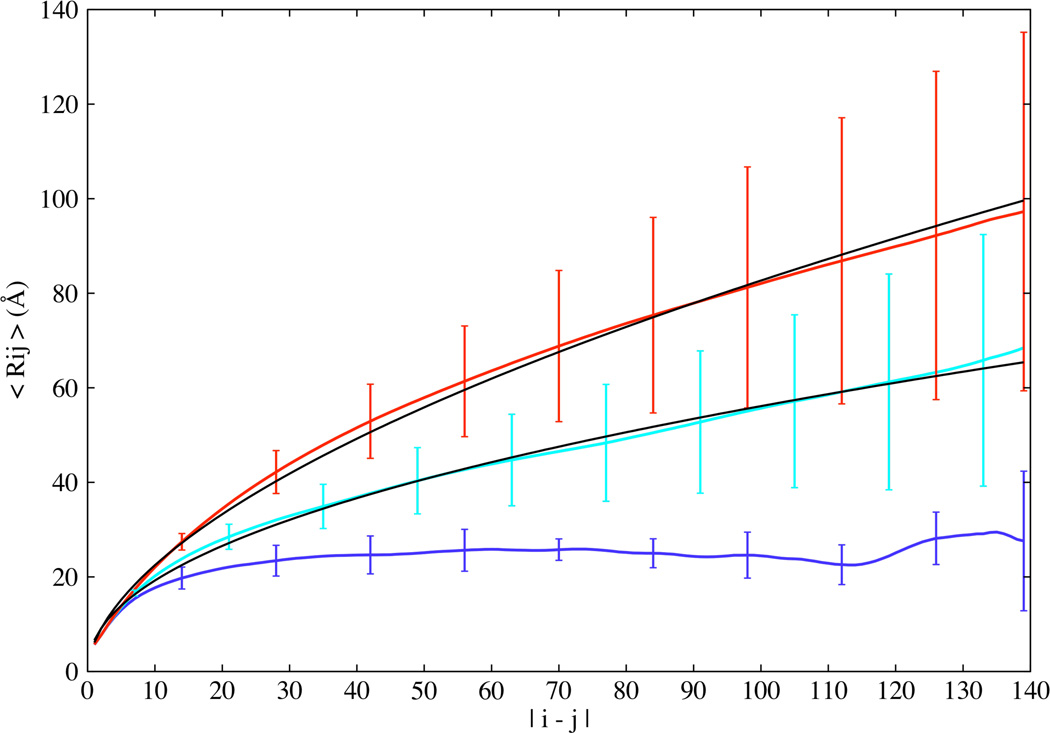
In Eq. 1, i and j are the amino acid indices, while m and n denote the atoms corresponding to residues i and j respectively and Z_ij is the total number of distances between the two residues. Fig. 3 shows the plot of R_ij as a function of sequence separation. At low temperature, R_ij plateaus, this is a signature of a collapsed chain, consistent with that expected for polymer chains in a poor solvent. At high temperature, R_ij scales with sequence separation as |i–j|^0.57, approaching the theoretical scaling exponent of 0.59 expected for polymer chains in good solvent ⁵⁰. At intermediate temperature, the polymer chain has a scaling exponent of 0.46.

Figure 3.

Scaling of average internal distances (R_ij) plotted as a function of sequence separation |i–j| for the low (blue), intermediate (cyan), and high (red) temperature ensembles. The fits to the intermediate and high temperature ensembles, shown as solid lines, have scaling exponents of 0.46 and 0.57 respectively. Error bars represent standard deviations displayed here only for select residues along the sequence for clarity.

The angular correlation function

The angular correlation function, which provides insights into the topology of the chain under different solvent conditions ³⁰, is calculated as a function of sequence separation as follows:

$$\langle \text{Cos}{\mathrm{\Theta }}_{\text{ij}}\rangle =\langle \frac{{\mathbf{l}}_{\mathrm{i}}·{\mathbf{l}}_{\mathrm{j}}}{{\mathrm{l}}^2}\rangle$$ (2)

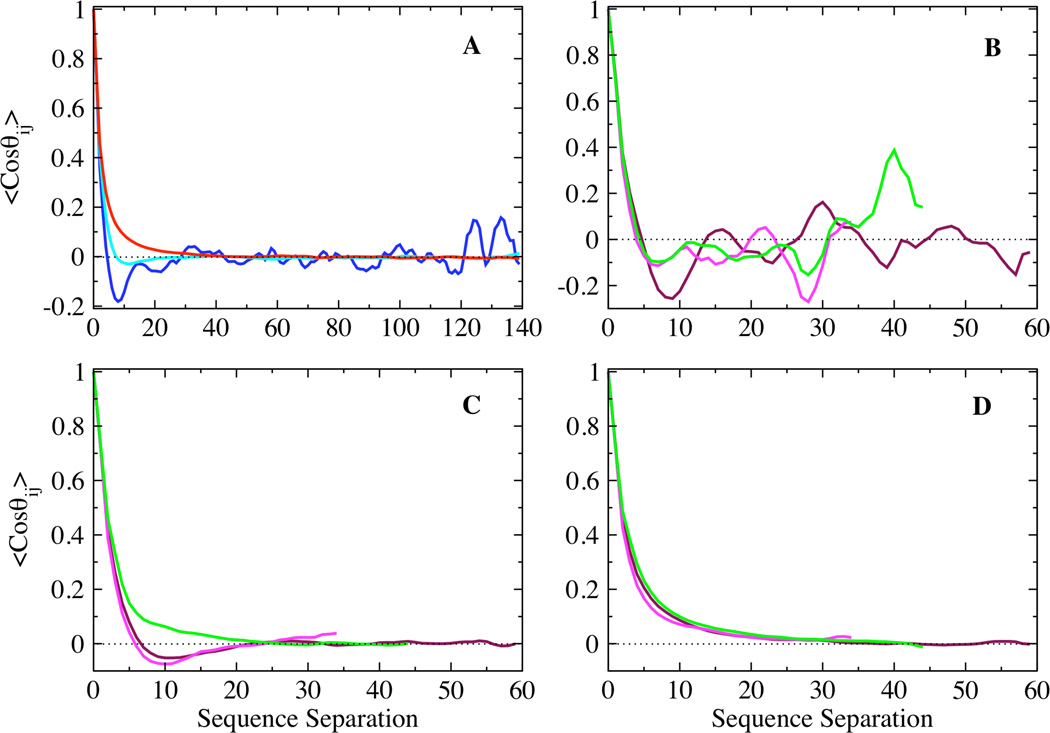
where l_i (l_j) represents the vector between the backbone nitrogen and carbonyl carbon of residue i (j) and l is the length of this bond vector. Fig. 4A shows the ensemble averaged angular correlation function plotted as a function of sequence separation for the low, intermediate and high temperature ensembles. The low temperature ensemble shows significant anti-correlations corresponding to chains with collapsed conformations, which on average reverse chain direction due to excluded volume effects. Strong correlations between residues separated by over 120 residues correspond to stable long-range interactions between residues in the N and C terminal regions. In contrast, the angular correlation function decays exponentially for the high temperature ensemble. The decay of the angular correlation function for the intermediate temperature ensemble is not exponential; it also shows anti-correlations similar to that observed for transient collapsed globular conformations, but suppressed in magnitude. Fig. 4 B–D show the angular correlations corresponding to the N, NAC and C-terminal regions for the low, intermediate and high temperature ensembles respectively. Significant anti-correlations are observed for the three regions at low temperature, while all three regions show exponential decay at high temperature, consistent with random coil distributions of conformations. However, the N, NAC and C-terminal regions show distinctly different topological characteristics at intermediate temperature (Fig. 4 C). The N and NAC regions show non-exponential decay of the angular correlation function, with anti-correlations corresponding to chains under a packing restraint. The C-terminal region however exhibits more complete angular averaging, decaying exponentially with sequence separation at intermediate temperature.

Figure 4.

Ensemble averaged angular correlation function plotted as a function of sequence separation for the (A) low (blue), intermediate (cyan), and high (red) temperature ensembles, and the N (maroon), NAC (magenta) and C (green) terminal domains of the (B) low, (C) intermediate, and (D) high temperature ensembles.

Persistence length

Persistence length provides information about the local intrinsic stiffness of polymer chains. We have calculated the persistence lengths for the low, intermediate and high temperature ensembles. The persistence lengths for the low and high temperature ensembles are ~ 3 Å and 12 Å respectively while the persistence lengths for the intermediate temperature ensemble is about 7 Å. To probe the effect of the heteropolymeric nature of α-synuclein on the persistence length, we calculated the persistence lengths separately for the N, NAC and C-terminal domains of the low, intermediate and high temperature ensembles. A comparison of the N, NAC and C-terminal regions shows no significant difference in the persistence lengths observed for the three regions at the extreme (low and high temperature) conditions. However, at intermediate temperature, the N-terminal and NAC regions have a persistence length around 6 Å while the C-terminal region has a persistence length of 11 Å, which also shows single exponential decay for the angular correlation function, corresponding to more extended random coil conformation in this region. The larger persistence length for the C-terminal region at intermediate temperature suggests that this region of the chain is significantly stiffer than the N and NAC regions, consistent with the high negative charge density in the C-terminal domain.

Residual Dipolar Couplings

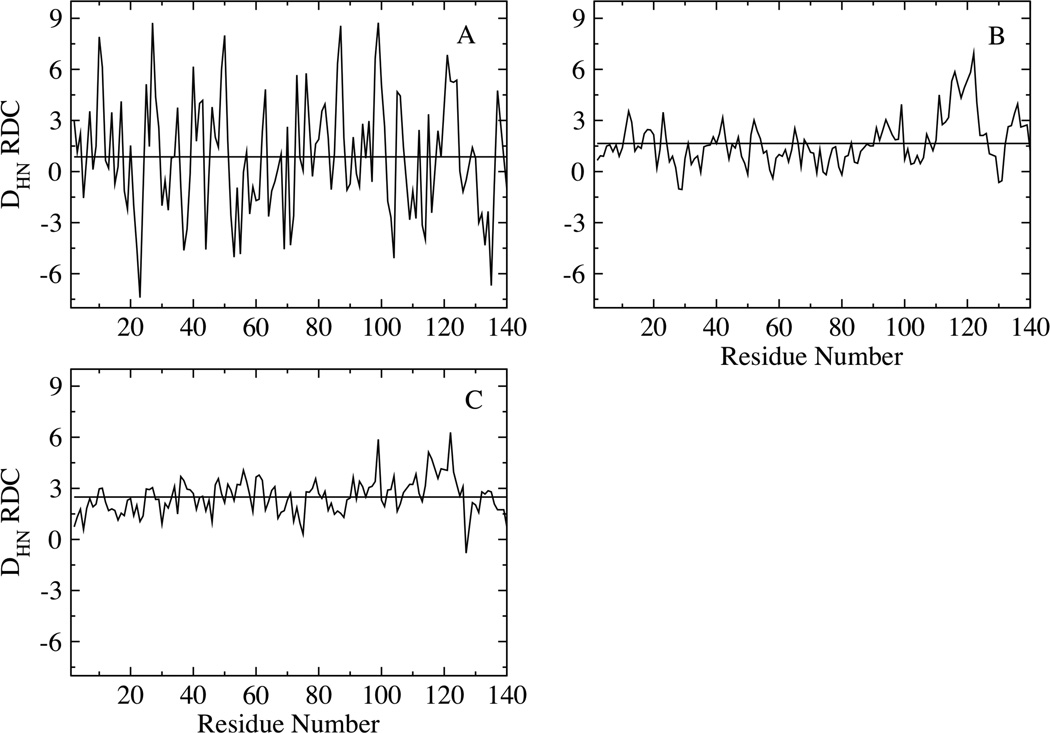
Fig. 5 shows the Residual Dipolar Coupling calculated using global alignment for the low (A), intermediate (B) and high temperature (C) ensembles. The RDCs are described below in terms of both 1) the range of values (difference between the magnitudes of the largest and smallest RDCs), and 2) the average values of the RDCs when averaged over the chain. The range of the RDCs is larger (~9 Hz) at low temperature, with both positive and negative values, while the RDCs averaged over the chain is close to zero (~0.86 Hz). At intermediate and high temperatures, the RDCs have a much smaller range compared to the low temperature values and are almost all the same sign (positive). The RDCs at high temperature (Fig. 5C) are the most uniform along the chain with higher magnitudes in the middle of the chain; the end segments have smaller values, consistent with those calculated for random flight chain models ⁵¹. The RDC averaged over the chain is also larger ~2.5 Hz at high temperature. At intermediate temperature, the C-terminal region exhibits larger RDCs, while the N-terminal and NAC regions show relatively smaller values (Fig. 5B).

Figure 5.

Residual Dipolar Couplings calculated based on global alignment for the (A) low, (B) intermediate and (C) high temperature ensembles. The horizontal lines represent the calculated RDCs averaged over the chains, with values of 0.86, 1.65 and 2.5 Hz for the low, intermediate and high temperature ensembles respectively.

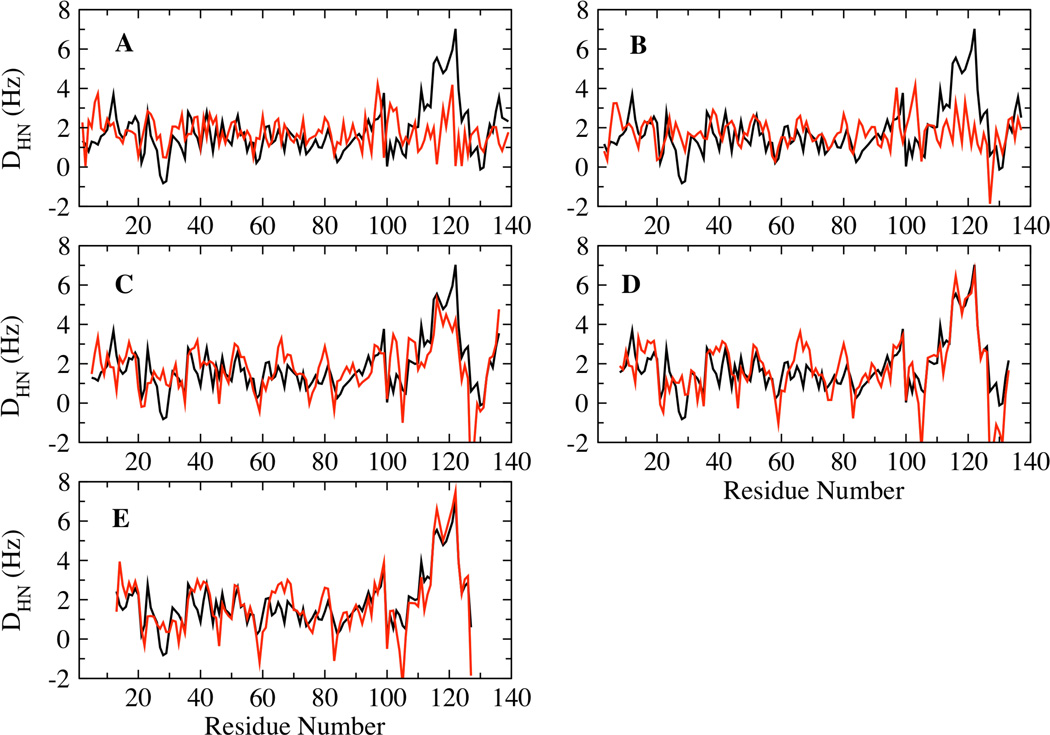
The concept of the Local Alignment Window (LAW) has been proposed previously, according to which RDCs are calculated by aligning short segments of the chain, instead of the whole chain, against the orienting medium ^52,53. This approach has been proposed to provide a good representation of the disordered state of polypeptide chains using fewer structures. We have analyzed the intermediate temperature ensemble to determine the LAW length best suited for calculating RDCs, by comparing the ability of LAWs of different lengths to reproduce the global alignment average. LAW lengths of 3, 5, 9, 15 and 25 residues were used for the calculation of the RDCs. The average RDCs of the different window lengths were scaled to fit the global alignment average. Fig. 6 A–E shows the accuracy of the RDCs calculated using the different LAWs compared to the global alignment average. These results show that LAW lengths of 9 residues and longer reproduce the global alignment average reasonably well for the entire length of the polypeptide chain, especially in the C-terminal region, which is not well fit by a smaller alignment window.

Figure 6.

Correlation between the RDCs calculated from global (black) and local (red) alignments using LAWs length − 3(A), 5 (B), 9 (C), 15 (D) and 25 (E).

Comparison between Simulations and NMR Experiments

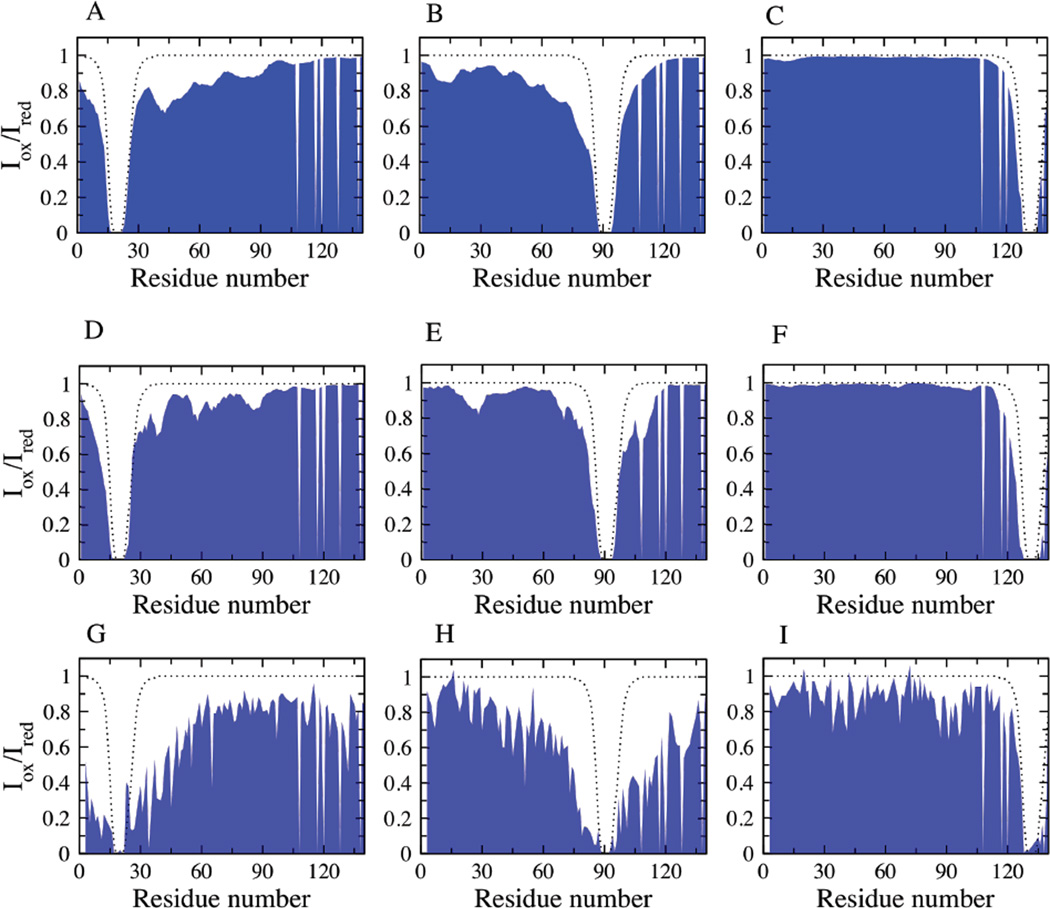
The presence of residual structure and long-range contacts involving the different regions of α-synuclein at neutral pH have been observed experimentally using NMR PREs ^10,19–21. The choice of the REMD ensemble for comparison with NMR experiments was based on the average hydrodynamic radius calculated for the simulation ensemble which best matches the experiments ^10,21. The intermediate temperature neutral pH REMD ensemble has an average R_H of ~30.5 Å, consistent with the size determined experimentally from PFG NMR diffusion measurements ²¹. Fig. 7 shows the comparison of the back-calculated PREs (Fig. 7 A–C) with that of the NMR data (Fig. 7 G–I). The calculated PREs are in reasonably good agreement with the experimental observations ¹⁰. This ensemble is characterized by a heterogeneous set of structures, with transient local and long-range interactions involving the residues in the N and NAC domains. The C-terminal residues (121–140 in particular), containing 8 negatively charged residues, show very few interactions with the rest of the protein chain.

Figure 7.

Conformational characteristics of the simulation ensembles correlating with experiment: PREs for the REMD ensemble (A, B, C), reconstructed ensemble (D, E, F) and NMR experimental data (G, H, I) for spin label at positions A19, A90 and G132 respectively. The dotted lines represent the theoretical PRE values calculated for α-synuclein with no long-range contacts, determined as described previously ²¹.

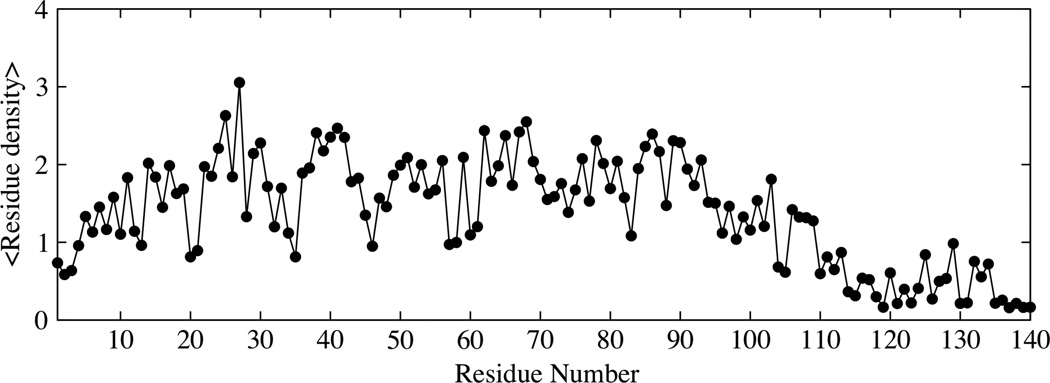
The lack of any significant transient interactions involving the last 20 residues of α-synuclein is also observed in the residue density plots shown in Fig. 8. Residue densities are obtained by calculating the average number of residues whose side chains are within 7 Å of any residue along the sequence. We note that the contributions from neighboring residues (up to 5 residues on either side of the given residue) were ignored in the calculation of the average densities. The residue density is significantly greater along the sequence for the N and NAC regions and up to residue 110 in the C-terminus. The regions with the highest average densities correspond to short stretches of hydrophobic residues. The residue density for the residues in the C-terminus is minimal indicating few contacts of residues in this region with the rest of the chain, consistent with the PRE data.

Figure 8.

Residue density along the sequence for the intermediate temperature ensemble of α-synuclein. The residue density is calculated as the count of the average number of residues within 7Å of the side chains of any residue along the sequence.

The conformational ensemble of α-synuclein that best fits the experimental RDCs and PREs

The REMD ensemble at intermediate temperature shows qualitative agreement with the average size and residue contacts (PREs) observed experimentally. However, the calculated average RDCs for this ensemble, shown in Fig. 9 A, are not in good agreement with the experimental data. The quality of the fit is assessed using the Q-factor ⁵⁴, calculated as the ratio of Root Mean Square (RMS) deviation between the experiment and calculated ensemble to that of the RMS average of the experimental RDCs. Q=0.78 for the REMD ensemble. Smaller values of the Q-factor correspond to a better fit, with a value between 0.1 and 0.3 observed for well ordered proteins ^55,56. To construct an ensemble of α-synuclein conformations with better agreement with experimental RDCs, we refine the conformational ensemble of α-synuclein using a reweighting approach elaborated in the methods section. Fig. 9 B shows that the average RDCs calculated for the reweighted ensemble is in good agreement with the experimental data. The reconstructed ensemble has a Q-factor of 0.35, showing a substantial improvement in the fit to experiment when compared with the fit from the original ensemble. The back-calculated RDCs left out of the fitting procedure are also in good agreement with experiment (Fig. S1) indicating that the data are not overfit. The Q-factors for the comparison of the REMD ensemble with experiment for the three spin label positions (A19C, A90C and G132C) are 0.37, 0.3 and 0.18, while the Q-factors for the comparison between the reconstructed ensemble and experiment are 0.24, 0.4 and 0.16 respectively. While the RDC values have changed, the calculated persistence length and the global shape characteristics of the reconstructed ensemble still closely resemble those of the original REMD ensemble. The persistence length for the reconstructed ensemble is ~ 6 Å, while the global shape characteristics reported as the average R_g (R_h), asphericity and shape parameter values are 30.7 Å (30.9 Å), 0.35 and 0.39 respectively. The long-range conformational characteristics of the reconstructed ensemble, estimated from the back-calculated PREs are similar to that of the experimental PREs (Fig. 7 D–F).

Figure 9.

Comparison of the experimental HN RDCs (black) with (A) the average RDC determined from global alignment of the intermediate temperature REMD ensemble (red), (B) RDCs calculated using local alignment for the weighted subset of the reconstructed ensemble (red).

Discussion

Polymer theory provides a statistical description of conformational properties of α-synuclein

We have used changes in temperature as a proxy for solvent quality to explore the polymeric properties of α-synuclein under different conditions which induce varying degrees of compaction. We report the average size in terms of the radius of gyration and the hydrodynamic radius, for comparison with measurements from SAXS and NMR diffusion experiments respectively. The relationship between R_g and R_h is dependent on the nature of the solute-solvent interactions. In poor solvents, R_g is smaller than R_h, while the inverse is true in a good solvent. Limiting ratios are provided by native, globular proteins for which R_g/R_h = 0.775 ⁵⁷ and excluded volume chains where R_g/R_h = 1.5 ⁵⁸. However, the ratio under strongly denaturing conditions, determined experimentally, has been reported to be 1.06 ⁴⁹, smaller than 1.5, predicted from the theoretical Zimm relationship ⁵⁸. For the low and high temperature ensembles for α-synuclein, we calculate R_g/R_h ratios of 0.808 and 1.14 respectively, values which are very close to those reported previously ^49,57.

The limiting values for the average size of heteropolymeric α-synuclein at the lowest and highest temperatures agree with predictions from the Flory theory of homopolymeric chains (Table 1). This is consistent with experimental observations that globular proteins in their native states behave like homopolymers in poor solvents, while denatured proteins scale like homopolymers in good solvents ⁴⁹. The R_g calculated for the intermediate temperature ensemble (30.5 Å) is different from that reported from SAXS measurements (~ 40 Å) ⁵⁹, while the R_h value closely match the NMR measurements. It appears that SAXS measurement of the size is not consistent with the estimates of size from NMR measurements. The larger value of the R_g reported from SAXS measurements is in contrast to values expected for polypeptide random coil models (41.5 Å), and close to a previous report of random coil simulations of α-synuclein ²³ where the attractive dispersion interaction between residues was turned off.

Table 1.

Comparison between the expected R_h, (R_g) and the calculated R_h (R_g) from REMD simulations. The expected values for Rh are determined using empirical equations which are based on a comparison of the hydrodynamic radii for a number of globular, disordered proteins and proteins under strongly denaturing conditions ^46,49. The R_g is calculated from the relationship R_g=R₀N^ν. The values for R₀ are used from previous reports of this constant value for globular ⁹⁹ and unfolded ¹⁰⁰ proteins.

REMD Ensemble	Expected Rh (Rg) Å	REMD simulation Rh (Rg) Å
Low temperature	20.1 (15.1)	23.15 (17.0)
Intermediate temperature	30.8	30.5
High temperature	35.1 (40.7)	36.36 (40.5)

Although the scaling of chain size is insensitive to the sequence at the extremes of solvent quality, the effects of chain heterogeneity are significant at intermediate solvent quality, represented here by the intermediate temperature ensemble of α-synuclein. This ensemble is heterogeneous with the N, NAC and C-terminal regions exhibiting distinctly different polymeric properties. Note that the internal distances at intermediate and high temperature are overlapping (Fig. 3). The C-terminal region of the protein has a predominance of acidic residues, with a net charge of −8 at neutral pH. It is mostly extended with very few contacts with other regions of the chain. The extended conformation is consistent with the expected polyelectrolyte behavior of a chain with a high net charge ^60,61. In contrast, the N-terminal region of the chain with a relatively large total charge density but small net charge shows transient contacts with other parts of the chain. Polyampholyte chains with unbalanced charges have also been shown to form globules in the charge-balanced regions, and one or more charged fingers corresponding to the charged regions ⁶², similar to conformations observed for the N-terminal domain of α-synuclein in the intermediate temperature ensemble.

The observation of transient contacts between the N-terminal and NAC regions for the intermediate temperature ensemble suggests that these interactions may be influenced by favorable electrostatic interactions through the formation of salt-bridges. The calculation of distances between all charged side-chains within a distance of 4.5 Å however shows salt bridge interactions in fewer than 10% of the population, for the intermediate temperature neutral pH ensemble. These ion-pair interactions are observed mostly between residues local in sequence rather than between distant residues suggesting locally collapsed regions, as shown for polyampholyte chains ⁶³.

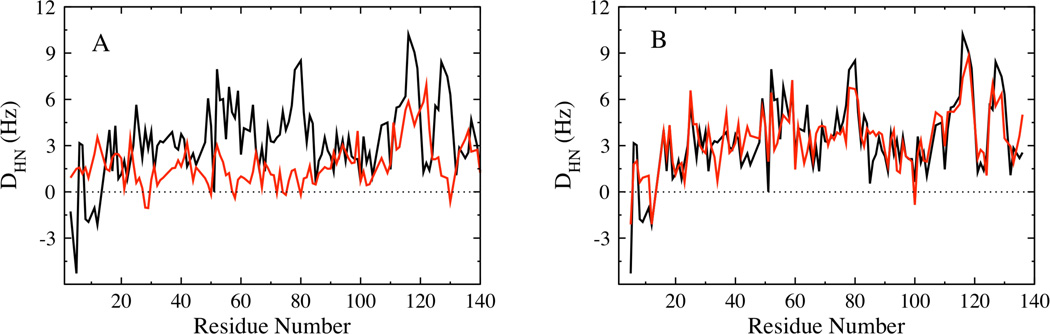
The effect of the charge-balanced state on the collapsed conformation of the N-terminal region of α-synuclein at neutral pH becomes more evident when compared to the conformations of this region at low pH (See supplementary material). The low pH ensembles were generated for a study published previously ¹⁰ and are used here to highlight the effect of charged residues on the conformational characteristics of α-synuclein. With a shift in pH from low to neutral pH, the residue density in the N-terminal region increases with a corresponding increase in the charge density (but lower net charge) while the C-terminal shows a decrease in residue density with an increased charge density (and higher net charge) (Fig. S2). Schuler et al ³⁶ showed the collapsed conformations of charge-balanced polypeptides due to attractive interactions between the opposite charges, consistent with our observations for the N and NAC regions, also consistent with observations from the theory of polyampholyte chains. In contrast, the expanded conformation of the C-terminal region at neutral pH with increase in charge density and the corresponding net charge arises due to charge repulsion, a result supported by similar observations reported by Pappu et al ⁹.

Correlating the polymer properties of α-synuclein with the calculated Residual Dipolar Couplings

By changing the solvent quality using temperature as a proxy, α-synuclein adopts a variety of conformations - near-spherical conformations at low temperature while at intermediate and high temperature akin to good solvent conditions, the chain adopts prolate ellipsoid conformations. The RDC averaged over the chain is close to zero (0.86 Hz) at low temperature, this average increases continually with increasing temperature to ~2.5 Hz at the highest temperature (Fig. 5). These observations highlight the strong influence of the shape of the chain on the averaged RDCs, with the average values increasing with increasing asphericity of the chain. This effect of the shape of the chain on average RDCs is also made clearer by comparisons of the angular correlations under these conditions (Fig. 4 A). Significant (anti-) correlations observed at low temperature, corresponding to collapsed conformations, correlate with RDCs with both large positive and negative values, whose average is close to zero. In contrast, the RDC patterns at intermediate and high temperature exhibit patterns similar to random flight chains ^51,64,65, where the RDCs are observed to all have the same sign, larger in the middle of the chain, with smaller RDCs at the ends. The corresponding angular correlation functions under these conditions show exponential decay. The average RDC at intermediate temperature within the N, NAC and C-terminal regions (Fig. 4 C) can also be related to the characteristic shapes within the three regions. The N and NAC regions, which show significant anti-correlations, have smaller average RDCs while the C-terminal region, which shows a single exponential decay of the angular correlation function for segments within this region corresponds to more extended conformations and greater asphericity in this region, leading to higher average RDCs (2.47 Hz). The range of the RDCs in the C-terminal region is also larger than the values of the N and NAC regions.

We note that while the averaged RDCs increase with increasing temperature, the range of RDCs sampled (both positive and negative) by individual residues is significantly larger at low temperature (upto ~ 9 Hz). The large range of the calculated RDCs suggests that there is local structural regularity within chains at low temperature. In contrast, at intermediate and high temperatures, where structures with more diverse conformational characteristics are sampled, the RDC pattern is closer to that of a random flight chain. The high temperature RDC pattern also shows a flat distribution of RDCs along the middle of the chain while terminal residues have smaller RDCs, consistent with the results from models of unfolded proteins described using random flight chains ^51,64.

The persistence length reflects the local chain stiffness, and is influenced by a number of factors including the nature of the monomeric units making up the polypeptide chain and the temperature or solvent quality. For a heteropolymeric chain like α-synuclein, the stiffness varies along the chain due the variation in the side chain groups and the resulting interactions between different segments of the chain with each other and with the solvent ^29,66. Our results show that the persistence length of α-synuclein increases from 3 to 12 Å going from low to high temperature, corresponding to a shift from poor to good solvent conditions. While the heteropolymeric nature of the chain has a negligible effect on the persistence length observed for the N, NAC and C-terminal domains at the lowest and highest temperatures (data not shown), significant differences are observed at intermediate temperature. For this ensemble, the N and NAC regions have a persistence length of about 6 Å, while the C-terminal shows a much larger persistence length of about 11 Å. This difference in the persistence lengths of the different regions can be explained based on the charge pattern, which is best described for the N-terminal region as a polyampholyte chain, with an unbalanced distribution of charges, while the C-terminal region has a predominance of acidic residues. The C-terminal region of the protein is characterized by the presence of 5 proline residues, which also increases the chain stiffness ⁶⁷.

Residual Dipolar Couplings in Intrinsically Disordered Proteins have been proposed to originate due to transient alignment of short segments of the chain, the length of which corresponds to the persistence length of the polymer chain ^39,64. Polymer persistence length has also been correlated with the size of the Local Alignment Window (LAW), a recently introduced concept ^52,53,68, which allows one to align individual fragments corresponding to the windows local in sequence separately to the ordering frame, rather than aligning the entire polypeptide chain. Analysis using the intermediate temperature ensemble shows that local alignments with LAW lengths 9 residues and higher reproduce the RDCs calculated from the global alignment data well (Fig. 6). However, average angular correlations for α-synuclein at intermediate temperature extend beyond nine residues. Our results show that for the intermediate temperature ensemble, the RDC pattern (the signs of the RDCs and the range) is sensitive to angular correlations that decay on a short length scale (over which the angular correlation function decays to 1/e of it's initial value), but that the longer range anti-correlations between HN groups separated by ten or more residues have little effect on the RDC pattern. The longer-range anti-correlations, however, are much smaller compared to that observed for the low temperature ensemble, indicating the lack of structural regularity of chains under these conditions. The results imply that the analysis of RDCs using local alignment windows is appropriate when the polypeptide chain obeys chain statistics that do not deviate markedly from random flight chain statistics.

Fitting to both the experimental RDCs and PREs provides a better representation for the conformational ensemble of α-synuclein

The structural characterization of α-synuclein has been carried out using a variety of experimental and computational methods ^{23,28,69–71}. We have previously shown that intermediate temperature ensembles obtained from REMD simulations fit experimental NMR measurements for model peptides ⁴⁵. Qualitative agreement of the α-synuclein conformational ensemble at intermediate temperature with experimental PREs ¹⁰ was also shown in a previous study where we noted the underdetermined nature of the problem of fitting conformational ensembles to experimental PREs resulting in different representative ensembles fitting the same PREs ¹⁰. A common problem encountered while constructing conformational ensembles for IDPs like α-synuclein is that many different ensembles with varying conformational propensities can fit any given experimental parameter. A number of approaches have been devised to deal with this problem of degeneracy of conformational ensembles ^72–74, but care must be taken to prevent overfitting the experimental data ^53,74. It has been suggested that the degeneracy problem encountered when fitting RDCs can be removed by fitting PREs as well ⁷⁵.

In our approach, ensembles were generated repeatedly by selecting sets of fifty structures from a large pool of conformers, with the subsequent introduction of a set of weights for each conformer that are adjusted to fit the RDC data. Cross validation has been used to avoid overfitting the data (Fig. S1). From the many ensembles that can be constructed in this way, we calculate the fit of each ensemble to the long range PREs, and then choose as the most representative ensemble the one with the best fit to both the short-range RDC data and the long range PRE data. We find that ensembles fitting only the RDCs do not always reproduce the global shape and size characteristics. Previous studies of α-synuclein, based on fits to experimental RDCs and PREs, suggest that RDCs agree better with experiment when the long-range information from PREs is explicitly included to fits obtained from local alignment windows ^25,76. We calculated RDCs based on local alignments, and further screened ensembles fitting the long-range PREs. The reconstructed ensemble fitting both of these parameters consistently retains the global shape and size properties observed for the REMD ensemble, in contrast to ensembles fitting either just the RDCs or the PREs alone.

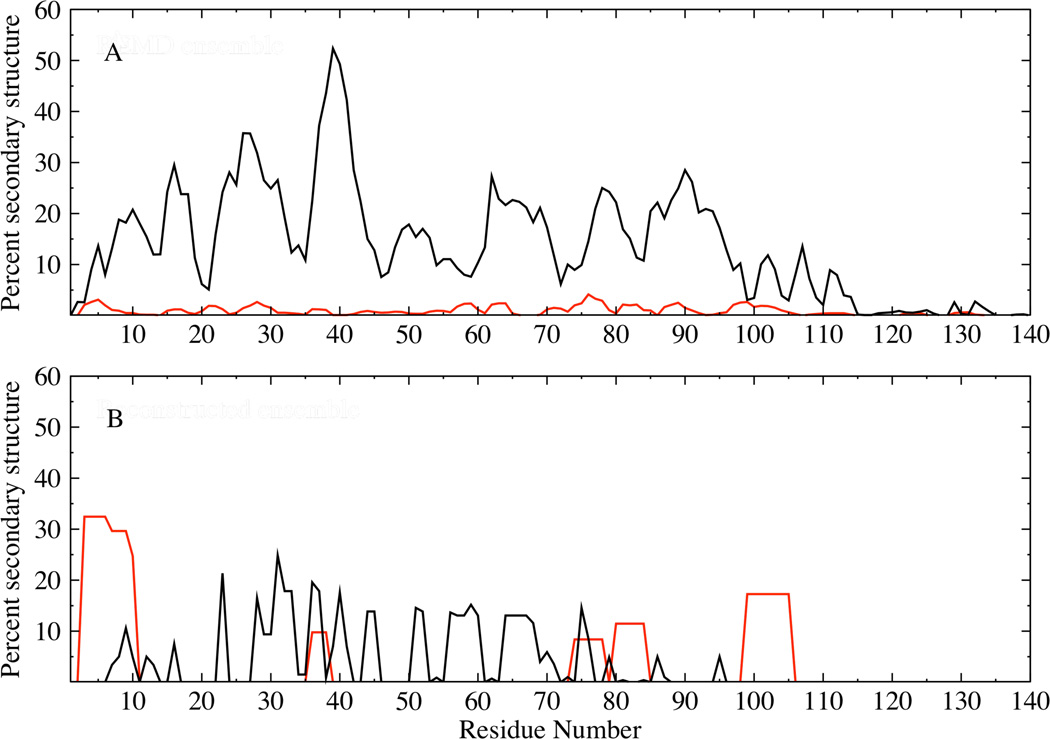
A comparison of the conformational characteristics between the reconstructed ensemble fitting both RDC and PRE measurements and the original REMD ensemble shows a significant change in the secondary structural properties, assigned using STRIDE ⁷⁷ (Fig. 10). The helical propensity of the reconstructed ensemble is enhanced upon fitting to the RDCs, with helicities being prominent over short stretches along the sequence including residues 1–13 which has been shown to form helices under crystallization conditions ⁷⁸. The strand propensity of the reconstructed ensemble is marginally diminished compared to the REMD ensemble, and is prominent in the N-terminal and NAC domains, encompassing regions predicted to have strand propensity in previous studies ⁷⁹.

Figure 10.

Ensemble averaged helix (red) and beta strand (black) propensities for the original REMD (A) and reconstructed (B) α-synuclein ensembles. Helix propensities were calculated by combining the alpha pi and 3–10 conformations, while the strand propensities were obtained by combining the extended and bridge conformations ⁷⁷.

This study focuses on the conformational characteristics of the monomeric disordered state of α-synuclein, which was long thought to be the physiological form of this protein. Two reports have challenged this view by suggesting that the physiological form of α-synuclein might actually be a stable helical tetramer ^80,81, while the most recent studies under similar conditions have been unable to confirm the report that α-synuclein forms a stable helical in mammalian cells. Instead evidence is presented that that α-synuclein remains a disordered monomer under cellular conditions and under conditions that contain the physiologically relevant N-terminal acetyl group ^{82, 102–104}. It remains to be seen if the helical tetramer is indeed the physiological form of α-synuclein. While this is still debated, it is essential to note the importance of the monomeric disordered state of α-synuclein. Changes in the environment change subpopulations of conformations in the monomeric state ¹⁰ which is presumed to eventually lead to aggregation. The monomeric conformations of α-synuclein have also been shown to associate with each other to form transient dimers ⁸³ which can proceed to form higher order aggregates and fibrils.

Implications for association and aggregation

Conformational characterization of the monomeric state of α-synuclein by experiment and computation have been performed in order to determine structural characteristics that might be associated with the aggregation propensity of α-synuclein. A variety of factors including secondary structure propensity ¹⁹ and long-range interactions ^{10,20,23,24,48} have been linked to the aggregation properties of α-synuclein. Our intermediate temperature ensemble, reconstructed by fitting both the experimental RDCs and PREs shows the secondary structural propensity to be predominantly turn and coil-like, and a small average propensity for alpha-helical and beta-strand conformations (Fig. 10 B). The propensity for helical conformations over short stretches along the chain suggests that these helical stretches could potentially act as seeds and accelerate the formation of a long contiguous helix under suitable conditions, including the lipid bound state ¹³ and the recently suggested tetrameric helical state ^80,81.

The observation of non-exponential decay of the angular correlations (including a sign change) in the N and NAC domains points to more collapsed conformation of these regions consistent with the transient long-range interactions observed between the N and NAC domains, while the C-terminal domain is largely extended. It seems likely that the collapsed conformation of the N and NAC regions, through transient contacts within these regions will retard intermolecular chain interactions. Coarse-grained modeling studies of polypeptide chains have suggested that stabilizing aggregation-prone conformations of chains can result in the formation of ordered fibrils with on-pathway oligomeric intermediates ⁸⁴. The propensity of α-synuclein to populate helical conformations in the N-terminal region is suggestive of a helix-mediated association between chains which can facilitate favorable intermolecular interactions between the aggregation-prone, hydrophobic NAC region, consistent with ideas proposed recently for natively unfolded chains ⁸⁵ and shown for α-synuclein in the form of helical intermediates ⁸⁶ under some conditions. It appears that in it’s monomeric state, α-synuclein shows a propensity for adopting a variety of conformations, which can facilitate either the formation of ordered structures or association to form higher order aggregates under suitable cellular conditions.

Materials and Methods

Set-up of Replica Exchange Molecular Dynamics Simulations

We have used Replica Exchange Molecular Dynamics (REMD) ^87,88 simulations to generate the conformational ensembles of α-synuclein. In this approach, a number of replicas are run in parallel over a specified temperature range. Adjacent replicas (T_i and T_j) are allowed to exchange periodically, with an acceptance criterion based on the following Metropolis transition probability.

$$\mathrm{W}\{{\mathrm{T}}_{\mathrm{i}},{\mathrm{T}}_{\mathrm{j}}\}\to \{{\mathrm{T}}_{\mathrm{j}},{\mathrm{T}}_{\mathrm{i}}\}=\text{min}(1,\text{exp}[-({\mathrm{\beta }}_{\mathrm{j}}-{\mathrm{\beta }}_{\mathrm{i}})({\mathrm{E}}_{\mathrm{i}}-{\mathrm{E}}_{\mathrm{j}})])$$ (3)

where, β_i(j) = 1/KT_i(j) and E_i(j) is the potential energy of the i^th (j^th) replica. This method generates canonical probability distributions for the ensembles over the specified temperature range. The REMD method has been implemented in the IMPACT simulation package ⁸⁹. Simulations were performed using the AGBNP implicit solvent model ⁹⁰ and the OPLS-AA force field ⁹¹.

All simulations were initiated with a fully extended conformation of the α-synuclein molecule. The simulations start with a short minimization using the conjugate gradient method followed by a production run for a total of 10ns each over 20 replicas at the following temperatures: 300, 308, 317, 325, 334, 343, 353, 362, 372, 382, 393, 403, 414, 426, 437, 449, 461, 474, 487 and 500K. The molecular simulation time-step was 1.5 fs and exchanges were attempted every 1ps. The cumulative simulation time, with a total of 25 ns for each of the 20 replicas, corresponds to a total of 500 ns.

Analysis of the global shape characteristics

The global shape characteristics of a chain are determined using the inertia tensor ^92,93 defined in equation 4 as:

$${\mathrm{T}}_{\mathrm{\alpha }\mathrm{\beta }}=\frac{1}{2{\mathrm{N}}^2}{\displaystyle \sum _{\mathrm{i},\mathrm{j}=1}^{\mathrm{N}}}({\mathrm{r}}_{\mathrm{i}\mathrm{\alpha }}-{\mathrm{r}}_{\mathrm{j}\mathrm{\alpha }})({\mathrm{r}}_{\mathrm{i}\mathrm{\beta }}-{\mathrm{r}}_{\mathrm{j}\mathrm{\beta }})$$ (4)

Here, N is the total number of atoms in the molecule; r_iα (r_jβ) is the α^th (β^th) component of the position of atom i (j) and α,β = x,y,z. The radius of gyration (R_g), asphericity (™) and shape parameter (S) can be derived from the eigenvalues of T_αβ, represented as λ₁, λ₂, λ₃, as follows:

$${\mathrm{R}}_{\mathrm{g}}=\sqrt{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3}$$ (5)

$$\mathrm{\delta }=1-3\left(\frac{{\mathrm{\lambda }}_1{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_2{\mathrm{\lambda }}_3+{\mathrm{\lambda }}_1{\mathrm{\lambda }}_3}{{({\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3)}^2}\right)$$ (6)

$$\mathrm{S}=27\frac{({\displaystyle \prod _{\mathrm{i}=1}^3}({\mathrm{\lambda }}_{\mathrm{i}}-\mathrm{\lambda ̅}))}{{({\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3)}^3},\mathrm{\lambda ̅}=\frac{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3}{3}$$ (7)

The asphericity values range from 0 for a sphere to 1 for a rod with intermediate values corresponding to ellipsoidal conformations. The range of the shape parameter is between −0.25 and 2. Negative values of S represent oblate conformations while positive values correspond to prolate conformations. The hydrodynamic radii of the structures were calculated using Hydropro ⁹⁴. Hydropro calculations were performed using the following values for the input parameters: Hydrodynamic model of each chain was obtained for non-hydrogen atoms using spherical elements of radii 3.1 Å. The resulting structure with overlapping spheres is used to obtain the shell model as described in the original reference ⁹⁴. The minimum and maximum radii of the beads in the shell were set to 1.5 and 2 Å respectively.

Error bars representing the standard deviations were calculated as the square root of the variance of the simulation data for the size and shape parameters.

Estimation of the persistence length of polymer chains

Persistence length is calculated as the average projection of the end-to-end vector onto every bond vector (l_i) along the sequence. Since the persistence length is calculated as an average over all possible sections along the chain of any given sequence separation, this method makes it easier to identify the effect of the varying stiffness along the sequence arising due to the heteropolymeric nature of the chain.

$${\mathrm{l}}_{\mathrm{p}}=\langle \frac{1}{\mathrm{N}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}{\displaystyle \sum _{\mathrm{j}=\mathrm{i}}^{\mathrm{N}}}\frac{{\mathbf{l}}_{\mathrm{i}}·{\mathbf{l}}_{\mathrm{j}}}{\left|{\mathrm{l}}_{\mathrm{i}}\right|}\rangle =\langle {\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}\frac{{\mathbf{l}}_{\mathrm{i}}·{\mathbf{l}}_{\mathrm{N}}}{\left|{\mathrm{l}}_{\mathrm{i}}\right|}\rangle$$ (8)

Ensemble Reconstruction by fragment assembly and ensemble selection by fitting to experimental parameters

To provide a coherent representation for the conformational ensemble of α-synuclein, we have designed an approach to fit both the experimental RDCs and PREs, which have been used most commonly for determining the structural properties of IDPs. The residual dipolar couplings between two nuclei (HN) are determined using Eq. 9 where the dipolar couplings are dependent on the angle θ between the internuclear vector and the magnetic field ⁹⁵. Here, γ_H (γ_N) corresponds to the gyromagnetic ratio of nuclei H (N) and r_HN is the internuclear distance.

$$\mathrm{D}=\frac{{\mathrm{\mu }}_0\mathrm{h}{\mathrm{\gamma }}_{\mathrm{H}}{\mathrm{\gamma }}_{\mathrm{N}}}{4\mathrm{\pi }{\mathrm{r}}_{\text{HN}}^3}\langle \frac{3{\text{Cos}}^2\mathrm{\theta }-1}{2}\rangle$$ (9)

Ensembles of weighted structures were selected from a large pool of structures, based on fits of the calculated average RDCs to the experimental RDCs. The pool of structures was generated by reconstructing the intermediate temperature REMD simulation ensemble. RDCs calculated using sliding windows over short overlapping segments of polypeptide chains have been used previously for structural motif determination of folded proteins ^96,97. In our approach, ensemble reconstruction was performed by first cleaving the structures generated from the REMD simulations into short fragments, each 14 residues long, which are subsequently spliced together to generate a new pool of structures. The RDCs for each of these new structures was calculated using a sliding window centered on a given residue, using the alignment tensor for this short segment. Fifty weighted structures were chosen at random from the pool of structures. The fits of this ensemble to the experimental RDCs were determined using the following selection criterion:

$${\mathrm{\chi }}^2={\displaystyle \sum _{\mathrm{i}}^{\mathrm{n}}}{({\displaystyle \sum _{\mathrm{j}}^{\mathrm{N}}}{\mathrm{D}}_{\text{ij}}^{\text{calc}}{\mathrm{w}}_{\mathrm{j}}-{\mathrm{D}}_{\mathrm{i}}^{\text{exp}})}^2$$ (10)

where w_j is the weight associated with structure j, i corresponds to the residue number, N the number of structures, n the number of RDCs, D_ij^calc the calculated HN couplings of residue i in structure j and D_ij^exp is the corresponding experimental HN couplings. The following constraints were applied to the weights assigned to chosen structures: (a) Sum of the weights should be equal to 1. (b) Weight associated with any structure should be greater than zero. The RDCs have been calculated based on alignment of individual structures using PALES ⁹⁸. Ensembles with the smallest χ² have been chosen for further analysis. Ensemble selection using a genetic algorithm for fitting to experimental RDCs, with selection criteria similar to that mentioned above, have been reported previously ⁵³.

This selection procedure was performed iteratively to obtain weighted ensembles best fitting to the RDCs. Cross-validation of RDC data not employed in the fitting were predicted and compared with experiment to evaluate the validity of the fitting procedure. The RDCs were calculated using a segment length determined based on extensive analysis of different segment lengths and their ability to reproduce the average global alignment of the RDCs.

The paramagnetic intensity ratios were back calculated for ensembles fitting the experimental RDCs, corresponding to the three spin-label sites used in the experiment. The distances were converted to intensity ratios using the following two relations.

The distance data (r) obtained from the coordinates of structures in the conformational ensemble is first converted to PREs (Г₂) using the following relation, where K is a constant (1.23×10⁻³²cm⁶S⁻²), τ_c is the correlation time (4 ns), ω_H is the proton larmor frequency.

$$\mathrm{r}={\left[\frac{\mathrm{K}}{{\mathrm{\Gamma }}_2}\right(4{\mathrm{\tau }}_{\mathrm{c}}+\frac{3{\mathrm{\tau }}_{\mathrm{c}}}{1+{\mathrm{\omega }}^2{\mathrm{\tau }}_{\mathrm{c}}^2}\left)\right]}^{\frac{1}{6}}$$ (11)

The PREs are then converted to intensity ratios using the following relation, where I_ox/I_red is the intensity ratio and t is the total relaxation time. The average intrinsic relaxation rate is set to 20 Hz, taken from experimental measurements ⁸³.

$$\frac{{\mathrm{I}}_{\text{ox}}}{{\mathrm{I}}_{\text{red}}}=\frac{{\mathrm{R}}_2\text{ exp}(-{\mathrm{\Gamma }}_2\mathrm{t})}{{\mathrm{R}}_2+{\mathrm{\Gamma }}_2}$$ (12)

Of the many ensembles that can be obtained using the above approach, the ensemble best fitting the experimental PREs was chosen as the representative ensemble. We note that multiple ensembles generated independently based on fits to both the RDCs and PREs have similar shape properties as described for the reconstructed ensemble presented here (data not shown).

Secondary structural assignments for the α-synuclein ensembles were determined using STRIDE ⁷⁷.