Abstract
Protein polymerization consists in the aggregation of single monomers into polymers that may fragment. Fibrils assembly is a key process in amyloid diseases. Up to now, protein aggregation was commonly mathematically simulated by a polymer size-structured ordinary differential equations (ODE) system, which is infinite by definition and therefore leads to high computational costs. Moreover, this Ordinary Differential Equation-based modeling approach implies biological assumptions that may be difficult to justify in the general case. For example, whereas several ordinary differential equation models use the assumption that polymerization would occur at a constant rate independently of polymer size, it cannot be applied to certain protein aggregation mechanisms. Here, we propose a novel and efficient analytical method, capable of modelling and simulating amyloid aggregation processes. This alternative approach consists of an integro-Partial Differential Equation (PDE) model of coalescence-fragmentation type that was mathematically derived from the infinite differential system by asymptotic analysis. To illustrate the efficiency of our approach, we applied it to aggregation experiments on polyglutamine polymers that are involved in Huntington’s disease. Our model demonstrates the existence of a monomeric structural intermediate  acting as a nucleus and deriving from a non polymerizing monomer (
acting as a nucleus and deriving from a non polymerizing monomer (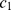 ). Furthermore, we compared our model to previously published works carried out in different contexts and proved its accuracy to describe other amyloid aggregation processes.
). Furthermore, we compared our model to previously published works carried out in different contexts and proved its accuracy to describe other amyloid aggregation processes.
Introduction
Protein aggregation and misfolding are involved in several fatal human disorders, such as Alzheimer’s, Prion, Huntington’s diseases [1], [2]. Certain types of aggregates display specific structural traits (e.g. a 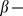 sheet enriched secondary structure) that characterize amyloid assemblies. Recent progress in solid state Nuclear Magnetic Resonance (NMR) has led to a better understanding of amyloid assemblies at the molecular level [3]. However, this structural knowledge constitutes only a snapshot of the dynamic processes. Protein aggregation involves a large amount of chain reactions, e.g. conformational exchange, nucleation (which is the formation of a first stable intermediate), polymerization by monomer, dimer or
sheet enriched secondary structure) that characterize amyloid assemblies. Recent progress in solid state Nuclear Magnetic Resonance (NMR) has led to a better understanding of amyloid assemblies at the molecular level [3]. However, this structural knowledge constitutes only a snapshot of the dynamic processes. Protein aggregation involves a large amount of chain reactions, e.g. conformational exchange, nucleation (which is the formation of a first stable intermediate), polymerization by monomer, dimer or 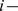 mer addition, coalescence, depolymerization (by loss of mono, di or oligomers), fragmentation (breakage into two or more polymers), protein degradation.
mer addition, coalescence, depolymerization (by loss of mono, di or oligomers), fragmentation (breakage into two or more polymers), protein degradation.
To explore the dynamics of amyloid assemblies, nucleation/polymerization reaction schemes have been applied, and to model them, ordinary differential equations (ODEs) have been used for many years [4]. An ODE means an equation containing only one independent variable (e.g. the chemical concentration of molecules) and its derivatives. Therefore in the case of polymerization, the number of equations should be at least equal to the number of sub-units constituting the longuest polymer. This value is extremely large in the case of amyloid fibrils (amyloid fibril sizes can go up to 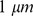 length [5]), therefore simplifying assumptions are commonly admitted, e.g. constant reaction rates, meaning that polymers of any size behave roughly in the same way [6]–[9]. Although such assumptions allow the system to be reduced from an infinite set of ODEs to a couple of equations [4], [7], assumptions of this nature are difficult to justify biochemically.
length [5]), therefore simplifying assumptions are commonly admitted, e.g. constant reaction rates, meaning that polymers of any size behave roughly in the same way [6]–[9]. Although such assumptions allow the system to be reduced from an infinite set of ODEs to a couple of equations [4], [7], assumptions of this nature are difficult to justify biochemically.
We propose here a new and global framework that can be adapted to most protein polymerization reactions. This method relies on partial differential equations (PDEs). In contrast to an ODE, a PDE permits formulation of problems involving functions of several variables. Instead of handling an infinite set of ODEs, we show that under reasonable assumptions, we can derive an equivalent model composed of a small number of ODEs coupled with a single size-structured PDE. The size variable of fibers replaces the infinite number of ODEs. To derive our model, we tune asymptotic methods from previously published works [10], [11]. A fully general model, which is much easier to handle both theoretically and numerically, is obtained. It allows much faster computations than for the full ODE set of equations. Moreover, recent analytical tools developed for PDE analysis can be applied. The obtention of size-distributions of polymers is a fundamental step [12], as it makes it possible to estimate quantitative reaction rates and build a predictive model by the means of recently developed inverse problem techniques [13].
To illustrate our method, we first formally derive the PDE model in a general case, and then apply our method to expanded polyglutamine (PolyQ) diseases. Finally, we compare our results to existing work [7], [8].
Results
The Infinite ODE System
Let us first recall how one can write the differential system describing all the reactions that occur during nucleated protein polymerization. We denote 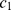 the protein monomeric concentration and
the protein monomeric concentration and 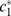 the one of a misfolded monomeric species which displays the ability to polymerize.
the one of a misfolded monomeric species which displays the ability to polymerize. 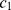 monomers transform into this monomeric species
monomers transform into this monomeric species 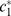 at the rate
at the rate 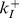 , and
, and 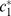 transform back to
transform back to 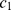 at the rate
at the rate 
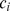 represents the concentration of polymers made up of
represents the concentration of polymers made up of  monomers. We assume that polymers and monomers are degraded with a size-dependent degradation rate denoted
monomers. We assume that polymers and monomers are degraded with a size-dependent degradation rate denoted 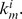 The misfolded monomers
The misfolded monomers 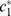 are able to polymerize to give rise to a nucleus
are able to polymerize to give rise to a nucleus 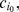 composed of
composed of 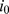 monomeric units, with the rate
monomeric units, with the rate 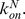 As proposed by Oosawa and co-authors [4], a nucleus is generated by the addition of an object to highly unstable entities that are too transitory to be observed. The object stabilizing the highly unstable entities can be a monomer (
As proposed by Oosawa and co-authors [4], a nucleus is generated by the addition of an object to highly unstable entities that are too transitory to be observed. The object stabilizing the highly unstable entities can be a monomer (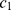 ). If we consider a nucleus
). If we consider a nucleus 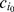 with a size
with a size 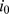 , its formation does not consist in a sequential addition of
, its formation does not consist in a sequential addition of 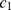 till
till 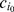 (where it would be represented by
(where it would be represented by 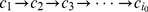 ), but follows an
), but follows an 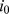 order kinetic (where
order kinetic (where 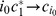 ).
).
This nucleus can dissociate at the rate 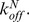 We make the reasonable assumption that there is an equilibrium between monomers and oligomers [4].
We make the reasonable assumption that there is an equilibrium between monomers and oligomers [4].
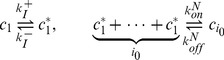 |
(1) |
Polymers of size  larger than
larger than 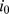 can polymerize or depolymerize, which is the gain or the loss of a single monomeric unit: the elongating species is assumed here to be
can polymerize or depolymerize, which is the gain or the loss of a single monomeric unit: the elongating species is assumed here to be 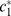 (our model is easy to adapt to other cases, e.g if the elongating species is a dimer or an oligomer [8]). Those reactions occur at the rate
(our model is easy to adapt to other cases, e.g if the elongating species is a dimer or an oligomer [8]). Those reactions occur at the rate 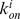 and
and 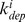 respectively.
respectively.
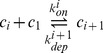 |
(2) |
Polymers can also coalesce with other polymers or break into two smaller polymers. For the sake of simplicity, we assume that a polymer can only break into two pieces at the exact same time (a breakeage into  or more pieces is generally much more hazardeous, so that it can be neglected). Coagulation of two polymers of respective size i and j occurs at the rate
or more pieces is generally much more hazardeous, so that it can be neglected). Coagulation of two polymers of respective size i and j occurs at the rate 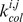 . Fragmentation of a polymer of size i gives rise to smaller polymers of size
. Fragmentation of a polymer of size i gives rise to smaller polymers of size 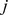 and
and 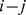 (where
(where 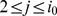 ), at the rate
), at the rate 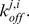
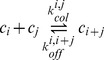 |
(3) |
We could have kept the same notation for fragmentation and depolymerization, by denoting 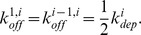 We prefered however to distinguish them, because they involve reactions of different kinds, so that the orders of magnitude may appear different.
We prefered however to distinguish them, because they involve reactions of different kinds, so that the orders of magnitude may appear different.
Let us define 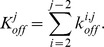 This represents the total rate with which a polymer of size
This represents the total rate with which a polymer of size 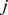 can break to give smaller polymers. By symmetry we have that
can break to give smaller polymers. By symmetry we have that 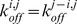 and
and 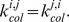
The following model is the exact deterministic transcription of the previously considered reactions. It could be completed by other reactions (polymerization pathways, other types of conformational exchange, for instance) to adapt to any possible case. The variation 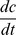 of the species
of the species 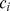 (or
(or 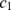 ,
, 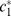 ) depends on two phenomena: 1) their rates of consumption, including depolymerization into a smaller polymer (or transformation into
) depends on two phenomena: 1) their rates of consumption, including depolymerization into a smaller polymer (or transformation into 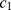 in the case of
in the case of 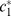 ), polymerization into a higher polymer (or transformation into
), polymerization into a higher polymer (or transformation into 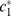 in the case of
in the case of 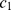 ) and degradation
) and degradation 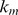 , and 2) their rates of production, i.e. polymerization from smaller polymer (or transformation from
, and 2) their rates of production, i.e. polymerization from smaller polymer (or transformation from 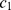 in the case of
in the case of 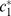 ) and depolymerization from higher polymer (or transformation from
) and depolymerization from higher polymer (or transformation from 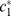 in the case of
in the case of 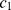 ). This induces the following equations.
). This induces the following equations.
| (4) |
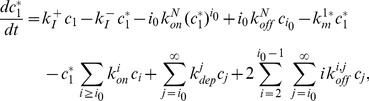 |
(5) |
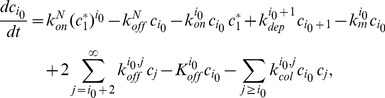 |
(6) |
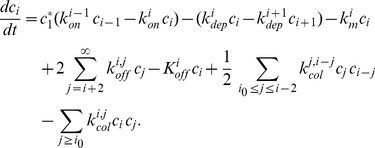 |
(7) |
This model and variants of it have been extensively studied, either in the general case in the mathematical literature (see [10], [14] and references therein), or when applying simplifying assumptions in the biological literature [4], [6]–[8]. It is an efficient tool to study protein aggregation when the average size of protein 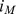 is of a reasonable order. However, for long polymer reactions, this modeling technique may be time-consuming and therefore inefficient to understand the underlying complexity. One can notice the resemblance between this infinite ODE model and a coupled PDE [15].
is of a reasonable order. However, for long polymer reactions, this modeling technique may be time-consuming and therefore inefficient to understand the underlying complexity. One can notice the resemblance between this infinite ODE model and a coupled PDE [15].
From ODEs to PDE: a New Size-structured Model
We propose here a new size-structured model composed of two ODEs and one PDE in the case of a large average size 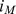 of polymers - i.e.,
of polymers - i.e., 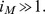 The main idea is to replace the discrete size
The main idea is to replace the discrete size  of a polymer by a continuous variable
of a polymer by a continuous variable 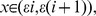 in which we have defined the small parameter
in which we have defined the small parameter 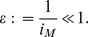 In the same way, the densities
In the same way, the densities 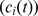 are replaced by a continuous-in-size function
are replaced by a continuous-in-size function 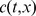 (see supplementary data S1 for more details). This model can be derived from the infinite set of ODEs if the two following assumptions hold.
(see supplementary data S1 for more details). This model can be derived from the infinite set of ODEs if the two following assumptions hold.
First, for most polymer sizes  there is only a slight difference between what happens for
there is only a slight difference between what happens for 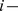 mers and for
mers and for 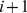 -mers. In other terms, even if quantities and reaction rates vary, it occurs in a “continuous” manner, implying only slight changes from one size
-mers. In other terms, even if quantities and reaction rates vary, it occurs in a “continuous” manner, implying only slight changes from one size  to its neighbor sizes
to its neighbor sizes 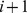 and
and  except for a small number of values. For instance, for degradation coefficients
except for a small number of values. For instance, for degradation coefficients 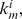 it is formalized as: There exists a constant, denoted below
it is formalized as: There exists a constant, denoted below 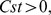 such that
such that
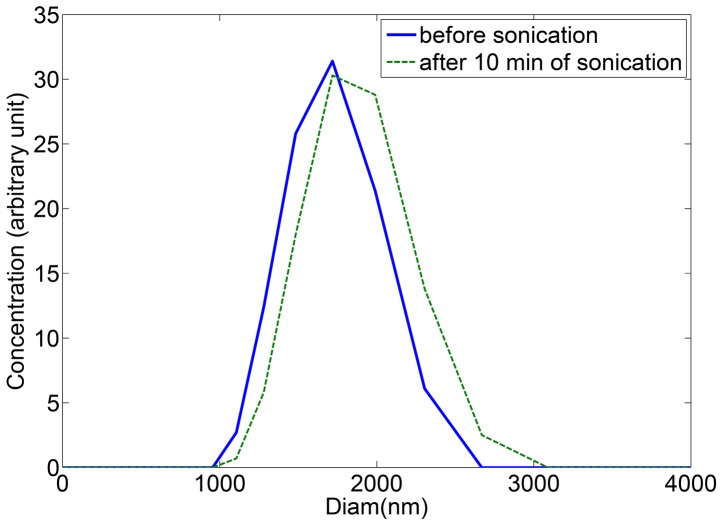
This assertion allows a continuous viewpoint on the equations for 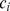 . It also means that disruptions in the concentrations or in the coefficients can only appear at some specific points, that will have to be identified, and that are meaningful biologically. Though, this assertion appears to be natural since the conformational changes in polymers only occur at specific sizes [16]. Moreover, having a look at experimental size distributions (Figure 1) confirms how natural it is to view the size of polymers as a continuous quantity.
. It also means that disruptions in the concentrations or in the coefficients can only appear at some specific points, that will have to be identified, and that are meaningful biologically. Though, this assertion appears to be natural since the conformational changes in polymers only occur at specific sizes [16]. Moreover, having a look at experimental size distributions (Figure 1) confirms how natural it is to view the size of polymers as a continuous quantity.
Figure 1. PolyQ41 Fibrils size distribution before (blue plain line) and after (dashed green) 10 min of sonication.
The absence of any change in the distribution shows that neither fragmentation nor coalescence occured.
The second and quite standard assumption is that at the beginning of the reaction, when polymer concentrations remain small compared to monomers, polymerization is the main process, whereas fragmentation and coalescence are secondary processes [4], [6]. This assumption can be replaced if necessary by a similar one, such as the existence of a dominant polymerization by 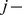 mer addition, with
mer addition, with 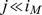 a relatively small oligomer. In such a case, the polymerization terms
a relatively small oligomer. In such a case, the polymerization terms 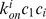 would be replaced by
would be replaced by 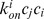 in the equations, and a similar treatment can apply.
in the equations, and a similar treatment can apply.
We refer to supplementary data S1 for a rigorous mathematical formulation of these two assertions. They are obtained when the system of equations is rescaled, and this allows us to estimate the relative contribution of each process to the overall dynamics.
Let us turn to the nucleus 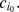 In this equation, the two assertions make it possible to ignore the influence of fragmentation and coalescence. Then as we are in the case where
In this equation, the two assertions make it possible to ignore the influence of fragmentation and coalescence. Then as we are in the case where 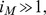 the time-dependency of the equation for
the time-dependency of the equation for 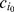 is much faster than the one for
is much faster than the one for 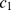 : it can be written
: it can be written 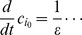 (see supplementary data S1). Hence, it is valid to suppose that it reaches its equilibrium instantaneously, and we can replace Equation (6) by
(see supplementary data S1). Hence, it is valid to suppose that it reaches its equilibrium instantaneously, and we can replace Equation (6) by
We thus obtain the following equality, which generalizes well-established formulas [6]
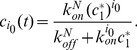 |
(8) |
We can now write the following coupled ODE and PDE system, where  is replaced by a continuous variable
is replaced by a continuous variable 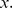 Differences are replaced by derivatives and sums by integrals.
Differences are replaced by derivatives and sums by integrals.
| (9) |
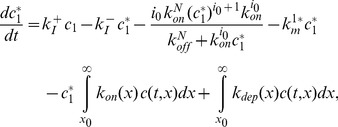 |
(10) |
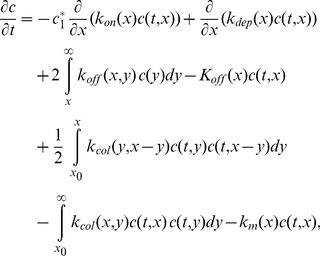 |
(11) |
| (12) |
Complete rigorous mathematical derivation can be found in supplementary data S1, and also shows that generally the third term in the right-hand side of Equation (10) (the ratio 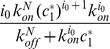 ) is negligible. Even mathematical approximation theorems can be written to validate the model, as is done for instance in [10], [11], [17].
) is negligible. Even mathematical approximation theorems can be written to validate the model, as is done for instance in [10], [11], [17].
The advantages are twofold. First, it allows us to investigate numerically, using standard and well-known numerical schemes (see [18]), how a change in the coefficients can influence the overall reaction, and, more specifically, the size distribution. Also, inverse problem techniques could allow size-dependent parameters to be estimated (see for instance [19], [20]). Secondly, it is easier to handle mathematically. Theoretical analysis can help us understand the intrinsic mechanisms and formulate new paradigms [21], [22].
Application to PolyQ Polymerization
Aggregation of polyglutamine (PolyQ)-containing proteins is responsible for several neurodegenerative disorders including Huntington’s disease. We have carried out biophysical analyses to investigate the aggregation kinetics of PolyQ41, which are peptides containing a repetition of 41 glutamine residues per monomer. Such a length of PolyQ repetition per molecule is sufficient to induce aggregation in vitro and in transfected cells [23].
Due to its simplicity, PolyQ provides an excellent model system to test our mathematical model. According to the experimental observations (Figure 1), fragmentation can be ignored. Indeed, in Figure 1, the size distribution of PolyQ41 fibrils did not change after 10 min of ultrasound treatments, showing that polymer-to-polymer reactions do not occur.
In order to determine whether coalescence occurs, we monitored simultaneously two types of measurements, polymer size and total polymerized mass. Polymer size was estimated by a static light scattering (SLS) signal. SLS is governed by the weighted average mass of oligomers and therefore highly depends on oligomer size. It can be viewed as a measurement of 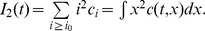 Total polymerized mass was followed by thioflavine T (ThT) fluorescence. Such fluorescence arises from interactions between ThT and the peculiar structure of amyloids, relatively independently of amyloid size (above a certain size threshold). ThT can be mathematically expressed by
Total polymerized mass was followed by thioflavine T (ThT) fluorescence. Such fluorescence arises from interactions between ThT and the peculiar structure of amyloids, relatively independently of amyloid size (above a certain size threshold). ThT can be mathematically expressed by 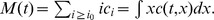 If there were coalescence, the weighted average polymer size would continue to grow even when the total polymerized mass
If there were coalescence, the weighted average polymer size would continue to grow even when the total polymerized mass 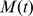 reached a plateau, so the second moment
reached a plateau, so the second moment 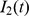 would continue to grow after the plateau has been reached by
would continue to grow after the plateau has been reached by 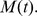 Here, however, both curves reach the plateau roughly simultaneously (see supplementary data S2). Therefore we conclude that coalescence is negligible. As described in Materials and Methods, the spontaneous polymerization of PolyQ41 is prevented by a glutathione s-transferase (GST) tag attached to PolyQ41 peptide. Such experimental system has the advantage of providing a system where only monomeric species are present at time
Here, however, both curves reach the plateau roughly simultaneously (see supplementary data S2). Therefore we conclude that coalescence is negligible. As described in Materials and Methods, the spontaneous polymerization of PolyQ41 is prevented by a glutathione s-transferase (GST) tag attached to PolyQ41 peptide. Such experimental system has the advantage of providing a system where only monomeric species are present at time  , i.e. no seeding was required for polymerization:
, i.e. no seeding was required for polymerization: 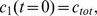
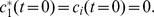 As the GST-polyQ41 does not constitute the pro-aggregative conformer, the PolyQ41 aggregation needs to be ignited by an irreversible enzymatic cleavage (here by thrombin hydrolysis), releasing the GST region apart from PolyQ41. This enzymatic cleavage can be assimilated to an activation process along which the poly Q41 monomer turns into a structurally activated form prone to aggregation. This led us to establish a minimal activation scheme in which the GST-polyQ41, denoted by
As the GST-polyQ41 does not constitute the pro-aggregative conformer, the PolyQ41 aggregation needs to be ignited by an irreversible enzymatic cleavage (here by thrombin hydrolysis), releasing the GST region apart from PolyQ41. This enzymatic cleavage can be assimilated to an activation process along which the poly Q41 monomer turns into a structurally activated form prone to aggregation. This led us to establish a minimal activation scheme in which the GST-polyQ41, denoted by 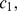 is converted into an active form denoted
is converted into an active form denoted 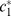 with a constant rate
with a constant rate  . The nucleus size
. The nucleus size 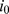 , of unknown value, can be equal to
, of unknown value, can be equal to  ,
, 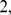
 or even more. With these assumptions, Model (4)–(7) becomes
or even more. With these assumptions, Model (4)–(7) becomes
| (13) |
| (14) |
| (15) |
| (16) |
and we use the continuous version of this model, given by (9)–(12), which becomes
| (17) |
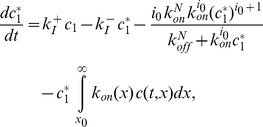 |
(18) |
| (19) |
| (20) |
As an initial approach, we tested piecewise linear polymerization rates. They are linear from 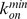 to
to 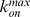 on
on 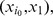 constantly equal to
constantly equal to  on
on 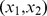 and linearly decreasing to zero on
and linearly decreasing to zero on 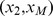 with
with 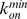 and
and 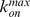 parameters to be calibrated. We arbitrarily set
parameters to be calibrated. We arbitrarily set 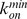 and
and 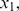 which led to
which led to 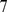 free parameters. We have also tested two different kinds of kinetics when
free parameters. We have also tested two different kinds of kinetics when 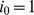 : first, the special case where there is no nucleus, i.e. the polymerization process starts directly from
: first, the special case where there is no nucleus, i.e. the polymerization process starts directly from 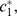 which means
which means 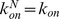 and
and 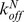 is negligible. This reaction scheme was unable to fit properly even a single experimental curve so we abandoned it. Second, the case when the previous model is unchanged but where
is negligible. This reaction scheme was unable to fit properly even a single experimental curve so we abandoned it. Second, the case when the previous model is unchanged but where 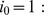 this means that the nucleus
this means that the nucleus 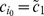 is a monomeric species differing only from
is a monomeric species differing only from 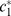 in its conformation. The elongating species remains the intermediate
in its conformation. The elongating species remains the intermediate 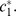 In the following,
In the following, 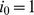 refers to this second case.
refers to this second case.
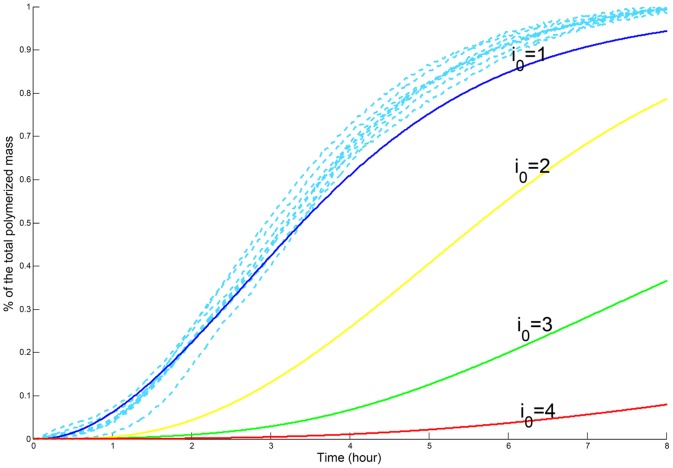
The parameters of this model were then estimated by fitting experimental data on PolyQ41 protein polymerization. We performed this in two successive ways. The first consists in fitting separately each experimental curve, corresponding to a given experiment, at a given concentration. The result is that whatever 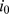 is, the fit is excellent for any curve, with a measurement error from
is, the fit is excellent for any curve, with a measurement error from 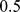 to
to 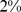 in
in  adimensioned norms (see supplementary data S2). It gives almost undistinguishable curves. However, the variability among the optimal coefficients was large, which led us to the second step. This consisted in fitting simultaneously all the curves of experiments carried out in identical experimental conditions, but for different concentrations. The global adimensioned error (in
adimensioned norms (see supplementary data S2). It gives almost undistinguishable curves. However, the variability among the optimal coefficients was large, which led us to the second step. This consisted in fitting simultaneously all the curves of experiments carried out in identical experimental conditions, but for different concentrations. The global adimensioned error (in 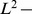 norm) diminished with
norm) diminished with  and reached its lowest level for
and reached its lowest level for 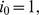 as shown in Figure 2. For larger values of the nucleus, the error is moreover too large for the model to be acceptable (results shown in supplementary data S2). It gives solid ground to the assumption, already suggested in the literature [24], that the nucleus is of size
as shown in Figure 2. For larger values of the nucleus, the error is moreover too large for the model to be acceptable (results shown in supplementary data S2). It gives solid ground to the assumption, already suggested in the literature [24], that the nucleus is of size 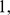 but with a specific and unconventional nucleation-elongation reaction scheme, where the elongating species
but with a specific and unconventional nucleation-elongation reaction scheme, where the elongating species 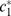 and the nucleus
and the nucleus 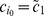 are distinct conformers.
are distinct conformers.
Figure 2. Simulation vs Experiments for Experimental Set 1, for an initial PolyQGST concentration of 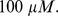 .
.
The parameters were first estimated for an experimental set of initial concentration 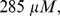 then we compared the experimental measures (dotted lines) for an initial concentration
then we compared the experimental measures (dotted lines) for an initial concentration 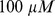 with the simulations (in solid lines) for
with the simulations (in solid lines) for 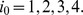 We see that the smaller
We see that the smaller  is, the closer the simulation to experimental curves.
is, the closer the simulation to experimental curves.
Another result of our simulations is that 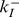 is negligible, thus we can suppose that
is negligible, thus we can suppose that 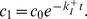 In the same way, we can compare
In the same way, we can compare 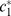 to the solution of the following differential equation
to the solution of the following differential equation
i.e., neglect the contribution of polymers in the equation for 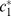 : it fits perfectly for the total duration of the lag phase.
: it fits perfectly for the total duration of the lag phase.
Application to the Knowles et al. Model [7]
As seen for the application to PolyQ, the fully general model (9)–(12) is not yet directly applicable, precisely because of its general character. It can be thought of as the departure point for numerical, biological and mathematical analysis; and it is indeed a powerful way to tackle polymerization issues. To illustrate our approach, we have applied our model to experimental data of amyloid protein aggregation from other authors and we have compared or transposed our model to the recently published models that were accompanying the data [7], [8].
In [7], Knowles and coauthors set up a model for polymerization of breakable filament assembly. This model is an analytical approximation that they have applied to (potential) experimental data and compared to exact equations representing the experimental data. For their approximation model, Knowles and coauthors made the following assumptions.
Polymerization at a constant rate independent of the size of the polymers,
no degradation of polymers neither monomers,
the size of the nucleus is
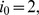
fragmentation rate depends linearly on the size of the polymer:
 constant,
constant,no coalescence,
nucleation disaggregation occurs with the same rate
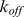 as depolymerization.
as depolymerization.
With these assumptions, it is well-known that the original ODE system simplifies by summation on a system of 2 non linear coupled ODEs (Equations (3a) and (3b) in [7]), namely:
| (21) |
| (22) |
where 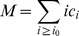 represents the total polymerized mass, and
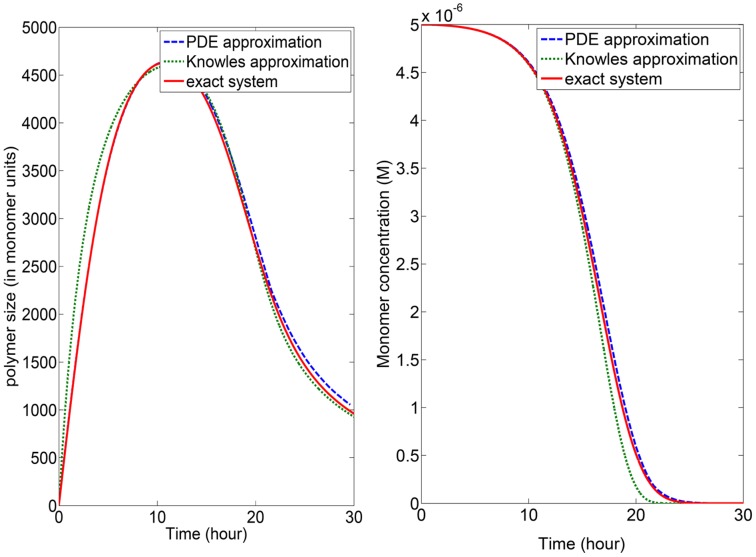
represents the total polymerized mass, and 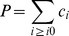 represents the total number of polymers. They approximate this system by an analytical formula, justified by a fixed point method and shown numerically to give a good approximation. To apply our method, we first look at the average size
represents the total number of polymers. They approximate this system by an analytical formula, justified by a fixed point method and shown numerically to give a good approximation. To apply our method, we first look at the average size 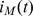 of polymers, which is given by
of polymers, which is given by 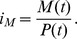 It is shown in Figure 3 for the parameter values
It is shown in Figure 3 for the parameter values 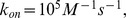
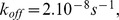
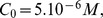
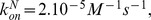
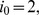
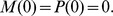 All these values, taken from [7] (fig. 1 of Knowles™ manuscript), directly represent the exact system of (potential) experimental data. We see that our assertion of large polymers is satisfied. Similarly, we check that the range of parameters that they proposed fit to our other assumptions, so that our method can be applied. The assumption on
All these values, taken from [7] (fig. 1 of Knowles™ manuscript), directly represent the exact system of (potential) experimental data. We see that our assertion of large polymers is satisfied. Similarly, we check that the range of parameters that they proposed fit to our other assumptions, so that our method can be applied. The assumption on 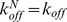 implies that the nucleus dissociation term in the equations for
implies that the nucleus dissociation term in the equations for 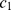 and
and  is negligible: indeed we have
is negligible: indeed we have 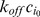 to be compared to
to be compared to 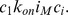
Figure 3. Numerical solution of Equation (21) (22) either using the exact equations, directly representing (potential) experimental data, the PDE approximation, or the analytical approximation proposed in [7].
Left: average size of polymers. Right: monomers concentration. It is clear that the PDE approximation gives excellent results. The parameters used for the exact equations (i.e. values for elongation rate, fragmentation rate and nucleus size) are those from Fig. 1 of [7].
We followed their modelling ideas but our method allows us to relax their assumptions in the following sense.
Polymerization is not necessarily constant, but values
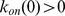 for small polymers of size
for small polymers of size  close to
close to 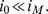
We neglect degradation of small polymers and of monomers, but we keep a degradation for large polymers,
I 0 = 2,
fragmentation rate does not necessarily depend linearly on the size of the polymer, but it is true for small polymers:
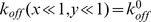 constant,
constant,coalescence is negligible compared to polymerization as long as
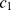 remains in the order of
remains in the order of 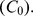
With these assumptions, System (9)–(12) can be simplified as follows:
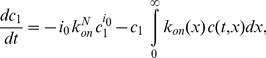 |
(23) |
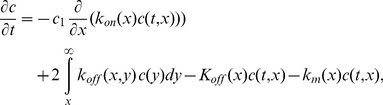 |
(24) |
| (25) |
If we take as in [7]
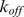 and
and 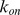 constant, we recover System (??)(??) by summation, but with the terms
constant, we recover System (??)(??) by summation, but with the terms  and
and 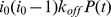 neglected. Numerical simulations are shown in Figure 3, and we see that this simplification allows a perfect fit with the complete model, fast simulations, and a better understanding of which reaction dominates at any moment (since we have access to size distributions, see Figure 4).
neglected. Numerical simulations are shown in Figure 3, and we see that this simplification allows a perfect fit with the complete model, fast simulations, and a better understanding of which reaction dominates at any moment (since we have access to size distributions, see Figure 4).
Figure 4. Adimensionned Distributions of the sizes of polymers for various times.
To obtain adimensionned distributions of polymer sizes, our model was applied to data taken from Figure 1 of [7]. From 6 to 18 hours one can see that the distribution remains roughly stable.
Comments on Size Distributions
For the size parameters taken from [7], fig. 1, we are able to observe the evolution of polymer size distributions over time: see Figure 4. At the beginning of the reaction (in this particular case, for a time between  and
and 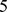 hours), the average size increases very fast. Then it reaches an equilibrium, and between
hours), the average size increases very fast. Then it reaches an equilibrium, and between  to
to 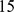 hours it reaches an exponential regime during which the whole size distribution, not only the average size, is quite steady. An explanation for this could be taken from [25] for instance. After this period, the average size decreases - and ultimately, the model shows that
hours it reaches an exponential regime during which the whole size distribution, not only the average size, is quite steady. An explanation for this could be taken from [25] for instance. After this period, the average size decreases - and ultimately, the model shows that 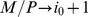 but this would be accomplished only after a very long period of time. A good test for the model proposed by [7] would be to check whether size distribution of polymers resembles such a one-peak distribution. If not, the assumptions would have to be relaxed, e.g. by taking variable coefficients [25].
but this would be accomplished only after a very long period of time. A good test for the model proposed by [7] would be to check whether size distribution of polymers resembles such a one-peak distribution. If not, the assumptions would have to be relaxed, e.g. by taking variable coefficients [25].
PDE Model Applied to the Xue et al. Model [8]
Xue and colleagues present a new strategy to analyse the self-assembly of misfolded proteins into amyloid fibrils [8]. They analysed fibril length distribution of 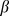 2-microglobulin, a protein involved in dialysis-related amyloidosis. Xue and colleagues have developed the following approach. Based on a large data set of experimental growth curves, transitional general parameters of the time-curve, namely the length of the lag phase (
2-microglobulin, a protein involved in dialysis-related amyloidosis. Xue and colleagues have developed the following approach. Based on a large data set of experimental growth curves, transitional general parameters of the time-curve, namely the length of the lag phase (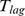 ) and the slope (
) and the slope (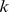 ) of the reaction curve at the inflexion point were extracted. Several theoretical models are simulated using the ODE formulation and the theoretical transitional parameters
) of the reaction curve at the inflexion point were extracted. Several theoretical models are simulated using the ODE formulation and the theoretical transitional parameters 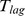 and
and 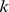 were extracted from the numerical growth curve in the same way as for the experimental curve (see Table S2 in Supplementary data S3). Then the best model and its parametrization were determined by comparing the theoretical values with the experimental data through least-squares analysis. This powerful approach is based on the simulation of a full ODE system (with one equation per size of aggregates) for each model investigated and no simplifications were made to reduce the dimension of this system. As a consequence, the method is time-consuming, which limits the number of mechanisms studied and the maximal polymer size (
were extracted from the numerical growth curve in the same way as for the experimental curve (see Table S2 in Supplementary data S3). Then the best model and its parametrization were determined by comparing the theoretical values with the experimental data through least-squares analysis. This powerful approach is based on the simulation of a full ODE system (with one equation per size of aggregates) for each model investigated and no simplifications were made to reduce the dimension of this system. As a consequence, the method is time-consuming, which limits the number of mechanisms studied and the maximal polymer size (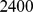 in [8]). In addition, estimation of the best fitting model is based only on general parameters of the curve, which do not seem much sensitive to the distribution of the fragmentation process (see supplementary data S3). To overcome these limitations, we propose transposing their approach using PDE models, allowing for i) faster simulations, ii) no limitation in the size of aggregates, and iii) development of inverse problem techniques ([26], [27]) to estimate parameters using the overall time evolution process.
in [8]). In addition, estimation of the best fitting model is based only on general parameters of the curve, which do not seem much sensitive to the distribution of the fragmentation process (see supplementary data S3). To overcome these limitations, we propose transposing their approach using PDE models, allowing for i) faster simulations, ii) no limitation in the size of aggregates, and iii) development of inverse problem techniques ([26], [27]) to estimate parameters using the overall time evolution process.
Xue et al investigated 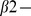 microglobulin growth, using models including different processes: a pre-polymerization step (characterized by either no pre-polymerization, or monomer-dimer equilibrium and dimer addition mechanism, or conformation exchange), an elongation of the aggregates following a one-step function, a linear function or a power function, and a possible secondary process such as fragmentation. Their best-fit model is given by:
microglobulin growth, using models including different processes: a pre-polymerization step (characterized by either no pre-polymerization, or monomer-dimer equilibrium and dimer addition mechanism, or conformation exchange), an elongation of the aggregates following a one-step function, a linear function or a power function, and a possible secondary process such as fragmentation. Their best-fit model is given by:
No conformational exchange, no coalescence and no degradation of polymers or monomers,
the size of the nucleus is
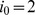 and nucleus dissociation occurs only through depolymerization,
and nucleus dissociation occurs only through depolymerization,polymerization and depolymerization follow a one-step function with the step at
 ,
,fragmentation into two smaller polymers occurs.
Thus, using the previously introduced notations, the original ODE system can be written
| (26) |
| (27) |
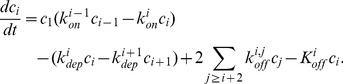 |
(28) |
For the particular choice of fragmentation made in [8], however, fragmentation in polymers of size  is close to
is close to  . This ODE system is then formally equivalent to the following PDE system:
. This ODE system is then formally equivalent to the following PDE system:
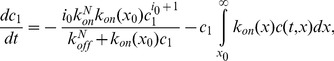 |
(29) |
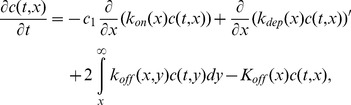 |
(30) |
| (31) |
Due to the shape of the polymerization process, which has a step at  (meaning that
(meaning that 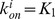 for
for 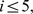
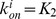 for
for 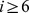 ), if the step is high, that is if
), if the step is high, that is if 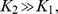 it is however preferable to keep all the ODEs occurring for
it is however preferable to keep all the ODEs occurring for 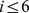 and to set up the PDE (30) only for
and to set up the PDE (30) only for 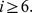 We then adapt the boundary condition (31) as shown in supplementary data S3. This can also be approximated by the Bishop and Ferrone model [6] by adjusting a nucleus critical size to
We then adapt the boundary condition (31) as shown in supplementary data S3. This can also be approximated by the Bishop and Ferrone model [6] by adjusting a nucleus critical size to 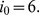 Similar work can be done for the different processes studied in [8]. Our study allowed us to enhance their approach by quick investigation of different fragmentation kernels, showing that the shape of the fragmentation does not influence the polymerization dynamics (see supplementary data S3).
Similar work can be done for the different processes studied in [8]. Our study allowed us to enhance their approach by quick investigation of different fragmentation kernels, showing that the shape of the fragmentation does not influence the polymerization dynamics (see supplementary data S3).
Discussion
We proposed a new model (9)–(12) to serve as a global framework to investigate the leading mechanisms of nucleation-elongation processes in amyloid fibrils’ assemblies. We applied it to PolyQ41 aggregation, demonstrating experimentally that coalescence and fragmentation were negligible, and predicting by our simulations that the monomer activation was irreversible. Moreover, it highlighted the early step of PolyQ41 nucleus formation and assemblies. With regard to the bibliography, the concept of nucleus in protein aggregation remains obscure. Here the analysis of PolyQ polymerization suggested a kinetic scheme in which 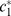 is at an equilibrium with
is at an equilibrium with 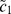 . These two species are monomeric and only differ in their conformation. According to the conventional model of nucleation-elongation process [4], the nucleus is thermodynamically stabilized by the addition of at least one monomer. Here we proposed an unconventional mechanism of nucleation in which the
. These two species are monomeric and only differ in their conformation. According to the conventional model of nucleation-elongation process [4], the nucleus is thermodynamically stabilized by the addition of at least one monomer. Here we proposed an unconventional mechanism of nucleation in which the 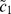 formation constitutes the limiting step in the polymerization process which is stabilized by an interaction with
formation constitutes the limiting step in the polymerization process which is stabilized by an interaction with 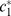 . Therefore, the formation of the
. Therefore, the formation of the 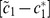 complex constitutes the first proaggregative species. Furthermore, during the formation of this complex, a structural information exchange should occur between
complex constitutes the first proaggregative species. Furthermore, during the formation of this complex, a structural information exchange should occur between 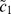 and
and 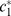 . To reach the formation of a nucleus, two changes of conformation are hence required. The first one arises from the GST-cleavage of
. To reach the formation of a nucleus, two changes of conformation are hence required. The first one arises from the GST-cleavage of 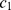 to a conformer
to a conformer 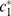 released as a random coil structure, that is not proaggregative. The second change of conformation is an internal change of the random coil
released as a random coil structure, that is not proaggregative. The second change of conformation is an internal change of the random coil 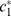 into a proaggregative species
into a proaggregative species 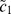 that is still monomeric.
that is still monomeric.
Our approach also proved highly efficient when applied to previously designed models [7], [8], where it can be adapted and used to pursue the research further. We believe it could be applied to many other cases, providing both a unified framework and an efficient way to carry out fast simulations, model discrimination [28], inverse problem methods and analysis.
Materials and Methods
Model Derivation
To derive the continuous model, we first write a rescaled version of the model, that makes use of typical orders of magnitude. Then, quantifying our assumptions, we approximate sums by integrals and differences by derivatives. Finally, from the equation for 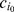 we deduce the boundary condition for
we deduce the boundary condition for 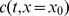 (full details in supplementary data S1).
(full details in supplementary data S1).
Numerical Implementation
To avoid useless conversions, we implemented the PDE model (9)–(12) with dimensioned numbers, and checked a posteriori that the considered orders of magnitude fit the assumptions. We use an explicit upwind scheme - finer methods can be used such as WENO [18].
Parameter Estimation
The parameter estimation was performed by a least-square approach. For 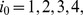 we searched for the optimal set of parameters such that it minimized the quadratic distance between the data points obtained by ThT measures and the simulated curve of the mass, represented by
we searched for the optimal set of parameters such that it minimized the quadratic distance between the data points obtained by ThT measures and the simulated curve of the mass, represented by 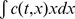 in the PDE model or by
in the PDE model or by 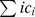 in the ODE one. The minimization task was performed by the CMAES algorithm [29]. It was run with 50 different initial parameters sets. Then the optimal solution was used as an initial guess and the minimization algorithm was run again 50 times.
in the ODE one. The minimization task was performed by the CMAES algorithm [29]. It was run with 50 different initial parameters sets. Then the optimal solution was used as an initial guess and the minimization algorithm was run again 50 times.
Experimental Results
GST-PolyQ production
The GST-Q41 expression vector was described by Masino et al [30]. GST-polyQ41 fusion protein was produced in E.Coli BL21DE3 and purified by affinity chromatography using Glutathione Sepharose affinity beads (Pharmacia).
Fragmentation experiments
The Fragmentation experiments were performed using an immersion sonotrod oscillating at 40 kHz. The size distributions of polyQ fibrils were monitored before and after sonication by dynamic light scattering (DLS, Wyatt).
Kinetic experiments
All polymerization experiments were performed at 33°C. Aggregation was initiated by thrombin addition (0.5 unit/µM of GST-PolyQ41) leading to the release of PolyQ41 peptide from GST. The aggregation was monitored either by Thioflavine T (Tht) (100  M) in a 96-well plate fluorescence spectrometer or by a homemade multiwavelength static light scattering/fluorescence system (SLS).
M) in a 96-well plate fluorescence spectrometer or by a homemade multiwavelength static light scattering/fluorescence system (SLS).
Supporting Information
Parameter estimation considering each curve separately. Time evolution of PolyQ41 polymerized mass for an initial PolyQGST concentration equal to 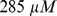 . The experimental results are plotted in dotted line and the best-fit curve in solide line.
. The experimental results are plotted in dotted line and the best-fit curve in solide line. 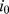 is set to 3. Best-fit parameters are
is set to 3. Best-fit parameters are 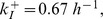
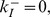
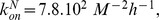
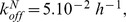

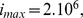
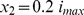 .
.
(TIF)
Parameter estimation for Experimental Set 1 when 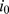 is set to 3. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to
is set to 3. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to 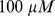 (A),
(A), 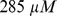 (B),
(B), 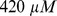 (C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in
(C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in 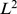 adimensioned norm was equal to 40% and the optimal parameters are very close to those of Figure 1.
adimensioned norm was equal to 40% and the optimal parameters are very close to those of Figure 1.
(TIF)
Parameter estimation for Experimental Set 1 when 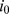 is set to 1. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to
is set to 1. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to 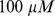 (A),
(A), 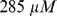 (B),
(B), 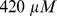 (C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in in
(C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in in 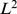 adimensioned norm was equal to 11%. The best-fit parameters are
adimensioned norm was equal to 11%. The best-fit parameters are 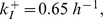
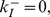
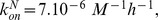
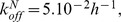
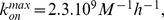

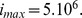
(TIF)
Left: Size distribution of the fragmentation rate for an aggregation of size 20, following a uniform distribution (black) or a mechanical-based distribution (red) of fragmentation. Right: Simulated normalized reaction progress curves of amyloid formation for a uniform distribution (black) and a mechanical-based distribution (red) of fragmentation. See below for the numerical values.
(TIF)
Examples of simulated size distribution of the aggregates for a uniform distribution (black) and a mechanical-based distribution (red) of fragmentation. See above for the numerical values.
(TIF)
Model derivation from ODE to PDE.
(PDF)
Application to PolyQ41 polymerization.
(PDF)
Effect of the fragmentation distribution on the kinetics of the Xue et al. model [1] .
(PDF)
Funding Statement
The work was partially financed by the French Agence Nationale de la Recherche, ANR grant 09-BLAN-0218-01. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. No additional external funding was received for this study.
References
- 1. Shastry BS (2003) Neurodegenerative disorders of protein aggregation. Neurochemistry International 43: 1–7. [DOI] [PubMed] [Google Scholar]
- 2. Ross C, Poirier M (2004) Protein aggregation and neurodegenerative disease. Nature Medicine 10(Suppl): S10–S17. [DOI] [PubMed] [Google Scholar]
- 3. Wasmer C, Lange A, Van Melckebeke H, Siemer AB, Riek R, et al. (2008) Amyloidfibrils of the het-s(218–289) prion form a beta solenoid with a triangular hydrophobic core. Science 319: 1523–1526. [DOI] [PubMed] [Google Scholar]
- 4.Oosawa F, Asakura S (1975) Thermodynamics of the polymerization of protein. Waltham, MA: Academic Press.
- 5.Dicko C, Kenney J, Vollrath F (2006) Fibrous Proteins: Amyloids, Prions and Beta- proteins, volume 73. Amsterdam: Elsevier. 17–53.
- 6. Bishop M, Ferrone F (1984) Kinetics of nucleation-controlled polymerization. a perturbation treatment for use with a secondary pathway. Biophysical Journal 46: 631–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Knowles TPJ, Waudby CA, Devlin GL, Cohen SIA, Aguzzi A, et al. (2009) An Analytical Solution to the Kinetics of Breakable Filament Assembly. Science 326: 1533–1537. [DOI] [PubMed] [Google Scholar]
- 8. Xue WF, Homans SW, Radford SE (2008) Systematic analysis of nucleation-dependent polymerization reveals new insights into the mechanism of amyloid self-assembly. PNAS 105: 8926–8931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Masel J, Jansen V, Nowak M (1999) Quantifying the kinetic parameters of prion replication. Biophysical Chemistry 77: 139–152. [DOI] [PubMed] [Google Scholar]
- 10. Doumic M, Goudon T, Lepoutre T (2009) Scaling limit of a discrete prion dynamics model. Communications in Mathematical Sciences 7: 839–865. [Google Scholar]
- 11. Collet JF, Goudon T, Poupaud F, Vasseur A (2002) The Becker–Döring system and its Lifshitz–Slyozov limit. SIAM J on Appl Math 62: 1488–1500. [Google Scholar]
- 12. Xue WF, Homans SW, Radford SE (2009) Amyloid fibril length distribution quantified by atomic force microscopy single-particle image analysis. Protein engineering design selection PEDS 22: 489–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Doumic M, Perthame B, Zubelli J (2009) Numerical solution of an inverse problem in sizestructured population dynamics. Inverse Problems 25: 045008. [Google Scholar]
- 14. Ball JM, Carr J (1990) The discrete coagulation-fragmentation equations: existence, uniqueness, and density conservation. J Statist Phys 61: 203–234. [Google Scholar]
- 15. Wulkow M (1996) The simulation of molecular weight distributions in polyreaction kinetics by discrete galerkin methods. Macromol Theory Simul 5: 396–416. [Google Scholar]
- 16. Desai A, Mitchison TJ (1997) Microtubule polymerization dynamics. Annual Review of Cell and Developmental Biology 13: 83–117. [DOI] [PubMed] [Google Scholar]
- 17. Laurençot P, Mischler S (2007) From the discrete to the continuous coagulation-fragmentation equations. Proceedings of the Royal Society of Edinburgh: Section A Mathematics 132: 1219–1248. [Google Scholar]
- 18. Gabriel P, Tine LM (2010) High-order WENO scheme for polymerization-type equations. ESAIM Proc 30: 54–70. [Google Scholar]
- 19. Doumic M, Maia P, Zubelli J (2010) On the calibration of a size-structured population model from experimental data. Acta Biotheoretica 58(4): 405–413. [DOI] [PubMed] [Google Scholar]
- 20. Banks H, Sutton K, Thompson W, Bocharov G, Roosec D, et al. (2010) Estimation of cell proliferation dynamics using cfse data. Bull of Math Biol 73(1): 116–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Calvez V, Lenuzza V, Oelz D, Deslys JP, Laurent P, et al. (2009) Size distribution dependence of prion aggregates infectivity. Math Biosci 1: 88–99. [DOI] [PubMed] [Google Scholar]
- 22. Alvarez-Martinez MT, Fontes P, Zomosa-Signoret V, Arnaud JD, Hingant E, et al. (2011) Dynamics of polymerization shed light on the mechanisms that lead to multiple amyloid structures of the prion protein. Biochimica et Biophysica Acta - Proteins and Proteomics 1814: 1305–1317. [DOI] [PubMed] [Google Scholar]
- 23. Scherzinger E, Sittler A, Schweiger K, Heiser V, Lurz R, et al. (1999) Self-assembly of polyglutamine-containing huntingtin fragments into amyloid-like fibrils: implications for huntingtons disease pathology. Proceedings of the National Academy of Sciences of the United States of America 96: 4604–4609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Kar K, Jayaraman M, Sahoo B, Kodali R, Wetzel R (2011) Critical nucleus size for disease-related polyglutamine aggregation is repeat-length dependent. Nature Structural and Molecular Biology 18: 328–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Calvez V, Lenuzza N, Oelz D, Deslys JP, Laurent P, et al. (2009) Size distribution dependence of prion aggregates infectivity. Math Biosci 1: 88–99. [DOI] [PubMed] [Google Scholar]
- 26. Ackleh AS, Fitzpatrick BG (1997) Modeling aggregation and growth processes in an algal population model: analysis and computations. Journal of Mathematical Biology 35: 480–502. [Google Scholar]
- 27. Bortz D, Jackson T, Taylor K, Thompson A, Younger J (2008) Klebsiella pneumoniae occulation dynamics. Bulletin of Mathematical Biology 70: 745–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Bernacki JP, Murphy RM (2009) Model discrimination and mechanistic interpretation of kinetic data in protein aggregation studies. Biophysical Journal 96: 2871–2887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hansen N (2006) The CMA evolution strategy: a comparing review. In: Lozano J, Larranaga P, Inza I, Bengoetxea E, editors. Towards a New Evolutionary Computation, volume 192. New York: Springer. 75–102.
- 30. Masino L, Kelly G, Leonard K, Trottier Y, Pastore A (2002) Solution structure of polyglutamine tracts in gst-polyglutamine fusion proteins. FEBS Letters 513: 267–272. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Parameter estimation considering each curve separately. Time evolution of PolyQ41 polymerized mass for an initial PolyQGST concentration equal to 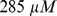 . The experimental results are plotted in dotted line and the best-fit curve in solide line.
. The experimental results are plotted in dotted line and the best-fit curve in solide line. 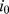 is set to 3. Best-fit parameters are
is set to 3. Best-fit parameters are 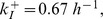
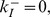
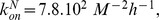
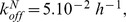

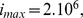
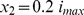 .
.
(TIF)
Parameter estimation for Experimental Set 1 when 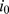 is set to 3. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to
is set to 3. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to 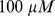 (A),
(A), 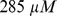 (B),
(B), 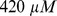 (C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in
(C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in 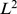 adimensioned norm was equal to 40% and the optimal parameters are very close to those of Figure 1.
adimensioned norm was equal to 40% and the optimal parameters are very close to those of Figure 1.
(TIF)
Parameter estimation for Experimental Set 1 when 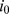 is set to 1. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to
is set to 1. Time evolution of the adimensioned PolyQ41 polymerized mass for an initial PolyQGST concentration equal to 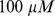 (A),
(A), 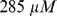 (B),
(B), 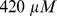 (C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in in
(C). Dotted curves represent experimental results. The solid curve is the best-fit. The global error in in 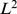 adimensioned norm was equal to 11%. The best-fit parameters are
adimensioned norm was equal to 11%. The best-fit parameters are 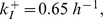
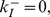
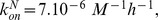
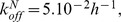
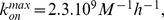

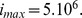
(TIF)
Left: Size distribution of the fragmentation rate for an aggregation of size 20, following a uniform distribution (black) or a mechanical-based distribution (red) of fragmentation. Right: Simulated normalized reaction progress curves of amyloid formation for a uniform distribution (black) and a mechanical-based distribution (red) of fragmentation. See below for the numerical values.
(TIF)
Examples of simulated size distribution of the aggregates for a uniform distribution (black) and a mechanical-based distribution (red) of fragmentation. See above for the numerical values.
(TIF)
Model derivation from ODE to PDE.
(PDF)
Application to PolyQ41 polymerization.
(PDF)
Effect of the fragmentation distribution on the kinetics of the Xue et al. model [1] .
(PDF)