Membrane mechanics as a probe of ion-channel gating mechanisms

Abstract

The details of conformational changes undergone by transmembrane ion channels in response to stimuli, such as electric fields and membrane tension, remain controversial. We approach this problem by considering how the conformational changes impose deformations in the lipid bilayer. We focus on the role of bilayer deformations in the context of voltage-gated channels because we hypothesize that such deformations are relevant in this case as well as for channels that are explicitly mechanosensitive. As a result of protein conformational changes, we predict that the lipid bilayer suffers deformations with a characteristic free-energy scale of 10k_BT. This free energy is comparable to the voltage-dependent part of the total gating energy, and we argue that these deformations could play an important role in the overall free-energy budget of gating. As a result, channel activity will depend upon mechanical membrane parameters such as tension and leaflet thickness. We further argue that the membrane deformation around any channel can be divided into three generic classes of deformation that exhibit different mechanosensitive properties. Finally, we provide the theoretical framework that relates conformational changes during gating to tension and leaflet thickness dependence in the critical gating voltage. This line of investigation suggests experiments that could discern the dominant deformation imposed upon the membrane as a result of channel gating, thus providing clues as to the channel deformation induced by the stimulus.

I. INTRODUCTION

The cell membrane is a richly inhabited landscape. Its undulating and dynamic terrain is peppered with proteins regulating what enters and leaves the cell. Various classes of membrane proteins interact with different environmental signals to determine when to allow molecular species such as ions to pass through the membrane. For example, voltage-gated ion channels are sensitive to millivolt-scale transmembrane electric potentials and respond to these voltages by undergoing a conformational change that allows selected ions to pass.

A growing body of work [1–5] suggests that the properties of the membrane influence the gating behavior of channels. In other words, the bilayer is not a passive bystander in membrane-protein function. This is demonstrated in the context of mechanosensitive channels whose function is acutely sensitive to properties of the surrounding bilayer such as lipid tail length, spontaneous curvature, and tension [2,6,7]. Previous theoretical work has focused on the observed connection between channel function and membrane elastic properties by examining membrane deformations at the protein-lipid interface [8–14].

Sensitivity to membrane mechanical properties is not unique to mechanosensitive channels. Voltage-gated ion channels also demonstrate sensitivity to applied membrane tension [3,4,15–17] and intrinsic elastic properties such as membrane stiffness, which has been shown to be correlated to deactivation of voltage-dependent sodium channels [7,18]. Therefore it is well established that the physical properties of the membrane influence channel gating, and in this work we exploit the channel-membrane interaction in the hope of learning about the structural changes of the channel itself. Our models are “coarse-grained” in the sense that the channel-membrane interactions are represented by different classes of membrane boundary conditions that replace the complex details of atomic-level motions.

An equivalent mindset that has proven useful for considering the connection between ion-channel function and membrane properties is the use of the so-called lateral pressure profile [19–21]. These profiles have been shown to be related to stability of conformational states of membrane-bound proteins. In our work, we consider the complementary elastic-deformation models, in which we assume that the important contributions from the lateral pressure are accounted for in their lowest order moments, in the form of membrane parameters such as bilayer and leaflet spontaneous curvature and tension.

A. Structure and function of voltage-gated ion channels

As an example of the type of problem this work addresses, we consider voltage-gated ion channels as a case study. Although the crystal structure of the well studied Shaker family K⁺ channel Kv1.2 is available in the open conformation [22], no voltage-gated channel structure has thus far been determined in both the closed and open conformations. The mechanism by which voltage-gated ion channels open and close in response to changing electric potentials remains uncertain; the goal of this paper is to explore the implications of different classes of structural models for membrane-protein interactions. The comparison is based on the channel’s sensitivity to bulk membrane mechanical properties.

All the channel mechanisms we explore contain two critical features: a pore region responsible for selectively blocking and passing ions across the membrane, and sensor regions that confer voltage sensitivity to the pore region. The voltage sensing motif is highly conserved across voltage-gated channels and consists of a bundle of four transmembrane helices [23]. At every third position on the fourth helix (named S4) there is a charged arginine or lysine residue that is responsible for voltage sensitivity [24–26]. In Shaker family channels, for example, these charged residues contribute 12 positive elementary charges per tetrameric channel [27], or three for each subunit. The conformational change to the conducting state decreases the electrostatic potential energy of these charged residues by a mechanism that remains uncertain. The charges either move through the electric potential or the channel manipulates and changes the electric field around them.

From the point of view of membrane deformations, the differences between the channel gating models are best described in terms of how the sensor regions move during opening and closing to modify the electrostatic environment of the charged residues. They may swing across the plane of the membrane as a paddle [28], or they may undergo a more subtle motion like a helical screw [29,30]. Some models do not rely upon the sensor domain actively transporting the charges across the membrane, but rather propose that its motion creates crevices that control how far the surrounding ionic solution penetrates into the protein, thus manipulating the electrostatic field itself. For a thorough description of various gating models and comparisons to experimental results, see Refs. [23,29,31].

The energy associated with changing the electrostatic environment of the residues is the voltage-dependent part of the gating energy, which we estimate using values for the Shaker family K+ channels. Assuming simple two-state Boltzmann statistics in which all four channel subunits occupy the same state at any given time, the probability that a channel is in the open state is given by 1

$$P_{\text{open}}=\frac{1}{1+e^{(\mathrm{\Delta }{G}_{\text{tot}}/k_{\text{B}}T)}},$$ (1)

where k_B is Boltzmann’s constant and T is temperature. In the absence of deactivation, the conductance of the membrane is proportional to P_open. We define ΔG_tot = G_open − G_closed, the total free energy difference between closed and open states. We can write ΔG_tot = ΔG_elec + ΔG_prot + ΔG_memb, where the terms represent the change in electrostatic gating energy, internal protein conformation free energy, and membrane-deformation free energy, respectively. We use a two-state model where “open” and “closed” describe the activation state of the pore. This is sufficient provided the conformations of the sensors and membrane are tightly correlated to that of the pore. Biological channels have many transition states which we assume have insignificant thermodynamic weight. Therefore the channel spends little time in those states, and we do not include them in our equilibrium model.

The energies calculated below also inform the kinetics of opening and closing. The free energy barriers for the kinetic transitions include membrane deformation energies of the transient states. The kinetics will therefore inherit membrane-parameter dependence through the membrane deformation energies. However, the many transition states may all have different transient membrane deformations, and extracting the membrane-parameter dependence of any one transition would be difficult. Equilibrium statistics, however, would not depend appreciably on these transient states.

We estimate the electrostatic energy using experimental results. The transmembrane voltage at which P_open = 0.5 is defined as V_0.5, where this half-activation voltage is typically negative and on the order of tens of millivolts. From Eq. (1), this voltage coincides with G_open − G_closed = 0, implying that at V_0.5 the electrostatic gating energy, ΔG_elec, balances the sum of membrane deformation and protein free energies: ΔG_elec = −(ΔG_memb + ΔG_prot). In other words, the internal energies of the system balance the energy supplied by the external electric field. Direct measurements of gating current give the effective charge per channel as Q = 12e_o [27], where e_o is one positive elementary charge (i.e., e_o = 1.6 × 10⁻¹⁹ C). We estimate an upper bound on the total electrostatic gating energy as ΔG_elec = −QV_0.5, assuming the charges move across the full potential. With V_0.5 = −35 mV as a typical transmembrane voltage at half activation for a potassium channel [27], one finds that ΔG_elec ≈ 16k_BT. Therefore an upper bound on the combined membrane and protein contribution to the gating free energy that balances the electrostatic contribution is −16k_BT. For comparison, measurements of conductance-voltage curves for wild-type Shaker channels have yielded electrostatic gating energies of 4 – 6k_BT per channel [32,33]. Kinetics measurements on potassium channels yield activation energies of about 20k_BT per channel [34]. Our calculated upper bound will serve as a benchmark against which we will compare membrane energetic contributions.

B. Conformation changes during gating

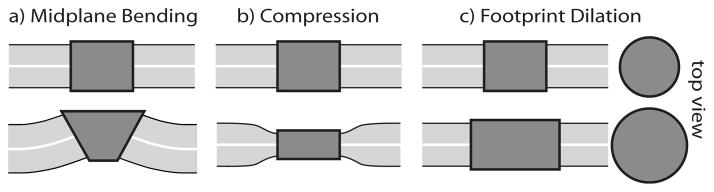
To focus on how the channel protein causes membrane deformation, we consider a coarse-grained model in which the protein is an axially symmetric shape that dictates the lipid-protein interface and creates deformations in the membrane. As the channel switches between open and closed states the membrane deforms and relaxes. We consider three types of deformations, as described in Fig. 1. Any small membrane deformation can be expressed as a combination of the three types. The deformed membrane may be associated with either the open or closed channel, so we commit to neither case and investigate both possibilities.

FIG. 1.

Models of gating in terms of three types of deformation induced in the membrane. We discard all molecular details of the channel and focus solely on how it deforms the membrane. The types of deformation are (a) bending of the midplane; (b) normal compression or stretching of the bilayer; (c) enlarging or shrinking of the channel areal footprint (shown with top view). The two rows represent protein shapes associated with different conformations. The figure exaggerates the deformations and does not specifically associate deformations with either the closed or open conformation because in general, deformations could be induced by either.

A relaxed membrane, with no spontaneous curvature, lies flat when undisturbed. The first type of deformation, called midplane bending, bends the bilayer away from the relaxed planar configuration. This deformation is induced by an effective protein shape with sloped sides [Fig. 1(a)] [35]. Such a shape could arise from a noncylindrical protein structure, such as a truncated cone. The next type of deformation compresses or stretches the membrane leaflets from their equilibrium thickness. This is referred to as compression deformation and is induced by dictating a nonequilibrium bilayer thickness at the membrane-protein boundary [Fig. 1(b)]. A difference in hydrophobic thickness between protein and lipid bilayer, called hydrophobic mismatch, causes this type of deformation [11,36]. The last type of deformation accompanies changes in the cross-sectional area of the protein. As the channel opens and closes, its areal footprint in the membrane may change, thus yielding to or pulling against the mechanical tension in the lipid bilayer. We refer to this as footprint dilation [Fig. 1(c)]. These three scenarios make the implicit assumption that the membrane shape is enslaved to the protein conformation. Although not mandatory, it is clear that some amount of frustration accompanied by an energy cost will result from a mismatch between the protein conformation and the natural lipid order. Our assumptions frame the simplest way to investigate the effect of this frustration on the channel activity.

C. Modeling strategy

The effective protein shape is, in principle, related to the atomistic details of the protein. It is determined by the geometry of the protein boundary and the locations and orientations of the hydrophobic and hydrophilic residues. However, the atomistic detail of the protein in the closed state is one of the unresolved issues, and we therefore avoid those details. Instead, we focus exclusively on the membrane deformations outlined in Fig. 1 and ask (i) which deformation types contribute an energy that is relevant in the total free energy budget? and (ii) how does gating couple to membrane parameters? We will demonstrate that those parameters which can be tuned experimentally, such as mechanical bi-layer tension and thickness, can be used as tools to determine if there is a dominant mode of deformation during gating.

Such a coarse-grained approach to investigating lipid-protein interactions has clear advantages over atomistic approaches, such as simplicity, broad applicability to a wide range of systems, and the ability to classify proteins based upon a generic shape deformation. However, such an approach has natural limitations as well. Elastic theory may poorly describe membrane mechanics at short length scales, and in this analysis, we do not probe noncircularly symmetric deformations. Furthermore, we assume only one deformation type is significant. If multiple types exist and the energetic contributions are comparable, the deformations would be difficult to identify. This work is a starting point, and to obtain detailed descriptions of gating for specific proteins, it must be supplemented with other data from structural studies and simulations.

Thus far, we have proposed a simple model of the protein. In Sec. II we model the bilayer as a continuous elastic sheet and describe deformations in terms of functions giving the height and thickness of the bilayer. This formulation allows us to concentrate on estimating the energy while discarding the details of individual lipids and their interactions. Section II A discusses the energy functionals for the deformations. In Sec. III we utilize analytic methods to find the deformation profiles that minimize the energy functionals subject to the boundary conditions imposed by the protein shapes in each deformation type. We then use these results and membrane-parameter values from the literature to compute equilibrium energies. Section IV interprets these results in terms of membrane-parameter dependence in V_0.5, and makes predictions for a new set of experiments.

II. ELASTIC PROPERTIES OF MEMBRANES

Utilizing well-developed models of membrane elasticity, we find the deformation energies by treating the bilayer as a fluid elastic sheet [8,9,37,38]. The local shape of the membrane can be characterized by two unique functions, one describing the membrane thickness and one the midplane height or deviation from a flat reference plane. We assume the protein has axial symmetry and work in cylindrical coordinates where r is the distance from the center of the channel (Fig. 2). We also assume that the membrane deformations are sufficiently small, i.e., the derivatives in the midplane slope and compression are small, so that all energies can be expressed at their lowest (quadratic) order.

FIG. 2.

Definition of the variables that characterize midplane bending and compression deformations. (a) h(r) describes the deviation of the midplane from the flat reference plane as a function of r, the distance from the center of the pore. R is the radius of the channel, and changes during footprint dilations. θ is a coarse-grained representation of the angle formed by the midplane at the protein-lipid interface. (b) u(r) describes the compression of the bilayer and d_o is the reference thickness of a leaflet. The size of the deformations in this schematic have been exaggerated for clarity.

In midplane-bending deformations, h(r) is the deviation of the bilayer midplane from the flat reference plane. The protein shape fixes the slope of the membrane midplane at the membrane-protein interface. Therefore in our small-deformation approximation, the boundary condition is $\frac{\partial h}{\partial r}{|}_{\text{r}=\text{R}}=-tan(\theta )\simeq -\theta$, where R is the radius of the protein and θ is the angle formed by the midplane with the perpendicular at the protein-lipid interface. For compression deformations, u(r) is the compression of each leaflet from the reference thickness d_o, the equilibrium hydrophobic thickness at zero tension far from the protein [Fig. 2(b)]. Positive values of u indicate leaflet compression for which the leaflet is thinner than d_o, whereas negative values indicate leaflet extension, where the leaflet is thicker than d_o. In compression deformations, the protein fixes the thickness of the membrane along its edge, imposing the boundary condition u(R) = U_o. Footprint dilations are characterized by the protein radius R, which can vary between the open and closed states.

A. Elastic free energies for the three deformation types

Having characterized the deformation of the membrane in terms of boundary conditions induced by the protein and the shape functions h(r) and u(r), we write free energy functionals for the three deformation types. Each functional includes contributions from different free energy sources, which are illustrated schematically in Fig. 3. Deviations from the equilibrium area per lipid, lipid tilt (relative to the midplane), and leaflet thickness all cost free energy. In Sec. III we solve for the shape functions h(r) and u(r) that minimize the free energy.

FIG. 3.

Schematic representation of sources of deformation energy. (a) A bilayer in the undeformed state. (b) Elastic compression or stretch leads to an increase in free energy that is accompanied by a change in leaflet thickness from its equilibrium value. (c) Yielding to membrane tension decreases free energy. This is modeled as a loading force applied to the edge of the membrane by weights hanging over pulleys. As the protein increases in size, the weights lower, thereby decreasing the total energy. (d) Bending deformations in the membrane are caused by torques on the membrane.

Elastic moduli measured in bulk membranes may not accurately describe the small-scale deformations along the protein-lipid interface. When packed against a protein, individual lipids lose degrees of freedom and therefore the free energy of the lipids depend upon their proximity to the protein. There are various ways to model this effect in terms of membrane deformations. These include utilizing radially dependent elastic moduli [39], adding an additional line energy term along the protein [40,41], or fixing the interface angle produced between the protein and the lipids [11]. These techniques can be tuned to give similar behavior [39]. Given that in this work we are most interested in an estimate of the magnitude of the deformation energy and how the free energy scales with the parameters, we choose the last technique for its simplicity.

The first type of deformation, midplane bending, has energy contributions from bending the bilayer and from the addition of membrane area due to the bending. We write the free energy as

$$G_{\text{bend}}={\int }_{{\mathcal{M}}^{\prime }}{d}^2\underset{\text{bending}}{\underbrace{\mathbf{r}\frac{{\kappa }_{\text{b}}}{2}{(2C_{\text{mean}}-C_{\text{o}}^{\text{b}})}^2}}+\underset{\text{area}\text{change}}{\underbrace{\alpha \mathrm{\Delta }A}},$$ (2)

where the integral is over the deformed membrane surface , α is the applied bilayer tension, and ΔA is the total bilayer area change due to the deformation. We define the free energy of an undeformed membrane [i.e., h(r) = 0], with no spontaneous curvature, as zero. The first term represents energy of curvature, where κ_b is the elastic curvature modulus of the bilayer. The energy depends upon the difference between the mean curvature C_mean, and the spontaneous curvature of the bilayer, $C_{\text{o}}^{\text{b}}$. To simplify calculations and analysis, we assume that the two leaflets of the bilayer are compositionally similar in which case $C_{\text{o}}^{\text{b}}$ vanishes. Whereas this can be the case in pure artificial bilayers, biological systems and some artificial bilayers possess compositional asymmetry which leads to a nonzero $C_{\text{o}}^{\text{b}}$ [42,43]. The second term represents the work done against mechanical tension when the bilayer area is modified. The change in area, ΔA, originates from a sloped midplane which has more area than a flat membrane with the same projection. Tension in artificial lipid bilayers is controlled by factors such as a pressure difference across the bilayer, the geometry of the bilayer and the material interfaces along the bilayer boundary, whereas the membrane tension of cells is thought to be regulated [44]. We use a single tension that is constant across the bilayer, because to a good approximation a simple bilayer acts as a two dimensional fluid with no shear stresses. This approximation breaks down in more complex systems such as a crowded membrane with structures of varying mobility.

For small deformations without spontaneous curvature, Eq. (2) can be rewritten as

$$G_{\text{bend}}=\frac{1}{2}{\int }_{\mathcal{M}}{d}^2\mathbf{r}[{\kappa }_{\text{b}}{({\nabla }^{2}h(r))}^2+\alpha {(\nabla h(r))}^2],$$ (3)

where the integral is now over the flat reference plane .

Compression deformations involve additional energy contributions and the combined free energy for both leaflets (assuming small deformations) is

$$G_{\text{comp}}={\int }_{{\mathcal{M}}^{\prime }}{d}^2\mathbf{r}\left[\underset{\text{compression}}{\underbrace{{\kappa }_{\text{e}}{\left(\frac{u(r)}{d_{\text{o}}}\right)}^2}}-\underset{\text{area}}{\underbrace{\alpha \frac{u(r)}{d_{\text{o}}}}}+\underset{\text{bending}}{\underbrace{{\kappa }_{\text{c}}{[{\nabla }^{2}u(r)-C_{\text{o}}]}^2}}+{\kappa }_{\text{gr}}{(\nabla u(r))}^2\right].$$ (4)

The first term represents deviations from the equilibrium leaflet thickness where κ_e is the elastic stretch modulus per leaflet [8,11,14]. Energy contributions are quadratic in this compressive strain. Although κ_e is typically applied to in-plane membrane stretch, thickness variations cause variations in total area because lipid bilayers largely conserve volume [45,46]. Therefore a small deformation in thickness results in a fractional change in area, $\delta A\approx \frac{u}{d_{\text{o}}}$. This also couples with the external tension and yields the second term. The third term represents the energy of curvature in each leaflet, where C_o is the leaflet spontaneous curvature and κ_c is the leaflet bending modulus. The final term represents the free energy cost of imposing a gradient in u(r), which imposes a slight asymmetry in the shape of each individual lipid molecule and increases the lipid-solvent interfacial area. We estimate a lower bound for the modulus κ_gr as the interfacial surface tension (not to be confused with the applied bilayer tension α) between the hydrophilic solvent layer and the hydrophobic tails. For the purposes of our estimates, we set κ_gr to this lower bound (see Table I).

TABLE I.

Parameters for a reference bilayer used to provide estimates of the contributions to membrane deformation energy.

Symbol	Parameter	Value
R	open channel radius	5 nm	[55]
α	applied bilayer tension	0.3kBT/nm2	a
κb	bilayer bending modulus	22kBT	[52]b
κe	leaflet stretch modulus	30kBT/nm2	[52]
do	leaflet thickness at zero tension	1.5 nm	[52]
Uo	boundary compression at zero tension	0.15 nm	c
κgr	compression-mode gradient-term modulus	5kBT/nm2	[53]a
κc	compression-mode leaflet bending modulus	11kBT	a

^aSee text for further discussion.

^bExperimental values are for C18:0/1 (1-oleoyl-2-stearoyl-sn-glycero-3-phosphocholine).

^cAssumed 10% of thickness.

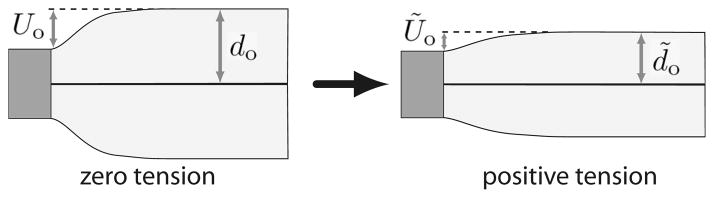
An applied tension thins the membrane according to ${\stackrel{\sim }{d}}_{\text{o}}=d_{\text{o}}(1-\frac{\alpha }{2{\kappa }_{\text{e}}})$. The thickness deformation is therefore shifted, and can be represented by rescaling u according to

$$\stackrel{\sim }{u}(r)=u(r)-d_{\text{o}}\frac{\alpha }{2{\kappa }_{\text{e}}}.$$ (5)

The thinning is accompanied by a rescaling of the compression at the channel-membrane interface from U_o to ${\stackrel{\sim }{U}}_{\text{o}}=U_{\text{o}}-d_{\text{o}}\frac{\alpha }{2{\kappa }_{\text{e}}}$. These effects are shown schematically in Fig. 4. We can rewrite the free energy functional in terms of the new compression variable ũ(r) as

FIG. 4.

Schematic demonstrating tension-induced thinning. Under tension, the bilayer (light gray region) thins, whereas the thickness along the protein (dark gray rectangle) remains unchanged. The membrane thickness decreases from d_o to d̃_o, and the boundary compression changes from U_o to Ũ_o. The effect is exaggerated in the figure for clarity.

$$G_{\text{comp}}[\stackrel{\sim }{u}(r)]={\int }_{\mathcal{M}}{d}^2\mathbf{r}\left[{\kappa }_{\text{e}}{\left(\frac{\stackrel{\sim }{u}(r)}{d_{\text{o}}}\right)}^2+{\kappa }_{\text{c}}{[{\nabla }^2\stackrel{\sim }{u}(r)-C_{\text{o}}]}^2+{\kappa }_{\text{gr}}{(\nabla \stackrel{\sim }{u}(r))}^2\right]+D,$$ (6)

where the constant D, representing the energy spent to attain the initial thickness d̃_o, is unimportant because we are only interested in changes between channel states at constant membrane tension. Note that we have eliminated the second term, thus simplifying the energy functional.

The free energy associated with footprint dilation is more straightforward. If the protein area increases, the membrane yields to the external tension α [as in Fig. 3(c)]. Therefore we can express the footprint dilation contribution to ΔG_tot in terms of the absolute change in channel area, ΔA_prot = A_open − A_closed,

$$\mathrm{\Delta }{G}_{\text{pore}}=-\underset{\text{area}}{\underbrace{\alpha \mathrm{\Delta }{A}_{\text{prot}}}}.$$ (7)

III. ENERGIES OF EQUILIBRIUM MEMBRANE PROFILES

In the previous section we presented the free energies associated with deformed membranes characterized by the shape functions h(r) and u(r). At equilibrium, the membrane will adopt a profile that minimizes the free energy and satisfies the boundary conditions imposed by the embedded protein. The different protein conformations impose different boundary conditions, and therefore each conformation is associated with a unique profile and free energy. In this section, we calculate the free energy costs for the three types of deformation and examine how these free energies might differ between the open and closed states.

The energy costs will depend upon the membrane parameters that appear in each functional. To compare the calculated deformation energies with phenomenological gating energies, we construct a reference membrane by choosing a value for each model parameter. Our reference values, given in Table I, are chosen to represent a “typical” phospholipid bilayer and the channel protein Kv1.2. The choice of a “typical” value, however, depends heavily upon the context. For example, the tension in a bilayer patch sealed against the inside of a pipette (as in a patch-clamp setup) could be very different from the tension in a living cell’s membrane. In the former, the tension is determined by external forces and the geometry of the glass-bilayer interface [6,47], and is on the order of 1k_BT/nm² (equivalent to 4 mN/m) [11]. In the latter, the tension is determined by a combination of cytoskeletal and exoskeletal structures, geometry, and osmotic pressure across the membrane [48,49]. Tensions in isolated plant membranes have been measured to be ≈0.03k_BT/nm² [50], whereas membrane tether force experiments give resting tensions in molluscan neurons an order of magnitude lower [51]. Vesicle micropipette aspiration techniques, in which suction is applied by a micropipette against a lipid vesicle, can tune and measure tensions of 3 × 10⁻⁴ − 3k_BT/nm². Note that the upper range is close to lytic tension for most lipid bilayers [52]. We choose 0.3k_BT/nm², or roughly 1.2 mN/m, as a reference tension for its applicability to experimental situations. As discussed above, we choose the interfacial surface tension between solvent and lipid as a lower estimate for κ_gr. We expect κ_c to be at most one-half the bilayer bending modulus κ_b. These reference values will provide estimates of the deformation energy. For further discussion of the values chosen, see the references cited in the table, and for an extended discussion of the range of these values, we direct the reader to [53,54].

A. Midplane bending

The free energy functional in Eq. (3) is minimized with respect to h(r), subject to the boundary conditions ∂h(r)/∂r|_r=R = −θ, and h(r → ∞) = 0. The minimization problem and the resultant free energies are solved in Appendix A and in [8,9,11,12,14]. The solutions for h(r) are Bessel functions with a tension dependent characteristic decay length of $\lambda =\sqrt{{\kappa }_{\text{b}}/\alpha }\approx 8\text{nm}$. The minimizing free energy is

$$G_{\text{bend}}={\kappa }_{\text{b}}\pi {\theta }^2\left(\frac{R}{\lambda }\right)\frac{{\mathcal{K}}_0(R/\lambda )}{{\mathcal{K}}_1(R/\lambda )},$$ (8)

where is the modified Bessel function of the second kind of order n.

We estimate the free-energy difference between open and closed states using the parameter values in Table I and assuming a range of small deformations at the protein boundary of 0.1<θ<0.5. The upper end of this range is consistent with structural models for the bacterial mechanosensitive channel MscS [56]. The free-energy difference between the deformed and undeformed (θ= 0) states is ΔG_bend = G(θ= 0) − G(θ) which adopts values ranging from −1 to −30k_BT for our reference membrane, a range comparable to our electrostatic benchmark energy.

B. Compression deformation

Next we turn to the case of compression deformations and minimize the energy given by Eq. (6) with respect to the compression profile ũ(r), subject to two boundary conditions. In addition to the condition ũ(R) = Ũ_o, we set $\frac{\partial \stackrel{\sim }{u}}{\partial r}{|}_{\text{r}=\text{R}}=0$. As discussed in Sec. II A, we fix the slope of the leaflets at the inclusion to model the packing of the lipids against the protein. This simplifies the problem and the mathematics while maintaining the essential parameter dependences and energy scales. In gramicidin, for example, the choice of zero slope predicts the correct channel lifetimes [38]. Furthermore, the zero-slope boundary condition yields a free energy that does not depend upon the spontaneous curvature, C_o [12,14].

As expected from the axial symmetry, the minimizing function ũ(r) is of the form ũ(r) = Ũ_o f(r), where f(r) is a combination of Bessel functions given in Appendix B, and Ũ_o is the compression at the boundary after tension rescaling. As shown in Appendix B (similar calculations are given in [8,11,14,38,57,58]), the minimizing free energy for both leaflets is given by $G_{\text{comp}}=\mathrm{\Omega }{\stackrel{\sim }{U}}_{\text{o}}^2$, where Ω ≈ 700k_BT/nm², assuming the parameters in Table I. Therefore the free energy G_comp inherits the tension dependence of Ũ_o explicit in Eq. (5) resulting in

$$G_{\text{comp}}=\mathrm{\Omega }{\left(U_{\text{o}}-d_{\text{o}}\frac{\alpha }{2{\kappa }_{\text{e}}}\right)}^2.$$ (9)

Note that a protein-lipid interface for which U_o = 0 yields a nonzero energy at nonzero tension. This result stems from the applied tension creating a deformation at the protein-lipid interface by thinning the bulk of the membrane. We write the difference in energy per leaflet between deformed and undeformed states as

$$\mathrm{\Delta }{G}_{\text{comp}}=G_{\text{comp}}(0)-G_{\text{comp}}(U_{\text{o}})=\mathrm{\Omega }\left(U_{\text{o}}{d}_{\text{o}}\frac{\alpha }{{\kappa }_{\text{e}}}-U_{\text{o}}^2\right),$$ (10)

where one state does not deform the membrane at zero tension and we have assumed that the radius of the channel is constant. We find that the free-energy difference between deformed and undeformed states is linear in bilayer tension α. Note that if U_o is positive, there exists a tension α for which the “deformed” state has zero free energy. The bilayer thins sufficiently so its thickness in the bulk matches that at the protein interface. We use the above equations to evaluate ΔG_comp for our reference membrane and find a typical value of roughly −14k_BT.

Given the previous discussion, the leaflet slope at the boundary u′(R) may be nonzero. In that case, there is an additional free energy term proportional to the leaflet bending modulus and the spontaneous curvature C_o [11,14]. Spontaneous curvatures of DOPE/DOPS mixtures in the H_|| hexagonal lattice phase have been measured to be between −0.3 and 0.07 nm⁻¹ depending on the mixture [59,60]. Given a small incident slope of u′(R) = 0.1, we make a free energy estimate of 4k_BT for a mixed composition leaflet of nominal C_o = 0.13 nm⁻¹. This term could account for the observed channel activity dependence on spontaneous curvature [7,18,57].

C. Footprint dilation

The free energy associated with the channel area is found by simply substituting the area into Eq. (7). Again, we are interested only in the free-energy difference between open and closed states, which is

$$\mathrm{\Delta }{G}_{\text{pore}}=\alpha \pi (R_{\text{closed}}^2-R^2).$$ (11)

R_closed is the unknown radius of the channel in the closed conformation. Assuming a small 5% decrease from the open state radius the corresponding free-energy change is −2.3k_BT. In general the radius could increase upon closing, giving a closed state with higher free energy.

In the analysis of midplane and thickness deformations, we assume the radius of the channel R is held constant. However, under footprint dilations the energetic contributions from midplane and thickness deformations increase with the circumference, even if those deformations are constant throughout the gating (i.e., U_o and θ are not state dependent). The deformations induce a line tension along the circumference resisting the dilation. This is precisely the mechanism studied in mechanosensitive channels such as MscL and MscS [2,56]. This implies that the footprint dilation mode inherits membrane-parameter dependence from state independent membrane deformations (those deformations that do not change as the channel opens and closes). Equation (11) must be modified to account for this additional energy.

Midplane deformations and compression deformations impose line tensions F_bend and F_comp, respectively. These are dependent upon both membrane parameters and channel radius. However, assuming the change in radius during gating is small, we neglect the radial dependence and approximate the line tensions as constant during dilation. Adding the additional terms to Eq. (11) gives a total energy shift between dilation states of

$$\mathrm{\Delta }{G}_{\text{pore}}=\alpha \pi (R_{\text{closed}}^2-R^2)+2\pi (R_{\text{closed}}-R)(F_{\text{bend}}+F_{\text{comp}}).$$ (12)

For the model membrane parameters and a change in radius of 5%, we estimate the total free energy change to now be −2.9k_BT. With the additional terms, ΔG_pore is no longer strictly linear in tension. It inherits the quadratic dependence of Eq. (9) and the square root dependence of Eq. (8). However, this effect is small, and the energy remains linear in α to a good approximation (see Fig. 5).

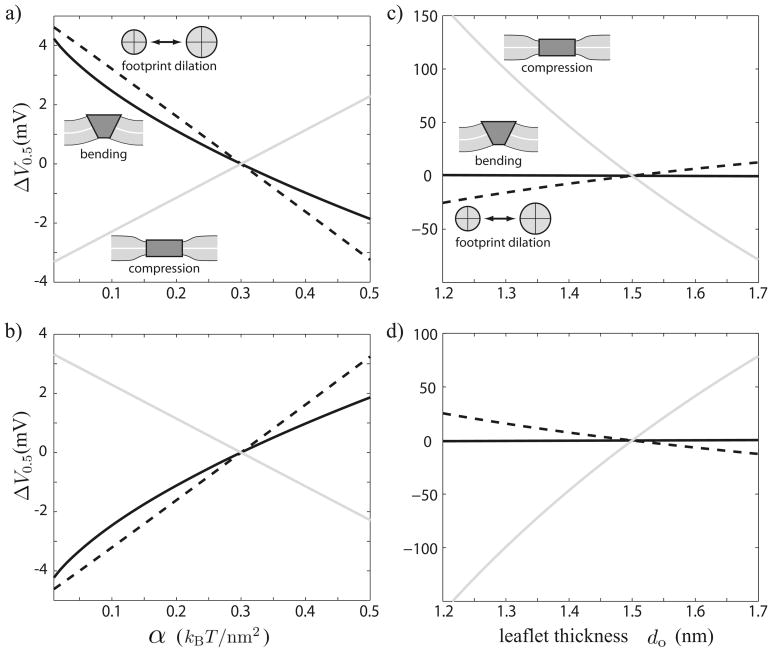
FIG. 5.

Expected shifts in half activation voltage as functions of tension (a), (b) and bilayer thickness (c), (d) for the three deformation types. ΔV_0.5 is expressed as a shift from V_0.5 at the reference tension and thickness in mV. The solid gray lines represent compression deformations, the dotted gray lines represent footprint dilations, and the solid black lines represent midplane-bending deformations. Plots (a) and (c) assume the closed channel state deforms the bilayer, whereas (b) and (d) assume the open channel deforms the bilayer. We present our results as though one type of deformation were dominant, though a physiological system may lack a dominant deformation type, existing as a mixture of different types.

IV. IMPLICATIONS FOR CHANNEL GATING

A. V_0.5 is a function of membrane energy

Electrophysiological experiments performed on voltage-gated ion channels typically measure the transmembrane current as a function of transmembrane voltage, and thus measure the conductivity of the composite membrane-protein system. If the channels are sufficiently dilute in the membrane, we ignore any possible cooperativity or frustration between channels and use the two-state Boltzmann statistics of Eq. (1).

In the preceding section, we showed that our benchmark gating energy of 16k_BT is comparable to the magnitude of the membrane deformation energies alone. Therefore the sample membrane deformations considered (≈10% change in area or hydrophobic mismatch, or θ ≈ 0.3) are energetically relevant when compared to electrostatic and protein conformation contributions. Therefore the voltage at half activation, V_0.5 ∝ (ΔG_memb + ΔG_prot), is sensitive to the membrane deformation energy. We can probe the sensitivity by measuring a shift in V_0.5 in response to a shift in applied tension,

$$\mathrm{\Delta }{V}_{0.5}({\alpha }_0,{\alpha }_1)=V_{0.5}({\alpha }_1)-V_{0.5}({\alpha }_0)=\frac{1}{Q}[\mathrm{\Delta }{G}_{\text{memb}}({\alpha }_0)-\mathrm{\Delta }{G}_{\text{memb}}({\alpha }_1)],$$ (13)

where α₀ and α₁ are experimentally determined initial and shifted values of membrane tension, respectively.

B. Membrane parameters are probes of the relevant deformations

In Sec. III we showed that membrane energy varies with bilayer tension differently for different deformation types. Above, we argue that V_0.5 is sensitive to membrane tension. Experiments can probe this dependence to distinguish which deformation types of the three may be dominant during gating. Figures 5(a) and 5(b) give expected shifts in V_0.5 as a function of applied membrane tension. To generate these plots, we use reference-membrane parameters and the analytic solutions of Sec. III. The upper plot a assumes closed channels deform the membrane and open channels leave the membrane undisturbed, whereas the lower plot b assumes the converse.

Experiments such as those described in [15–17] have demonstrated tension dependence in peak current by inducing pressure across the membrane. The results suggest that increasing the stretch of the membrane, and therefore the tension, increases the open channel probability. These papers explore stretch dependence in activation and deactivation kinetics, which, as discussed above, could involve membrane deformation. Unfortunately, the current literature does not yield quantitative measurements of tension, so establishing accurate relationships between tension and V_0.5 is not possible with available data. Furthermore, the analysis we suggest requires channel conductivity without the interference of deactivation, as can be derived from time traces of the current [17]. To calculate tension from the measured pressure, the patch clamp technique utilized in the experiments [15–17] must be combined with measurements of the geometry of the membrane and the membrane-pipette interface [2,61–63]. Unfortunately, as noted in [17], visualization of the interface is very difficult given physical limitations on the pipette and hardware.

Nevertheless, using a comparison between observed rupture pressures on the order of 100 mmHg and rupture tensions of about 4k_BT/nm² [64], the study by Morris and Juranka demonstrates that tensions on the order of 0.4k_BT/nm² are consistent with shifts in V_0.5 of 2 – 3 mV in voltage-gated sodium channels. These measurements are smaller than the voltage shifts calculated for our model membrane system (see Fig. 5), and perhaps correspond to smaller deformations.

The above discussion centers on tension dependence in the gating free energy. The energy also depends upon material membrane parameters, such as leaflet thickness and bending modulus. These parameters are not independent but rather interrelated. For example, the ratio of bending modulus to stretch modulus is observed to vary quadratically with leaflet thickness [52]. Therefore, in addition to influencing compression deformations, variations in leaflet thickness influence midplane-bending deformations via k_b [14] as well as footprint dilations via F_bend and F_comp. Over a range of hydrophobic thickness from 1.2 to 1.7 nm, Rawicz and coauthors find that κ_e changes by less than 10% whereas κ_b changes by over 100%. We ignore changes in κ_e and let the bending modulus scale as ${\kappa }_{\text{b}}^{\prime }={\kappa }_{\text{b}}{(d_o^{\prime }/d_o)}^2$ where the prime indicates the value for modified thickness (the compression-mode leaflet bending modulus κ_c scales identically). In this way we calculate expected critical voltage shifts as a function of bilayer thickness for each deformation type, and plot them in Figs. 5(c) and 5(d).

V. CONCLUSIONS AND OUTLOOK

We have argued that the lipid membrane is not a passive bystander in the functioning of ion channels. The membrane envelopes the channel, and as such, is intimately coupled to conformational changes of the channel protein. In the case of voltage-gated ion channels, the role and location of the S4 helix in the protein structure and evidence that the helix moves during gating [65] implies protein motion at the protein-lipid interface. It follows that the conformation change during opening must induce local deformations in the lipid membrane. To change conformation, the channel must pay the energetic cost of bending and compressing the bi-layer.

Our estimates above place the cost of membrane deformations on the order of 10k_BT for the representative deformations, in agreement with other theoretical estimates [19–21]. This is comparable to experimental estimates of total energies that drive the gating. As a result, we claim that the energetics of membrane deformations should not be ignored. Furthermore, the membrane’s influence upon gating can be exploited to learn about the channel conformational change. Varying the applied bilayer tension and leaflet thickness modifies gating energetics which are observable through open channel statistics. This suggests a class of experiments in which the half activation voltage is measured as a function of those membrane parameters:

1. The model predicts a systematic shift in half activation voltage with applied tension. A square-root dependence indicates midplane deformation is dominant, whereas a linear shift indicates footprint dilation or bilayer compression is dominant. The sign of the slope indicates whether the open or closed conformation deforms the membrane.

2. The model also predicts a shift in half activation voltage with lipid tail length. Supplemented with the understanding of how the elastic moduli depend upon the lipid tail length, the model distinguishes among deformation types based upon how the half activation voltage shifts with tail length. Bending deformations are least sensitive to leaflet thickness, whereas compression deformations are very sensitive and exhibit the most nonlinear dependence.

This line of investigation could therefore place constraints on how the protein conformation changes during gating. By tuning membrane parameters, we can exploit the information stored in the membrane’s deformation and probe the protein itself.

APPENDIX A: MIDPLANE-BENDING EQUILIBRIUM SOLUTIONS

To find the equilibrium solutions for the bilayer profile under midplane-bending deformations, we begin by writing the bending energy functional of Eq. (3) in dimensionless units. By factoring out the length scale $\lambda =\sqrt{\frac{{\kappa }_{\text{b}}}{\alpha }}$ and the energy scale κ_b we obtain

$$\overline{g}[\overline{h}(\mathbf{s})]=\frac{1}{2}{\int }_{\mathcal{M}}{d}^2\mathbf{s}[{({\nabla }^2\overline{h})}^2+{(\nabla \overline{h})}^2],$$ (A1)

where ḡ = g/b, h̄ = h/λ, and s= r/λ. The Euler-Lagrange equation is 0 = ∇⁴h̄ − ∇²h̄, where ${\nabla }^2\equiv \frac{{\partial }^2}{\partial {\overline{x}}^2}+\frac{{\partial }^2}{\partial {\overline{y}}^2}$ [11]. With cylindrical symmetry and the boundary conditions applied, the solutions that are finite at large distances satisfy

$${\nabla }^2{\mathcal{K}}_0(k_{\pm }s)=k^2{\mathcal{K}}_0(k_{\pm }s),$$ (A2)

where is the modified Bessel function of the second kind. Solving for k yields k_±= {1, 0} and the height function is of the form

$$\overline{h}(s)=A_{+}{\mathcal{K}}_0(s)+A_{-}{\mathcal{K}}_0(0).$$ (A3)

Demanding the height function is finite at the protein interface fixes A₋ = 0, whereas the imposed slope condition at the interface sets the other constant via $\frac{\partial \overline{h}(s)}{\partial s}{|}_{s=\overline{R}}=-\theta =-A_{+}{\mathcal{K}}_1(\overline{R})$, where R̄ = R/λ. The equilibrium height function that satisfies all boundary conditions is

$$\overline{h}(s)=\frac{\theta }{{\mathcal{K}}_1(\overline{R})}{\mathcal{K}}_0(s).$$ (A4)

We now calculate the deformation energy given our height profile Eq. (A4) by evaluating Eq. (A1) using partial integration. The Laplacian squared term is evaluated as

$$\begin{array}{l}\int d^2\mathbf{s}{\nabla }^{2}h{\nabla }^{2}h=\int d^2\mathbf{s}{\nabla }^{4}h-\oint ({\nabla }^{2}h\nabla h-h{\nabla }^{3}h)·d\widehat{\mathbf{n}}\\ =\int d^2\mathbf{s}{\nabla }^{4}h,\end{array}$$ (A5)

where we evaluate the boundary term using the Euler-Lagrange relationship. Likewise, the gradient squared term is

$$\int d^2\mathbf{s}\nabla h\nabla h=-\int d^2\mathbf{s}{\nabla }^{2}h+\oint h\nabla h·d\widehat{\mathbf{n}}.$$ (A6)

Combining the two results yields

$$\overline{g}=\frac{1}{2}\int d^2\mathbf{s}({\nabla }^4\overline{h}-{\nabla }^2\overline{h})+\frac{1}{2}\oint d\widehat{\mathbf{n}}·\overline{h}\nabla \overline{h},$$ (A7)

where we have adopted our scaled coordinates and again utilized the Euler-Lagrange relation to remove the first term. The remaining boundary integral is easily solved using the height profile of Eq. (A4) and evaluating along the inclusion boundary. After restoring units, the energy is

$$g={\kappa }_{\text{b}}\pi {\theta }^2\left(\frac{R}{\lambda }\right)\frac{{\mathcal{K}}_0(R/\lambda )}{{\mathcal{K}}_1(R/\lambda )}.$$ (A8)

APPENDIX B: COMPRESSION-DEFORMATION EQUILIBRIUM SOLUTIONS

We begin by writing the Hamiltonian for compression deformations, Eq. (6), in a dimensionless form by factoring out a length scale $\varsigma =\sqrt{\frac{{\kappa }_{\text{c}}}{{\kappa }_{\text{gr}}}}$ and energy κ_c:

$$\overline{g}[\overline{u}(s)]={\int }_0^{\infty }{d}^2\mathbf{s}[{({\nabla }^2\overline{u})}^2-2{\nabla }^2\overline{u}{\overline{C}}_o+{(\nabla \overline{u})}^2+\beta {\overline{u}}^2],$$ (B1)

where the overbars indicate scaling out ς or κ_c, s = r/ς and $\beta \equiv \frac{{\kappa }_{\text{e}}{\kappa }_{\text{c}}}{{\kappa }_{\text{gr}}^2{d}_{\text{o}}^2}$. Since C_o is independent of the conformation of the channel, we have removed the $C_o^2$ term. The Euler-Lagrange equation, 0 = ∇⁴ū − ∇²ū + βū, yields solutions of the form

$$\overline{u}(s)=A_{+}{\mathcal{K}}_0({\lambda }_{+}s)+A_{-}{\mathcal{K}}_0({\lambda }_{-}s),$$ (B2)

where

$${\lambda }_{+}\equiv \sqrt{\frac{1\pm \sqrt{1-4\beta }}{2}}.$$ (B3)

Complex values of λ_± are allowed because the physical quantity ū(s) remains real. By restoring units to ū(s) we uncover a second length scale, $\gamma ={(\frac{{\kappa }_{\text{c}}{d}_{\text{o}}^2}{{\kappa }_{\text{e}}})}^{1/4}$. The physical decay length of the Bessel functions is a combination of these two length scales. We now impose the boundary conditions ū(s)|_S = Ū_o and $\frac{\partial \overline{u}}{\partial s}{|}_S=0$, where S = R/ς. We solve for A_±:

$$A_{\pm }=\frac{{\overline{U}}_o{\mathcal{K}}_1({\lambda }_{\mp }S){\lambda }_{\mp }}{{\mathcal{K}}_0({\lambda }_{\mp }S){\mathcal{K}}_1({\lambda }_{\mp }S){\lambda }_{\mp }-{\mathcal{K}}_0({\lambda }_{\mp }S){\mathcal{K}}_1({\lambda }_{\mp }S){\lambda }_{\mp }}.$$ (B4)

This solution applied to Eq. (B1) gives the equilibrium energy. Alternatively, we can utilize the same trick as with midplane deformations where partial integration upon the free energy functional results in a boundary integral along the inclusion. The unitless energy turns out to be

$$\overline{g}=\oint ({\nabla }^2\overline{u}\nabla \overline{u}-\overline{u}{\nabla }^3\overline{u}+\overline{u}\nabla \overline{u}-2C_o\nabla \overline{u})·d\widehat{\mathbf{n}},$$ (B5)

where assuming cylindrical symmetry and the boundary condition ∇ū|_S = 0 yields

$$\overline{g}=-2\pi S(-\overline{u}{\nabla }^3\overline{u})·-d\widehat{\mathbf{s}}{|}_{s=S}.$$ (B6)

This expands to

$$\overline{g}={2\pi S\overline{u}\left({\partial }_s^3\overline{u}+\frac{1}{s}{\partial }_s^2\overline{u}-\frac{1}{s^2}{\partial }_s\overline{u}\right)|}_{s=S},$$ (B7)

which we evaluate along the inclusion of radius R = ςS and boundary deformation $\varsigma {\overline{U}}_o={\stackrel{\sim }{U}}_{\text{o}}=U_{\text{o}}-d_{\text{o}}\frac{\alpha }{2{\kappa }_e}$. We then restore the energy g = ḡκ_c.