Non-polarizing broadband multilayer reflectors in fish

Abstract

Dielectric multilayer reflectors that are non-polarizing are an important class of optical device and have numerous applications within optical fibres [1], dielectric waveguides [2] and LEDs [3]. Here we report analyses of a biological non-polarizing optical mechanism found in the broadband guanine-cytoplasm “silver” multilayer reflectors of three species of fish. Present in the fish stratum argenteum are two populations of birefringent guanine crystal, each with their optic axes either parallel to the long axis of the crystal or perpendicular to the plane of the crystal. This arrangement neutralizes the polarization of reflection due the different interfacial Brewster’s angles of each population. The fish reflective mechanism is distinct from existing non-polarizing mirror designs [4, 5, 6, 7] with the important feature that there is no refractive index contrast between the low index layers in the reflector and the external environment. It is a mechanism that could be readily manufactured and exploited in synthetic optical devices.

Multilayer reflectors occur extensively in nature. They are used by animals to create iridescent signals for communication [8], crypsis for camouflage [9] and as reflectors to increase low light sensitivity in many eyes [10]. Silvery reflections from fish are produced by multilayer “stacks” of high refractive index guanine crystals separated by low refractive index cytoplasm gaps [11]. Many fish have two separate forms of these stacks: a) those in the stratum argenteum, a sub-dermal layer of the skin, and b) those that lie on the inner surface of the scales [12, 13]. These reflecting structures provide cryptic camouflage in the near-axially symmetric underwater light field, with reflections matching the intensity of rays from behind [13]. For optimal concealment, the reflecting structures must produce both spectrally broadband and high percentage, nonpolarizing reflectivity over all angles of incidence. Non-polarizing reflectors are advantageous as they are not subject to a reduction in overall reflectivity as angles of incidence approach Brewster’s angle. Multilayer mechanisms capable of producing broadband reflectivity in fish are well understood [14, 15], with the random layer thickness variation in the sub-dermis reported by McKenzie et al.[15] providing the biological analogue of disordered synthetic dielectric mirrors [16]. Past experimental studies have suggested that reflections from fish are of low polarization [17, 18]. However, this property of reflection has never been explained and all existing optical models [10, 15, 19, 20] predict full Fresnel polarization at Brewster’s angle.

Initially, we used reflectance spectrophotometry to characterize the polarization dependence of the reflectivity from two species of fish, Clupea harengus (Atlantic Herring) and Sardina pilchardus (European Sardine), (refer to Methods for details of experimental set-up). We measured the specular component of reflectivity for light polarized perpendicular and parallel to the plane of incidence, R_σ(λ, θ ) and R_π(λ, θ), and calculated the degree of polarization

$$d(\lambda ,\theta )=\left(\frac{R_{\sigma }-R_{\pi }}{R_{\sigma }+R_{\pi }}\right)$$ 1

for reflected light. In accordance with previous studies [17, 18] the polarization by reflection is very different to a Fresnel dielectric with low polarization across all wavelengths and at all angles of incidence. Measurements of d(θ) at λ=600 nm about the azimuthal (dorsoventral) and latitudinal (rostrocaudal) axes of illumination for C. harengus are shown in Fig. 1(a). We estimated the percentage error of the experimental arrangement for an ideal flat sample to be ~ 1% by measuring d(θ) for a glass microscope slide and comparing our measured values to theoretical values for double image Fresnel equations [21] (Fig. 1(a)). Both fish data sets have maximum polarization values ~ 0.35 at θ = 60° and suggest that the polarization behaviour is near-independent of axis of rotation. At all angles of incidence the reflection spectra are broad bandwidth with no gaps in the high reflectance region (Fig. 1(b) and Fig. 1(c)). Measurements from samples of S. pilchardus exhibit very similar generic reflection and polarization behaviour (refer to supplementary material, Fig. S1).

Figure 1. Optical reflectivity measurements.

a Measurements of the degree of polarization, d(θ), at λ = 600 nm for azimuthal (dorsoventral; red cardinal crosses) and latitudinal angles of illumination (rostrocaudal; blue oblique crosses) from Clupea harengus. The black solid circles and black line represent a positive control and are experimental data and a theoretical curve for a double surface Fresnel reflection (front and back reflection) from a glass microscope slide with refractive index 1.50, in air. b, c Reflection and degree of polarization spectra at (b) 30° and (c) 60°. In (b) and (c) the black solid line is R_σ(λ), the black dashed line is R_π(λ) and the green solid line is d(λ).

All previous multilayer models of fish reflectors [10, 15, 19, 20], assume the crystals behave as optically isotropic layers with refractive index ~1.83. These crystals, however, are actually highly birefringent, being a mixture of pure guanine and hypoxanthine which have refractive indices of (1.93, 1.91, 1.47) and (1.85, 1.78, 1.42) [22]. The guanine-hypoxanthine ratio varies between fish, with the crystals found in C. harengus reported to have refractive index values of (1.85, 1.81, 1.46) [13, 22]. It has conventionally been thought that the optic axes of the crystals all have a common orientation in the multilayer, with the low refractive index value aligned with the short axis of the crystal and the direction of stacking (by convention, the z axis) [13]. However, it has recently been demonstrated that the relative axial growth rate of crystals in fish are subject to biological control mechanisms, with some crystals being very different to the predicted lowest energy state [23]. This motivated us to reexamine the optical properties of individual guanine crystals from the stratum argenteum and the inner surface of teleost scales. We used a digital holographic transmission microscope to measure the ratio of the refractive indices along the two planar crystal axes (refer to Methods for a description of this technique).

In three species of clupeid teleost we identified two distinct populations of guanine crystals that are morphologically identical but have different optical properties. In the stratum argenteum there exists both Type 1 crystals and Type 2 crystals with planar refractive index ratios of ~ 1.025 and ~ 1.250 respectively (Fig. 2 and supplemental information Fig. S2). Under the scales, there exists only Type 1 crystals, but these crystals have a different lower aspect ratio morphology compared with the crystals from the argenteum. These differences in shape have been reported before by Denton and Nicol [12] and Denton [13]. It is also worth noting here that whilst the opercula (gill covers) of both fish species have no scales, the skin contains both physical shapes of Type 1 crystals in addition to Type 2 crystals. In agreement with the literature [13, 22], our measurements of Type 1 crystals imply that the low refractive index value is aligned with the z-axis. The measurements for Type 2 crystals are very different to the optical properties reported to date and imply that the low refractive index value is orientated in the (x, y) plane.

Figure 2. Refractive index ratios of guanine crystals.

Measurements (mean ± s.d.) of the planar refractive index ratios in Type 1 and Type 2 guanine crystals in Clupea harengus, Sardina pilchardus and Spratus spratus. The multilayers under the scales of C. harengus contained only Type 1 crystals.

We used the anisotropic 4×4 matrix technique [24, 25] to calculate the reflectivity of a guanine-cytoplasm multilayer that contains these two populations of crystals (details of the theory are provided in the Methods section). In this model, the weakly biaxial crystals were approximated as uniaxial birefringent planar layers with ordinary refractive index n_o = 1.83 and extraordinary refractive index n_e = 1.46. A schematic example of the modelled structure is given in Fig. 3(a) illustrating the two populations of guanine crystals and their associated refractive indices. Each crystal layer was randomly assigned a ‘population state’ with Type 1 crystals having mixing ratio f and Type 2 crystals having mixing ratio (1 – f). Refractive index vectors for each population are given by:

$${\mathrm{n}}_g=(n_o,n_o,n_e),$$ 2

$${\mathrm{n}}_g=(\sqrt[]{{\cos }^2\left(\varphi \right)n_o^2+{\sin }^2\left(\varphi \right)n_e^2},\sqrt[]{{\cos }^2\left(\varphi \right)n_e^2+{\sin }^2\left(\varphi \right)n_o^2},n_o),$$ 3

where is a uniformly distributed random variable on the interval [0, π]. n_o and n_e are the ordinary and extraordinary refractive indices respectively. The isotropic cytoplasm layers and the external environment (water) both have a refractive index 1.33 [19]. The broad bandwidth of our reflection spectra are best accounted for by assuming that the thicknesses for guanine and cytoplasm layers can be modelled as uniformly distributed random variables [15]. Our model used a thickness sampling interval of [55, 110] nm for the thickness of guanine crystals [14], with the bounds for cytoplasm layer thicknesses allowed to vary freely over physiologically plausible values [15]. The in (x,y) plane symmetry of the reflection spectra in Fig. 1(a) indicates rotational invariance of the macroscopic structure, therefore, we average over 500 multilayer structures to account for the variation at the microscopic scale (as modelled).

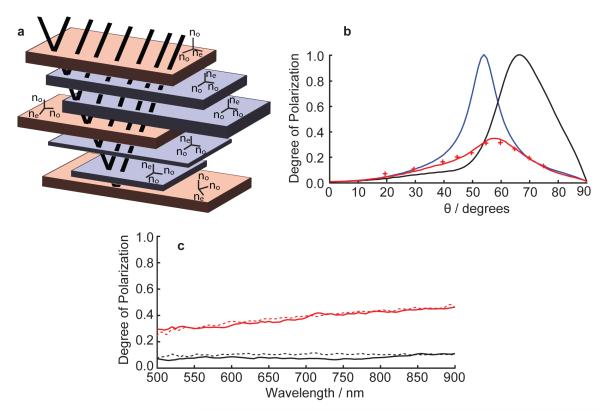
Figure 3. Optical structure, modelling and parametric fit to experimental data.

a Schematic diagram illustrating the multilayer model used and the two populations of guanine crystals: Type 1 crystals (purple) and Type 2 crystals (orange). The orientation of the principle refractive indices coordinate axes of each crystal layer are indicated. b Simulations of the degree of polarization, d(θ), at different angles of incidence (θ) and at λ = 600 nm for three classes of multilayer model, including a parametric fit to experimental data from Clupea harengus. The black line is for a multilayer of Type 1 crystals (f = 1), the blue line is for isotropic crystals (n_o = n_e = 1.83), the solid red line is a parametric best fit for a mixture of Type 1 and Type 2 crystals with f=0.75, and the red crosses are the mean of the azimuthal and latitudinal data from Fig. 1(a). Our model explained 95% of the variation in the data, assessed by the R² from linear regression. There was no systematic difference between model and data (mean pairwise difference and s.d. 0.0044 ± 0.0132, t = 0.7512, df = 9, p = 0.472). The best fit parameters are N=37 crystal layers in each multilayer structure, with the sampling intervals for guanine and cytoplasm thicknesses [55, 110] nm and [30, 300] nm respectively. c Simulated degree of polarization, d(λ), for the parametric best fit in Fig. 3(b) (solid black line θ = 30° and solid red line θ = 60°), and experimental d(λ) from C. harengus (dashed black line θ = 30° and dashed red line θ = 60°) as in Fig. 1(b) and 1(c).

Our optical model predicts that multilayers with only Type 1 crystals (f = 1) have a fully polarizing Brewster’s angle at 67° (black line in Fig. 3(b)). This polarization behaviour is anticipated by the anisotropic interfacial reflection coefficients for each individual layer [26], which have a Brewster’s angle, θ_B, given by the relation

$$\tan \left({\theta }_B\right)=\left(\frac{n_{g,z}}{n_c}\right)\sqrt[]{\left(\frac{n_c^2-n_{g,x}^2}{n_c^2-n_{g,z}^2}\right)},$$ 4

where the left subscripts (c, g) indicate cytoplasm or guanine and the right subscripts (x, z) indicate Cartesian components (Orfanidis, S. Electromagnetic waves and antennas. http://www.ece.rutgers.edu/~orfanidi/ewa/. Online book, accessed Sept 2012). This is standard Fresnel behaviour and similar to that which occurs if the crystals are assumed to be isotropic, in which case equation (4) reduces to $\text{tan}\left({\theta }_B\right)=\left(\frac{n_g}{n_c}\right)$ and the Brewster’s angle is at 53° (blue line in Fig. 3(b)). However, when there are two populations of crystal present in the multilayer, low-polarization reflections over all angles of incidence can occur. We applied a parametric grid search to the experimental data from C. harengus in Fig. 1(a), allowing for N, f and the sampling interval bounds upon the cytoplasm thickness to vary. We found f = 0.75, N = 37 and thickness bounds [30, 300] nm to give the best parametric fit. Our model explained 95% of the variation in the data, assessed by the R² from linear regression. There was no systematic difference between model and data (mean pairwise difference and s.d. 0.0044 ± 0.0132, t = 0.7512, df = 9, p = 0.472) (red solid in line in Fig. 3(b) and refer to supplementary material (Fig. S1) for a similar analysis of data from S. pilchardus). The values of N for the parametric fits for both fish are in excellent agreement with past histological surveys [14]. Figure 3(c) further shows the similar agreement between the experiment and modelled results for both θ = 30° (black lines) and θ = 60° (red lines) as a function of wavelength. The reason underlying this non-trivial polarization behaviour is the different interfacial Brewster’s angles between the isotropic layers and either the Type 1 crystals or the different orientations in the plane of the Type 2 crystals which can lie anywhere in the interval [33, 53]° (equation (4)). One further possible explanation for this polarization behaviour that has been considered is polarization mode mixing in the multilayer structure. With changes in polarization occurring due to the changing orientation of optic axes of the birefringent layers, a contribution might always exist perpendicular to the plane of incidence and therefore be reflected. However, we have both experimentally measured and theoretically calculated (using the best-fit parameters above) both R_πσ and R_σπ for C. harengus (see Fig. S3 in supplemental information). In both the experimental measurements and optical modelling, the contributions of these cross terms are extremely small and cannot account for the polarization response of the structure.

Clearly the real biological multilayer reflectors of C. harengus and S. pilchardus are weakly polarizing. However, by increasing the number of layers in the multilayer, the optical mechanism can produce true polarization-neutral reflections. This property is demonstrated in Fig. 4(a) which indicates a monotonic decrease in the degree of maximum polarization with increasing N, and Fig. 4(b) which shows a reflectance band for both σ and π polarizations approaching 100 percent reflectivity at θ = 60° (this is approximately the angle of highest polarization). Natural photonic structures are proving to be of inspiration for optical technologies [27], with the organisation of birefringent materials in animals leading to the fabrication of novel biomimetic devices [28, 29]. Common to all existing non-polarizing mirror designs is the employment of a refractive index contrast between the low-index layers in the reflector and the external environment (e.g. [4, 5, 6, 7]), that enables the reflector to be screened from angles of incidence where polarization occurs. The fish reflective mechanism places no such restriction, and is instead dependent upon having both birefringent layers with different interfacial Brewster’s angles and there being a high variation in the optical thickness of the layers. Highly birefringent polymers with similar refractive indices to the fish have already been used in multilayer mirror designs [26], although these studies do not discuss the production of non-polarized reflections through two different populations of birefringent layers. The polarization properties of a biomimetic design that replaces the two populations of crystals with two uniaxially birefringent populations of layers with refractive indices (1.83, 1.83, 1.33), (1.33, 1.33, 1.83) are illustrated in Fig. 4(c) and Fig. 4(d). This biomimetic design captures the essential physics of the fish reflective mechanism, but improves the efficiency of polarization neutralisation by maximising the disparity between the interfacial Brewster’s angles of the two populations (equation (4)). It is important to be clear that the mechanism of polarization-neutral reflections described here is radically different from that of photonic-bandgap based non-polarizing mirrors. Unlike existing non-polarizing reflectors, the biomimetic design permits the environmental media and the low index layers to be made from the same material, and would provide an advantage in applications where the thermal and mechanical properties of the reflector benefit from being constructed with the same material externally and within the structure.

Figure 4. A biologically inspired mechanism of polarization-neutral reflection.

Simulated degree of polarization, d(θ), at different angles of incidence (θ) and λ = 600 nm for N = 20, 40, 200, 400 crystal layers (red, black, blue and green solid lines respectively) and accompanying reflection and polarization spectra at 60° for (a,b) the fish reflective structure and (c,d) a biomimetic design with 2 uniaxial populations of layers with refractive indices given by (1.83, 1.83, 1.33) and (1.33, 1.33, 1.83). N=400 in (b) and N=200 in (c). The black solid line is R_σ(λ), the black dashed line is R_π(λ) and the green solid line is d(λ). In all plots the layer thicknesses are sampled from uniform distributions on the intervals [55, 110] nm for the birefringent layers and [30, 300] nm for the isotropic layers, with f = 0.75 and the (1.83, 1.83, 1.33) layers being defined as Type 1 in the biomimetic design.

In the context of an animal’s visual ecology, to perfectly background-match an axially symmetric light field over all angles of incidence, any vertical dielectric reflector must produce non-polarizing broadband reflections, as well as having high reflectivity. By producing a high degree of polarization neutrality for reflections over all angles of incidence, the mechanism discovered in these species of fish ensures a greater total reflected intensity that more closely matches the open water background light field. Whilst previous works have emphasised how the spectral properties of biological multilayer structures arise and the relationship that this has to biological function [14, 19], our study exposes the fact that, provided one of the constituent materials has high birefringence, polarization properties, as well as spectral properties, can play a role in their structural organisation. It is an intriguing possibility that the selection of polarization properties in the biological reflectors examined in this work are a direct adaptation to better intensity-match the pelagic light environment. It is worth adding that several aquatic animals including fish, cephalopods and crustaceans have polarization vision [30, 31]. In an axisymmetric light environment, a consequence of a non-polarizing mechanism of intensity-matching is that the reflector also matches the polarization of the background [32]. Finally, it is likely that birefringence is key to the optical properties of other animal multilayer reflectors. The optical properties of silver reflectors in certain cephalopods [33] and the polarizing guanine-cytoplasm structures in the tapeta of some spiders [34] both still require explanations.

Methods

Reflectance spectrophotometry

Thin areas of fish skin and underlying tissue ~ 3 mm in thickness and 30×30 mm in size were taken from the vertical lateral flank of each animal and mounted on a black perspex slide. Data were recorded about the azimuthal (dorsoventral) axis and latitudinal (caudorostral) axis, with the latitudinal angle of incidence at 90° when viewing the fish from the ventral direction and the azimuthal angle of incidence at 90° when viewing the fish its rostral end (0° being normal incidence to the tissue in both cases). The sample was placed in the centre of an optically clear, cylindrical, Perspex™ tank filled with water, with the incident and reflected beams locally perpendicular to the tank surface. An Ocean Optics DH2000 halogen lamp was used as an illuminant, with an Ocean Optics QE65000 spectrometer used as a photon detector over a range of angles from 20° to 75°. Light from the lamp was directed onto the fish skin via a fibre optic (Ocean Optics P600-2-UV/VIS), terminated with an Ocean Optics 74-UV lens (NA = 0.24), and reflected light was collected and directed to the spectrometer by an identical lens and fibre combination. The beam spot size was 5 mm diameter. The lenses were mounted to rotating arms, with the centre of rotation coincident and above the surface of the sample. Glan-Thompson achromatic polarizers were placed in the beam path before (all measurements) and after the sample (when measuring the four polarization mode combinations, R_ππ, R_πσ, R_σσ and R_σπ ).

Digital holographic microscopy

We isolated the individual crystals using the methods described by Denton and Land [14]. We measured the phase retardation parallel and perpendicular to the long axis of the crystal (indicated by red arrow and black arrows in supplemental information Fig. S2(a) and Fig. S2(b)) using a digital holographic microscope. A detailed description of the technique is set out by Coulomb et. al [35]. We made 6 separate measurements of the phase retardation parallel and perpendicular to the long axis of each crystal and used the two retardations to calculate the mean planar refractive index ratio. For each species (and sample area) we measured 20 crystals, calculating the mean and standard deviation of measurements (Fig. 2).

Optical modelling

The optical model assumes that the guanine-cytoplasm stack can be approximated as a planar stratified medium with alternating isotropic and uniaxial birefringent layers. The coordinate system was chosen so that z-axis is aligned with the direction of stacking and the σ polarization is aligned with the y-axis. Each crystal layer was orientated at a random planar angle, , where is a uniformly distributed random variable on [0, π]. The reflectivity was calculated using the 4×4 matrix method [24, 25]. In this formulation, the dielectric properties of each crystal layer are represented by the differential propagation matrix Δ. For the Type 1 crystals this is of the form

$${\Delta }_1=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 1-\frac{n_I^2\sin {\left({\theta }_I\right)}^2}{{∊}_e}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {∊}_o\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {∊}_o-n_I^2\sin {\left({\theta }_I\right)}^2\hfill & \hfill 0\hfill \end{array}\right),$$ 5

and for Type 2 crystals this is of the form

$${\Delta }_2=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill 1-\frac{n_I^2\sin {\left({\theta }_I\right)}^2}{{∊}_o}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {∊}_o\cos {\left(\varphi \right)}^2+{∊}_e\sin {\left(\varphi \right)}^2\hfill & \hfill 0\hfill & \hfill \frac{1}{2}({∊}_o-{∊}_e)\sin \left(2\varphi \right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill \frac{1}{2}({∊}_o-{∊}_e)\sin \left(2\varphi \right)\hfill & \hfill 0\hfill & \hfill {∊}_o\sin {\left(\varphi \right)}^2+{∊}_e\cos {\left(\varphi \right)}^2-n_I^2\sin {\left({\theta }_I\right)}^2\hfill & \hfill 0\hfill \end{array}\right)$$ 6

where ${∊}_o=n_o^2,{∊}_e=n_e^2,n_I$, n_I is the refractive index of the incident medium and θ_I is the angle of incidence. The isotropic cytoplasm layers have the same form of Δ matrix as Type 1 crystals, but with ${∊}_c=n_I^2$ substituted for ε_o and ε_e respectively. The transfer matrices for each layer were obtained using the procedure described by Azzam and Bashara [25]. The transfer matrix for the overall multilayer system was obtained by taking a matrix product over all layers and reflectivity coefficients, R_σ = R_σσ + R_σπ and R_π = R_ππ + R_πσ were then calculated using standard formulae [25]. In order to equate the microscopic structure with the bulk optical response and simulate a representative model, we sampled and averaged over 500 multilayer structures.