Mouth asymmetry in the textbook example of scale-eating cichlid fish is not a discrete dimorphism after all

Abstract

Individuals of the scale-eating cichlid fish, Perissodus microlepis, from Lake Tanganyika tend to have remarkably asymmetric heads that are either left-bending or right-bending. The ‘left’ morph opens its mouth markedly towards the left and preferentially feeds on the scales from the right-hand side of its victim fish, and the ‘right’ morph bites scales from the victims’ left-hand side. This striking dimorphism made these fish a textbook example of their astonishing degree of ecological specialization and as one of the few known incidences of negative frequency-dependent selection acting on an asymmetric morphological trait, where left and right forms are equally frequent within a species. We investigated the degree and the shape of the frequency distribution of head asymmetry in P. microlepis to test whether the variation conforms to a discrete dimorphism, as generally assumed. In both adult and juvenile fish, mouth asymmetry appeared to be continuously and unimodally distributed with no clear evidence for a discrete dimorphism. Mixture analyses did not reveal evidence of a discrete or even strong dimorphism. These results raise doubts about previous claims, as reported in textbooks, that head variation in P. microlepis represents a discrete dimorphism of left- and right-bending forms. Based on extensive field sampling that excluded ambiguous (i.e. symmetric or weakly asymmetric) individual adults, we found that left and right morphs occur in equal abundance in five populations. Moreover, mate pairing for 51 wild-caught pairs was random with regard to head laterality, calling into question reports that this laterality is maintained through disassortative mating.

1. Introduction

Morphological variation plays an important role in the ecology and evolution of natural populations. One particularly interesting case of phenotypic variation is ‘left-right asymmetry’, where phenotypic traits of left or right individuals differ asymmetrically [1]. Left–right asymmetry can be found in several phyla of animals, for example, in eye side in flatfishes (Pleuronectiformes) [2], direction of shell coiling in the snails, Euhadra species [3], the major claws of the male mud shrimp, Neotrypaea californiensis [4] and direction of the mouth-opening in the scale-eating cichlid fish, Perissodus microlepis [5].

The adaptive radiations of cichlid fishes in the great East African lakes, including Lakes Malawi, Tanganyika and Victoria, consist of hundreds of endemic species [6]. The coexistence of so many species demands astonishingly precise ecological specializations, to avoid competitive exclusion. Perissodus microlepis, a scale-eating cichlid fish from Lake Tanganyika, is a textbook example of the evolution of a pronounced morphological asymmetry and of a striking trophic specialization [5]. Most of the nine described species of cichlids of the monophyletic tribe Perissodini from Lake Tanganyika [7], including P. microlepis, are specialized to feed predominantly on the scales of other fishes [6,8,9]. In P. microlepis, individuals are even more specialized: in individual fish, the mouth bends either to the left (‘left’ morph; L) or to the right (‘right’ morph; R; figure 1). L-morphs preferentially attack the right flank of their prey, while R-morphs attack their victim's left flank [5,10–12]. Some textbooks in evolutionary biology hence present the asymmetrical mouth of P. microlepis as a typical example of antisymmetry (AS), where two distinct forms coexist (i.e. dimorphic asymmetry) [13].

Figure 1.

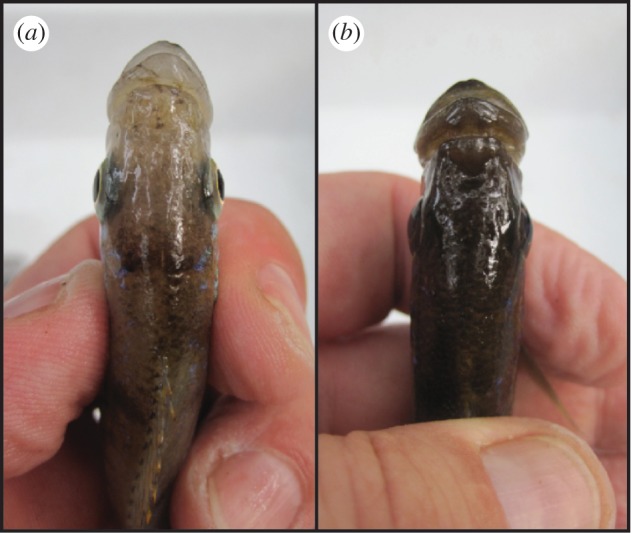
Dorsal view of relatively pronounced (a) right-bending and (b) left-bending mouth-morphs of the Lake Tanganyikan scale-eating cichlid fish, Perissodus microlepis.

Mouth laterality in P. microlepis is thought to facilitate efficient scale-eating because the contact area between the predator's teeth and the flank of the prey fish is enlarged [5]. The frequency of L- and R-morphs in natural populations of P. microlepis was found to fluctuate about an approximately 50 : 50 ratio over more than a decade of sampling [5], and negative frequency-dependent selection has been invoked to explain the relative stability of this 50 : 50 ratio [5]. The more common morph is thought to suffer a fitness disadvantage since prey fish would be more often attacked from the preferred side, making them more alert to attacks from that direction. Therefore, the more common morph of the predator would be expected to succeed less often in removing scales than the less-common morph, which in turn would be favoured [5].

Although P. microlepis is well known among evolutionary biologists, many fundamental questions about this fish remained unanswered [14]. Contradictory hypotheses have been proposed about the trait distribution and the inheritance of mouth asymmetry in this fish. It has been claimed that differences in the mouth asymmetry between L- and R-morphs of adult as well as juvenile fish are sufficiently pronounced to be discernable upon visual inspection by trained observers [5,15]. A strictly bimodal distribution (‘strong’ AS) [16] of the asymmetry has been previously reported for this species [5,15]. However, the bimodality of this asymmetry has been called into question owing to recent reports of unimodally distributed mouth asymmetry at the late larval stage [17] as well as from adult P. microlepis [10]. Furthermore, mouth asymmetry in adults of this species was found to conform to ‘weak’ AS [10]—where the trait distribution is rather platykurtic than strictly bimodal [16]. Yet the degree and distribution of mouth asymmetry in juvenile fish has not been investigated so far.

Moreover, the degree of genetic determination of this remarkable asymmetry remains unknown. Previously, two alleles at a single Mendelian locus were thought to determine the directionality of mouth asymmetry [5,15,17]. However, a recent review [14] pointed out that the observed phenotype frequencies among offspring of breeding pairs of different morph combinations were inconsistent with models of Mendelian inheritance. Additionally, reported intraspecific brood mixing [18] could affect phenotype frequencies within broods collected in the field, which would make interpretation of field data, particularly without genetic knowledge on parentage, difficult.

Disassortative mating—where individual P. microlepis fish preferentially mate with individuals of the opposite morph—was thought to be an additional mechanism in stabilizing the variation in morph frequency over time [19], because offspring frequencies exhibited a 1 : 1 ratio of L- to R-individuals for disassortatively breeding pairs, a 1 : 2 ratio for RR pairs and a 1 : 0 ratio for LL pairs. These offspring frequencies were explained by a complex inheritance pattern involving two alleles at a single locus where R is dominant over L and R is homozygous lethal [15,19]. However, phenotypically plastic responses to handed foraging behaviour have recently been suggested to give rise to these mouth asymmetries [10]. Furthermore, because no genetic basis for laterality has been found in most cases of AS [1,20], phenotypic plasticity may be an important source of phenotypic variation in this system.

The suggested disassortative mating pattern in P. microlepis is difficult to reconcile with two recent findings: (i) phenotypic plasticity apparently affects mouth asymmetry [10] and (ii) genetic evidence suggests that random mating occurs in natural populations [11]. The sample size of pairs of P. microlepis caught in the field so far has been rather small (n = 24) [19] and a reasonable explanation for how mating partners should recognize each others' laterality was lacking.

Here, we address these open questions surrounding mouth laterality of this species by revisiting the mating pattern and population-based relative abundances of mouth morphs and by assessing the (multivariate) phenotypic trait distributions of adults and juveniles. In particular, we test whether mouth asymmetry of P. microlepis displays dimorphic (antisymmetric) variation, either strong or weak, as has been so far believed.

2. Material and methods

(a). Sample collection, and assessments of equal abundance and mating pattern

We sampled 287 adult individuals of P. microlepis from five different locations around Mpulungu (Zambia) on the southern tip of Lake Tanganyika in April 2010 from water depths up to 7 m (table 1). Most specimens were caught by gill nets and sampled randomly with respect to mouth-opening direction. All fish were photographed live from a lateral view and then preserved in 97 per cent ethanol and vouchered in the fish collection at the University of Konstanz. Standard length (SL) was determined from digital photographs.

Table 1.

Abundance of lateral morphs in P. microlepis from five different populations. (Sample sizes–relative frequencies in parentheses. Bold numbers indicate the number of specimens that could not be unambiguously assigned.)

	right morph	left morph	total	χ2	p-value
Crocodile Island (8°42.1′ S, 31°7.2′ E)	2–(50%)	2–(50%)	4	–	–
Kasakalawe Village (8°46.8′ S, 31°4.8′ E)	22–(43%)	29–(57%)	51 + 3	0.7	0.403
Katoto Village (8°48.2′ S, 31°1.3′ E)	33–(56%)	26–(44%)	59 + 3	0.6	0.431
Mbita Island (8°45.3′ S, 31°5.4′ E)	21–(47%)	24–(53%)	45 + 13	0.1	0.777
Toby Veall's Lodge (8°37.4′ S, 31°12′ E)	57–(54%)	48–(46%)	105 + 4	0.6	0.439
all locations pooled	135–(51%)	129–(49%)	264 + 23	0.1	0.752

In addition, 65 juveniles from five different broods (of three RR pairs and two RL pairs) were caught and transported to the animal care facility at the University of Konstanz. The broods were raised in separate 40 l and later 200 l aquaria on Artemia nauplii with flake food as diet. These juvenile P. microlepis were used for quantitative measures of mouth asymmetry as well as for laboratory feeding experiments [21]. Owing to the observed surprisingly high levels of brood-mixing (H. J. Lee, V. Heim & A. Meyer 2012, unpublished data), we could not reliably investigate inheritance patterns of mouth asymmetry and therefore only focus on trait distributions.

Assessments of morph abundance and mating pattern were based upon visual determination of mouth laterality in the field. Laterality of 287 live adult fish was judged by eye by two independent observers (H.K. and A.M.). ‘Mouth-opening direction’ was the criterion for laterality (i.e. the relative orientation of the ascending process of the premaxillary bone, while the mouth is opening and the jaw protruding). Ambiguous specimens (n = 23), defined as those individuals where the two observers made no or different calls (i.e. symmetric or weakly asymmetric individuals), were excluded from the Chi-square (χ²) analyses to test whether the ratio of L- and R-morphs deviated from equal abundance.

To assess the mating pattern in P. microlepis, 54 breeding pairs were collected by diving with hand nets at Toby Veall's Lodge (8°37.4′ S, 31°12′ E), about 20 km northeast of Mpulungu at the southern tip of Lake Tanganyika. Three of the 54 pairs were excluded from the analysis because one breeding partner was found to be ambiguous with respect to laterality by the two observers (n = 2) or scored with opposite scores (n = 1). Expected numbers of RR, RL and LL pairs were calculated from the laterality frequencies in our sample and compared with observed frequencies with χ²-statistics.

(b). Quantifications of mouth asymmetry in adult Perissodus microlepis

We used statistical tools developed for fluctuating asymmetry (FA) analyses [22] to test whether mouth asymmetry in P. microlepis corresponded to dimorphic variation (e.g. AS), even though we recognize that the jaw asymmetry variation in this species may have predictable genetic or environmental causes [10], i.e. it may not be owing solely to developmental noise, as is normally assumed for FA variation.

Mouth asymmetry in adult fish was quantified by estimating mouth-bending angle [15], ‘α L − β R’ (in degrees) for 249 preserved individuals from standardized photographs from a dorsal view. A randomly selected sub-sample (n = 33) was photographed twice independently, and replicate and blind measurements were carried out from the repeated photographs to assess measurement error (ME) caused by photographing. Potential ME caused by preservation could not be assessed. ME1—average difference between pairs of measurements on each L and R side (∑|M₁ − M₂|/n) [22]—was calculated. ME3—ME as a percentage of non-directional asymmetry (non-DA; FA and AS)—was further estimated from results of a two-way mixed model ANOVA (100 × MS_error/MS_{sides × individuals}) ([22]; see below).

Mouth angles were measured in TPSDIG v. 2.16 [23]. On each image, a triangle connecting the anterior-most points of the eye sockets and the tip of the snout was drawn to calculate angles, α L (angle of the vertex by the left eye) and β R (angle of the vertex by the right eye; see below). Negative values of α L − β R indicate right-bending specimens, whereas positive values indicate left-bending individuals. The most extreme fish (mouth-bending angles deviating by more than 15°; n = 11) were excluded from analyses because these fish or parts of them seemed to have been deformed during preservation.

A detailed analysis of mouth-bending angle was performed in R [24] to test whether mouth asymmetry in P. microlepis represented dimorphic variation (e.g. AS; a bimodal or platykurtic distribution),  DA (a significant departure of mean asymmetry from zero) or FA (a continuous normal distribution of mean zero). First, the trait mean for the whole sample as well as for each separate population (with large sample sizes of n = ca 50) was calculated and analysed for a departure of the mean from zero to test for DA [25]. As suggested in Van Dooren et al. [10], the dip statistic [26], a specific test for a unimodal distribution was used to evaluate any presence of a ‘strong’ AS. One would expect a bimodal distribution if AS were strong [16]. Linear regression analyses were also conducted to test for a significant relationship between degree of mouth asymmetry and body size [15].

Using repeated measurements (angles) from replicate images of the sub-sample that was used for the assessment of ME, a two-way mixed model ANOVA (sides = fixed; individuals = random) was carried out to test if mouth asymmetry exhibits DA or non-DA as suggested by other studies [27,28]. This analysis tests for the significance of DA (effects of ‘sides’) and non-DA (effects of ‘sides × individuals’) relative to the variation expected owing to ME [28].

To further test whether the observed trait distribution consisted of more than a one-component normal distribution, a mixture analysis was performed. An Anscombe–Glynn test for platykurtosis [29] in the trait distribution was used to evaluate the presence of a potential ‘weak’ AS following [10]. A broad-peaked, but still unimodal (i.e. platykurtic) distribution would be expected if AS were weak [16]. Furthermore, using an expectation–maximization (EM) algorithm-based approach [30] implemented in the mixtools package [31], mixtures of two single-component normal distributions were fitted to the mouth asymmetry data and their fit was inspected (see the electronic supplementary material, figure S1). A parametric bootstrap test (1000 iterations) using the output of the EM mixture model fits was performed to test whether the trait distributions consisted of one or two components [31].

(c). Quantifications of mouth asymmetry in juvenile Perissodus microlepis

For the live juvenile P. microlepis, we employed two different methods to quantify mouth asymmetry from photographs: (i) mouth-bending angle [15] and (ii) geometric morphometric analysis based on mouth landmarks. Each live test-fish was photographed from a dorsal view in a standardized position using a Zeiss Axiophot digital microscope (Zeiss, Germany). Mouth-bending angle was measured at two ontogenetic stages, of ca 3 months (n = 65) and ca 7 months (n = 54) of age. A sub-sample of 24 individuals from each of the two age groups was photographed twice independently to quantify ME, as was performed in adults (see above). Statistical analyses were conducted as carried out in adults.

We also performed geometric morphometric analyses on landmark configurations for the combined age groups. A set of 10 landmarks defining mouth shape was digitized using TPSDIG v. 2.16, consisting of two un-paired landmarks (snout tip; mid-point between the frontal eye sockets) as well as four paired landmarks (see the electronic supplementary material, S1 for detailed description).

Using MorphoJ v. 1.02e [32], we applied a generalized Procrustes superimposition taking object symmetry into account [33–35]. This method compares the original mouth shapes to their respective mirror-images and partitions total variation in mouth shape into components of symmetry as well as of asymmetry [35]. Symmetric components represent variation in the left–right averages of mouth shape, whereas asymmetric components indicate the left–right mouth asymmetries within individuals [35]. Therefore, we only considered the asymmetric components of variation in mouth shape.

Principal component analysis (PCA) was used to identify the major patterns of shape change in the asymmetric component of shape variation that relate to mouth orientation. Individual loadings on the most important asymmetric component affecting mouth asymmetry (PC-1) were extracted and their distribution was analysed in the same way as the mouth-bending angle data (see above). Moreover, discriminant function analysis (DFA) was performed between both age groups (3- versus 7-month-old fish) to test for effects of age (body size) on the mouth asymmetry means. DFA is a commonly used ordination-based multivariate method to examine whether a priori determined two groups can be distinguished reliably [36–39]. Levene's test [40] was further conducted using individual PC-1 scores to investigate whether variance in mouth asymmetry differed significantly between both age groups.

To statistically test for the magnitude of DA and non-DA relative to ME, we landmarked a sub-sample of 24 individuals twice on replicate images, and further conducted Procrustes analysis of variance (ANOVA) as well as multivariate analysis of variance (MANOVA) on each age group [33,35]. For the latter analysis, only the asymmetric component of shape variation was considered. The Procrustes ANOVA procedure considers fewer parameters than the MANOVA model, but assumes equal amount and direction of variation in each landmark [35], whereas the MANOVA procedure avoids such assumptions [33]. These statistical analyses have been commonly applied in studies of multivariate shape analyses in relation to left–right asymmetry [35,41–43].

The morphological data (e.g. mouth-bending angle, body size) and morphometric data have been deposited in DRYAD, entry doi:10.5061/dryad.4605c.

3. Results

(a). Equal abundance of mouth morphs and random mating in Perissodus microlepis

The direction of mouth laterality could be unambiguously assigned for 92 per cent (264 of 287 individuals) of the field-collected adult P. microlepis by visual inspection (table 1). Only 18 individuals (6%) were independently scored as no calls (ambiguous) and five individuals (2%) were scored differently by both experimenters (H.K. and A.M.). The average fish SL was 7.95 cm (range: 5.52–11.13 cm; s.d. = 1.21 cm). None of the five sampling locations showed deviations from an equal ratio of R- to L-morphs (table 1), corroborating the earlier hypothesis of equal abundance [5,11].

The specimens used for our investigation of mating patterns consisted of 55 R- and 47 L-morphs that formed 51 pairs. Thirteen pairs were RR, nine were LL and 29 were RL. Although RL pairs were proportionally more common than expected, the observed pair frequencies were not significantly different from expected frequencies under the assumption of random mating (χ₂² = 1.06, p = 0.59; figure 2).

Figure 2.

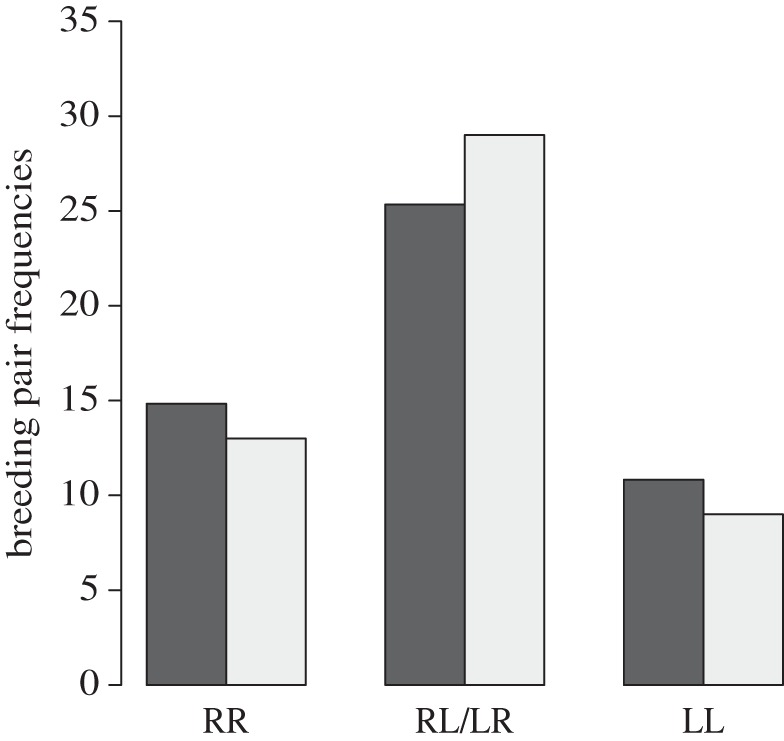
Random mating in P. microlepis. Observed (grey bars) pair frequencies (RL: n = 29; RR: n = 13; LL: n = 9) did not differ from expected (black bars) frequencies (n = 25.3, n = 14.8 and n = 10.8).

(b). Mouth asymmetry in adult Perissodus microlepis

The ME1 of angles α L and β R was 1.71° and 1.91°, respectively, which accounts for 11.3 per cent of non-DA (FA and AS) variation (ME3), a finding similar to that of other studies reported in Palmer & Strobeck [28]. Note that when referring to this variation as FA, we do so only in the sense of the shape of the frequency distribution of mouth asymmetry variation; we do not mean to imply that the primary cause of this variation is developmental noise, as is generally assumed in studies of FA variation.

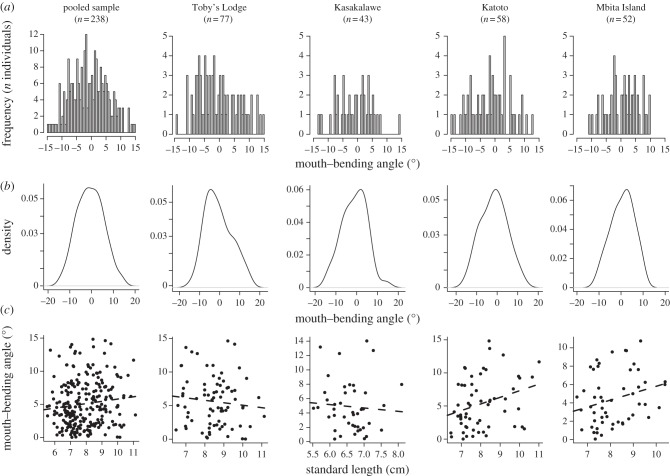
The outcome of our detailed analysis of mouth-bending angle of 238 specimens revealed that mouth asymmetry did not significantly depart from unimodality in any of the populations or in the pooled sample (table 2 and figure 3), ruling out the possibility of strong AS. The trait mean was always found not to be significantly different from zero (table 2), indicating no DA. The two-way mixed model ANOVA confirmed the initial indication of no DA in our sample, whereas it revealed highly significant non-DA relative to ME (table 3).

Table 2.

Statistical analyses of traits related to mouth asymmetry in adult and juvenile P. microlepis. (These analyses include the dip tests for unimodality [26], one sample t-tests for the assessment of the deviation of the trait mean from zero, Anscombe–Glynn tests for platykurtosis [29], mixture analyses to determine the number of components, and linear regression analyses to test for a significant correlation between mouth-bending angle and body size. p-values in boldface denote statistical significance. (a) Mouth-bending angle of wild-caught adult specimens (whole sample and listed by population). (b) Mouth-bending angles of laboratory-reared juvenile specimens. (c) Individual PC-1 scores, derived from a PCA on the asymmetric component of shape variation.)

			dip test		one sample t-test		platykurtosis	mixture analysis		linear regression analysis
	n	trait mean	dip	p-value	t-test	p-value	p-value	n components	p-value	slope	F	r²	p-value
(a)
Toby's Lodge	77	−0.53 (°)	0.028	>0.5	−0.69	0.49	0.18	1	0.16	−0.37	0.84	0	0.36
Kasakalawe	43	−1.13 (°)	0.046	>0.5	−1.24	0.22	1	1	0.78	−0.47	0.22	−0.02	0.64
Katoto	58	−1.57 (°)	0.036	>0.1	−1.85	0.07	0.3	1	0.75	1	5.34	0.07	0.02
Mbita Island	52	0.62 (°)	0.046	>0.1	0.86	0.39	0.2	1	1	0.75	3.64	0.05	0.06
all samples	238	−0.58 (°)	0.015	>0.5	−1.46	0.15	0.06	1	0.47	0.34	3.35	0.01	0.07
(b)
ca 3 months	65	0.58 (°)	0.029	>0.5	1.84	0.07	0.18	1	0.39	—	—	—	—
ca 7 months	54	0.64 (°)	0.047	>0.1	1.95	0.06	0.63	1	0.9	0.11	0.04	0.001	0.85
(c)
ca 3 months	65	3.31 × 10−5	0.037	>0.5	0.03	0.98	<0.01	1	0.06	—	—	—	—
ca 7 months	54	−3.99 × 10−5	0.036	>0.5	−0.02	0.99	0.27	1	0.23	—	—	—	—

Figure 3.

Frequency distribution of mouth asymmetry in adult P. microlepis from four wild populations. Left panel: pooled sample; four right panels: analyses at the population level. (a) Histograms of the distribution of mouth-bending angle in the respective samples; (b) smoothed histograms to exclude potential effects that might be caused by the number of bins; and (c) linear regression between standard body length and degree of mouth asymmetry.

Table 3.

Statistical tests for the significance of DA (‘sides’) and non-DA (‘sides × individuals’; FA and AS) relative to measurement error (ME, imaging error) using two-way mixed-model ANOVA (sides = fixed, individuals = random) following [28]. (p-values in boldface denote statistical significance.)

effect	MS	d.f.	F	p-value
(a) adults
sides	16.614	1	0.65	0.426
individuals	25.222	32	0.986	0.516
sides × individuals	25.579	32	8.823	<0.001
ME	2.899	66
(b) ca 3 months
sides	13.104	1	2.394	0.135
individuals	4.545	23	0.831	0.670
sides × individuals	5.473	23	7.706	<0.001
ME	0.710	48
(c) ca 7 months
sides	14.420	1	2.344	0.139
individuals	3.088	23	0.502	0.947
sides × individuals	6.151	23	17.354	<0.001
ME	0.354	48

The Anscombe–Glynn tests revealed no significant platykurtosis in the asymmetry distribution, and the mixture analyses along with the parametric bootstrap test strongly suggest that a single-component normal distribution best fitted our sample, both as a whole and at the population level (table 2; see the electronic supplementary material, figure S1). However, in the pooled sample platykurtosis was only marginally non-significant (p = 0.06), which does not allow us to exclude the possibility of weak AS.

Furthermore, no significant correlation was detected between the size of the fish and mouth-bending angle except in one population (Katoto Village: table 2 and figure 3), which suggests that mouth asymmetry does not necessarily increase with body size as hypothesized by Hori et al. [15]. However, in the pooled sample the effect was on the borderline of being significant (p = 0.07; table 2), so this association cannot be rejected with confidence.

(c). Mouth asymmetry in juvenile Perissodus microlepis

The ME1 of angles in the 3-month-old juvenile fish was 0.93° (α L) and 1.02° (β R), while the ME1 of the 7-month-old juvenile fish was smaller, 0.58° (α L) and 0.76° (β R). This amount of ME accounts for 13.0 per cent and 5.8 per cent of the non-DA variation (ME3) for the 3- and 7-month-old fish, respectively.

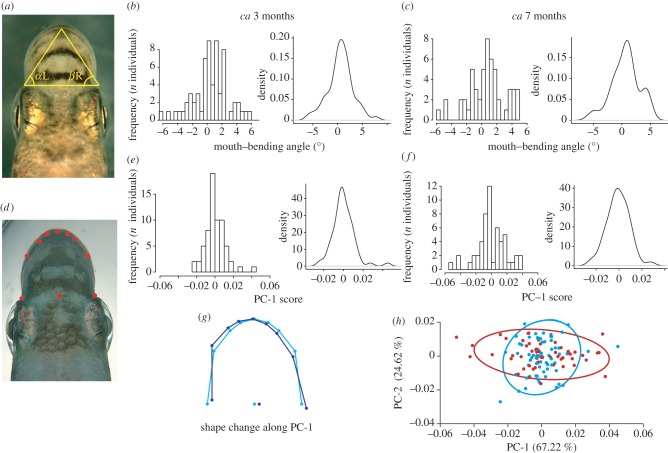
The degree of mouth asymmetry in juvenile fish was considerably lower than in wild-caught adults and showed a continuous and unimodal distribution across the two different ontogenetic stages (table 2 and figure 4). These data reject the hypothesis of strong AS. Twenty-one of the 65 3-month-old fish (32%) displayed nearly symmetric mouth morphologies (i.e. mouth-bending angles ranging between −1° and +1°; figure 4a–c) as did 18 out of 54 individuals (33%) measured at 7 months of age. The average mouth-bending angle was 0.58° and 0.64° for the 3- and 7-month-old fish, respectively, and was not significantly different from zero despite being close to statistical significance (table 2). The two-way mixed ANOVA of each age group provided no support for DA, but a highly significant non-DA relative to ME was detected (table 3). No sign of platykurtosis was detected and a single-component normal distribution best fitted the samples of both age groups (table 2; see the electronic supplementary material, figure S1). Also in the 7-month-old laboratory-reared fish, the laterality did not increase significantly with body size (table 2).

Figure 4.

Frequency distribution of traits related to mouth asymmetry in laboratory-reared juvenile P. microlepis. (a) The triangle indicates connection lines between the frontal points of the two eye sockets and the upper-jaw intersection, drawn to calculate angle differences between α L (angle of the vertex by the left eye) and β R (angle of the vertex by the right eye) on a juvenile P. microlepis [15]. Histograms and density plots of mouth-bending angles of (b) 3- and (c) 7-month-old fish. (d) A juvenile P. microlepis displaying the landmark set that was used for geometric morphometric analyses (see the electronic supplementary material, S1 for detailed description of how the landmark set was defined). Histograms and density plots of individual PC-1 scores for (e) 3- and (f) 7-month-old fish. (g) Shape changes that are associated with PC-1. Lines drawn in light blue represent an average consensus mouth shape, whereas dark blue lines indicate the shift in mouth shape that is associated with 0.1 units in the positive direction on PC-1 in (h). (h) The plot of PC-1 versus PC-2 displays the difference in variance along PC-1 between both age groups. Individual scores and 95% CIs indicated in blue and red for 3- and 7-month-old fish, respectively.

Similar to the outcome of the analysis of mouth-bending angles, individual PC-1 scores also exhibited a continuous and unimodal distribution (table 2 and figure 4d–f). However, the 3-month-old fish showed significant platykurtosis in the PC-1 distribution. Nevertheless, the distribution most probably consisted of only one-component normal distribution (see the electronic supplementary material, figure S1). PC-1 accounted for 67.22 per cent of the total variation in asymmetric mouth shape components. The shape change along PC-1 was clearly associated with the expected pattern of mouth asymmetry (figure 4g). The DFA on the asymmetric component of shape variation showed that mouth shape means of both age groups were not significantly different (Procrustes distance = 0.0023; p = 0.63). However, shape variance (as inferred from PC-1) was significantly higher in the 7-month-old fish than in the 3-month-old fish (Levene's test; F = 11.625; p = 0.001; figure 4h).

The multivariate analysis of mouth orientation also showed that the trait distributions in both age groups fitted better to non-DA than to DA. The Procrustes ANOVA of geometric morphometric data showed that non-DA (sides × individuals) was statistically highly supported for both age groups, although DA (sides) was also slightly significant only for the 3 month group (see the electronic supplementary material, table S1). Considering the MANOVA (non-isotropic model), both DA and non-DA were statistically highly significant in the 3-month-old fish, but not in the 7-month-old fish (see the electronic supplementary material, table S1).

4. Discussion

The pronounced laterality of the foraging behaviour and asymmetry in the morphology of P. microlepis has made this species a textbook example [13] of both their astonishing degree of adaptation and specialization and of negative frequency-dependent selection [5]. Yet, many questions about this species, including its ecology, mating and extent, distribution and origin of its laterality remained uncertain or untested until now. How this asymmetrical head morphology evolved [7], what bones are actually involved in bringing about the head asymmetry, and what the underlying genetic and/or environmental contributions are, are all questions that are still either completely unanswered or debated [10,14,17]. Also how this mouth asymmetry manifests itself throughout the ontogeny of the fish remained unknown, although some progress on this issue has been made [10,17]. From an ecological standpoint, it is still not fully understood how it is maintained in natural populations. Our study investigated the degree and distribution of mouth asymmetry in juveniles as well as adults, collected information on the relative abundance of morphs in wild-caught individuals from several populations and tested previous hypotheses on mating preferences. Combined with our behavioural data on the interaction of foraging behaviour and mouth asymmetry [21], we advance the understanding of the evolution and ecological maintenance of the interesting laterality in this species.

(a). Equal dimorphism and random mating between mouth morphs

In five populations of P. microlepis, we found both R- and L-morphs to be equally abundant, confirming the results of previous investigations [5], in spite of their sampling sites being separated from ours by hundreds of kilometres of coastline.

Based on the largest field sample of mated pairs collected for P. microlepis to date, we detected random mating with regard to laterality (figure 2). This contradicts previous reports based on smaller sample sizes that claimed to have found disassortative mating [19]. These new field data are consistent with our previous work that revealed no genetic differentiation between morphs based on both, mitochondrial and nuclear DNA markers, but that provided genetic support for the random mating hypothesis [11]. Hypothetical selective advantages for breeding assortatively or disassortatively were thus not reflected or detected by genetic analyses. The disagreement between our results and those of previous investigations [19] may be owing to their use of an insufficient sample size. Alternatively, there might be heretofore unreported intraspecific variation in mating preferences among populations—instances of this are known from other vertebrates [44]. Geographical aspects might play a role in mating pattern variation, especially when considering that genetic isolation by (small) distances between populations of P. microlepis has been reported along rocky shorelines of southern Lake Tanganyika [11,45]. Although we observed a slightly higher number of disassortative pairs (n = 29) than expected by chance (n = 25.34), this difference was not statistically significant. A larger sample size might again reveal evidence for disassortative mating [19]. However, even if such a slight deviation from random mating existed, it would not be likely to stabilize morph frequencies [19]. The suggestion that phenotypic plasticity plays a large role in shaping mouth asymmetry in this species [10] would indirectly support our findings of random mating with regard to laterality.

(b). Trait variation in mouth asymmetry is not a discrete dimorphism

We show that mouth asymmetry is continuously and unimodally (generally non-platykurtic) distributed in both adult and juvenile P. microlepis, which contrasts rather strongly with the previous reports about the discreteness and bimodality of this trait [5,15].

By quantifying mouth-opening direction in a large number of individuals, we show that many juveniles and adults have virtually symmetrical mouths (figures 3 and 4), which argues against the previous hypothesis that mouth laterality of P. microlepis is determined exclusively by two alleles at a single genetic locus [5,15,17]. If that hypothesis were correct then symmetrical or near-symmetrical fish would not be expected to be present unless environmental variation also plays a role in the determination of mouth directionality [46].

Trait means, regardless of the measurement technique, were not different from zero in either adult or juvenile fish. Similarly, the ANOVA and MANOVA analyses of mouth asymmetry (table 3; see the electronic supplementary material, table S1) generally favour non-DA. Each specific dataset (e.g. mouth-bending angle, PC-1 score) most probably consisted of a single component and not two components as would be expected if the trait were strongly antisymmetric (see the electronic supplementary material, figure S1). However, in the pooled adult sample the test for platykurtosis in the distribution of mouth-bending angle was nearly significant (p = 0.06) and in the laboratory-reared 3-month-old fish, platykurtosis in the distribution of PC-1 score was significant. Thus, the possibility of weak AS cannot be excluded. On the whole, in the context of left–right asymmetry our data suggest that mouth asymmetry variation in this scale-eating cichlid fish is much more continuously distributed than previously believed and is not a discrete dimorphism at all. Consequently, if mouth laterality in P. microlepis has any genetic basis at all, it is weak and coupled with significant environmental input [46].

In spite of the general non-significant relationship, mouth asymmetry of adult P. microlepis is inclined to increase with body size in two sampling locations as well as in the pooled field sample (table 2). This (weak) positive association would be expected if mouth asymmetry were to amplify over individual's lifetime as a phenotypically plastic response to repeated attacks at a particular prey-side [10,14], assuming that behavioural handedness is not particularly plastic [10,21]. Platykurtosis was also marginally non-significant in the pooled sample. It is therefore conceivable that if our sampling included a greater number of larger fish, this positive trend and platykurtosis would become significant, which in turn leaves room for the possibility of weak dimorphic asymmetry.

Several further lines of evidence support the hypothesis that mouth asymmetry is not a discrete dimorphism. In a previous study, we [11] also found that 11 out of 128 (9%) individuals of adult P. microlepis from two populations from southern Lake Tanganyika could not, based on visual inspection, be unambiguously assigned to a particular laterality morph. Similarly, more than 10 per cent (5 out of 47) adults from a northern population from Lake Tanganyika were also almost perfectly symmetrical (mouth-bending angle less than 1°) [10]. The results of Van Dooren et al. [10] further suggest that mouth asymmetry is difficult to assess without a quantitative measure of mouth asymmetry. Nevertheless, many wild-caught adult individuals still have a mouth that bends strongly to the left or the right (figure 3). However, our assessments of both pooled and population samples showed that variation in mouth asymmetry is unimodally distributed.

Furthermore, even with the aid of a dissecting microscope, it was difficult to judge mouth laterality in the 3-month (approx. 3–4 cm total length (TL)) and 7-month (approx. 8.0 cm in TL)-old fish. This does not agree with previous reports that laterality is readily discernible in juvenile fish whose TL is greater than 1.2 cm [15]. When mouth-bending angle was estimated for juveniles of a single P. microlepis brood, mouth laterality could be confidently assigned for only 93 of 141 (66%), while the mouths of the remaining 48 individuals were nearly symmetrical [17]. Thus, the frequency of mouth asymmetry in that study [17] of juveniles showed a unimodal trait distribution, which would not be the case if it were a discrete dimorphism.

In comparison to wild-caught fish, the rather symmetrical mouth morphology in our laboratory-reared 7-month-old juveniles lends indirect support to the hypothesis that phenotypic plasticity considerably contributes to mouth laterality [10]. This is because the fish were fed almost exclusively by Artemia nauplii and flake food, but they were not provided with prey fish that would allow them to feed on scales. One might speculate that they might have developed apparent asymmetry if they had the regular opportunity to prey on scales [21].

We here document a generally unimodal and non-platykurtic distribution (with the mean not being different from zero) of mouth asymmetry. The measurements from photographs taken from a dorsal view suggest that the trait variation in mouth laterality of P. microlepis does not reflect a discrete dimorphism. We recognize that this type of measurement (e.g. mouth-bending angle) may not fully capture the existing mouth laterality of this species. In the assessments of laterality in live P. microlepis, one can open the mouths by pulling down the upper jaw. In most specimens, the laterality of the mouth-opening direction becomes much more apparent and can thus be less ambiguously scored, based on the relative orientation of the ascending process of the premaxillary bone and the laterality of mouth-opening direction. Our scoring of mouth asymmetry of live fish overwhelmingly fit their later foraging decisions [21]. We are currently investigating the relative roles of environmental and genetic influences in bringing about morphological and behavioural laterality in this species.