Spatial organization of foreshocks as a tool to forecast large earthquakes

Abstract

An increase in the number of smaller magnitude events, retrospectively named foreshocks, is often observed before large earthquakes. We show that the linear density probability of earthquakes occurring before and after small or intermediate mainshocks displays a symmetrical behavior, indicating that the size of the area fractured during the mainshock is encoded in the foreshock spatial organization. This observation can be used to discriminate spatial clustering due to foreshocks from the one induced by aftershocks and is implemented in an alarm-based model to forecast m > 6 earthquakes. A retrospective study of the last 19 years Southern California catalog shows that the daily occurrence probability presents isolated peaks closely located in time and space to the epicenters of five of the six m > 6 earthquakes. We find daily probabilities as high as 25% (in cells of size 0.04 × 0.04deg²), with significant probability gains with respect to standard models.

The existence of different initiation processes leading to large and small earthquakes is still a central question in the debate on seismic predictability¹. The organization in space, time and magnitude of seismicity before mainshocks probably represents the most suitable tool to enlighten possible differences. The central question is the existence of some features that discriminate events before large shocks from other earthquakes. Foreshocks are usually retrospectively identified on different temporal scales, ranging from hours up to months before mainshocks, and, in general, their number increases as the mainshock time is approaching, consistently with a power law²,³,⁴. Some studies have suggested that the magnitude distribution of foreshocks is different from the distribution of other earthquakes⁵,⁶,⁷ and have shown correlations between the size of the foreshock zone and the magnitude of the subsequent earthquake⁸,⁹,¹⁰,¹¹. These observations are consistent with a scenario where foreshocks are the manifestation of an initiation process leading to the mainshock¹²,¹³. However, the above features have been attributed to biases introduced by the foreshock selection criterion¹⁴,¹⁵,¹⁶,¹⁷. In fact, single mode triggering models, where mainshocks, aftershocks and foreshocks are treated on the same footing, are able to reproduce the above features of foreshock time-magnitude organization. In these models magnitudes are assumed to be independent of past seismicity and therefore no information on mainshock magnitude can be obtained from foreshock properties. Within this approach seismicity before large earthquakes presents no distinct features.

In this study we show that the spatial organization of foreshocks can be used to forecast large mainshock occurrence. We first consider small mainshocks following the original approach proposed by Felzer & Brodsky (FB)¹⁸ to unveil the physical mechanisms behind aftershock occurrence. The great advantage of the FB approach is that a very large number of mainshock-aftershock couples can be analyzed, allowing for an accurate statistical study.

Results

Foreshocks before mainshocks with magnitude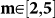

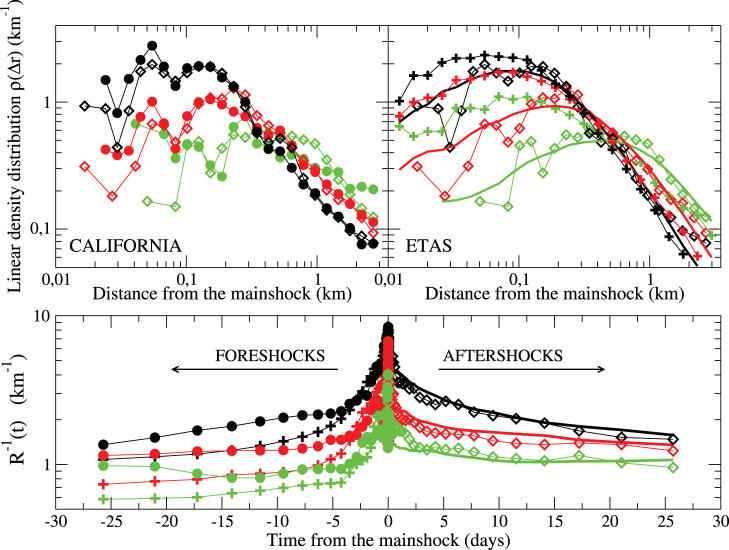
According to the FB procedure (see Methods), an event is identified as a mainshock if it is sufficiently far in time and space from larger earthquakes. Aftershocks (foreshocks) are events occurring just after (before) the mainshock and close in space. We consider a linear density probability ρ(Δr) defined as the number of aftershocks (foreshocks) with epicenters at a distance in the interval [Δr, 1.2Δr] from the mainshock, divided by 0.2Δr and by their total number, i.e. the linear density evaluated in ref.s ^{18, 19} divided by the total number of identified aftershocks (foreshocks). This normalization allows us to compare directly the functional form of the foreshock and aftershock distributions, even if their number are usually very different. In the left panel of Fig. 1 we compare ρ(Δr) for foreshocks and aftershocks in the Southern California Catalog²⁰, with mainshock magnitude 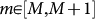and M = 2, 3, 4. Parameters of the FB procedure are listed in Table 1. The linear density probabilities before and after mainshocks are very similar in the whole spatial range and for all values of M. Fig. 1 indicates that, not only for aftershocks but also for foreshocks, ρ(Δr) depends on the mainshock magnitude. We have explicitly verified that the distributions for different M tend to collapse on the same master curve if Δr is rescaled by 10^ηM, with η = 0.39±0.05, in agreement with the scaling form ρ(Δr) = L(M)F(Δr/L(M)) and L(M) = 0.05 × 10^ηM km. This result, well established for the aftershock distribution²¹,²² indicates that the typical size of the foreshock zone also scales like 10^ηm with the mainshock magnitude m, in agreement with previous estimates for larger mainshocks⁹. In a recent publication the symmetry in the spatial organization of seismicity before and after M = 2 mainshocks has been attributed to artifacts of the mainshock selection criterion¹⁹. In the supplementary information we have deeply checked the stability of the results with respect to different parameters of the FB procedure. Furthermore, we have also verified that other mainshock selection criteria²¹,²³ provide similar results. Here, we show that the FB mainshock procedure leads to expected features for the aftershock occurrence: First, we argue that a biased mainshock selection cannot produce a coherent pattern like the dependence of ρ(Δr) on the mainshock magnitude. Second, we analyze the inverse average distance from the mainshock 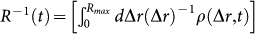, with R_max = 3 km (lower panel of Fig. 1). This quantity shows that, for all M, the mainshock occurrence time represents a singular point for R⁻¹(t), i.e., R⁻¹(t) grows before the mainshock occurrence and decreases after. This indicates that mainshocks are not part of a sequence triggered by large events that occurred before the time window used in the FB procedure. Finally, we find that both the number of aftershocks and foreshocks grow exponentially with the mainshock magnitude, consistently with a productivity law (see Supplementary Fig. 6). We note that the existence of reasonable productivity coefficients indicates that mainshocks are correctly selected.

Figure 1. Aftershocks and foreshocks spatio-temporal organization in Southern California.

Left upper panel. The linear density probability ρ(Δr) for foreshocks (filled circles) and aftershocks (empty diamonds) are obtained considering all events occurring within 12 hours from the mainshock. Different colors correspond to mainshocks in different magnitude classes, m ∈ [M, M + 1), and M = 2, 3, 4 for black, red and green symbols respectively. We restrict the distribution to Δr ≤ 3 km in order to reduce the contribution from background seismicity. Right upper panel The linear density probability ρ(Δr) averaged over 50 independent realizations of synthetic catalogs generated by the ETAS model. Details on the numerical procedure are given in the Methods. Data for aftershocks and foreshocks in numerical catalogs are indicated as continuous lines and pluses, respectively. Open diamonds refer to the aftershock ρ(Δr) in the experimental catalog. Black, red and green colors correspond to M = 2, 3, 4 respectively. Lower Panel. The inverse average distance 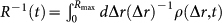is plotted as function of time from the mainshock. Here ρ(Δr, t) is the linear density probability in the interval [–1.2t, –t] ([t, 1.2t]) before (after) mainshocks for foreshocks (filled circles) and aftershocks (empty diamonds), respectively. We average 1/Δr, instead of Δr, in order to reduce the influence of background seismicity and, for the same reason, we fix R_max = 3 km. The same symbols as in upper panels are used.

Table 1. Parameters of the FB criterion and number of mainshocks, aftershocks and foreshocks selected by the FB criterion for each mainshock class. Aftershocks (foreshocks) are events occurring within 3 km and 12 hours after (before) the mainshock.

FB parameters	Value	Description
L	100 km	spatial range
y1	3 days	interval before
y2	12 hours	interval after

Once established the efficiency of the FB method in the identification of correlated couples, the crucial question is if events identified as foreshocks provide information on the subsequent mainshock magnitude. We emphasize that results reported in Fig. 1 (left panel) cannot be reproduced by single mode triggering models, where earthquakes are either independent (mainshocks) or triggered events (aftershocks). In these models, earthquakes identified as foreshocks are by construction mainshocks followed by a larger earthquake. Their asymptotic spatial decay is similar to the aftershock one, as observed in ref.24, but ρ(Δr) only weakly depends on the mainshock magnitude class M. In order to explicitly verify this point we have performed extended numerical simulations of the ETAS model²⁵,²⁶. More precisely we implement experimental parameters obtained from the likelihood maximization²⁷,²⁸ in a numerical code (see Methods). We therefore apply the FB procedure to identify foreshocks and aftershocks. Fig. 1 (right panel) shows that, as expected, the aftershock linear density probability depends on M whereas ρ(Δr) for foreshocks is weakly M-independent. As a consequence, ρ(Δr) for aftershocks and foreshocks are different, with discrepancies more pronounced for increasing M.

On the other hand, some features of the organisation in time, space and magnitude of experimental foreshocks are recovered in ETAS catalogs. These are consequences of the fact that, in numerical catalogs, most of the events identified as mainshocks, and preceded by close-in-time earthquakes, are aftershocks triggered by smaller earthquakes. Therefore, stacking several couples of such events leads to apparent clustering features. For instance, numerical foreshocks exhibit a productivity law with the mainshock magnitude as well as an increase both in the number of events (inverse Omori law) and in the inverse average distance R⁻¹(t) as the time approaches the mainshock. However, the growth of R⁻¹(t) is not symmetrical for aftershocks and foreshocks differently than the observed behavior in the experimental catalog (Fig. 1 lower panel). We wish to stress that differences are also observed in the number of identified foreshocks. A recent study¹⁴, indeed, has evidenced a deficit of foreshocks in synthetic ETAS catalogs with respect to the number of foreshocks in real seismic catalogs. This discrepancy has been attributed either to lack of aftershocks due to catalog incompleteness, or to a potential indication of the existence of a preparatory process leading to mainshock occurrence. In the Suppl.Fig.s 6,7 we present results of numerical simulations of the ETAS model confirming the foreshock deficit. The number of foreshocks in the synthetic catalog also increases exponentially with the mainshock magnitude. However, the coefficient of this growth is always significantly smaller than the experimental value and does not depend on the catalog incompleteness (see Suppl.Fig. 6).

Foreshocks before mainshocks with m > 6

The above observations suggest that seismic spatial and temporal clustering represents a potential tool to forecast mainshock occurrence. In the following we develop an alarm-based model for m > 6 mainshocks that implements results of Fig. 1 obtained for smaller mainshocks. We divide the Southern California region in cells of area dΣ = 0.04° × 0.04° and indicate with 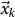the coordinates of the k-th cell center. We evaluate the daily expected number of earthquakes per cell 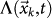, in the k-th cell position at the time t by means of the ETAS model (see Methods). Then, assuming that 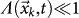, the daily probability to have at least one event in the k-th cell is given by 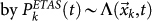. 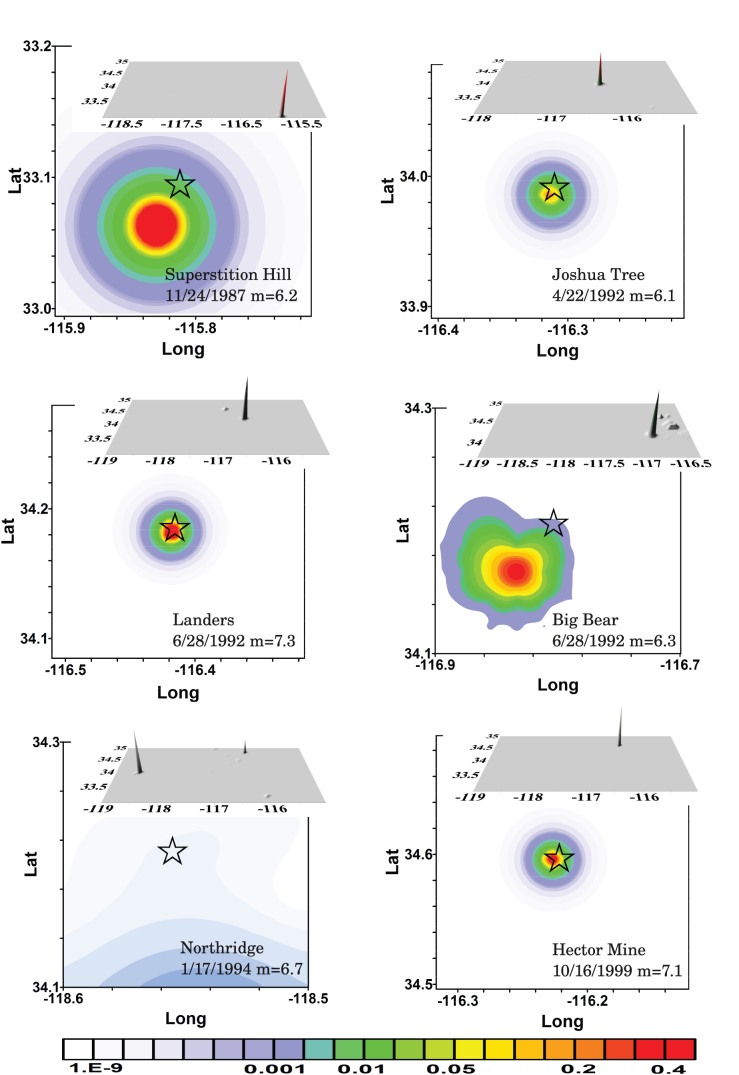For each m > 6 mainshock, the quantity 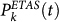is evaluated at the time t of the last m ≥ 2.5 earthquake preceding the mainshock. All seismic maps (see Suppl. Fig. 8) present sharp maxima (in the range [2E − 3, 2E − 2]) that are closely located (up to 5 kms) to the future mainshock epicenter, except for the Northridge earthquake. In this case a smaller peak (of amplitude 1.2E − 6) is located 25 km away from the future epicenter. The presence of sharp maxima in P_k(t) can be attributed to the occurrence of small earthquakes near the mainshock epicenter from few days up to few minutes before the mainshocks.

Within the ETAS scenario, these small events trigger other earthquakes whose magnitude is randomly chosen from a Gutenberg-Richter law; therefore a sequence that anticipates a large event does not have any distinctive feature. Results of Fig. 1 show a different scenario. In particular, the lower panel of Fig. 1 provides a possible mechanism to discriminate between spatial clustering due to foreshocks and aftershocks. In the case of foreshocks, indeed, we expect that for each sequence the inverse average distance R⁻¹ is an increasing function of time, whereas R⁻¹ decreases soon after mainshock occurrence. This indicates that seismicity tends to reduce the spatial variability approaching the mainshock in a characteristic way, concentrating in an area surrounding the future epicenter, and then to spread out after the mainshock occurrence. This scenario is in agreement with recent observations of earthquake migration towards the rupture initiation point of the mainshock, during the month preceding the 2011 Tohoku-Oki Earthquake²⁹. In the following we implement foreshock spatial clustering in a forecasting model. 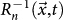At each event occurrence time t, we define in position the quantity which represents the inverse distance averaged over the last n events, with m ≥ 2.5, before time t. Moreover, we indicate with t_b < t the occurrence time of the (n + 1)-th earthquake before t, and evaluate 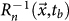as the inverse average distance for n events before t_b. We then introduce the quantity 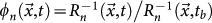which is expected to be φ_n > 1 before mainshock occurrence and φ_n < 1 soon after. This result is confirmed in Suppl.Fig. 9 for all m > 6 mainshocks. We then define a foreshock based (FS) alarm function 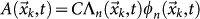in the k-th cell at time t, where C is a constant and Λ_n is the occurrence probability given by the ETAS model restricted to the last n earthquakes with m ≥ 2.5. This definition implies that our forecasting takes into account only n events closer in time to the future mainshock. When 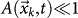, the daily probability to have at least one event in the k-th cell is finally given by 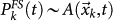. The constant C is, then, fixed by the condition the total number of expected events with m > 6 in the FS and in the ETAS model coincide, i.e., 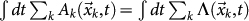, where the sum extends to all cells and the integral covers the entire catalog duration. This new procedure introduces only one additional parameter n with respect to the ETAS model. We have verified that results weakly depend on n for 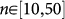, in the following we show results for n = 20. In Table 2 we list the daily occurrence probability in the cell containing the mainshock epicenter for the six m > 6 earthquakes, for both the ETAS and the FS model. Fig. 2 shows that before each mainshock a sharp maximum of 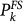is present at a small distance (few kilometers) from the future mainshock epicenter. Only in the case of the Northridge earthquake, the maximum location is 30 kms from the epicenter. For all mainshocks, in the cells containing the future epicenter, 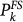is larger than the value obtained by the ETAS model. The most striking result is for the Landers earthquake, where a daily occurrence probability 24.75% is observed in the cell containing the future epicenter. Cells with even higher probabilities (39.2%) are observed before the Superstition Hill earthquake, where the mainshock epicenter is located at a distance of roughly 4 km from the maximum of P_k. The small value of 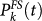before the Northridge earthquake can be attributed to the lack of close in time earthquakes leading to a very small Λ_n. Interestingly, the function 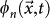shows evidence of spatial clustering even in this case (see Suppl.Fig. 9). The joint occurrence probability of all six m > 6 events, Π^FS is simply given by the product of the six 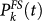at the time t just before the six mainshocks in the cells including the epicenter. The same quantity is evaluated for the ETAS model. We obtain a ratio Π^FS/Π^{ET AS} = 2.8E7 indicating a significant gain for the FS model with respect to the ETAS model.

Table 2. Information about forecasting maps. For each m > 6 earthquake the table lists the value of the probability evaluated by the FS model at the mainshock epicenter, and the same quantity evaluated by the ETAS model.

Mainshock	Mainshock Probability FS	ETAS Probability
SuperstitionHill	0.007	5E-4
JoshuaTree	0.04	2E-3
Landers	0.25	7E-3
BigBear	0.0025	8E-4
Northridge	1.2E-6	1E-7
HectorMine	0.075	1E-3

Figure 2. Daily occurrence probability just before m > 6 earthquakes.

The probability 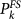to have a m > 6 earthquake within 1 day in a cell of side 0.04°, is evaluated for the 6 largest events in Southern California just after the occurrence of the last event before mainshock. For each mainshock, we plot 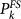over the entire Southern California region (upper panels), and a zoom over a box centered in the future mainshock epicenter (front panels). Black stars indicate the mainshock epicenter location and the values of 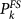can be obtained from the color code bar.

In Fig. 3 we apply a standard procedure outlined in ref.30, 31 to compare the FS forecasting model with the ETAS and the relative intensity (RI) model³². In the latter model, the occurrence probability 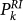is time independent and implements spatial clustering on the basis of smoothed historical seismicity. In the following 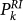is obtained using the parameters suggested by Rundle et al. and used in 31 to compare the RI model with a pattern informatics (PI) model³³ and with the United States Geological Survey National Seismic Hazard Map (NSHM)³⁴. Results have shown that neither PI nor NSHM provide significant performance gain relative to the RI reference model. The comparison is performed by means of standard Molchan diagrams, a plot of miss rate H versus the fraction of space–time occupied by alarms τ. The value (0, 0) in the plot represents perfect prediction with zero missed events and perfectly localized alarms. The descending diagonal from (0, 1) to (1, 0), conversely, represents the line with performance gain G = (1 − H)/τ = 1, i.e., the same performance for the two models. We use this procedure to compare the different models. More precisely, we evaluate 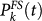in all cells and, for different thresholds P_th, we declare an alarm at the time t in those cells with 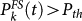. In this way we obtain 6 different values of miss rates. For each value of P_th, the fraction of space–time occupied by alarms is given by the integral in time and space of 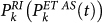over all cells with 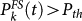. All points below the descending diagonal indicate that the FS model performs better than the other model. In particular, perfect prediction by the FS model corresponds to points lying on the vertical axis. Fig. 3 indicates that the FS model performs much better than the other models. We introduce the average gain 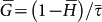, where 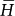and 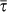are the average values of H and τ for the six points on the Molchan diagram. 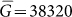The FS model exhibits an average gain with respect to the RI model , which becomes if the Northridge earthquake is not included in the average. The comparison with the ETAS model gives 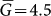. This result is weakly affected by the implementation of different spatial kernels in the ETAS model.

Figure 3. Space-time Molchan diagrams.

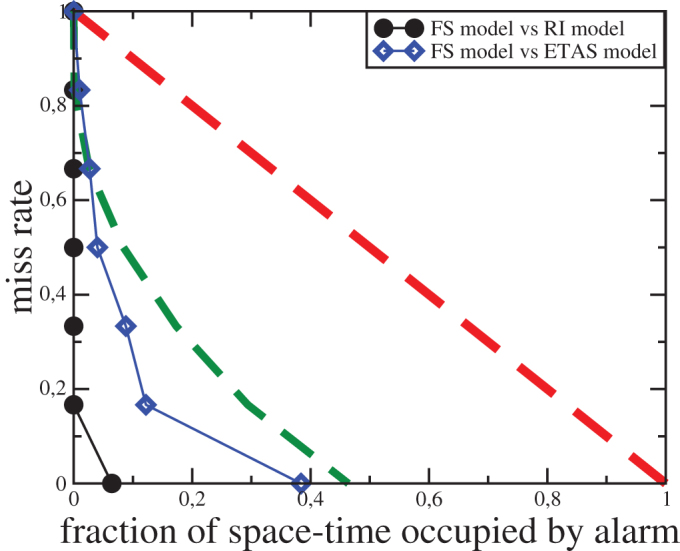
The Molchan trajectories of the FS model relative to the RI reference model (black filled circles) and to the ETAS reference model (blue open diamonds). Points on the descending diagonal (red curve) indicate equivalent model performance. For points below the dot-dashed green line, the null hypothesis (equivalent probability for the two models) can be rejected with a confidence level larger than 99,99%.

Discussion

It is interesting to notice that the large improvement is obtained only on the basis of the last few events before mainshock and it does not contain any information on the fault structure and historical seismicity. As final remark, we emphasize that all these results have been obtained retrospectively. An unbiased evaluation of the forecasting performances will be obtained through prospective tests. For this reason the next step will be to submit this model in the prospective experiments conducted by the Collaboratory for the Studies of Earthquake Predictability³⁵.

Methods

Mainshock, aftershock and foreshock selection criterion

According to the FB method an event is identified as a mainshock if a larger earthquake does not occur in the previous y days and within a distance L. In addition a larger earthquake must not occur in the selected area in the following y₂ days. Typical values used by FB are L = 100 km, y = 3 and y₂ = 0.5. Aftershocks and foreshocks are all events occurring, respectively, in the subsequent or in the preceding time interval δt = 12 h and within a circle of radius R = 3 km from the mainshock epicenter. Other parameter values provide similar results (see Suppl. Fig. 1).

ETAS model parameters and numerical simulations

In the ETAS model, the daily occurrence seismic rate in the position 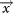at time t is evaluated on the basis of all the earthquakes with magnitude m_i ≥ m_c, epicentral location 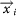and occurrence time t_i < t and is given by

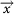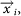where d_i is the angular distance between and , and 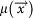is a time independent contribution related to the occurrence probability of Poisson events. Events with m < m_c cannot trigger future earthquakes.

For 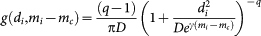, the model parameters, µ, B, α, c, p, D, q and γ, can be estimated by maximizing the likelihood function. In the specific case m_c = 2.5 the parameters have been kindly provided by J. Zhuang who obtained them by means of an iterative algorithm²³,²⁷,²⁸. Their values are B = 0.618, α = 1.198, c = 0.0024 days, p = 1.05, D = 9E – 7 deg², q = 1.034. µ is finally obtained on the basis of the procedure described in ref.17. The quantity 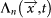used in the evaluation of 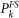is given by Eq.(1) restricting the sum over to the n events occurring before t. The spatial kernel used for results in Fig. 1 is obtained according to the following procedure: we fix for m = 2 g(Δr, m) = ρ(Δr), where ρ(Δr) is the linear density probability obtained for M = 2 in the experimental catalog (see Fig. 1 left panel). For m > 2, g(Δr, m) is obtained from g(Δr, m = 2) assuming the scaling relation ρ(Δr) = L(m)^–1F(Δr/L(m)), that fits experimental data with L(m) = L(m = 2)10^0.4(m–2).

Numerical simulations are performed according to the algorithm proposed by Zhuang et al. (Ref.¹⁷). In order to simulate a catalog with 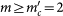, we assume that seismic properties do not depend on the lower magnitude threshold. This implies that the new set of parameters B′, α′, c′, p′, D′, q′, γ′, can be obtained from the m_c = 2.5 parameters, taking α′ = α, c′ = c, p′ = p, q′ = q γ′ = γ, 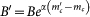and 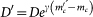. We have also implemented a different choice of model parameters and verified that results plotted in Fig. 1 (upper right panel) do not depend on the specific parameter set.

Author Contributions

E.L., L.de A. and C.G. were involved in all of the phases of this study. W.M. contributed to the development of the forecasting model and to paper writing. E.L. performed the analyses and numerical simulations.

Supplementary Material

Supplementary Information

SUPPLEMENTARY MATERIALS