Reverse engineering the euglenoid movement

Abstract

Euglenids exhibit an unconventional motility strategy amongst unicellular eukaryotes, consisting of large-amplitude highly concerted deformations of the entire body (euglenoid movement or metaboly). A plastic cell envelope called pellicle mediates these deformations. Unlike ciliary or flagellar motility, the biophysics of this mode is not well understood, including its efficiency and molecular machinery. We quantitatively examine video recordings of four euglenids executing such motions with statistical learning methods. This analysis reveals strokes of high uniformity in shape and pace. We then interpret the observations in the light of a theory for the pellicle kinematics, providing a precise understanding of the link between local actuation by pellicle shear and shape control. We systematically understand common observations, such as the helical conformations of the pellicle, and identify previously unnoticed features of metaboly. While two of our euglenids execute their stroke at constant body volume, the other two exhibit deviations of about 20% from their average volume, challenging current models of low Reynolds number locomotion. We find that the active pellicle shear deformations causing shape changes can reach 340%, and estimate the velocity of the molecular motors. Moreover, we find that metaboly accomplishes locomotion at hydrodynamic efficiencies comparable to those of ciliates and flagellates. Our results suggest new quantitative experiments, provide insight into the evolutionary history of euglenids, and suggest that the pellicle may serve as a model for engineered active surfaces with applications in microfluidics.

Unicellular microorganisms have developed effective ways of locomotion in a fluid, overcoming fundamental physical constraints such as the time reversibility of low Reynolds number (Re) hydrodynamics (1). Amongst eukaryotes, most species swim beating cilia or flagella. Yet, through a long evolutionary history, some protists have developed unconventional functional strategies, accomplished by highly diverse subcellular structures (2). A notable example is the euglenoid movement, or metaboly, executed by some species of euglenids (3). This peculiar motility mode is characterized by elegantly concerted, large-amplitude distortions of the entire cell with frequencies of about f ≈ 0.1 Hz (4). Euglenids have attracted the attention of scientists since the earliest days of microscopy, when van Leeuwenhoek referred to them in 1674 as microscopic motile “animalcules” that were green in the middle, which challenged the classification of organisms into animals and plants (5). More recently, metaboly has inspired models for artificial microswimmers (6), although even its locomotory function remains unclear. In contrast with flagellar or ciliary motion, the euglenoid movement has not undergone close biophysical scrutiny, and fundamental questions remain open, including a precise understanding of the actuation mechanism leading to the body shape changes, or its hydrodynamic efficiency. Because all euglenids move primarily with their flagella, it is difficult to discern the role of the body distortions in the observed motion.

Euglenids are abundant in a wide range of aquatic environments and, with typical sizes from tens to hundreds of micrometers, are easily observed by optical microscopy. They display a striking diversity in terms of morphology, nutrition (phagotrophs, phototrophs, osmotrophs), and motility, making of euglenids an excellent system to study evolution (7, 8). As other protists, they cannot resort to cell specialization to accomplish vital functions. Instead, they encapsulate all the functionality required for survival in a single cell, with an elaborate machinery revealed by ultrastructual studies. Euglenids are enclosed by a striated surface with two opposing poles called pellicle. The pellicle, the major trait of morphological diversity in the group, is a cortical complex consisting of the plasma membrane, a set of interlocking proteinaceous strips, microtubules, and tubular cisternae of endoplasmic reticulum arranged along the strips (3). The ability of euglenids to undergo metaboly has been correlated with the morphology of the pellicle. Flexible pellicles possess a large number of articulated strips (a few tens) often wrapped helically around the cell, whereas rigid pellicles can have as few as four fused strips arranged either helically or along the meridians of the cell. Some euglenids exploit their body flexibility to merely round up, elongate, or gently bend. Here, we focus on the most extreme oscillatory motions displayed by some species.

Detailed observations of Euglena fusca, possessing a pellicle decorated by easily traceable particles, have shown that shape changes are accompanied by sliding between adjacent pellicle strips (9, 10); as the shape changes, the pellicle strips retain their length and width, but change their helicity. This mechanism is consistent with the commonly observed twisting motions around the long axis of the cell accompanying metaboly. These pellicle rearrangements are thought to be driven by the sliding of microtubule complexes relative to the proteinaceous strips and controlled by calcium sequestration in the tubular cisternae of endoplasmic reticulum. Although the molecular motor has not been identified, the active motions are thought to be fueled by ATP (11). Further experimental interrogation of metaboly with modern biophysical techniques is still lacking.

The euglenoid movement confronts us with far-reaching biological and biophysical questions. One such issue is the competitive advantage of metaboly. Although metaboly is an oddity in microscopic locomotion, it has persisted through natural selection coexisting within individuals with flagellar motility in a significant part of the phylogenic tree of euglenids. Another intriguing aspect of metaboly is the operation of the distributed machine that elegantly and robustly executes the body motions, and that may inspire man-made active envelopes. As a first step, our goal here is to understand the kinematics and hydrodynamics of the euglenoid movement. For this purpose, we quantitatively analyze movies of metaboly recorded by others, representative of common observations by protistologists and physical scientists interested in motility (4). We examine these recordings with statistical learning methods. We then propose a model for the pellicle kinematics, which establishes a precise connection between distributed actuation and shape changes. Finally, we assess by numerical simulations the hydrodynamic features of the euglenoid movement.

Quantitative Observations

Data and Methods.

We start from video recordings of four photosynthetic specimens, labelled euglenid #1 through #4, three of which are of the genus Eutreptiella, and the fourth belongs to either a Euglena or a Eutreptiella species. We assume that these euglenids remain essentially axisymmetric as they undergo metaboly, in agreement with their general description (12) and with detailed scrutiny of the movies studied here (see Fig. S1). Therefore, they can be described by their generating curve in the symmetry plane.

From the viewpoint of low Re locomotion, a swimming stroke is a closed path in shape space, which needs to be nonreciprocal to accomplish net motion. We next propose a method to identify and parametrize such a path for further quantitative examination (see Fig. 1). In recent years, statistical learning methods have been increasingly used to understand stereotyped animal behavior; see, e.g., related studies on the motility of Caenorhabditis elegans (13, 14). Because the stroke is expected to be a nonlinear manifold of dimension one, here we resort to a nonlinear dimensionality reduction technique called Isomap (15). This method identifies nonlinear correlations of high-dimensional data points (here snapshots of the cells describing their shape) by embedding them in low dimensions in a geometry-preserving manner.

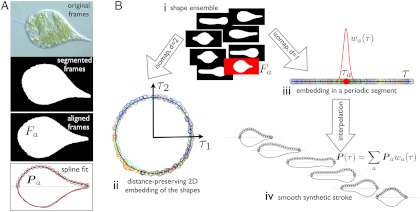
Fig. 1.

Quantitative analysis of the movies: method. (A) The frames are segmented and aligned to obtain images of F_a containing information about the shape alone, devoid of translation, rotation, or textures. A B-spline curve, given by its control polygon P_a (black circles), is fitted to the boundary of F_a and is a generating curve of the axisymmetric representation of the pellicle. Original frame image courtesy of Richard E. Triemer. (B) The segmented and aligned frames (i), representative of the shapes adopted by the cell, are embedded in low dimensions by a nonlinear dimensionality reduction technique called Isomap (15). The algorithm maps each frame to a low-dimensional point (circles in ii and iii, color labeling chronological order), so that the intrinsic distance between frames (shape dissimilarity) is preserved as much as possible by the low-dimensional representation. The embedding in the plane (τ₁, τ₂) (ii), shows that the stroke is a closed nonreciprocal path in shape space. Consequently, it can be most compactly described by embedding the frames in a periodic 1D segment (iii), from which we parametrize the stroke as a function of τ by interpolation (iv) with smooth basis functions w_a(τ). At any given τ, the synthetic stroke is a weighted average of the curves fitting video frames whose 1D embedding is in the vicinity of τ. The parameter τ is not proportional to physical time, ignored by the manifold learning algorithm, but rather to arc length in shape space. See SI Text, section Video Processing and Parametrization of the Stroke, for technical details.

First (Fig. 1A), we gather the collection of shapes adopted by each euglenid by segmenting and aligning the video frames. We represent numerically the shape of each frame by fitting a spline curve to the boundary of the aligned segmentation. Second (Fig. 1B), we identify the geometric structure underlying the set of shapes (i) with Isomap. We embed the shapes in 2D (ii) to examine the nature of the path described by the euglenids in shape space. Because the shape ensemble is essentially a one-dimensional loop, we further embed the shapes in a periodic 1D segment labelled by τ (iii), where the frames are ordered by shape proximity. With the 1D embedding, we parametrize the geometric stroke smoothly (iv). This procedure filters some of the noise while closely following the data; see Fig. S2 A and B. The resolution of the result is limited by optical artifacts and images out of focus, which bias the segmentation, and possibly by slight departures from axisymmetry. Yet, the quality of the numerical stroke is sufficient for quantitative examination (see Movie S1).

Because our method is based on geometric similarity, τ measures arc length in shape space rather than physical time. The hydrodynamic efficiency depends on the relative rate at which different parts of the stroke are executed (the net displacement after one cycle does not). To inspect the pace along the stroke, we obtain from the data the relation between τ and normalized physical time t.

Results.

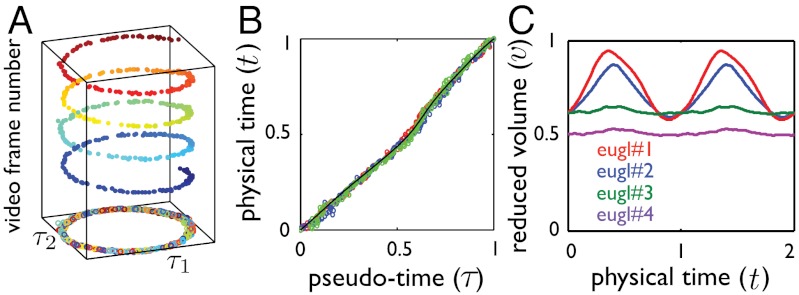
We find that nonlinear dimensionality reduction reveals vividly the signature of low Re swimming for each of the four euglenids, with well-defined nonreciprocal paths in shape space over the many cycles captured in the movies (Fig. 2A and Fig. S3A). Different specimens perform geometrically distinct strokes (Fig. S2C), and, for a given specimen, each stroke is executed multiple times with the same pace; i.e., the relation between τ and t is nearly the same over several strokes (Fig. 2B and Fig. S3D). With the numerical stroke at hand, we first examine elementary features such as the surface area S(t) and the volume V(t) enclosed by the pellicle. We express volume in nondimensional terms as the reduced volume 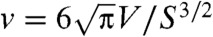, the ratio between the cell volume and the volume of a sphere with the same surface area. Thus, v ranges between 0 to 1. We find that the surface area of the four euglenids remains nearly constant along the stroke, with deviations below 5% (Fig. S3C). This observation is consistent with the hypothesis that pellicle deformation is mediated by relative sliding of pellicle strips, which retain their length and width (9). Such a deformation is called simple shear in continuum mechanics, and preserves area locally. The small area deviations may be due to the systematic errors in the data acquisition mentioned earlier, or to a slight area deformability of the pellicle. Strikingly, the body volume behaves very differently for euglenids #1 and #2 and for euglenids #3 and #4; see Fig. 2C. The former exhibit reduced volume deviations of around 20% and average reduced volumes of around 0.75, while the latter show essentially constant reduced volume of smaller magnitude. The volume-changing euglenids necessarily flow significant amounts of fluid in and out of their body quite rapidly during the stroke. The contracting vacuole of euglenids, connected to an invagination called reservoir located at one end of the cell, is known to regulate water, although generally at longer time scales. The motion of the internal organelles during metaboly, clearly seen in the movies, suggests that the volume variations are accommodated by a distributed fluid permeation rather than by localized jets.

Fig. 2.

Quantitative analysis of the movies: results. (A) Two-dimensional embedding of a stroke plotted against video frame number, showing the shape and pace uniformity of the stroke over several realizations. Isomap identifies similar shapes from different realizations (here about four cycles) and yields a single geometric stroke. (B) Pseudo-time parameter τ against normalized physical time t during three full strokes represented in different colors, showing that path in shape space is traveled with a well-defined pace (here, euglenid #3). The black line shows the fit used to reparameterize time. (C) Reduced volume, v, as a function of time during two strokes. We distinguish two distinct motility styles: a volume-changing style for euglenids #1 and #2, and a volume-preserving style for euglenids #3 and #4. See Fig. S3 for the full data.

Pellicle Kinematics

Theory.

The information about the kinematics of the pellicle obtained above is incomplete, because shape alone does not report on the motion of material particles; specifically, no quantitative data is available about the tangential motions within the symmetry plane and in the azimuthal direction. A careful inspection of some of the movies reveals that, while changing shape, the cell body twists nonuniformly around the symmetry axis. We next describe a theory for the pellicle kinematics, which allows us to recover the full velocity field of the pellicle and also provides a precise understanding of the concerted actuation leading to metaboly.

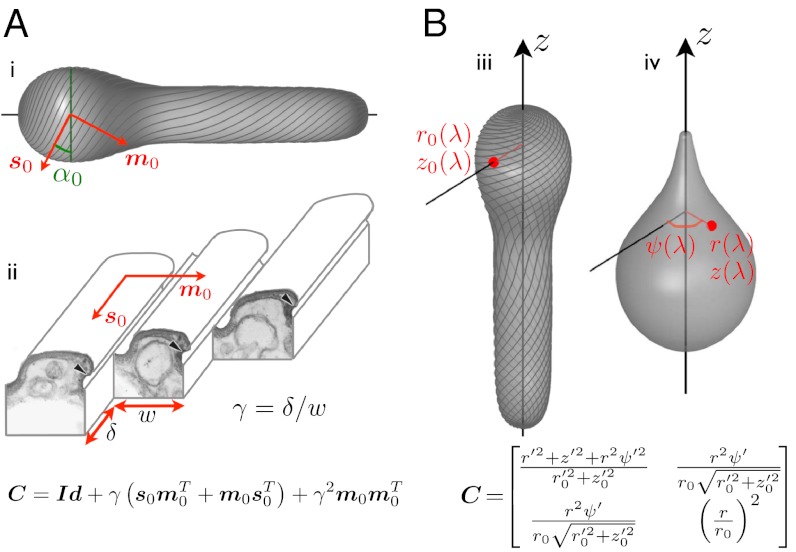
The key assumption in this theory, as discussed earlier, is that the pellicle deforms by simple shear γ along the strips (Fig. 3A). Consequently, the pellicle deformation is locally area preserving, and we can label the material parallels of the axisymmetric pellicle with a body coordinate λ, measuring the fraction of total area delimited by a given parallel (see Fig. S4). By time differentiation of the generating curve at fixed λ, we can compute the pellicle velocity within the symmetry plane.

Fig. 3.

Pellicle kinematics: theory. (A) Surface strain (the 2 × 2 matrix C) is derived assuming simple shear along the strips, γ, acting on a reference pellicle. The reference pellicle conformation (i,iii) is defined by a shape and a pellicle conformation, given by the tangent vector fields s₀ and m₀, along the strips and perpendicular to them, or by the angle α₀ between the pelliscle strips and the surface parallels. (ii) Ultrastructure of the pellicle (transmission electron micrograph from ref. 7, Copyright 2001 The Society for the Study of Evolution), and depiction of the sliding between adjacent strips causing the pellicle shear γ. (B) Surface strain, C, is now derived by comparing a reference configuration, (iii), given by r₀(λ) and z₀(λ), where λ is the body coordinate, and a deformed configuration (iv), given by r(λ), z(λ) and the azimuthal displacement relative to a fixed direction ψ(λ). The red point denotes a material particle attached to the pellicle, and ()^′ denotes differentiation with respect to λ. Matching the microstructural (A) and the shape-derived (B) expressions for the strain, we find equations relating pellicle shear, pellicle orientation, shape changes, and azimuthal motions.

We next recover the azimuthal motions and the pellicle shear. Consider an arbitrary but fixed conformation of the pellicle, given by its generating curve [r₀(λ) and z₀(λ)] and by the orientation of the pellicle strips, which could be obtained by in vivo imaging. This orientation is given mathematically by the vector field s₀ along the strips, or by the angle the strips form with the surface parallels α₀(λ) (Fig. 3A). We take this conformation as a reference. The strain of the pellicle surface relative to the reference configuration can be characterized at each point by the Cauchy–Green deformation tensor C (16), which by axisymmetry only depends on the body coordinate λ. From the actuation viewpoint, we obtain a first expression for C, depending on the reference pellicle orientation and the pellicle shear; Fig. 3A. On the other hand, comparing the reference state with a new configuration, given by r(λ), z(λ), and the azimuthal displacement ψ(λ), we obtain a second expression for C; Fig. 3B. Matching the two expressions, we find the relation between the global conformation (including shape and pellicle helicity) and the local actuation; see SI Text, section Pellicle Kinematics, for details and Fig. S5 for a validation.

Here, we have obtained from the movies a trajectory of shapes, r(λ,t) and z(λ,t). The theory then provides expressions for the associated azimuthal displacement ψ(λ,t) and the pellicle shear γ(λ,t), from which in turn we evaluate the full velocity field and the conformation of the deformed pellicle strips along the stroke. The theory can also be used to evaluate the deformed pellicle shape and helicity resulting from a prescribed pellicle shear γ(λ,t) acting on a reference conformation, although we do not explore here the design of strokes.

The theory imposes a constraint on the shapes achievable from a given reference pellicle; namely, r/r₀≥| sin α₀|. Consider a reference pellicle with strips parallel to the meridians; i.e., α₀(λ) = π/2. Then the shape at instant t is accessible from the reference pellicle if r(λ,t)≥r₀(λ), consistent with the fact that thin parts of flexible pellicles display strips with almost no helicity. We can access all the shapes of the stroke by defining r₀(λ) as the smallest radius adopted by the material parallel λ, and integrate z₀(λ) from local area preservation. This procedure defines an optimal reference pellicle for each euglenid, which achieves the observed shapes with minimal pellicle shear at every point; we adopt this reference pellicle in the absence of detailed imaging.

Results.

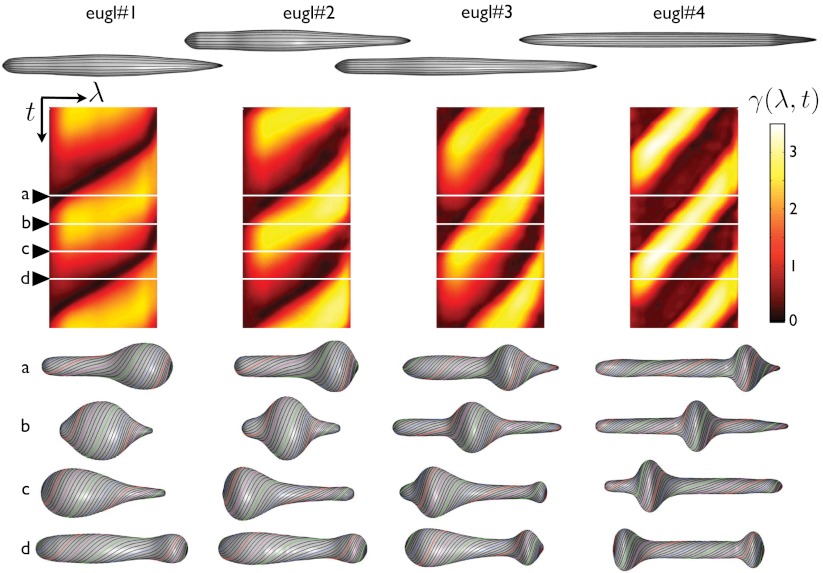
Fig. 4 summarizes the application of our theory to the four euglenids, highlighting the link between distributed actuation, pellicle conformation, and shape. The reconstructed pellicle shears γ(λ,t) of the four euglenids exhibit distinct patterns, but also common features. A bump of high pellicle shear near the head of the cell (snapshot a) travels toward the tail (snapshots b and c). This traveling shear bump reflects in the shape as a bulge that moves from head to tail, reminiscent of peristaltic movements. When it reaches the tail, the shear bump decays while a new one appears at the head (snapshot d) before the cycle closes. Euglenid #1 exhibits the bluntest pattern and shape trajectory, and only reaches pellicle shears of 250%. In contrast, euglenid #4 executes a remarkably sharp and regular pattern of pellicle shears, reaching 340%, with a corresponding well-defined bulge that slides along a cylindrical body of nearly constant radius. Some species of osmotrophic genera, such as Astasia and Distigma, exhibit a similar swimming style to the photosynthetic euglenid #4. With an estimated pellicle width of w ≈ 250 nm, we predict a sliding displacement between adjacent strips of up to δ ≈ 850 nm for this euglenid. By differentiating the map of γ(λ,t) in Fig. 4, we find that 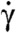reaches 20f Hz, leading to a maximum sliding velocity of 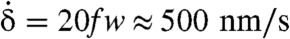, consistent with the velocities of molecular motors along microtubules (17, 18). The similarity between our pellicle reconstructions and observations of flexible pellicles, with a clear correlation between radius and pellicle orientation, is remarkable.

Fig. 4.

Stroke kinematics: relationship between the local actuation and shape changes. Reference conformation of the pellicle for each euglenid (top), exhibiting very small reduced volumes. Map of the pellicle shear recovered from the observations as a function of time and body coordinate γ(λ,t) (center), shown for two full synthetic strokes. The pellicle shear distributions acting on the reference configurations produce the shapes and pellicle conformations shown below.

Hydrodynamics of the Stroke

Combining the movie processing and the theory for the pellicle kinematics, we compute the surface velocity during the strokes, and analyze the hydrodynamics by placing the model euglenids in a Newtonian fluid. With a typical size of 50 μm and a stroke frequency f ≈ 0.1 Hz, we estimate Re ≈ 10^-4. We solve the Stokes equations with a boundary integral method, and the linear velocity along z and the azimuthal spin of the cell are calculated from the self-propulsion condition (19); see SI Text, section Hydrodynamics, for details. We assume that volume changes are accommodated by a uniform normal permeation velocity. The fluid velocity at the pellicle is then the surface velocity plus the permeation velocity, which is not very significant even for the volume changing euglenids #1 and #2 (see Fig. S6).

Table 1 summarizes the kinematic features and swimming performance of the four euglenids (see Table S1 for additional data). We evaluate the swimming performance with the linear displacement in one stroke U, measured in units of body length 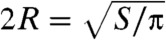, and with Lighthill’s efficiency Eff_L. This conventional notion of efficiency is defined as the ratio between the power needed to drag the swimmer at the average velocity W = U/T and the average power exerted by the swimmer on the surrounding fluid during the stroke, P^out. Because our swimmers change shape continuously, we consider 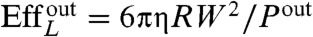, where η is the fluid viscosity. We find that all euglenids move by a few tenths of a body length in one stroke, and exhibit efficiencies in the order of 1%. With the typical frequencies of metaboly, the swimming speeds are very low, W ≈ 1–2 μm/s, between one and two orders of magnitude slower than during flagellar locomotion. Remarkably, the hydrodynamic efficiency is comparable to that estimated for ciliates and flagellates (20). We find that euglenid #1 is the slowest and least efficient swimmer, followed by #2 and #3, with comparable performance, and finally #4 is the best, with a displacement of 40% of the body length per stroke and 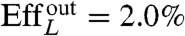. The table suggests that swimming performance is correlated with maximum pellicle shear. The best swimmer is a volume-preserving specimen with the lowest reduced volume, although there is no clear trend in this respect. See Movie S2 for a visual depiction of the stroke kinematics and the resulting linear and angular motion for the four euglenids.

Table 1.

Summary of the kinematic features and swimming performance of the four strokes

Euglenid		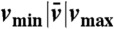γmax	U	, %	, %
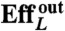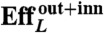#1	0.58|0.76|0.95	2.5	0.16	0.71	0.24
#2	0.60|0.72|0.87	3.0	0.27	1.6	0.57
#3	0.61|0.63|0.65	3.0	0.25	1.6	0.48
#4	0.50|0.51|0.53	3.4	0.40	2.0	0.76

U denotes the net displacement in one stroke, in units of body length 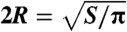(the diameter of a sphere with the surface area of the swimmer). Eff_L denotes the Lighthill efficiency, accounting for either the outer, or both the outer and inner fluids. denotes the average reduced volume during the stroke.

The hydrodynamics in the symmetry plane are completely decoupled from the azimuthal hydrodynamics, by the linearity and symmetry of the equations. Thus, the azimuthal energy dissipation in the fluid is a toll on the swimmer efficiency resulting from the mechanism used by the pellicle to change shape. It accounts for about 20% of the outer fluid dissipation (see Table S1). Lighthill’s efficiency disregards the internal energy losses, passive or metabolic, known to be dominant in other microorganisms (21). Without attempting to evaluate these, we now view the swimmer as an isolated active surface embedded in a fluid, and consider the inner fluid dissipation as well. Remarkably, the inner dissipation is very large, about three times the outer counterpart, resulting in efficiencies about three times smaller.

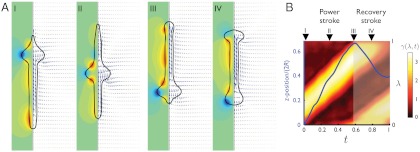
Fig. 5 illustrates the fluid flow patterns around euglenid #4 and correlates these with the forward displacement during the stroke. Similar results are obtained for the other euglenids. We can clearly distinguish between a power and a recovery phase. During the power stroke, a bulge slides down the slender body, producing a characteristic flow pattern that propels the swimmer forward monotonically. During the recovery stroke, the swimmer moves backward and the bulge at the tail disappears at the expense of a growing bulge at the head. This requires a considerable forward rearrangement of fluid and pellicle mass, clearly noticeable in the flow pattern. The large internal streaming during this phase agrees with the motion of the organelles observed in movies of metabolic euglenids. While the energy dissipation in the outer fluid is quite uniformly distributed along the stroke for all four euglenids, the average dissipation power of the inner fluid is three to four times larger during the recovery phase than during the power phase. Because optimal strokes with respect to a dissipation metric exhibit uniform dissipation rate (22), this shows that the observed strokes do not minimize internal dissipation, despite that being the largest contribution. Fig. 5B summarizes the correspondence between the distributed actuation mechanism and the resulting forward motion during the power and recovery phases.

Fig. 5.

Stroke hydrodynamics of euglenid #4. (A) Flow pattern around the pellicle at selected instants along the stroke. The fluid velocity field in the symmetry plane is indicated by blue arrows, and the azimuthal component is shown with isocontours, where green is zero, blue negative, and red positive. (B) Relationship between actuation and forward motion, where the vertical axis is the body coordinate λ for the color map of γ(λ,t) and z position (average between the head and the tail) in units of body length for the curve in blue. Both the actuation pattern and the forward motion clearly delineate a power and a recovery phase in the stroke.

Discussion

Our study suggests many new questions. A number of quantitative experiments could test and complement our theory. A detailed kinematical picture of the pellicle during metaboly can be obtained in vivo by light microscopy under ultraviolet illumination (23), while particle image velocimetry (24) can resolve the hydrodynamics and shed light on the inflow and outflow management of volume-changing euglenids. Our observation about the volume variations challenges the predominant conceptual models of swimming at low Re (6, 25), although swimmers permeating fluid across a fixed body shape have been analyzed (26). It is not clear if volume changes are passive, as a consequence of the pellicle deformation, or if these two phenomena are regulated in concert. Experiments on extracted cell models suggest that the euglenoid movement is mediated by a spatiotemporally nonuniform calcium sequestration, which triggers the pellicle activity (11). This mechanism could osmotically drive water permeation, which may enhance the exchange of nutrients and wastes. It is known that photosynthetic euglenids can acquire nutrients by osmotrophy.

Having established that metaboly is a competent motility mode, the evolutionary benefit of such a large biological investment remains unclear, when coexisting with flagella, an alternative strategy of demonstrated success. Current evolutionary theories suggest that the earliest ancestors, rigid and feeding on small bacteria, developed a flexible pellicle to engulf larger eukaryotic prey. Photosynthetic species evolved from phagotrophs after engulfing green algae, and some of these lost the pellicle flexibility by strip fusing (8). Presumably, the pellicle flexibility may have found a secondary utility, besides mediating in eukaryovory, and may have persisted because of this in photosynthetic euglenids such as those studied here, as well as in some osmotrophs. The benefit of metaboly may be related to the stirring of the cytosol or the surrounding medium, or to locomotion. Interestingly, many euglenids live in interstitial, soil-rich, or eutrophic water, suggesting that metaboly may be particularly well-suited to move in “difficult” conditions such as confined environments, or in media of complex rheology, known to affect flagellar efficiency (20, 27). This hypothesis is supported by a marine photosynthetic species, lacking emergent flagella but exhibiting strong metaboly, known to migrate vertically through the sand of the benthic zone in diurnal cycles (28). Thus, the heterogeneity of the biophysical traits of metaboly could complement the morphological and molecular data used in current phylogenic studies of euglenids, and provide new clues about their evolutionary history.

Besides complementing experimental observations to obtain a complete kinematical picture of metaboly, the theory for the pellicle deformation provides the background for further biophysical studies. It is possible to optimize the pellicle shear to achieve maximal efficiency, and investigate the role of volume constraints or different dissipation metrics. Similar studies have brought new insight for cilia (29), flagella (30, 31), and model swimmers undergoing full body distortions (22, 32, 33). Furthermore, the theory can be used to compute the resisting forces, arising from the internal and external friction and from the pellicle bending elasticity, that need to be overcome by metabolic activity.

The pellicle suggests itself as an appealing design concept for an active material (34). The local actuation of the pellicle produces a local strain incompatible with the current geometry, which is only realizable by further curving and producing shape changes (35). Similar concepts of material-as-machine relying on martensitic materials have been put forth (36, 37), and actually operate in biological organisms such as the tail sheath of bacteriophage T4 (38). Viewed as an active surface, the pellicle exhibits an interesting balance between shape flexibility and controllability, which explains why metaboly is such an elegantly concerted motion as compared, e.g., with the amoeboid movement. The pellicle has a single degree of freedom available for the local surface deformation, the pellicle shear, which nevertheless is sufficient to realize a wide family of shapes. Observations show that flexible euglenids can perform bending and torsional maneuvers of remarkable agility, including sharp turns. A general theory considering nonuniform pellicle shears in the azimuthal direction may delimitate the possibilities of this shape actuation concept, which may find applications in artificial microswimmers or peristaltic micropumps.

Conclusions

We have provided a detailed biophysical analysis of the euglenoid movement, a widely appreciated but poorly understood motility mode of euglenids. We have developed a statistical learning methodology to analyze strokes and applied it to four movies recorded by others. We have established the shape and pace uniformity of the strokes, and have parametrized the motions in a computer model. Some euglenids exhibit very large variations of their body volume during the stroke, while others keep their volume constant. A kinematical theory, assuming that the cell surface deforms by simple shear along pellicle strips, provides a precise link between distributed actuation and shape changes, explains common observations about the pellicle helicity, and provides the input for hydrodynamics. Metaboly is found to be a slow but efficient motility mode in water, which enhances stirring of the cytosol and the surrounding fluid, and may be advantageous in granular or complex media.