Calcium-dependent folding of single calmodulin molecules

Abstract

Calmodulin is the primary calcium binding protein in living cells. Its function and structure depend strongly on calcium concentration. We used single molecule force spectroscopy by optical tweezers to study the folding of calmodulin in the physiologically relevant range. We find that full-length calmodulin switches from a rich and complex folding behavior at high calcium to a simple folding pathway at apo conditions. Using truncation mutants, we studied the individual domains separately. Folding and stability of the individual domains differ significantly at low calcium concentrations. With increasing calcium, the folding rate constants increase while unfolding rate constants decrease. The complete kinetic as well as energetic behavior of both domains could be modeled using a calcium-dependent three-pathway model. We find that the dominant folding pathway at high calcium concentrations proceeds via a transition state capable of binding one calcium ion. The folding of calmodulin seems to be designed to occur fast robustly over a large range of calcium concentrations and hence energetic stabilities.

Proteins interact with numerous partners when they function in our body. This interaction naturally also affects their structure and energetics. In extreme cases, proteins can only fold if they interact with a specific binding partner (1). Understanding of protein structure formation hence requires that the folding process be studied in the presence of those binding partners.

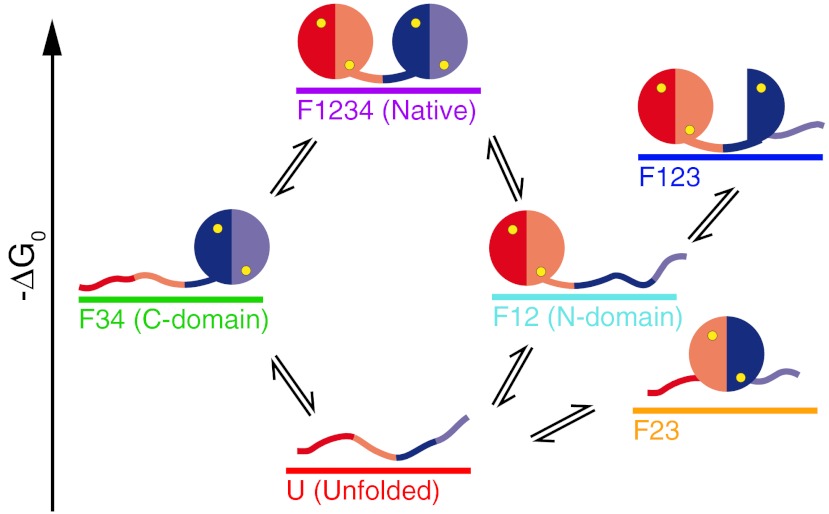
Calmodulin (CaM) is the most important calcium binding protein in our body and is involved in the regulation of numerous calcium-dependent pathways (2). Calcium binding as well as peptide binding properties have been studied in detail over the last decades (3–7). Despite its outstanding relevance, however, not much is known about the folding of calmodulin at physiologically relevant calcium concentrations. At very high calcium concentrations, we reported a complex folding pathway of calmodulin in a recent study (8). In this earlier study, we found that while calmodulin folds fast and robustly when its individual domains fold sequentially, its overall folding time is slowed whenever it folds into one of two off-pathway intermediates. Those intermediates involved, in one case, the non-native pairing of the EF hands 2 and 3, and in the other case the collapse of EF hand 3 onto the already folded N-terminal domain in a non-native conformation. We found that all of the on and off pathway states bind one calcium per folded EF-hand (Fig. 1). However, in vivo calcium concentrations are low. At those conditions, calmodulin switches between structurally distinct apo and holo conformations. Calcium-calmodulin dependent regulation of cellular processes critically relies on those conformations. A first characterization of the calcium-dependent folding of calmodulin at high calcium concentrations was performed in earlier experiments using AFM (9). However, technical limitations in resolution and drift stability limited the accessible range in calcium concentration as well as kinetics. In this paper, we use optical tweezers (10–12) to study single molecule folding/unfolding properties of calmodulin around physiologically relevant calcium concentrations.

Fig. 1.

Cartoon of the folding network of full-length calmodulin at high calcium. At high calcium, full-length calmodulin folds in a complex network of states (8). From the unfolded state (U, red), the molecule can proceed to the native state (F₁₂₃₄, purple) via an intermediate with only the C-terminal domain folded (F₃₄, green), or an intermediate where only the N-terminal domain is folded (F₁₂, light blue). From F₁₂, an additional EF hand can fold to form the off-pathway intermediate F₁₂₃ (dark blue). From U, the protein can populate another off-pathway intermediate where the EF hands 2 and 3 form a pair with non-native contacts (F₂₃, orange).

Results

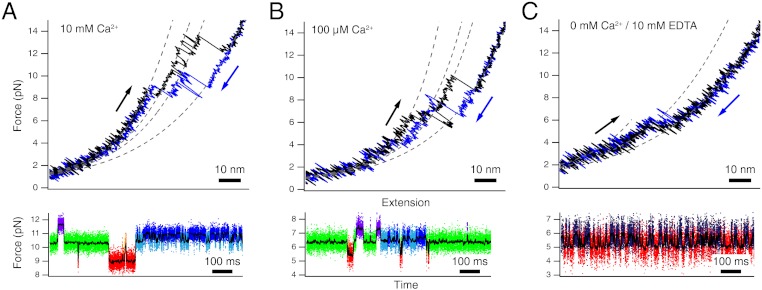
In a first set of experiments, we investigated the folding/unfolding mechanics of full-length calmodulin at calcium concentrations of 10 mM, 100 μM, and 0 μM Ca²⁺. We recorded both stretch and relax cycles at a pulling velocity of 500 nm/s (Fig. 2 A–C, upper traces) as well as made measurements where the trap centers were held at a constant separation and hence imposed an average force-bias on the fluctuating molecule (Fig. 2 A–C, lower traces). Assignment of states indicated by different colors in the constant trap separation measurements was performed using a Hidden-Markov-Model (SI Text).

Fig. 2.

Full-length calmodulin at varying calcium concentrations. Stretch-and-relax cycles (Upper) and constant trap separation traces (Lower) of full-length calmodulin at 10 mM Ca²⁺ (A), 100 μM Ca²⁺ (B) and 0 mM Ca²⁺/10 mM EDTA conditions (C). The constant trap separation traces are shown at intermediate biasing forces where all states are populated. Raw data points are colored after classification by a Hidden-Markov model. At 10 mM Ca²⁺ and 100 μM Ca²⁺, all six states described in Fig. 1 were identified. At 0 mM Ca²⁺/10 mM EDTA conditions, only two states remained. The colors in the lower parts of (A) and (B) correspond to the coloring in Fig. 1. The colors in the lower part of (C) are red: unfolded, dark blue: N-domain folded.

At 10 mM Ca²⁺, we find the complex pattern of various intermediate states reported earlier (8). In brief, calmodulin can populate the six states sketched in Fig. 1: fully folded (purple), N-terminal domain unfolded (green), C-terminal domain unfolded (light blue), one EF-hand of the C-terminal domain unfolded (dark blue), non-native pairing of EF-hands 2 and 3 (orange), fully unfolded (red). At concentrations of 100 μM, the pattern of populated states essentially remains, albeit at lower forces (8) (Fig. 2B). It is important to note that even at a concentration of 100 μM, calcium binding sites are saturated with calcium (13). At 0 mM calcium (Fig. 2C), the observed kinetic pattern changes drastically. The richness of intermediate states, observed under high calcium, can no longer be observed. In stretch-and-relax cycles (Fig. 2C, Upper), a rapid conformational transition close to equilibrium can be clearly observed at forces around 5 pN. This is further supported by constant trap separation measurements (lower traces of Fig. 2C). A two state transition (dark blue and red) with millisecond kinetics can be observed. The contour length change during this transition (24.4 nm, Fig. 2C) suggests that, in full length calmodulin, only one domain exhibits sufficient thermodynamic stability so that its folding under force can be readily observed in our experiments. An additional transition at lower lengths can only be vaguely inferred from contour lengths fit to the very low force regime (< 3 pN) of the force-extension curve (Fig. 2C). To investigate the changes in kinetics and stability of calmodulin at various calcium concentrations in more detail, we studied the N- and C-terminal domains separately using truncation constructs (Figs. 3 and 4 and Table S1). In the following, the N-terminal domain containing EF-hands 1 and 2 is called CaM₁₂; the C-terminal domain with EF-hands 3 and 4 is called CaM₃₄ (SI Text).

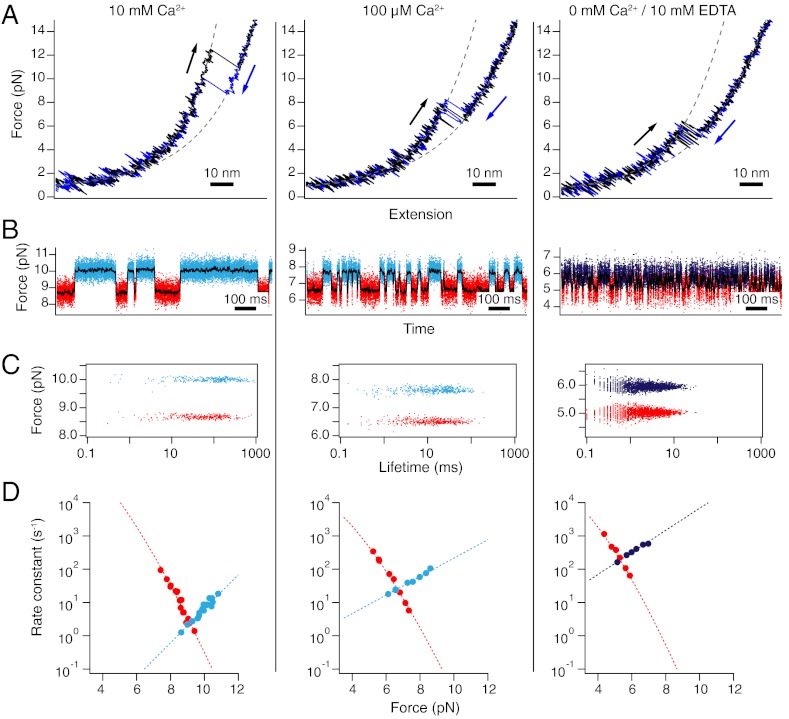
Fig. 3.

The N-terminal domain at calcium concentrations of 10 mM (Left), 100 μM (Middle) and 0 mM (Right). Shown are data from three individual molecules. (A) Stretch (black) and relax (blue) cycles at 500 nm/s. Dashed lines are fits to the folded and unfolded stretches. (B) Constant-trap separation traces at intermediate forces. The raw data are colored according to the classification by a Hidden-Markov model. Red: unfolded state, light blue: domain folded with calcium bound, dark blue: domain folded with no calcium bound. (C) Force-lifetime scatter plot for the traces shown in (B). Each dot is represented by the average force of one dwell plotted against its lifetime. (D) Force-dependent folding (red) and unfolding (blue) rate constants. Dotted lines are fits to the data.

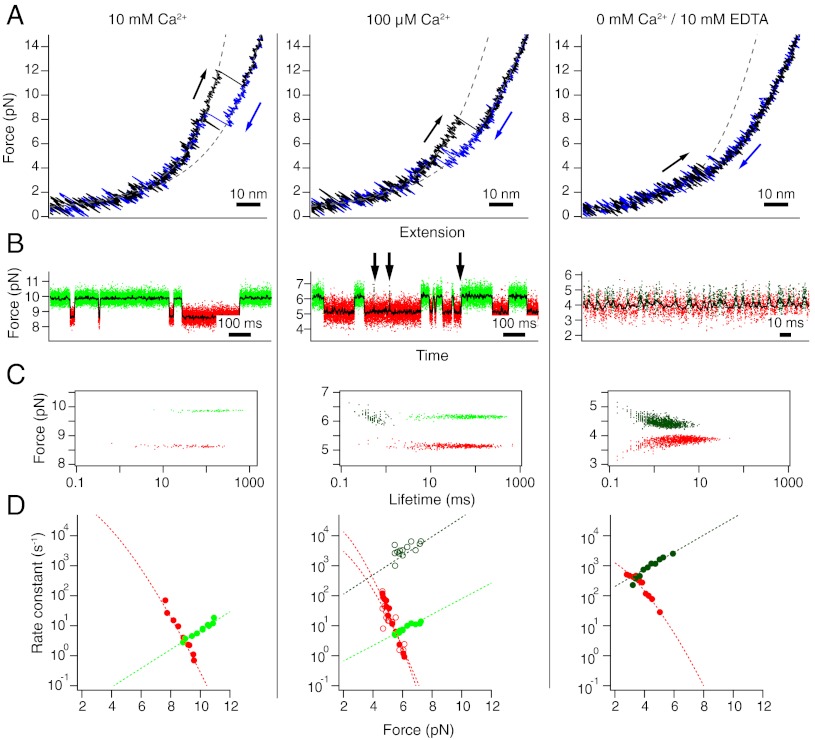
Fig. 4.

The C-terminal domain at calcium concentrations of 10 mM (Left), 100 μM (Middle), and 0 mM (Right). Shown are data from three individual molecules. (A) Stretch (black) and relax (blue) cycles at 500 nm/s. Dashed lines are fits to the folded and unfolded stretches. (B) Constant-trap separation traces at intermediate forces. Arrows indicate occurrences of short-lived folded states incompatible with lifetimes of the light-green folded state. The raw data are colored according to the classification by a Hidden-Markov model. Red: unfolded state, light green: domain folded with calcium bound, dark green: domain folded with no calcium bound. (C) Force-lifetime scatter plot for the traces shown in (B). Each dot is represented by the average force of one dwell plotted against its lifetime. (D) Force-dependent folding (red) and unfolding (green) rate constants. Dotted lines are fits to the data.

Isolated N-Terminal Domain.

Sample traces for stretch and relax curves, as well as constant trap separation measurements obtained at different calcium concentrations on CaM₁₂, are shown in Fig. 3. We observe clear two-state behavior under all calcium conditions. Forces drop while the midpoint transition kinetics get faster with decreasing calcium concentration. To distinguish the holo conformation of calcium-bound calmodulin from the calcium-free apo conformation, we used different coloring for the folded state (light blue vs. dark blue). In the absence of calcium under 10 mM EDTA (Fig. 3 Right), the transitions are indistinguishable both in length and kinetics from the transition observed in full-length calmodulin (Fig. 2C). The dwell-times and forces of the respective states are shown in the scatter plots in Fig. 3C. This analysis corroborates our assumption of a two state process. All dwell-times follow a single exponential distribution (Fig. S1A and SI Text). For a more complete kinetic characterization, we measured the force-dependence of the folding and unfolding rate constants (Fig. 3D). We found that both the folding and the unfolding branches shift as calcium concentrations change. To obtain folding/unfolding rate constants under zero-load conditions, we extrapolated the measured data points to zero force using established methods [(14), see Methods for details, dotted lines in Fig. 3D]. The curvature in the extrapolation of the folding branch is due to the non-linear entropic elasticity of the unfolded polypeptide contracting against load. Since transition state positions for unfolding under force generally lie close to the folded state, we used a linear extrapolation (Bell model) for the unfolding branch.

Isolated C-Terminal Domain.

Similar calcium-dependent measurements were performed for CaM₃₄. In stretch and relax cycles, a clear drop in mechanical stability can be observed with decreasing calcium concentrations. The differences between holo (Fig. 4, Left) and apo states (Fig. 4, Right) are even more pronounced than for CaM₁₂. As with CaM₁₂, the folding/unfolding kinetics become faster with decreasing calcium concentrations. A Hidden-Markov analysis shows that kinetics is two-state at very high calcium (Fig. 4, Left). In the absence of calcium, the midpoint forces of the transition drop to very low values of around 3.5 pN (Fig. S2). The respective Hidden-Markov analysis yields dwell times in the millisecond range, even faster than for CaM₁₂. The respective rate vs. force plot is shown in Fig. 4D, Right. An interesting effect can be observed at intermediate calcium concentrations. The constant trap separation measurements (Fig. 4, Middle) show that in addition to the long dwells marked in light green, also very rapid transient populations of the folded state marked in dark green can be observed. The two populations can be easily discriminated in a scatter plot (Fig. 4C). In addition to the stretched out data cloud at long lifetimes (light green), also, a cloud centered at lifetimes below 1 ms can be observed. This lifetime is identical to the expected lifetime of the apo-state at the respective forces of 5–6 pN. Apparently, for CaM₃₄, at low calcium concentrations a mixture of apo and holo states can be observed online in the single molecule experiments. The rate constants of the whole kinetic network, including the unfolded state (red), the holo state (light green) and the apo state (dark green) can now be extracted from the lifetime measurements (Fig. S1 B and C). The full circles in Fig. 4D indicate folding and unfolding to/from the holo state, while the open circles indicate folding and unfolding to/from the apo state.

Calcium-Dependent Kinetics.

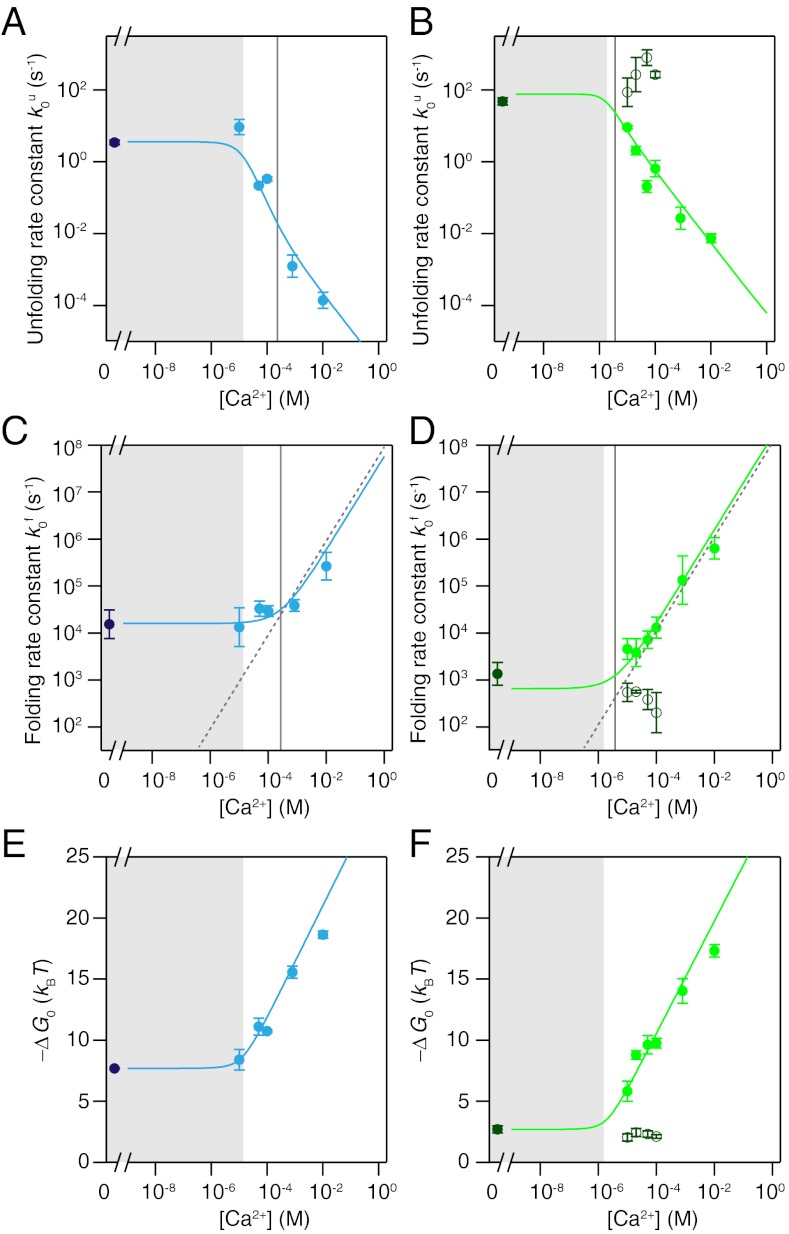
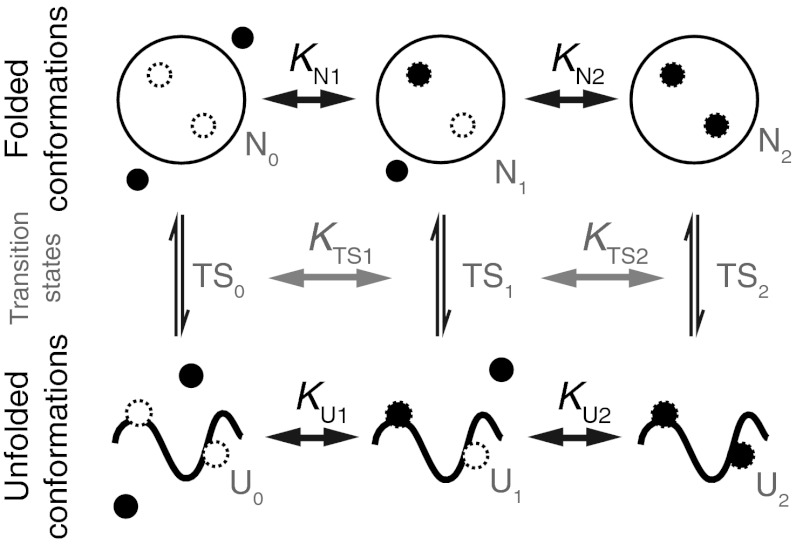
In order to compare the effect of calcium on the folding kinetics, we extrapolated the measured rate constants of folding and unfolding to zero load using the models described above. Fig. 5 A–D shows zero-load folding and unfolding rate constants for CaM₁₂ and CaM₃₄ at calcium concentrations between 0 and 10 mM. Both folding and unfolding rate constants depend on calcium concentration. In the absence of calcium, the unfolding rate constants are approximately 3 s^-1 and approximately 50 s^-1 for CaM₁₂ and CaM₃₄, respectively (Fig. 5 A and B). Above 10^-4 M the unfolding rate constants for CaM₁₂ drop while CaM₃₄ already deviates from apo behavior above 10^-5 M. The folding rate constants (Fig. 5 C and D) show an opposite trend. Apo folding rate constants were approximately 13000 s^-1 and approximately 1400 s^-1 for CaM₁₂ and CaM₃₄. The folding and unfolding rate constants for the apo C-terminal domain are consistent with values obtained in T-jump experiments (4). Folding rate constants for CaM₁₂ rise beyond 10^-3 M, while for CaM₃₄ they rise already beyond 10^-5 M. The dependence of both folding and unfolding rate constants on calcium can be modeled quantitatively using a kinetic model with a folding transition state able to bind calcium. The kinetic scheme we used is shown in Fig. 6. We assume that the exchange of calcium ions in the folded as well as unfolded state occurs in rapid equilibrium (15, 16). Calcium exchange in the transition state, however, is assumed to be slow compared to its life-time (15, 16). Analytical solutions for the model can be found in the methods section (SI Text).

Fig. 5.

Kinetic and equilibrium information for CaM₁₂ (left) and CaM₃₄ (Right) at varying calcium concentrations. (A, B) Zero-force extrapolated unfolding rate constants. (C, D) Zero-force extrapolated folding rate constants. (E, F) Equilibrium free energies of folding. Dashed lines in (C) and (D) are the calculated diffusion-limited on-rates for one calcium ion assuming a rate limit of 10⁸ M^-1 s^-1. Filled circles represent averages over several molecules at a particular concentration. Empty circles in (B, D, F) are values for the short-lived state as shown in Fig. 4, Middle. Error bars represent the SEM. Colored continuous lines are fits to the data. Vertical grey lines in (A–D) represent the value of K_TS1 as obtained from the fit. The shaded areas are the concentration range below 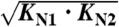, where the protein is predominantly ligand-free.

Fig. 6.

Model for folding and unfolding of an isolated domain. The folded state can exist in three conformations: unligated, with one calcium ion bound, and with two calcium ions bound. Similarly, the unfolded state can exist in all three conformations. Folding and unfolding can occur via a transition state that also can bind up to two calcium ions. We assume that the barrier crossing times are faster than the equilibrium of the transition state. Using this scheme, we can calculate the effective folding and unfolding rates. Of the two possible conformations for N₁ and U₁, only one is shown. They are indistinguishable in our assay.

A global fit to both the unfolding and folding rate data in Fig. 5 A–D using literature values for the calcium affinities K_N1, K_N2 [log ₁₀K_N1 = -4.62, log ₁₀K_N2 = -5.17 in molar units for CaM₁₂, log ₁₀K_N1 = -5.32, log ₁₀K_N2 = -6.21, for CaM₃₄ (13)] of the folded state was applied to the data. The unfolded state was assumed to have low affinity K_U1, K_U2 for calcium in excess of 1 M. The only free parameters were the folding and unfolding rate constants at 0 M calcium and the calcium affinities K_TS1, K_TS2 of the transition state for folding. In molar units, log ₁₀ K_TS1 was -3.6 for CaM₁₂ and -5.4 for CaM₃₄. Consistently, for both domains, the affinity for binding of a second calcium ion to the transitions state K_TS2 was very low. Hence, in the probed range of calcium concentrations, the transition state for folding/unfolding of calmodulin can only bind one calcium ion with a lower affinity of the N-terminal domain as compared to the C-terminal domain. As pointed out earlier, CaM₃₄ at low calcium concentrations exhibits a mixture of apo and holo states. The open circles in Fig. 5 show the calcium-dependence of the short apo states. As expected, the folding/unfolding rate constants for apo calmodulin do not depend on calcium concentration and exhibit values consistent with the measured values under apo conditions (solid dark green circles in Fig. 5).

Equilibrium Free Energies.

Beyond kinetic information, our assay allows us to extract equilibrium folding free energies from the data taken at various loads. Using probability distributions for the population of the folded and the unfolded state as a function of force (Fig. S3), the free energy difference between those two states can be calculated by taking into account the known elastic properties of the DNA and peptide linkers as well as the trap spring constant (12) (SI Text). The apo values we find for CaM₁₂ and CaM₃₄ are 7.7 and 2.5 k_BT, respectively. The calcium dependence (Fig. 5 E and F) can be modeled using an equilibrium version of the model above (5). Beyond the calcium affinities of CaM₁₂ and CaM₃₄ (approximately 10^-5 M and approximately 10^-6 M, respectively), the stability increases with a slope corresponding to the energy gain of 2· ln(10)k_BT per decade of calcium concentration expected from the solution chemical potential when two ions bind (see lines in Fig. 5 E and F).

Discussion

Holo to Apo Transition in Full-Length Calmodulin.

At high calcium concentrations, calmodulin folding and unfolding proceeds through a network of six states (see Fig. 1). This network has been described in detail in an earlier study (8). The high calcium concentrations in the millimolar range used in the earlier study are extreme considering normal cellular conditions where calcium concentrations vary in a range from hundreds of nanomolar to micromolar (17). The goal of this study was observing the changes in calmodulin folding as calcium concentrations fall close to the physiologically relevant range and holo to apo conformational changes occur. As long as calcium concentrations remain so high that all intermediate states within this network remain saturated, a qualitative change in the folding pathways is not to be expected. This is confirmed by the data in Fig. 2B taken at 100 μM. Even though the overall stability and hence folding/unfolding forces of all intermediate states drop as compared to 10 mM calcium, the connectivity as well as the number of states remain. If, however, the ligand is not present anymore, more drastic changes in folding pathways are expected. Such a drastic change indeed occurs when calcium is absent under EDTA conditions (Fig. 2C). Stretch and relax cycles now only reveal a single dominant two-state transition while another transition can only be inferred at very low forces (see dashed fits in Fig. 2C, Upper). From bulk experiments, it is known that under apo conditions the N-terminal domain is more stable than the C-terminal domain. Hence, the dominant transition in Fig. 2C represents unfolding of the N-domain while the less pronounced transition corresponds to unfolding of the C-domain. Interestingly, in full-length calmodulin the apo C-domain appears even weaker than for the isolated construct CaM₃₄ (Fig. 4, Right). This is in accord with an earlier report that in full-length calmodulin under apo conditions, the C-domain is weakened at the expense of the N-domain (5).

Even though, under apo conditions, from our data alone we cannot completely exclude a presence of non-native intermediates like F₁₂₃ or F₂₃ (see structural cartoons in Fig. 1), the absence of calcium will likely prevent their formation, thus simplifying the overall folding pathway as compared to higher calcium concentrations. Supporting this conclusion, solution experiments have shown that F₂₃ cannot form in the absence of calcium (18). Even though the individual domains of calmodulin fold more slowly at low calcium, an absence of intermediates and kinetic traps can increase its overall folding speed. While the average folding time at 10 mM calcium lies in the range of seconds (8), under apo conditions, in the absence of folding traps the average folding time will be in the millisecond range. Hence at low calcium conditions, which typically are found in a living cell, calmodulin will fold fast and robustly.

Calcium-Dependence of Folding Kinetics and Free Energies of the Isolated Domains.

Our experiments on the isolated N-terminal domain (CaM₁₂) readily reveal this domain as the stable domain also in full-length calmodulin under EDTA conditions. Both the kinetics as well as the midpoint forces of unfolding are identical to the dominant transition observed in wild-type (compare Fig. 2C to Fig. 3 A and B, Right). The isolated C-terminal apo domain (CaM₃₄) (Fig. 4, Right) is considerably less stable than apo CaM₁₂ (2.5 k_BT vs. 7.7 k_BT). The stability values we extract from our single molecule measurements for both domains are consistent with bulk values (13).

For a discussion of the calcium-dependence of folding and unfolding rate constants, it is important to note that we also observe changes of the transition state positions with calcium concentration. This can be seen in the rate vs. force plots of Fig. 3D where the slopes of the folding as well as unfolding branches differ among different calcium conditions. Hence, to compensate for this effect and simplify modeling of calcium-dependence, we extrapolated all folding and unfolding rate constants to zero force conditions (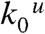 and 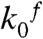in Fig. 5 A–D). Interestingly, both folding and unfolding rate constants depend on calcium. In an earlier study, an effect of calcium was only reported on the calmodulin folding rate constant (9). However, in this earlier study, measurements were performed in the presence of a calmodulin binding peptide. Moreover, a separation of folding and unfolding kinetics was not directly possible due to limited resolution in those measurements. The overall dependence of folding and unfolding of CaM₁₂ and CaM₃₄ could be successfully modeled by the kinetic scheme in Fig. 6 (SI Methods). 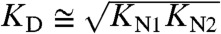At calcium concentrations below the dissociation constant for calcium binding, the folding and unfolding rate constants for both CaM₁₂ and CaM₃₄ remain constant (shaded areas in Fig. 5 A–D). Above K_D, folding rate constants increase while unfolding rate constants decrease with calcium. The slope of the increase of the folding rate constants towards high calcium concentrations directly reveals that, as soon as K_TS1 is exceeded, one calcium ion binds to the transition state during folding even at the highest calcium concentrations measured. A detailed calculation of the number of calcium ions bound to the native state as well as the transition state for both domains can be found in Fig. S4. Hence the dominant folding pathway for both domains at high calcium concentrations (Fig. 6) involves rapid and weak binding of one calcium ion to the unfolded state (U₀ → U₁) and subsequent fast folding over the one calcium bound transition state TS₁ into the native state N₁. Binding of a second calcium ion will occur rapidly in a diffusion-controlled manner (N₁ → N₂). Unfolding occurs in the reverse order. For the N-terminal domain, the transition state apparently exhibits a somewhat lower affinity to calcium (approximately 250 μM) such that in a range between 10 and 250 μM calcium, the domain folds with no calcium bound and two calcium ions then bind later to the folded state. It is important to note that all the structural interpretation we give here do not come from direct time-resolved structural evidence but are a consequence of the transition state model of protein folding (Fig. 6).

The dashed lines in Fig. 5 C and D represent a diffusion limited binding of calcium ions with a rate constant of 10⁸ M^-1 s^-1 (6, 19). Apparently, at high calcium, the folding rate constants are limited by the binding of calcium to calmodulin. This observation also explains why folding rate constants for the two domains differ under apo conditions but converge at high calcium.

We note that the kinetic scheme of Fig. 6 does not distinguish between a calcium-free protein that adopts a holo-like fold and calmodulin in the apo conformation. A rapid equilibrium of such conformations has been postulated in NMR experiments (20) as well as from MD simulations (21). Since the energetic difference between such conformations is low, we cannot distinguish them in our experiments. Likewise, we do not distinguish between holo calmodulin and apo calmodulin with bound calcium ions (22, 23).

Direct Observation of the Coexistence of Holo and Apo Conformations.

A great advantage of single molecule measurements over bulk studies is their ability to directly observe sub-populations without ensemble averaging. For slowly exchanging ligands with strong affinity, single molecule mechanical measurements have shown that a stable ligand-bound form can coexist with a mechanically weaker apo form (24–26). However, in the case of calmodulin, the exchange is rapid and so far, only average properties could be measured in single molecule assays (9). At calcium concentrations that lie in the transition regime from apo to holo conformations, one would expect to observe a simultaneous coexistence of apo and holo conformations. We could indeed observe such a mixture for CaM₃₄ (Fig. 4, Middle, and Fig. 5, open symbols); however, not for CaM₁₂. At first sight, this comes as a surprise because both domains should exhibit such a coexistence regime albeit at different calcium concentrations. The important difference between the N-terminal domain CaM₁₂ and the C-terminal domain CaM₃₄ lies in their calcium exchange kinetics. At calcium concentrations of 100 μM, the diffusion-limited on-rate constant for calcium binding is 10⁴ s^-1 (3, 6). To observe unfolding from an apo state, it is necessary that the apo state lifetime lie below the binding rate constant for calcium, because otherwise, calmodulin would have bound calcium and subsequently switched to the holo conformation. The sample trace in Fig. 4B (Middle) for CaM₃₄ at 100 μM calcium is recorded at forces of 5–6 pN. At these forces, apo CaM₃₄ will unfold at a rate constant of ca. 2000 s^-1 (Fig. 4D, Right). This value is comparable to the rate constant of calcium binding and hence, in a significant number of events (approximately 17%), the apo conformation will unfold before it is transformed to the holo conformation and we will record a short lived event (arrows in Fig. 4B, Middle). For CaM₁₂, the forces where folding/unfolding is observed in equilibrium lie around 6.5–7.5 pN (see sample trace in Fig. 3B, Middle). Apo CaM₁₂ will unfold at a rate constant of 400 s^-1 at those forces (Fig. 3D, Right). Hence, in most cases (> 96%), calcium will bind before the apo domain unfolds. This rapid binding therefore likely prevents the observation of pure apo states and lifetimes will be distributed single exponentially.

Conclusion

In summary, we were able to study the calcium-dependent folding of a single molecule of calmodulin in a physiologically relevant regime around the apo to holo transition. We were able to identify the kinetic folding pathway in detail. It has been reported that in the calcium free state, calmodulin undergoes rapid transitions between apo and holo-like conformations (20, 21). Distinguishing such populations in our single molecule assay will be an important challenge for the future. So far, this has not been possible, owing to limitations in time and force resolution. Moreover, it will be interesting to see how the kinetic folding pathway couples to the simultaneous interaction with calmodulin binding targets, which is the primary function of this calcium-sensing molecule.

Methods

Experimental Procedures.

CaM₁₂ (CaM₃₄) comprised residues 2–78 (76–149) of human calmodulin (P62158). The construct was genetically inserted between two ubiquitins with terminal cysteines that served as spacers (8). Using the cysteines as attachment points for thiol-modified DNA handles with biotin/digoxigenin functionalized ends of a length of approximately 180 nm each, we attached the construct to micron-sized neutravidin/anti-digoxigenin silica beads in a dumbbell configuration. Data were collected on a custom-built dual beam optical tweezers setup. Measurements were performed in 50 mM Tris/150 mM KCl, pH 8 with varying concentrations of CaCl₂ or EDTA (SI Text).

Data Analysis.

Transitions between states were detected using a Hidden-Markov model on the unfiltered raw data of the difference signal of the two traps [(27, 28), SI Text].