Energy landscape of knotted protein folding

Abstract

Recent experiments have conclusively shown that proteins are able to fold from an unknotted, denatured polypeptide to the knotted, native state without the aid of chaperones. These experiments are consistent with a growing body of theoretical work showing that a funneled, minimally frustrated energy landscape is sufficient to fold small proteins with complex topologies. Here, we present a theoretical investigation of the folding of a knotted protein, 2ouf, engineered in the laboratory by a domain fusion that mimics an evolutionary pathway for knotted proteins. Unlike a previously studied knotted protein of similar length, we see reversible folding/knotting and a surprising lack of deep topological traps with a coarse-grained structure-based model. Our main interest is to investigate how evolution might further select the geometry and stiffness of the threading region of the newly fused protein. We compare the folding of the wild-type protein to several mutants. Similarly to the wild-type protein, all mutants show robust and reversible folding, and knotting coincides with the transition state ensemble. As observed experimentally, our simulations show that the knotted protein folds about ten times slower than an unknotted construct with an identical contact map. Simulated folding kinetics reflect the experimentally observed rollover in the folding limbs of chevron plots. Successful folding of the knotted protein is restricted to a narrow range of temperature as compared to the unknotted protein and fits of the kinetic folding data below folding temperature suggest slow, nondiffusive dynamics for the knotted protein.

Knotted proteins are an interesting and important class of proteins (1–4). They are found across all kingdoms of life and they cover more than 1% of the Protein Data Bank (PDB) entries. Recent results show that protein knots, instead of being discarded through the process of evolution, are often strongly conserved (5). This conservation suggests that the knots are somehow advantageous and important to the function of the protein. Presently though, the direct influence of a knot on a protein’s function is unknown. A possible connection to function is through the effect of the topological barrier on the folding of the protein. Lengthy folding times can cause misfolded or partially unfolded states that result in useless or possibly even harmful proteins via aggregation, which is known to be connected to neurodegenerative disorders. Knotted proteins are involved in some human neurodegenerative diseases (6, 7) and HIV (8). Thus, the manner of efficient folding is of fundamental interest for knotted proteins because of the deep connections between a protein’s folding and its function (9).

Theoretical investigations (10, 11) have suggested knotted proteins fold through two major steps: (i) formation of a twisted native loop and (ii) threading one of the termini across the loop. A twisted loop is a necessary precursor to folding any knot, and its formation is guided by the formation of native contacts. The threading event proceeds through a plugging (i.e., threading a needle) or a slipknot intermediate (10–15), or in the case of the most complex protein discovered to date, a loop flip (4). One study suggests a less ordered mechanism that includes nonnative interactions (12). The key question about folding knots is how the protein is able to effectively traverse the entropic and topological barrier of threading a terminal through a loop in the polypeptide. It is not clear if the signal is contained simply in the geometry of the protein fold or if the chemical nature of the amino acids in the threading terminal and loop regions are of a special nature to encourage knotting. Exploring this question will require close collaboration between experiment and theory.

Experimental investigation of the folding of knotted proteins is complicated by the persistence of knots in the denatured ensemble (16). Only recently has in vitro folding from an unknotted denatured state to the knotted native state been observed (by monitoring the folding of YibK immediately following translation) (17). Therefore, it is now clear that the information necessary to fold a knot is wholly contained in the amino acid sequence. Simulations have shown that YibK can be kinetically folded and tied with structure-based models (SBMs), protein models containing information about only the native conformation (10). In addition, a smaller knotted protein has been thermodynamically characterized using SBM, including reversible folding and unfolding transitions (11). These results suggest that native-based protein folding models, which are validated across myriad protein folds (18, 19), are also appropriate for studying the free energy landscape and folding process of knotted proteins.

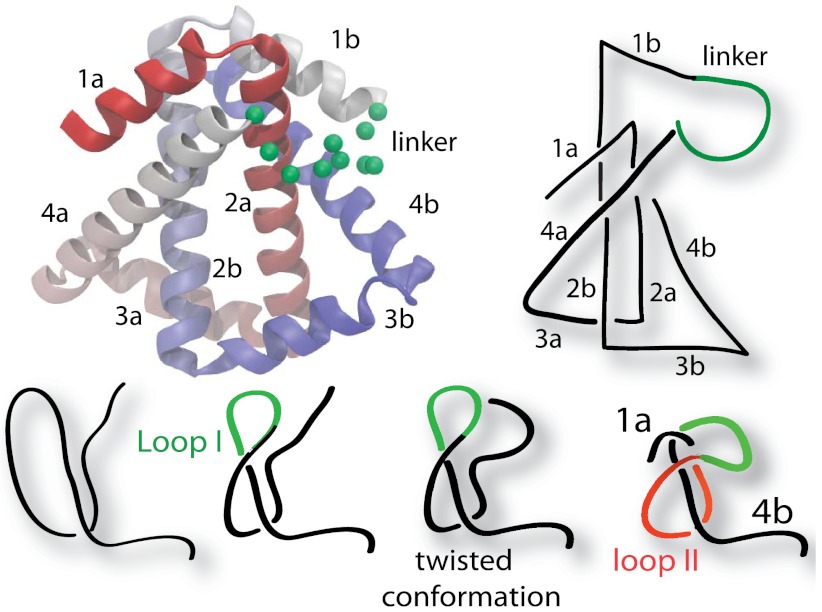
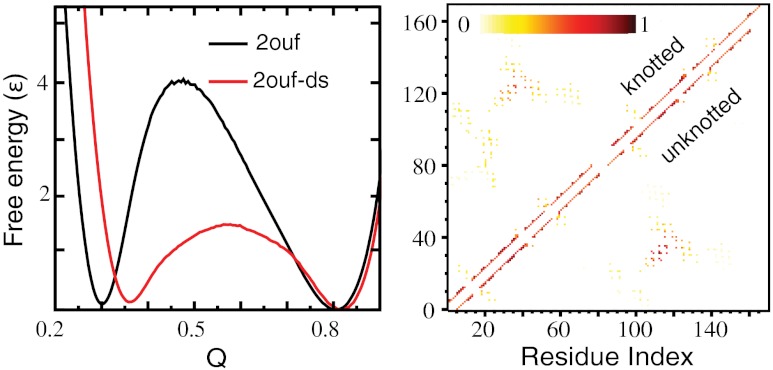
A cleverly constructed knotted protein from the Yeates group, 2ouf (20), gives us a unique opportunity to explore the knotting mechanism. This protein was constructed through domain fusion. The monomers of a dimeric protein were linked, such that if the newly fused monomer folded to the same structure as the dimer, it would have to form a 3₁ knot (Fig. 1). Experimental measurements strongly suggested that 2ouf was able to reversibly unfold and fold (including unknotting and knotting). Experimental reversibility makes 2ouf an ideal system to collaboratively explore knotting between theory and experiment. Additionally, the folding of 2ouf has been compared to 2ouf-ds, a construct where the monomers are instead connected by a disulfide bridge in the protein core (SI Appendix, Fig. S1). Thus, 2ouf has a nearly identical native fold, despite having a trivial topology due to the lack of the linker.

Fig. 1.

Cartoon representation of the designed knotted protein 2ouf. (Left). The protein 2ouf with green spheres indicating the C_α positions of the linker. (Right) Schematic of 2ouf. Letters a and b indicate helices from first and second monomer in sequence. (Lower) Schematic of the folding pathway.

Here, because the domain fusion used to create 2ouf mimics a possible evolutionary pathway for knotted proteins, we study various perturbations to the energetics and geometry in the threading regions of 2ouf to probe how evolution could optimize the threading process (5, 21). First, we present a detailed study of the folding of 2ouf through simulation. Our results show that 2ouf is able to fold and knot reversibly. We then investigate various perturbations to the energetics and geometry in the threading regions of 2ouf to probe how the knotting process can be optimized. We test the dependencies of the threading process and the overall folding on the helicity of the threading terminal helix and on the stiffness, length, and specificity of the linker. Because we obtain a statistically significant number of folding (and knotting) events with the SBM of 2ouf, we can compare our results with the experimentally measured thermodynamics, kinetic folding rates, and chevron plots. Connections can then be made between the microscopic structural data in the simulation and the macroscopic experimental observables. Finally, we predict that the folding nuclei of 2ouf and 2ouf-ds are the same, giving evidence that comparing the two proteins can elucidate the effects of the topological constraint. We suggest possible explanations for experimentally observed rollover in chevron plots. The overall result, based on the threading efficiency and similarity to experiment, is that the most appropriate geometry is represented by the experimentally designed geometry. Also, the best model is given by the unperturbed model parameters.

Results and Discussion

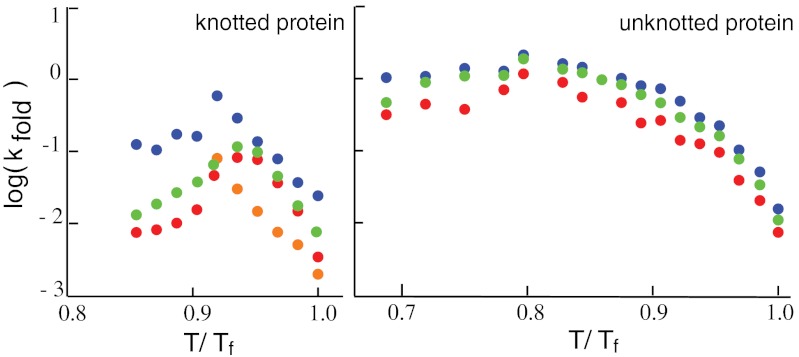
The knotted protein 2ouf was created through genetic fusion of a tandem repeat of the gene for the unknotted dimeric protein HP0242 from Helicobacter pylori (PDB ID codes 2ouf and 2bo3). The two subunits of this protein intertwine in such a manner that connecting the C terminus of the first monomer to the N terminus of the second monomer by a linker creates a trefoil, 3₁ knot topology in the fused monomeric protein, called 2ouf (Fig. 1). This construction creates a deep knot with left and right termini in position 18 and 124, respectively. The unknotted protein 2ouf-ds, which is also composed of the two chains of the dimer, is linked by an intermolecular disulfide bridge (L44C mutation) in the middle of each chain and does not introduce a knot (SI Appendix, Fig. S1). Both proteins, 2ouf and 2ouf-ds are unimolecular and have a similar fold, differing only in their topology.

Simulations of 2ouf and 2ouf-ds performed in this work are constructed based on structures provided directly by the Yeates group (20), instead of the structures deposited in the PDB. These structures have a higher resolution, and thus are more suitable for use with SBMs. Also, unlike the deposited structure, the C_α coordinates of the linker residues in 2ouf are resolved. We reconstructed the five Ser side chains from the linker to determine native contacts. We found that 11 contacts are created with the rest of the structure through these side chains. The other linker amino acids are Gly, which does not have side groups.

Folding Mechanism of the Designed Protein 2ouf.

The protein 2ouf contains a 3₁ twisted knot (i.e., unknotting number one) and thus must thread one terminus across a twisted loop to fold. The 2ouf, like all proteins with a 3₁ knot, contains two possible loops to thread, one for each terminus (Fig. 1). Loop I is threaded by the N terminus and is composed of helix 4a, linker, and helices 1b and 2b. Loop II is threaded by the C terminus and is composed of helices 2a, 3a, and 4a. Inspection of the structure would suggest that 2ouf likely folds by the N terminus threading Loop I. First, the N terminus needs to thread only 18 residues, whereas the C terminus is 45 residues deep. Second, Loop II and the C-terminal end of the knot form a hydrophobic core (2a-2b), making early formation likely. Third, Loop I contains the linker, which is likely looser and more conducive to threading.

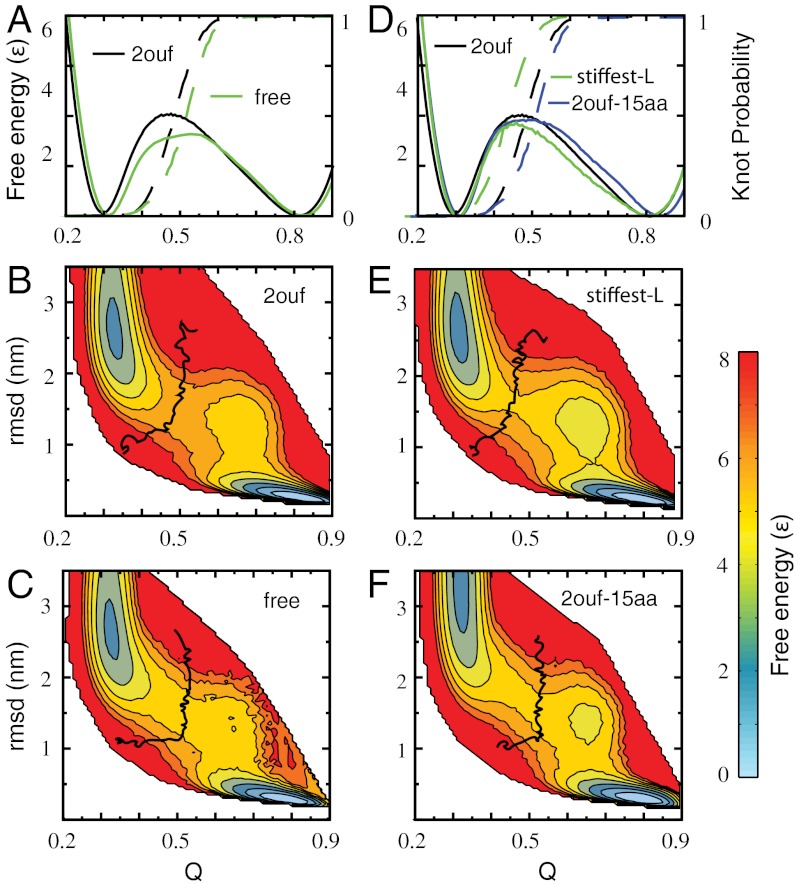
The folding of 2ouf was studied by molecular dynamics simulation with an SBM (22, 23). An advantage of simulation is that the topology of the protein can be monitored at each step, allowing study of the interplay between folding and knotting. The obtained folding trajectories show that 2ouf is able to avoid significant topological traps, unlike the case of YibK (10). To monitor the folding progress we use the fraction of native contacts formed, Q, and rmsd from the native state as reaction coordinates. The free energy, F(Q), suggests that 2ouf is a two-state folder (Fig. 2A). The probability to form a knot during folding, K(Q), shows that the knot formation coincides with the free energy barrier to folding. The low and high Q ensemble corresponds to unfolded/unknotted and folded/knotted protein, respectively. Additional information about the landscape comes from a second reaction coordinate that monitors the global similarity, rmsd. The two-dimensional landscape F(Q,rmsd) shows hidden complexities within the folding/unfolding mechanism (Fig. 2B). A population of metastable states is seen at Q ∼ 0.6 for compact protein (low rmsd). It corresponds to helix 4b being disordered and extended. The contour of K(Q,rmsd) = 0.5 shows where the knot is formed 50% of the time, it signifies the ensemble change in topology from trivial to knotted. Knotting coincides with the rate-limiting step at the top of the barrier.

Fig. 2.

Free energy landscape of knotted proteins measured by the fraction of native contacts formed Q and rmsd for 2ouf and three mutants. (A) One-dimensional free energy F(Q) for 2ouf with 2ouf-free, and corresponding knot probability K(Q). (B and C) Two-dimensional free energy landscape of 2ouf and 2ouf-free. (D) One-dimensional free energy F(Q) for 2ouf-stiffer-L and 2ouf-15aa (longest linker). The 2ouf-stiffer-L shows the slowest knotting kinetics (Fig. 4). (E and F) Two-dimensional free energy landscape of 2ouf-stiffer-L and 2ouf-15aa. All F(Q, rmsd) show that the folding mechanism of knotted protein is composed of complex events, as seen by the chair-like shapes of the transition states and the metastable states around Q = 0.75 and rmsd = 1.2. Black curve on (B, C, E, F) shows the contour of knot probability K(Q,rmsd) = 0.5. This contour lies across the transitions state, thus coinciding with the rate-limiting step to folding. (B and E) When the contacts between the linker and the rest of the protein are included K(Q,rmsd) has the gradually curved “)” shape. (C and F) Proteins with free linkers are characterized by “⌋” shape contours. F(Q) and F(Q,RMSD) for other constructs is shown in SI Appendix, Fig. S2.

Detailed analysis of the individual folding (unfolding) events (SI Appendix, Tables S1–S3) shows that there is a dominant route of formation of the native contacts. First the protein creates the hydrophobic core interactions 2a-2b followed by 2a-3a. Formation of these contacts defines the stable twisted native loop across which the N terminus can be threaded to form the knot. Contact between linker-1b brings the protein to the top of the free energy barrier, Q ∼ 0.4. Next, the N-terminal threads the correctly twisted Loop I via a dominant plugging route, dragging the N-terminal through the loop, similar to threading a needle. There is a less populated knotting route of flipping the linker over an already docked N-terminal. The loop flipping consists mainly of linker-1b moving from an extended state to the native position. The native knot forms contacts 4a-2b, and the last step is the packing of the C-terminal tail. In summary, the folding pathway consists of forming a twisted loop and threading the N-terminal across the loop or flipping loop over the N-terminal.

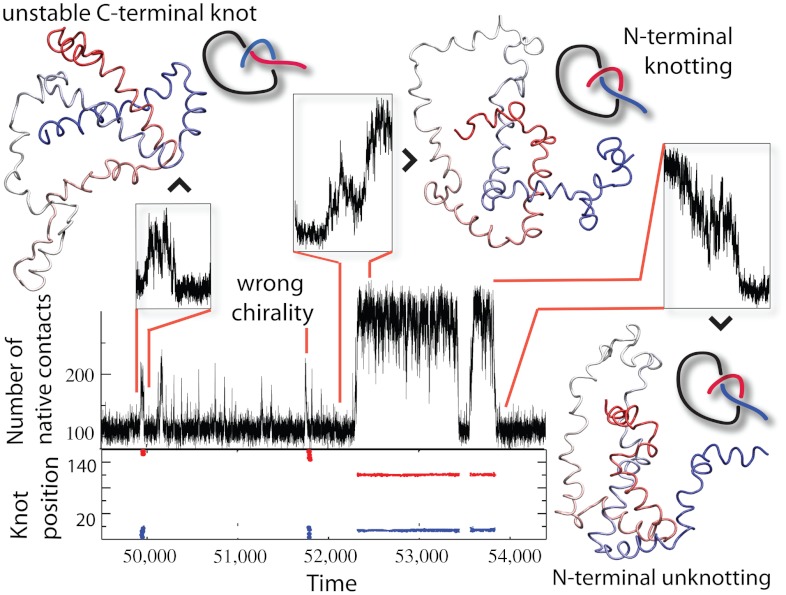
Whereas K(Q) shows knots are mainly formed after the formation of the transition state, it is also very interesting to ask whether any unstable, transient knots are formed in the unfolded basin. This intriguing question has not yet been previously explored. A closer look at typical trajectories shows examples of transiently knotted structures in the unfolded basin (SI Appendix, Fig. S4). To quantify their abundance, all tying/untying events are counted, where the knot is formed for more than twice the velocity relaxation time. The ratio of folding/unfolding events to tying/untying events is 0.38, N_trans/N_knot (Table 1). Thus, roughly half of the knots will backtrack instead of leading to the native knotted state. The transient structures correspond mostly to three knotted configurations: incorrect chirality, knotting by the C terminus, and very extended knotted conformation with low Q, revealing why these unfolded ensemble knots cannot act as nucleation spots for folding (SI Appendix, Fig. S4). Configurations with an incorrect chirality always must backtrack. Knotting via the C terminus is much less likely because it must thread twice as deep as the N terminus. The shallow N-terminal knots at low Q are unlikely to reach the native knotted configuration without some nonnative bias to facilitate threading. Amazingly, we also notice three structures with the more complicated knot 4₁. This knot must first untie to fold a 3₁ knot. Unlike for 5₂ or 6₁ (24), there is no direct route from 4₁ to 3₁. So, even though over 50% of the tying events were observed in the unfolded basin, these knots do not contribute to the shown free energy landscape due to their short lifetimes. These knots indicate that the unfolded basin at T_f samples topologically complex configurations as would be expected from any homopolymer of similar length.

Table 1.

Thermodynamic and topological parameters for the set of mutants

Label		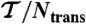Ntrans/Nknot	ΔF	Tf		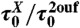Description of difference from 2ouf
2ouf	5.6e4	0.38	4.1	1.05	1.0	Contains 21 contacts between linker and protein
2ouf-free	3.5e4	0.27	3.3	1.03	1.3	No contacts between linker and protein
2ouf-soft-N	3.8e4	0.52	3.2	1.04	1.5	Reduced native dihedral bias (εD) in the N-terminal helix (1a) by 1/2
2ouf-stiff-N	7.2e4	0.65	4.1	1.06	1.2	Increased native dihedral bias (εD) in the N-terminal helix (1a) by 2
2ouf-soft-L	5.6e4	0.61	3.8	1.05	1.2	Reduced native dihedral bias (εD) of the linker by 1/2
2ouf-stiff-L	9.5e4	0.72	4.1	1.07	1.7	Increased native dihedral bias (εD) in the linker (1a) by 2
2ouf-stiffer-L	7.5e4	0.63	3.7	1.08	2.1	The same as stiff-L and additional 5 amino acids from each side of the linker
2ouf-6aa	6.6e4	0.39	3.7	1.03	1.5	No contacts between linker and protein, and 6 amino acid linker
2ouf-12aa	3.0e4	0.39	3.1	1.03	1.3	No contacts between linker and protein, and 12 amino acid linker
2ouf-15aa	4.0e4	0.51	3.7	1.02	0.91	No contacts between linker and protein, and 15 amino acid linker
2ouf-ds	—	—	1.5	1.07	—	Unknotted construct, dimer connected by disulfide bridge at residue 44

Last column describes how the mutant differs from 2ouf. Structures denoted as 2ouf-6aa, 2ouf-12aa, 2ouf-15aa are based on modeled linker, all other structures are built based on experimentally determined positions of amino acids. In particular, 2ouf-free is built based on the native positions of C_α atoms in the linker, but without taking into account 21 contacts between the linker and the rest of the structure (included in 2ouf). Abbreviations are, as follows: 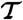, total simulation time; N_trans, number of transitions (between folded/unfolded protein); N_knot, number of knotting/unknotting events; ΔG, barrier high from F(Q);T_f, folding temperature; and 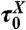, the characteristic reconfiguration time on the barrier of construct X.

Perturbation of Geometry and Chain Stiffness in the Knotted Region.

The relative ease of overcoming the topological barrier, shown by the lack of long-lived topological traps, suggests that the experimental observation of reversible knotting was correctly interpreted. Here, we test the robustness of this theoretical result by perturbing the chain in ways that evolution could use to select for optimized folding of knots. The set of mutants was chosen to explore the effect of varying the properties of the loop and terminal residues involved in the threading event at the top of the free energy barrier (Table 1). The folding and knotting is compared between 2ouf and four sets of perturbations: (i) a free linker without native contacts, 2ouf-free, (ii) flexibility of the linker, 2ouf-soft-L, 2ouf-stiff-L, and 2ouf-stiffer-L, (iii) varying linker length, 2ouf-6aa, 2ouf-12aa, and 2ouf-15aa, and (iv) altered helicity of the N-terminal helix, 2ouf-soft-N and 2ouf-stiff-N (only discussed in SI Appendix, Section S2.4 and Table S4). First, in the following sections, we compare the folding mechanisms and knotting propensity in turn. Then, we compare the relative diffusion rates on the top of the barrier where the knot is being formed. In all cases, the protein is observed to reversibly fold and knot during the simulations. The diffusion constant of knot formation varies by less than a factor of three, and shows that folding knots in 2ouf is a robust feature of its native-based energy landscape.

Removing the Native Bias from the Linker.

Because the linker was artificially designed in the experiment, it has no evolutionary pressure to be specific and minimally frustrated (25) as native contacts imply. To test the opposite extreme from a protein-like linker in 2ouf (i.e., a polymer-like linker), we deleted the 21 native contacts (11 contacts with 2a, 3 with 4b, and 7 with 1b) between the linker and the rest of the protein. This construct is called 2ouf-free.

The comparison of F(Q) for 2ouf-free and 2ouf shows a broader, more asymmetrical, and lower barrier for 2ouf-free (Fig. 2 A and C). The polymer-like linker of 2ouf-free increases the general knotting propensity. N_trans/N_knot is smaller than for native 2ouf, meaning a larger relative abundance of nonproductive knots. Detailed analysis of folding routes shows that 2ouf-free has the same characteristic folding events as 2ouf, however the knot is formed later during the folding process (SI Appendix, Tables S2 and S3). Indirect influence comes from the earlier formation of 3a-2a and 2a-3b, which as before, defines the twisted loop. Although the linker does not form contacts with these pieces, it implies that the linker modulates the ability to close and twist Loop I. Lacking specific contacts means that the linker is easier to bend. The second step of loop threading occurs over a broad range of Q, instead of concurrently at Q = 0.48. 2a-4a orders earlier (Q = 0.4), setting up the N-terminal threading, but the contacts between 1a-4a, which signal the final packing of the N-terminal knot, order later (Q = 0.56). Interestingly, removing the linker contacts removes the competition between linker-4b and 1b-4b formation that causes backtracking, a signal of geometrical frustration (26). During folding transitions in 2ouf, as the knot is threaded the contacts between 1b-4b tend to temporarily break in favor of linker-4b. But in 2ouf-free, the linker does not interfere with these contacts and no backtracking is observed.

Varying the Stiffness of the Linker.

The stiffness of the linker determines how easily Loop I can hold its shape open for the N terminus to thread. The stiffness is modulated by reducing the dihedral bias by a factor of 2 for 2ouf-soft-L, and increasing by a factor of 2 for 2ouf-stiff-L and 2ouf-stiffer-L. The free energy barrier slightly decreases for 2ouf-soft-L and 2ouf-stiffer-L, and the latter has an asymmetric barrier (SI Appendix, Fig. S2). Additionally F(Q,rmsd) shows a pronounced population of the high Q metastable state. K(Q) indicates that the knot is formed earlier for stiff-L and stiffer-L, and later for softer L. The ratio of folding events to total knotting events increases for all linker perturbations. Stiff-L and stiffer-L are almost double that of 2ouf.

The route measure R(Q) (26) of 2ouf-soft-L is almost the same as for 2ouf and stiff-N (SI Appendix, Fig. S3), whereas the route measures for stiff-L and stiffer-L show increased polarization in late transition states 0.48 < Q < 0.65. This range exactly corresponds to the metastable states in F(Q,rmsd). The resulting bottleneck is most pronounced for stiffer-L. Detailed analysis of the folding routes shows that soft-L folds similarly to 2ouf where stiff-L and stiffer-L switch the early fold events. Details are explained in SI Appendix, Section S2.3 and Table S4.

Varying the Length of the Linker.

To address the sensitivity of the folding to the linker length we inserted or deleted residues of a free linker (no native contacts) (Table 1). The protein 2ouf-6aa has a linker shorted by three residues with respect to the 9 amino-acids native length of linker, the smallest construct that we were able to build (shorter linker caused steric clashes). Proteins, 2ouf-12aa and 2ouf-15aa are lengthened by 3 and 6 amino acids, respectively (SI Appendix, Fig. S1).

The free energy landscape indicates that in all cases it is possible to reversibly fold the proteins (Fig. 2 and SI Appendix, Fig. S2). The barrier height depends in a nonlinear way on linker size, where 2ouf-12aa has a significantly lower barrier than 2ouf-15aa. The shorter linker 2ouf-6aa shows earlier knot formation, whereas both longer linkers show later knot formation. Of the ten mutants, the high Q metastable state is the most pronounced in the linker length mutants. Not only do they disrupt the native structure, but they also have no contacts with helix 4b, the helix that frays. The abundance of nonproductive knots N_trans/N_knot is surprisingly the same for 2ouf, 2ouf-6aa, and 2ouf-12aa, and only marginally increases for 2ouf-15aa. Thus, the size of the loop is not the primary determinant of the propensity to form random and nonproductive knots. The route measure shows that in all cases the protein starts folding by the formation of the twisted loop, the first peak in the route measure (SI Appendix, Fig. S3).

T_f of all mutant proteins changes weakly with chain length, however the insertion of 6 amino acids inside the knotted loop destabilizes the protein more than insertion of 3 amino acids suggesting that the unstructured linker provides a weak energetic penalty (Table 1). This result agrees with experimental results for the chymotrypsin inhibitor-2 (CI2) (27) and other proteins (28) where it was shown that insertion of residues destabilizes a protein, although, the amount of destabilization is sensitive to insertion position. In 2ouf the free energy barrier is lowered by the insertion or deletion of up to 3 amino acids to the linker, but insertion of 6 residues causes a compensating increase in barrier height relative to 2ouf-12aa. Whereas the 2ouf-15aa trend is opposite to the change of rate constant upon loop extension in CI2, the barrier is still smaller than 2ouf. It should be noted that these previous results were obtained from unknotted loops or covalently closed loops (27–29).

Let us point out a few interesting things about these linker length mutants. In the case of 2ouf-6aa we observed a significant number of unfolding fluctuations (Q < 0.4) that remained tied (SI Appendix, Fig. S5). These tied but unfolded configurations form a nucleation spot from which protein can fold rapidly to a native state. This process mirrors what was experimentally observed for YibK (16), fast folding from preknotted states. Also, in 2ouf-15aa, even though the contour of K(Q,rmsd) = 0.5 is located at higher Q, we observed an unprecedented successful folding/knotting event that started from low Q (Fig. 3). The small fraction of native contacts (27 pairs) corresponds to a correctly twisted Loop I, which possesses only contacts between 3a-3b and a few contacts with 2b. The N terminus threads across a rather unstructured and extended conformation of Loop I. This observation implies that in some cases proteins can successfully knot even if the driving force from native contacts is indirect.

Fig. 3.

Knotting, folding, and unfolding events observed for 2ouf-12aa. Trajectory insets show (Top Left) random knotting by the C-terminal, (Top Middle) folding via knotting at low Q (unique to 2ouf-12aa), and (Top Right) unknotting and unfolding by unplugging the N-terminal. Corresponding configurations are shown next to the insets. (Bottom) Topological signature of the protein measured by the position of the knot along the sequence. Knot termini are shown by blue and red dots.

Protein-Like 2ouf has Fast Knotting Kinetics.

Folding probed by a one-dimensional reaction coordinate Q can be approximated as a Brownian barrier crossing process with a diffusion constant D(Q) (30). Thus, the barrier crossing time τ_trans can be approximated with the free energy barrier height exp(ΔF/kT) (31) and the diffusion on the top of the barrier D(Q^†). The height of the barrier ΔF is determined by the fraction of time the protein spends in the transition state. Differences in height caused by mutations are caused by two different factors: The mutation alters (i) the global favorability of the transition state ensemble or (ii) diffusion of the threading process. To separate out the global effects and focus on the mutations’ effects on knotting diffusion, we normalize the folding time by the barrier height. 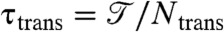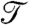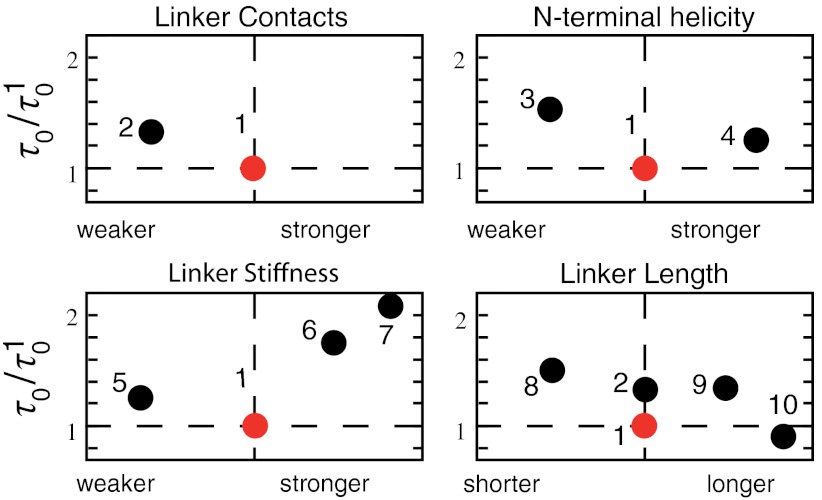From the simulation, , where is the total simulation time and N_trans is the number of observed folding/unfolding transitions at T_f and 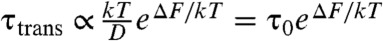, where τ₀, the ratio of the transition time and barrier height, is then a characteristic time that quantifies the change in kinetic difficulty of folding the knot upon perturbation (Fig. 4 and Table 1). The fastest, and therefore most efficient, knot tying constructs are 2ouf and 2ouf-15aa, followed by 2ouf-stiff-N. The fast knotting kinetics of 2ouf-15aa arises in a complex combination between ease of threading a larger loop mixed with the difficulty of threading while lacking much of the native bias. The kinetic benefit of the longer linker must be contrasted with the stability cost. This protein has the lowest T_f of all mutants. The slowest dynamics is observed for the 2ouf-stiffer-L.

Fig. 4.

Characteristic knotting time τ₀ measured relative to the protein-like construct 2ouf (red points). Ordered as in Table 1. (1) 2ouf, (2) free, (3) soft-N, (4) stiff-N, (5) soft-L, (6) stiff-L, (7) stiffer-L, (8) 6aa, (9) 12aa, (10) 15aa.

Folding Mechanism of 2ouf is Similar to the Unknotted Protein 2ouf-ds.

An advantage of studying 2ouf is the existence of an unknotted version of the protein (2ouf-ds) with an identical native contact map. Instead of the linker, 2ouf-ds is connected with a disulfide bridge at position 44 in each monomer. Isolating the effect of the knot is difficult because of the the changes in contact order introduced by the different monomer linkages. Interestingly, analysis of the folding of 2ouf-ds shows that the early folding events are almost the same between 2ouf and 2ouf-ds, contacts are first formed between the hydrophobic core helices 2a-2b (Fig. 5 and SI Appendix, Fig. S6). This ordering is obvious for 2ouf-ds because the disulfide bridge connects these segments. Thus, after the nuclei are formed, the later stages of folding have very similar effective contact orders, making the comparison meaningful as a measure of the topological barrier in 2ouf.

Fig. 5.

Comparison of knotted (2ouf) and unknotted (2ouf-ds) proteins. (A) Free energy as a function of Q shows a lower barrier for 2ouf-ds. (B) Contact formation probabilities at Q = 0.45 for 2ouf (Top) and 2ouf-ds (Bottom). The folding nuclei are nearly identical.

The experimental results suggested that 2ouf folds 20 times slower than a homologous unknotted monomer 2ouf-ds (20). An estimate of the difference in kinetic folding rate is from the difference in free energy barrier height. This value is on the same order as the experimental result, exp(4.1/1.05 - 1.4/1.07) ≈ 13. The comparison of folding kinetics (discussed in the next section) shows that 2ouf is indeed folding more slowly than 2ouf-ds in the simulation, and that folding the knot poses a topological barrier for 2ouf. It is interesting to note that all of the perturbations to 2ouf resulted in a smaller free energy barrier, supporting the notion that the protein-like treatment of the linker in 2ouf is the most appropriate.

Kinetics and Comparison to Experimental Results.

Experimental kinetic data of the knotted and unknotted proteins represented as chevron plots show rollover in the folding limbs and suggest a complex folding mechanism (20). We performed kinetic folding simulations to more fully explore the effect of the knotted topology on the dynamics of the folding event and to calculate observables to compare with the experiments.

Simulations were started from random unfolded configurations, each run for an equal amount of time, and considered folded when they both reached a high Q indicative of the folded basin and contained a native-like knot. SI Appendix, Fig. S7 compares the fraction of correctly folded protein between 2ouf and 2ouf-ds over broad range of temperatures. Compared to 2ouf-ds, 2ouf has a narrow range of temperature where it can be consistently correctly folded. However, note that there is a broader range of temperature where Q reaches native-like values, but with the structures still lacking the native knot. The existence of a knot was not determined for the experimental protein ensemble, but is crucial for the correct interpretation of the kinetics of knotted proteins. It suggests an explanation of the experimentally observed rollover in the chevron plot at low denaturant. At low denaturant, analogous to low temperature in the simulation, the protein folds into a collapsed configuration lacking the knot, which then must repeatedly backtrack in an attempt to fold, thus slowing folding.

For a more direct comparison to the experiment, the simulated kinetics data were used to extract folding rate constants for different temperatures at and below T_f to create chevron plots (Fig. 6). The folding limbs of the chevron plots qualitatively reproduce the experimental data, most notably the rollover at low temperature (low denaturant) and the slower folding of the knotted 2ouf. Numerical analysis reveals that kinetics of 2ouf-ds is best modeled by a biexponential fit; same as that suggested by the experiment (example fits to single and double exponentials are shown in SI Appendix, Fig. S8). A double exponential is characterized by a slow and fast phase. The folding trajectories suggest that the slower phase describes backtracking from an incorrect packing of the protein terminals as they wrap around one another during folding. Interestingly, at low temperature, the kinetics can be well-fit by a single exponential, suggesting that these incorrectly packed intermediates are relatively destabilized at lower temperature.

Fig. 6.

Folding limbs of chevron plot from simulated kinetics. Rate constants k_fold are obtained by fitting the folding kinetics to single (green), double (red and blue), and compressed (orange) exponentials. Left and Right correspond to 2ouf and 2ouf-ds.

The kinetics of 2ouf can be adequately described by a double exponential, but it is seemingly best modeled by a compressed exponential with β = 1.4: A exp[-(kt)^β] (SI Appendix, Fig. S8). Whereas kinetics with β > 1 is very rare for proteins, it is common for jammed soft materials (32). In colloidal gels, β > 1 corresponds to nondiffusive, slow relaxation processes. It models the relaxation of stress in the jammed system. In the case of knotted proteins, jammed states might correspond to the knotting events (dragging/flipping of the loop across/above terminal). Relaxation of the stress can be connected with the finalized knotting process or escaping from topological traps. A fit to a double exponential suggests fast and slow phases, which corresponds to immediate knotting versus a slow threading of terminal across knotted loop. The temperature at which more than 20% trajectories do not reach the correctly folded and knotted state (SI Appendix, Fig. S7) has an interesting characteristic: the best fit changes from compressed to stretched, i.e., β < 1. β = 1 is the point where the rollover begins in the chevron plots.

Double or even compressed exponentials imply complex folding with intermediate states. The F(Q,rmsd) plots show possible intermediate states near the folded basin (Fig. 2B), however, the likely culprits of the complex folding kinetics would be intermediates on the unfolded side of the transition state ensemble. Deeper analysis is needed to uncover coordinates that are able to reveal the hidden complex kinetics in the unfolded basin and near the transition state. Similar effects were observed in the experiment, as no stable intermediates were observed based on fluorescence spectra, but were based on CD spectra (20). In summary, the kinetic data shows that the folding mechanism is complicated and is composed of intermediate steps and/or multiple routes as was suggested experimentally. The analysis additionally reveals that successful folding depends strongly on temperature.

Conclusions

Our primary goal was to determine how nature could select structures that are more efficient at folding knots. Along these lines, we performed structural and energetic modifications to the designed knotted protein 2ouf to find where the bottleneck for folding and threading is located on the free energy landscape. With the SBM, 2ouf was seen to be reversibly folded and knotted over the whole set of mutants. We did observe that as the knotting loop (specifically the linker) is lengthened or altered in stiffness the number of nonproductive knots decreases. Even so, knotting in the folding basin was always rare, and the few events that are seen rarely lead to the native state. The driving force to tie the knotted protein comes from the native contacts present in the preordered intermediate.

We validated our results through direct comparison to the experimental folding data of 2ouf and 2ouf-ds (20). Simulated thermodynamics data confirmed that the knotted protein 2ouf has a higher folding free energy barrier than the homologous unknotted 2ouf-ds. Experimental folding rate constants, based on both single or double exponential fits, showed a rollover in the folding limbs of the chevron plots, which suggested a complex folding mechanism. We observed a similar rollover in our simulated chevron plots. Possible sources for this rollover are transition from nondiffusive, slow relaxation processes to diffusive in the prefactor of the folding rate that is suggested by the change of best fit for the folding kinetics from a compressed exponential to a stretched exponential. Another possibility is that under good folding conditions, i.e., low temperature or low denaturant, the protein collapses more quickly than the knot threading process, creating several trapped intermediates. These are just a couple of examples of the possible sources of rollover in such a complicated system.

In summary, even though the knotted protein folds slower than the unknotted construct, efficient folding is observed in both experiment and simulation. Our simulation data suggests that the experimentally designed 2ouf represents the most efficient construct over our range of structural and energetic mutants. The simulations and experimental results highlight the possible role of gene fusion as a mechanism open to evolution when selecting for new knotted proteins.

Materials and Methods

Structure-Based Protein Simulations.

The protein is modeled as a bead of C_α atoms with a popular coarse-grained structure-based model (22, 23). All energetic terms stabilize the native structure. Tertiary pair interactions are included between any residue pairs with atoms within 7 Å and separated by more than three in sequence. Contacts are modeled with 10-12 Lennard–Jones potentials. The folding of all mutants were studied through constant temperature molecular dynamics simulations using a Nose–Hoover thermostat with coupling 0.025. Trajectories were run near folding temperature (T_f) and sampled folding/knotting and unfolding/unknotting several times in each run.

Knots Detection.

Algorithm to detect knots is described in SI Appendix.