Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2012 Oct 17;13(11):3823–3832. doi: 10.1021/bm301283f

Normal and Shear Interactions between Hyaluronan–Aggrecan Complexes Mimicking Possible Boundary Lubricants in Articular Cartilage in Synovial Joints

Jasmine Seror †, Yulia Merkher ‡, Nir Kampf †, Lisa Collinson §, Anthony J Day §, Alice Maroudas ‡, Jacob Klein †,✉
PMCID: PMC3497856  PMID: 23074968

Abstract

graphic file with name bm-2012-01283f_0001.jpg

Using a surface force balance, normal and shear interactions have been measured between two atomically smooth surfaces coated with hyaluronan (HA), and with HA/aggrecan (Agg) complexes stabilized by cartilage link protein (LP). Such HA/Agg/LP complexes are the most abundant mobile macromolecular species permeating articular cartilage in synovial joints and have been conjectured to be present as boundary lubricants at its surface. The aim of the present study is to gain insight into the extremely efficient lubrication when two cartilage surfaces slide past each other in healthy joints, and in particular to elucidate the possible role in this of the HA/Agg/LP complexes. Within the range of our parameters, our results reveal that the HA/Agg/LP macromolecular surface complexes are much better boundary lubricants than HA alone, likely because of the higher level of hydration, due to the higher charge density, of the HA/Agg/LP layers with respect to the HA alone. However, the friction coefficients (μ) associated with the mutual interactions and sliding of opposing HA/Agg/LP layers (μ ≈ 0.01 up to pressure P of ca. 12 atm, increasing sharply at higher P) suggest that such complexes by themselves cannot account for the remarkable boundary lubrication observed in mammalian joints (up to P > 50 atm).

Introduction

Mammalian synovial joints are among the most efficiently lubricated systems known in nature, with friction coefficients μ between the sliding articular cartilage surfaces as low as ca. 0.001 under pressures of up to 100 atm or higher, over a range of shear rates from rest up to order 106 s–1.1 Many models2−6 have been proposed to explain this extreme lubrication. These include the main concepts deriving from engineering tribology, such as hydrodynamic, elastohydrodynamic, and boundary lubrication, as well as specific effects such as interstitial pressurization3,6,7 and models that take account of the particular properties of the articular cartilage itself (a network-like structure comprising about 70% water, permeated by a large number of molecular and macromolecular species, as well as the cells that produce them), and of the synovial fluid permeating the joint.2,4,5,8−15 At high pressures (up to 100 atm) and limitingly low shear rates, conditions that are frequently typical of mammalian joints and where intervening fluid layers would be squeezed out, one expects the boundary lubrication regime to dominate. In this regime slip occurs at the interface between layers at the outer boundary of each cartilage surface, resulting in frictional dissipation as the contacting layers slide past each other. The molecular composition of the very outer surface of articular cartilage is not precisely known, though it has been conjectured4 that it must include mobile macromolecules that permeate the cartilage itself as they diffuse out into the synovial fluid. That is, since macromolecules (such as HA and Agg) are produced within the relatively widely separated cells, yet permeate the cartilage uniformly, they must undergo diffusion in order to achieve such uniform permeation, and it is this diffusive motion that eventually brings them also to the outer cartilage surface (as also discussed in ref (4)). In addition, there is the possible presence of macromolecules adsorbed from the synovial fluid itself.5,16 Thus an important question concerns the role of macromolecular species or complexes, similar to those that may be present at the outer surfaces of the articular cartilage, as boundary lubricants.

A related question concerns the detailed molecular mechanism whereby very low friction could result as such compressed macromolecular layers slide past each other at high physiological pressures. Several studies17−20 have shown that highly hydrated molecules, such as ions,17 polyelectrolytes,19 polyzwitterionic brushes,18 or phosphatidylcholine liposomes,20 may act as extremely efficient lubricants via the “hydration lubrication” mechanism17 (not to be confused with hydrodynamic lubrication, which is a very different mechanism21). In this, water is tightly bound in hydration layers surrounding charges on the molecular species, which therefore are capable of supporting high normal loads. At the same time, such hydration layers are capable of very rapid relaxation arising from the rapid exchange of hydration water molecules with those in the surrounding bulk water (∼109 s–1 in optimal cases17), which ensures that they behave in a fluid-like manner under shear as long as the shear rates are lower than their relaxation rate. As was directly observed in several studies,18,20,22 the hydration lubrication mechanism can result in friction coefficients μ ≈ 0.0001 (or even lower) up to physiological pressures (of order 100 atm). Thus in principle, given appropriate vectors (such as macromolecules) to “deliver” hydration layers at the articular cartilage surface, this mechanism could account for the very efficient lubrication of synovial joints.

Hyaluronan (known also as hyaluronic acid or HA for short) is the most common macromolecular component of synovial fluid. HA was long conjectured to be the “lubricating” molecule23 responsible for low joint friction, because of its high bulk viscosity;24 it is still often injected as a visco-supplement between the articular surfaces of knees and hips affected by osteoarthritis (OA). Several more recent studies,25 however, have suggested that the main clinical indications of such visco-supplement injection might be a mildly anti-inflammatory benefit together with a placebo effect25 since, at physiological shear rates, the HA solution viscosity drops to values similar to those of water.4,24 Radin et al.26 first suggested that rather a hyaluronate-free fraction of proteins is responsible for the friction reduction, and this protein (actually a proteoglycan) was later given the name lubricin.14 The lubricating properties of this macromolecule have been examined directly,27 although with little indication of any remarkable lubricating ability at physiological pressures. Hills5,28,29 on the other hand has claimed that so-called surface active phospholipids (SAPL)11,30—lipids synthesized by synoviocytes and adsorbed onto the cartilage surface—rather than proteins/proteoglycans are responsible for the lubrication of synovial joints. The Hills mechanism conjectured that the SAPL formed boundary layers on the cartilage surface resembling classical boundary lubricants, exposing hydrophobic tails that contacted and slid past each other during cartilage articulation. It has been pointed out,31 however, that such a mechanism would lead to friction coefficients (μ ≈ 0.05)32 rather than the much lower values (μ ≈ 0.001) in human joints. Clearly, the relative contributions of the cartilage or synovial joint macromolecular components to boundary lubrication of joints have not yet been resolved. Our present study is part of an overall goal to systematically investigate each one of the main cartilage macromolecules, in order to shed light on this central question of cartilage boundary lubrication in mammalian synovial joints.

While HA is the most abundant macromolecule in synovial fluid, it is the proteoglycan known as aggrecans (Agg) that is the most abundant macromolecule present within the collagen fibril network comprising articular cartilage (at a concentration of ca. 8%4,33). Agg is composed of a protein backbone and highly negatively charged34,35 glycosaminoglycan chains of chondroitin sulfate (CS, see structure in Figure 1B) and keratan sulfate (KS) covalently attached to it34,36−39 in a bottlebrush-like configuration. Within the cartilage tissue, Agg exist mostly as complexes with HA, where up to a hundred or more Agg molecules are noncovalently attached to a single HA chain via the HA-binding region, a globular domain called G1 at the N-terminus of the Agg core protein,36,40−42 stabilized by link proteins (LPs). Such HA/Agg/LP aggregates, ubiquitous in the cartilage, may thus also be present at its surface.4

Figure 1.

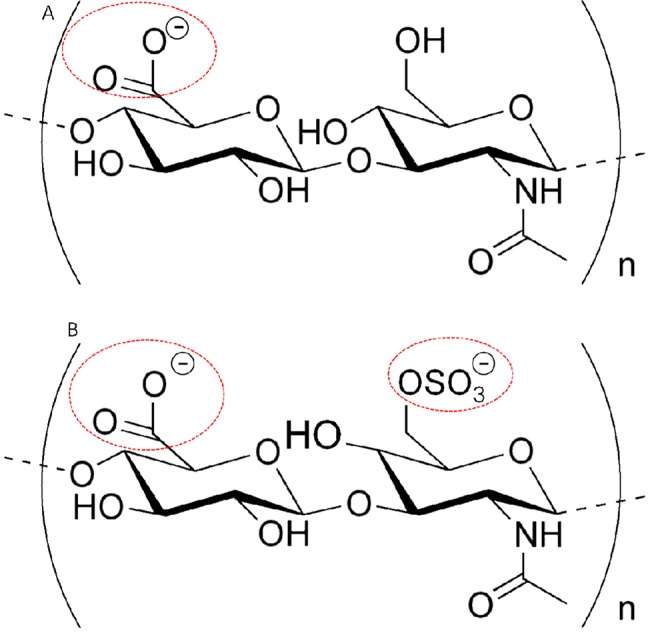
Figure 1

Open in a new tab

(A) Structural formula of HA. (B) Structural formula of CS. In both the molecules, the ionized sites are rounded in red. In physiological conditions, usually HA has one negative charge per disaccharide, and CS has two negative charges per disaccharide.

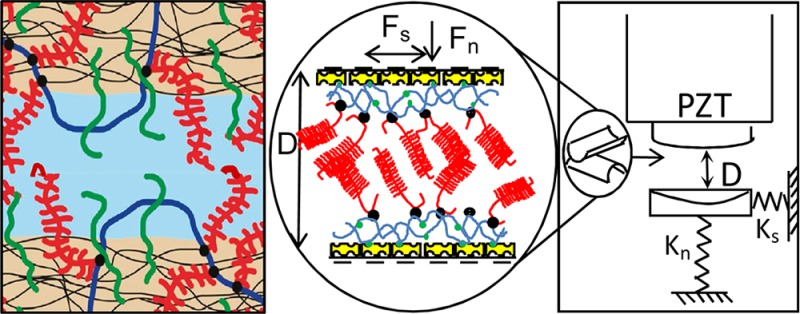
In an earlier study,43 the nature and properties of a single layer of HA/Agg/LP complexes attached to a molecularly smooth surface were examined in some detail, by measuring the interactions of such a layer with a second, molecularly smooth, bare solid (mica) surface. These interactions were determined stage by stage as the HA/Agg/LP layer was progressively constructed; this is crucial to reveal the properties not only of the final layer but also of the intermediate stages, such as the HA layer prior to its complexation with Agg/LP. It was thus possible to deduce the charge density of the HA/Agg/LP layer, its macromolecular configuration on the surface and its areal density, and the mechanical response of such a layer to compression, as well as shear interactions between the layer and the bare, smooth (negatively charged) solid surface. These previously determined properties43 of the single HA/Agg/LP layer serve as a useful reference for the present study, although clearly in order to emulate sliding friction between cartilage surfaces a symmetrical situation is required (i.e., the presence of similar HA/Agg/LP layers on opposing surfaces). The main idea of the present work, therefore, is to create identical surface layers of such complexes on two opposing, mutually compressed surfaces in order to examine their capability for reducing friction at low shear rates (where the boundary lubrication regime is expected to apply) and, particularly, at salt concentrations and pressures resembling those in the joint.

Materials and Methods

Materials

Water for the surface force balance (SFB) experiments was purified with a Barnstead water purification system (Barnstead NANOpure Diamond, resistivity = 18.2MΩ, total organic content (TOC) < 1 ppb; so-called conductivity water), Ruby Muscovite mica grade 1 supplied by S & J Trading, Inc., New York, was utilized for the SFB experiments. Avidin from egg white (A9275) and PBS (phosphate buffered saline tablet, Tru-Measure Chemical (P4417)) were supplied by Sigma Aldrich, Israel. MILLEX HV Duropore PVDF 0.45 μm Membrane filters were supplied by Millipore, Ireland.

Bovine articular cartilage was obtained from femoral heads of 15–18 months old animals. Tissue was visually normal, and frozen at −20 °C until analyzed in order to keep its properties close to live tissue.

The biotinylation of HA, and the extraction and isolation of Agg proteoglycans and cartilage LP were described in ref (43). For the present study, we use the same materials as in ref (43).

Methods

SFB Measurement Procedure

The SFB technique and the detailed experimental procedure to measure normal and shear interactions between molecularly smooth sheets of mica have been described elsewhere;17,44,45 a schematic of the SFB is shown as the inset to Figure 2. The stage-by-stage preparation procedure of the HA/Agg/LP surface-attached complexes on each mica sheet is described in detail in ref (43) and is repeated briefly in what follows.

Figure 2.

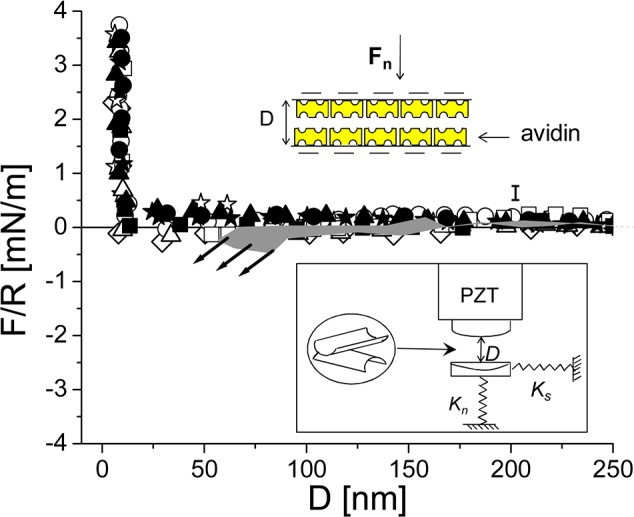
Figure 2

Open in a new tab

Normal force profiles normalized by the radius of curvature (R) as a function of the surface separation (D) between two avidin-bearing surfaces in pure water. Filled symbols are approaching profiles; empty symbols are receding profiles. Error bar represents uncertainty in the value of a datum point within a given run; scatter between different runs may be larger. Shaded area: interaction between an avidin-bearing surface and bare mica (from ref (43)); the arrows indicate jump into adhesive contact. Lower inset: schematic of an SFB, where Ks and Kn are the shear and the normal spring, respectively (Ks = 300 N/m and Kn = 137 N/m). Upper inset: schematic of two interacting avidin-bearing surfaces.

In order to reconstruct the HA/Agg complexes on the mica surface to be as similar as possible to their native configuration, we used lightly biotinylated HA (bHA).43,46 bHA attaches to a layer of positively charged avidin, previously adsorbed on the negative charged mica sheets, due to the avidin–biotin biochemistry (but also in part to the electrostatic interactions between the negative HA and the positive avidin). After the calibration of bare-mica/bare-mica contact in air and water, the lenses were soaked in 0.01 mg/mL avidin aqueous solution for around 30 min and then rinsed in water for 1–2 min. Normal and shear interactions between the two avidin-bearing surfaces were then measured. The bHA was then added to the avidin layer by filling overnight the meniscus between the lenses with an aqueous solution of 49 μg/mL bHA. The interface between the lenses was rinsed while filling the bath with water. After normal and shear interactions were measured between the two avidin-bHA bearing surfaces, the meniscus was filled overnight with a previously mixed solution of 0.1 mg/mL Agg +7.7 ± 0.6 μg/mL cartilage LP. This ratio corresponds to ∼3 LP molecules for each Agg (considering 47 000 Da and 2.5 × 106 Da to be the molecular weight of LP and Agg, respectively). Following measurements between the avidin-bHA/Agg/LP layers, the water was replaced with PBS solution (0.15 M) paying attention not to expose the surfaces to air. Normal and shear interactions were then measured in PBS solution.

Agg solution was prepared about 40 h prior to measurements and stored at 4 °C. After ca. 25 h (to ensure through dissolution), the solution was filtered through a 0.45 μm pore-size filter (Millipore, Ireland) to remove any residual particulate, and mixed with LP.

Mean pressures P on the confined macromolecular layers were estimated using Hertzian contact mechanics to evaluate the flattened area A at the point of closest approach, as A = π(FnR/K)2/3,47 where Fn is the applied normal load in the SFB, R (≈ 1 cm, determined separately at each contact point) is the mean radius of curvature of the mica surfaces, and K is the mean effective modulus of the mica/glue combination (determined separately as K ≈ 5 × 109 N/m2,22 via monitoring of the flattening at different loads, although this value may differ between contact points22). A is somewhat smaller than the total area over which the macromolecular layers overlap, but represents the region of closest approach and thus the greatest compression of the surface layers, which is taken to contribute the most to the sliding friction. The effective mean pressure is thus P = Fn/A (for interacting polymer-coated colloid particles, where the modulus is on the order of 1011 N/m2 and R is on the order of micrometers, the flattened Hertzian contact becomes unphysically small, and the effective contact area may be taken as that over which the polymers overlap48).

Results

As in our earlier single HA/Agg/LP layer study,43 it is essential to carry out the interaction measurements stage-by-stage, progressively, as it is only in this controlled approach that we can be confident that our surfaces are coated as designed. After calibrating the zero distance between the surfaces both in air and in water, normal and shear interactions between two avidin-bearing surfaces across conductivity water were determined, as shown in Figure 2. In the earlier one-layer study43 (where the corresponding stage was avidin vs bare mica instead of avidin vs avidin) the surfaces experienced a long-range jump into contact, arising from electrostatic attraction between the positively charged avidin and the negatively charged bare mica (shown as a shaded band in Figure 2). In the present symmetric case, the two avidin-bearing surfaces experience a weak repulsion, indicating a (weak) net positive charge on each avidin-coated mica surface, until a “hard wall” is reached at the closest surface separation D = 8.5 ± 0.4 nm, corresponding to an avidin monolayer on each mica surface.49 The interaction profiles are reversible, i.e. the decompression traces (empty symbols in Figure 2) are identical (within the scatter) to the compression ones (filled symbols in Figure 2).

Following addition of bHA, normal force (Fn(D)) versus closest-surface-separation (D) profiles, normalized by the mean radius of curvature (R) between two avidin-bHA-bearing surfaces across conductivity water are shown in Figure 3. Monotonic repulsions commence at ca. 300 nm, and increase roughly exponentially as might be expected from an electrostatic double layer interaction (inset Figure 3); this arises because the negative charge on the bHA overcompensates the positively charged avidin-coated mica, forming a weakly negatively charged surface. Deviations to a much steeper increase in the Fn(D)/R profiles at D ≈ 40 ± 10 nm indicate the onset of steric repulsions, while on strong compression a “hard-wall” separation of 14.6 ± 0.7 nm is reached, only about 6 nm thicker than the underlying avidin layers.43 From the far-field fit to the linearized Poisson–Boltzmann theory,50 the solid line in Figure 3, the avidin-bHA coated mica surfaces have an effective net surface charge density of ca. −e/200 nm2, while the bulk ion concentration corresponds to C = 10–5 M. These values are similar to those estimated earlier for the asymmetric case (σavidin+bHA ≈ −e/300 nm2 facing σmica ≈ –e/30 nm2, C ≈ 2 × 10–5 M).43

Figure 3.

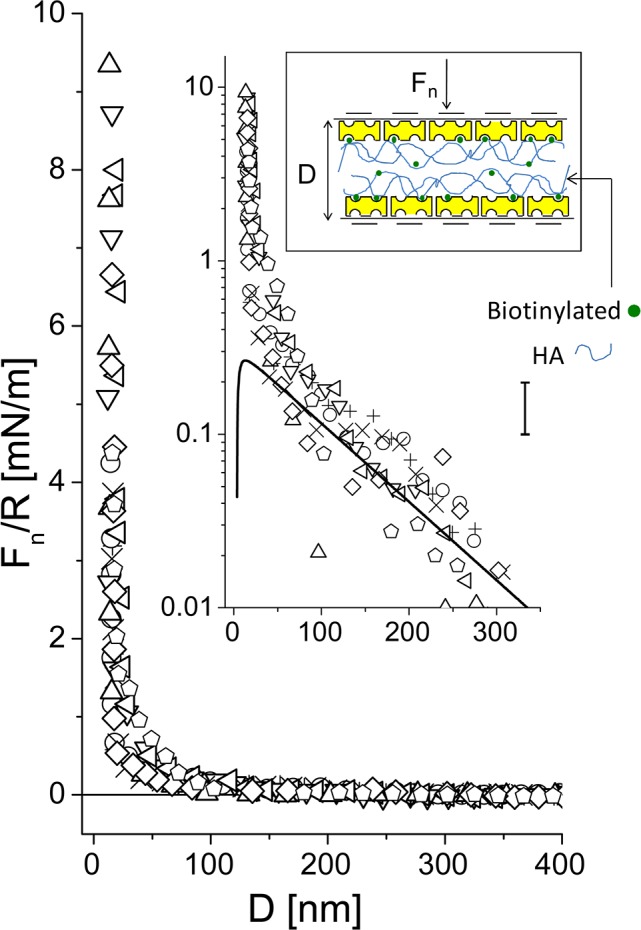
Figure 3

Open in a new tab

Normal force profiles normalized by the radius of curvature (R) as a function of the surface separation (D) between two avidin-bHA-bearing surfaces in pure water. The solid line in the upper graph is the DLVO fit (σavidin+bHA = −e/200 nm2, C = 10–5 M). The inset is a cartoon representing two avidin-bHA-bearing surfaces.

Following overnight incubation of the surfaces in an Agg and LP solution, normal and shear interactions were measured between the surfaces bearing the LP stabilized Agg/bHA complexes across conductivity water (Figure 4). A stronger, longer-ranged repulsion is now experienced between the surfaces, setting on at D > 300 nm and increasing monotonically to a ‘hard wall’ separation of 17.8 ± 1 nm under strong compression (mean pressure P = ∼12 atm). In our earlier paper, a single-layer bHA/Agg was compressed to 12 nm, at 18 atm, suggesting the hard wall should be at 24 nm now rather than 18 nm as observed. The shaded red area in Figure 4 recalls the normal interactions between a single avidin-bHA/Agg/LP-bearing surface against bare mica.43 When both surfaces are covered with the Agg/bHA complexes, the steric repulsion onsets at roughly double the separation of the single layer, and the ‘hard wall’ thickness is around one-third higher as noted above. Upon substituting water with PBS solution (0.15 M), the range of repulsion sharply decreases (half and blue symbols in Figure 4), repulsion appears around D ≈ 100 nm and increases sharply up to D = 16.4 ± 1.8 nm, similar within the scatter to the hard-wall in conductivity water. This is reasonable since the hard-wall value reflects the amount of polymer adsorbed (once most of the water has been squeezed out), which is little affected by the salt. Finally, upon decompression, the force profiles show, both in pure water and high salt solution, a small hysteresis: this may be due to a slower relaxation of the compressed molecules to their equilibrium configuration, which would result in a somewhat shorter range of repulsion on decompression, as seen in the profiles.

Figure 4.

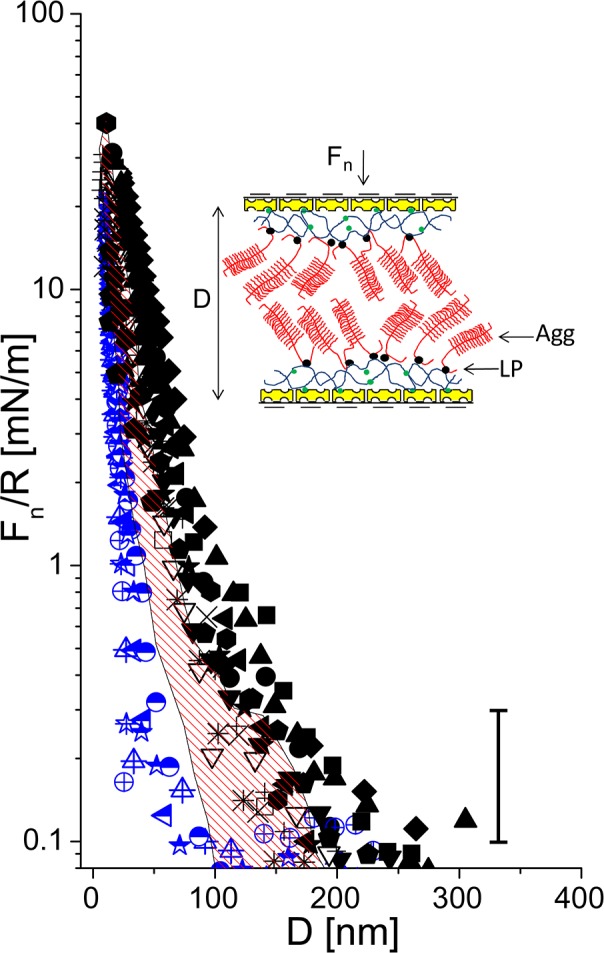
Figure 4

Open in a new tab

Normal force profiles normalized by the radius of curvature (R) as a function of the surface separation (D) between two avidin-bHA/Agg/LP-bearing surfaces: black symbols are the normal profiles in pure water, blue half symbols are normal profiles in PBS. Full and half symbols are approaching profiles; empty and crossed symbols are receding profiles. The shaded area (red online) recalls the data of the normal force profiles between an avidin-bHA/Agg/LP-bearing surface against bare mica, from ref (43). The inset is a schematic representation of two avidin-bHA/Agg/LP-bearing surfaces (see also earlier schematic for description of cartoon symbols).

At the same time as the Fn(D) profiles, shear interactions (i.e., frictional forces Fs) were also measured by moving the upper surface laterally back and forth past the bottom one at different separations and pressures. In Figures 5 and 6 are reported typical shear traces taken directly from the SFB when two avidin-bHA- and two avidin-bHA/Agg/LP-bearing surfaces, respectively, slide past each other in conductivity water, while in Figure 7 are the shear traces for two avidin-bHA/Agg/LP-coated surfaces sliding past each other in PBS solution. In all the figures, trace A represents the back and forth motion of the upper surface as a function of time, while the following traces are the shear forces, Fs (recorded from the bending of the lateral springs), at different surface distances and normal pressures at a given contact point. As in the earlier study,43 we have used the frequency analysis (FFT) of the shear force versus time graphs to extract those values of Fs that are too weak to be evaluated directly from the Fs versus time curves.

Figure 5.

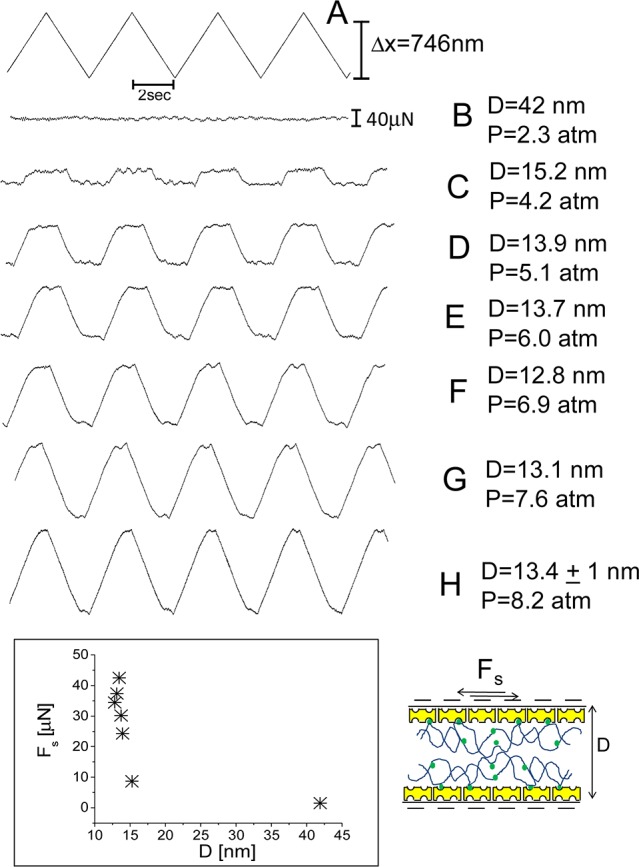
Figure 5

Open in a new tab

Typical shear force (Fs) versus time traces between two avidin-bHA-bearing surfaces across water. Trace A is the back and forth motion of the upper surface on top of the lower one at driving frequency of 0.25 Hz. Traces B–H are the shear forces recorded by the bending of the lateral springs at given pressures and surface separations. Bottom left inset: typical shear force Fs as a function of surface separation D. On the right is a schematic of two avidin-bHA-bearing surfaces shearing one on top of the other (see also earlier schematic for description of cartoon symbols).

Figure 6.

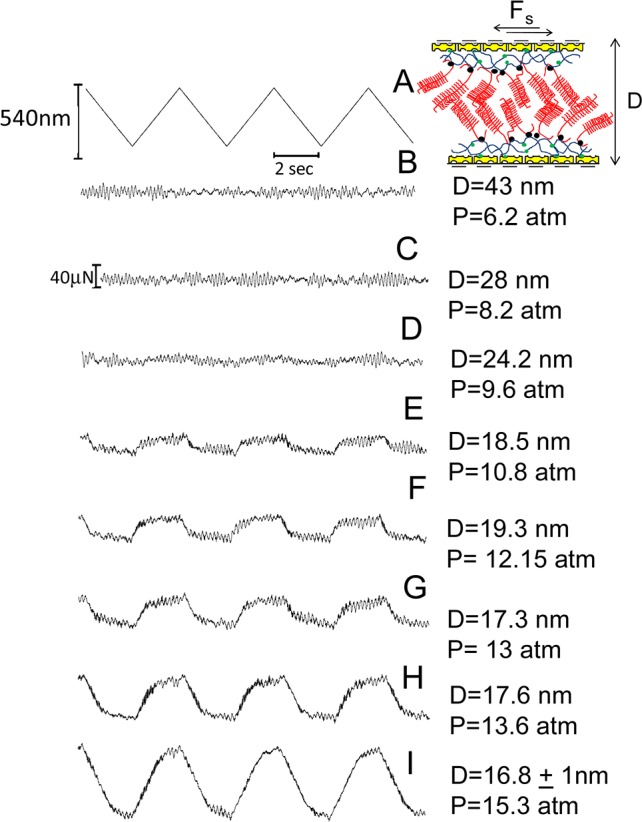
Figure 6

Open in a new tab

Typical shear force (Fs) versus time traces between two avidin-bHA/Agg/LP-bearing surfaces across water. Trace A is the back and forth motion of the upper surface on top of the lower one at driving frequency of 0.25 Hz. Traces B–I are the shear forces recorded by the bending of the lateral springs at given pressures and surface separations. On top is a schematic of two avidin-bHA/Agg/LP-bearing surfaces shearing one on top of the other (see also earlier schematic for description of cartoon symbols).

Figure 7.

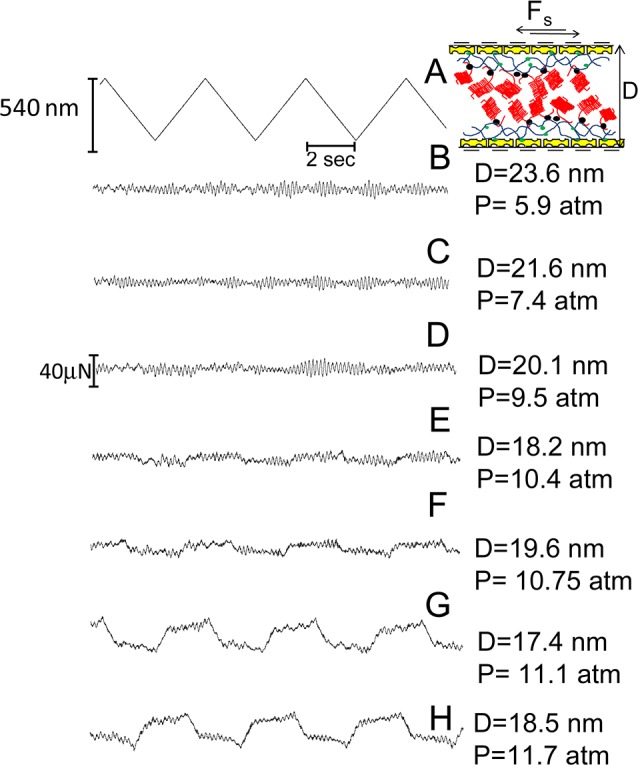
Figure 7

Open in a new tab

Typical shear force (Fs) versus time traces between two avidin-bHA/Agg/LP-bearing surfaces across PBS. Trace A is the back and forth motion of the upper surface on top of the lower one at a driving frequency of 0.25 Hz. Traces B–H are the shear forces recorded by the bending of the lateral springs at given pressures and surface separations. On top is a schematic of two avidin-bHA/Agg/LP-bearing surfaces shearing one on top of the other in a collapsed configuration (see also earlier schematic for description of cartoon symbols).

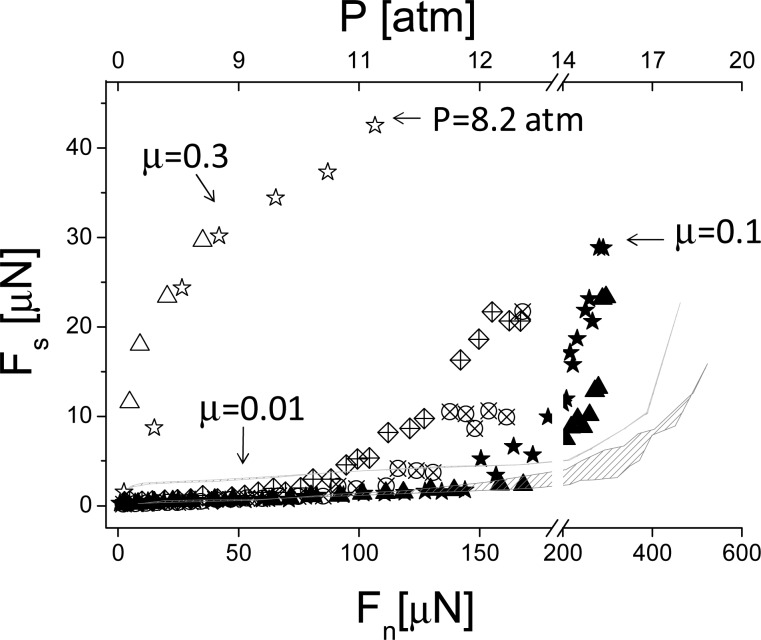
Variation of the shear forces Fs for the three configurations as a function of the normal loads Fn are summarized in Figure 8 and yield the effective friction coefficients for the different cases. In conductivity-water, when the surfaces are covered only with an avidin-bHA layer, the coefficient of friction is high (μ = 0.4 ± 0.05) already at low pressures (starting from ca. 2 atm). In contrast, once Agg/LP complexes with the previously attached HA, the friction coefficient decreases significantly (μ = 0.014 ± 0.004) up to P ≈ 12 atm. At stronger compression, the friction coefficient increases (reaching μ ≈ 0.1 from Figure 8 at P ≈ 16 atm), but is still much lower than between two sliding avidin-bHA layers. In the presence of high salt concentration, despite clear differences in the normal force profiles, the sliding friction remains similar, if slightly higher, leading to similar coefficients of friction (μ = 0.015 ± 0.007), up to P ≈ 9 atm, but then increases significantly at higher pressures as shown by the crossed symbols in Figure 8.

Figure 8.

Figure 8

Open in a new tab

Shear forces as a function of normal forces. Open symbols: interactions between two avidin-bHA-bearing surfaces across water; closed symbols: interactions between two avidin-bHA/Agg/LP-bearing surfaces across water; crossed symbols: interactions between two avidin-bHA/Agg/LP-bearing surfaces across PBS. The top axis indicates the pressure calculated according to Hertzian contact mechanics. The pressure depends on the radius of curvature (R) which is measured for each contact point; in the top axis R = 8.04 mm, corresponding to the radius of curvature of the ★ profile (for other profiles, where R is somewhat different, the pressure axis serves as an approximate value).

Discussion

The main thrust of this study was to examine the frictional forces between two sliding surfaces, each coated with HA–Agg aggregates (stabilized by LP, i.e, HA/Agg/LP layers). These complexes are known to comprise the most abundant macromolecules in articular cartilage, and thus our results may provide insight into the nature of boundary lubrication in synovial joints. Our earlier study43 established the properties of each such HA/Agg/LP layer attached to molecularly smooth mica surfaces (which serve as the substrates for these macromolecular surface phases), and in particular enabled estimates of their structure, surface charge density, and areal density on the mica surfaces. The present study too was carried out by constructing the final layers on each of the two interacting surfaces step by step, including control measurements at each stage. This is a crucial protocol, which enables a direct stage-by-stage examination of the intermediate layers—avidin, then avidin-bHA—and is necessary to have confidence that the ultimate configuration is indeed that of HA/Agg/LP layers attached to the avidin-coated mica substrate.

We first consider briefly the nature of the interactions between these intermediate layers. The two interacting avidin–coated surfaces (Figure 2) experience a weak long-ranged repulsion consistent with a net positive surface charge43 and come into contact at a “hard-wall” separation of ca. 8.5 nm. This compares with the single avidin layer versus bare mica interaction,43 which shows a strong attraction to adhesion at a hard wall separation at D ≈ 6 nm, and suggests, since the bilayer thickness is less than twice that of the monolayer, that there is some interpenetration of the two opposing avidin layers. This would be consistent with the nature of the avidin adsorption, which AFM micrographs (see Figure 1 in the Supporting Information) of the avidin-coated mica reveal to be a dense, although not close-packed, array of adsorbed avidin molecules covering roughly half the surface area. Shear force measurements between the contacting avidin-coated surfaces show a large friction force as soon as the surfaces are pressed together (see Figure 2 in the Supporting Information). This is likely due to local adhesive contact between some of the (positively charged) avidin molecules with the exposed (negatively charged) mica patches on the opposing surface, again consistent with the picture of layer interpenetration, although the net interaction between the surfaces remains repulsive.

Once bHA attaches to each surface (via specific biotin–avidin adhesion as well as through physisorption on the oppositely charged avidin molecules) the net surface charge reverses to become weakly negative,43 and the normal interactions (Figure 3) indicate a weak, long-ranged, electrostatic double layer repulsion followed by a more-sharply increasing (though still weak) steric repulsion setting on at ca. 40 ± 10 nm as the opposing HA segments come into overlap. This suggests the unperturbed thickness of each bHA layer is about 20 ± 5 nm, and is consistent with the thickness of a single avidin-bHA indicated in our earlier study.43 The frictional forces (Figures 5 and 8) between the avidin-bHA coated surfaces are quite low (almost within the scatter of the data), until the surfaces are compressed almost to their “hard-wall” separation, D ≈ 15 nm, and pressures up to ca. 3 atm (Figure 8), whereupon they rise very rapidly. The weak frictional dissipation at low pressures (P < 3 atm) is attributed to hydration lubrication arising from the hydrated, negatively charged HA segments sliding past each other, where the low friction is due to the fluid nature of the bound hydration layers.17 The rapid rise of friction at D < ca. 15 nm suggests that bHA molecules are bridging to make contact with avidin molecules on the opposing surface as the layers interpenetrate under compression: frictional dissipation occurs as such bridges are dragged along during the sliding.51,52 Alternatively, it may be due to the removal of the hydration layers about the negatively charged HA monomers, if such hydration layers about the charged COO– groups (see Figure 1) are only weakly bound, as is known to be the case with simple hydrated anions such as Cl– or Br–.53 Removal of the water of hydration would eliminate the hydration lubrication mechanism, resulting in higher frictional dissipation as HA segments rubbed past each other (see later). This would be consistent with the abrupt rise in friction between negatively charged polymer brushes observed in earlier studies,19,54 which also occurs at pressures larger than about 3 atm. The relatively large friction between compressed HA layers is also consistent with earlier direct friction studies on such layers.55−57

The most relevant indications arise once the Agg molecules have attached to the avidin-bHA layer. As noted, bottlebrush-like configurations of HA–Agg aggregates are abundant in articular cartilage. They have been conjectured4 to be present at the outer cartilage surface as they pass through it into the synovial fluid, and may play a role as boundary lubricants in cartilage articulation. The repulsive steric interactions between two HA/Agg/LP layers across water (Figure 4) have a range that is somewhat under twice that of the repulsion between a single HA/Agg/LP layer and bare mica43 (shaded band in Figure 4). On a logarithmic plot of the data, as shown in Figure 9, the profile appears to have two linear regimes: a longer-ranged one, from D ≈ 300 nm (when the repulsion first exceeds the scatter in the data) to D ≈ 70 nm, and another for D < ca. 70 nm. As in our previous study, the overall repulsion may be considered as the sum of a longer-ranged double-layer electrostatic repulsion term arising from the net residual charge on the avidin-HA/Agg/LP layers (due to trapped counterions, c/i), and a repulsion that arises once the Agg layers overlap so that steric interactions between their monomers become dominant.

Figure 9.

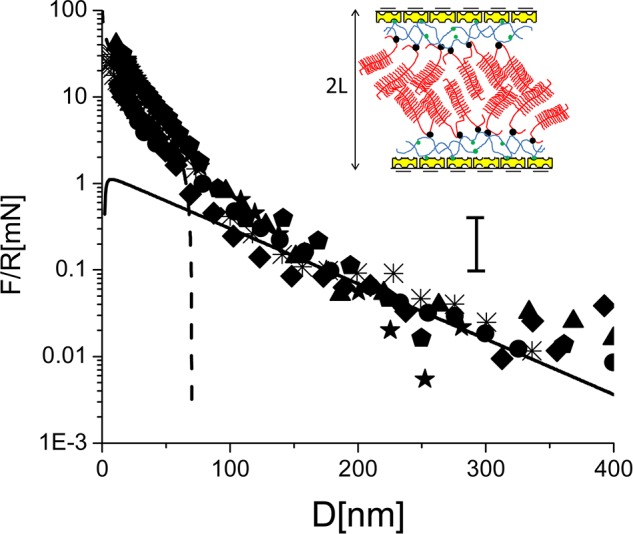
Figure 9

Open in a new tab

Normal interactions, normalized by the radius of curvature (R), as a function of surface separation (D) of two avidin-bHA/Agg/LP-bearing-surfaces in water. Solid line: fit to the linear Poisson–Boltzmann theory (DLVO) corresponding to σavidin-bHA/Agg/LP = −e/9 nm2, C = 2 × 10–5 M, which describes the long-range interaction. Dashed line: fit to eq 2 (see text), which describes the short-range interaction. (See also earlier schematic for description of cartoon symbols.)

A simple model to account for compression of a single HA/Agg/LP layer in terms of pressures Πc/i ≈ nkBT, and Πmon ≈ (ϕ2/ν)kBT, due to counter-ion osmotic pressure and monomer steric contribution, respectively, was developed in ref (43). Here n is the number of counterions per unit volume, kB is the Boltzmann constant, T is the temperature (T = 296 K), ν is the volume of a disaccharide monomer on the CS moieties on the Agg molecules, and ϕ is the monomer volume fraction (volume of disaccharide monomers per unit volume). The overall pressure between flat parallel surfaces obeying the same force–distance law as the curved mica surfaces at separation D is given by Π(D), where

graphic file with name bm-2012-01283f_m001.jpg 1

and, in terms of the normal force (Fn)–distance (D) profile between the mica surfaces (mean radius of curvature R), we find43

graphic file with name bm-2012-01283f_m002.jpg 2

Here 2L is the range of the steric interaction. The prediction of eq 2 for the present force–distance profile, assuming the long-ranged electrostatic interaction for D > 2L, and eq 2 for D < 2L, using values of n and D-dependent ϕ that are twice those deduced earlier43 (since we are dealing with a symmetric configuration), are shown in Figure 9. The reason why the range of the steric interactions between the two layers is somewhat less than twice that between a single layer and mica is attributed in part as follows: in the case of two HA/Agg/LP layers, there is some interpenetration between them before the osmotic steric repulsion dominates the electrostatic double layer repulsion, while for the case of a single layer facing bare mica, steric effects are expected to be substantial as soon as contact with the impenetrable surface is made. We note that in a PBS environment with physiological level salinity, the repulsion between two HA/Agg/LP layers (Figure 4) is considerably reduced, both with respect to onset separation and at higher compressions, compared to the conductivity water environment. This is due to reduction of the Debye screening length at high salt, which reduces both the range of the electrostatic double layer repulsion between the opposing layers, and the short-ranged repulsions between the Agg macromolecules on each surface, resulting in a less extended configuration. We recall that at 1:1 electrolyte salt concentrations of ca. 3 × 10–5 M and 0.13 M, corresponding to conductivity water and to PBS solution, the Debye screening lengths are ca. 55.5 and 0.8 nm, respectively. At the same time, the limiting (“hard-wall”) separation at the highest compressions is little changed, at D ≈ 17–18 nm (Figure 4), as it reflects the overall amount of polymer on the surfaces. An additional suggestive indication may be extracted from Figure 9, which shows the surface charge density of each HA/Agg/LP layer to be ca. e/9 nm2. This corresponds to 0.018 C/m2, which is within a factor 2 of the measured surface charge density of 0.037 C/m2 on the articular cartilage surface58

Sliding frictional forces between the HA/Agg/LP layers at physiological pressures are of particular interest. The only other studies, that we are aware of, of friction between Agg-bearing surfaces used lateral force microscopy with an AFM cantilever tipped by a 2.5 μm-radius colloidal particle,48,59 where the Agg core proteins extend normal to the substrates. These results indicate friction coefficients in the range μ ≈ 0.02–0.07 at salt concentrations of 10–3–1 M. However, the relation of these results to the present work is not clear. This is because in these AFM experiments48,59 the mean pressures over the Agg–Agg contact areas are very low (up to ca. 1 atm at most), which is much lower than in our study, and is indeed about 2 orders of magnitude lower than in the major joints where synovial lubrication is active. In addition, sliding past the soft Agg layers of a micrometer-sized bead may involve substantial ploughing dissipation, which does not occur in the SFB (where the radius of curvature of the surfaces, R ≈ 1 cm, is about 3–4 orders of magnitude higher).

The shear forces as the HA/Agg/LP layers slide past each other, Figures 7–9, reveal a rather low friction between them, with an effective friction coefficient μ ≈ O(0.01), up to mean pressure P ≈ 12 atm. This may be interpreted largely in terms of two effects. The first is the reluctance of segments from the charged, brush-like Agg molecules extending from each surface43 to interpenetrate, in line with earlier work on polymer brushes;19,54 this would result in a weakly entangled interfacial layer, and thus low viscous dissipation on shear. At the same time, one expects the hydration layers about the charged groups on the Agg molecules, largely the COO– and the SO3– groups on the CS moieties, to provide lubrication via the hydration lubrication mechanism.17 The magnitude of the frictional dissipation, expressed at the simplest level through the friction coefficient μ, then provides clues as to the nature of the interactions. We note first that the frictional dissipation between the two avidin-bHA/Agg/LP layers as they slide past each other (μ ≈ 0.01 up to P ≈ 12 atm) is significantly lower than for two sliding avidin-bHA layers, where the friction becomes very large at P > ca. 3 atm. This is also in line with the higher friction between HA segments relative to Agg molecules sliding past bare mica.43 Part of this may be due to HA adhering to the opposing bare mica (as seen previouisly),43,55 or bridging to adhere to opposing avidin-coated mica in the present work, but the indications are also that the hydrated groups on the Agg molecules are more efficient in reducing friction than the hydrated groups of the HA layers.

We may examine this in more detail with the help of Figure 1. There we see that in the case of Agg, the CS monomers—the dominant component of Agg—have, on average, one COO– and one SO3– charged groups per disaccharide monomer, while the charged HA monomers have only one charged COO– group per disaccharide. Moreover, the density of the charged CS moieties on each Agg is considerably larger than that of the HA,43 per unit area occupied by each of the macromolecules.43 Thus we expect a considerably higher density of hydrated charged groups per unit area of interaction for the Agg when compared with the HA layers, and this may well account for the much more efficient Agg versus Agg lubrication relative to HA versus HA lubrication. We may quantify this as follows: From our study of the single avidin-bHA and avidin-bHA/Agg/LP layers,43 we estimated an area AHA ≈ 1.6 × 105 nm2 per HA molecule on the mica surface, a number nHAds ≈ 2.6 × 103 disaccharide units per HA molecule, each with a single hydrated charge, and nAgg ≈ 20 Agg molecules complexed to each surface-attached HA chain. Each Agg bears nCSds ≈ 5.5 × 103 CS disaccharide units (as in Figure 1B), each with two hydrated charged groups. Thus the ratio of hydrated groups associated with the Agg relative to those associated with the HA, per unit area of the surface, is (2nCSds·nAgg/nHAds) ≈ 80. Even if not all the hydrated groups on the aggrecn are active in reducing the friction via the hydration lubrication mechanism, it is clear that the Agg layers must expose very many more such groups per unit area of interaction than the surface-attached HA alone. We attribute the better lubrication by the Agg layers mainly to that. Indeed, the overall areal density of hydrated charged groups on the Agg (either COO– or SO3–) is close to 1 hydrated-charge/nm2, although, because of the bottle-brush like structure of the Agg, many of these will be screened from interacting with the opposing surface.

At the same time, we recall that lubrication between brushes of the polymer poly(methacryloylphosphorylcholine) (pMPC)18 whose monomers consist of phosphorylcholine groups (similar to the headgroups of phosphatidylcholine lipids), as well as lubrication by close-packed liposomes on mica surfaces,20,22 is very much more efficient still (μ ≈ 10–4), and to much higher pressures (P = O(100 atm)) than the Agg versus Agg lubrication in the present study. This is likely to be due to the highly hydrated nature of the zwitterionic phosphocholine groups, as well as their higher surface density. The liposomes, for example, expose 1 highly hydrated phosphocholine group per 0.7 nm2, and these higher areal densities, together with the high level of hydration, account for the much more efficient lubrication by the phosphocholine-exposing layers relative to Agg. However, the issue of the precise extent, binding energy, and fluidity of bound hydration layers, which affect the hydration lubrication mechanism, and how these vary between different charged or zwitterionic groups, is complex. It is influenced not only by the nature of the hydrated groups themselves but also by their local charge environment.60 We expect that, group for group, phosphocholine groups provide better hydration lubrication than the charged COO– and SO3– groups on Agg, because SO3– groups are rather weakly hydrated. For example, SO3– is known to desolvate and adsorb onto gold electrodes from sulphuric acid solution, in contrast to highly hydrated alkali metal ions such as Na+ or K+.61−63 Additionally, in experiments using polyelectrolyte brushes19 where the charged groups on the chains were SO3–, the friction, in contrast to the pMPC brushes,18 was found to increase rapidly at pressure > ca. 3 atm, suggesting that lubrication by these hydrated SO3– groups is quite weak.

We remark also on the effect of a higher salt environment on the Agg versus Agg friction seen in Figure 8. At the physiological-level salt concentration in the PBS solution, ca. 0.15M, compared with an effective 1:1 salt concentration of ca. 3 × 10–5 M in conductivity water, we note a systematically higher friction by up to a factor of 3-fold or so. This is in line with earlier observations on the hydration lubrication mechanism, such as between pMPC brushes18 and between phosphatidylcholine liposome surface layers.22 This higher friction at higher salt is attributed, as in the other cases,18,22 to the reduced extent of hydration in the presence of a high salt concentration, as is known from independent studies,64 resulting in less efficient hydration lubrication.

Finally, we note the differences between Agg layers sliding past bare mica, and sliding past each other, as indicated in Figure 8. Assuming that the dominant mechanism for reducing the friction arises from the hydration layers on the Agg, we note that, for the case of Agg versus bare mica (shaded regions in Figure 8 taken from ref (43)), the friction force is very similar to that for Agg versus Agg up to P ≈ 12 ± 2 atm. At higher pressures, however, the former is significantly lower than the latter. We may attribute this as additional viscous dissipation upon sliding, arising from the increased interpenetration of the opposing Agg layers at higher P,52 relative to the case of an Agg layer sliding against bare mica, which is smooth and impenetrable.

Conclusions

The present study is part of broader effort to gain insight into the origin of the very low friction in synovial joints at physiological pressures. In particular, we examined whether the most common macromolecules present in synovial fluid and in the articular cartilage itself, namely, HA and Agg and their complexed aggregates, could provide boundary lubrication consistent with this low friction. Our findings show that, at pressures up to around 12 atm, friction coefficients between sliding surfaces bearing the HA–Agg aggregates (stabilized by cartilage LP) were relatively low, although at a value of μ ≈ 0.01, increasing to 0.1 at ca. 16 atm, they were substantially higher than values characteristic of synovial joint lubrication, which is around μ ≈ 0.001–0.005 up to physiological pressures (on the order of 50–100 atm).4 The larger friction is attributed to the relative weakness of the hydrated groups associated with the Agg molecules (COO–, SO3–) in providing efficient hydration lubrication. Thus we conclude that, on their own, such HA–Agg aggregates at the cartilage surface are unlikely to provide boundary lubrication with the observed low friction properties of synovial joints. The boundary lubrication properties of the main macromolecular components of both articular cartilage and synovial fluid, i.e., HA,55,56 Agg,35,36,48,59 and the HA–Agg complex (our previous43 study and the present study), as well as lubricin,27 have now all been examined directly. The results show clearly that, on their own, these macromolecules cannot account for the remarkably efficient boundary lubrication in the major joints, and that the origin of this must lie elsewhere, possibly in a synergistic effect arising from a combination of the relevant components at the cartilage surface.

Acknowledgments

We thank the Charles W. McCutchen Foundation for sustained support of this study. We also acknowledge support from the European Research Council and from the Petroleum Research Fund (Grant 45694-AC7) and the Ministry of Industry and Trade (Israel) through their Kamin programme. A.J.D. and L.C. acknowledge the support of Arthritis Research UK (18472).

Supporting Information Available

Figure 1: Atomic force microscope (AFM) image of a mica sheet covered with avidin. Tapping mode in air. Figure 2: Shear force versus time traces between two avidin- bearing mica surfaces. This information is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Supplementary Material

bm301283f_si_001.pdf (264.3KB, pdf)

References

  1. Dowson D.; Yao J. Proc. 16th Leeds–Lyon Symp. Tribol. 1990, 17, 91–102. [Google Scholar]
  2. Schmidt T. A.; Gastelum N. S.; Nguyen Q. T.; Schumacher B. L.; Sah R. L. Arthritis Rheum. 2007, 56, 882–891. [DOI] [PubMed] [Google Scholar]
  3. McCutchen C. W. Wear 1962, 5, 1–17. [Google Scholar]
  4. Klein J. Proc. Inst. Mech. Eng., Part J 2006, 220, 691–710. [Google Scholar]
  5. Hills B. A.; Butler B. D. Ann. Rheum. Dis. 1984, 43, 641–648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ateshian G. A.; Wang H.; Lai W. M. J. Tribol. 1998, 120, 241–251. [Google Scholar]
  7. McCutchen C. W. Nature 1959, 184, 1284–1285. [DOI] [PubMed] [Google Scholar]
  8. Chang D. P.; Abu-Lail N. I.; Coles J. M.; Guilak F.; Jay G. D.; Zauscher S. Soft Matter 2009, 5, 3438–3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chang D. P.; Abu-Lail N. I.; Guilak F.; Jay G. D.; Zauscher S. Langmuir 2008, 24, 1183–1193. [DOI] [PubMed] [Google Scholar]
  10. Gale L. R.; Chen Y.; Hills B. A.; Crawford R. Acta Orthop. 2007, 78, 309–314. [DOI] [PubMed] [Google Scholar]
  11. Hills B. A. Intern. Med. J. 2002, 32, 242–251. [DOI] [PubMed] [Google Scholar]
  12. Schwarz I. M.; Hills B. A. Br. J. Rheumatol. 1998, 37, 21–26. [DOI] [PubMed] [Google Scholar]
  13. Swann D. A.; Radin E. L.; Nazimiec M.; Weisser P. A.; Curran N.; Lewinnek G. Ann. Rheum. Dis. 1974, 33, 318–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Swann D. A.; Slayter H. S.; Silver F. H. J. Biol. Chem. 1981, 256, 5921–5925. [PubMed] [Google Scholar]
  15. Yu J.; Urban J. P. G. J. Anat. 2010, 216, 533–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hills B. A. J. Rheumatol. 1989, 16, 82–91. [PubMed] [Google Scholar]
  17. Raviv U.; Klein J. Science 2002, 297, 1540–1543. [DOI] [PubMed] [Google Scholar]
  18. Chen M.; Briscoe W. H.; Armes S. P.; Klein J. Science 2009, 323, 1698–1701. [DOI] [PubMed] [Google Scholar]
  19. Raviv U.; Giasson S.; Kampf N.; Gohy J. F.; Jerome R.; Klein J. Nature 2003, 425, 163–165. [DOI] [PubMed] [Google Scholar]
  20. Goldberg R.; Schroeder A.; Silbert G.; Turjerman K.; Barenholz Y.; Klein J. Adv. Mater. 2011, 23, 3517–3521. [DOI] [PubMed] [Google Scholar]
  21. Wen S.; Huang P.. Principles of Tribology; John Wiley & Sons: New York, 2012. [Google Scholar]
  22. Goldberg R.; Schroeder A.; Barenholz Y.; Klein J. Biophys. J. 2011, 100, 2403–2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ogston A. G.; Stanier J. E. J. Physiol. 1953, 119, 244–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fouissac E.; Milas M.; Rinaudo M. Macromolecules 1993, 26, 6945–6951. [Google Scholar]
  25. Richette P.; Ravaud P.; Conrozier T.; Euller-Ziegler L.; Mazieres B.; Maugars Y.; Mulleman D.; Clerson P.; Chevalier X. Arthritis Rheum. 2009, 60, 824–830. [DOI] [PubMed] [Google Scholar]
  26. Radin E. L.; Swann D. A.; Weisser P. A. Nature 1970, 228, 377–&. [DOI] [PubMed] [Google Scholar]
  27. Zappone B.; Ruths M.; Greene G. W.; Jay G. D.; Israelachvili J. N. Biophys. J. 2007, 92, 1693–1708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hills B. A.; Crawford R. W. J. Arthroplasty 2003, 18, 499–505. [DOI] [PubMed] [Google Scholar]
  29. Hills B. A. Ann. Biomed. Eng. 1995, 23, 112–115. [DOI] [PubMed] [Google Scholar]
  30. Hills B. A. Intern. Med. J. 2002, 32, 170–178. [DOI] [PubMed] [Google Scholar]
  31. Faraday Discuss. 2012, 156, 295-6. [Google Scholar]
  32. Briscoe B. J.; Evans D. C. B. Proc. R. Soc. London., Series A 1982, 380, 389–407. [Google Scholar]
  33. Maroudas A.; Bayliss M. T.; Venn M. F. Ann. Rheum. Dis. 1980, 39, 514–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Dudhia J. Cell. Mol. Life Sci. 2005, 62, 2241–2256. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ng L. J. Doctor of Philosophy in Biological Engineering Thesis, University of California, 2005. [Google Scholar]
  36. Ng L.; Grodzinsky A. J.; Patwari P.; Sandy J.; Plaas A.; Ortiz C. J. Struct. Biol. 2003, 143, 242–257. [DOI] [PubMed] [Google Scholar]
  37. Doege K. J.; Sasaki M.; Kimura T.; Yamada Y. J. Biol. Chem. 1991, 266, 894–902. [PubMed] [Google Scholar]
  38. Dean D.; Seog J.; Ortiz C.; Grodzinsky A. J. Langmuir 2003, 19, 5526–5539. [Google Scholar]
  39. Hascall V. C.; Sajdera S. W. J. Biol. Chem. 1970, 245, 4920–4930. [PubMed] [Google Scholar]
  40. Hardingham T. E.; Fosang A. J. FASEB J. 1992, 6, 861–870. [PubMed] [Google Scholar]
  41. Watanabe H.; Cheung S. C.; Itano N.; Kimata K.; Yamada Y. J. Biol. Chem. 1997, 272, 28057–28065. [DOI] [PubMed] [Google Scholar]
  42. Seyfried N. T.; McVey G. F.; Almond A.; Mahoney D. J.; Dudhia J.; Day A. J. J. Biol. Chem. 2005, 280, 5435–5448. [DOI] [PubMed] [Google Scholar]
  43. Seror J.; Merkher Y.; Kampf N.; Collinson L.; Day A. J.; Maroudas A.; Klein J. Biomacromolecules 2011, 12, 3432–3443. [DOI] [PubMed] [Google Scholar]
  44. Klein J.; Kumacheva E. J. Chem. Phys. 1998, 108, 6996–7009. [Google Scholar]
  45. Klein J. J. Chem. Society, Faraday Trans. 1 1983, 79, 99–&. [Google Scholar]
  46. Mahoney D. J.; Blundell C. D.; Day A. J. J. Biol. Chem. 2001, 276, 22764–22771. [DOI] [PubMed] [Google Scholar]
  47. Israelachvili J.Intermolecular and Surface Forces, 2nd ed.; Accademic Press: London, 1992. [Google Scholar]
  48. Han L.; Dean D.; Mao P.; Ortiz C.; Grodzinsky A. J. Biophys. J. 2007, 93, L23–L25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Darst S. A.; Ahlers M.; Meller P. H.; Kubalek E. W.; Blankenburg R.; Ribi H. O.; Ringsdorf H.; Kornberg R. D. Biophys. J. 1991, 59, 387–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Derjaguin B. V.; Churaev N. V.; Muller V. M.. Surface Forces: Plenum Publishing Corporation: New York, 1987. [Google Scholar]
  51. Klein J.; Raviv U.; Perkin S.; Kampf N.; Chai L.; Giasson S. J. Phys.: Condens. Matter 2004, 16, S5437–S5448. [Google Scholar]
  52. Raviv U.; Tadmor R.; Klein J. J. Phys. Chem. B 2001, 105, 8125–8134. [Google Scholar]
  53. Cotton F. A.; Wilkinson G.; Murillo C. A.; Bochmann M.. Advanced Inorganic Chemistry; Wiley-Interscience: New York, 1999. [Google Scholar]
  54. Raviv U.; Giasson S.; Kampf N.; Gohy J. F.; Jerome R.; Klein J. Langmuir 2008, 24, 8678–8687. [DOI] [PubMed] [Google Scholar]
  55. Benz M.; Chen N. H.; Israelachvili J. J. Biomed. Mater. Res., Part A 2004, 71A, 6–15. [DOI] [PubMed] [Google Scholar]
  56. Tadmor R.; Chen N. H.; Israelachvili J. N. J. Biomed. Mater. Res. 2002, 61, 514–523. [DOI] [PubMed] [Google Scholar]
  57. Yu J.; Banquy X.; Greene G. W.; Lowrey D. D.; Israelachvili J. N. Langmuir 2012, 28, 2244–2250. [DOI] [PubMed] [Google Scholar]
  58. Minassian A.; O’Hare D.; Parker K. H.; Urban J. P. G.; Warensjo K.; Winlove C. P. J. Orthop. Res. 1998, 16, 720–725. [DOI] [PubMed] [Google Scholar]
  59. Han L.; Dean D.; Ortiz C.; Grodzinsky A. J. Biophys. J. 2007, 92, 1384–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. See discussion in http://www.lsbu.ac.uk/water/ions.html and references therein.
  61. Bartlett B. N. University of Southampton, U. K., private communication.
  62. Zelenay P.; Ricejackson L. M.; Wieckowski A. J. Electroanal. Chem. 1990, 283, 389–401. [Google Scholar]
  63. Faraday Discuss. 2012, 156, 293. [Google Scholar]
  64. Rappolt M.; Pabst G.; Amenitsch H.; Laggner P. Colloids Surf., A 2001, 183–5, 171–181. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

bm301283f_si_001.pdf (264.3KB, pdf)

Articles from Biomacromolecules are provided here courtesy of American Chemical Society

RESOURCES