CS Informativeness Governs CS-US Associability

Abstract

In a conditioning protocol, the onset of the conditioned stimulus (CS) provides information about when to expect reinforcement (the US). There are two sources of information from the CS in a delay conditioning paradigm in which the CS-US interval is fixed. The first depends on the informativeness, the degree to which CS onset reduces the average expected time to onset of the next US. The second depends only on how precisely a subject can represent a fixed-duration interval (the temporal Weber fraction). In three experiments with mice, we tested the differential impact of these two sources of information on rate of acquisition of conditioned responding (CS-US associability). In Experiment 1, we show that associability (the inverse of trials to acquisition) increases in proportion to informativeness. In Experiment 2, we show that fixing the duration of the US-US interval or the CS-US interval or both has no effect on associability. In Experiment 3, we equated the increase in information produced by varying the C̅/T̅ ratio with the increase produced by fixing the duration of the CS-US interval. Associability increased with increased informativeness, but, as in Experiment 2, fixing the CS-US duration had no effect on associability. These results are consistent with the view that CS-US associability depends on the increased rate of reward signaled by CS onset. The results also provide further evidence that conditioned responding is temporally controlled when it emerges.

Substantial evidence indicates that animals learn and encode the duration of events in conditioning protocols, and that the temporal parameters of a conditioning protocol have a profound impact on conditioned responding (Blaisdell, Denniston, & Miller, 1998; Gallistel & Gibbon, 2000; Gibbon & Balsam, 1981; Miller & Barnet, 1993; Savastano & Miller, 1998; see Balsam, Drew, & Gallistel, 2010, for review). Encoded intervals have at least two behavioral effects. First, they control timing of conditioned responding (e.g., Bevins & Ayers, 1995; Davis, Schlesinger, & Sorenson, 1989; Delamater & Holland, 2008; Fanselow & Stote 1995; Holland, 2000; Kehoe, Graham-Clark, & Schreurs, 1989; Kirkpatrick & Church, 2000; LaBarbera & Church, 1974), often from very early in training (Balsam, Drew, & Yang, 2002; Drew, Zupan, Cooke, Couvillon, & Balsam, 2005; Kirkpatrick & Church, 2000). Second, they determine rate of acquisition (Balsam, Fairhurst & Gallistel, 2006; Gibbon & Balsam, 1981; Gibbon, Baldock, Locurto, Gold, & Terrace, 1977; Gottlieb, 2008; Holland, 2000; Lattal, 1999).

Associability, or the ability of a CS to enter into an association with the US, is a fundamental concept in associative learning theory, often appearing as a free parameter in formal models (e.g., Rescorla & Wagner, 1972; Mackintosh, 1975; Pearce & Hall, 1980). Balsam and Gallistel (2009) proposed a specific measure of associability: the inverse of trials to acquisition. This measure has two advantages: First, it captures the widely shared intuition that the greater the associability, the faster the learning (this is true in all of the just cited formal models). Second, when associability is measured in this way, it enters into a simple quantitative law proposed by Gallistel and Balsam (2009): Associability is proportional to informativeness, where informativeness is defined to be the factor by which the onset of the CS shortens the expected time to reinforcement. Put more formally,: A ≡ 1 N_r ∝ C̅/T̅ ≡ I, where A stands for associability, N_r is the number of trials required for the appearance of a conditioned response, C̅ is the average interval between unconditioned stimuli (USs), T̅ is the average interval from the onset of the conditioned stimulus (CS) to the onset of the US (average CS-US interval) and I stands for informativeness.

Informativeness is interesting from an information-theoretic standpoint, because Balsam and Gallistel (2009) showed that it determines one component of the Shannon information that CS onsets convey about the timing of US onsets. The information that the onset of a CS conveys about the timing of the next US is measured by the reduction in the subject's uncertainty about when that US will occur. The uncertainties before and after CS onset are quantified by the entropies of probability distributions, which are computed using Shannon's formula: $H=p{\displaystyle \sum }\text{log}\left(\frac{1}{p}\right)$. The information conveyed is the difference between the entropy of the probability distribution before CS onset and the entropy of the distribution after CS onset.

When both C and T are approximately exponentially distributed, then the information in bits provided by CS onset is log₂ (C̅/T̅). However, in the more common delay-conditioning protocol, where T has a fixed duration, there is a second component to the information provided. Because of the scalar uncertainty in animals' subjective representation of temporal intervals (Gibbon 1977; Gallistel and Gibbon 2000), the magnitude of this second component does not depend on protocol parameters; rather it depends on the subject's Weber fraction, which measures how precisely the subject can measure and/or remember elapsed intervals (Balsam et al., 2006; Balsam et al., 2010; Balsam & Gallistel, 2009). The amount of information provided by fixing the duration of the CS is very substantial: Given that empirical estimates of the Weber fraction in both pigeons and mice are around .16 (e.g., Gallistel & King, 2004), fixing the CS-US interval provides approximately 2 additional bits of information regardless of the duration of this interval (see Balsam & Gallistel, 2009; Balsam et al., 2010, for the derivation).

In the present experiments, we measured the contribution of both types of information to associability. Although many studies using autoshaping preparations in pigeons have demonstrated the effect of C̅/T̅ on associability, it is unclear to what extent these results generalize to appetitive protocols in rodents. The few studies of this phenomenon conducted with rodents have reported effects of absolute C̅ and T̅ durations, aside from the effects of C̅/T̅ (e.g., Holland, 2000; Kirkpatrick & Church, 2000; Lattall, 1999). Based on these results, some have suggested that associability is governed separately by C̅ and T̅, not simply by their ratio (e.g., Holland, 2000; Kirkpatrick & Church, 2000). Therefore, in Experiment 1, we determined the effects of varying C̅/T̅ on associability in mice, using different values of T̅. In Experiment 2, we assessed the impact of having either fixed vs. variable cycle and CS durations on associability with a single C̅/T̅. Experiment 3 examined the effect of both C̅/T̅ and fixed-vs.- variable CS durations on associability. In all three experiments, associability was fully determined by informativeness. Together, these results establish the critical role of CS informativeness in determining CS-US associability.

Experiment 1

Method

Subjects

Forty seven C57/BL6 mice (Taconic) were used. Mice were housed in individual cages for the duration of the experiment and maintained at 90% of their free feeding weights by post session feeding as necessary.

Apparatus

Eight matching experimental mouse-testing chambers (Med-Associates, St. Albans, VT) were used. The chambers measured 22 × 18 × 13 cm, and the floor consisted of metal rods placed 0.87 cm apart. Each chamber was equipped with a pellet dispenser (Med-Associates) with which 14 mg pellets (Bio-Serve) could be delivered. A feeder trough was centered on one wall of the chamber with a recessed light located at the top of the feeder receptacle. An infrared photocell detector inside the trough was used to detect and record head entries into the trough. Each chamber was equipped with two retractable levers mounted on the same wall as the feeder trough. Each chamber was enclosed in a sound attenuating shell, and white noise and chamber ventilation fans masked extraneous noise. Control of experimental protocols and data recording were accomplished via a computer in an adjacent room running Med-PC software.

Procedure

Mice were trained to eat food pellets in two stages. First, mice were given 10 pellets in a dish in the home cage. Following 2–3 days of this exposure, mice were placed in the experimental chamber for 15 minutes with 5 pellets in the food trough to accustom the mice to eating pellets from the trough. Food pellet training continued in this manner for 3 sessions, after which the experiment proper began.

The procedure was an appetitive conditioning protocol in which mice received 25 presentations of a feeder light CS followed by a food pellet US in each of 16 daily sessions. Each group of mice experienced a single combination of C̅ (seconds between successive USs; ITI + CS) and T̅ (CS duration in seconds) according to the group designations 32/8 (n=8), 80/8 (n=7), 224/8 (n=9), 96/24 (n=8), 240/24 (n=7), 672/24 (n=8). Thus, three C̅/T̅ ratios (4, 10, and 28) were arranged, with two different values of T̅. Intertrial interval durations were variable and were randomly sampled from exponential distributions with mean values appropriate to the different group C̅/T̅ ratios. CS durations were fixed. Sessions were conducted 5 days a week at approximately the same time each day.

Data analysis

The number of head entries into the feeder receptacle during the entire CS duration and during an equivalent portion of the pre-CS period (the last T̅ seconds of the ITI) was recorded for every trial. These measures were used to calculate a difference score as the primary measure of conditioning by subtracting the rate of responding in the pre-CS period from the rate of responding during the CS. A programming error in groups 80/8 and 240/24 resulted in the food pellet being delivered .8 s prior to CS termination, rather than after the CS as in the other groups. All statistical analyses were conducted with a significance level of p<.05.

Results

Conditioned responding across training

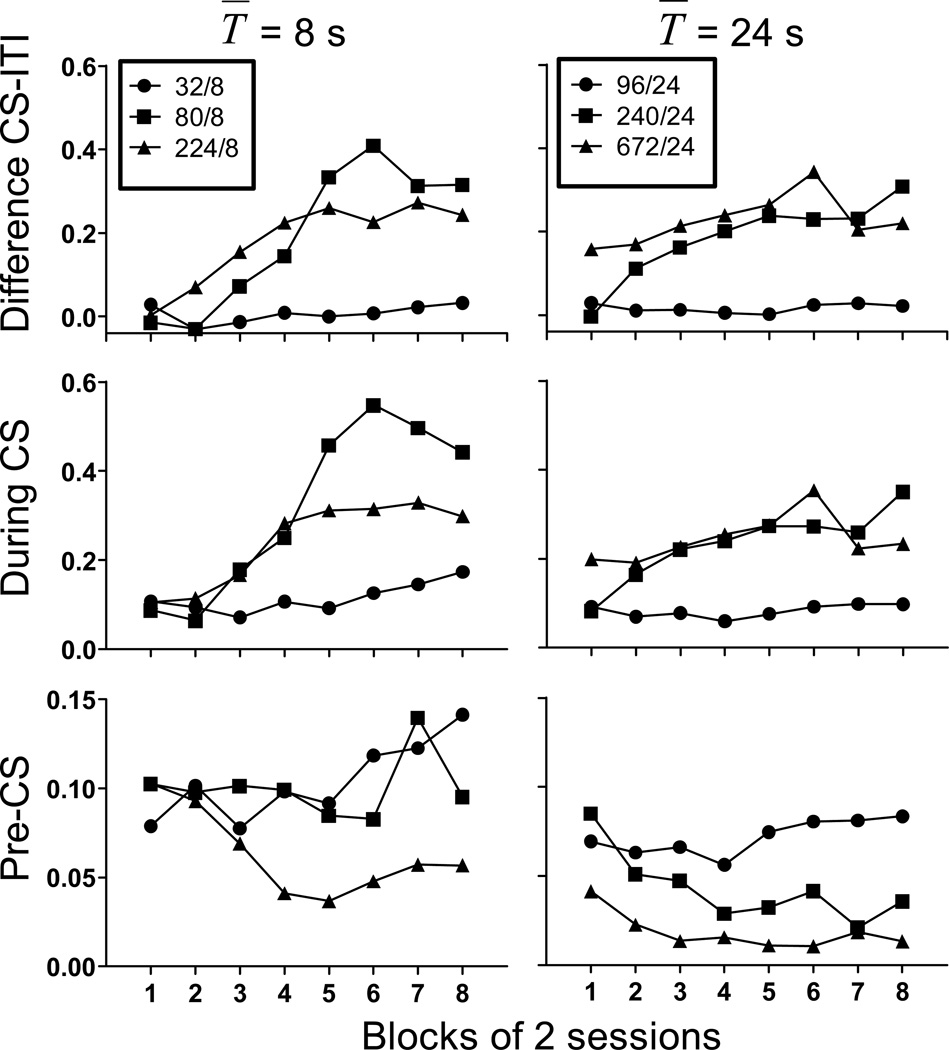
Figure 1 shows the average rate of responding (responses per second) during the CS and the pre-CS period as well as the difference scores for all groups of mice over the course of conditioning. These data were analyzed with session block × C̅/T̅ × CS duration (T̅) ANOVAs. Across all groups, the difference score and the rate during the CS increased as training progressed (main effect of session block, F(7,280)=13.64 and 13.10, respectively) but increased more slowly for the groups trained with the C̅/T̅ = 4 as compared to the other groups, which was reflected in the significant C̅/T̅ × session block interaction (F(14,280)=5.43 and 4.77). In addition, the groups trained with the lowest ratio never responded as much as the other groups. The value of T̅ had no overall effect on the difference score (Fs<1.50) indicating that the ratio of C̅ toT̅ rather than the value of T̅ determined the rapidity with which the difference score increased. Lastly, there was a significant interaction between all three factors (F(14,280) = 3.63 and 3.87) perhaps because of the higher asymptotic difference scores and CS rates in the group with the 8 sec CS trained at C̅/T̅ = 10 than in the other groups. For pre-CS responding, response rate was lowest at the highest C̅/T̅ (groups 224/8 and 672/24) and increased with lower C̅/T̅ (main effect of C̅/T̅ ; F(2,40) = 6.28). This likely indicates an effect of decreased cycle time. In addition, pre-CS response rates were lower overall in groups with T̅ = 24s (main effect of T̅ ; F(1,40) = 15.49). This pattern of results likely reflects the decreased cycle time between the different C̅/T̅ ratio groups as well as the overall longer cycle times in group T̅ = 24s.

Figure 1.

The difference in responses per second during the ITI and CS (top row), response rate during the CS (middle row), and response rate during the pre-CS period (bottom row) as a function of blocks of training sessions for all groups of subjects in all conditions of Experiment 1. Groups with T̅ =8 s are shown in the left panels, while groups with T̅ =24 s are shown in the right panels. Note the different scales of the y-axes.

Temporal control of responding in the CS

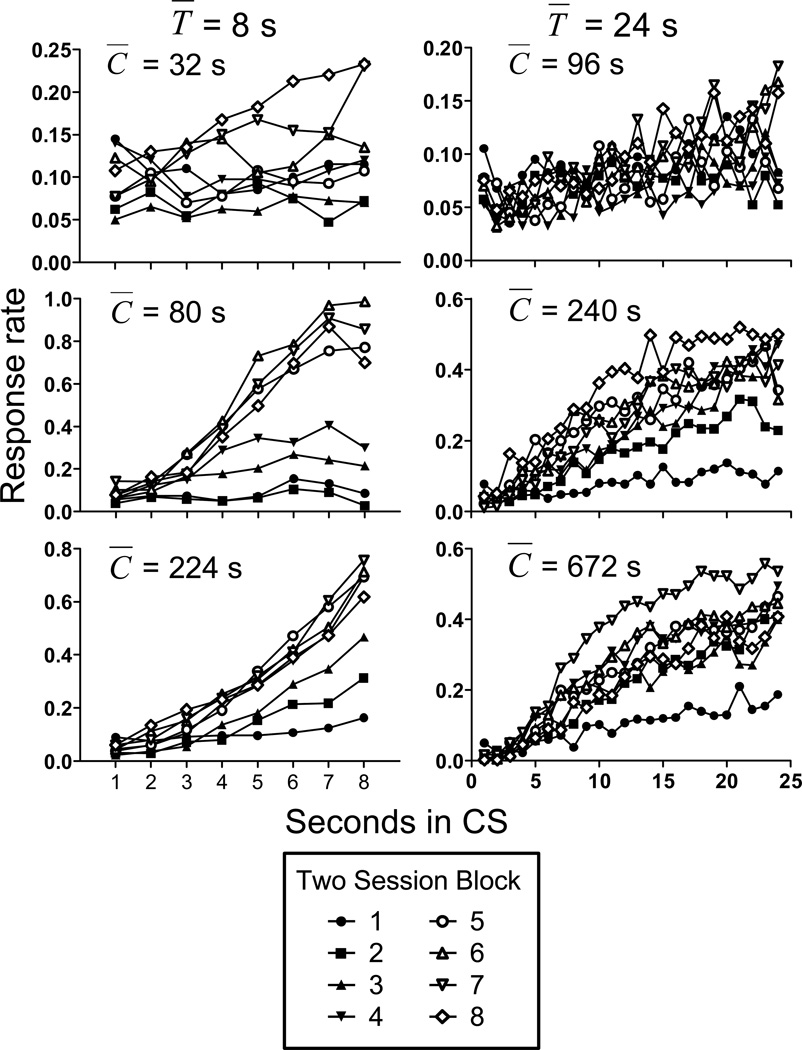
To investigate the temporal pattern of responding during the CS across blocks of training sessions, Figure 2 shows average response rate across the CS for all groups during the course of training. Separate C̅/T̅ × session block × time in CS repeated measures ANOVAs were conducted for groups T̅ = 8s and T̅ = 24s. For groupT̅ = 8s, the ANOVA found a significant effect of session block [F(7,147) = 14.82], reflecting the increased rate of responding across blocks. Rate of responding increased across the CS interval, indicating temporal control (F(7,147) = 33.86, for the main effect of time in CS). The C̅/T̅ did not have a significant effect on the overall rate of responding [F(2,21) = 3.08], but the magnitude of response rate increase across blocks varied with C̅/T̅, resulting in a block × C̅/T̅ interaction [F(14,147) = 3.70]. Temporal control of responding increased across blocks, evidenced by the response rate functions becoming steeper (F(49,1029) = 9.01, for the block × time in CS interaction). In addition, responding by the group with C̅/T̅ = 4 was less temporally controlled than responding by groups C̅/T̅ = 10 and 28, resulting in a significant time in CS × C̅/T̅ interaction [F(14,147) = 7.76]. Finally, the three way block × C̅/T̅ × time in CS interaction was also significant [F(98,1029) = 3.17]. For group T̅ = 24s, overall response rates were lower, but the pattern of responding was similar to group T̅ = 8s. The main effects of session block [F(7,140)=6.81], C̅/T̅ [F(2,20)=4.53], and time in CS [F(23,460)=50.81] were significant, as were all interactions (p<.05). Together, these results show that temporal control of conditioned responding increased across blocks of training, and that the overall rate of responding and steepness of the temporal gradient increased with increasing C̅/T̅.

Figure 2.

Responses per second as a function of CS duration for all groups in Experiment 1. Response rate is shown across blocks of two training sessions. Other details as in Figure 1.

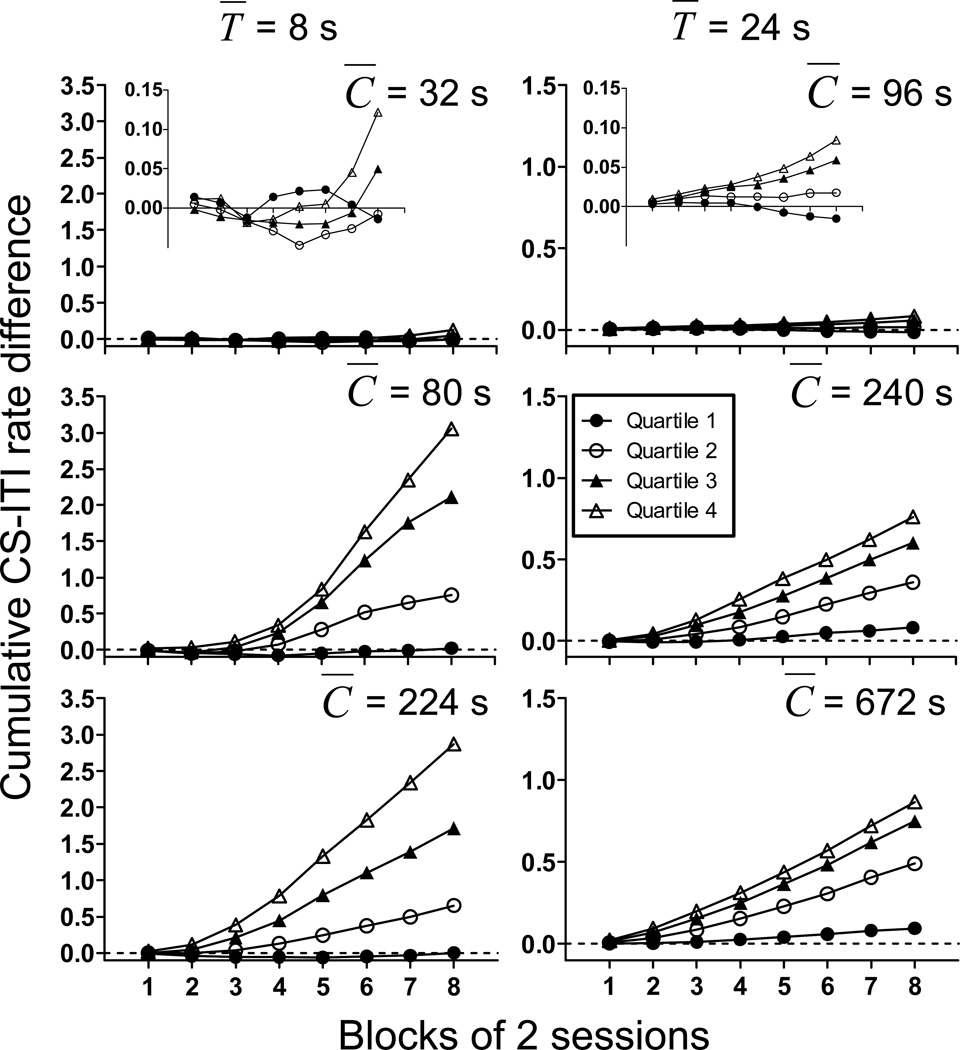
To examine the relation between the emergence of conditioned responding and temporal control of that responding, we calculated cumulative difference scores for each quartile of the CS duration. To calculate this measure, we divided responding during the CS into successive quartiles and calculated response rate in each quartile. We then subtracted the responding in the pre-CS period from responding in each quartile of the subsequent CS. The cumulative plots in Figure 3 show the cumulative rate difference between the CS and pre-CS period across blocks of training sessions for each group of mice. Three aspects of the figure are readily apparent. First, with the exception of Quartile 1, the cumulative difference scores in all groups increase over the course of training. Second, the increase in the cumulative difference scores is greater in later quartiles. In fact, the cumulative difference in response rate is ordered with increasing quartile for all groups. Finally, conditioned responding first appears in the later quartiles (not the earlier quartiles as might be expected if the response was simply to CS onset).

Figure 3.

Cumulative difference in responses per second in the pre-CS period and the CS for different quarters of the CS as a function of blocks of training sessions for all groups in Experiment 1. Note the difference in scaling of the y-axes for groups T̅ =8 and T̅ =24 s.

We calculated an average difference score for each subject for each block and subjected these data to a mixed model ANOVA with CS quartile and session block as within subjects’ factors and C̅/T̅ ratio and T̅ as between-subjects factors. This analysis indicated a significant four way interaction between quartile, session block, C̅/T̅ ratio, and T̅ (F(42,861)=2.55). We therefore conducted tests for simple main effects separately on the groups within the three C̅/T̅ ratios. For groups with a C̅/T̅ ratio of 4 (groups 32/8 and 96/24), there was a main effect of quartile (F(3,42)=8.27), and a significant interaction between quartile and session block (F(21,294)=2.56) indicated by the separation of quartiles later in training (see inset of Figure 3). For groups with a C̅/T̅ ratio of 10, conditioned responding was greater in the later quartiles for both groups with T̅ =8 s and T̅ =24 s (F(3,36)=35.74, main effect of quartiles), and increased across session blocks (F(7,84)=11.50, main effect of block). There was also a greater rate of increase in conditioned responding across session blocks in the later quartiles (quartile × session block interaction; (F(21,252)=7.41). Finally, the interaction between session block, quartile, and T̅ was significant (F(21,252)=3.92), possibly reflecting the tendency for conditioned responding to be overall less in group 80/8 than in group 240/24. The results from the tests for simple main effects in groups with C̅/T̅ ratio of 28 (groups 224/8 and 672/24) revealed the same pattern of statistically significant main effects and interactions as for the C̅/T̅ 10 ratio groups with the exception of the lack of a significant 3 way (session block × quartile × T̅) interaction.

Acquisition of conditioned responding: Change point analyses

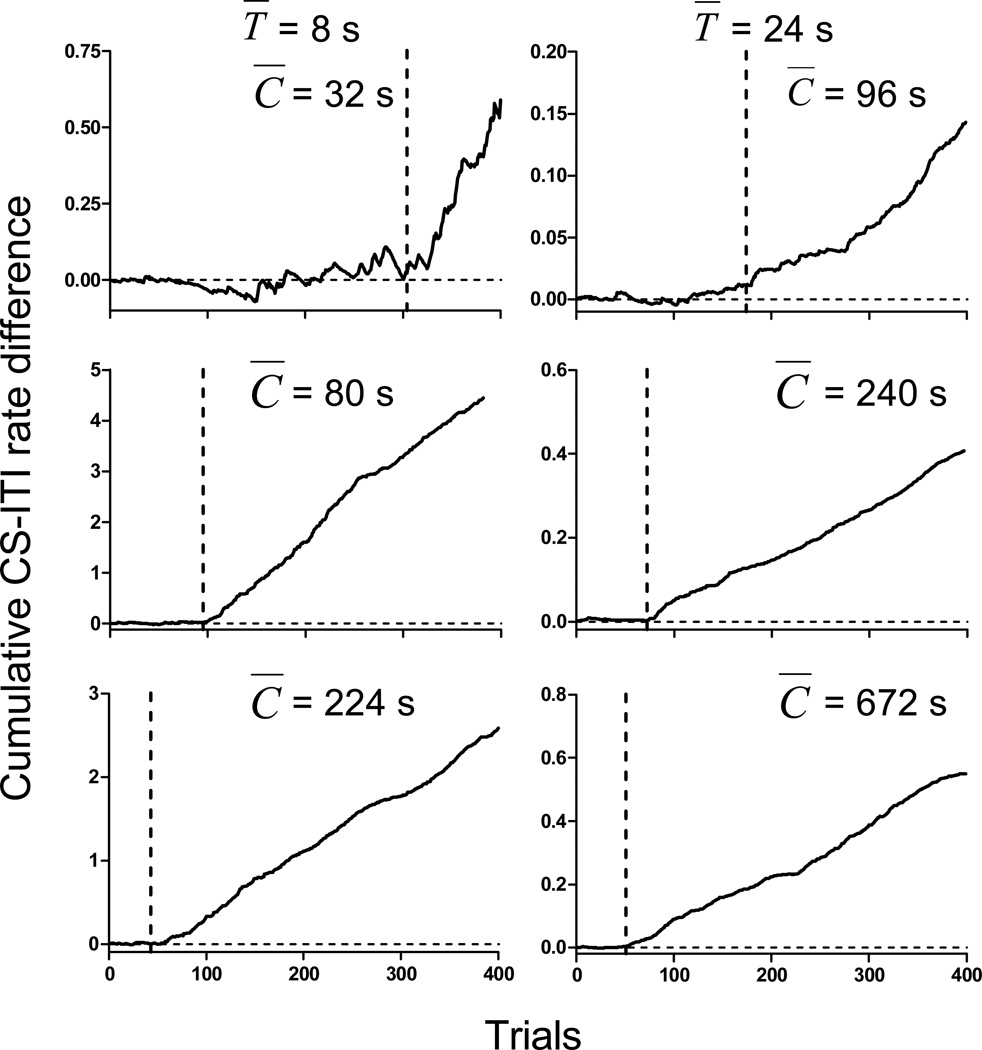
To quantify associability we used an algorithm that finds change points in response rates over time (Balsam, Fairhurst, & Gallistel, 2006; Gallistel, Fairhurst, & Balsam, 2004). In the typical mouse, the poking rate during the CS is at first no higher than during the intertrial interval preceding CS onset. At some point in the course of training, the poking rate becomes higher during the CS. This change is evident in the cumulative record of the trial-by-trial difference in the two rates; the record is flat early in training, then upwardly sloped. The change in slope is typically abrupt and readily apparent. The trial on which it is judged to occur is the trial on which the conditioned response emerged. To make the decision about this trial independent of our judgment, we sought an algorithm that satisfied two constraints. First, it should find the visually obvious inflection points (change in slope) well in a majority of subjects. Second, it should have a minimum of free parameters. Although a few individual fits could be improved by the inclusion of additional free parameters, the general result remained similar when we used a variety of change point algorithms, which differed in complexity and the number of free parameters. For the sake of parsimony, we present the data from the simplest algorithm. For this analysis, we identified the first positive change point (see Balsam et al., 2006; Gallistel et al., 2004) after the cumulative CS/ITI rate difference function reached its’ minimum. The algorithm we used proceeds datum by datum through the cumulative record testing for the occurrence of a change in slope. The algorithm finds the minimum of the cumulative difference function and then for all subsequent data points in the record, the algorithm finds a putative change point (i.e., a would-be change point) prior to that datum. This putative change point is the previous datum that deviates maximally from a straight line drawn from the origin of the plot (or previous change point once one is detected) to the current cumulative record datum. It divides the prior data into those up to and including the putative change point and those after it up to and including the current datum. The algorithm then calculates the log of the odds against the null hypothesis that the observations on the two sides of the putative change point come from the same rate process (see Gallistel et al., 2004, for more details). This change-point analysis yields for each subject an estimate of the trials to acquisition, that is, the trial at which a statistically significant positive difference between the CS rate and the ITI rate consistently appeared. It has only one free parameter, the alpha level in the change-point algorithm. Taken across subjects, a wide range of alpha levels yielded similar summary statistics. For the analyses we now report, we used α = .01. Figure 4 shows the cumulative record of trial-by-trial difference scores for a representative subject in each group, with the change point identified by the algorithm indicated by a vertical dashed line.

Figure 4.

Cumulative difference functions for representative subjects in each group. Vertical dashed line shows the learning trial identified by the change-point algorithm (see text for details). Note the different scales of the y-axes.

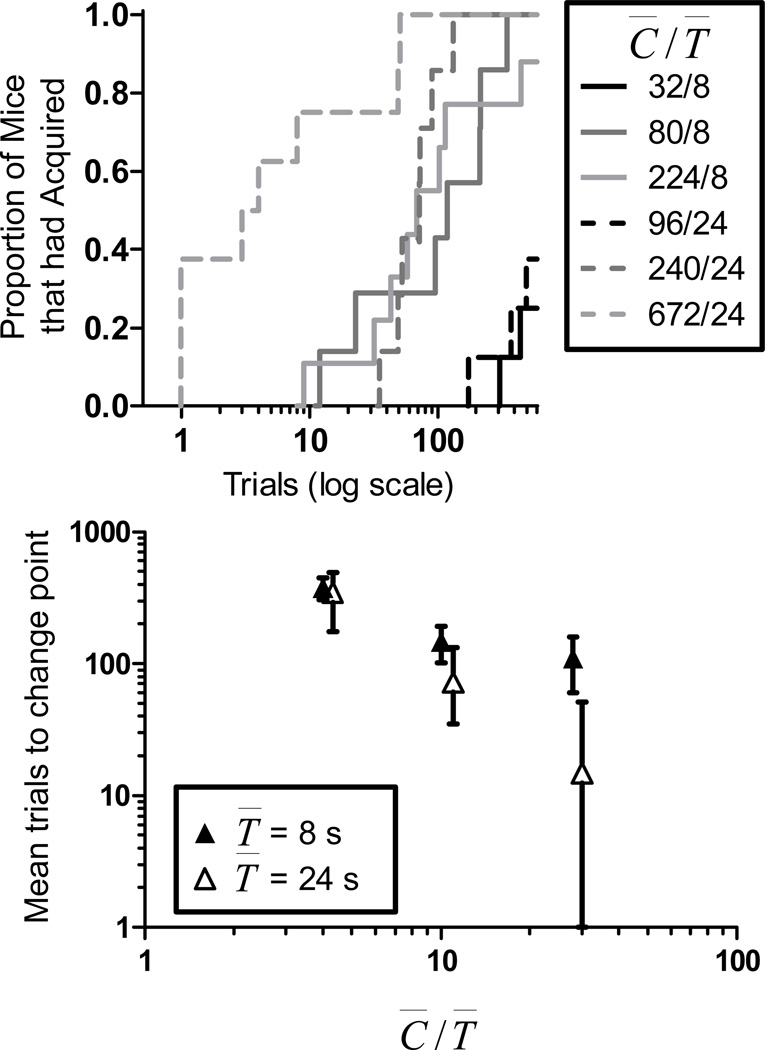
The top panel of Figure 5 presents the cumulative distributions of acquisition scores for each group of mice. The figure plots the proportion of mice that had acquired (for which a change point had been determined) as a function of conditioning trials. For both groups with T̅ = 8s (solid lines) and T̅ = 24s (dashed lines) the cumulative distributions are shifted to the left with increasing C̅/T̅, indicating faster acquisition. For group T̅ = 8s, there was no increase in associability from C̅/T̅ = 10 to C̅/T̅ = 28, while in group T̅ = 24s, the increase in associability between these ratios was substantial. A lower percentage of mice in both groups met the acquisition criterion at the lowest C̅/T̅, which is why the rightmost plots do not rise to 1.

Figure 5.

The left panel shows cumulative acquisition distributions showing the proportion of mice that had acquired (for whom a change point had been determined) as a function of trials (CS-US pairings) for all groups in Experiment 1. See text for details. The right panel shows mean trials to change point as a function of C̅/T̅ ratio for all groups in Experiment 1. Error bars show the standard error of the mean.

A more familiar summary is given in the bottom panel of Figure 5, which shows the mean trials to change point (the measure of acquisition) as a function of C̅/T̅ for all groups. These data were analyzed with a C̅/T̅ × T̅ ANOVA. Mice for which a change point could not be determined were excluded from this analysis. The number of mice excluded on these grounds was six in group 32/8, one in group 224/8, and five in group 96/24. Change points were determined for all other mice. The ANOVA found a significant effect ofC̅/T̅. Trials to acquisition decreased as C̅/T̅ increased (F(2,29)=5.38). The effect of T̅ was not significant (F(1,29)=1.82), nor was the interaction between C̅/T̅ and T̅ (F(2,29)=0.84).

Discussion

In the present experiment, associability increased with increases in C̅/T̅, replicating previous results with other species (e.g., Gibbon et al., 1977; Gottlieb, 2008; Holland, 2000; Lattall, 1999). Some caution is warranted in interpretation of these results, as many mice in the group with the smallest C̅/T̅ ratio did not acquire a statistically reliable conditioned response in the number of sessions conducted. Nevertheless, the data clearly show an effect of the C̅/T̅ ratio on acquisition, in that mice with the smallest C̅/T̅ ratio took much longer to acquire, or did not acquire at all. In addition, response rates in the CS increased and response rates in the pre-CS period decreased with increasing values of C̅/T̅, replicating previous results (e.g., Holland, 2000; Lattall, 1999). Thus, both associability and the probability of conditioned responding increase with informativeness.

Although the C̅/T̅ ratio has consistently been found to be a major determinant of measures of conditioned performance such as probability or rate of responding, some have reported that when C̅/T̅ is held constant, some measures of conditioned performance show effects of varying the absolute values of C̅ and/or T̅ (Holland, 2000; Lattal, 1999). We note that these experiments have not determined associability, the inverse of trials to acquisition, which is a fundamentally different kind of measurement than post acquisition measures of performance. Associability is measured by the value of a protocol parameter (trials) required to produce a fixed behavioral effect, the onset of conditioned responding. Measuring associability as a function of informativeness gives a trade-off function, whereas measuring performance (response rates over trials) as a function of informativeness gives a psychometric function. Trade-off functions reveal quantitative properties of underlying mechanisms whereas psychometric functions generally do not (Gallistel, Shizgal, & Yeomans, 1981). Given the fundamental differences in the measurements, interpretation of the effects of C̅ and T̅ alone on conditioned performance across studies is difficult.

Further complications in interpretation arise because measures of performance are also almost always reported as group averages, whereas associability is determined for each subject. As is clear from the cumulative distributions of trials to acquisition in this and our subsequent experiments, there are large individual differences in trials-to-acquisition within conditions (as is also true for measures of conditioned performance). Moreover, at some parameter values, some percentage of the subjects fail to acquire a conditioned response at all. This makes group averaging problematic, both for associability and for measures of conditioned performance, which is why we prefer to show the distributions.

The present data provide further evidence for the early emergence of temporally controlled conditioned responding in Pavlovian protocols. Responding in the CS was temporally controlled from early in training in all groups (Figure 2) and conditioned responding was temporally controlled when it emerged (Figure 3). These results are in accordance with theoretical accounts which suggest that the times of protocol intervals are learned rapidly at the outset of training (see Balsam et al., 2002, for discussion). The present experiment cannot distinguish whether timing preceded or occurred simultaneously with acquisition.

The temporal control observed at the emergence of conditioned responding in the present experiment is similar to results reported by Kirkpatrick and Church (2000b). They exposed rats to a procedure similar to that used in the present experiment and found that the stimulus discrimination ratio (index of differential responding during the CS as opposed to the ITI) and the timing discrimination ratio (index of increasing responding as a function of time in the CS) increased at about the same time in training, suggesting that when anticipatory (that is, conditioned) responding emerges it is temporally controlled. Similarly, Holland (2000) reported that temporal control of responding during the CS was evident at the appearance of conditioned responding in an appetitive conditioning protocol with rats. The relative lack of temporally controlled responding during the CS for the two groups with the lowest C̅/T̅ ratios is indicative of a lack of acquisition; mice that acquired in these groups showed temporal control of responding (Figure 3). These results suggest that reports of late emergence of timing in the CS (e.g., Delamater & Holland, 2008) may be the result of averaging together subjects who have and have not acquired.

Experiment 2

The results of Experiment 1 are consistent with the fact that associability is a function of informativeness (C̅/T̅). However, it is unclear from Experiment 1 whether the extra information provided when the CS-US interval is fixed contributes to associability above and beyond the contribution made by CS informativeness. Although there have been some studies on the effects of fixed vs. variable CS-US durations on CR learning in aversive preparations, only a few have characterized acquisition. These studies have reported no effect of fixed vs. variable CS-US durations on speed of acquisition of avoidance responding in a shuttle box paradigm by rats (Kamin, 1960; Low & Low, 1962), eyeblink conditioning in rabbits (Patterson, 1970), or acquisition of a CR in an aversive conditioning preparation in goldfish (Berger, Yarczower, & Bitterman, 1965). Thus, the available evidence from these disparate paradigms suggests that there is no difference in speed of acquisition with fixed vs. variable CS-US intervals in aversive conditioning protocols. We are unaware of any studies examining this question in appetitive conditioning protocols.

The few studies that have compared acquisition with fixed or variable ITIs or cycle times have reported conflicting results. Levine and England (1960) reported that rats learned an avoidance response in a shuttle box paradigm more quickly with fixed than with variable ITI durations (although this interpretation of their results is complicated by different overall and asymptotic levels of avoidance between groups). Gibbon et al. (1977), however, reported similar speed of acquisition with fixed and variable ITI times in a pigeon autoshaping preparation. In an appetitive conditioning protocol with rats, Kirkpatrick and Church (2000a) assessed acquisition of a conditioned head poke in two different experiments with fixed or variable interfood intervals. Although they did not directly compare speed of acquisition between groups and there were small procedural changes across experiments, inspection of the acquisition data (their Figure 2 and Figure 6) suggests that the group with the fixed interfood interval may have acquired faster than the group with the variable interfood interval.

Figure 6.

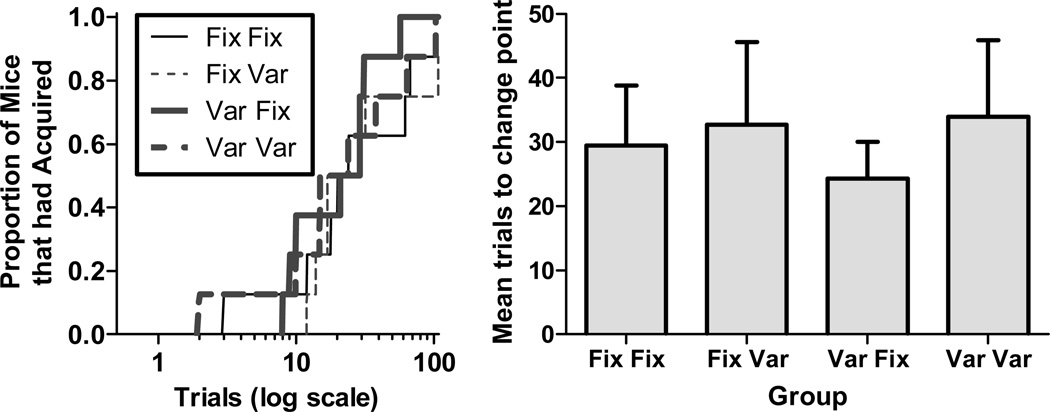
The left panel shows the proportion of mice that had acquired (for whom a change point had been determined) as a function of trials for all groups in Experiment 2. The right panel shows the mean trials to acquisition for all groups. Error bars indicate standard error of the mean.

As is clear from the discussion above, when the studies to date on the effects of fixed vs. variable CS and cycle times on speed of acquisition are considered, no clear picture emerges. The relatively small number of previous studies, together with the differences in species and experimental preparations across studies, make general conclusions difficult. We therefore assessed speed of acquisition in separate groups of mice with either fixed or variable cycle times and fixed or variable CS durations. The comparison of most interest is between the group with a variable CS-US interval and a fixed cycle time and the group with a fixed CS-US interval and a variable cycle time. Given the programmed C̅/T̅ = 72s 8s = 9 in the present protocol, a variable CS-US interval with a fixed cycle time provides roughly 1 bit of information, while a fixed CSUS interval with a variable cycle time (the usual arrangement in delay conditioning protocols) provides roughly 5 bits of information (see Appendix for the calculations). The 4-bit variation in the Shannon information conveyed by the onset of the CS is the theoretical equivalent of a 16-fold increase in C̅/T̅. If associability depends on the total information provided by the CS, rather than solely on the factor by which the expected time to reinforcement is shortened (i.e., informativeness), the difference in acquisition between these two groups should be very large. If, however, associability depends not on the total information conveyed by the CS, but rather only on the component that varies with C̅/T̅, then there should be no difference in the speed of acquisition between groups.

Method

Subjects

Thirty two C57/BL6 mice (Taconic) were used. Mice were housed 4 to a cage for the duration of the experiment. Mice were maintained at 90% of their free feeding weights by post session feeding as necessary.

Apparatus

Eight matching experimental chambers (Med-Associates, St. Albans, VT) were used. The chambers measured 22 × 18 × 13 cm, and the floor consisted of metal rods placed 0.87 cm apart. A dipper receptacle was centered on one wall of the chamber and provided access to one drop (approximately 15–20 µl) of evaporated milk which could be delivered from a raised dipper. An infrared photocell detector inside the trough was used to detect and record head entries into the receptacle. Each chamber was equipped with two retractable levers mounted on the same wall as the dipper receptacle. Each chamber was enclosed in a sound attenuating shell and white noise and chamber ventilation fans masked extraneous noise. Control of experimental protocols and data recording were accomplished via a computer in an adjacent room running Med-PC software.

Procedure

First, mice were taught to consume the liquid reward from the raised dipper. During this phase, the chambers were modified in visual, tactile, and olfactory ways to be contextually distinct from the chambers during the conditioning phase. The chamber modification consisted of scented vanilla pads being placed in the chamber tray, Plexiglas sheets covering the floor grid, and black and white striped paper being fastened to the walls of the chamber. Mice were placed inside the chamber with the dipper raised. The dipper was lowered 10-s after the first head entry in the feeder trough, followed by a variable intertrial interval (mean=30s), after which another trial was initiated. The session ended after 30 min or 20 dipper presentations. On the following day, mice received a similar session, except that the dipper was raised for 8 s and then lowered. One additional session of this sort was conducted, after which all mice made head entries during at least 20 of 30 dipper presentations.

Next we pre-exposed mice to the chambers to be used in the conditioning phase. We did this to eliminate to the extent possible conditioned head poking induced by the dipper training experience before the conditioning phase. To this end, mice were placed in the chambers (the vanilla scented pads, Plexiglas flooring, and striped walls had been removed), the houselight was turned on, and the session lasted for 30 min. This phase lasted for four sessions.

Mice then received 12 presentations of a dipper light CS followed by a 5 s dipper presentation US in each of 15 daily sessions. Sessions were conducted 5 days per week and occurred at approximately the same time each day. The cycle and CS durations were fixed or variable according the group designations Fix/Fix, Fix/Var, Var/Fix, and Var/Var (8 mice per group). Across groups, T̅ and C̅ were 8 s and 72 s, respectively. In group Fix/Fix, these times were fixed at 8s and 72s, respectively. In group Fix/Var, the CS duration was selected randomly each trial from a truncated exponential distribution with a minimum duration of 2.03 s and a maximum duration of 19.60 s (mean of 8 s) and the ITI duration was varied from 52.40 s to 69.97 s to maintain a fixed cycle time (the sum of the ITI and CS duration) of 72s. In group Var/Fix the CS duration was fixed at 8 s and the ITI duration was selected randomly each trial from a truncated exponential distribution with a minimum duration of 14.27 s and a maximum duration of 119.50 s (mean of 64 s). Finally, in group Var/Var, the CS duration (T̅) was varied from 2.03 s to 19.60 s and the ITI duration was varied from 14.27 s to 119.50 s. In the latter group the CS and ITI duration were selected independently each trial, but C̅ (the mean of their sum) was 72s. The primary dependent measure for assessing acquisition was the difference in rate of responding in the last 8 s of the ITI and the first 8 s of the CS (except in cases where the CS was shorter than 8 s, in which case we analyzed responding during the entire CS). Change point analyses were conducted on these differences, as described for Experiment 1.

Results

Acquisition with fixed or variable CS and cycle times

The left panel of Figure 6 shows the superimposed cumulative distributions of trials to acquisition for the four groups. As in Experiment 1, these distributions show the proportion of mice that had acquired (for which a change point had been determined) as a function of successive trials. With the exception of one mouse in the Fix/Var group, all mice acquired statistically reliable conditioned responding. As is clear from the figure, there was no difference in associability between any of the groups, that is, the distributions fall more or less on top of one another. This result is also shown in the more traditional form in the right panel of Figure 6, which depicts the mean trials to acquisition for all groups. A one way ANOVA found no significant differences in trials to acquisition between any of the groups [F(3,27)=0.18]. This result, however, gives no indication of the strength of the support that the data offer for the conclusion that there is no effect of fixing either the cycle period or the CS duration or both; for that we need a Bayes factor. The Bayes factor for the comparison of the null (no-effect) hypothesis and the "some-effect" hypothesis, gives odds of 8.7:1 in favor of the null. The some-effect hypothesis that we contrasted with the null (no-effect) hypothesis was that there was a shift of anywhere between 0 and the 16-fold shift predicted if acquisition depended on all the information given at CS onset, (the computation of a Bayes factor is explained and illustrated in the Supplemental Materials. It requires a contrasting hypothesis, because the Bayes factor is the amount by which the data change the relative likelihood of the two contrasted hypotheses). We conclude that what matters in acquisition is not the total amount of information that CS onset provides about when the next US may be expected, but rather only the component that depends on the informativeness of the CS, the factor by which its onset shortens the expected time to the onset of the US.

Temporal control of responding during the CS and ITI

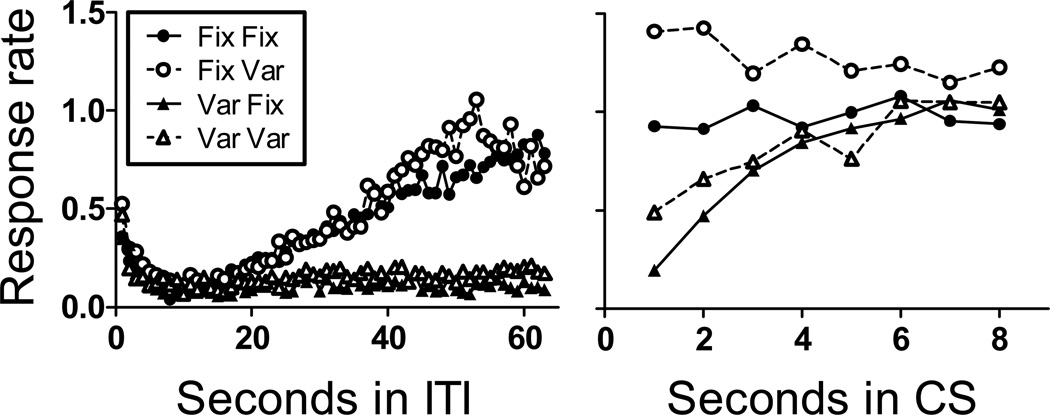
Next we examined the influence of fixed and variable cycle and CS times on temporal control of head poking during the ITI and CS. Figure 7 shows response rates as a function of time in the ITI and in the CS for all groups. For this analysis, we used sessions 10–12 because all mice who would acquire had done so by this point in training. We calculated average response rates during the first 64 s of the ITI and during the first 8 s of the CS in all groups. During the ITI (left panel) response rates were initially low for all groups (with the exception of increased rates following US delivery, likely due to consummatory behavior). For the groups with fixed cycle durations response rate generally increased over the course of the ITI until presentation of the CS. For groups with variable cycle durations, response rate remained low throughout the ITI. These impressions were confirmed by the results of a mixed model ANOVA which showed significant effects of time in ITI, cycle condition (fixed vs. variable), and a significant time in ITI × cycle condition interaction (Fs>16.00). The effect of CS condition (fixed vs. variable) was not significant, nor were any of its interactions (Fs<1).

Figure 7.

Mean response rate (responses per second) as a function of time in the ITI (left panel) and CS (right panel) for all groups in Experiment 2. See text for details.

Response rate during the CS is shown in the right panel of Figure 7. For both groups Fix/Fix, and Fix/Var response rates increased somewhat from the terminal ITI rate (with the greatest increase for group Fix/Var) and remained relatively constant across the duration of the CS. For group Var/Fix the rate of responding increased across the duration of the CS. In group Var/Var responding increased but less steeply than group Var/Fix but it was not completely flat as in group Fix/Fix. A mixed model ANOVA with time in CS as a within subjects factor and CS and cycle condition (fixed vs. variable) as between groups factors indicated a significant effect of time in CS (F(7,196)=6.45). The effect of CS condition was not significant, but the interaction between time in CS and CS condition was (F(7,196)=2.13). In addition, there was a significant time in CS by cycle condition interaction (F(7,196)=10.17), evidenced by the differing temporal patterning of behavior across the CS duration in the fixed vs. variable cycle groups.

Discussion

When C̅/T̅ was held constant, there was no effect on associability of fixing or varying from trial to trial either T̅ or C̅ or both, despite clear evidence of appropriately timed anticipatory behavior (during the ITI in both fixed cycle groups and during the CS in the Var/Fix group). The mice learned the durations of fixed delays of reinforcement and fixed cycles (US-US intervals), but the large variations in the information about US timing at CS onset that results from fixing these intervals or allowing them to vary had no effect on associability. Associability appears to depend solely on the contrast between the average rate of reward in the context and the average rate of reward in the presence of the CS, that is, on informativeness (Gallistel & Gibbon, 2000; Balsam & Gallistel, 2009).

The pattern of responding during the ITI in the fixed vs. variable cycle conditions replicates previous reports in the literature (e.g., Catania & Reynolds, 1968; Kirkpatrick & Church, 2000a, 2000b; 2003). In addition, the temporal control of responding during the CS in group Var/Fix replicates the results from Experiment 1 and numerous other results. In both groups Fix/Var and Fix/Fix, there was an overall increase in response rate at the onset of the CS that remained relatively constant across the 8 s of the CS, rather than a graded increase in response rate with time in the CS as in group Var/Fix (and to a lesser extent, group Var/Var). This increase in response rate across the CS in these groups is consistent with a general increase in anticipation engendered by the passage of time during the CS. The relatively flat temporal control exhibited in the CS by group Var/Var (compared to group Var/Fix), following the low rates of responding during the ITI, is consistent with less finely tuned temporal responding, or responding during the CS being initiated with some latency, but then being relatively constant.

The lack of temporal control of responding during the CS in group Fix/Fix was surprising, and appears at odds with reports of temporal control of responding during fixed cycle and CS conditions in other preparations (e.g., Kirkpatrick & Church, 2000b). One possibility is that the CS duration was too short for temporal control to be manifest in the context of the high ITI response rates generated by the fixed cycle time. The fixed CS durations used by Kirkpatrick and Church were considerably longer, with the shortest being nearly double the CS duration used in the present experiment, possibly better enabling a cessation of responding following ITI termination before resumption of temporally graded responding in the CS. In addition, Gibbon et al. (1977) showed that with pigeons the pattern of temporal responding during the CS in an autoshaping preparation depended on the C̅/T̅ ratio. In their Experiment 2, in which both the CS and ITI durations were fixed, the shallowest temporal gradients were displayed by the pigeons with the lowest C̅/T̅ ratio, regardless of the specific CS duration. While direct comparison across experiments is not possible given procedural and species differences, the present results are nevertheless not without precedent. Perhaps testing with longer CS durations or greater C̅/T̅ ratios would reveal more timing in the Fix/Fix case.

Experiment 3

The results of Experiment 2 suggest that associability depends only on the informativeness of a CS, that is, the factor by which its onset reduces the expected time to reinforcement. Notwithstanding the 4 bit variation in information provided by fixing the CS duration in the Var/Fix group as compared to the Fix/Var group, there was no difference in associability between these groups. If the information provided by fixing either C̅ or T̅ affected associability there would have been a 16-fold difference in trials to acquisition.

To further explore the generality of the finding that variation in T̅ (CS duration) did not affect associability, in Experiment 3 we examined the Var/Fix vs. Var/Var manipulation at two different C̅/T̅ values. The two values for this ratio were chosen such that changing the ratio had the same effect on the Shannon information as did fixing the interval between CS onset and the US. At C̅/T̅ 's of 8.05 and 24.4 (see calculations below), we compared associability between Var/Fix and Var/Var groups. Given the threefold difference in C̅/T̅ between groups, we predicted threefold faster acquisition with C̅/T̅ = 24.4 than with C̅/T̅ = 8.05. We also picked parameter values such that if associability is governed by the total amount of information conveyed by the CS, then the Var/Fix groups should also acquire three times faster than Var/Var groups. If on the other hand, as suggested by the results of Experiment 2, associability depends only on CS informativeness, fixing the duration of T should have no effect on associability regardless of C̅/T̅.

Method

Subjects

The subjects were 23 male C57bl/6j mice, obtained from Jackson labs, weighing between 13 and 25 grams on arrival in the lab and 18 – 27 grams at the beginning of testing.

Apparatus

The experimental environments were Med Associates ENV-307 mouse testing chambers, 22 × 18 cm in plan and 13 cm high, with two opposing aluminum walls and the other two walls of Plexiglas, and stainless-steel-bar flooring. Three feeding hoppers (Med Associates ENV-303-R2W) were set into one metal wall, but only the left one was used in this experiment. Each test chamber was connected by a 3.5 cm in diameter acrylic tube to a 18.5 × 28 × 12.7 cm polypropylene mouse housing tub topped by a cover of stainless steel bars, with a water bottle. The mouse moved between the tub and the test chamber by way of the connecting tube. The bottom of the tub was covered with bedding. These nest-tub-test-box combinations were housed two to a shelf on the 4 shelves of a 122 × 46 × 198 cm steel cabinet, with a solid black 1 cm thick plastic partition separating the two environments on a shelf. A 3 watt light in each test box provided a 12:12 hr light-dark cycle.

The interior of the active hopper was illuminated by an LED to signal the impending delivery of a pellet (an autoshaped head-entry protocol, with a hopper-illumination CS). The pellets were Research Diets NOYES Precision Pellets, PJAI-0020, Rodent Food Pellet, Formula A/I, 20 mg. The entrance to each hopper was monitored by an infrared (IR) beam, which the mouse interrupted when it poked into the hopper. There was another IR beam at the bottom of the V-shaped hopper, the interruption of which signaled the arrival of the pellet. The monitoring of the latency between pellet release and pellet arrival allowed us to know whether pellet delivery was operating reliably. A 6.2 cm length of 4 cm diameter polyvinyl tubing in the nest box provided a snug for the mouse. Water was available at all times. Remote computers running MedPC 2.4.10 programmed and recorded the times of events (lights-on, lights-off, hopper illumination, pellet delivery) and recorded the times of IR beam interruptions to the nearest 20 ms.

Procedure

The mice lived in the nest-tub-test-box combination throughout the experiment, obtaining their daily food ration from the approximately 80 20-mg pellets delivered by the conditioning protocols during the feeding phases of the protocols.The delivery of each pellet was signaled by the illumination of the hopper prior to pellet release. No pretraining was conducted and all mice were exposed to the experiment proper immediately.

The parameters in this experiment are summarized in Table 1. There were four groups: Small C̅/T̅ Fixed CS, Small C̅/T̅ Variable CS, Large C̅/T̅ Fixed CS, and Large C̅/T̅ Variable CS. For mice in the groups with a fixed CS duration, the latency between hopper illumination and pellet delivery was 20 s. For mice in the groups with a variable CS duration, the pre pellet duration of hopper illumination was sampled randomly each trial from a gamma distribution with shape parameter 4 and scale parameter 5. The expectation of a gamma distribution is the product of its shape and scale parameters, so the average latency to pellet release (T̅) was 20 s. The parameters of this distribution were chosen so that even the shortest CS lasted long enough for the mice to get to the hopper and poke into it prior to pellet release. 99% of the releases occurred more than 5.9 s after hopper illumination and 95% occurred more than 8.4 s after; at the other end of the distribution, 99% occurred within 47 s of hopper illumination and 95% occurred within 37 s.

Table 1.

Parameters in Experiment 3. Shown in bold is the information conveyed by the CS in each set of conditions.

	Fixed Duration CS		Variable Duration CS
	CS Dist	fixed @ 20 s	CS Dist	gamma(4,5)
	E(CS dur)	20	E(CS dur)	20
	ITI Dist	gamma(3,46.67)	ITI Dist	gamma(3,46.67)
	E(ITI dur)	140	E(ITI dur)	140
	E(US-US)	160	E(US-US)	160
Small C̅/T̅	C̅/T̅	8	C̅/T̅	8
	Pellets/Hr	22.5	Pellets/Hr	22.5
	SessDur	3.5 hrs	SessDur	3.5 hrs
	Hcs-us	6.95 bits*	Hcs-us	8.56 bits†
	Hus-us	11.56 bits†	Hus-us	11.56 bits†
	ΔH	4.6 bits	ΔH	3 bits
	CS Dist	fixed @ 20	CS Dist	gamma(4,5)
	E(CS dur)	20	E(CS dur)	20
	ITI Dist	gamma(3,156)	ITI Dist	gamma(3,156)
	E(ITI dur)	468	E(ITI dur)	468
Large C̅/T̅	E(US-US)	488	E(US-US)	488
	C̅/T̅	24.4	C̅/T̅	24.4
	Pellets/Hr	7.4	Pellets/Hr	7.4
	SessDur	10.6 hrs	SessDur	10.6 hrs
	Hcs-us	6.95 bits*	Hcs-us	8.56 bits*
	Hus-us	13.16 bits†	Hus-us	13.16 bits†
	ΔH	6.2 bits	ΔH	4.6 bits

^*Assuming a cv of .16 and temporal resolution of .1 s

^†Assuming temporal resolution of .1 s

Note. E(CS dur) is the expected duration of the CS (aka T̅). E(ITI dur) is the expected duration of the intertrial interval. E(US-US) is the expected duration of the US-US interval (aka C̅). Hcs-us is the entropy of the distribution of CS durations. When CS duration is fixed, it is assumed to have the entropy of a gauss(20,3) distribution. When CS duration varies, the entropy is taken to be the entropy of the gamma(4,5) distribution of CS durations. Hus-us is the entropy of the distribution of US-US intervals. ΔH is Hus-us - Hcs-us, which is the Shannon information communicated to the subject by the onset of the CS. Entropy calculations were done numerically, assuming a temporal resolution of 0.1 s. (The resolution assumed has no effect on the entropy differences, provided it is small relative to the width of the distributions.) The increase in C̅/T̅ from the Small to Large conditions increases ΔH by 1.6 bits. The difference in information communicated by CS onset between the fixed and variable conditions (the difference in the ΔH 's between columns within rows) is also 1.6 bits.

The ITI distributions were gamma distributions chosen so as to make the informativeness of the CSs in the Large C̅/T̅ conditions greater than the informativeness in the Small C̅/T̅ conditions by a factor of roughly 3 (3.05). Increasing the informativeness by a factor of 3 increases the Shannon information conveyed by CS onset by log₂ (3)= 1.6 bits. On the assumption that the precision with which a mouse can estimate an elapsed interval is scalar with a Weber fraction of .16, the entropy of the effective distribution in the fixed-CS-duration conditions, that is, the measure of the subject's uncertainty about the time to the next US after CS onset when CS duration is fixed, is the entropy of a normal distribution with a mean of 20 and a standard deviation of (.16 × 20) *** 3. The additional information available at CS onset in the fixed-CS-duration conditions beyond that available at CS onset in the variable-CS-duration conditions is the difference between the entropy of the gamma(4,5) distribution and the entropy of the Gaussian(20,3) distribution. This difference is 1.6 bits (see Table 1). Thus, both the size of the C̅/T̅ change and the fixing or varying of CS duration changed the information communicated by CS onset by 1.6 bits (see Table 1). Based on the previous two experiments, we predicted that the first manipulation would have a threefold effect on associability (2^1.6 = 3), whereas the second would have no effect.

For mice in the small C̅/T̅ conditions, pellets were delivered at 22.5 pellets per hour, whereas for those in the large C̅/T̅ condition, the rate was 7.4 per hour. We held total pellets delivered in each 24 hours to approximately 78, by restricting the total amount of time that the pellet-releasing schedule operated to 10.6 hours in the large C̅/T̅ conditions and 3.5 hours in the small C̅/T̅ conditions. In the large-ratio conditions, the schedule operated from 1 hour after the house light went out until 24 minutes before it came back on. In the small-ratio conditions, it operated for 1.75 hours, starting 1 hour after the house light went out, and then for another 1.75 hours, starting 1.75 hours before the house light came back on.

For data analysis, the rate of hopper entry during the last T̅ seconds of the ITI was subtracted from the rate during the CS to yield a difference score. The estimation of the learning trial was based on the cumulative record of these difference scores, using the same algorithm as in the previous two experiments.

Results

Acquisition as a function of C̅/T̅ and fixed or variable T

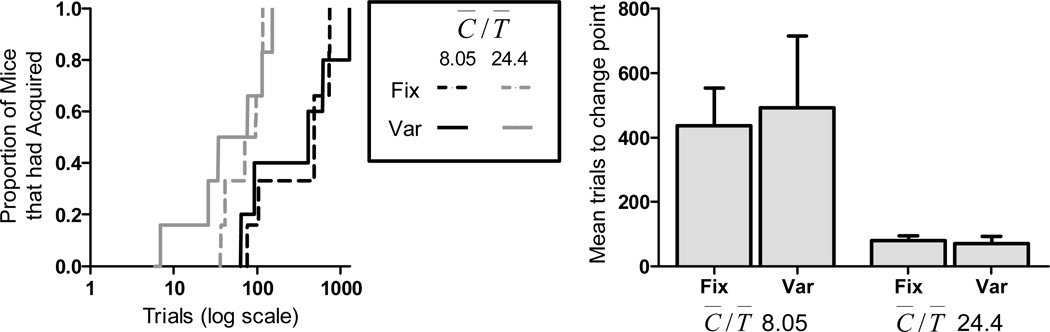
The left panel of Figure 8 shows cumulative acquisition distributions for all groups. All of the mice in each of the four groups acquired statistically reliable conditioned responding. However, there is a large difference in the rapidity of acquisition between groups with a small and large C̅/T̅, as evidenced by the rightward shift of the cumulative distribution of trials to acquisition when C̅/T̅ is reduced. There was no effect of fixing the CS duration on associability; the distributions from the fixed and variable CS duration groups fall largely on top of one another. The right panel of Figure 8 shows the more traditional way of displaying these data. We conducted a two factor C̅/T̅ by Fix-vs.-Var ANOVA on the acquisition scores. There was a main effect of C̅/T̅ [F(1,19 = 15.76], with no effect of Fix vs. Var CS duration [F(1,19) = 0.44], and no interaction [F(1,19) = 0.18].

Figure 8.

The left panel shows the cumulative acquisition distributions for all groups in Experiment 3. The right panel shows the mean trials to acquisition for all groups. Error bars indicate standard error of the mean.

The ANOVA does not measure the extent to which the data favor contrasting conclusions that might be drawn from the results. More importantly, it does not measure the strength of the support for our quantitative predictions: 1) tripling informativeness triples associability and 2) the associability when CS duration is fixed is the same as when it varies widely. To remedy these deficiencies, we computed Bayes factors.

Bayes factors give the relative degree of support (relative likelihood) for differing conclusions one might draw from the data. For example, we can determine if data offer more or less support for our prediction (a 3-fold increase in associability) than for the more cautious claim that increasing the C̅/T̅ by a factor of 3 increases associability by somewhere between 1 and 3. The more cautious claim subsumes the more precise claim, so one might suppose that the data could not support it more strongly than the more cautious claim, but this is not so. The Bayes factor for this comparison favors the exactly-3 claim over the more cautious claim by odds of almost 28:1. It does so because Bayesian analysis translates possible conclusions into prior probability distributions. These may be thought of as bets that the possible conclusions make about the size of the shift, before seeing the data. Both potential conclusions bet the same unit mass of prior probability, because probability distributions always integrate to 1. They differ in how they spread it around. The cautious one spreads it cautiously over the range from no shift to a 3-fold shift (from 0 to 1.6 on a log-base-2 axis); the more precise one puts it all on 3. If the likelihood function puts the bulk of the likelihood at and beyond 3, as it does given these data, then the more precise conclusion is more strongly supported. It places more of the unit mass of prior probability out where the data imply the true mean is. The more cautious conclusion “wastes” prior probability by putting the bulk of it on shifts less than 3, which are unlikely given the data. The Bayes factor tells us which claim makes the better bet and how much better it is. Thus, we conclude that increasing C̅/T̅ by a factor of 3 produced a threefold increase in associability.

Similar reasoning applies to the claim that there is no effect of fixing the delay of reinforcement (CS duration) rather than allowing it to vary widely. A more cautious claim is that this manipulation may have some effect. We make this a testable claim by putting limits on 'some.' In this case, we put a lower limit of 1 (no effect) and an upper limit of 3. We put an upper limit of 3 because we have no reason to expect this manipulation to have an even greater effect than the effect of increasing the C̅/T̅ by an informationally equivalent factor. In this case, too, the more cautious conclusion subsumes the more precise one. But here too, the more cautious conclusion spreads its unit mass of prior probability across a range of possible empirical results, whereas the more precise one puts it all on a single possibility--no effect. If the likelihood function puts the bulk of the likelihood at a factor of 1 and below, as it does in this case, then we are not surprised that the Bayes factor favors the conclusion that there is no effect, though in this case only by odds of 2.7:1. The smallish odds in favor of the null are to be expected because the samples are relatively small and very noisy. The smaller the samples and the noisier they are, the lower the upper limit on the extent to which the Bayes factor may favor the null hypothesis. This limitation is asymmetric; Bayes factors disfavoring the null may be arbitrarily large, even with small and noisy samples, if the samples do not overlap. Again, for those unfamiliar with Bayesian analysis, the computations are described and illustrated in the Online Supplemental Materials.

Temporal control of responding during the CS and ITI

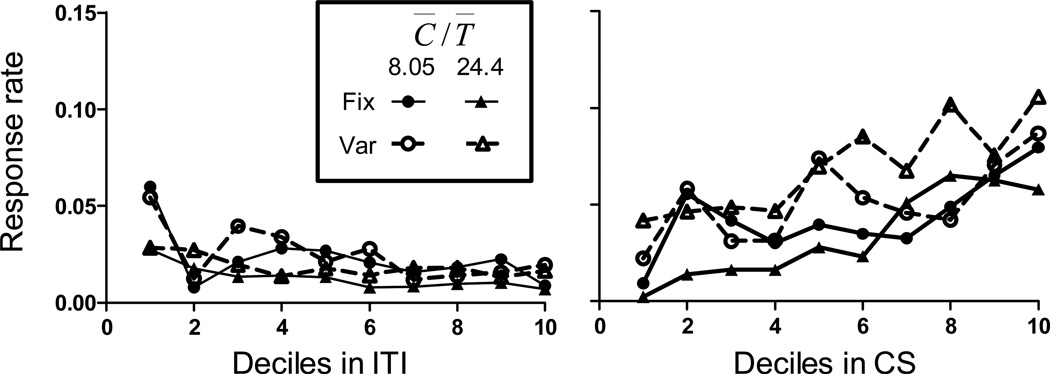
To assess temporal control of responding in the CS and ITI, we calculated response rate during the CS and ITI for the 36 trials following acquisition (as in Experiment 2) and calculated an average response rate for each mouse. We then calculated the average response rate per decile in the ITI and CS for all groups. Because the duration of the ITI was variable, we only calculated response rates for the first I seconds, where I is the average duration of the ITI. Similarly, response rates in the CS were only calculated for the first 20 seconds. Figure 9 shows the results of this analysis. During the ITI (left panel), response rates were generally low (with the exception of increased responding in the first decile, likely due to consummatory behavior) and did not increase or decrease systematically with time elapsed in the ITI. Response rate tended to be higher in groups with a C̅/T̅ of 8.05 than in groups with a C̅/T̅ of 24.4 (particularly in early deciles). We conducted a mixed model repeated measures ANOVA with decile as a within subjects factor and Fix vs. Var and C̅/T̅ ratio as between subjects factors. The ANOVA found a significant effect of decile [F(9,171) = 14.86] and C̅/T̅ ratio [F(1,19) = 6.96], with a significant interaction [F(9,171)] = 6.15]. The effect of Fix vs. Var was not significant [F(1,19) = 1.53], neither were any of its interactions.

Figure 9.

Mean response rate (responses per second) as a function of time in the ITI (left panel) and CS (right panel) for all groups in Experiment 3. See text for details.

The right panel of Figure 9 shows that response rates increased across the CS for all groups. In addition, response rates of groups with a variable CS duration tended to be somewhat higher than those of groups with fixed CS durations. We conducted a mixed model repeated measures ANOVA with decile as a within subjects factor and Fix vs. Var and C̅/T̅ ratio as between subjects factors. The ANOVA found a significant effect of decile [F(9,171) = 5.76]. The effect of Fix vs. Var was not significant [F(1,19) = 3.39]. The effect of C̅/T̅ was not significant, and there were no significant interactions.

Discussion

The results of Experiment 3 confirm the dependence of associability on C̅/T̅. Groups with C̅/T̅ = 24.4 acquired faster than groups with C̅/T̅ = 8.05. In addition, there was no effect of fixing the duration of the CS on associability. This result confirms the result of Experiment 2 in a somewhat different experimental preparation and in a paradigm that is sensitive to a primary determinant of associability (variation of C̅/T̅). Together, these results provide strong support for the claim that associability depends on the informativeness of the CS-US relation, that is, the factor by which CS onset reduces the expected time to the next reinforcement. Notwithstanding the additional information conveyed by fixing the CS duration, associability in the present experiment depended entirely on the average rates of reward in the cycle and CS.

In both Experiment 2 and Experiment 3, we statistically compared the conclusion that the additional information from fixing CS duration had no effect on associability with the hypothesis that it had an effect somewhere between no effect and the effect predicted by the resulting increase in the Shannon information at CS onset. In both tests, the Bayes factor favored the no-effect conclusion. Because they are odds ratios, the Bayes factors from the same comparison in different experiments may be multiplied to obtain the strength of the evidence from the combined experiments. The product of the two Bayes factors (2.7 × 8.7) favors that conclusion by odds of better than 27:1. We therefore conclude that fixing the duration of the CS, although it greatly increases the overall information conveyed by CS onset, has no effect on associability.

Our results further confirm the temporal control of conditioned responding when the time to the next reinforcement is predictable. The pattern of minimal responding in the ITI, when time to reinforcement was unpredictable, was similar to that obtained in Experiment 1 and to that from the groups with a variable ITI in Experiment 2. As in Experiments 1 and 2, mice in Experiment 3 displayed temporal control of responding during the CS, indicating that they had learned the duration of the CS. Interestingly, temporal control of responding was evident in groups with fixed and variable CS durations. Similar results were obtained from the Var/Var group in Experiment 2, although the temporal response gradient was shallower than in group Var/Fix. Together with these results, the trend toward higher overall responding in the variable groups in Experiment 3 could suggest that CS onset engenders an overall increased anticipation and somewhat less temporally tuned responding, as the duration of the CS is unpredictable. In addition, temporal control of responding in the variable CS condition in Experiment 3 could result because the hazard function of a gamma(4,5) distribution increases monotonically with elapsed time. The hazard function specifies the probability of reinforcement in the next moment. It is flat only when the distribution of reinforcement delays is exponential.

General Discussion

The present experiments examined the relationship between temporal variables in appetitive conditioning protocols and associability. In Experiment 1, associability increased with increasing C̅/T̅, confirming the importance of this temporal relation in acquisition of conditioned responding. In addition, conditioned responding, when it appeared, was temporally controlled. The results of Experiment 2 indicate that associability was not affected by the increased information provided by fixing the CS or cycle durations. Rather, associability depended entirely upon the average rate of reward in the cycle and CS: informativeness. The results of Experiment 3 confirmed the results of both Experiments 1 and 2: associability was faster with a greater C̅/T̅ and it was not affected by fixing the duration of the CS. Together, these results are consistent with theoretical accounts that posit rapid learning of the duration of events in conditioning protocols (e.g., Balsam & Gallistel, 2009; Balsam et al., 2010). In addition, these results indicate that although mice can learn the CS and cycle durations when they are fixed, as evidenced by temporally controlled responding in all three experiments, this information does not play a role in determining associability. Indeed, associability appears to depend only on the information that the CS conveys about the average reward rate in its presence compared to the average reward rate in the context (Balsam & Gallistel, 2009; Balsam et al., 2010; Gallistel & Gibbon, 2000).

Our results are at odds with some reports of lack of temporal control of conditioned responding until well after acquisition (e.g., Delamater & Holland, 2008; Rescorla, 1967). As noted above, these results may reflect averaging of subjects who have and have not acquired at different points in training. As training progresses more subjects will have acquired the CR and the average function relating responding to time in the CS will become steeper. In addition, apparent sharpening of temporal control as a function of training can result from an increase in the overall rate of conditioned responding during training. In preparations in which there is a nonzero level of the CR during the ITI, timing will appear to sharpen during training as the background level of responding becomes a smaller proportion of the total response output (see Balsam et al., 2002; Drew et al., 2005, for discussion). Finally, temporal control of responding not apparent in one CR may be apparent in other anticipatory responses (see Balsam et al., 2009; Brown, Hemmes, & Cabeza de Vaca, 1997).

The present analysis is relevant to the question of how temporal parameters alter whether to respond and when to respond (see Ohyama, Gibbon, Deich, & Balsam, 1999). According to rate estimation theory (RET; Gallistel & Gibbon, 2000), acquisition of a timed response (when to respond) to the CS cannot occur until after the whether criterion has been met. The fact that in some cases timing of responding occurs simultaneously with or precedes acquisition (Drew et al., 2005; Ohyama & Mauk, 2001; the present data) suggests that the whether decision need not precede the when decision. Indeed, we have argued before that learning of times in conditioning protocols may be a necessary precursor to the emergence of conditioned responding (e.g., Balsam et al., 2002; Drew et al., 2005; Balsam & Gallistel, 2009). Empirical support for the idea that the temporal relation between CS and US is learned before the emergence of conditioned responding comes from an experiment in which Ohyama and Mauk (2001) trained rabbits in an eye blink conditioning protocol with tone-shock pairings with a 750 ms ISI. They stopped training before the CS evoked a CR and then trained the rabbits on a shorter 250 ms ISI until strong conditioned responding was established. When subsequently tested with long-duration probe trials (1250 ms), the rabbits blinked at both the short and long times since probe onset, indicating that they had learned the longer time even though conditioned responding had not yet emerged. Results such as these and the present results showing that CRs are appropriately timed when they first emerge indicate that animals are encoding times of events prior to (or in the absence of) the emergence of statistically reliable acquisition. Nevertheless, two behavioral manifestations of this encoded temporal information, namely temporal control of responding and associability, appear to be independent.

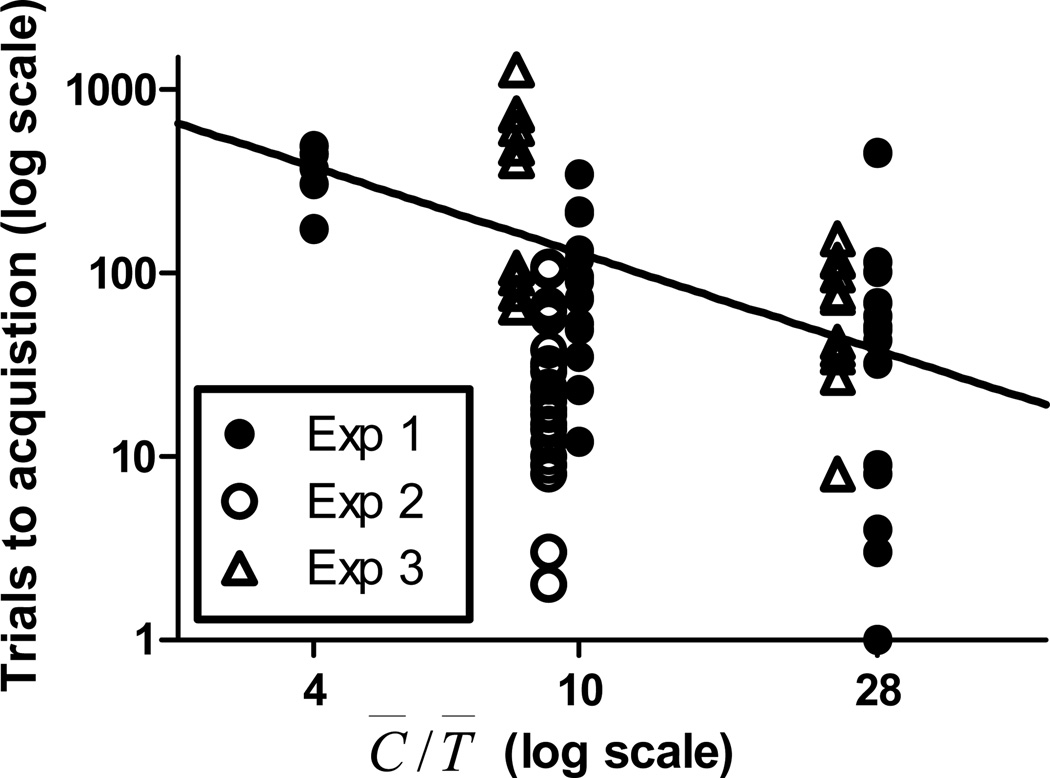
Our results strengthen the evidence that CS-US associability is proportional to informativeness. Evidence for this quantitative law goes back to Gibbon and Balsam (1981), who plotted median trials-to-acquisition in a large number of pigeon autoshaping experiments from many different laboratories against the C̅/T̅, on double-logarithmic coordinates. The strong inverse relation was obvious in their plot; as C̅/T̅ increased, trials to acquisition decreased. Gallistel and Gibbon (2000) were, however, the first to fit a line to the data in this plot and to note that its slope did not differ significantly from −1, which is its value under the assumption that associability is strictly proportional to informativeness. The slope in Gallistel and Gibbon (2000) was somewhat less than −1, whereas when we combine the data on the effect of the C̅/T̅ on associability in the current experiments and compute the regression (Figure 10), the slope is somewhat greater than −1. In both cases, however, it does not differ significantly from −1, suggesting proportionality between associability and C̅/T̅. Given the few data points at the smallest C̅/T̅ ratio in the present studies (Experiment 1), confirmation of strict proportionality between associability and the C̅/T̅ ratio in mice must await further research.

Figure 10.

Trials to acquisition as a function of the C̅/T̅ ratio in all three of the present experiments. The line through the data shows the best fitting linear regression. Note that both axes are on logarithmic coordinates.

Proportionality of associability to informativeness has important implications at the psychological level of analysis. First, it implies that there is no window of associability, no critical interval within which the CS and US signals must fall in order for an association to form (c.f., Gluck & Thompson, 1987). Second, temporal pairing is relative; what matters is the average delay of reinforcement (T̅) relative to the expected interval between USs (C̅). This implies greater computational complexity in the causal path from experience to association formation than has commonly been assumed. If the appearance of the conditioned response is to be understood in associative terms, then the fact that associability is proportional to informativeness requires that the strength of the associative bond between CS and US be a function of the ratio of these two expectations. These expectations are themselves the means of sequences of intervals experienced over many episodes, often over many days. They could not be computed unless the individual experiences of which they are the average were themselves encoded in memory in a manner that made them (or their sum) accessible to computation. Thus, it would seem that the path from experience to the formation of the associative bond must include the computation of the expectations of these two sets of intervals (the CS-US intervals and the US-US intervals) and of the ratio of these expectations.

These results also have important implications for attempts to link conditioned responding to long-term potentiation (LTP; e.g., Bauer, LeDoux, & Nader, 2001; Kwon & Choi, 2009; McKernon & Shinnick-Gallagher, 1997; Rogan, Staubli, & LeDoux, 1997; but see Shors & Matzel, 1997). If plastic changes at synapses (LTP) mediate the appearance of conditioned responding, then the number of CS-US pairings required for the (appropriately aggregated) magnitude of those changes to reach a given level must be inversely related to the factor by which CS onset shortens the expected time to reinforcement (informativeness). This constraint applies regardless of whether sensitivity to "temporal pairing" is a circuit-level property or a synapse-level property of the underlying neurobiology. If the changes at the synaptic level are insensitive to the relative duration of T̅ and C̅, then they cannot be the neurobiological alteration that mediates the appearance of the conditioned response (see Gallistel, et al, 1981 for a discussion of why behavioral trade-off functions constrain quantitative properties of the underlying neurobiological mechanisms).

That fixing the CS-US interval does not increase associability is surprising from an information-theoretic perspective, because manipulating the variability of CS and ITI duration can greatly vary the amount of information that CS onset gives regarding when to expect reinforcement. When the ITI is exponentially distributed and T (CS-US interval) is fixed, CS onset provides 4 bits more information about when to expect the US than when the ITI is fixed and the delay of reinforcement is exponentially distributed with expectation T̅ (see Appendix). To increase the information by the same amount by increasing C̅/T̅ would require a 16-fold increase, from, for example, 8 to 128. The results from Experiments 2 and 3 support the conclusion that this additional information has no effect on trials to acquisition. This is all the more surprising given the clear evidence from the timing of anticipatory poking that subjects learn both the US-US interval and the CS-US interval and that they differentiate between the case when these intervals are fixed and the case when they vary randomly with the same expectation. Nevertheless, as far as associability is concerned, the critical aspect of information conveyed by the CS is the degree to which its onset reduces the expected time to the next US.

Finally, we would stress that we consider it unlikely that it is the growth in the evidence of a CS-US contingency that explains the eventual appearance of a conditioned response (the assumption made in Gallistel and Gibbon, 2000). In many mice, the number of trials required for this appearance is much too long. By the time the CR appears, the evidence of contingency is astronomical. Rather, we think the effect of informativeness is motivational. The increase in reinforcement density arouses food seeking behavior; the greater the increase, the greater the arousal. This view is consistent with other theoretical conceptualizations about the relationship between motivation/arousal and reinforcement rate (e.g., Killeen & Fetterman, 1988; Rescorla & Soloman, 1967). More recently, it has been shown that the information that a CS conveys about the average time to the next US directly impacts overall response rates; the greater the informativeness, the higher the response rate (Harris & Carpenter, 2011). As far as the effect of informativeness on associability is concerned, we suggest that there must be a countervailing motivation, such as fear of exposure to predation, which wanes with continued exposure to the protocol until it is weak enough to be overcome by the arousal from the increase in expected reinforcement density that occurs at CS onset.

Appendix

Computing the information that the CS provides about the timing of the next US The information that the CS provides about the timing of the next US is the difference in the entropy between the (subjective) distribution of the possible occurrence times in the absence of the CS and the subjective distribution after CS onset. The derivations depend therefore on the entropy of an exponential distribution (in the case where either or both C̅ and T̅ vary approximately exponentially) and the entropy of a Gaussian distribution in which the standard deviation is proportional to the mean (scalar variability). This latter distribution represents the subjective uncertainty about exactly when the US will occur when that occurrence comes at a fixed delay after some earlier event, such as CS onset.

The entropy in bits of an exponential distribution with expectation T̅ is:

$${\text{log}}_2\mathrm{T̅}+{\text{log}}_2\left(\frac{e}{\mathrm{\Delta }\tau }\right)$$

where Δτ is the resolution with which time is measured.

The entropy in bits of a Gaussian distribution with expectation T̅ and standard deviation wT̅ is:

$$\frac{1}{2}{\text{log}}_2\left[2\mathrm{\pi }e\frac{{\left(w\mathrm{T̅}\right)}^2}{\mathrm{\Delta }{\tau }^2}\right]$$

The scalar, w is the Weber fraction, whose empirical value is about .16. In each derivation, the entropy of the CS-US distribution is subtracted from the entropy of the US-US distribution.

Variable CS-US and Variable US-US condition:

$$H=[{\text{log}}_2(\mathrm{C̅})+{\text{log}}_2(\frac{e}{\mathrm{\Delta }\tau }\left)\right]-[{\text{log}}_2(\mathrm{T̅})+{\text{log}}_2(\frac{e}{\mathrm{\Delta }\tau }\left)\right]={\text{log}}_2\left(\frac{\mathrm{C̅}}{\mathrm{T̅}}\right)={\text{log}}_2(9)=3.2\text{ bits}$$

Fixed CS-US Fixed US-US condition:

$$H=\frac{1}{2}{\text{log}}_2\lfloor 2\mathrm{\pi }e\frac{{\left(w\mathrm{C̅}\right)}^2}{\mathrm{\Delta }{\tau }^2}\rfloor -\frac{1}{2}{\text{log}}_2\lfloor 2\mathrm{\pi }e\frac{{\left(w\mathrm{T̅}\right)}^2}{\mathrm{\Delta }{\tau }^2}\rfloor ={\text{log}}_2(\mathrm{C̅})-{\text{log}}_2(\mathrm{T̅})={\text{log}}_2\left(\frac{\mathrm{C̅}}{\mathrm{T̅}}\right)={\text{log}}_2(9)=3.2\text{ bits}$$

Variable CS-US and Fixed US-US condition:

$$H=\frac{1}{2}{\text{log}}_2\left[2\mathrm{\pi }e\frac{{\left(w\mathrm{C̅}\right)}^2}{\mathrm{\Delta }{\tau }^2}\right]-[{\text{log}}_2\mathrm{T̅}+{\text{log}}_2(\frac{e}{\mathrm{\Delta }\tau }\left)\right]=\frac{1}{2}{\text{log}}_2(2\mathrm{\pi })+\frac{1}{2}{\text{log}}_2(e)+{\text{log}}_2(w)+{\text{log}}_2(\mathrm{C̅})-{\text{log}}_2(\mathrm{\Delta }\tau )-{\text{log}}_2(\mathrm{T̅})-{\text{log}}_2(e)+{\text{log}}_2(\mathrm{\Delta }\tau )={\text{log}}_2\left(\mathrm{C̅}\right)-{\text{log}}_2\left(\mathrm{T̅}\right)+{\text{log}}_2(w)+\frac{1}{2}{\text{log}}_2(2\mathrm{\pi })-\frac{1}{2}{\text{log}}_2(e)={\text{log}}_2\left(\frac{\mathrm{C̅}}{\mathrm{T̅}}\right)+{\text{log}}_2(w)+\frac{1}{2}{\text{log}}_2\left(\frac{2\mathrm{\pi }}{e}\right)={\text{log}}_2(9)+{\text{log}}_2(0.16)+\frac{1}{2}{\text{log}}_2(2.31)=1.1\text{ bits}$$

Fixed CS-US and Variable US-US condition:

$$H=\left[{\text{log}}_2\right(\mathrm{C̅})+{\text{log}}_2(\frac{e}{\mathrm{\Delta }\tau }\left)\right]-\frac{1}{2}{\text{log}}_2\left[2\mathrm{\pi }e\frac{{(w\mathrm{T̅})}^2}{\mathrm{\Delta }{\tau }^2}\right]={\text{log}}_2\left(\mathrm{C̅}\right)+{\text{log}}_2(e)-{\text{log}}_2(\mathrm{\Delta }\tau )-\frac{1}{2}{\text{log}}_2(2\mathrm{\pi }e)-{\text{log}}_2\left(w\mathrm{T̅}\right)+{\text{log}}_2(\mathrm{\Delta }\tau )={\text{log}}_2\left(\mathrm{C̅}\right)-{\text{log}}_2\left(\mathrm{T̅}\right)+{\text{log}}_2(e)-\frac{1}{2}{\text{log}}_2(e)-\frac{1}{2}{\text{log}}_2(2\mathrm{\pi })-{\text{log}}_2(w)={\text{log}}_2\left(\frac{\mathrm{C̅}}{\mathrm{T̅}}\right)+\frac{1}{2}{\text{log}}_2\left(\frac{e}{2\mathrm{\pi }}\right)-{\text{log}}_2(w)={\text{log}}_2(9)+\frac{1}{2}{\text{log}}_2(0.43)-{\text{log}}_2(0.16)=5.2\text{ bits}$$