Matching 3D Prone and Supine CT Colonography Scans Using Graphs

Abstract

In this paper, we propose a new registration method for prone and supine computed tomographic colonography (CTC) scans using graph matching. We formulate 3D colon registration as a graph matching problem and propose a new graph matching algorithm based on mean field theory. In the proposed algorithm, we solve the matching problem in an iterative way. In each step, we use mean field theory to find the matched pair of nodes with highest probability. During iterative optimization, one-to-one matching constraints are added to the system in a step-by-step approach. Prominent matching pairs found in previous iterations are used to guide subsequent mean field calculations. The proposed method was found to have the best performance with smallest standard deviation compared with two other baseline algorithms called the normalized distance along the colon centerline (NDACC) (p=0.17) with manual colon centerline correction and spectral matching (p<1e-5). A major advantage of the proposed method is that it is fully automatic and does not require defining a colon centerline for registration. For the latter NDACC method, user interaction is almost always needed for identifying the colon centerlines.

I. Introduction

Colon cancer is the second leading cause of cancer-related deaths in the United States, with about 150,000 new cases and 50,000 deaths every year [1]. Computed tomographic colonography (CTC) has been shown to be effective in the detection of colorectal polyps and for cancer screening [2] while computer-aided detection systems (CAD) [3–11] are now starting to be applied in CTC. CAD systems have been shown to improve radiologist detection performance.

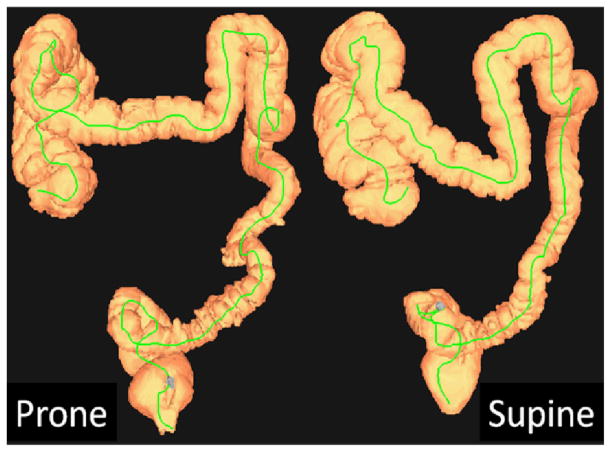
In CTC, a patient will be scanned twice, once supine and once prone, to improve the sensitivity for polyp detection [12]. In Fig. 1 we show two typical 3D colon CTC surface reconstructions of a patient. Registering the prone and supine CTC scans is expected to improve CTC interpretation by reducing interpretation times and potentially improving detection sensitivity.

Fig. 1.

Prone and supine three-dimensional CTC surface reconstructions of the colon of a 65 year old man. Colon centerlines shown in green.

Previous work on CTC registration focused on centerline registration which is a simplified approach compared with full 3D colon registration. For example, Li et al. proposed a heuristic algorithm for the colon centerline registration that employed the coordinate information of the centerline [13]. Summers et al. used the normalized distance along the colon centerline (NDACC) to register prone and supine scans [14]. To make full use of the centerline and colon shape information, Wang et al. used correlation optimized warping (COW) and canonical correlation analysis (CCA) for CTC registration [15]. Suh et al. considered topological changes between prone and supine scans [16]. Zeng et al. employed teniae coli and quasi-conformal mapping to register flattened colons [17]. Roth et al. reduced the complexity of the registration task from 3D to 2D by using cylindrical parameterization [18].

In all the methods described above, the colonic centerline is required for the registration. But in reality, centerline extraction is still a very challenging problem [19]. For some complicated cases the centerline may be erroneous and these errors adversely affect registration accuracy. A main cause of centerline errors is poor colon distention resulting in disconnected colonic segments. In CTC practice, manual corrections are required for such errors. In this work we treat the problem from the point of view of graphs and propose a new graph matching method for CTC colon registration to avoid centerline extraction problems and human interventions in CTC registration. Graph matching develops a correspondence between two similar graphs represented by nodes and edges under a set of constraints. State-of-the-art graph matching algorithms include spectral matching [20] and convex relaxation [21]. While graphs built from colon segmentations are affected by colon segmentation errors, graph matching reduces the dependence on accurate segmentations compared with centerline-based registration methods by utilizing 3D structure information from a limited number of key points.

The outline of the paper is as follows: in Sec. 2, we formulated the colon registration problem in CTC as a graph matching problem. In Sec. 3, we discuss the use of mean field theory and we propose an iterative optimization method to solve the graph matching problem. Sec. 4 includes the experimental results and comparisons with the baseline algorithms NDACC and spectral matching. Sec. 5 contains the discussions.

II. Problem Formulation

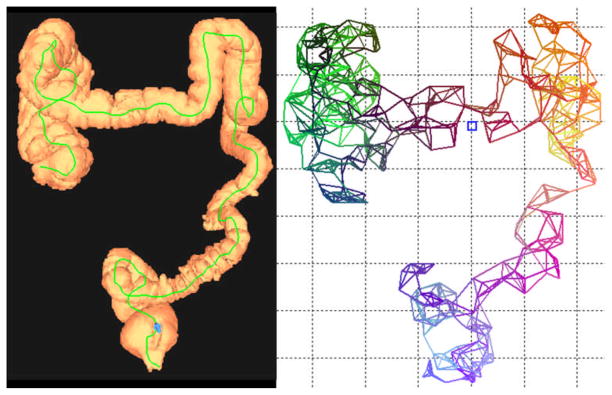
In our approach, we used region growing to segment the colon in CTC scans. With the colon segmented, we applied n-Dimensional Scale Invariant Feature Transform (n-SIFT) to find key points on the surface of the colon. n-SIFT is a registration method which extracts and matches salient features from images of arbitrary dimensionality [22]. For a given image, it builds image pyramids and uses Gaussian smoothing to find spatial extreme key points. These key points usually contain anatomical landmarks. Due to deformation of the colon between prone and supine scans, some key points or landmarks from one scan may not have correspondences in the other scan. In the following section, we propose a new graph matching method to find matched pairs with highest probability of node and graph structure similarities between the two scans. With a set of matched prominent pairs, we show in the experimental results that we can register prone and supine CTC scans accurately, and reduce the influence of segmentation errors and incorrect/wrong “non-prominent” landmarks significantly. With detected key points in both the prone and supine segmented colon, we built graphs using a K-nearest neighbor criterion. In Fig. 2 we show a 3D colon surface rendering exemplar along with the graph built using our algorithm.

Fig. 2.

A 3D graph constructed from a CTC scan. Colored lines represent links between key points identified by the n-SIFT algorithm. For each link, its color in RGB color space is determined by its XYZ coordinates, respectively. Blue square shows location of a colonic polyp.

Given two graphs from prone and supine CTC scans to be matched, we can assume for example that the prone graph is defined as model graph G_M and the supine graph is defined as data graph G_D or vice versa. The model graph is a graph constructed from an exemplar object to be matched; the data graph is a graph constructed from a real object that may be in a cluttered environment that usually contains noise. Each graph is depicted by a set of vertexes and edges: G_M=G(V_M, E_M), G_D=G(V_D, E_D). Each element of the vertex set is a feature vector which describes the characteristics of the vertex and its surroundings. The edge sets contains structural information of a graph. They can be binary which means they indicate the connectivity between two vertexes; or they can be feature vectors which contain additional information pertaining to the link. The matching of two sets of vertexes can be described by a matching matrix M whose elements are binary: 0 or 1. The size of M is |V_D|×|V_M|. A one-to-one or one-to-many correspondence limitation can be incorporated in the matching matrix M by requiring that the summation of row or column of M sum to one or they sum to more than one, respectively. In this paper, we assume that the data graph is smaller than the model graph (it has fewer vertices) and each vertex of G_D has one and only one correspondent vertex in graph G_M. A vertex in model graph G_M has at most one corresponding vertex in G_D. The above constraints can be formulated as follows:

$$\sum _{\alpha \in {\mathbf{V}}_{\mathbf{M}}}\mathbf{M}(a,\alpha )=1,\forall a\in {\mathbf{V}}_{\mathbf{D}}\text{and}\sum _{a\in {\mathbf{V}}_{\mathbf{D}}}\mathbf{M}(a,\alpha )\le 1,\forall \alpha \in {\mathbf{V}}_{\mathbf{M}},$$

where a is the index for a node in the data graph and α is the index for a node in the model graph.

Now let us consider similarities between the two graphs. The matching quality between G_D and G_M can be depicted by vertex similarity and link compatibility. We use a matrix W to contain the similarities of each vertex of V_D and each vertex of V_M. The size of W is |V_D|×|V_M|. The link compatibility is a measure equivalent to the co-existing probability of a pair of links between G_D and G_M. We use a matrix Q to represent the link compatibility whose size is |V_D||V_M|×|V_D||V_M|. For the convenience of presentation, we convert matrices M and W into one dimensional vectors m and wwhose elements are taken column-wise from M and W, respectively. With all these notations, the objective of the graph matching problem can be formulated as follows [21]:

$$\begin{array}{c}\underset{m}{max}{m}^T\times w+m^T\mathbf{Q}m\\ s.t.{\mathbf{A}}_{\mathbf{R}}\times m=e_R,{\mathbf{A}}_{\mathbf{C}}\times m\le e_C,\text{and}m\in {\{0,1\}}^{\mid {\mathbf{V}}_{\mathbf{D}}\mid \mid {\mathbf{V}}_{\mathbf{M}}\mid },\end{array}$$ (1)

where e_R is a |V_D|×1 vector whose elements are all one, e_C is a |V_M|×1 vector whose elements are all one, ${\mathbf{A}}_{\mathbf{R}}={\mathbf{I}}_{\mid {\mathbf{V}}_{\mathbf{D}}\mid }\otimes e_C^T$ and ${\mathbf{A}}_{\mathbf{C}}=e_C^T\otimes {\mathbf{I}}_{\mid {\mathbf{V}}_{\mathbf{D}}\mid }$.

III. Graph Matching Based on Mean Field Theory

The matching problem expressed by eq. (1) is a quadratic integer program which is non-deterministic polynomial-time hard (NP-hard) and has no known polynomial-time solver. To solve this problem efficiently, we drop the one-to-one constraint first and treat the problem in a probabilistic manner. More specifically, the objective function is expressed by the following probabilistic model which has the exact same form as an Ising model with quadratic interaction [23]:

$$p(m)=\frac{\rho (m)}{Z(w,\mathbf{Q})}exp\left[\sum _{i<j}{m}_i{\mathbf{Q}}_{ij}{m}_j+\sum _i{w}_i{m}_i\right],$$ (2)

where $\rho (m)={\displaystyle \prod _i}\rho (m_i)$ models the distribution for each single variable in which we can encode all the prior knowledge or constraints to be satisfied by m_i (discreteness, bounds on the range, etc.); Z(w, Q) is called the partition function where: $Z(w,\mathbf{Q})=\int {\displaystyle \prod _j}\left({dm}_j\rho \left(m_j\right)\right)exp\left[{\displaystyle \sum _{i<j}}{m}_i{\mathbf{Q}}_{ij}{m}_j+{\displaystyle \sum _i}{w}_i{m}_i\right]$. The partition function is the integration of a target function across all the states of the function variables. It describes the statistical properties of the system or model. The binary constraint of the matching problem can be encoded in the following way by using the Delta function: $\rho (m_i)=\frac{1}{2}\delta (m_i-1)+\frac{1}{2}\delta (m_i+1)$. In eq. (2), the item in the exponential function corresponds to the target function in eq. (1); the prior item $\rho (m)={\displaystyle \prod _i}\rho (m_i)$ corresponds to the constraint m ∈ {0, 1}^|V_D||_VM| in eq. (1). Since we drop the one-to-one constraint in eq. (1) for now, eq. (2) is equivalent to eq. (1) without the one-to-one constraint between model and data graphs. The probabilistic model shown in eq. (2) with binary constraint is an Ising model where w_i, i = 1, 2, …, |V_D||V_M| is called the external field. An Ising model is a probabilistic energy model describing ferromagnetism with variables called spins in this statistical model having only two energy states [24]. Mean field theory provides an effective way to compute approximate values for the moments of the spins/variables m_i and for the free energy −lnZ [23].

According to mean field theory, the expectation of m_i can be approximated as $\langle m_i\rangle =\partial ln{Z}_0^{(i)}/\partial w_i$, where $Z_0^i=\int {dh}_i{dm}_i\rho (m_i)e^{m_i(h_i+w_i)}p(h_i\backslash m_i)$. Here h_i = Σ_j Q_ijm_j is called the “cavity” field and its distribution p h_i\m_i) at the location of vertex i can be approximated by a Gaussian distribution with mean 〈 h_i 〉_\i = Σ_j Q_ij 〈 m_j 〉 − V_i 〈 m_i 〉 and variance V_i.

With the mean field approximation, the integer quadratic optimization problem shown in eq. (1) without matching constraints can be solved in a probabilistic manner. The expectation of matching variables 〈 m_i 〉, i = 1, 2,…, |V_D||V_M|, can be viewed as confidence that a vertex in graph G_D is matched to a vertex in graph G_M. The next step is to incorporate the one-to-one matching constraint in the mean field solution. Here we propose an iterative technique for mean field calculation and for adding the matching constraints. The basic idea comes from human visual perception. When a person looks at two graphs, he/she will try to match the most prominent points in the two graphs which are similar in shape, color, surroundings, etc. Less similar points are matched with guidance from the prominent points previously matched. Similar to human visual perception, our algorithm first matches the most prominent points in the data and model graphs. We keep the external field w_i corresponding to variable m_i having the highest expectation value and set all other external fields which conflict with m_i to zero in order to develop a one-to-one matching constraint. The overall algorithm is summarized in Fig. 3.

Fig. 3.

The proposed graph matching algorithm based on mean field theory.

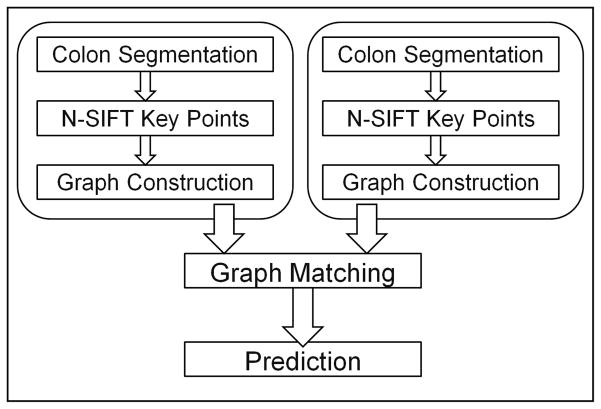
Figure 4 shows a diagram of our registration system. For each prone and supine scan, we first segment the colon, apply key point detection using n-SIFT algorithm, and construct the graph using a stepwise K-nearest neighbor approach. Once graphs for both the prone and supine scans have been defined, we match these two graphs using mean-field theory. The result of the graph matching step is registered prone and supine graphs, where a corresponding point in either the prone and supine graph can be matched to a distinct location in the other graph.

Fig. 4.

System diagram of the proposed non-centerline based prone/supine registration method.

IV. Experimental Results

Our institution’s Office of Human Subjects Research declared this project to be exempted from IRB review. Our evaluation dataset consists of CTC examinations from 39 patients collected from three medical centers. Each patient was scanned in the prone and supine positions. Each scan was done during a single breath hold using a 4 or 8 detector row CT scanners. CT scanning parameters included 1.25- to 2.5-mm section collimation, 15 mm/s table speed, 1-mm reconstruction interval, 100 mAs, and 120 kVp. Each patient had one or more polyps. We randomly picked a single polyp for algorithm evaluation if a patient had more than one polyp. We selected a total of 39 polyps 6–25 mm in size. The polyps were confirmed by both traditional optical colonoscopy and CT colonography. The whole dataset was split into training and test sets with 19 and 20 patients, respectively.

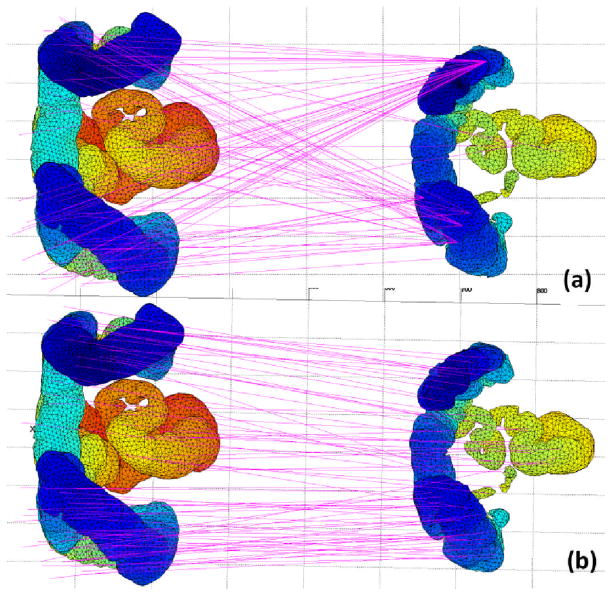
Fig. 5(a) shows the matching result of the n-SIFT algorithm alone. The n-SIFT features employed for matching are orientation histograms of gradient magnitude and orientation in the region around the keypoint [22]. From it we see that the n-SIFT alone produces problematic matching results: key points from the descending colon are matched to key points in the ascending colon. Because n-SIFT matches key points from different scans based on the Euclidean distance between the features of the two key points, a key point in one scan may attract a number of key points from the other scan. Fig. 5(b) shows the matching result of our proposed method. Compared with n-SIFT, our method shows improved matching. The different segments of the colon were found to be well-matched visually (parallel pink lines). The figure also shows the advantage of utilizing the graph structure of the colon during the matching process, (i.e., matching with constraints). Statistical features from key points are only one set of factors in our matching process. The graph structure appears to play a more important role in limiting mismatches along the colon.

Fig. 5.

Matching results of (a) n-SIFT and (b) our proposed algorithms. We show 3D renderings of the segmented colon from prone (left) and supine (right) CTC scans. Pink lines between the scans indicate matched key points on prone and supine colons.

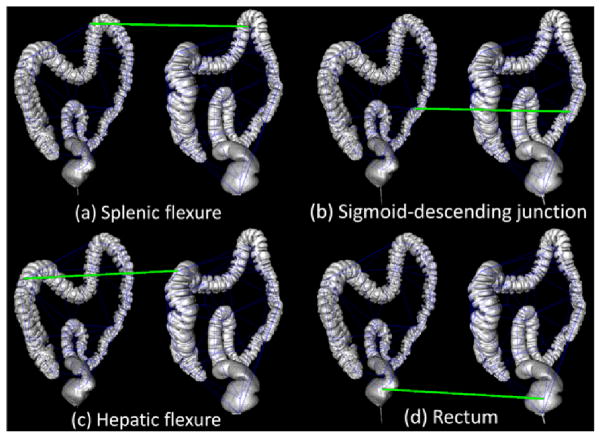
The anatomy of the colon plays an important role in CTC reading. It is known that a colon can be partitioned into segments using six anatomical landmarks. These landmarks are the cecum, rectum, two flexures (splenic and hepatic) and two junctions (rectum-sigmoid and sigmoid-descending). In general, the shapes of the splenic and hepatic flexures tend to be preserved between the prone and supine scans and are therefore considered as reliable landmarks [25]. The registration of prone and supine colon can be improved by employing prior knowledge of colon anatomy. In Fig. 6, we show four landmarks which were matched using our algorithm. These matched vertices rank high in the mean field calculation. This suggests that our proposed automatic matching algorithm behaves similarly to human visual perception: where the most prominent landmarks are first identified and subsequent matching proceeds using these key points as a guide.

Fig. 6.

Four landmarks matched by our algorithm (shown by green line between scans). The constructed graphs are shown in blue lines overlapped on the 3D renderings of scans. The ranks of the four matched vertices are 1, 3, 6 and 7 from (a) to (d), respectively. There are 50 ranked vertices for each scan. The rank of a matching link is defined as the order it is identified or fixed during the iterative optimization process.

To quantitatively evaluate our registration method, we conducted a registration experiment based on the correspondence in the polyp location between the prone and supine scans. The baseline algorithms for comparison were NDACC and spectral matching. For the three methods compared, we used the same colon segmentation results to provide a fair comparison among the methods.

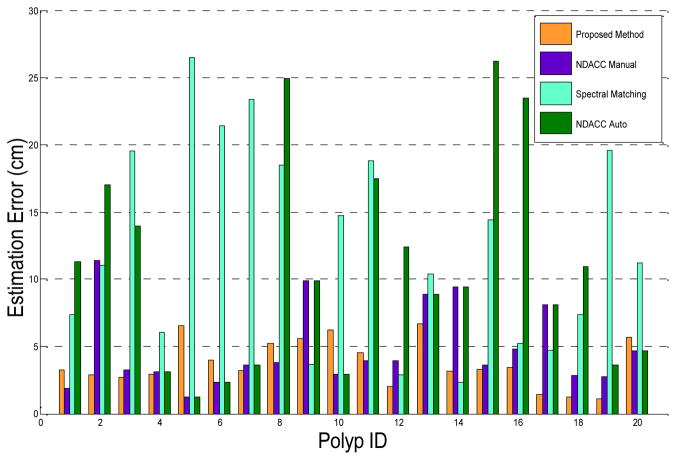
Fig. 7 shows the registration errors for the polyps across the three methods on the test data set. The registration error is defined as the Euclidean distance between a polyp’s actual location and estimated location. For NDACC, we show results with and without manual correction of the colon centerline. The average registration error for our method is 3.76cm (std. 1.74 cm). The average registration error of NDACC with manual centerline correction is 4.82 cm (std. 2.98 cm) and without manual centerline correction is 10.78 cm (std. 7.73 cm). The average registration error of spectral matching is 12.46 cm (std. 7.51 cm). The 95% confidence intervals of the four sets of results are [2.94 cm, 4.57 cm], [3.43 cm, 6.22 cm], [7.17 cm, 14.40 cm] and [8.95 cm, 15.97 cm], respectively. The proposed method had better performance on the test set compared to NDACC with manual centerline correction (p=0.17) and spectral matching (p<0.001). There were 5 cases in which the registration error of NDACC with manual centerline correction was greater than 8cm. None of the registration errors of the proposed method was greater than 8cm.

Fig. 7.

Registration errors for the three colon registration methods on the test set. For NDACC, we show results with and without manual correction of the colon centerline. The proposed method, NDACC with manual centerline correction, and spectral matching had lowest registration errors on 11, 7 and 2 polyps, respectively.

V. Discussion and Conclusion

Registration of prone and supine CTC scans plays a key role in CTC practice and utilizing the colonic centerline for registration in CTC has been a critical part of most mainstream registration method. However, this can also be a major limitation of these methods when the centerline extraction gives erroneous results and needs manual correction complicating the registration process and increasing registration error. With this limitation in mind, we have proposed a new approach to solve the CTC registration problem that does not rely on a centerline. Our approach characterized the colon using graphs and then implemented a new graph matching method to register prone and supine graphs. The proposed method showed significantly better performance on the test set compared with a state-of-the-art graph matching method and with NDACC when manual colon centerline correction was not utilized.

In this paper, we employed NDACC as a baseline algorithm in our comparison with centerline based registration method due to its simplicity and effectiveness. As we introduced in Sec. 1, more advanced and accurate methods for colon registration in CTC were developed in the past two years. For example, Zeng et al. employed teniae coli and quasi-conformal mapping to register flattened colons. They showed 0.57 cm average registration error on 20 pairs of polyps from 6 datasets [17]. But their method requires the accurate identification of both the colon centerline and teniae coli which are still very difficult to automatically identify in a large population of patients. Suh et al. considered topological changes between prone and supine scans. They reported 2.23 cm registration error for a validation dataset of 24 patients [16]. The core of their method is feature-based registration by centerline analysis. So for state-of-the-art colon registration methods, colon centerline/teniae coli and manual intervention are important factors in their success. From the viewpoint of clinical practice, our graph matching method resulted in a somewhat larger registration error compared to some of these other state-of-the-art methods. The large registration error mainly came from the sparse graph representation of the original colon segmentation. However, it was found to adequately localize colonic polyps between prone and supine scans and in a fully automated manner. The relatively small difference in the errors between the approaches is likely to only have a small impact in the clinical setting because usually in 3D flythrough mode the colon region radiologists observe is longer than 4cm. Similar to our method, spectral matching identifies salient links between the two graphs using a stepwise approach. But the rating of salient links is mainly based on eigenvalue decomposition while the matching constraints are part of a separate post-processing procedure. On the contrary, our method identifies salient links based on the mean field calculation in each step which essentially interweaves salient link identification and the matching constraints procedures together. Including the matching constraints within each step allowed our registration algorithm to guide the identification of salient links in the following steps and allowed it to achieve improved performance.

For our graph matching method, computation time is a big issue because graph matching is a quadratic integer programming problem with computation time that increases exponentially as the number of variables increases. On a workstation with two Intel® Xeon® Processor X5550 Xeon CPU (8M Cache, 2.66 GHz) and 24G memory, to register two CTC scans with about 30 key points from each scan, the whole registration process takes about 5 minutes. If the number of key points increases to 100, the computational time is about 24 hours. This is too long to be practical for routine CTC practice. Finding an efficient approach to solve the quadratic optimization problem is another open problem. Fortunately, we found that usually 30 nodes per graph will give us acceptable registration results (around 4cm) already which makes this registration method practical for clinical use.

We conducted a grid search to find the optimal number of key points for registration using our training set. Experimental results showed that 100 key points from each scan achieved the best performance. Given a polyp candidate from CTC CAD in one scan, the prediction of its correspondence in the other scan is a function of the key points of both scans. In theory, more key points should reduce the registration error. But our experiments on the training set showed that the performance of the proposed method degenerated after 100 key points. The degeneration was likely caused by the iterative matching identifying a local minimum instead of the global minimum as the number of key points increased. Clearly, the optimization task is more difficult and prone to getting stuck in local minima as the number of potential matches increases. How to find the global solution and avoid local minima for large scale registration problems, how to balance the number of key points (related to the precision of the registration), and how to optimize the accuracy of the matching algorithm and the time needed to perform the optimization are all important areas in need of additional research.

Key point detection is a critical part of a successful graph matching method. Currently we are using the n-SIFT algorithm to detect key points. Given the advantage that teniae coli bear the same deformation trend as colon, it makes them more stable anatomic landmarks on the colon surface compared with n-SIFT key points. Restricting the key points only in teniae coli may reduce the matching error significantly. Currently the extraction of teniae coli requires the colon centerline. In the future work, it is also worth trying to use teniae coli as reference coordinate system to match prone and supine CTC if teniae coli can be detected in a fully automatic way without the colon centerline [26].

In this work, we focused on solving the CTC registration problem. However, the proposed graph matching method using mean field theory to find probabilistic approximations of the quadratic integer programming problem is a general new graph matching method in itself. In future work, it will be interesting to extend this new method to other medical registration problems such as registration of organs on serial scans or across modalities.

In conclusion, our graph matching registration method is a fully automatic registration approach (i.e., no human interaction required) and was found to be robust compared with other CTC colon registration methods, e.g. NDACC and COW, because our method is less dependent on segmentation quality. Future improvements could include the incorporation of other anatomical landmarks such as the spine, liver and kidney. The graph matching method showed improved performance on real CTC datasets compared to NDACC with manual colon centerline correction and may be useful for clinical practice.

Biographies

Shijun Wang received his PhD degree in Control Science and Engineering from Tsinghua University, China, where his research focused on machine learning and complex systems. He earned a BS in Electronic Engineering at Beihang University and an MS in Communication at Second Aerospace Science Academy, China. He is currently a staff scientist in the Imaging Biomarkers and Computer-Aided Diagnosis Laboratory, US National Institutes of Health National Clinical Center, Dept. of Radiology and Imaging Sciences. Dr. Shijun Wang’s current research interests include machine learning, statistical image analysis and their applications in computer aided diagnosis. He is an associate editor of Medical Physics and reviewer for IEEE TMI, IEEE TBME, Journal of Artificial Intelligence Research, Journal of Magnetic Resonance Imaging, Medical Physics, Pattern Analysis & Applications, and Journal of Theoretical Biology. He is a program committee member of Asian Conference on Machine Learning.

Nicholas Petrick is currently at the Center for Devices and Radiological Health, U.S. Food and Drug Administration where he is Deputy Director for the Division of Imaging and Applied Math and Leader of the Image Analysis Laboratory. He also holds an Adjunct Appointment in the UM Medical School. He has authored or coauthored over 160 scientific articles with 75 appearing in the peer-reviewed literature. Dr. Petrick’s current research interests include quantitative image analysis, computer-aided diagnosis and the development of assessment methods for medical imaging and computer assessment devices.

Robert L. Van Uitert is currently a Senior Director of Global Product Marketing at iCAD, Inc. His research interests are in the field of virtual colonoscopy and computer-aided detection for cancer in mammography, CT colonoscopy, and dynamic contrast MR images.

Senthil Periaswamy received the Ph.D. degree in Computer Science from Dartmouth College, Hanover, NH, in 2003. He is currently Director of Research at iCAD Inc., Nashua, NH. His research interests include computer vision and pattern recognition applied to medical images.

Zhuoshi Wei received the B.S. degree in Electronic Engineering from Beijing Jiaotong University, Beijing, China, and the Ph.D. degree in Pattern Recognition and Intelligence System from Institute of Automation, Chinese Academy of Sciences, Beijing, China. She is currently a Postdoctoral Fellow in the Department of Radiology and Imaging Sciences, National Institutes of Health, Bethesda, MD. Her research interests include pattern recognition and image processing.

Ronald M. Summers received the B.A. degree in physics and the M.D. and Ph.D. degrees in Medicine/Anatomy & Cell Biology from the University of Pennsylvania. He completed a medical internship at the Presbyterian-University of Pennsylvania Hospital, Philadelphia, PA, a radiology residency at the University of Michigan, Ann Arbor, MI, and an MRI fellowship at Duke University, Durham, NC. In 1994, he joined the Diagnostic Radiology Department at the NIH Clinical Center in Bethesda, MD where he is now a tenured Senior Investigator and Staff Radiologist. He is currently Chief of the Clinical Image Processing Service and directs the Imaging Biomarkers and Computer-Aided Diagnosis (CAD) Laboratory. In 2000, he received the Presidential Early Career Award for Scientists and Engineers, presented by Dr. Neal Lane, President Clinton’s science advisor. His research interests include virtual colonoscopy, CAD, multi-organ multi-atlas registration and development of large radiologic image databases. His clinical areas of specialty are thoracic and gastrointestinal radiology and body cross-sectional imaging. He is a member of the editorial boards of the journals Radiology and Academic Radiology. He is a program committee member of the Computer-aided Diagnosis program of the annual SPIE Medical Imaging conference. He has co-authored over 200 journal, review and conference proceedings articles and is a coinventor on 10 patents.