Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jan 7.
Published in final edited form as: J Theor Biol. 2012 Sep 30;316C:42–48. doi: 10.1016/j.jtbi.2012.09.029

Mechanical Buckling of Arterioles in Collateral Development

Qin Liu 1, Hai-Chao Han 1
PMCID: PMC3498525  NIHMSID: NIHMS411518  PMID: 23034307

Abstract

Collateral arterioles enlarge in both diameter and length, and develop corkscrew-like tortuous patterns during remodeling. Recent studies showed that artery buckling could lead to tortuosity. The objective of this study was to determine arteriole critical buckling pressure and buckling pattern during arteriole remodeling. Arterioles were modeled as elastic cylindrical vessels with an elastic matrix support and underwent axial and radial growth. Our results demonstrated that arteriole critical buckling pressure decreased with increasing axial growth ratio and radius growth ratio, but increased with increasing wall thickness. Arteriole buckling mode number increased (wave length decreased) with increasing axial growth ratio, but decreased with increasing radius growth ratio and wall thickness. Our study suggests that axial growth in arterioles makes them prone to buckling and that buckling leads to tortuous collaterals. These results shed light on the mechanism of collateral arteriole tortuosity.

Keywords: arteriole buckling, tortuosity, critical pressure, remodeling, axial growth ratio, radius growth ratio, artery, modeling

1. Introduction

Vessel tortuosity often occurs during arteriogenesis, the growth of preexisting arterioles. Arterioles develop into tortuous collateral arteries after occlusion of a major artery. “Corkscrew” collaterals have been reported in coronary and peripheral arteries (Schaper and Buschmann 1999; Cai et al. 2003; Shireman and Quinones 2005). Tortuosity increases the flow resistance in collateral arterioles (Heil and Schaper 2004; Eitenmuller et al. 2006). Tortuosity may also activate platelets and consequently induce thrombosis in microvessels (Liu et al. 2008; Chesnutt and Han 2011). On the other hand, an increase in capillary tortuosity could increase the interface area of capillary to tissue, thus promoting muscle tissue oxygenation (Goldman and Popel 2000; Charifi et al. 2004). Arterioles around tumor cells often develop tortuous shapes, and the tortuosity level has been associated with the malignancy of tumors (Bullitt et al. 2005; Pries et al. 2009; Vakoc et al. 2009). Therefore, it is important to understand the relationship between microvessel development and tortuosity.

Tortuous vessels are also often observed in medium to large arteries and veins in humans and animals (Han 2012), and are often associated with hypertension, aging, and atherosclerosis (Smedby and Bergstrand 1996; Del Corso et al. 1998; Pancera et al. 2000; Hiroki et al. 2002; Thore et al. 2007; Han 2012). Genetic defects and other pathologic changes such as degenerative vascular diseases have also been linked to artery tortuosity (Dobrin et al. 1988; Wagenseil et al. 2005; Callewaert et al. 2008). While it is speculated that arterial growth may lead to tortuosity, the physical mechanisms and the quantitative relation remain unclear.

Collateral arteriole growth begins with a rapid onset of proliferation leading to outward remodeling in seven days after the occlusion, which is followed by extensive remodeling (Ito et al. 1997). During the development of collateral arterioles, smaller vessels regress, and larger ones increase in diameter. However, the enlargement in diameter is often limited. In optimal conditions, 35 – 40% of the maximal flow can be recovered by collateral arteries (Lazarous et al. 1996; Ito et al. 1997). Though creating an arterio-venous shunt may completely restore the maximal collateral flow (Eitenmuller et al. 2006), it is hard to achieve clinically. One possible reason for the incomplete recovery of blood flow could be the tortuosity of collateral arterioles. However, how tortuosity is generated in collateral arterioles and its relationship to arteriole remodeling remain unclear.

Recent studies have shown that arteries may lose stability and buckle when their lumen pressure is elevated or axial tension is reduced (Han 2007; Han 2009; Lee et al. 2012). Artery buckling causes arteries to deform into tortuous shapes, starting with a small lateral deflection and developing into a large deflection if the pressure continues to increase. In vivo experiments showed that rabbit carotid arteries under reduced axial tension adapted over time and became permanently tortuous (Jackson et al. 2005), suggesting that buckling could lead to tortuosity. However, the effects of growth on arterial mechanical stability and buckling behavior have not been investigated.

Therefore, the objective of this study was to determine arteriole critical buckling pressure and buckling pattern change due to axial and radial growth and remodeling using model simulations.

2. Methods

2.1. Buckling equation

Arterioles were modeled as nonlinear elastic circular cylinders surrounded by soft tissues. The tissues were modeled as linear elastic matrices. Accordingly, arteriole buckling pressure pcr was determined using the artery buckling equation given by (Han 2009):

pcr=NπRi2+EIπRi2(nπl)2+ksπRi2(lnπ)2 (1)

where N is the axial force, Ri is the lumen radius, EI is the cross sectional bending rigidity, ks is the Young’s modulus of the surrounding matrix, l is the vessel length, and n is the buckling wave mode number. N was determined by the transmural pressure p and the strain. The bending rigidity EI is a function of arteriole cross sectional dimensions and the strain components as given in detail previously (see appendix in (Han 2011)). EI is also affected by the lumen pressure and axial stretch ratio since the strain components are functions of pressure and axial stretch ratio. The critical pressure pcr of an arteriole with given Ri, l, and ks, was determined following the iteration steps decreased previously (Han 2009). Briefly, for each assumed wave number n, the buckling pressure was determined through iterations using Equation 1. The process was repeated for a range of n values (>1. The corresponding pcr value first decreases and then increases with increasing n). The actual critical buckling pressure was determined by finding the n value that gave the minimum pcr value (Han 2009).

2.2. Determination of arteriole wall material constants

The mechanical behavior of arteriolar walls was characterized by Fung’s exponential strain energy function (Fung 1993):

w=12b0eQ+K[(1+2Er)(1+2Eθ)(1+2Ez)-1]Q=b1Eθ2+b2Ez2+b3Er2+2b4EθEz+2b5EzEr+2b6ErEθ (2)

where b0 – b6 are the material constants, and K is a Lagrangian multiplier for incompressibility. Eθ, Ez, and Er are the Green strain components in the circumferential, axial, and radial directions, which all refer to the zero-stress state. By solving the equilibrium equation for a cylindrical arteriole under axial load and internal pressure, the internal pressure p and axial force N in the vessel were expressed as (Fung 1990; Humphrey 2002; Han 2008; Han 2009):

p=∫RiRe[(1+2Eθ)(b1Eθ+b4Ez+b6Er)-(1+2Er)(b6Eθ+b5Ez+b3Er)]b0eQdξξN=πRi2p+π∫RiRe[2(1+2Ez)(b4Eθ+b2Ez+b5Er)-(1+2Er)(b6Eθ+b5Ez+b3Er)-(1+2Eθ)(b1Eθ+b4Ez+b6Er)]b0eQrdr (3)

wherein Ri and Re are the inner and outer radii, respectively. The material constants b0 – b6 were determined by fitting Eq. (3) to a previously reported pressure-diameter relation of cat mesenteric arterioles incorporating the initial dimensions (outer/inner radius and wall thickness t) (Gore 1974). Residual strain was not measured in this previous study (Gore 1974). However, since our previous studies have shown that residual strain (opening angle) had little effect on the critical pressure (Han 2009; Liu and Han 2012), the residual strain in the arteriole was neglected in current simulations (opening angle = 180°). We also assumed that the arterioles were free to expand in the mesentery, and thus the axial force was N =πr2p. Using a custom code in Matlab (Lee et al. 2012; Liu and Han 2012), we obtained b1 = 2.0, b2 = 0.001, b3 = 2.0, b4 = 0.2555, b5 = 0.001, b6 = 1.996, and b0= 38.949 kPa.

2.3. Arteriole parameters and simulation conditions

In our simulations, arteriole length l was assumed to be 10 mm, with the initial lumen radius Ri = 50 μm and outer radius Re = 60 μm. The arteriole was pre-stretched axially at a stretch ratio of 1.5. The stiffness of supporting matrix was ks = 5 kPa, unless otherwise specified.

To describe the growth of arterioles, we defined growth ratio as the percentage of dimension change due to growth from the original length under no-load condition. Collateral arterioles elongate while enlarging radially (outward remodeling). So we examined arterioles with combinations of axial growth ratios and radial growth ratios. The axial growth ratios were examined in the range of 0 to 30% (Herzog et al. 2002). Since arteriolar wall cross section area might decrease (hypotrophic), increase (hypertrophic), or remain the same (eutrophic) (Mulvany 1999), both lumen diameter and wall thickness (thus the outer diameter) changes were examined. The lumen diameter and wall thickness were assumed to increase up to 2-fold and 2.5-fold, respectively, following a previous experimental observation (Herzog et al. 2002).

Arteriole buckling was simulated first for axial growth alone and then for combined axial and radial growth.

3. Results

3.1. Effect of axial growth on arteriole critical buckling

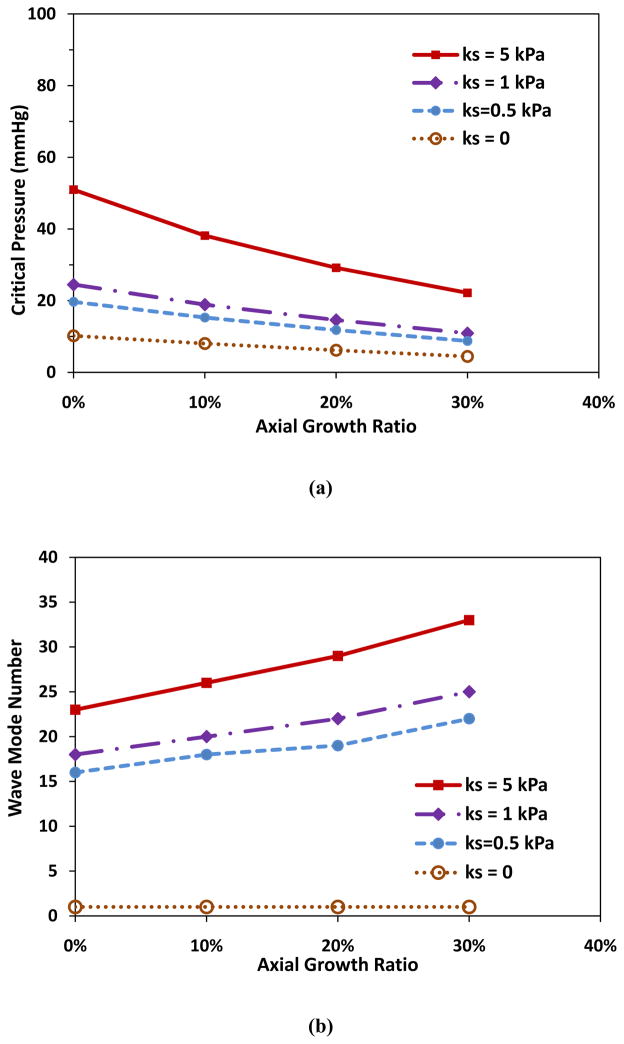
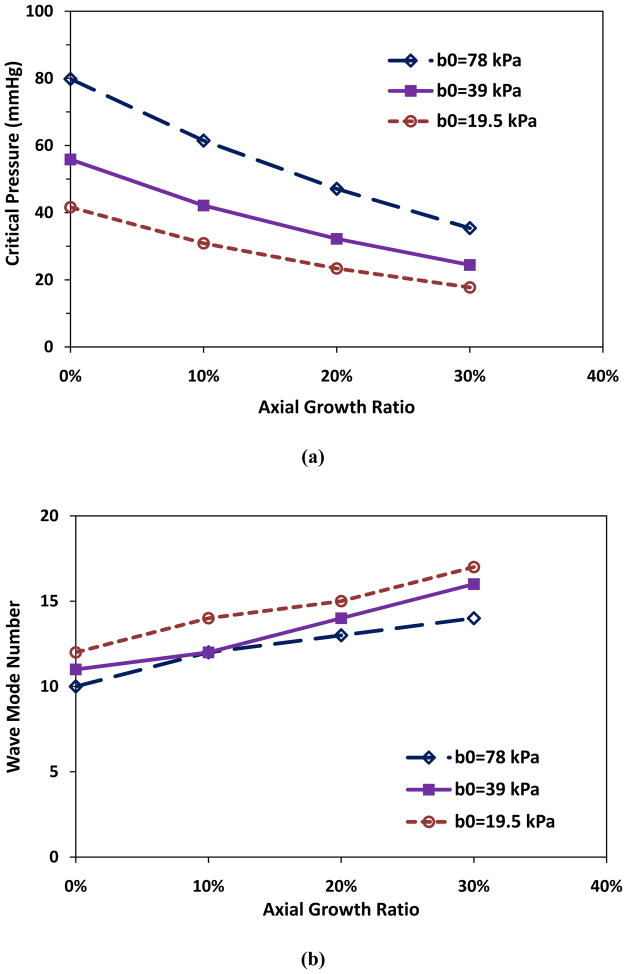
Simulations showed that axial growth of arterioles reduced the critical buckling pressure. For an arteriole (Ri = 50 μm, t = 10 μm, and l = 10mm) within a surrounding matrix of stiffness ks = 5 kPa, when the axial growth ratio increased from 0 to 30% while the lumen radius and wall thickness remained unchanged, the critical buckling pressure decreased from 51.0 to 22.2 mmHg (■, Fig. 1a). Accordingly, the buckling wave mode number increased from the 23rd to the 33rd mode (■, Fig. 1b). The wave length decreased from 435 to 303 μm. These results indicate that at a higher axial growth ratio the arteriole more easily buckled and became more tortuous. Figure 1c illustrates the first seven wave mode shapes for arteriole buckling.

Figure 1.

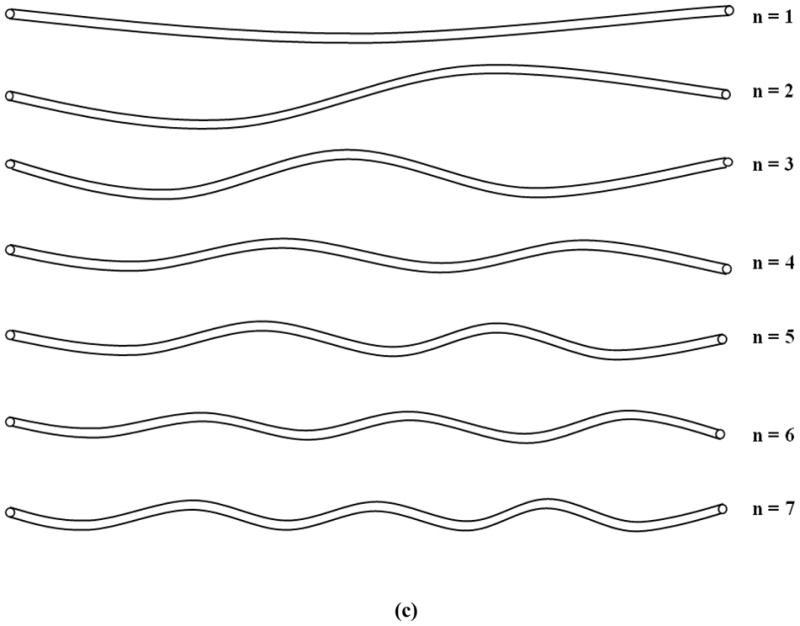
Figure 1

Figure 1

Open in a new tab

Critical buckling pressure (a) and buckling mode (b) plotted as functions of axial growth ratio at different matrix stiffness. The lumen radius Ri, wall thickness t, and length of the collateral arteriole l were 50 μm, 10 μm, and 10 mm respectively. (c) Illustration of buckling wave mode shapes.

3.2. Effect of supporting tissue stiffness on arteriole critical buckling

The stiffness of the surrounding matrix affects the critical buckling pressure and buckling mode. Arterioles without supporting tissue (ks = 0) buckle into the base mode (n = 1) under increasing lumen pressure. However, with supporting tissue (ks = 0.5, 1 and 5 kPa), arterioles buckled into higher order mode shapes (Fig. 1b) and at higher critical pressures (Fig. 1a). Stronger supporting tissue (ks = 5) led to higher critical buckling pressures and higher wave shape modes in arterioles with the same axial growth ratio. For example, for the arteriole with the lumen radius 50 μm, wall thickness 10 μm, and length 10 mm, at axial growth ratio 10%, the critical buckling pressures were 15.3, 18.9, and 38.2 mmHg, and the corresponding wave modes were 18, 20, and 26 for ks = 0.5, 1, and 5 kPa, respectively.

3.3. Effect of arteriole radius growth on critical buckling

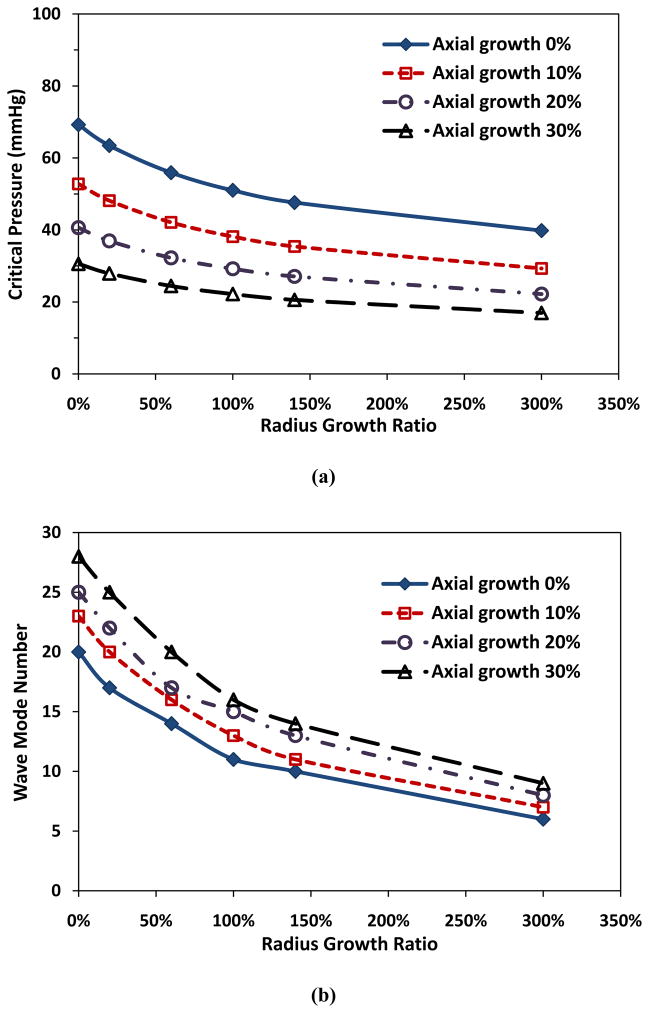
Radius growth of arterioles also reduced the critical pressure. For an arteriole maintaining a constant thickness, both the critical pressure and buckling wave number decreased with increasing radius growth ratio (Fig. 2). For example, at a given wall thickness t = 20 μm and axial growth ratio 10%, when arteriolar radius growth ratio increased from 0 to 3 (an increase of radius from 50 to 200 μm), the critical pressure pcr decreased from 52.8 to 29.3 mmHg, and buckling wave mode number changed from 23rd to 7th.

Figure 2.

Figure 2

Open in a new tab

Critical buckling pressure (a) and buckling mode (b) plotted as functions of arteriolar radius growth ratio at a constant wall thickness (t = 20 μm). Arteriole initial length l = 10 mm, initial lumen radius Ri = 50 μm, and ks = 5 kPa.

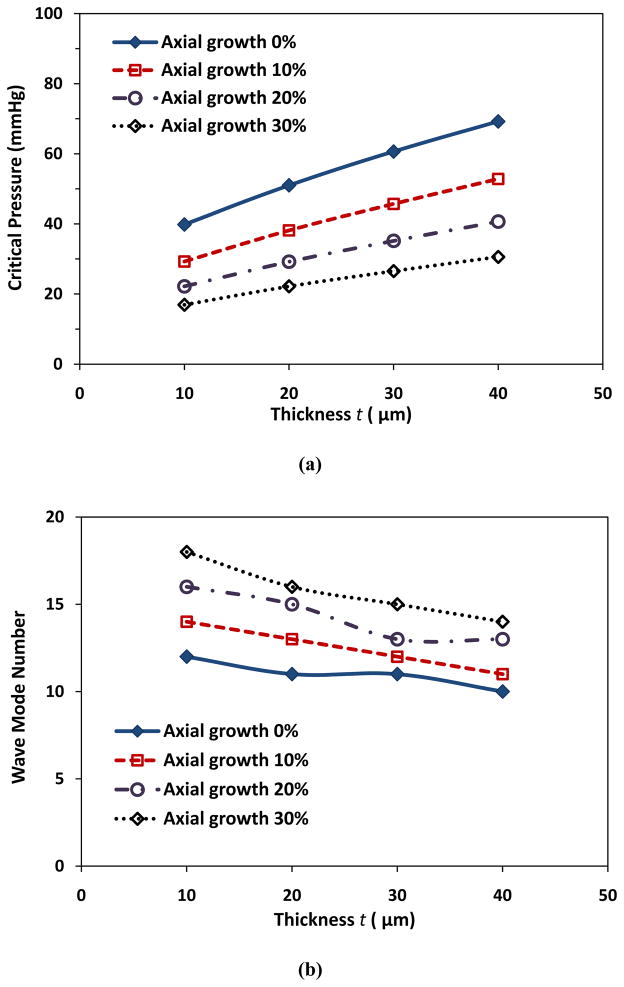
In addition, for a given radius growth ratio and axial growth ratio, the growth in wall thickness increased the critical pressure (Fig. 3a) and reduced the buckling wave mode number (Fig. 3b). For example, at a given lumen radius growth ratio of 2 (Ri = 100 μm) and axial growth ratio of 10%, with the increase of wall thickness from 10 to 40 μm, the critical buckling pressure increased from 29.3 to 52.8 mmHg and the corresponding buckling wave mode number decreased from 14th to 11th.

Figure 3.

Figure 3

Open in a new tab

Critical buckling pressure (a) and buckling mode (b) plotted as functions of wall thickness with constant lumen radius (Ri = 100 μm). Arteriole length l = 10 mm and ks = 5 kPa.

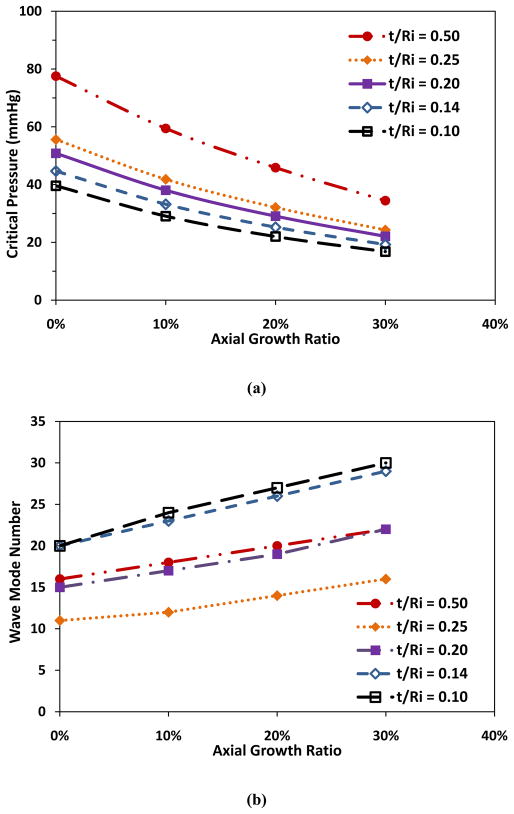
Having noticed the same critical pressure (52.8 mmHg) for the two vessels of the same wall thickness to radius ratio (but different thickness and radius), we further analyzed the effect of arteriole dimensions on the critical pressure. Our results demonstrated that the final remodeled wall thickness to lumen radius ratio t/Ri was a determinate parameter for the critical buckling pressure, though not the buckling mode shape (Fig. 4). Table 1 illustrates t/Ri values and types of remodeling at various changes in Ri and Re, as well as the corresponding wave modes. It is seen that the change of wave mode with t/Ri value was not monotonic but biphasic.

Figure 4.

Figure 4

Open in a new tab

comparison of critical buckling pressure (a) and buckling mode (b) plotted as functions of axial growth ratio at different t/Ri ratios. Arteriole Ri, t, and l were 50 μm, 10 μm, and 10 mm respectively, and ks = 5 kPa.

Table 1.

Arteriolar buckling modes under axial and radial growth, initial radius Ri = 50 μm, Re = 60 μm and length l=10 mm

Lumen Radius Growth Ratio Final Dimension Buckling Mode Number
Lumen Ri (μm) Outer Re (μm) t/Ri Remodeling Type Axial growth ratio
0% 10% 20% 30%
1.2 60 90 0.50 hypertrophic 16 18 20 22
1.5 75 90 0.20 hypertrophic 15 17 19 22
2 100 125 0.25 hypertrophic 11 12 14 16
1.2 60 68.6 0.14 eutrophic 20 23 26 29
1.2 60 66 0.10 hypotrophic 20 24 27 30
Open in a new tab

3.4. Effect of wall material property changes on critical buckling

To mimic the changes in material properties of collateral arteriolar walls, we considered the changes in material constant b0, which directly reflects the stiffness of arteries at all strain levels. Our results demonstrated that elevation of material stiffness increased the critical buckling pressures (Fig. 5). For example, at the same axial growth ratio of 10%, when the value of b0 (38.95 kPa) decreased to 0.5b0 (19.47 kPa) or increased to 2b0 (77.90 kPa), the critical pressure decreased to 30.9 mmHg or increased to 61.5 mmHg, respectively (Fig. 5a), and the corresponding buckling wave mode increased from 12th to 14th, or remained unchanged 12th, respectively (Fig. 5b).

Figure 5.

Figure 5

Open in a new tab

Comparison of critical buckling pressure (a) and buckling mode (b) plotted as functions of axial growth ratio at different arterial wall material properties (b0). Arteriole Ri,t, and l were 50 μm, 10 μm, and 10 mm respectively, and ks = 5 kPa.

4. Discussion

This study illustrated the relation between collateral arteriole growth/remodeling and mechanical buckling. Our results showed that arteriolar axial growth reduced the critical buckling pressure, making arterioles prone to buckling and consequently leading to tortuous collaterals. In addition, radius growth at a given wall thickness reduced the critical pressure, and wall thickening at a given radius elevated the critical pressure.

4.1 Effects of dimensional growth on critical pressure

The effects of dimensional growth on the critical buckling pressure can be explained using a buckling equation, which illustrated that arterial buckling pressure decreased with reduced axial stretch ratio and wall thickness to radius ratio (Han 2007; Han 2008; Han 2009).

First, axial growth reduced the axial stretch ratio of the arteriole since the distance between the up- and down-stream branching points of a collateral arteriole was restricted by the anatomic positions. Therefore, an arteriole with a higher axial growth ratio would have a lower stretch ratio and thus a lower critical buckling pressure. These results are consistent with the conclusion that the reduction of axial tension in rabbit carotid arteries led to tortuous arteries in a previous in vivo study (Jackson et al. 2005). The study also showed that the reduction of axial tension elevated the proliferation rates of both endothelial cells and smooth muscle cells. These results indicated that reduced axial tension may stimulate arteriole growth and remodeling, and suggested a possible dynamic feedback mechanism that needs to be investigated in the future.

Second, increasing arteriole radius at a given wall thickness reduced the wall thickness to radius ratio and thus reduced the critical buckling pressure making arterioles prone to buckling. Although the change of critical pressure with lumen radius is biphasic in general (Han 2007; Datir 2010), the critical pressure reduced monotonically in the radius growth range discussed (from 50 to 200 μm) for arterioles. On the other hand, wall thickening at a given radius increased the critical pressure. However, when arteriolar lumen radius and outer radius both increased at the same ratio, the wall thickness to radius ratio remained the same and the critical buckling pressure did not change. The critical buckling pressure increased only when the wall thickness increased at a higher ratio than the lumen radius did, i.e., when the ratio of wall thickness to lumen radius (t/Ri) increased. These results demonstrated that the determining parameter was the final wall thickness to lumen radius ratio, not the wall thickness per se (Han 2007; Han 2008; Han 2009).

One interesting finding of this study is that the radial growth of an arteriole alone, without any axial length change or wall thickening, would reduce the critical buckling pressure. Collateral arterioles both enlarge their diameters and elongate their lengths during remodeling. These combined radius and axial growths intensify the reduction in critical pressure. Thus collateral arterioles are very often seen to be tortuous.

4.2. Determination of matrix stiffness ks

Arterioles were surrounded by supporting tissue. Our simulation presumed that collateral arterioles did not buckle at the beginning of the remodeling, where the critical buckling pressure should be above the lumen pressure in the arterioles. After remodeling started, with the axial and/or radial growth, arterioles could buckle. The lumen pressure measured in collaterals after the ligation of the femoral artery was 30 – 40 mmHg (Chen et al. 1994; Unthank et al. 1995; Unthank et al. 1996). Therefore, a matrix stiffness ks = 5 kPa was used in the simulations so that the estimated critical buckling pressure (51.0 mmHg) of the arteriole was above the normal pressure. The critical buckling pressure dropped below the normal pressure at various axial and radius growth ratios. While further studies are needed to determine the actual stiffness that may vary depending on the surrounding matrix, we expect that the trend demonstrated by our simulation will remain similar.

4.3. Estimation of buckling wave mode number

The non-monotonic change of buckling wave modes with t/Ri ratio could be explained using the theoretical equation for buckling wave mode number n (Han 2009)

n2(n+1)2=ksEI(lπ)4 (4)

Approximating I = πR3t for cylindrical arterioles and assuming E is a constant yield

n≈lπRiksEπ41t/Ri4 (5)

It is seen that wave mode number n is not determined by t/Ri ratio alone but by both t and Ri. For arterioles with constant thickness t, the wave mode number decreased with the increase of Ri (decrease of t/Ri). For arterioles with constant Ri, the wave mode number decreased with the increase of t (increase of t/Ri).

4.4. Model limitations

A limitation of current study is that the supporting tissue was assumed to be linear elastic. The linear elastic matrix assumption was used due to its simplicity and to be consistent with our previous study (Han 2009). Since arterioles had very small lateral deflection when buckling occurred initially, the reaction force generated by the matrix could be assumed to be linearly related to the deflection. Thus, the linear elastic matrix assumption was reasonable. In addition, the comparison of the critical buckling of arterioles at different axial and radial growth ratios was done for linear elastic matrix of the same stiffness. So we expected that the linear elastic matrix assumption did not affect the overall conclusion.

Another assumption was that arteriole growth was axially and circumferentially uniform. The newly-grown parts did not change the uniformity of the whole vessel. Even though previous simulation results showed that geometric variations could slightly reduce or increase the buckling pressure (Datir 2010), the effects of these imperfections were expected to be small.

Our simulations showed that changes in the mechanical properties affect the critical pressure and wave mode. However, it is unclear how changes in mechanical properties of the arteriole wall are associated with axial growth or radial growth. A previous study demonstrated that the stiffness of arterioles increased ~25% during the development of diabetes (Liu and Fung 1992). Our simulations showed that a 2-fold increase in stiffness (b0) increased pcr by ~50% at each axial growth ratio, and a 25% increase in stiffness might only increase pcr by approximately 2 – 3 mmHg. Further studies are needed to experimentally measure the material properties of collateral arterioles during the remodeling process.

4.5. Clinical relevance

Collateral arterioles expand in diameter to increase blood flow to the ischemic tissue after a main artery is occluded. The increased flow increases fluid shear stress, which has been considered as a trigger for collateral growth through a complex signaling process involving monocyte chemotactic protein-1 (MCP-1), angiotension, vascular endothelial growth factor, which results in increased monocyte deposition, cell proliferation, and matrix metalloproteinase activities (Ito et al. 1997; Shireman 2007; van Royen et al. 2009). Growth of collateral arterioles could result in axial growth (elongation), which reduces the axial tension in the arterioles and often makes collateral arterioles tortuous. Reduction in axial tension could further stimulate cell proliferation and generate tortuosity (Jackson et al. 2005; Lee et al. 2012). However, the maximal flow can only be partially recovered by collateral arterioles (Lazarous et al. 1996). One possible reason is the increase of flow resistance due to the development of tortuosity in collateral arterioles (Heil and Schaper 2004; Eitenmuller et al. 2006). Although the molecular mechanisms that stimulate and regulate arteriole growth still remain to be investigated, the current model helps us to understand the formation of the tortuous shape in the process. Our results also suggest that raising the critical buckling pressure of the arteriole, by changing the wall material property (stiffening the wall) or stiffening the supporting matrix, will make the arteriole more stable. This is consistent with previous reports that showed enhancing tissue support would prevent vessel tortuosity (Lu et al. 1993; Han et al. 1998; Hamza et al. 2003). Our study sheds new light on the mechanism of the development of tortuous collaterals.

On the other hand, buckling of arterioles could be beneficial. For people with α–thalassemia disease where more muscle tissue oxygenation is wanted (Vincent et al. 2010), increasing capillary tortuosity may increase the contact area of capillaries to tissue (Goldman and Popel 2000; Charifi et al. 2004). Factors that reduce the critical buckling pressure in the capillary would be potential targets for treatment.

In conclusion, growth and remodeling in arterioles can lead to mechanical buckling. Arteriole buckling pressure decreases with axial growth, but increases with increasing wall thickness to lumen radius ratio. Arteriolar buckling mode number increases with axial growth, but decreases with increasing radius and wall thickness. Collateral arterioles become prone to buckling with growth in radius and axial length, which could be a mechanism for the development of tortuous collaterals.

Understanding the mechanisms of tortuosity initiation and development in the microvasculature has wide implications in vascular physiology and pathology, as well as in tissue regeneration. This understanding will help us to develop new approaches for the prevention and treatment (reduction or augmentation) of arteriolar tortuosity.

Highlights.

  • We modeled arteriole buckling behavior associated with growth and remodeling

  • Arteriole length growth decreases the buckling pressure and buckling wave length

  • Radius growth decreases the buckling pressure but increases buckling wave length

  • Increasing wall thickness increases the buckling pressure and buckling wave length

  • Adaptive growth makes arterioles prone to buckling & leads to tortuous collaterals

Acknowledgments

This work was supported by CAREER award #0644646 from the National Science Foundation and grant R01HL095852 from the National Institutes of Health.

Footnotes

Conflict of interest statement

The authors have no conflict of interest.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bullitt E, Zeng D, Gerig G, Aylward S, Joshi S, Smith JK, Lin W, Ewend MG. Vessel tortuosity and brain tumor malignancy: A blinded study. Acad Radiol. 2005;12(10):1232–40. doi: 10.1016/j.acra.2005.05.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Cai WJ, Koltai S, Kocsis E, Scholz D, Kostin S, Luo X, Schaper W, Schaper J. Remodeling of the adventitia during coronary arteriogenesis. Am J Physiol Heart Circ Physiol. 2003;284(1):H31–40. doi: 10.1152/ajpheart.00478.2002. [DOI] [PubMed] [Google Scholar]
  3. Callewaert BL, Willaert A, Kerstjens-Frederikse WS, De Backer J, Devriendt K, Albrecht B, Ramos-Arroyo MA, Doco-Fenzy M, Hennekam RC, Pyeritz RE, Krogmann ON, Gillessen-kaesbach G, Wakeling EL, Nik-zainal S, Francannet C, Mauran P, Booth C, Barrow M, Dekens R, Loeys BL, Coucke PJ, De Paepe AM. Arterial tortuosity syndrome: Clinical and molecular findings in 12 newly identified families. Hum Mutat. 2008;29(1):150–8. doi: 10.1002/humu.20623. [DOI] [PubMed] [Google Scholar]
  4. Charifi N, Kadi F, Feasson L, Costes F, Geyssant A, Denis C. Enhancement of microvessel tortuosity in the vastus lateralis muscle of old men in response to endurance training. J Physiol. 2004;554(Pt 2):559–69. doi: 10.1113/jphysiol.2003.046953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chen DS, Gu YD, Su YC. [distal blood pressure changes after ligation of the femoral artery or vein in the rat] Zhonghua Wai Ke Za Zhi. 1994;32(6):374–5. [PubMed] [Google Scholar]
  6. Chesnutt JK, Han HC. Tortuosity triggers platelet activation and thrombus formation in microvessels. J Biomech Eng. 2011;133(12):121004. doi: 10.1115/1.4005478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Datir P, Lee AY, Lamm SD, Han HC. Effect of geometric variations on the vuckling of arteries. Int J Appl Mech. 2010;3(2):385–406. doi: 10.1142/S1758825111001044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Del Corso L, Moruzzo D, Conte B, Agelli M, Romanelli AM, Pastine F, Protti M, Pentimone F, Baggiani G. Tortuosity, kinking, and coiling of the carotid artery: Expression of atherosclerosis or aging? Angiology. 1998;49(5):361–71. doi: 10.1177/000331979804900505. [DOI] [PubMed] [Google Scholar]
  9. Dobrin PB, Schwarcz TH, Baker WH. Mechanisms of arterial and aneurysmal tortuosity. Surgery. 1988;104(3):568–71. [PubMed] [Google Scholar]
  10. Eitenmuller I, Volger O, Kluge A, Troidl K, Barancik M, Cai WJ, Heil M, Pipp F, Fischer S, Horrevoets AJ, Schmitz-Rixen T, Schaper W. The range of adaptation by collateral vessels after femoral artery occlusion. Circ Res. 2006;99(6):656–62. doi: 10.1161/01.RES.0000242560.77512.dd. [DOI] [PubMed] [Google Scholar]
  11. Fung YC. Biomechanics: Motion, flow, stress, and growth. New York: Springer-Verlag; 1990. [Google Scholar]
  12. Fung YC. Biomechanics: Mechanical properties of living tissues. New York: Springer-Verlag; 1993. [Google Scholar]
  13. Goldman D, Popel AS. A computational study of the effect of capillary network anastomoses and tortuosity on oxygen transport. J Theor Biol. 2000;206(2):181–94. doi: 10.1006/jtbi.2000.2113. [DOI] [PubMed] [Google Scholar]
  14. Gore RW. Pressures in cat mesenteric arterioles and capillaries during changes in systemic arterial blood pressure. Circ Res. 1974;34(4):581–91. doi: 10.1161/01.res.34.4.581. [DOI] [PubMed] [Google Scholar]
  15. Hamza LH, Dang Q, Lu X, Mian A, Molloi S, Kassab GS. Effect of passive myocardium on the compliance of porcine coronary arteries. Am J Physiol Heart Circ Physiol. 2003;285(2):H653–60. doi: 10.1152/ajpheart.00090.2003. [DOI] [PubMed] [Google Scholar]
  16. Han HC. A biomechanical model of artery buckling. J Biomech. 2007;40(16):3672–8. doi: 10.1016/j.jbiomech.2007.06.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Han HC. Nonlinear buckling of blood vessels: A theoretical study. J Biomech. 2008;41(12):2708–13. doi: 10.1016/j.jbiomech.2008.06.012. [DOI] [PubMed] [Google Scholar]
  18. Han HC. Blood vessel buckling within soft surrounding tissue generates tortuosity. J Biomech. 2009;42(16):2797–801. doi: 10.1016/j.jbiomech.2009.07.033. [DOI] [PubMed] [Google Scholar]
  19. Han HC. Determination of the critical buckling pressure of blood vessels using the energy approach. Ann Biomed Eng. 2011;39(3):1032–40. doi: 10.1007/s10439-010-0212-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Han HC. Twisted blood vessels: Symptoms, etiology and biomechanical mechanisms. J Vasc Res. 2012;49(3):185–197. doi: 10.1159/000335123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Han HC, Zhao L, Huang M, Hou LS, Huang YT, Kuang ZB. Postsurgical changes of the opening angle of canine autogenous vein graft. J Biomech Eng. 1998;120(2):211–6. doi: 10.1115/1.2798304. [DOI] [PubMed] [Google Scholar]
  22. Heil M, Schaper W. Influence of mechanical, cellular, and molecular factors on collateral artery growth (arteriogenesis) Circ Res. 2004;95(5):449–58. doi: 10.1161/01.RES.0000141145.78900.44. [DOI] [PubMed] [Google Scholar]
  23. Herzog S, Sager H, Khmelevski E, Deylig A, Ito WD. Collateral arteries grow from preexisting anastomoses in the rat hindlimb. Am J Physiol Heart Circ Physiol. 2002;283(5):H2012–20. doi: 10.1152/ajpheart.00257.2002. [DOI] [PubMed] [Google Scholar]
  24. Hiroki M, Miyashita K, Oda M. Tortuosity of the white matter medullary arterioles is related to the severity of hypertension. Cerebrovasc Dis. 2002;13(4):242–50. doi: 10.1159/000057850. [DOI] [PubMed] [Google Scholar]
  25. Humphrey JD. Cardiovascular solid mechanics: Cells, tissues, and organs. New York: Springer; 2002. [Google Scholar]
  26. Ito WD, Arras M, Winkler B, Scholz D, Schaper J, Schaper W. Monocyte chemotactic protein-1 increases collateral and peripheral conductance after femoral artery occlusion. Circ Res. 1997;80(6):829–37. doi: 10.1161/01.res.80.6.829. [DOI] [PubMed] [Google Scholar]
  27. Jackson ZS, Dajnowiec D, Gotlieb AI, Langille BL. Partial off-loading of longitudinal tension induces arterial tortuosity. Arterioscler Thromb Vasc Biol. 2005;25(5):957–62. doi: 10.1161/01.ATV.0000161277.46464.11. [DOI] [PubMed] [Google Scholar]
  28. Lazarous DF, Shou M, Scheinowitz M, Hodge E, Thirumurti V, Kitsiou AN, Stiber JA, Lobo AD, Hunsberger S, Guetta E, Epstein SE, Unger EF. Comparative effects of basic fibroblast growth factor and vascular endothelial growth factor on coronary collateral development and the arterial response to injury. Circulation. 1996;94(5):1074–82. doi: 10.1161/01.cir.94.5.1074. [DOI] [PubMed] [Google Scholar]
  29. Lee AY, Han B, Lamm SD, Fierro CA, Han HC. Effects of elastin degradation and surrounding matrix support on artery stability. Am J Physiol Heart Circ Physiol. 2012;302(4):H873–84. doi: 10.1152/ajpheart.00463.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Liu Q, Han HC. Mechanical buckling of artery under pulsatile pressure. J Biomech. 2012;45(7):1192–8. doi: 10.1016/j.jbiomech.2012.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Liu Q, Mirc D, Fu BM. Mechanical mechanisms of thrombosis in intact bent microvessels of rat mesentery. J Biomech. 2008;41(12):2726–34. doi: 10.1016/j.jbiomech.2008.06.013. [DOI] [PubMed] [Google Scholar]
  32. Liu SQ, Fung YC. Influence of stz-induced diabetes on zero-stress states of rat pulmonary and systemic arteries. Diabetes. 1992;41(2):136–46. doi: 10.2337/diab.41.2.136. [DOI] [PubMed] [Google Scholar]
  33. Lu Y, Huang Y, Zhao L, Li R, Shi K, Ma P, Chu X. Management of major arterial injuries of limbs: A study of 166 cases. Cardiovasc Surg. 1993;1(5):486–8. [Google Scholar]
  34. Mulvany MJ. Vascular remodelling of resistance vessels: Can we define this? Cardiovasc Res. 1999;41(1):9–13. doi: 10.1016/s0008-6363(98)00289-2. [DOI] [PubMed] [Google Scholar]
  35. Pancera P, Ribul M, Presciuttini B, Lechi A. Prevalence of carotid artery kinking in 590 consecutive subjects evaluated by echocolordoppler. Is there a correlation with arterial hypertension? J Intern Med. 2000;248(1):7–12. doi: 10.1046/j.1365-2796.2000.00611.x. [DOI] [PubMed] [Google Scholar]
  36. Pries AR, Cornelissen AJ, Sloot AA, Hinkeldey M, Dreher MR, Hopfner M, Dewhirst MW, Secomb TW. Structural adaptation and heterogeneity of normal and tumor microvascular networks. PLoS Comput Biol. 2009;5(5):e1000394. doi: 10.1371/journal.pcbi.1000394. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Schaper W, Buschmann I. Arteriogenesis, the good and bad of it. Eur Heart J. 1999;20(18):1297–9. doi: 10.1053/euhj.1999.1686. [DOI] [PubMed] [Google Scholar]
  38. Shireman PK. The chemokine system in arteriogenesis and hind limb ischemia. J Vasc Surg. 2007;45(Suppl A):A48–56. doi: 10.1016/j.jvs.2007.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Shireman PK, Quinones MP. Differential necrosis despite similar perfusion in mouse strains after ischemia. J Surg Res. 2005;129(2):242–50. doi: 10.1016/j.jss.2005.06.013. [DOI] [PubMed] [Google Scholar]
  40. Smedby O, Bergstrand L. Tortuosity and atherosclerosis in the femoral artery: What is cause and what is effect? Ann Biomed Eng. 1996;24(4):474–80. doi: 10.1007/BF02648109. [DOI] [PubMed] [Google Scholar]
  41. Thore CR, Anstrom JA, Moody DM, Challa VR, Marion MC, Brown WR. Morphometric analysis of arteriolar tortuosity in human cerebral white matter of preterm, young, and aged subjects. J Neuropathol Exp Neurol. 2007;66(5):337–45. doi: 10.1097/nen.0b013e3180537147. [DOI] [PubMed] [Google Scholar]
  42. Unthank JL, Nixon JC, Burkhart HM, Fath SW, Dalsing MC. Early collateral and microvascular adaptations to intestinal artery occlusion in rat. Am J Physiol. 1996;271(3 Pt 2):H914–23. doi: 10.1152/ajpheart.1996.271.3.H914. [DOI] [PubMed] [Google Scholar]
  43. Unthank JL, Nixon JC, Lash JM. Early adaptations in collateral and microvascular resistances after ligation of the rat femoral artery. J Appl Physiol. 1995;79(1):73–82. doi: 10.1152/jappl.1995.79.1.73. [DOI] [PubMed] [Google Scholar]
  44. Vakoc BJ, Lanning RM, Tyrrell JA, Padera TP, Bartlett LA, Stylianopoulos T, Munn LL, Tearney GJ, Fukumura D, Jain RK, Bouma BE. Three-dimensional microscopy of the tumor microenvironment in vivo using optical frequency domain imaging. Nat Med. 2009;15(10):1219–23. doi: 10.1038/nm.1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. van Royen N, Piek JJ, Schaper W, Fulton WF. A critical review of clinical arteriogenesis research. J Am Coll Cardiol. 2009;55(1):17–25. doi: 10.1016/j.jacc.2009.06.058. [DOI] [PubMed] [Google Scholar]
  46. Vincent L, Feasson L, Oyono-Enguelle S, Banimbek V, Denis C, Guarneri C, Aufradet E, Monchanin G, Martin C, Gozal D, Dohbobga M, Wouassi D, Garet M, Thiriet P, Messonnier L. Remodeling of skeletal muscle microvasculature in sickle cell trait and alpha-thalassemia. Am J Physiol Heart Circ Physiol. 2010;298(2):H375–84. doi: 10.1152/ajpheart.00812.2009. [DOI] [PubMed] [Google Scholar]
  47. Wagenseil JE, Nerurkar NL, Knutsen RH, Okamoto RJ, Li DY, Mecham RP. Effects of elastin haploinsufficiency on the mechanical behavior of mouse arteries. Am J Physiol Heart Circ Physiol. 2005;289(3):H1209–17. doi: 10.1152/ajpheart.00046.2005. [DOI] [PubMed] [Google Scholar]

RESOURCES