Multi-GPU Jacobian Accelerated Computing for Soft Field Tomography

Abstract

Image reconstruction in soft-field tomography is based on an inverse problem formulation, where a forward model is fitted to the data. In medical applications, where the anatomy presents complex shapes, it is common to use Finite Element Models to represent the volume of interest and to solve a partial differential equation that models the physics of the system. Over the last decade, there has been a shifting interest from 2D modeling to 3D modeling, as the underlying physics of most problems are three-dimensional. Though the increased computational power of modern computers allows working with much larger FEM models, the computational time required to reconstruct 3D images on a fine 3D FEM model can be significant, on the order of hours. For example, in Electrical Impedance Tomography applications using a dense 3D FEM mesh with half a million elements, a single reconstruction iteration takes approximately 15 to 20 minutes with optimized routines running on a modern multi-core PC. It is desirable to accelerate image reconstruction to enable researchers to more easily and rapidly explore data and reconstruction parameters. Further, providing high-speed reconstructions are essential for some promising clinical application of EIT. For 3D problems 70% of the computing time is spent building the Jacobian matrix, and 25% of the time in forward solving. In the present work, we focus on accelerating the Jacobian computation by using single and multiple GPUs. First, we discuss an optimized implementation on a modern multi-core PC architecture and show how computing time is bounded by the CPU-to-memory bandwidth; this factor limits the rate at which data can be fetched by the CPU. Gains associated with use of multiple CPU cores are minimal, since data operands cannot be fetched fast enough to saturate the processing power of even a single CPU core. GPUs have a much faster memory bandwidths compared to CPUs and better parallelism. We are able to obtain acceleration factors of 20 times on a single NVIDIA S1070 GPU, and of 50 times on 4 GPUs, bringing the Jacobian computing time for a fine 3D mesh from 12 minutes to 14 seconds. We regard this as an important step towards gaining interactive reconstruction times in 3D imaging, particularly when coupled in the future with acceleration of the forward problem. While we demonstrate results for Electrical Impedance Tomography, these results apply to any soft-field imaging modality where the Jacobian matrix is computed with the Adjoint Method.

1. Introduction

Soft field tomographic techniques are based on the application of a sensing field to an anatomic region of the body and on measuring responses to this field. Processing of these responses allows reconstructing the distribution of physical properties inside a volume of interest. Examples of such tomographic techniques are: Electrical Impedance Tomography (EIT) (Holder 2004), Microwave Tomography (MWT) (Rubk et al. 2007), and Diffuse Optical Tomography (DOT) (Boas et al. 2001). In EIT, for example, a set of electrodes attached to the body are used for injecting low intensity, low frequency alternating currents. Potential differences that result at the electrodes from these excitations are recorded. In MWT, a set of antennas is used to impose an electromagnetic field on the body, and these same antennas are used for sensing scattered responses. In DOT, a set of optic fibers is used for shining infrared light on parts of the body, and the same optic fibers are used for sensing the light scattered by the tissues. Image reconstruction for soft-field tomography is usually based on an inverse problem formulation, where a model of the anatomical region of interest is constructed, the Partial Differential Equation (PDE) describing the physics of the method is solved by standard numerical techniques, and the computed fields are fitted to the measured ones by iterative regularized least squares formulations. In practice algorithms are typically based on the Gauss-Netwon method (Polydorides & Lionheart 2002) (De Zaeytijd et al. 2007) (Schweiger et al. 2005), which requires three main steps: forward solving, computing the Jacobian matrix that maps the model parameters to measured data, and computing the update of the model parameters.

While use of Graphic Processing Units (GPUs) as a computing medium in other medical imaging modalities such Magnetic Resonance Imaging (MRI) (Stone et al. 2008), Computed Tomography (CT) imaging (Jia et al. 2010), and in medical physics in general (Pratx & Xing 2011) has been explored in numerous works, this technology has been explored much less in soft-field tomography. Image reconstruction in MRI and CT is highly parallelizable and lends itself particularly well to direct implementation on GPUs, while algorithms for soft-field tomography do not necessarily present this peculiarity. Two works are known in soft-field literature, the work of Fang et. al. (Fang & Boas 2009) where the forward problem in DOT is solved by Markov Chain Monte Carlo (MCMC) approaches on graphic processing units, and the work by Schweiger (Schweiger 2011), where linear systems arising from the FEM discretization of the forward model are solved with iterative methods on GPUs. In the field of Microwave Imaging no known work is specifically focused on tomographic reconstruction. However, there is significant industrial interest in speeding up the solution of the Maxwell equations; the work of Klöckner et. al. is an example in which Discontinuous Galerkin methods are used for solving the time-domain Maxwell equations on GPUs. In the specific field of EIT, early examples of parallelized reconstruction algorithms based on the use of Transputer networks have been suggested. For example, in (Smith et al. 1995) a network of four transputers was used to speed up image reconstruction and data acquisition control. Similar unpublished work was conducted by researchers at Oxford Brookes University. These early works date to the mid 90s and were directed at 2D reconstruction. The availability of more and more powerful Central Processing Units (CPUs) in the late 90s and early 2000s provided enough computing power for solving 2D problems quickly, and transputer technologies were later abandoned in favor of the simplicity offered by traditional programming on CPUs. The interest in using parallel architectures has again become important as dense 3D forward FEM meshes have been shown to be critical for accurately modeling arbitrary tissue geometries; this has significantly increased the demand for more computing power.

In certain clinical applications of EIT, difference imaging is used (e.g. lung imaging); this is a technique in which the forward solution and the Jacobian are computed once and then stored for later use. Conversely, absolute imaging applications (e.g. cancer imaging) require that the forward solution and Jacobian be computed at each iteration of a multi-iteration reconstruction algorithm; therefore, speeding up these computations is critical for achieving a close to real-time imaging modality. The current trend in clinical applications of EIT is to use patient-specific Finite Element Method (FEM) meshes to solve the forward problem, since this is an important aspect in improving the accuracy of the forward solution (Gibson et al. 2003) (Bayford et al. 2008) (Tizzard et al. 2010) (Forsyth et al. 2011). When patient specific meshes are produced, forward solutions and Jacobian need to be computed for each patient, irrespective of whether the reconstruction is absolute or difference-based. Therefore, the ability to quickly compute the Jacobian matrix for dense 3D meshes is becoming more and more desirable for clinical applications of EIT.

In the present paper we focus on speeding up the Jacobian computation, which in our framework for image reconstruction is the step that takes the longest; we also show that this parallelizes well on GPUs. For the soft-field techniques mentioned above, EIT, MWT, and DOT, and possibly in others, the Jacobian is computed in a very similar fashion, with what is called the Adjoint Method (Polydorides & Lionheart 2002), (El-Shenawee et al. 2009), (Arridge & Schweiger 1995). This method involves computing point-by-point in the imaging volume the dot product of two fields and integrating this product over the elements that form the image. While not a complex computation, this step consumes the majority of computing time spent in image reconstruction; this is especially true if the problem is large. As an example in EIT, Borsic (Borsic et al. 2008) showed that, for 3D FEM forward models with 300,000 to 750,000 elements, the time spent constructing the Jacobian is approximately 70% of the total computing time, and that this proportion increases with the problem size. Speeding up the computation of the Jacobian is therefore desirable, as the overall performance of reconstruction algorithms can be increased significantly.

Methods for speeding up the Jacobian, on traditional computing architectures in the context of EIT have been considered for example in (Graham & Adler 2006) and (Borsic et al. 2008). In (Borsic et al. 2008) multithreaded optimizations have been pursued both for the forward solving phase and for the Jacobian computation, and shown to reduce computing times by up to 7.6 times.

In this manuscript, we consider further methods for increasing the speed of the Jacobian computation. Firstly, we show how the Jacobian computation time is bound on PCs by the memory bandwidth between the Random Access Memory (RAM) and the CPU, and how this limits scalability with multicore platforms: using multiple cores in the computation of the Jacobian produces very marginal speed gains. Secondly, we consider computing the Jacobian on Graphic Processing Units (GPUs). GPUs are computing architectures that have been optimized for video-gaming performance, to the point that their raw-computing power and other characteristics are far superior, for certain tasks, to CPUs. In the last 5 years use of GPUs for scientific computing has been successfully considered and significant performance gains have been demonstrated (Nickolls & Dally 2010).

In Section 2.1 we introduce Electrical Impedance Tomography (EIT) as an example problem and discuss how the Jacobian matrix is computed. In Section 3 we discuss the optimized computation of the Jacobian on a CPU and consider factors that limit further speed-up. In Section 4 we discuss the use of single and multiple GPUs for computing the Jacobian matrix, which results in significant performance gains. Finally, we comment on results and future work. While traditional PC architectures have been considered for parallelization of EIT reconstruction, to the best of our knowledge no other work on the use of GPUs in the field of EIT is known at this stage.

2. Image Reconstruction in Electrical Impedance Tomography

2.1. Forward Model

We briefly outline in this section how images are reconstructed in Electrical Impedance Tomography. Besides the PDE which describes the physics of the problem, similar methods are used in MWT and DOT (De Zaeytijd et al. 2007) (Schweiger et al. 2005).

The forward problem is modeled with a low-frequency approximation, where the electric field is considered conservative and the conduction currents dominant with respect to the displacement currents; this leads to the following partial differential equation:

$$\nabla ·\sigma \nabla u=0\text{on}\mathrm{\Omega }$$ (1)

where σ is the conductivity or admittivity of the body to be imaged, u is the electric potential, and Ω the body to be imaged. Electrodes are modeled using the Complete Electrode Model (Somersalo et al. 1992), resulting in the following boundary condition for each portion of the boundary ∂Ω_ℓ underneath electrode ℓ:

$${\int }_{\partial {\mathrm{\Omega }}_{\ell }}\sigma \frac{\partial u}{\partial \mathbf{n}}=I_{\ell }\ell =1\dots \text{L}$$ (2)

where I_ℓ is the current injected at electrode ℓ and L is the number of electrodes. The electrode currents resulting from the applied voltages are calculated by integrating the current density over the surface of each electrode ℓ. Also the following condition applies:

$$u+z_c\sigma \frac{\partial u}{\partial \mathbf{n}}=V_{\ell }\text{on}\partial {\mathrm{\Omega }}_{\ell }\ell =1\dots \text{L}$$ (3)

where z_c is the contact impedance and V_ℓ is the potential that develops at electrode ℓ. Underneath inter-electrode gaps, the following boundary condition is applied:

$$\frac{\partial u}{\partial \mathbf{n}}=0\text{on}\partial \mathrm{\Omega }\backslash \{\partial {\mathrm{\Omega }}_1\cup \dots \cup \partial {\mathrm{\Omega }}_{\text{L}}\}$$ (4)

Equations (1) to (4) can be used to compute the electrode voltages V_ℓ for any given conductivity distribution σ, and usually are solved with the Finite Element Method (FEM).

2.2. Parameter Estimation

Reconstruction in EIT is commonly formulated as a standard non–linear Least Squares, Tikhonov regularized inversion, based on a finite element implementation of the forward model (Holder 2004) as:

$${\mathit{\sigma }}_{\mathit{rec}}=arg\underset{\mathit{\sigma }}{min}\frac{1}{2}{\left|\right|\mathbf{V}(\mathbf{\sigma })-{\mathbf{V}}_{\text{meas}}\left|\right|}^2+\alpha \frac{1}{2}{\left|\right|L(\mathit{\sigma }-{\mathit{\sigma }}^{\ast })\left|\right|}^2$$ (5)

where, having discretized the imaging domain, σ is a vector of conductivities (admittivities for the complex valued case). Specifically, σ_rec is the vector of the reconstructed conductivities, V(σ) is the vector of electrode voltages resulting from the forward solver, V_meas is the vector of measured electrode voltages, α is the Tikhonov factor, L is a regularization matrix and σ^* is the initial conductivity distribution. The application of the Gauss Newton method to (5) results in the iterative formula:

$$\delta {\mathit{\sigma }}_n=-{(J_n^T{J}_n+\alpha L^{T}L)}^{-1}[J_n^T(\mathbf{V}({\mathit{\sigma }}_n)-{\mathbf{V}}_{\text{meas}})-\alpha L^{T}L({\mathit{\sigma }}_n-{\mathit{\sigma }}^{\ast })]$$ (6)

where n is the iteration number, δσ_n is the conductivity update iteration n, and J_n is the Jacobian of the forward operator V(σ) calculated for σ = σ_n, and L a regularization matrix. The conductivity is updated as:

$${\mathit{\sigma }}_{n+1}={\sigma }_n+\beta \delta {\mathit{\sigma }}_n$$ (7)

where β is a scalar value resulting from a line search procedure (Gill et al. 1982). Equation 6 is solved iteratively, updating the forward solution V(σ_n), the Jacobian matrix, and the update δσ_n at each cycle. Since computing the Jacobian matrix consumes approximately 70% of the total time, we concentrate on accelerating this step. The next session briefly discusses how the Jacobian matrix is computed, followed by a discussion of how its implementation can be optimized on CPUs and GPUs.

2.3. Computating the Jacobian Matrix

The element J_(i,j) of the Jacobian matrix J is defined as $J_{(i,j)}=\frac{\partial V_{(i)}}{\partial {\mathit{\sigma }}_{(j)}}$, where V_(i) is the i-th measured potential and σ_(j) the j-th discrete conductivity element of the imaging domain. Considering a tetrapolar imaging EIT system, which are the most common, the measurement ∂V_(i) would result from the application of a current between an electrode pair (m, n) and from sensing a potential difference at electrodes (k, p). With this convection the Jacobian matrix can be computed efficiently by what is called the Adjoint Method (Polydorides & Lionheart 2002) (De Zaeytijd et al. 2007) (Schweiger et al. 2005):

$$J(i,j)={\int }_{\mathrm{\Omega }}{\psi }_j{\mathbf{E}}_{\mathit{applied}}(m,n)·{\mathbf{E}}_{\mathit{lead}}(k,p)$$ (8)

where E_applied(m, n) is the electric field applied to the body by the current injection electrode pair (m, n) during the i-th measurement, and E_lead(i) is the lead field, or the field that would result from the application of a unit current stimulus to the electrode pair (k, p) which is used for sensing the i-th voltage difference; ψ_j is the characteristic function that describes the support of the conductivity element σ_(j).

It is common in EIT to use the Finite Element Method to solve the forward problem. Generally first order elements are used, where the electric potential u is piecewise linear, the resulting electric fields E_applied(m, n) and E_lead(k, p) are piecewise constant, and the conductivity vector, σ, stores the conductivity value of each tetrahedra. In this case, the Jacobian is simply computed as:

$$J(i,j)={\mathcal{T}}_j{\mathbf{E}}_{\mathit{applied}}{(m,n)}_j·{\mathbf{E}}_{\mathit{lead}}{(k,p)}_j$$ (9)

where 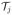is the volume of the j-th FEM tetrahedra corresponding to the j-th conductivity element σ_(j), and E_applied(m, n)_j and E_lead(k, p)_j are the values of the applied and lead fields on the j-th element of the mesh.

A whole row of the Jacobian can thus be computed as:

$$J_i=T[E_{\mathit{applied}}^x(m,n)\ast E_{\mathit{lead}}^x(k,p)+E_{\mathit{applied}}^y(m,n)\ast E_{\mathit{lead}}^y(k,p)+E_{\mathit{applied}}^z(m,n)\ast E_{\mathit{lead}}^z(k,p)]$$ (10)

where T is a diagonal matrix holding the tetrahedra volumes 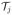of the mesh elements, E^x, E^y and E^z are the vectors holding the x, y, and z components of the electric fields on each element of the mesh, and the symbol “*” indicates the element–wise vector product. For real valued problems, the above computation involves 3 vector-wise products and a diagonal matrix multiplication. For complex valued problems real and imaginary parts of the fields have to be considered; this results in 12 vector-wise products and a diagonal matrix multiplication.

Often in tomography applications it is useful to use a fine grid for computing the fields, and a coarse grid on which the inverse parameters are estimated. A fine grid, with hundreds of thousands or millions of elements, enables accurate forward computations, while use of a coarse grid reduces the number of inverse parameters to be estimated to a few thousands. In this case, the Jacobian on the coarse grid is still computed row-by-row with (10) on the fine grid, and then projected on the coarse grid as $J_i^c=J_{i}P$, where $J_i^c$ is a row of the coarse Jacobian and P is a sparse matrix that describes the interpolation between the two grids. Apart from the multiplications by T and P, which are very sparse, the bulk of the Jacobian computation is determined by the element-wise products of the vectors holding the electric fields. This product can be optimized on CPUs, however certain limits exist on the maximum achievable speed-ups.

3. Optimizing Jacobian Computation on CPUs and Performance Limits

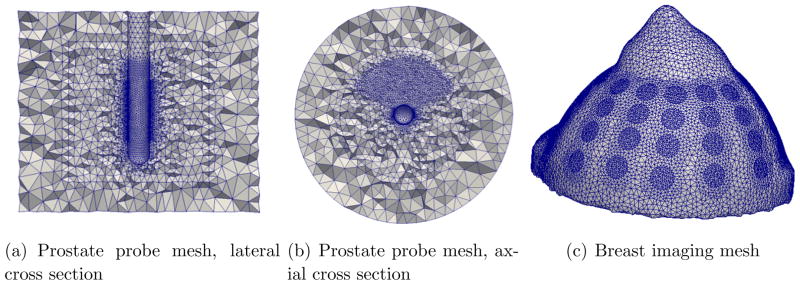
Despite the simplicity of the operations involved in (10), the computation of the Jacobian is the most expensive step in image reconstruction (Borsic et al. 2008) (Boyle et al. 2012). We consider a numerical test case related to an EIT imaging application: a fine 3D mesh with 97,973 nodes and 541,604 elements is used for forward modeling, and 2430 potential measurements are collected in the experiment, which is representative for 3D EIT imaging. Figures 1(a) and 1(b) show this mesh, which we use in the numerical experiments, and Figure 1(c) shows a second representative example of meshes being used in 3D EIT - a breast mesh with approximately 500,000 tetrahedral elements.

Figure 1.

The above figure illustrates two meshes used in 3D EIT imaging. The left and center figures are cross sections of an FEM mesh modeling a transrectal EIT probe used for imaging the prostate. This mesh has 541,604 tetrahedral elements and it is used for the simulations and timing results presented in this paper. The mesh showed in the right is a 3D mesh modeling a breast with 48 electrodes attached. Also this mesh has approximately 0.5 million elements. The capability of using larger meshes, that describe well the anatomy of the body and the physics of the forward problem is becoming more and more attractive in terms of offering higher image quality, this movitates the need to accelerate image reconstruction with modern computing architectures, to address the increased computing demands.

In computing the Jacobian equation (10) needs to be solved 2430 times with different applied and lead fields; this corresponds to the excitation and sense pairs for each measurement. Electric field vectors have a length equal to the number of mesh elements, 541,604 in this case. This corresponds to 541, 604 · 3 · 2430 = 3, 948, 293, 160 floating point operations, or 3.9 Gflops, for real valued problems, and to 541, 604 · 12 · 2430 = 15, 793, 172, 640 or 15.8 Gflops for complex valued problems.

One way to optimize performance in the MATLAB environment, which we use for image reconstruction, is to implement time consuming portions of the code in C-language mex files. Because these C-constructs are basaed on a native non-interpreted language, these routines execute at maximum speed. In our implementation, we use C-mex files and, where possible, rely on function calls to the Intel MKL (Math Kernel Library) and IPP (Integrated Performance Primitives) libraries, which are multithreaded and highly optimized. In (10) we use the ippsAddProduct64f from IPP to implement the element-wise products of vectors holding electric field values. Because this function is multithreaded, it is able to use multiple cores on modern computing architectures.

We conducted performance testing experiments on a Dell Power Edge 1955 Blade Server. The server is based on two quad-core Xeon 5355 “Clovertown” CPUs, with an internal clock frequency of 2.66GHz and front-side bus speed of 1.33GHz. The total computing time on the mesh with 541,604 elements and 2430 measurements was 297.5 seconds for a real valued problem and 745.5 seconds for a complex valued problem. Though these computing times can be 5 to 10 times faster than a conventional scripted MATLAB implementation (Borsic et al. 2008), it still requires 5 minutes to compute a real-value Jacobian and 12 minutes for the complex-valued case. Considering that the reconstruction algorithm involves forward solving and typically 3 to 5 iterations, this renders the reconstruction of problems of this size non-interactive, and brings the total reconstruction time to the order of 1 hour or more.

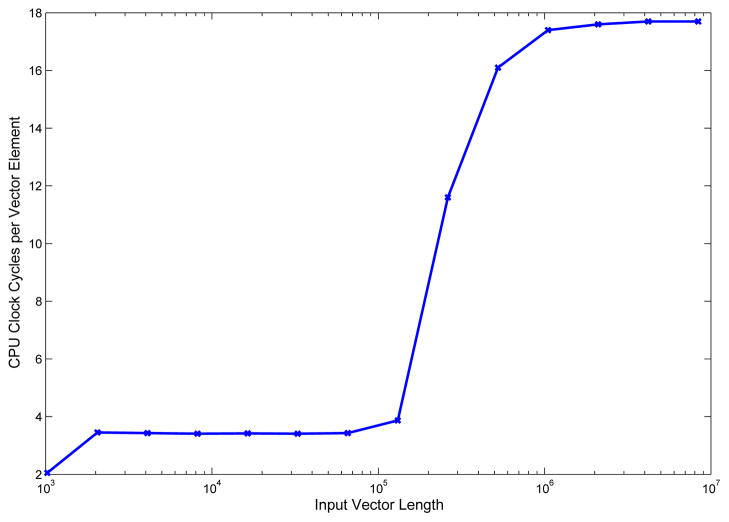
The problem was analyzed to seek ways of further reducing computing times. It was noticed that using a single core or up to 8 cores on the Xeon PC produced only marginal gain, on the order of 10%. Further analysis suggested that the performance of the algorithm is bounded by the bandwidth between main memory and CPU. The vectors holding electric fields have a length of 541,604 elements (determined by the number of tetrahedra in the mesh), and are represented in double precision, requiring 4.3MB each for storage. Vectors of this size do not fit in the cache memory of the CPU, which needs to fetch them element-by-element from main memory as it is computing the element-wise product. While the element-by-element product is trivial, and computed in a few clock cycles, fetching data from memory requires several clock cycles and slows down the overall execution of the algorithm. To verify this, test functions of the IPP library were used to measure how many CPU clock cycles are required to compute the element-by-element product with different length sizes of the input vectors. For vectors of small length, which are expected to fit in cache memory, the product is expected to execute faster, for larger vectors which do not fit in cache memory the number of clocks per operation is expected to increase, as operands need to be fetched from the slower main memory. Figure 2 shows results from testing ippsAddProduct64f performance with input vectors of different lengths, ranging from 30 to 10 million elements. The horizontal axis indicates in logarithmic scale the length of the vector, while the vertical axis indicates the number of clock cycles necessary to multiply two elements of the input vectors. For vector lengths of less than 100,000 elements the product takes 4 clock cycles per element. For vectors with more than 100,000 elements the number of required clock cycles increases sharply to 18. This behavior arises from the fact that smaller test vectors fit completely in the L2 cache, and are fetched from this with a 256 bit wide bus, with higher throughput and lower latency compared to main memory.

Figure 2.

Number of CPU clocks per product of vector element. The graph represents vertically the number of CPU clocks that are required for performing a product of two elements of input vectors in an element-wise product of two vectors. Horizontally is represented the length of the input vectors in logarithmic scale. For vectors of a small length, with up to 100,000 elements, the multiplication of two elements takes on average 4 clock cycles. For input vectors of larger size, the element-wise product takes 18 clock cycles per element, on average. This decreased performance is due to the fact that operands do not fit in cache memory and need to be fetched directly from RAM, requiring much longer access times.

The total computing cost, as anticipated previously, is of 3.9 Gflops and of 15.8 Gflops respectively for real and complex valued problems. Since the raw computing power of the Xeon processor in use is of approximately 70Gflops, the Jacobian potentially could be computed in under 1 second, if the data were supplied at a sufficient rate to all 8 processor cores. The Jacobian computation takes much longer than a second; this signifies that it is bound by memory bandwidth, which is not sufficient to saturate even a single core (8.75 Gflops). An implication of this is that algorithms do not benefit from use of multiple cores. As data are not fed at a sufficient rate to saturate the computing power of a single CPU core, speed cannot be improved by using more cores: they share the same access to memory, and all the cores except one would be idle. As our tests demonstrated, using 8 cores only provides a speed improvement of 10% compared to execution on a single core. Further speed gains are therefore possible only by computing on different architectures that offer faster access to data compared to current PC technologies. The typical peak CPU to memory bandwidth on PCs is 25GB/s, but only a fraction of this bandwidth can be obtained as the bus connecting the CPU to memory is shared by other peripherals. Modern CPU architectures exhibit higher clock frequencies and an increased number of cores, resulting in a much increased computing power. Despite this, memory bus speeds have increased very little. An alternative computing platform is instead represented by GPUs, which are highly optimized for performance and for memory bandwidth, some of them having bandwidths of 400GB/s.

4. Optimizing Jacobian Computation on GPUs

Graphic Processing Units (GPUs) have been highly optimized for gaming performance, and rely on very specialized processors that for certain tasks are orders of magnitude more powerful than CPUs and have much faster access to on-board RAM. In the last 5 years, the use of these architectures for scientific computing has been considered, and significant accelerations have been possible in many different areas of application. Based on these features, we explored implementing the Jacobian computation on single and multiple GPUs as way of speeding up the computations.

In these experiments, an NVIDIA Tesla C1070 solution was employed. This is a rack mount system developed by NVIDIA consisting of 4 GPUs connected together and enclosed in a chassis. The system connects to a conventional PC via a dedicated cable and a PCIe adapter card. The S1070 is capable of delivering 4 Teraflop/s in single precision, 345 Gigaflop/s in double precision, has a memory bandwidth of 409 GB/s, and it comprises 960 computing cores (240 per each GPU).

The S1070 can be programmed with an NVIDIA proprietary language, CUDA, which is based on C with proprietary extensions. NVIDIA also supplies the cuBLAS numerical library, a CUDA specific implementation of BLAS. In this GPU implementation of the Jacobian computation, C-mex files were programmed using calls to functions from the the CUDA and cuBLAS libraries, to transfer data from the CPU to the GPU/GPUs and backwards, and to perform the computations. The element wise products in (10) have been implemented with calls to cuBLAS, while the sparse matrix products involving the T and P matrices have been implemented with ad-hoc kernels similar to the ones proposed in (Bell & Garland 2008). All the routines have been implemented in double precision arithmetic to preserve the same precision used on CPU implementations.

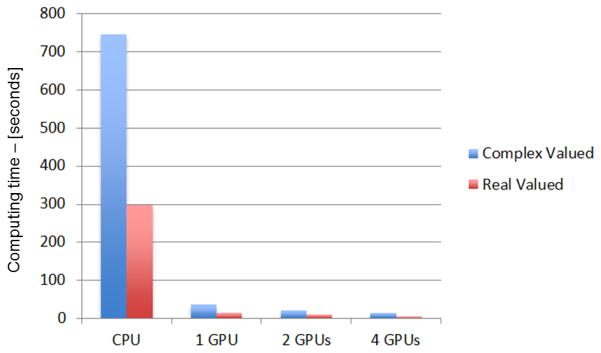
First, Jacobian computing was implemented and tested on a single GPU. The implementation of this routine is simpler than the multi-GPU implementation, as all the data (computed electric fields and matrices T and P) are transferred to a single GPU where all computations occur. Significant performance gains were obtained compared to the CPU optimized routine. Table 1 reports the computing time for the Jacobian matrix, which for a real valued problem on an Intel Xeon PC is 297.5 seconds. This time was reduced to 14.2 seconds by using a single GPU. For a complex valued problems times are respectively 745.4s on a PC and 35.4s on a single GPU. These times also include the transfer operations from CPU to GPU and back. Relative gains are reported in Table 2. In both the real and complex valued cases, the use of a GPU resulted in an acceleration of 20 times. This gain is significant and reduces the computing time of the Jacobian from several minutes to several seconds. It is important to note that this computational speed-up does not result in any loss of precision, the Tesla S1070, similar to other GPUs, computes in double precision according to the IEEE 754 standard, which is the standard for floating point computing largely adopted by the computer industry. We evaluated whether any numerical differences existed between the Jacobian computed on the CPU, which we label J_CPU, and the Jacobian computed on the GPU, labeled J_GPU, and found that ||J_CPU − J_GPU ||_∞ = 4.44 × 10⁻¹⁴, that is: the maximum discrepancy between any two elements of the Jacobian matrices is 4.44 × 10⁻¹⁴. Differences of the same order of magnitude were found in the reconstructed conductivities computed using J_CPU or J_GPU, these differences are therefore negligible and probably attributable to different rounding mechanisms. They maintain a very limited effect on the image as the regularization suppresses contributions from higher singular vectors, which would be potentially sensitive to this small rounding differences.

Table 1.

Execution times for real valued (top) and complex valued (bottom) computation of the Jacobian matrix. Performance results are reported for an optimized routine on an Intel Xeon based PC, and for optimized routines using 1, 2 or 4 GPUs of an NVIDIA Tesla S1070 unit. Timing includes the transfer of data from CPU to GPU and transfer of the computed Jacobian matrix back to the CPU.

Computing Time - Real Valued Case
	CPU	1 GPU	2 GPUs	4 GPUs
Time [s]	297.5	14.2	8.3	5.6

Computing Time - Complex Valued Case
	CPU	1 GPU	2 GPUs	4 GPUs
Time [s]	745.4	35.4	20.8	14.7

Table 2.

Speed gain compared to optimized routine on an Intel Xeon PC for routines using 1,2, and 4 GPUs. The top table reports results for real valued problems, the bottom table reports results for complex-valued problems on an NVIDIA Tesla S1070 unit.

Speed Gain - Real Valued Case
CPU	1 GPU	2 GPUs	4 GPUs
-	20.9	35.7	53.5

Speed Gain - Complex Valued Case
CPU	1 GPU	2 GPUs	4 GPUs
-	21.0	35.8	50.7

In order to further accelerate the computation we explored the use of multiple GPUs by developing a second routine that distributes data and performs computation across multiple graphic processors. The NVIDIA S1070 has 4 GPUs; we conducted tests using 2 and 4 GPUs. This is achieved by splitting vectors $E_{\mathit{applied}}^x,E_{\mathit{lead}}^x,E_{\mathit{applied}}^y,E_{\mathit{lead}}^y,E_{\mathit{applied}}^z$, and $E_{\mathit{lead}}^z$ in two or four parts and by sending each part to a single GPU to compute one half, one fourth, of a row of the Jacobian. Each part of the row is then transferred back to the CPU and assembled to form an entire row of the Jacobian. This computation is repeated over rows to form the entire matrix.

Additional speed gains were obtained with this approach. For the real valued case, the computing time was reduced from 297.5s on the CPU to 8.3 and 5.6 using 2 or 4 GPUs, respectively. For the complex valued case the time was reduced from 745.4s on the CPU to 20.8s and 14.7s using 2 or 4 GPUs, respectively. The resulting speed-ups are of 35.7 and 53.5 times for the real case, and of 35.8 and 50.7 times for the complex valued case. The speed-ups achievable by the use of multiple GPUs are very significant. For complex valued problems, the times for computing the Jacobian can be reduced from 12.5 minutes to 14s. Speed-ups of this order are not common for GPU-based acceleration, but are algorithm dependent. The computation of the Jacobian matrix is parallelizable as the element-wise product of vectors can be split over several GPUs by splitting the input vectors in several sub-vectors of, for example, one half or one-forth the size. The sparse products for the matrices T and P, the first holding the volumes of the tetrahedral elements, and the second representing the projection to a coarse mesh, are parallelized by splitting these matrices by rows, in such a way the partial products (e.g. top half matrix times top half vector) can be performed independently on single GPUs. These operations can therefore be mapped to multiple cores without requiring inter-communication. The significant acceleration results also from the higher bandwidth that GPUs have compared to CPUs. Unfortunately, the algorithm in its current form does not scale optimally with the number of GPUs. Given a gain of 20 times on a single GPU one would potentially expect a gain of 80 times on 4 GPUs, however the actual gain is of order 50 times. This non-linear scalability is caused by memory transfer operations between the CPU and the 4 GPUs. It might be possible in the future to further improve these figures by solving the forward problem on the GPUs. If the computed electric fields $E_{\mathit{applied}}^x,E_{\mathit{lead}}^x,E_{\mathit{applied}}^y,E_{\mathit{lead}}^y,E_{\mathit{applied}}^z$, and $E_{\mathit{lead}}^z$ required for the computation of the Jacobian are in fact already present in the memory of the GPU, this would reduce the transfer operations between CPU and GPU. Further, the conductivity update (6) could also be computed on the GPU/GPUs; in this case the Jacobian would not be transferred back to the CPU and a speed gain of 80 times, or very close, might be realistic on 4 GPUs.

5. Conclusions and Future Work

By using Graphic Processing Units as a computing architecture, speed gains of up to 50 times were possible in the computation of the Jacobian matrix for a representative 3D problem in Electrical Impedance tomography, total computing time reduced from 12 minutes to 14 seconds. The Jacobian computation is the most intensive step in image reconstruction, consuming typically 70% of the overall time. The second most intensive step is typically forward solving, which consumes approximately 25% of the total time. Our goal is to render 3D image reconstruction on fine FEM meshes at an almost interactive to facilitate more rapid data exploration and ultimately providing near real-time imaging for clinical applications.

Accelerating the Jacobian computation, as reported here, is a significant step in this direction. Ongoing efforts to accelerate the forward solver via GPU implementation are expected to provide an additional reduction in computation time. Dense linear algebra operations, such as the ones involved in computing the Jacobian, accelerate better on GPUs. Despite this, we still expect that gains of 10–15 times might be possible with a multi-GPU forward solver implementation, which involves sparse linear algebra operations. If these results are achieved, an image reconstruction step for the 3D problem we consider would require approximately 40 seconds, allowing for an almost-interactive 3D reconstruction environment. We would like to highlight that the results reported here apply to other soft-field imaging modalities, including Microwave Tomography and Diffuse Optical Tomography, since the Jacobian matrix is computed almost identically in these techniques.

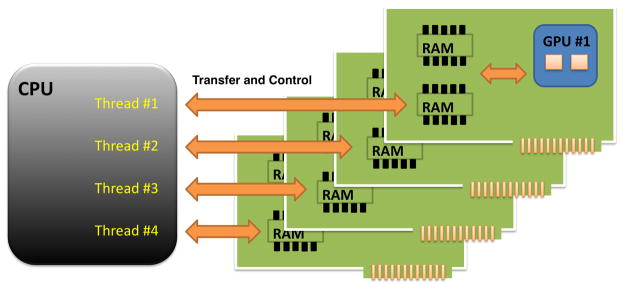
Figure 3.

Sketch of the multi-GPU architecture: the NVIDIA Tesla S1070 computing solutions consists of 4 GPUs which are housed in a chassis that provides power and a dedicated interconnection to a PC. At the software level, 4 threads are instantiated on the CPU; each thread communicates with one GPU and is responsible for splitting the data, and transferring the data to the associated GPU, launching the Jacobian computation on the GPU, transferring the results back to the CPU. As each GPU processes one fourth of the Jacobian matrix, results are re-assembled to form the full matrix on the CPU. With the above overheads, accelerations of 50 times have been possible using the 4 GPUs provided be the S1070 computing solution.

Figure 4.

Bar graph of the time, expressed in seconds, required to compute the Jacobian matrix on an Intel Xeon based PC with an optimized C-language mex file, and with dedicated routines on 1, 2, and 4 GPUs on a S1070 computing solution from NVIDIA. The blue bars report times for the complex-valued case, and red bars report times for the real-valued case.