Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Nov 15;2:861. doi: 10.1038/srep00861

Initial geometries, interaction mechanism and high stability of silicene on Ag(111) surface

Junfeng Gao 1, Jijun Zhao 1,a
PMCID: PMC3498736  PMID: 23155482

Abstract

Using ab initio methods, we have investigated the structures and stabilities of SiN clusters (N ≤ 24) on Ag(111) surface as the initial stage of silicene growth. Unlike the dome-shaped graphene clusters, Si clusters prefer nearly flat structures with low buckling, more stable than directly deposition of the 3D freestanding Si clusters on Ag surface. The p-d hybridization between Ag and Si is revealed as well as sp2 characteristics in SiN@Ag(111). Three types of silicene superstructures on Ag(111) surface have been considered and the simulated STM images are compared with experimental observations. Molecular dynamic simulations show high thermal stability of silicene on Ag(111) surfaces, contrast to that on Rh(111). The present theoretical results constitute a comprehensive picture about the interaction mechanism of silicene on Ag(111) surface and explain the superiority of Ag substrate for silicene growth, which would be helpful for improving the experimentally epitaxial growth of silicene.

Stimulated by the graphene boom, silicon monolayer (ML) with honeycomb geometry, namely, silicene, has been theoretically predicted1,2,3,4,5 and experimentally synthesized6,7,8,9,10,11,12,13,14,15. Similar to its graphene counterpart, freestanding silicene sheet is also composed of hexagonal rings but with a slight buckling of about 0.44 Å according to density functional theory (DFT) calculations2. Very excitingly, the band structures of low-buckled silicene resemble those of graphene, that is, π and π* bands cross linearly at the Fermi level of the Brillouin zone, forming the so-called “Dirac cones”1,2,16,17,18. Hence, the charge carriers in silicene behave like Dirac massless fermions with ultrahigh Fermi velocity of the magnitude of 105~106 m/s1,2,13,19,20. Besides, it was recently demonstrated that silicene with topologically nontrivial electronic structures can realize the quantum spin Hall effect in an experimentally accessible low temperature regime21. Though pristine silicene is a semimetal, tunable band gap in silicene monolayer can be opened up at the Fermi level by either applying external electric field22,23,24,25 or chemical functionalization with hydrogen26,27,28,29 and halogen elements29,30. In addition to the infinite silicene sheet, fascinating electronic and magnetic properties for the silicene nanoribbons have been predicted by first-principles calculations16. With these outstanding electronic and transport properties, integration of silicene into microelectronic devices is rather tempting since it is compatible with the mature silicon-based semiconductor technology.

Experimentally, silicene in the form of nanoribbons has been synthesized on Ag(001)6 and Ag(110)7,8,9,10 surfaces, respectively. Especially, the silicene nanoribbons on Ag(110) surface presented a magic width of 1.6 nm and aligned parallelly with each other in a well distributed way7,8,9,10. Reflection electron energy loss spectroscopy (REELS) measurement attested sp2-like hybridization of valence orbitals in the silicene nanoribbons10, whereas graphene-like band dispersion in the silicene nanoribbons has been testified by angle-resolved photoelectron spectra (ARPES)8. Moreover, these silicene nanoribbons on Ag(110) substrate show strong resistance towards oxidation10.

Beyond the nanoribbons, Vogt et al. have epitaxially synthesized large area silicon monolayer on Ag(111) surface13, making the theoretical predicted silicene ML comes true. With ARPES measurement, they demonstrated that the Dirac cone, which is the most intrinsic property of silicene distinguishing from common silicon, exists in the epitaxially silicene on Ag(111). Besides, compelling evidences for silicene honeycomb lattice, such as the Si 2p and Ag 4d core level emission, the STM images, and the LEED pattern, were provided. Based on the experimental observations and DFT calculations, they proposed a superstructure of (3×3) silicene on (4×4) Ag(111) surface (which is usually called Ag(111)−(1×1) lattice).

In addition, several other groups also synthesized silicene monolayer on Ag(111) surface and revealed the (4×4) superstructure, separately11,12,14. Wu's group observed one-atom-thick silicene sheet across the step edges of the Ag(111) surface without losing continuity of the atomic lattice12, and they further proved the existence of massless Dirac fermions in silicene@Ag(111)20. Besides, several other probable superstructures of silicene monolayer on Ag(111) surface were also proposed, such as 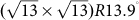Inline graphic11 and Inline graphic14, implying that the interaction mechanism of silicene on Ag(111) surface is rather complicated and still unclear. Except for the Ag(111) substrate, Fleurence et al. obtained epitaxial silicene ML through surface segregation on the ZrB2 thin films grown on Si wafers15. The successful synthesis of silicene ML opens a new opportunity towards many potential applications, such as field effect transistor, ultra-sensitive chemical sensors, and solar cells31,32.

A prerequisite for future utilization of silicene-based materials and devices is the mass production of silicene of high-quality. Clearly, elucidating the growth mechanism of silicene is imperative for the rapidly growing silicene research. Indeed, the growth behaviors of graphene on various transition metal (TM) substrates have been recently explored using ab initio calculations33,34,35,36,37,38,39 and molecular dynamics (MD) simulations40,41. The behaviors of metal supported carbon clusters in the very initial stage of graphene growth, such as the ground state structures and the critical size for sp to sp2 transition (i.e., from linear chain to 2D island), were found to be quite different from those of freestanding carbon clusters33,34. On metal surfaces, graphene nanoclusters form dome-shaped islands spontaneously because the carbon-metal interaction mainly occurs at the edge atoms of the graphene patches35. In addition, the metal surfaces have significant influence on the diffusion and dissolution behaviors of carbon atoms40,42, as well as the edge reconstruction of graphene38. Unlike carbon preferring sp2 bonding, silicon favors sp3 hybridization and there is no graphite-like sp2 allotrope for silicon solids. Intuitively, there must be some differences in the growth behaviors of silicene and graphene on the metal substrates. Hence, exploring the structures and stabilities of the TM-supported silicene clusters (as the early stage of growth) and silicene ML of different superstructures is of key importance. However, to the best of our knowledge, no such study was reported yet.

In this paper, we systematically investigate the interaction mechanism and stability of silicene clusters and monolayers on Ag(111) surface using ab initio calculations. We show that the energetically unfavorable two-dimenstional (2D) honeycomb silicon clusters (up to 24 atoms) in vacuum can be stabilized by Ag substrate. Due to hybridization between silicene cluster and metal surface, no dome-shaped silicon island is found on Ag(111) surface, in contrast to the metal-supported carbon clusters. The buckling of small silicene clusters on Ag(111) surface is lower than periodic silicene sheet either in vacuum or on Ag(111) surface. Analysis of electronic structures demonstrates that the 2D Si24 cluster on Ag(111) surface retain certain sp2 character. Ab initio molecular dynamics (AIMD) simulations at 500 K confirm high stability of silicene ML on Ag(111) surface, but not on Rh(111) surface. Our theoretical results not only illustrate why Ag(111) surface is superior for epitaxial growth of silicene but also provide some useful insights into the synthesis of high-quality silicene on other probable metal surfaces.

Results

To characterize the stability of a silicon cluster on metal substrate, its formation energy is defined as:

graphic file with name srep00861-m1.jpg

where εT is the total energy for the silicon cluster and the metal substrate, N is the number of atoms in the silicon cluster, εSi is the energy per atom of silicon solid with diamond lattice, εSub is the energy of the substrate. In the case of freestanding clusters in vacuum, εT becomes the total energy for the silicon cluster only, and the εSub term vanishes.

Structures of SiN clusters in vacuum and on Ag(111) surface

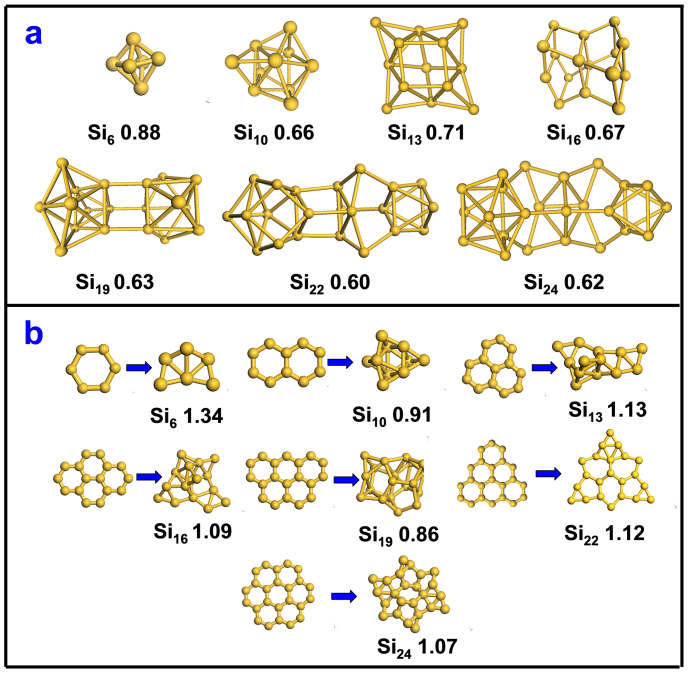
Previously, Zeng's group has extensively explored the lowest-energy structures of freestanding SiN clusters (N ≤ 30)43,44,45. Smaller Si6 and Si10 with sphere-like octahedron and tetracapped trigonal prism configurations are the magic clusters with exceptional stability43. The most stable configurations for the larger SiN clusters can be then obtained from the small clusters (like Si6 and Si10) as building units by adding atoms, fusing two clusters44, or assembling two clusters via some bridge atoms45. These ground state (abbreviated as GS in the following) structures are adopted here and their geometries and formation energies are presented in Fig. 1a. To examine the stability of sp2 silicene fragments without TM substrate, we constructed a series of 2D SiN clusters (N = 6, 10, 13, 16, 19, 22, 24) as aggregates of six-membered rings (6MRs), which can be viewed as embryos of silicene ML. However, none of them are even metastable on the potential energy surface. After relaxation, these planar SiN clusters transform into severely buckled configurations spontaneously (see Fig. 1b). In vacuum, these highly distorted SiN clusters are less stable than the lowest-energy GS structures, with formation energy difference of about 0.25 ~ 0.52 eV/atom.

Figure 1.

Figure 1

Open in a new tab

(a) Most stable structures and their formation energies (eV per atom) for SiN clusters (N = 6, 10, 13, 16, 19, 22, 24) in vacuum; (b) planar SiN clusters constructed by hexagonal rings (left) and their spontaneous transformation into severely distorted structures (right) after relaxation in vacuum.

For the purpose of comparison, we have explored selected freestanding planar CN clusters with the same 6MR-based configurations46. The detailed results are given in Supplementary Fig. S1 of the Supporting Information (SI) online. Except for C10, which transforms from a double-hexagon configuration into a ten-membered ring after relaxation, the hexagon rings in all other freestanding CN clusters are well preserved upon optimization, even though they may not be the ground state configurations for these cluster sizes. The distinct difference between Si and C clusters suggests that the freestanding silicon clusters can not form stable sp2 structures spontaneously. However, low buckled 2D silicene sheets have been synthesized on Ag(111) surface in experiments11,12,13,14. Clearly, Ag(111) surface must be responsible for the stability of these 2D silicene structures and thus significantly affect the nucleation and growth behaviors of silicene clusters.

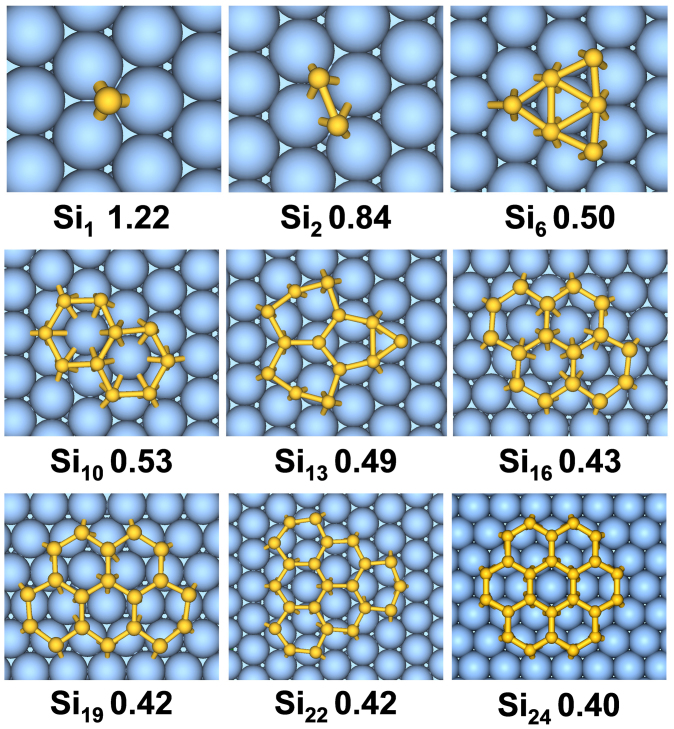
Fig. 2 depicts the equilibrium geometries and formation energies of silicon monomer, dimer and 6MR-based silicene-like clusters on Ag(111) surface. For reference, the geometries and formation energies of CN clusters on Ag(111) substrate are computed and shown in Supplementary Fig. S2 online. Different from the Ag-supported C6 cluster which retains its hexagon ring structure well, a hexagonal ring of Si6 placed on the Ag(111) surface is distorted into triangle-based configuration upon relaxation. In sharp contrast to severe deformation in vacuum, starting from Si10, the planar SiN clusters (N = 10, 13, 16, 19, 22, 24) formed by multiple hexagons remain stable after optimization; only Si13 (with three hexagons) undergoes moderate deformation at the periphery. Certainly, Ag(111) surface as the only external factor is responsible for preserving the 2D structure of silicene clusters, similar to the improved stability of silicon cages and nanotubes by metal stuffing47,48. This effect will be discussed in details later. Nevertheless, the well persevered six-membered rings in silicon clusters on Ag(111) substrate imply the existence of sp2 bonding character, which has been evidenced by experiments with STM, REELS, and ARUPS techniques10,13,15,20.

Figure 2. Geometries and formation energies (eV per Si atom) of 2D SiN clusters on Ag(111) surface.

Figure 2

Open in a new tab

The observation of triangle-based Si6 cluster suggests a possible competition between hexagonal and triangular structural motifs for Ag-supported Si clusters. To examine the stability of the larger triangle-based silicon clusters, we have constructed one Si10 and two Si13 configurations composed by triangular networks on Ag(111) surface. Their atomic structures before and after optimization are shown in Supplementary Fig. S3 online. After relaxation, none of them can retain the initial triangular structures, and they all transform into some irregular shapes with higher formation energies (ΔE = 0.10 eV for Si10, ΔE = 0.13 eV or 0.26 eV for Si13) compared to the hexagon-based structures. In particular, for the Si13-t1 isomer with initial triangular structure, a hexagon would be formed spontaneously upon structural relaxation, implying the tendency of structural transformation from triangles to hexagons. The transition from triangular to hexagonal motif at Si10 may play an important role in nucleation of silicene patch, beyond which honeycombed silicene lattice can be synthesized on Ag(111) surface.

Formation energies of SiN clusters and interactions with Ag(111) surface

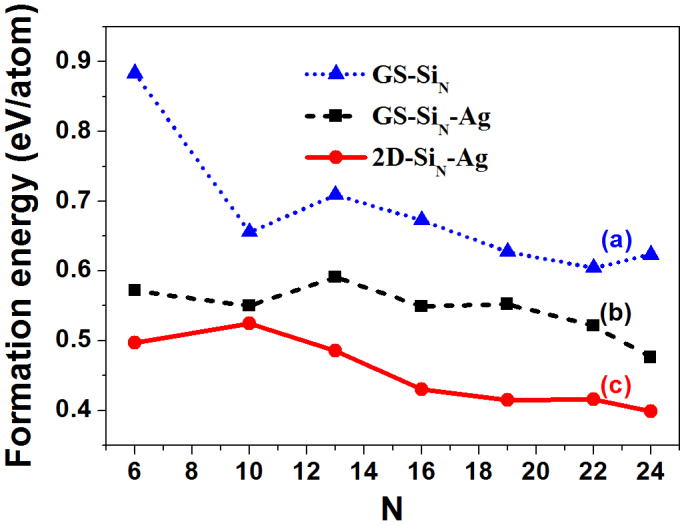
To explore the early stage of silicene nucleation, we considered two competitive structural motifs for SiN clusters (N = 6, 10, 13, 16, 19, 22, 24) on Ag(111) substrate: (i) 2D silicene-like configurations as aggregates of up to seven 6MRs (Fig. 2); (ii) 3D structures that are the ground state geometries in vacuum (see Supplementary Fig. S4 online). The formation energies of these two kinds of metal-supported silicon clusters are compared in Fig. 3, along with those for freestanding clusters. When a gas-phase GS silicon cluster is deposited on the Ag(111) surface, its formation energies drops substantially by about 0.07 ~ 0.31 eV/atom. This can be easily attributed to the passivation effect of metal surface, that is, the dangling bonds in the unsaturated atoms of isolated SiN clusters being passivated by the free electrons of the metal. Very interestingly, the 2D silicene-like clusters on Ag(111) surface are more stable than those 3D GS isomers, entirely opposite to the vacuum situation discussed above. Again, this finding can be explained by the passivation effect of Ag(111) surface. As shown in Supplementary Fig. S4, the metal surface only interacts with the bottom part of a 3D GS silicon cluster, leaving the top Si atoms unsaturated. On the contrary, for a 2D silicene cluster lying on the metal surface, all these under-coordinated Si atoms (with typical vertical distance of 2.2 Å~2.5 Å from the Ag substrate) can be passivated. In other words, 2D SiN cluster has a larger contact area with the Ag surface than the 3D one. As a natural extension of 2D Si24 clusters with seven 6MRs, one can speculate that an appreciably large silicene patch should be stabilized by the metal surface.

Figure 3. Formation energies of SiN clusters in vacuum and on Ag(111) surface:

Figure 3

Open in a new tab

(a) freestanding SiN clusters with ground state configurations in vacuum (GS-SiN); (b) direct deposition of GS-SiN clusters on Ag(111) surface (GS-SiN-Ag); (c) 2D silicene-like clusters on Ag(111) surface (2D-SiN-Ag).

As shown in Fig. 3, the formation energy of silicon cluster increases from Si6 (0.50 eV/ Si atom) to Si10 (0.53 eV/ Si atom). After Si10, the formation energy of Ag(111)-supported SiN cluster reduces smoothly as cluster size increases (see Fig. 3b). Thus, Si10 composed of two 6MRs can be considered as the nucleation size from thermodynamic point of view, which is very crucial to the growth of 2D silicene crystal. As shown in Supplementary Fig. S5a online, the diffusion barrier of silicon monomer on Ag(111) surface is only 0.031 eV; in other words, motion of Si adatoms on Ag substrate is nearly barrierless at room temperature. Thus, once overcoming the critical size of Si10, silicene patch would grow continuously until the concentration of silicon atoms from the source is not sufficient.

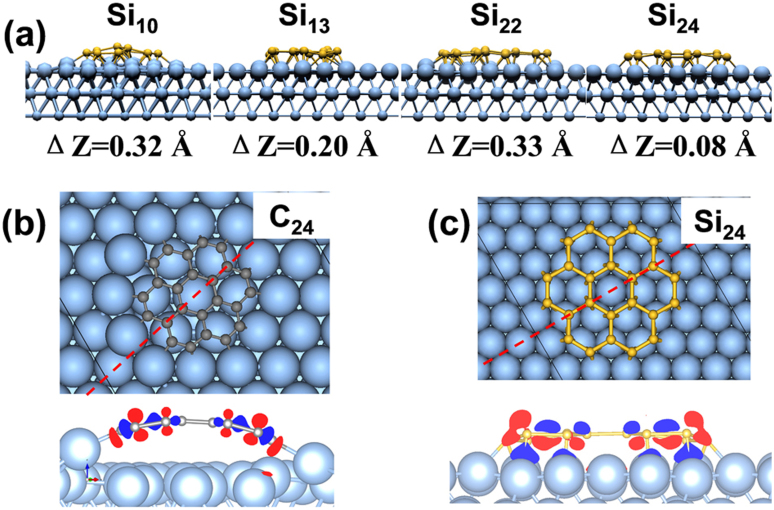
To gain deeper insight into the interaction mechanism between silicon clusters and silver surface, the side view of selected 2D SiN clusters (N = 10, 13, 22, 24) are shown in Fig. 4a, along with the height difference ΔZ between upper and bottom Si atoms for each cluster. The detailed buckling information of these 2D SiN clusters is provided in the Supplementary Fig. S6 online. To explore the difference between silicene and graphene, we considered a series of 6MR-based carbon clusters on Ag(111) surface. Their equilibrium geometries and formation energies are shown in provided in the Supplementary Fig. S2 online. On Ag(111) surface, the smaller C10 and C13 clusters prefer upright standing, while the larger ones (C22 and C24) form dome-like shape, similar to the previous observation of carbon nanoislands on Ir(111) surface35. Different from carbon clusters, silicon clusters explored here sit more flatly on Ag(111) surface with slight buckling of less than 0.33 Å (see Fig. 4a and Fig. S6). The geometry difference between SiN and CN clusters implies that their interactions with Ag(111) surface must be rather different.

Figure 4. Side view plots for atomic structures of (a) selected SiN clusters on Ag(111) surface.

Figure 4

Open in a new tab

Charge differential densities of hexagon-based (b) C24 and (c) Si24 on Ag(111) surface, respectively. In (b) and (c), the cleaved planes are along the red line, and red (blue) zone loses (gains) charge.

As shown in Fig. 4 (b) and (c), the interactions of Si24 and C24 clusters with metal surface are visualized by charge differential density. No charge density is found between the six inner carbon atoms of C24 and Ag(111) surface, implying weak van der Waals (vdW) interaction rather than strong chemical bonds. Strong charge distribution between the edge of carbon cluster and Ag(111) surface illustrates that carbon clusters bond to metal surface mainly at the edge35. As for Si24@Ag(111), Si-Ag charge transfer occurs both at the periphery and inner regions of Si24 cluster, suggesting that every silicon atoms interact with Ag(111) surface. Note that the standard DFT method used here is only able to distinguish the interactions between C and Si clusters with Ag(111) surface qualitatively, whereas accurate description of the vdW interaction between the dome-like carbon clusters and Ag(111) surface requires more elaborate methods such as DFT-D2 and vdW-DF approaches.

Previous DFT calculations predicted a slight buckling of about 0.44 Å in freestanding silicene sheet2, which was also experimentally confirmed in Ag-supported silicene ML with buckling amplitude of about 1 Å11,12,13,14. Here we also observed low buckling in 2D silicene clusters, as shown in Fig. 4a and the Supplementary Fig. S6 online. However, the buckling heights for silicene clusters (0.2~0.33 Å for Si10,13,22 and only 0.08 Å for Si24) are less pronounced than those for the free-standing and Ag(111)-supported silicene sheet. This phenomenon can be explained by the following picture. In vacuum, as the π bonding is weakened, puckering of silicene sheet would introduce dehybridization. Hence, the perpendicular pz orbital combining with the s orbital is crucial to stabilize the freestanding silicene. While on Ag(111) slab, metal passivation helps reduce the buckling of silicene on the one side; but lattice mismatch of periodic superstructures of silicene and Ag(111) would introduce more seriously undulate patterns on the other side. The latter effect is dominant for periodic silicene superstructures; thus high buckling of ΔZ ~ 1 Å is observed experimentally11,12,13,14. In contrast, the small silicene clusters without constraint of periodic boundary condition can accommodate the Ag(111) surface better since the edge atoms have more degree of freedom for adjusting the adsorption position.

Moreover, the population analysis of Mulliken charge49 of Si24 on Ag(111) surface is shown in the Supplementary Fig. S7 online. The on-site charges of Si atoms in Si24@Ag(111) system range between −0.13 |e| and −0.08 |e|. The slight variation of on-site charges can be associated with small height difference due to low buckling of silicene cluster (see Supplementary Fig. S6d online). Nevertheless, the nearly homogeneous charge transfer between Si atoms and Ag surface (and consequently the Si-Ag interaction) is surely beneficial for continuous growth of silicene patch on Ag substrate.

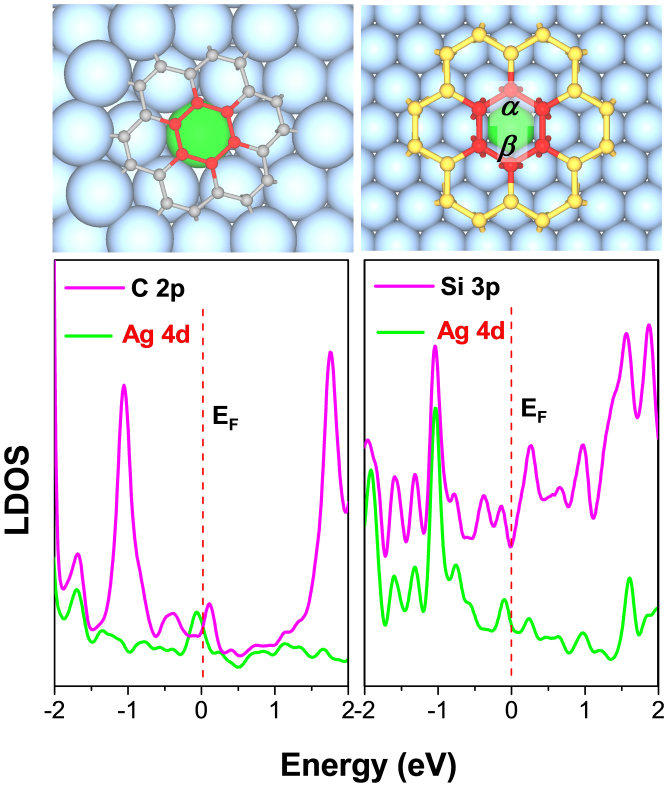
To further illustrate the interaction between Si clusters and Ag(111) surface, we calculated the LDOS for selected atoms of Si24@Ag(111) and C24@Ag(111), respectively, which are displayed in Fig. 5. Clearly, the 3p states of Si atoms coincide with the Ag-4d states in the vicinity of the Fermi level, suggesting the pz electrons of silicon atoms hybrid with the 4d electrons of Ag(111) surface. In contrast, there is no such correspondence between 2p orbitals of carbon atoms and 4d orbitals of Ag(111) surface, in line with the charge differential density plot (Fig. 4c) which implies vdW interaction between inner carbon hexagon and Ag substrate. This is because that the hybridization between C 2p and Ag 4d states will break the delocalized π bonds in the graphene sheet that are very stable; on the contrary, strong interaction between Si 3p states and Ag 4d states is expected for silicene because of the reluctance of Si in forming π bonds. In addition, the bond angles of the inner hexagon in Si24 split into two staggered angles: α = 120°~121° and β = 115°~118°, corresponding to sp2 and sp2/sp3 hybridization, respectively. Similar distribution of bond angles was found in a recent study on silicene sheet on Ag(111) surface13. Moreover, the LDOS of 3p states of silicon exhibits a distinct pseudogap at the Fermi level like the freestanding graphene and silicene, implying that the partial sp2 characters10,13,20,50. In short, the pz orbital of Si interacts substantially with Ag substrate while sp2 hybridization still exists in these 2D silicene-like clusters on metal. Different from graphene with mainly sp2 states, the partially sp2-hybridization characteristics in Ag(111)-supported silicene might lead to some novel applications.

Figure 5. Atomic structures (upper) and local density of states (LDOS, lower) of C24@Ag(111) (left) and Si24@Ag(111) (right) systems.

Figure 5

Open in a new tab

The LDOS comes from the central six carbon atoms (2p orbital) or silicon atoms (3p orbital) highlighted by red balls as well as the Ag atoms (4d orbital) highlighted by green ball right underneath the C or Si hexagon. Two characteristic bond angles (α, β) for central Si6 hexagon are labeled: α = 120° – 121°, β = 115° – 118°.

Silicene monolayer superstructures on Ag(111) surface

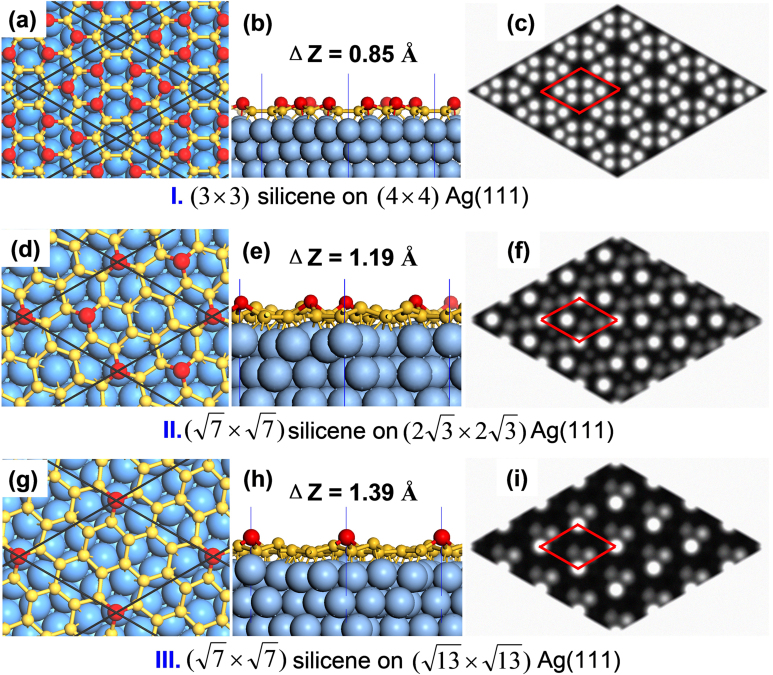
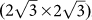To further understand the interaction between silicene and Ag(111) surface and to directly compare with available experiments, we considered three types of co-periodic silicene@Ag(111) superstructures: (I) (3×3) silicene on (4×4) Ag(111) surface (usually named Ag(111)−(1×1) surface or (4×4) silicene11,12,13,14); (II) Inline graphic silicene on Inline graphic Ag(111) surface14; (III) 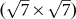Inline graphic silicene on 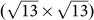Inline graphic Ag(111) surface11. The atomic structures as well as the simulated STM images are shown in Fig. 6. The detailed structural information such as the supercell dimension, mismatch, bond length, are summarized in the Supplementary Table S8 online.

Figure 6. Atomic structures and simulated STM images of three types of silicene@Ag(111) superstructures.

Figure 6

Open in a new tab

(a), (d), (g) are the top views; (b), (e), (h) are the side views; (c, f, h) are the STM images with a constant height of 2 Å to the topmost Si and a bias of −1.5 V. The topmost Si atoms are highlighted by red balls.

As displayed in Fig. 6, due to passivation of metal surface and lattice mismatch, the buckling behavior of Ag(111)-supported silicene sheet is quite different from the freestanding ones. In the frequently found superstructure of type I, there are only 1/3 of Si atoms at the top (highlighted by red balls), resulting a wheel-shaped double ring STM pattern (Fig. 6c) composed by six spots on the internal ring and twelve spots on the external ring, in excellent agreement with experimental images11,12,13. Within the silicene@Ag(111) supercell of type II, there are only two Si atoms (1/7 of Si atoms) on the top sites, resulting a honeycombed STM image (Fig. 6f); however, the nearest distance between two spots is about 5.76 Å14. In the superstructure of type III, there is only one topmost Si atom per cell corresponding to the lightest spot in STM image (Fig. 6i). The present theoretical result for type III can be related to recent experimental STM image by Lin et al.11, in which they observed one spot per rhombus supercell of 10.4 Å in dimension.

The heights of buckling in these three types of silicene superstructure are 0.85 Å, 1.19Å and 1.39 Å, respectively. Considering the corresponding lattice mismatches of −0.86 %, +2.73 % and −1.24 %, no clear correlation is found between the buckling amplitude and the lattice mismatch. As listed in the Supplementary Table S8 online, the Si-Si bond lengths of these three types of superstructures range between 2.285 Å and 2.436 Å, in accordance with previous theoretical calculations and experimental data11,12,13,14. The average Si-Si bond length of Ag(111)-supported silicene ML superstructures are 2.351 Å for (4×4), 2.322 Å for 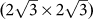Inline graphic and 2.357 Å for 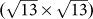Inline graphic, respectively. Interestingly, the variation of Si-Si bond length is roughly proportional to the mismatch between silicene superstructure and Ag(111) surface.

Thermal stability of silicene monolayers on Ag(111) and Rh(111) surfaces

The above analyses indicate that the 2D silicene-like clusters are stabilized by Ag(111) surface due to passivation of the unsaturated edge Si atoms and p-d hybridization between inner Si atoms and Ag substrate. Due to the lattice mismatch between Ag(111) and silicene lattice as well as the energy difference between different adsorption sites on metal surface, deposition of large-scale silicene sheet on the metal substrate would introduce extra local tension on silicene. At finite temperature, thermal perturbation would trigger some structural defects associated with such local tension and thus disturb the geometry integrity of silicene sheet. This effect must be considered during the fabrication and processing of the silicene-based materials and devices. Previously, phonon calculations have been conducted to assess the stability of the freestanding silicene ML2; but such simulation is unable to examine the finite-temperature behavior and the thermal stability.

To assess the thermal stability of silicene on metal substrates, we preformed AIMD simulation on the type I silicene@Ag(111) superstructure as a representative. The initial geometry of silicene ML on Ag(111) was fully optimized (see Fig. 6a,b and Fig. 7a). AIMD simulations were then carried out at 500 K (experimental growth temperature) for more than 7.5 ps. Interestingly, the silicene monolayer is found to be very stable on Ag(111) surface. At 500 K, no topological defect was ever generated during the entire simulation time of 7.5 ps (Fig. 7b), confirming its high thermal stability on Ag(111) surface. This can be attributed to the passivation effect as well as low local tension of silicene network on the metal surface. As shown in Supplementary Fig. S6 online, the local energy difference of silicon monomer on different sites of Ag(111) surface is lower than 0.031 eV, implying a very small local tension.

Figure 7. Snapshots from AIMD simulation of silicene monolayers on Ag(111) at 500 K.

Figure 7

Open in a new tab

(a) initial configuration and (b) structure after 7.5 ps for (3×3) silicene on (4×4) Ag(111) surface (i.e., type I defined above); (c) initial configuration and (d) structure after 5.6 ps for (5×5) silicene on (7×7) Ag(111) surface with 3.8% lattice mismatch.For each graph, Ag atoms are not shown in top view.

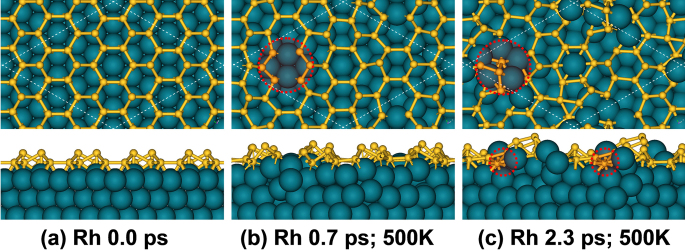
To understand the role of Ag(111) surface, the Rh(111) surface, which has relatively stronger interaction with Si, was assumed as substrate of silicene monolayer. A silicene@Rh(111) superstructure, including (4×4) silicene cells and (6×6) Rh(111) cells with 3.7% mismatch, was constructed. Upon DFT relaxation, silicene on Rh(111) surface can retain its honeycomb lattice well (Fig. 8a). Comparative AIMD simulation at 500 K was then carried for this silicene@Rh(111) superstructure up to 2.3 ps. In sharp contrast to that on Ag(111) surface, the silicene lattice on Rh(111) surface start collapsing via breaking up two Si-Si bonds after only 0.7 ps simulation time (Fig. 8b). Once such a defect is created, silicene monolayer became more and more unstable on Rh(111) surface. After the entire duration of 2.3 ps, an amorphous Si-Rh interface is formed (Fig. 8c).

Figure 8. Snapshots from AIMD simulation of silicene on Rh(111) at 500 K.

Figure 8

Open in a new tab

(a) initial structure; (b) structure at 0.7 ps with two Si-Si bonds broken; (c) structure after 2.3 ps, showing an amorphous Si-Rh interface.The important local disruptions of silicene 2D lattice are labeled by red dash rings for guide of eyes.

The thermal instability of silicene ML on Rh(111) may be interpreted by the larger local energy difference of Si atom on Rh surface. As shown in Supplementary Fig. S5b online, the diffusion barrier of silicon monomer on Rh(111) surface is 0.306 eV, about ten times than that on Ag(111) surface. However, the co-periodic silicene@Rh(111) supercell considered here has a large lattice mismatch of 3.7%, which might also account for the instability of silicene ML. To exclude this factor, we further adopted a (5×5) silicene on (7×7) Ag(111) surface (Fig. 7c) with 3.8 % lattice mismatch for AIMD simulation. During the simulation time (5.6 ps), silicene lattice is well preserved on Ag(111) surface and not even a defect is produced at 500 K. Interestingly, even at a higher temperature of 900 K, the topological structure of silicene lattice is still retained for 5 ps (see Supplementary Fig. S9 online for details). Thus we can conclude that the instability of silicene on Rh(111) surface is mainly originated from high local energy difference. These results suggest that the local energy difference of silicon atoms on surface might be a key factor to justify whether a metal substrate is suitable for epitaxial growth of silicene.

Discussion

In summary, using ab initio calculations, the structures and stabilities of SiN clusters (N ≤ 24) in vacuum and on Ag(111) surface are investigated and compared with those of CN clusters. Planar configurations based on aggregates of hexagons are highly unstable for the isolated silicon clusters in vacuum and will be severely reconstructed to 3D distorted structures spontaneously. However, due to passivation effect of metal surface, these 2D silicon clusters as embryo of silicene patch can be stabilized by Ag(111) substrate. No dome shape is found for Ag(111)-supported SiN clusters, in contrast to graphene nanoclusters on TM surfaces. Analysis of electronic structures reveals significant p-d hybridization between Si and Ag surface, and sp2 characteristics in silicone clusters. Three types of silicene superstructures on Ag(111) surface are investigated and the simulated STM images agree well with available experimental observations. Compared to the buckling of about 0.44 Å in freestanding silicene sheet, the buckling heights in 2D silicene clusters (0.08~0.33 Å) on Ag(111) substrate are smaller and those in Ag(111)-supported silicene sheet (0.85~1.39 Å) are larger. AIMD simulations on two kinds of silicene@Ag(111) superstructures and comparing with that on Rh(111) surface confirm excellent thermal stability of silicene monolayer on Ag surface, which can be attributed to the passivation effect by Ag and low local energy difference of silicon adatoms on different sites of Ag(111) surface. These theoretical results not only are very helpful for understanding the atomic structures, the initial growth behaviors, and the interaction of silicene on Ag(111) surface, but also provide some useful guidelines for finding new appropriate substrate for epitaxial growth of silicene beyond Ag surface.

Methods

Ab initio calculations were performed by using density functional theory (DFT) and plane wave basis, as implemented in the Vienna Ab-initio Simulation Package (VASP)51,52. Generalized gradient approximation (GGA) with the RPBE functional was adopted to describe the exchange-correlation interaction, which was elaborately developed for the calculations of surface systems53. The core electrons were described by the projected augmented wave (PAW) method54. The kinetic energy cutoff of 400 eV for the plane wave basis was used.

In this study, we chose the Ag(111) surface as substrate since it was the major metal surface for growing large-scale silicene sheet till now11,12,13,14. The Ag(111) surface was modeled by a three-layer slab model within periodic boundary condition, which was cleaved from bulk fcc silver solid with the experimental lattice constant of 2.89 Å. The validity of this three-layer slab model was assessed by our previous studies37,39 as well as our test calculations on a five-layer slab. To avoid the interactions between adjacent periodic images, a large (7×7) supercell with dimension of 20.22 Å×20.22 Å was used for the slab model, while the supercell dimension perpendicular to the Ag(111) surface was chosen as large as 30 Å. With fixed supercell parameters, the three-layer slab model was further relaxed with the fixed bottom layer to mimic the semi-infinite solid. Then, different sized SiN and CN clusters (up to N = 24) were placed on the optimized (7×7) slab model of Ag(111) surface and the entire cluster-substrate systems were fully relaxed (also with the bottom layer of Ag atoms fixed). During the geometry optimization, a (2×2) k-point mesh including the Γ point was used to sample the reciprocal space due to the large supercell. For LDOS calculation, the k-point mesh was increased to (7×7) in order to obtain more accurate information on the electronic structures. To simulate the diffusion behavior of Si atom on Ag(111) and Rh(111) surface, the climbing image nudged elastic band (cNEB) method with convergence criterion of 0.02 eV/Å for force was used to find the diffusion path55.

The structure of Silicene@Ag(111) were investigate by three selected silicene superstructures on Ag(111) surface by compressing silicene lattice slightly to fit the metal surface56. The k-point meshes are divided into smaller than 0.03 Å−1 for silicene metal superstructures. The STM images of silicene superstructures were simulated by using the Tersoff−Hamann approximation57 with a constant height of 2 Å above the topmost Si atoms. To examine the thermal stability of silicene ML on Ag(111) surfaces, ab initio molecular dynamics simulation within the NVT ensemble58 were performed using VASP. The system for AIMD simulation refers to the most observed superstructure composed of (3×3) silicene cells and (4 × 4) Ag(111) cells with only −0.86 % mismatch. AIMD simulation at 500 K (which is the typical experimental growth temperature) lasted for 7.5 ps. To shed light on the role of Ag(111) surface, a comparative AIMD simulation of silicene ML on a strongly interacting Rh(111) surface was carried out and the simulation supercell included (4×4) silicene cell on (6×6) cell of Rh(111) surface (3.7 % mismatch). Furthermore, to distinguish whether the large mismatch or Rh(111)'s self caused worse thermal stable of silicene, a larger silicene@Ag(111) co-periodic superstructure, including (5×5) silicene cells on (7×7) Ag(111) cells (3.8% mismatch) was used to compare that of 3.7 % mismatched silicene@Rh(111) superstructure upon more than 5.0 ps AIMD simulation. The time step for all AIMD simulations was 1.0 fs. In all situations, the convergence criterion of total energy for self-consistent field (SCF) calculations was set as 10−4 eV and the convergence criterion of 0.02 eV/Å for force was used during geometry optimization.

Author Contributions

Junfeng Gao and Jijun Zhao wrote the manuscript and prepared the figures. Junfeng Gao did the calculations. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Initial geometries, interaction mechanism and high stability of silicene on Ag(111) surface

srep00861-s1.doc (12.9MB, doc)

Acknowledgments

This work was supported by the National Natural Science Foundation of China (11134005), Program for Changjiang Scholars and Innovative Research Team in University of China, Fundamental Research Funds for the Central Universities of China (No. DUT12YQ05), and Program for SCI@guoshi of CETV.

References

  1. Guzmán-Verri G. G. & Lew Yan Voon L. C. Electronic structure of silicon-based nanostructures. Phys. Rev. B 76, 075131 (2007). [Google Scholar]
  2. Cahangirov S., Topsakal M., Aktürk E., Şahin H. & Ciraci S. Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium. Phys. Rev. Lett. 102, 236804 (2009). [DOI] [PubMed] [Google Scholar]
  3. Morishita T., Nishio K. & Mikami M. Formation of single- and double-layer silicon in slit pores. Phys. Rev. B 77, 081401 (2008). [Google Scholar]
  4. Takeda K. & Shiraishi K. Theoretical possibility of stage corrugation in Si and Ge analogs of graphite. Phys. Rev. B 50, 14916–14922 (1994). [DOI] [PubMed] [Google Scholar]
  5. Yang X. & Ni J. Electronic properties of single-walled silicon nanotubes compared to carbon nanotubes. Phys. Rev. B 72, 195426 (2005). [Google Scholar]
  6. Léandri C., Oughaddou H., Aufray B., Gay J. M., Le Lay G., Ranguis A. & Garreau Y. Growth of Si nanostructures on Ag(0 0 1). Surf. Sci. 601, 262–267 (2007). [Google Scholar]
  7. Aufray B., Kara A., Vizzini S., Oughaddou H., Leandri C., Ealet B. & Le Lay G. Graphene-like silicon nanoribbons on Ag(110): A possible formation of silicene. Appl. Phys. Lett. 96, 183102–183103 (2010). [Google Scholar]
  8. De Padova P., Quaresima C., Ottaviani C., Sheverdyaeva P. M., Moras P., Carbone C., Topwal D., Olivieri B., Kara A., Oughaddou H., Aufray B. & Le Lay G. Evidence of graphene-like electronic signature in silicene nanoribbons. Appl. Phys. Lett. 96, 261905–261903 (2010). [Google Scholar]
  9. De Padova P., Quaresima C., Olivieri B., Perfetti P. & Le Lay G. Strong resistance of silicene nanoribbons towards oxidation. J. Phys. D: Appl. Phys. 44, 312001 (2011). [Google Scholar]
  10. De Padova P., Quaresima C., Olivieri B., Perfetti P. & Le Lay G. sp2 like hybridization of silicon valence orbitals in silicene nanoribbons. Appl. Phys. Lett. 98, 081909–081903 (2011). [Google Scholar]
  11. Lin C.-L., Arafune R., Kawahara K., Tsukahara N., Minamitani E., Kim Y., Takagi N. & Kawai M. Structure of Silicene Grown on Ag(111). Appl. Phys. Express 5, 045802 (2012). [Google Scholar]
  12. Feng B., Ding Z., Meng S., Yao Y., He X., Cheng P., Chen L. & Wu K. Evidence of silicene in honeycomb structures of silicon on Ag(111). Nano Lett. 12, 3507–3511 (2012). [DOI] [PubMed] [Google Scholar]
  13. Vogt P., De Padova P., Quaresima C., Avila J., Frantzeskakis E., Asensio M. C., Resta A., Ealet B. & Le Lay G. Silicene: Compelling Experimental Evidence for Graphenelike Two-Dimensional Silicon. Phys. Rev. Lett. 108, 155501 (2012). [DOI] [PubMed] [Google Scholar]
  14. Jamgotchian H., Colignon Y., Hamzaoui N., Ealet B., Hoarau J. Y., Aufray B. & Bibérian J. P. Growth of silicene layers on Ag(111): unexpected effect of the substrate temperature. J. Phys. Condens. Matter 24, 172001 (2012). [DOI] [PubMed] [Google Scholar]
  15. Fleurence A., Friedlein R., Ozaki T., Kawai H., Wang Y. & Yamada-Takamura Y. Experimental Evidence for Epitaxial Silicene on Diboride Thin Films. Phys. Rev. Lett. (2012). [DOI] [PubMed] [Google Scholar]
  16. Ding Y. & Ni J. Electronic structures of silicon nanoribbons. Appl. Phys. Lett. 95, 083115–083113 (2009). [Google Scholar]
  17. Lebègue S. & Eriksson O. Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 79, 115409 (2009). [Google Scholar]
  18. Şahin H., Cahangirov S., Topsakal M., Bekaroglu E., Akturk E., Senger R. T. & Ciraci S. Monolayer honeycomb structures of group-IV elements and III–V binary compounds: First-principles calculations. Phys. Rev. B 80, 155453 (2009). [Google Scholar]
  19. Liu C.-C., Jiang H. & Yao Y. Low-energy effective Hamiltonian involving spin-orbit coupling in silicene and two-dimensional germanium and tin. Phys. Rev. B 84, 195430 (2011). [Google Scholar]
  20. Chen L., Liu C.-C., Feng B., He X., Cheng P., Ding Z., Meng S., Yao Y. & Wu K. Evidence for Dirac Fermions in a Honeycomb Lattice Based on Silicon. Phys. Rev. Lett. 109, 056804 (2012). [DOI] [PubMed] [Google Scholar]
  21. Liu C.-C., Feng W. & Yao Y. Quantum Spin Hall Effect in Silicene and Two-Dimensional Germanium. Phys. Rev. Lett. 107, 076802 (2011). [DOI] [PubMed] [Google Scholar]
  22. Ni Z., Liu Q., Tang K., Zheng J., Zhou J., Qin R., Gao Z., Yu D. & Lu J. Tunable Bandgap in Silicene and Germanene. Nano Lett. 12, 113–118 (2011). [DOI] [PubMed] [Google Scholar]
  23. Drummond N. D., Zólyomi V. & Fal'ko V. I. Electrically tunable band gap in silicene. Phys. Rev. B 85, 075423 (2012). [Google Scholar]
  24. Kamal C. Controlling Band Gap in Silicene Monolayer Using External Electric Field. arXiv:1202.2636v1[cond-mat.mes-hall] (2012). [Google Scholar]
  25. O'Hare A., Kusmartsev F. V. & Kugel K. I. A Stable “Flat” Form of Two-Dimensional Crystals: Could Graphene, Silicene, Germanene Be Minigap Semiconductors? Nano Lett. 12, 1045–1052 (2012). [DOI] [PubMed] [Google Scholar]
  26. Osborn T. H., Farajian A. A., Pupysheva O. V., Aga R. S. & Lew Yan Voon L. C. Ab initio simulations of silicene hydrogenation. Chem. Phys. Lett. 511, 101–105 (2011). [Google Scholar]
  27. Houssa M., Scalise E., Sankaran K., Pourtois G., Afanas'ev V. V. & Stesmans A. Electronic properties of hydrogenated silicene and germanene. Appl. Phys. Lett. 98, 223107–223103 (2011). [Google Scholar]
  28. Wang X.-Q., Li H.-D. & Wang J.-T. Induced ferromagnetism in one-side semihydrogenated silicene and germanene. Phys. Chem. Chem. Phys. 14, 3031–3036 (2012). [DOI] [PubMed] [Google Scholar]
  29. Ding Y. & Wang Y. Electronic structures of silicene fluoride and hydride. Appl. Phys. Lett. 100, 083102–083104 (2012). [Google Scholar]
  30. Gao N., Zheng W. T. & Jiang Q. Density functional theory calculations for two-dimensional silicene with halogen functionalization. Phys. Chem. Chem. Phys. 14, 257–261 (2012). [DOI] [PubMed] [Google Scholar]
  31. Kara A., Enriquez H., Seitsonen A. P., Lew Yan Voon L. C., Vizzini S., Aufray B. & Oughaddou H. A review on silicene — New candidate for electronics. Surf. Sci. Rep. 67, 1–18 (2012). [Google Scholar]
  32. Jose D. & Datta A. Structures and electronic properties of silicene clusters: a promising material for FET and hydrogen storage. Phys. Chem. Chem. Phys. 13, 7304–7311 (2011). [DOI] [PubMed] [Google Scholar]
  33. Gao J., Yip J., Zhao J., Yakobson B. I. & Ding F. Graphene Nucleation on Transition Metal Surface: Structure Transformation and Role of the Metal Step Edge. J. Am. Chem. Soc. 133, 5009–5015 (2011). [DOI] [PubMed] [Google Scholar]
  34. Gao J., Yuan Q., Hu H., Zhao J. & Ding F. Formation of Carbon Clusters in the Initial Stage of Chemical Vapor Deposition Graphene Growth on Ni(111) Surface. J. Phys. Chem. C 115, 17695–17703 (2011). [Google Scholar]
  35. Lacovig P., Pozzo M., Alfè D., Vilmercati P., Baraldi A. & Lizzit S. Growth of Dome-Shaped Carbon Nanoislands on Ir(111): The Intermediate between Carbidic Clusters and Quasi-Free-Standing Graphene. Phys. Rev. Lett. 103, 166101 (2009). [DOI] [PubMed] [Google Scholar]
  36. Wu P., Jiang H., Zhang W., Li Z., Hou Z. & Yang J. Lattice Mismatch Induced Nonlinear Growth of Graphene. J. Am. Chem. Soc. 134, 6045–6051 (2012). [DOI] [PubMed] [Google Scholar]
  37. Yuan Q., Gao J., Shu H., Zhao J., Chen X. & Ding F. Magic Carbon Clusters in the Chemical Vapor Deposition Growth of Graphene. J. Am. Chem. Soc. 134, 2970–2975 (2011). [DOI] [PubMed] [Google Scholar]
  38. Gao J., Zhao J. & Ding F. Transition Metal Surface Passivation Induced Graphene Edge Reconstruction. J. Am. Chem. Soc. 134, 6204–6209 (2012). [DOI] [PubMed] [Google Scholar]
  39. Cheng D., Barcaro G., Charlier J.-C., Hou M. & Fortunelli A. Homogeneous Nucleation of Graphitic Nanostructures from Carbon Chains on Ni(111). J. Phys. Chem. C 115, 10537–10543 (2011). [Google Scholar]
  40. Meng L., Sun Q., Wang J. & Ding F. Molecular Dynamics Simulation of Chemical Vapor Deposition Graphene Growth on Ni (111) Surface. J. Phys. Chem. C 116, 6097–6102 (2012). [Google Scholar]
  41. Amara H., Bichara C. & Ducastelle F. Formation of carbon nanostructures on nickel surfaces: A tight-binding grand canonical Monte Carlo study. Phys. Rev. B 73, 113404 (2006). [Google Scholar]
  42. Wu P., Zhang W., Li Z., Yang J. & Hou J. G. Communication: Coalescence of carbon atoms on Cu (111) surface: Emergence of a stable bridging-metal structure motif. J. Chem. Phys. 133, 071101–071104 (2010). [DOI] [PubMed] [Google Scholar]
  43. Zhu X. & Zeng X. C. Structures and stabilities of small silicon clusters: Ab initio molecular-orbital calculations of Si7 – Si11. J. Chem. Phys. 118, 3558–3570 (2003). [DOI] [PubMed] [Google Scholar]
  44. Zhu X. L., Zeng X. C., Lei Y. A. & Pan B. Structures and stability of medium silicon clusters. II. Ab initio molecular orbital calculations of Si12 – Si20. J. Chem. Phys. 120, 8985–8995 (2004). [DOI] [PubMed] [Google Scholar]
  45. Yoo S. & Zeng X. C. Structures and relative stability of medium-sized silicon clusters. IV. Motif-based low-lying clusters Si21 – Si30. J. Chem. Phys. 124, 054304–054306 (2006). [DOI] [PubMed] [Google Scholar]
  46. Kosimov D. P., Dzhurakhalov A. A. & Peeters F. M. Carbon clusters: From ring structures to nanographene. Phys. Rev. B 81, 195414 (2010). [Google Scholar]
  47. Kumar V. Nanosilicon. (Elsevier Science, 2007). [Google Scholar]
  48. Wang J., Zhao J., Ma L., Wang G. & King R. B. Stability and magnetic properties of Fe encapsulating in silicon nanotubes. Nanotechnology 18, 235705 (2007). [Google Scholar]
  49. Mulliken R. S. Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I. J. Chem. Phys. 23, 1833–1840 (1955). [Google Scholar]
  50. Kara A., Vizzini S., Leandri C., Ealet B., Oughaddou H., Bernard A. & Le Lay G. Silicon nano-ribbons on Ag(110): a computational investigation. J. Phys. Condens. Matter 22, 045004 (2010). [DOI] [PubMed] [Google Scholar]
  51. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  52. Kresse G. & Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996). [DOI] [PubMed] [Google Scholar]
  53. Hammer B., Hansen L. B. & Nørskov J. K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 59, 7413–7421 (1999). [Google Scholar]
  54. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
  55. Henkelman G., Uberuaga B. P. & Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000). [Google Scholar]
  56. Giovannetti G., Khomyakov P. A., Brocks G., Karpan V. M., van den Brink J. & Kelly P. J. Doping Graphene with Metal Contacts. Phys. Rev. Lett. 101, 026803 (2008). [DOI] [PubMed] [Google Scholar]
  57. Tersoff J. & Hamann D. R. Theory and Application for the Scanning Tunneling Microscope. Phys. Rev. Lett. 50, 1998–2001 (1983). [Google Scholar]
  58. Windiks R. & Delley B. Massive thermostatting in isothermal density functional molecular dynamics simulations. J. Chem. Phys. 119, 2481–2487 (2003). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Initial geometries, interaction mechanism and high stability of silicene on Ag(111) surface

srep00861-s1.doc (12.9MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES