SUMMARY
How cells form global, self-organized structures using genetically encoded molecular rules remains elusive. Here, we take a synthetic biology approach to investigate the design principles governing cell polarization. First, using a coarse-grained computational model, we searched for all possible simple networks that can achieve polarization. All solutions contained one of three minimal motifs – positive feedback, mutual inhibition, or inhibitor with positive feedback. These minimal motifs alone could achieve polarization under limited conditions; circuits that combined two or more of these motifs were significantly more robust. With these design principles as a blueprint, we experimentally constructed artificial polarization networks in yeast, using a toolkit of chimeric signaling proteins that spatially direct the synthesis and degradation of phosphatidylinositol (3,4,5)-trisphosphate (PIP3). Circuits with combinatorial motifs yielded clear foci of synthetic PIP3 that can persist for nearly an hour. Thus, by harnessing localization-regulated signaling molecules, we can engineer simple molecular circuits that reliably execute spatial self-organized programs.
INTRODUCTION
A hallmark of living cells is their ability to form complex structures that are essential for their function. Remarkably, such cellular structures arise through a process of self-organization – the individual molecules in a cell function as a coherent system to create global order, despite the fact that these molecules are distributed and can only execute simple local regulatory rules (Kirschner et al., 2000; Karsenti, 2008; Liu and Fletcher, 2009; Loose et al., 2011). How molecular self-organizing systems dynamically shape the spatial organization of the cell remains a central question in cell biology. Ultimately, if we could understand how to engineer spatial self-organizing systems, this would have important implications in controlling cellular shape, movement, and function, or in the engineering of complex non-biological molecular systems (Rafelski and Marshall, 2008).
One of the most fundamental examples of cellular spatial self-organization is polarization – the asymmetric distribution of key molecules within the cell (Drubin and Nelson, 1996; Shapiro et al., 2002; Macara and Mili, 2008). Polarization is a fundamental building block upon which many other more complex spatial behaviors are constructed. Motile cells must polarize to generate a distinct front and back, one associated with extension and the other with contraction, thus allowing them to move in one direction (Mogilner and Oster, 2003; Wang, 2009; Swaney et al., 2010). Similarly, epithelial cells must polarize to yield distinct apical and basal surfaces (St Johnston and Ahringer, 2010; McCaffrey and Macara, 2011). During development, key cells polarize before undergoing asymmetric cell division, leading to daughter cells that inherit distinct molecular components and ultimately, distinct fates (Doe, 2001; St Johnston and Ahringer, 2010; Nance and Zallen, 2011). In the developing nervous system, neurons polarize to form distinct dendritic and axonal structures (Inagaki et al., 2011). Even a single-celled organism such as Saccharomyces cerevisiae must polarize during the processes of budding and mating (Drubin and Nelson, 1996; Irazoqui and Lew, 2004; Wedlich-Soldner et al., 2004; Slaughter et al., 2009; Johnson et al., 2011).
Prior theoretical work has explored potential mechanisms for cell polarization, from simple models based on local positive feedback and global inhibition, to far more detailed models that attempt to explicitly explain the molecular interactions in specific examples of cell polarization (Gierer and Meinhardt, 1972; Meinhardt and Gierer, 2000; Wedlich-Soldner et al., 2003; Jilkine and Edelstein-Keshet, 2011; Mogilner and Odde, 2011; Mogilner et al., 2012). Nevertheless, a unified picture of the overall design principles of polarization circuits has been elusive. For example, do we understand polarization sufficiently that we know how to design polarization circuits from scratch?
This type of synthetic biology question presents an alternative and complementary approach to investigating cell polarization, focusing on how one can design molecular systems that polarize, rather than focusing on any one particular example of polarization. Such an approach can potentially reveal the design principles that govern polarization by raising a unique set of questions. At the network level, what are the simplest circuits that can robustly achieve polarization? Are there multiple general classes of solutions, and if so, do they have distinct functional advantages and limitations? Can we use our understanding to construct novel polarization systems in which an engineered set of genetically encoded molecules and their local interactions can control global cellular organization?
Most work in synthetic biology to date has focused on engineering circuits that control scalar output quantities (e.g. gene expression) over time, and relatively little work has explored how to engineer spatial control circuits (Purnick and Weiss, 2009; Khalil and Collins, 2010; Nandagopal and Elowitz, 2011). Thus, if we want the ability to synthetically control spatial behaviors, we will need to develop components that can encode and transmit spatial regulatory information.
Here, we integrate theory and experiment to explore the design principles underlying cell polarization. Using a coarse-grained computational model, we enumerated all possible one- and two–node circuits that can polarize. We compared the functional constraints and robustness of the core networks that emerged. Using this computational analysis as a guide, we genetically engineered artificial polarization circuits that produce phosphatidylinositol (3,4,5)-trisphosphate (PIP3) poles when expressed in yeast. The links in these synthetic circuits were implemented by fusing catalytic modules that create or degrade PIP3 to recognition modules that spatially target these catalytic activities. This combination of computational and experimental analysis results in a more general understanding of the core requirements for locally-driven interaction networks that can yield polarization and demonstrates that it is possible to program artificial self-organizing spatial control circuits in living cells.
RESULTS
Coarse-grained computational framework for simulating cell polarization
We sought to enumerate all possible simple molecular regulatory networks that could yield polarization to better understand the design principles governing this fundamental self-organizing behavior (Figure 1A). In natural networks, core network motifs may be obscured by evolutionary history and pleiotropic function (Ma et al., 2006; 2009).
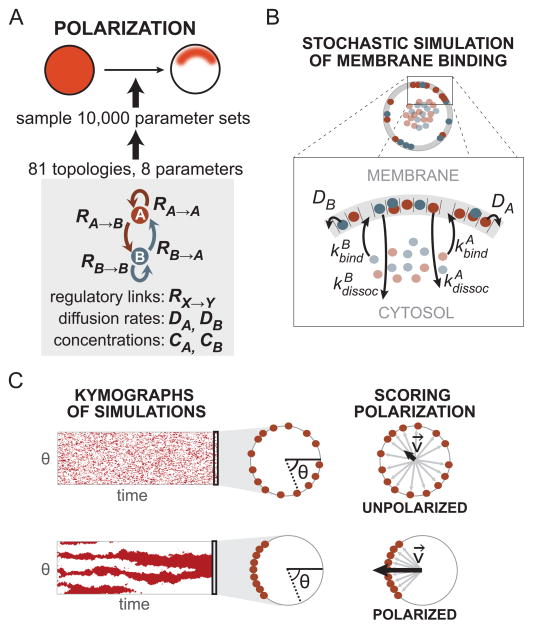
Figure 1. Coarse-grained computational model for cell polarization.
(A) Self-organizing cell polarization is defined as the spontaneous asymmetric organization of a polarity marker (red) within the cell. All 81 regulatory network topologies consisting of one or two components were tested for their ability to generate polarization. Each network topology was sampled using sets of parameters representing strengths of regulatory links (RX→Y), diffusion rates (DX), and component concentrations (CX). (B) The cell is modeled as a one-dimensional membrane lattice with a well-mixed cytosol. Simple binding and dissociation reactions, as well as lateral diffusion of membrane-bound components, are simulated at each lattice location using a stochastic simulation algorithm. (C) The spatial distribution of membrane-bound polarity markers changes throughout the simulation, as can be seen on the kymographs. After the system has reached steady-state, a polarity score P is calculated as the magnitude of the vector sum of all membrane-bound polarity markers, normalized by the maximum possible magnitude for a lattice of size L (see Extended Experimental Procedures). For all subsequent analyses, systems with P>0.6 are classified as polarized.
We developed a computational framework simple enough to enable efficient screening of a large number of network architectures, yet complex enough to represent the essential spatial behavior of polarization. We decided to explore the full space of two-node networks. The two nodes represent two molecular species – a “polarity marker” species whose distribution we measure, and a second, “regulatory” species that has the potential to alter the behavior of the polarizing species (Figure 1A). The full circuit space is defined by different combinations of regulatory links between the two nodes (either positive, negative, or no link), as well as self-regulation (positive, negative, or no feedback), yielding a total of 81 possible network architectures.
We implemented a coarse-grained model in which the plasma membrane is represented by a one-dimensional circular lattice (of size 100) surrounding a “cytosolic” pool of the two molecules (Figure 1B). Many examples of cell polarization involve localization of molecules to the plasma membrane. Thus, we defined reactions to be simple membrane-binding and dissociation reactions (Figure 1B) and polarization as the asymmetric distribution of the polarity marker along the membrane.
We used a stochastic algorithm to simulate binding and dissociation events (Gillespie, 1977). Thus, at lattice location i, a signaling component X bound to the membrane with rate kXbind(i) or a membrane-bound component X dissociated into the cytosol with rate kXdissoc(i). Regulatory interactions due to membrane-bound molecules at neighboring positions in the lattice act by modifying the binding and dissociation rates, kXbind(i) and kXdissoc(i) respectively. Lateral diffusion rates for each component within the membrane were also defined as parameters in the model (DX, Figure 1B). We treated the cytosol as a well-mixed reservoir and simulate only lateral diffusion on the membrane, assuming that membrane binding and dissociation occur on a much slower timescale than cytosolic diffusion.
In natural polarization circuits, local regulatory interactions between molecules can occur through mechanisms such as enzymatic reactions, physical recruitment, and cytoskeletal transport. We chose a generalizable, abstract representation of local regulatory interactions that modeled the overall effect of regulation rather than its implementation. The regulatory links in our model affected the local apparent membrane affinities of the signaling components by changing basal binding and dissociation reaction rates (see Extended Experimental Procedures for full equations). A positive regulatory link from node X to Y (RX→Y > 0) increased the binding rate of Y, kYbind(i), and decreased the dissociation rate of Y, kYdissoc(i), as a function of the local concentration of membrane-bound X at lattice location i. This effectively increased the local concentration of membrane-bound Y in the vicinity of membrane-bound X, leading to “positive feedback” when Y=X or “cross activation” when Y ≠ X. The reverse was true for negative, “inhibitory” links.
We enumerated all network topologies by combinatorially varying the possible regulatory links between two network nodes (Figure 1A). Note that a network topology only encodes the types of regulatory interactions between the nodes, whereas the magnitudes of these regulatory interactions are specified as parameters.
Scoring polarization and searching parameter space for robust networks
After each simulation reached steady state, a polarization score (P) was calculated as the normalized magnitude of the vector sum of each of the membrane-bound polarity markers (Figure 1C, see Extended Experimental Procedures). A non-polarized cell with a random distribution of membrane-bound polarity markers resulted in many randomly oriented vectors and thus, low P (Figure 1C, top). In a polarized cell with a cluster of membrane-bound polarity markers, many aligned vectors resulted in a high P (Figure 1C, bottom).
To test the robustness of each network topology, we sampled the performance of the network topology with 10,000 parameter sets (Figure 1A). Each network had at most eight associated parameters - the strengths of the four network regulatory links, the lateral membrane diffusion rates of the two molecular species, and the concentrations of the two molecular species. We scored each network topology by its polarization robustness, Q, the fraction of parameter sets that polarized with P > 0.6 (Dassow et al., 2000). More robust topologies are most likely to emerge through a semi-random process such as evolution and are also likely the easiest targets for engineering of polarization networks.
Identification of three minimal network motifs for cell polarization
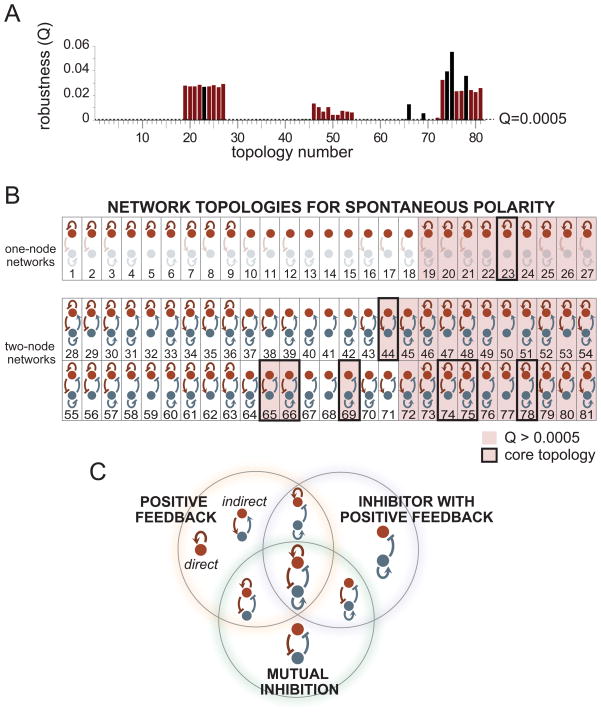
Within the complete set of 81 network topologies, 33 (or 41%) were able to polarize with a robustness of Q>0.0005 (Figure 2A). The performance of these 33 candidate topologies consistently stood out above background, even when we altered the basal conditions of the simulations (Figure S1A). Further, to confirm that our parameter sampling was sufficient, we tested a subset of representative topologies using five times larger sample size (50,000 parameter sets) and found that robustness values did not change significantly (Figure S1B).
Figure 2. Three minimal motifs drive robust self-organizing cell polarization.
(A) For each of the 81 network topologies, a robustness score Q was calculated as the fraction of parameter sets that resulted in a polarized distribution of membrane-bound polarity markers. Topologies with Q>0.0005 were chosen as candidates for further analyses. Core topologies are indicated as black bars. (B) Within the set of candidate network topologies, eight were identified as core network topologies for cell polarization after elimination of degenerate topologies. Note that although topologies 1–27 do not contain a link from the regulator node back to the polarity marker and are therefore equivalent to single-node topologies consisting only of the polarizing species, they were nonetheless tested individually. (C) Each of the eight core network topologies contains one or more minimal motifs: positive feedback, mutual inhibition, and inhibitor with positive feedback. See also Figures S1 and S2.
We hypothesized that some of the candidate topologies were degenerate, i.e. they contain regulatory links that are either extraneous or detrimental to performance. We compared the Q value of each network topology with the Q values of all its “ancestor” topologies consisting of one fewer regulatory links (Figure S2A). If a network topology was more robust than all of its ancestors, then all of the regulatory links were indeed essential and we considered it to be a new core network topology. If a network topology failed to display increased robustness in comparison to at least one of its ancestors, then some of its regulatory links were unnecessary elaborations, and the topology was considered degenerate. After this analysis, only 8 out of the 33 candidate topologies were classified as core network topologies (Figure 2B), all of which achieve polarization over similar ranges of time scales depending on parameters (Figure S2B).
Within the core network topologies, we observed three recurring minimal motifs: positive feedback on the polarizing molecule, either direct (topology 23) or indirect (topology 44); an inhibitor with positive feedback (topology 69); and mutual inhibition (topology 65). All of the eight core topologies that emerged from our analysis were found to contain one or more of these three minimal motifs (Figure 2C). Note that for simplicity, direct and indirect positive feedback are considered to be different implementations of the same minimal motif of positive feedback. But as subsequent analyses will show, these two implementations in fact display distinct robustness behaviors.
Minimal motifs only achieve polarization within constrained regions of parameter space; combination motifs are more robust
Since all of the identified core network topologies could be constructed using one or more of these three minimal motifs (Figure 2C), we asked if there were functional differences between minimal motifs and topologies that contained motif combinations. We explored how distinct topologies performed when biological parameters, such as component concentrations, diffusion constants, and regulation strengths, were varied.
We first investigated each topology’s robustness to variation in concentrations of signaling components. For each of the three minimal motifs, we performed finer sampling (100,000 parameter sets), binned parameter sets by concentrations, and calculated each motif’s robustness Q to variation in the remaining parameters (regulation strengths and diffusion constants). We visualized the robustness landscape as a heatmap in two-dimensional concentration space (Figure 3A, i–iv).
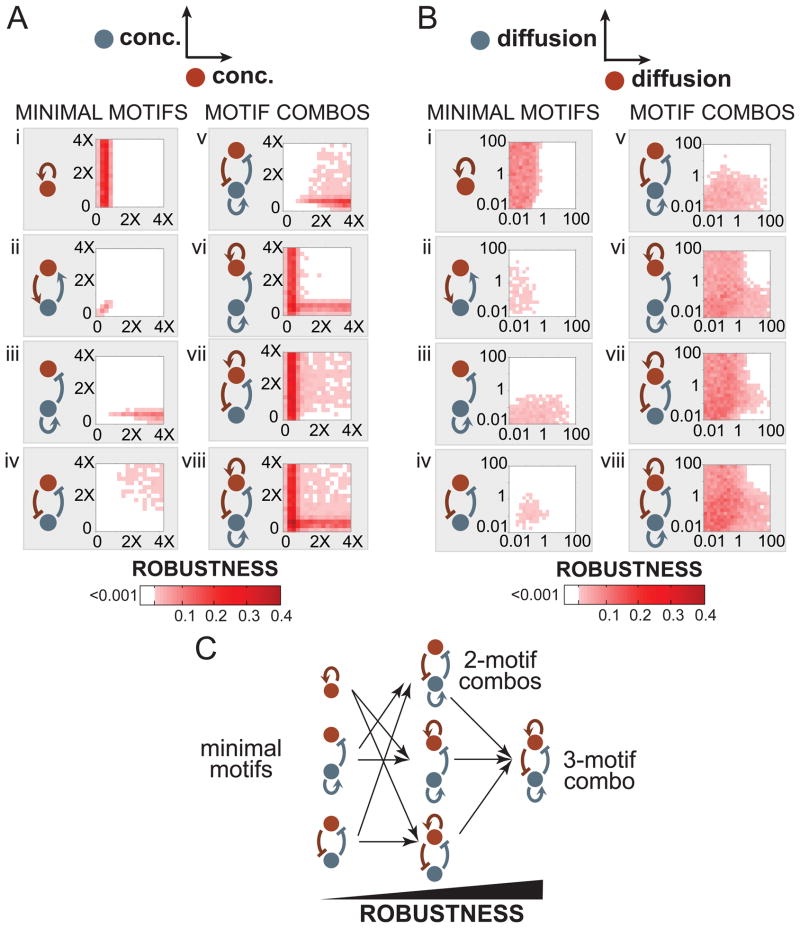
Figure 3. Combining minimal motifs increases robustness to variation in component concentrations and lateral diffusion rates.
Robustness landscapes are projected onto a two-dimensional parameter space representing either (A) component concentrations, defined relative to the total number of binding sites or (B) component lateral diffusion rates, defined as dimensionless ratios relative to the basal binding rate kon. Projections are visualized as heatmaps with robustness indicated by color. In both cases, minimal motifs alone (i to iv) can polarize robustly only in small, limited regions of parameter space, while topologies consisting of motif combinations (v to viii) can polarize robustly in expanded regions of parameter space. (C) Combining minimal motifs into more complex circuitry enables self-organizing polarization over larger ranges of parameter values and thus, increases the topology’s robustness to parameter variations. See Figure S3.
The positive feedback minimal motif can achieve polarization, but only within a limited region of concentration space (Figure 3A, i). For direct positive feedback, polarization requires a limiting concentration of the polarizing species -- less than the number of total binding sites on the membrane. This observation is consistent with previous studies in which a network combining self-activation with limiting concentrations (a form of “local activation and global inhibition”) was capable of both polarization and pattern formation (Gierer and Meinhardt, 1972; Meinhardt and Gierer, 2000; Altschuler et al., 2008). Intuitively, a network with positive feedback and an excess concentration of molecules fails to robustly polarize because the molecules simply promote each other’s binding, leading to symmetric saturation of the membrane. Our analysis also shows that indirect positive feedback networks (involving a secondary activator) are even more constrained in concentration space (Figure 3A, ii). Because the feedback loop involves both of the network nodes, both red and blue molecules must be present in limiting concentrations to yield asymmetric membrane binding.
The inhibitor with positive feedback motif displays distinct robustness constraints (Figure 3A, iii). The inhibitor must be present in limiting concentrations, and an excess concentration of the polarity marker is required. The inhibitor’s positive feedback combined with a limiting concentration effectively implements asymmetric clustering of the inhibitor on the membrane. The asymmetric spatial organization of the inhibitor then restricts the localization of the polarity marker, resulting in polarization.
The third minimal motif we observed was mutual inhibition between the two nodes. Although cross-antagonism between two components (a double negative feedback loop) can in some contexts be considered to be equivalent to positive feedback (Meinhardt and Gierer, 2000), our results indicate that in this spatial context, this motif is actually highly distinct in behavior (Figure 3A, iv). Specifically, mutual inhibition can drive polarization in the presence of excess concentrations of both signaling components, and limiting concentrations actually hinder its ability to self-organize polarization.
Thus, although each minimal motif can generate cell polarization, it is only able to do so in limited regions of concentration space. Combining motifs into more complex topologies, however, increases robustness to concentration variations. For example, coupling mutual inhibition to an inhibitor with positive feedback enables polarization in a larger fraction of concentration space (Figure 3A, v–viii) when compared to either of the minimal motifs alone. Combining all three motifs resulted in the most robust self-organizing polarization topology (Figure 3A, viii).
A similar increased robustness of combinatorial networks was also observed with respect to variation of other parameters such as diffusion constants and regulatory strengths. In “diffusion space” where lateral diffusion rates of the molecular species were varied (Figure 3B) and in “regulation space” where regulatory link strengths were varied (Figure S3), combinatorial networks drove polarization with higher tolerance to parameter variations. In all three situations, a topology containing all three minimal motifs is the most robust (Figure 3C).
Engineering synthetic PIP3 polarization in yeast: Building new regulatory interactions using combinations of modular localization and catalytic domains
Our computational analysis defines the landscape of possible polarization circuits and provides a guide for the design of new polarization circuits. To test these findings, we attempted to construct synthetic polarization circuits and to systematically probe the in vivo requirements for spatial self-organization.
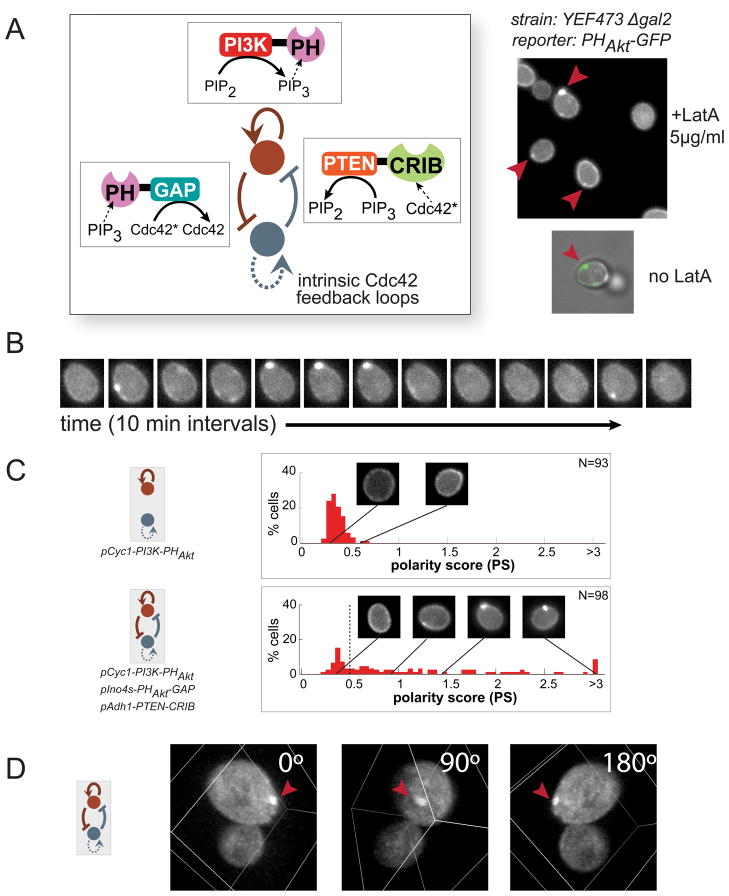
We chose the membrane-associated phospholipid species, phosphatidylinositol (3,4,5)-trisphosphate (PIP3) as a novel polarity marker in S. cerevisiae (Figure 4A). Although PIP3 is an important polarization marker in higher eukaryotic cells, PIP3 is not normally present in budding yeast (Dove et al., 1997; Rodríguez-Escudero et al., 2005). The total amount of PIP3 in yeast can be controlled by expressing lipid kinases and phosphatases from higher eukaryotes – PI3 kinase, which converts PIP2 to PIP3, and PTEN, the lipid phosphatase that converts PIP3 to PIP2 (Rodríguez-Escudero et al., 2005). Thus variants of these enzymes could be engineered to act as specific regulatory links controlling PIP3 generation and degradation, if we could find a way to spatially target their activities. The spatial distribution of PIP3 can also be easily tracked with an in vivo reporter (the PH domain of Akt).
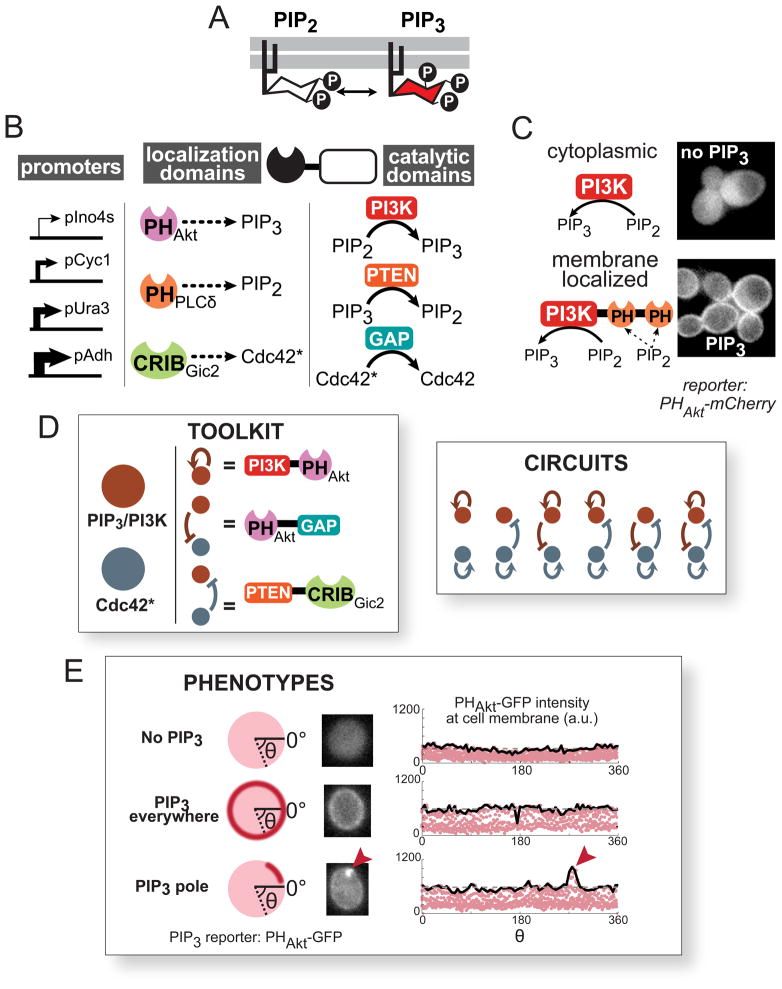
Figure 4. Construction of a synthetic polarization system using PIP3, a phospholipid not normally found in S. cerevisiae.
(A) Phosphatidylinositol (4,5)-bisphosphate (PIP2) can be reversibly phosphorylated to become PIP3. (B) Modular localization domains can be fused to catalytic domains to direct enzyme activity to specific subcellular locations. Pleckstrin homology (PH) domains bind specific phospholipid headgroups, and the CRIB (Cdc42/Rac interactive binding) domain of Gic2 localizes to activated Cdc42 (herein denoted as Cdc42*). Catalytic domains were truncated or mutated to achieve localization-dependent activity. Expression was tuned using a set of different strength constitutive yeast promoters. (C) PI3K does not produce PIP3 unless localized by the PH domain of PLCδ (PHPLCδ) to its substrate, PIP2, at the plasma membrane. The PH domain of Akt (PHAkt) fused to mCherry is used as a reporter for PIP3. See also Figure S4. (D) Using the localization and catalytic domains described above, a toolkit of enzymatic fusions is created analogous to the regulatory links in the computational model. Using this toolkit, we experimentally tested a subset of the predicted core network topologies and determined the resulting phenotypes. (E) Using 2xPHAkt-2xGFP as a reporter, we classify cells into three phenotypes: no visible PIP3, PIP3 everywhere on the plasma membrane, and a localized pole of PIP3 (see Extended Experimental Procedures). Fluorescence images of individual cells are cropped to contain only one cell, and pixel intensities at the cell membrane are plotted (red dots, right). The maximum intensity along the cell membrane (solid black line) is used to calculate the polarity score (See Figure S4). A cell without PIP3 (top) displays uniform, low intensity background fluorescence along its periphery. A cell with PIP3 everywhere (middle) displays uniform high intensity fluorescence along its edge. A cell with a PIP3 pole (bottom) has a fluorescence intensity peak indicating a local concentration of PIP3 (red arrow).
To build specific spatially-controlled links in PIP3 regulatory circuits, we fused the catalytic domains from PI3K or PTEN to different localization domains (Figures 4B, 4C, and S4). For example, to generate a positive feedback regulatory link for PIP3, we fused a PIP3-binding domain (PHAkt) to the PI3K catalytic domain (p110α). This fusion protein should produce more PIP3 at a location that already has PIP3 (i.e. “IF PIP3, THEN make more PIP3”). Using this strategy, fusion proteins made from combinations of localization and catalytic domains can be used to create diverse spatially-controlled regulatory links in a PIP3-generating network.
A fusion protein will only function as a conditional regulatory link if its catalytic function depends on its localization. We demonstrated that the PI3K catalytic domain (p110α) does not produce PIP3 at the membrane unless properly localized. Expression of the catalytic domain alone does not lead to membrane localization of a PIP3 reporter, 2xPHAkt-2xGFP (Figure 4C). However, when PI3K is targeted to the plasma membrane (where PIP2 is present), PIP3 is produced. Similar localization dependent function is observed for the PTEN phosphatase catalytic domain (Figure S4).
To create a second regulatory node to serve as an inhibitor of the polarizing molecule, we utilized the endogenous GTPase protein Cdc42 as an opposing landmark. Cdc42, which exists in two distinct states (one active GTP-bound and one inactive GDP-bound), is an ideal inhibiting regulatory node. Active Cdc42 localizes to the membrane in a highly polarized manner via a combination of catalytic- and actin transport-mediated positive feedback (Figure 4B and 4D) (Kozubowski et al., 2008). We created synthetic mutually inhibitory links between activated Cdc42 (Cdc42*) and PIP3 as follows. By fusing a Cdc42* binding domain (from the protein Gic2) to the PTEN phosphatase domain, we encoded the regulatory link: “IF Cdc42* THEN dephosphorylate PIP3”. Conversely, by fusing a PIP3 binding domain (PHAkt) to a Cdc42 GAP domain (inactivates Cdc42*) from the protein Rga1, we could encode the following regulatory link: “IF PIP3, THEN inactivate Cdc42*”.
We generated a set of chimeric enzymes corresponding to the regulatory links in the coarse-grained model (Figure 4D). By selectively transforming combinations of enzymes from this set of links into yeast, we re-created a subset of the topologies identified through our computational analysis. We could alter the strength of individual links in the circuit by altering the strength of the constitutive promoter used to express each synthetic fusion protein.
To detect the distribution of PIP3 in cells containing these synthetic circuits, we expressed a reporter protein consisting of a fluorescent protein fused to a domain that binds PIP3 (2xPHAkt-2xGFP). To simplify the automated analysis of polarization, we pretreated the cells with the drug Latrunculin A (LatA), which disrupts actin polymerization, thus preventing budding, resulting in cells which maintained their shape over a longer period of time (hours). LatA also disrupts the actin transport based positive feedback on Cdc42* (Ayscough et al., 1997) but leaves the Bem1/Cdc24 protein-based positive feedback loop intact (Ziman et al., 1993; Wedlich-Soldner et al., 2003; 2004; Kozubowski et al., 2008).
We classified cells bearing these synthetic circuits into three phenotypes (Figure 4E): 1) no visible PIP3 (and therefore no PIP3 pole), 2) PIP3 observed throughout the plasma membrane (no pole), or 3) a concentrated region of PIP3 (a PIP3 pole). We used a simple metric for the polarity score: the ratio of the maximum to the mean cell-edge intensity minus one (see Figure S4B for more detail). The fraction of PHAkt-GFP recruited to the membrane (indicating PIP3 production) was also calculated and termed the “production score.” Cells with a low average production score (<0.3) were classified as “no PIP3.” Those cells with a higher production score were divided into “polarized” (maximum observed polarity score>0.5) and “PIP3 everywhere.”
Synthetic circuit that includes positive feedback and mutual inhibition can generate artificial PIP3 poles in living cells
Our model predicted the combination of all three minimal motifs to be the most robust to variations in component concentration and diffusion rates. We implemented this three-motif combination circuit by expressing all of the components of our enzymatic toolkit in one strain: PIP3 positive feedback (PI3K-PHAkt), dephosphorylation of PIP3 in response to Cdc42* (CRIBGic2-PTEN), and deactivation of Cdc42* in response to PIP3 (PHAkt-GAPRga1). This circuit combined synthetic positive feedback on PIP3 with mutual inhibition between PIP3 and Cdc42* (Cdc42* also has native positive feedback regulation). This combinatorial circuit was expected to be the most robustly performing network and thus the easiest network to implement without parameter fine-tuning.
As predicted, many (65%) of the cells expressing these three synthetic signaling proteins exhibit strong PIP3 poles (Figure 5A). Two-dimensional time-lapse images (Figures 5B and S5) show that the poles are relatively stable, lasting for tens of minutes. A three-dimensional reconstruction of one of these synthetic PIP3 poles is shown in Movie S1 and Figure 5D. Analysis of cells that have not been treated with LatA shows PIP3 poles are located roughly opposed to the bud, where Cdc42* is localized (Figures 5A and S6A). More detailed three-dimensional reconstructions of confocal time courses show that PIP3 polarization is, overall, highly persistent. In some cases, stable PIP3 polarization is observed for more than 45 minutes (Movie S2A; 50 minutes in Movie S2D). The PIP3 poles, however, are also dynamic, appearing/disappearing or dividing/fusing on the minute timescale as well as moving rapidly throughout the plasma membrane (Movie S2). Thus, two-dimensional time analysis probably underestimates pole persistence, as poles move out of the plane of focus.
Figure 5. Experimental design of synthetic PIP3 polarization networks.
(A) Three regulatory links were introduced into a yeast strain by expressing all three synthetic fusion proteins from our toolkit. Several cells in one field of view show PIP3 polarization with this most robust combination of polarization motifs (top right). In most cases, cells were treated with 5μg/ml Latrunculin A (LatA) before imaging to prevent budding. When omitting LatA treatment, PIP3 (green) polarizes away from the bud site (phase), where Cdc42* is concentrated. (B) Timecourse of PIP3 polarization demonstrates that they are dynamic but can persist for over tens of minutes (10 minute intervals between images). (C) Histograms of polarity scores (PS). Positive feedback alone (top) produces a small number of weak poles. The three-motif (bottom) combination produces significantly larger numbers of strong poles. Example images of a range of polarity scores are shown. N indicates the number of individual cells analyzed with each network topology. Maximum polarity score for each cell through observation is shown. See also Figures S5 and S6. (D) A three-dimensional rendering of a cell with polarized PIP3 (See also Movies S1 and S2).
For comparison, we also constructed an identical circuit lacking the mutual inhibitory links (PIP3 positive feedback only). To assess the frequency of polarization in both types of circuits, we analyzed ~70 cells for each circuit and measured their polarity scores. The cells containing the three-motif circuit showed a distribution with high polarity scores; cells containing only the PIP3 positive feedback motif were all clustered at low polarity scores (Figure 5C). Cells with positive feedback alone occasionally had weak poles (polarity score≥0.5), but cells with the full circuit had stronger poles with a much higher frequency. Only 5% of cells with positive feedback alone exhibited poles, with most having PIP3 everywhere on the plasma membrane. In cells with the engineered three-motif circuit, 65% of cells had PIP3 poles, many of which were much stronger than any seen with positive feedback alone. In addition, polarization in the three-motif circuit persisted longer than polarization in cells expressing positive feedback alone (Figure S6B).
Requirements for synthetic polarization: Analysis of circuit variants underscores the importance of combinatorial motifs
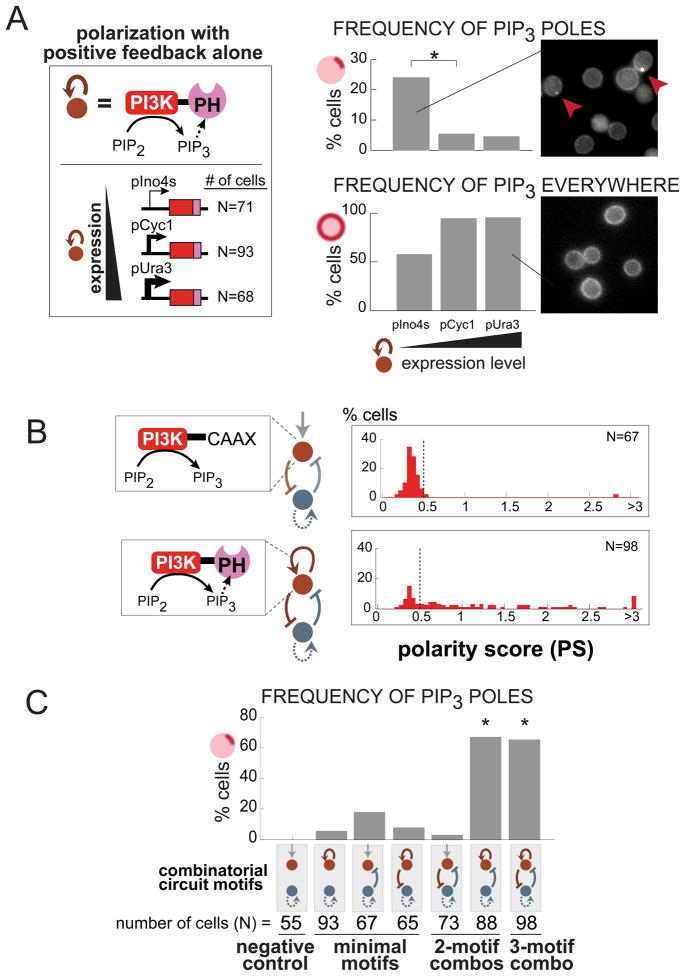
We explored the circuit requirements for PIP3 polarization, perturbing individual circuit links in our designed networks by either omitting them or altering the expression levels of the equivalent fusion protein. As described in the previous section, cells expressing only the PIP3 positive feedback loop (PI3K-PHAkt) from a medium strength promoter (pCyc1) did not show significant polarization. However, our model suggested that this class of circuit could generate polarization but would only do so in limiting concentration regimes (Figure 3A, i). A small amount of PI3K-PHAkt could create an initial quantity of PIP3 stochastically, as the enzyme encounters its substrate PI(4,5)P2 incidentally (without recruitment). This initial PIP3 would be amplified by positive feedback as PI3K-PHAkt is recruited and would phosphorylate nearby lipids. This positive feedback loop could generate transient PIP3 polarization. If the concentration of the positive feedback node (PI3K-PHAkt) is too high, however, PIP3 is likely to overtake the membrane symmetrically. We varied the expression level of the PIP3 positive feedback fusion protein alone using different constitutively active promoters (Figure 6A). In this designed circuit, PIP3 and the positive feedback fusion protein (PI3K-PHAkt) can be considered to be a single virtual node, where the concentration of the fusion protein has the potential to be limiting.
Figure 6. Network topologies with motif combinations produce PIP3 polarization more frequently, demonstrating their increased robustness.
(A) Using different strength promoters, we varied the level of PI3K-PHAkt expression. With positive feedback alone, low expression of PI3K-PHAkt produces more PIP3 poles than high expression of PI3K-PHAkt (top). High expression of PI3K-PHAkt floods the membrane with PIP3, eliminating polarization (bottom). Differences in polarization frequency between low and medium PI3K-PHAkt expression (starred) are significant with p<0.005 (Fisher’s two-tailed exact test). (B) Circuits expressing only the mutual inhibition minimal motif do not lead to strong PIP3 polarization, even when PI3K is tethered to membrane constitutively via CAAX motif fusion (without positive feedback). Thus, addition of a positive feedback link for PIP3 synthesis is necessary for strong polarization. (C) A combination of minimal motifs leads to a higher frequency of PIP3 poles compared to positive feedback alone. Starred bars are significantly different than positive feedback alone with p<0.001 (Fisher’s two-tailed exact test). See Figure S4 for details on how polarization is measured and Figures S5 and S7 for additional polarization timecourses and score histograms.
We observed that cells with lowest expression of the PIP3 positive feedback regulatory link alone (weak promoter: pIno4s) showed higher frequencies of polarization; at the lowest concentration of positive feedback, one in four cells polarized (Figure 6A). As the expression level of PI3K-PHAkt increased, fewer cells displayed polarization and instead showed more uniform PIP3 over their plasma membrane. Thus, the positive feedback only circuit can yield polarization but is highly sensitive to enzyme concentration, consistent with theoretical predictions (Figure 3A, i) and previous work (Altschuler et al., 2008). In kinetic experiments, when positive feedback alone (pGal10-PI3K-PHAkt expression) is rapidly induced, PIP3 polarization can be transiently observed before PIP3 becomes distributed throughout the plasma membrane (Figure S6C).
Next we dissected which interactions allowed the full three-motif circuit (Figure 5A) to produce robust PIP3 poles. We constructed a series of circuit variants in which individual regulatory link proteins were omitted and determined the percentage of PIP3-polarizing cells. Removal of the PIP3 positive feedback link resulted in loss of polarization (Figure 6B). Conversely, induction of PIP3 positive feedback in cells constitutively expressing the mutual inhibition regulatory links resulted in the rapid induction of strong polarization (Figure S6D). Moreover, expression of the mutual inhibitory links with a version of PI3K that is either cytoplasmically or plasma membrane targeted (but not positive feedback regulated) also failed to yield polarization (Figures 6B and S7B). Thus, despite the intrinsically strong polarization of Cdc42*, the mutual inhibition circuit between PIP3 and Cdc42* alone is not sufficient to confer robust PIP3 polarization (Figure 6B and S7B).
Based on this link deletion analysis, positive feedback on PIP3 and cross-inhibition from Cdc42* to PIP3 seem to be the most critical links in the network, consistent with our computational results. The PIP3 to Cdc42* inhibitory link appears less critical than predicted by modeling, perhaps because Cdc42* is endogenously a strong pole which may not require the additional spatial sharpening of this inhibitory link. The combinatorial two- or three-motif circuit that balances self-propagation with competition appears to be a circuit that is optimized for robust performance, rather than an overly complex solution to a simple biological problem.
DISCUSSION
Design principles of self-organizing cell polarization
In this study, we computationally defined the rules capable of driving self-organizing cell polarization. In the full space of simple two-node network topologies, there are eight core topologies capable of producing polarization, constructed using three minimal network motifs. Although the minimal motifs achieve polarization, each only functions in a limited and distinct regime of parameter space. Thus, if one builds the simplest possible polarizing system using one of these minimal motifs, there will be a tradeoff of having limited tolerance to parameter variation.
Combining minimal motifs into more complex networks expands the parameter space over which the system is functional. The theoretical solution most robust to variations in component concentrations, lateral diffusion rates, and regulation strengths was the combination of all three minimal motifs. Using these principles as a guide, we built synthetic polarization circuits in yeast that yielded PIP3 polarization. Consistent with our computational analysis, a circuit combining all three minimal motifs displayed strong and sustained PIP3 poles more frequently than the minimal motifs alone. Intuitively, these results suggest that the combination of self-propagation (positive feedback) balanced by competition with an opposing molecule (mutual inhibition) is one of the most robust ways to define a spatially asymmetric domain. In our experiments, we sampled a relatively small set of points throughout concentration space using the limited range of promoters available. Further varying or tuning the relative concentrations of each regulatory link could further optimize the behavior of these circuits.
Comparison to natural polarization circuits
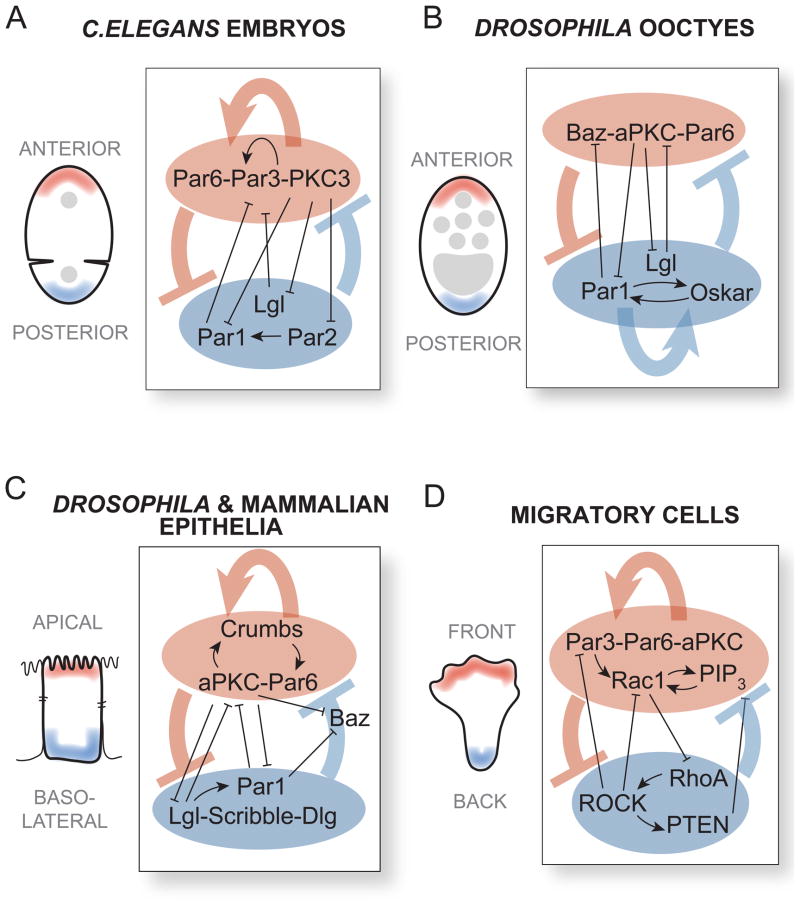
Our results suggest that natural cell polarization systems would tend to converge upon the more robust network topologies. Although natural cell polarization circuits often have highly complex architectures, examination reveals that many of these systems consistently have a combination of positive feedback and mutual inhibition at their core (Figure 7). In C. elegans embryos, the asymmetric localization of distinct proteins to the anterior and posterior domains is critical for proper development (Figure 7A) (Goldstein and Macara, 2007; St Johnston and Ahringer, 2010; Nance and Zallen, 2011). The anterior Par6/Par3/PKC-3 complex enhances its own cortical flow to the anterior domain of the embryo, effectively implementing a positive feedback loop critical for polarization (Munro et al., 2004). At the same time, phosphorylation of the posterior proteins Par2 and Lgl by PKC-3 inhibits their association with the anterior cortex (Hao et al., 2006; Hoege et al., 2010), providing one branch of cross inhibition. The posterior protein Par2 recruits Par1, preventing the localization of the anterior Par complex to the posterior cortex, supplying opposing mutual inhibition (Cuenca et al., 2003; Hao et al., 2006). Similarly, Lgl also inhibits the localization of the anterior Par complex to the posterior by a process of “mutual elimination” (Beatty et al., 2010; Hoege et al., 2010). Thus, the C. elegans embryo polarization system employs a motif-combination circuit predicted to be more robust.
Figure 7. Network topologies consisting of motif combinations are found in many well-studied polarization pathways.
(A) In C. elegans embryos and (B) Drosophila oocytes, the establishment of the anterior and posterior domains is driven by a network topology that combines positive feedback with mutual inhibition. Similar network topologies are also thought to robustly generate (C) apical and basolateral domains in Drosophila and mammalian epithelial cells as well as (D) the fronts and backs of migrating cells.
Other polarization systems also reveal regulatory networks with a similar combination of positive feedback and mutual inhibition. These include polarization of Drosophila oocytes (Figure 7B) and epithelial cell polarization (Figure 7C) (Goldstein and Macara, 2007; St Johnston and Ahringer, 2010; Nance and Zallen, 2011). Likewise, the self-organization of Rac1 and RhoA proteins to opposite poles in migratory cells such as neutrophils, fibroblasts, and Dictyostelium is directed by a regulatory circuit containing positive feedback and mutual inhibition (Xu et al., 2003; Charest and Firtel, 2007; Iden and Collard, 2008; Swaney et al., 2010). Recent studies in yeast suggest that Cdc42 polarization also involves a combination of positive feedback and negative regulation (Howell et al., 2012). Such combinatorial architectures may allow cell polarization systems to operate under a wide range of conditions.
Circuit enumeration to define design principles of spatial organization
The goal of most cell polarization models has been to explain the observed behavior of naturally polarizing systems. In this study, we adopted a different but complementary, bottom-up approach and looked for all possible solutions to the problem of cell polarization. We intentionally used network topologies containing abstract nodes and components instead of modeling specific proteins from specific polarization pathways in order to explore the general design principles of cell polarization in a system agnostic way.
While our approach is different from previous studies on cell polarization, we recover many of the earlier findings. As an example, in our study, positive feedback alone only generates polarization when the concentration of polarity marker is limiting, similar to a framework where global inhibition is implemented via a limiting pool of substrate (Gierer and Meinhardt, 1972). Without this constraint, positive feedback will symmetrically saturate the membrane with polarity markers. The minimal motif of an inhibitor with positive feedback also requires a limiting concentration of inhibitors, in order to polarize. The polarity marker becomes polarized as a consequence of the inhibitor’s spatial organization.
Our observation that mutual inhibition is the third minimal motif in polarization networks is also consistent with several previous studies. In studies of mutual inhibition in the absence of positive feedback, mutual inhibition alone has spontaneous polarization capability but only in small regions of parameter space (Gamba et al., 2005; Narang, 2006). Other groups have speculated that mutual inhibition is a useful motif when a system needs to generate both a front and a back simultaneously, as in the case of a migrating cell (Narang, 2006; Onsum and Rao, 2007).
Our theoretical analysis is broadly consistent with previous studies, but we further defined the parameter conditions under which each of the minimal motifs is capable of polarization. In doing so, we mapped the robustness landscape of polarization topologies, identifying regions of network space with highest likelihood of polarization. This network space is smooth, with clusters of network topologies capable of polarization, and motifs that combine to produce the most robust polarization. The smoothness of this landscape suggests that an evolutionary random walk could also converge on the same combinatorial networks as solutions for cell polarization.
Designing synthetic polarization: global organization by programming local molecular interactions
One of the most exciting aspects of this work is our use of computational results as a design guide for constructing an artificial polarization circuit in yeast that yields PIP3 poles. Our theoretical predictions pointed us to the set of regulatory networks with the highest probability of achieving a desired function, greatly streamlining the design process. These findings also demonstrate that it is possible to harness the molecular programming language of self-organization to generate cell polarization. Spatial control circuits can be constructed from simple protein signaling modules by localizing specific catalytic functions to diverse spatial targets. The modular separation of catalytic and localization functions makes the creation of new spatial regulatory links relatively straightforward. These types of molecular modules could potentially be harnessed by synthetic biologists to program even higher order cellular structures from the bottom up, such as complex cellular morphologies or even multicellular structures. Since cell polarization is a fundamental building block for many of these complex structures, understanding its design principles is critical for learning the rules that can control cell shape, movement and assembly.
EXPERIMENTAL PROCEDURES
Computational Framework
The plasma membrane was modeled as a 1D periodic lattice of size 100. Each lattice location has a single polarity marker membrane-binding site (A) and a single regulator membrane-binding site (B). The cytosol was treated as a well-mixed reservoir.
The system evolved over the course of the simulation as a result of binding and dissociation reactions (defined at each lattice location i). Membrane-bound A and B diffused laterally on the membrane with rates DA and DB, respectively. Reaction rates were functions of basal reaction rates and the strengths of the regulatory links in a particular network topology. Local concentrations of membrane-bound signaling components near a lattice location modulate the binding and dissociation rates of signaling components at that lattice location, weighted by the strengths of the regulatory links.
For each network topology, we used the Latin hypercube method to generate 10,000 sets of parameter combinations representing the concentrations, lateral diffusion rates of each signaling component, and strengths of all non-zero regulatory links (Table S1) (McKay et al., 1979). We simulated each of these parameter combinations using a spatially-extended variant of Gillespie’s stochastic simulation algorithm (Gillespie, 1977). After the system reached a steady state, we calculated a polarity score for each simulation run using the metric described in the main text. Refer to Extended Experimental Procedures for equations and further details on our computational methods.
Construction and expression of plasmids
Fragments encoding key domains were amplified from a plasmid or genomic DNA using PCR (Table S2), ligated into a “donor” vector, digested with the restriction enzyme AarI and ligated into a yeast integrating vector containing a promoter and terminator using the combinatorial cloning method described in (Peisajovich et al., 2010). Yeast integrating vectors were linearized and transformed into yeast strains (Table S3). Yeast cultures were grown with shaking in synthetic complete media overnight at 30°C and diluted 1:100 into fresh media the morning of the experiment. Cells were grown for 3–5 hours before imaging. See Extended Experimental Procedures and Tables S4 and S5 for more details.
Imaging conditions
96-well glass-bottomed plates were coated with Concanavalin A and washed twice with sterile water. Cells were sonicated briefly, Latrunculin A (5 μg/ml) was added and then cells were spun down into coated 96-well plates. Cells were imaged on a Nikon TE-2000 with a Nikon Apo TIRF 100X objective every 10 minutes for up to three hours. Four images were taken at each timepoint: one out-of-focus image (used for cell edge detection), one in-focus bright-field image, one mCherry fluorescence image and one GFP fluorescence image. NIS Elements files were converted into TIFF stacks with ImageJ and read into Matlab (Mathworks) for edge detection and analysis. Refer to Extended Experimental Procedures for more details.
Automated detection of polarization
Isolated cells without buds were selected for analysis. The plasma membrane was automatically detected using custom image processing software (Matlab). Pixel intensities within the membrane mask were recorded as a function of θ (Figure S4). The ratio between the maximum (Amax) and average (Amean) PIP3 signal around the membrane minus one was the “polarity score”. PHAkt recruitment was calculated as the ratio of total fluorescence at the membrane versus within the whole cell (“production score”).
Supplementary Material
HIGHLIGHTS.
Computational model identified three minimal network motifs for cell polarization
Combining minimal motifs increased robustness of polarization to parameter variation
We designed PIP3 polarization networks using engineered chimeric signaling proteins
Synthetic networks combining minimal motifs yield strong, sustained PIP3 poles
Acknowledgments
Thanks to A. Houk, C. Baker, W. Marshall, K. Mostov, D. Mullins, O. Weiner, W. Ma, C. Lee and the Lim lab, especially J. Zalatan, R. Williams and E. Puchner, for valuable comments and discussion. We thank M. Molina, V. Cid, L. Chan, E. Bi, and O. Weiner for strains and plasmids. Thanks to J. Baker-LePain and the QB3 shared computing cluster for technical support of the computational work, and the Shokat lab for PI3K inhibitor. This work was supported by an Achievement Rewards for College Scientists (ARCS) Foundation scholarship (A.H.C.), NIH NRSA fellowship 5F32GM093475 (J.M.W.), an NSF Graduate Research Fellowship (J.G.), NIH grant P50 GM081879 (W.A.L and C.T.), NIH grants PN2 EY016546 and RO1 GM062583 (W.A.L.), NSF grants DMR-0804183 and CMMI-0941355 (C.T.) and the NSF Synthetic Biology Engineering Research Center EEC-0540879 (W.A.L).
Footnotes
Supplemental Information includes Extended Experimental Procedures, seven supplemental figures, two supplemental movies and five supplemental tables.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Altschuler SJ, Angenent SB, Wang Y, Wu LF. On the spontaneous emergence of cell polarity. Nature. 2008;454:886–889. doi: 10.1038/nature07119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayscough KR, Stryker J, Pokala N, Sanders M, Crews P, Drubin DG. High rates of actin filament turnover in budding yeast and roles for actin in establishment and maintenance of cell polarity revealed using the actin inhibitor latrunculin-A. J Cell Biol. 1997;137:399–416. doi: 10.1083/jcb.137.2.399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beatty A, Morton D, Kemphues K. The C. elegans homolog of Drosophila Lethal giant larvae functions redundantly with PAR-2 to maintain polarity in the early embryo. Development. 2010;137:3995–4004. doi: 10.1242/dev.056028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charest PG, Firtel RA. Big roles for small GTPases in the control of directed cell movement. Biochem J. 2007;401:377–390. doi: 10.1042/BJ20061432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuenca AA, Schetter A, Aceto D, Kemphues K, Seydoux G. Polarization of the C. elegans zygote proceeds via distinct establishment and maintenance phases. Development. 2003;130:1255–1265. doi: 10.1242/dev.00284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Dassow G, Meir E, Munro EM, Odell GM. The segment polarity network is a robust developmental module. Nature. 2000;406:188–192. doi: 10.1038/35018085. [DOI] [PubMed] [Google Scholar]
- Doe CQ. Cell polarity: the PARty expands. Nat Cell Biol. 2001;3:E7–9. doi: 10.1038/35050684. [DOI] [PubMed] [Google Scholar]
- Dove SK, Cooke FT, Douglas MR, Sayers LG, Parker PJ, Michell RH. Osmotic stress activates phosphatidylinositol-3,5-bisphosphate synthesis. Nature. 1997;390:187–192. doi: 10.1038/36613. [DOI] [PubMed] [Google Scholar]
- Drubin DG, Nelson WJ. Origins of cell polarity. Cell. 1996;84:335–344. doi: 10.1016/s0092-8674(00)81278-7. [DOI] [PubMed] [Google Scholar]
- Gamba A, de Candia A, Di Talia S, Coniglio A, Bussolino F, Serini G. Diffusion-limited phase separation in eukaryotic chemotaxis. Proc Natl Acad Sci USA. 2005;102:16927–16932. doi: 10.1073/pnas.0503974102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik. 1972;12:30–39. doi: 10.1007/BF00289234. [DOI] [PubMed] [Google Scholar]
- Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- Goldstein B, Macara IG. The PAR proteins: fundamental players in animal cell polarization. Dev Cell. 2007;13:609–622. doi: 10.1016/j.devcel.2007.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao Y, Boyd L, Seydoux G. Stabilization of cell polarity by the C. elegans RING protein PAR-2. Dev Cell. 2006;10:199–208. doi: 10.1016/j.devcel.2005.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoege C, Constantinescu AT, Schwager A, Goehring NW, Kumar P, Hyman AA. LGL can partition the cortex of one-cell Caenorhabditis elegans embryos into two domains. Curr Biol. 2010;20:1296–1303. doi: 10.1016/j.cub.2010.05.061. [DOI] [PubMed] [Google Scholar]
- Howell AS, Jin M, Wu CF, Zyla TR, Elston TC, Lew DJ. Negative feedback enhances robustness in the yeast polarity establishment circuit. Cell. 2012;149:322–333. doi: 10.1016/j.cell.2012.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iden S, Collard JG. Crosstalk between small GTPases and polarity proteins in cell polarization. Nat Rev Mol Cell Biol. 2008;9:846–859. doi: 10.1038/nrm2521. [DOI] [PubMed] [Google Scholar]
- Inagaki N, Toriyama M, Sakumura Y. Systems biology of symmetry breaking during neuronal polarity formation. Dev Neurobiol. 2011;71:584–593. doi: 10.1002/dneu.20837. [DOI] [PubMed] [Google Scholar]
- Irazoqui JE, Lew DJ. Polarity establishment in yeast. J Cell Sci. 2004;117:2169–2171. doi: 10.1242/jcs.00953. [DOI] [PubMed] [Google Scholar]
- Jilkine A, Edelstein-Keshet L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comput Biol. 2011;7:e1001121. doi: 10.1371/journal.pcbi.1001121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JM, Jin M, Lew DJ. Symmetry breaking and the establishment of cell polarity in budding yeast. Curr Opin Genet Dev. 2011;21:740–746. doi: 10.1016/j.gde.2011.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karsenti E. Self-organization in cell biology: a brief history. Nat Rev Mol Cell Biol. 2008;9:255–262. doi: 10.1038/nrm2357. [DOI] [PubMed] [Google Scholar]
- Khalil AS, Collins JJ. Synthetic biology: applications come of age. Nat Rev Genet. 2010;11:367–379. doi: 10.1038/nrg2775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirschner M, Gerhart J, Mitchison T. Molecular “vitalism”. Cell. 2000;100:79–88. doi: 10.1016/s0092-8674(00)81685-2. [DOI] [PubMed] [Google Scholar]
- Kozubowski L, Saito K, Johnson JM, Howell AS, Zyla TR, Lew DJ. Symmetry-breaking polarization driven by a Cdc42p GEF-PAK complex. Curr Biol. 2008;18:1719–1726. doi: 10.1016/j.cub.2008.09.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu AP, Fletcher DA. Biology under construction: in vitro reconstitution of cellular function. Nat Rev Mol Cell Biol. 2009;10:644–650. doi: 10.1038/nrm2746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loose M, Kruse K, Schwille P. Protein self-organization: lessons from the min system. Annu Rev Biophys. 2011;40:315–336. doi: 10.1146/annurev-biophys-042910-155332. [DOI] [PubMed] [Google Scholar]
- Ma W, Trusina A, El-Samad H, Lim WA, Tang C. Defining network topologies that can achieve biochemical adaptation. Cell. 2009;138:760–773. doi: 10.1016/j.cell.2009.06.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma W, Lai L, Ouyang Q, Tang C. Robustness and modular design of the Drosophila segment polarity network. Mol Syst Biol. 2006;2:70. doi: 10.1038/msb4100111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macara IG, Mili S. Polarity and differential inheritance--universal attributes of life? Cell. 2008;135:801–812. doi: 10.1016/j.cell.2008.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaffrey LM, Macara IG. Epithelial organization, cell polarity and tumorigenesis. Trends Cell Biol. 2011;21:727–735. doi: 10.1016/j.tcb.2011.06.005. [DOI] [PubMed] [Google Scholar]
- McKay MD, Beckman RJ, Conover WJ. Technometrics. Vol. 21. United States: 1979. Comparison the three methods for selecting values of input variable in the analysis of output from a computer code; p. 2. [Google Scholar]
- Meinhardt H, Gierer A. Pattern formation by local self-activation and lateral inhibition. Bioessays. 2000;22:753–760. doi: 10.1002/1521-1878(200008)22:8<753::AID-BIES9>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- Mogilner A, Allard J, Wollman R. Cell polarity: quantitative modeling as a tool in cell biology. Science. 2012;336:175–179. doi: 10.1126/science.1216380. [DOI] [PubMed] [Google Scholar]
- Mogilner A, Odde D. Modeling cellular processes in 3D. Trends Cell Biol. 2011;21:692–700. doi: 10.1016/j.tcb.2011.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Oster G. Polymer motors: pushing out the front and pulling up the back. Curr Biol. 2003;13:R721–33. doi: 10.1016/j.cub.2003.08.050. [DOI] [PubMed] [Google Scholar]
- Munro E, Nance J, Priess JR. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev Cell. 2004;7:413–424. doi: 10.1016/j.devcel.2004.08.001. [DOI] [PubMed] [Google Scholar]
- Nance J, Zallen JA. Elaborating polarity: PAR proteins and the cytoskeleton. Development. 2011;138:799–809. doi: 10.1242/dev.053538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nandagopal N, Elowitz MB. Synthetic biology: integrated gene circuits. Science. 2011;333:1244–1248. doi: 10.1126/science.1207084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narang A. Spontaneous polarization in eukaryotic gradient sensing: a mathematical model based on mutual inhibition of frontness and backness pathways. J Theor Biol. 2006;240:538–553. doi: 10.1016/j.jtbi.2005.10.022. [DOI] [PubMed] [Google Scholar]
- Onsum M, Rao CV. A mathematical model for neutrophil gradient sensing and polarization. PLoS Comput Biol. 2007;3:e36. doi: 10.1371/journal.pcbi.0030036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peisajovich SG, Garbarino JE, Wei P, Lim WA. Rapid diversification of cell signaling phenotypes by modular domain recombination. Science. 2010;328:368–372. doi: 10.1126/science.1182376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purnick PEM, Weiss R. The second wave of synthetic biology: from modules to systems. Nat Rev Mol Cell Biol. 2009;10:410–422. doi: 10.1038/nrm2698. [DOI] [PubMed] [Google Scholar]
- Rafelski SM, Marshall WF. Building the cell: design principles of cellular architecture. Nat Rev Mol Cell Biol. 2008;9:593–602. doi: 10.1038/nrm2460. [DOI] [PubMed] [Google Scholar]
- Rodríguez-Escudero I, Roelants FM, Thorner J, Nombela C, Molina M, Cid VJ. Reconstitution of the mammalian PI3K/PTEN/Akt pathway in yeast. Biochem J. 2005;390:613–623. doi: 10.1042/BJ20050574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro L, McAdams HH, Losick R. Generating and exploiting polarity in bacteria. Science. 2002;298:1942–1946. doi: 10.1126/science.1072163. [DOI] [PubMed] [Google Scholar]
- Slaughter BD, Smith SE, Li R. Symmetry breaking in the life cycle of the budding yeast. Cold Spring Harb Perspect Biol. 2009;1:a003384. doi: 10.1101/cshperspect.a003384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St Johnston D, Ahringer J. Cell polarity in eggs and epithelia: parallels and diversity. Cell. 2010;141:757–774. doi: 10.1016/j.cell.2010.05.011. [DOI] [PubMed] [Google Scholar]
- Swaney KF, Huang CH, Devreotes PN. Eukaryotic chemotaxis: a network of signaling pathways controls motility, directional sensing, and polarity. Annu Rev Biophys. 2010;39:265–289. doi: 10.1146/annurev.biophys.093008.131228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F. The signaling mechanisms underlying cell polarity and chemotaxis. Cold Spring Harb Perspect Biol. 2009;1:a002980. doi: 10.1101/cshperspect.a002980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedlich-Soldner R, Wai SC, Schmidt T, Li R. Robust cell polarity is a dynamic state established by coupling transport and GTPase signaling. J Cell Biol. 2004;166:889–900. doi: 10.1083/jcb.200405061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedlich-Soldner R, Altschuler S, Wu L, Li R. Spontaneous cell polarization through actomyosin-based delivery of the Cdc42 GTPase. Science. 2003;299:1231–1235. doi: 10.1126/science.1080944. [DOI] [PubMed] [Google Scholar]
- Xu J, Wang F, Van Keymeulen A, Herzmark P, Straight A, Kelly K, Takuwa Y, Sugimoto N, Mitchison T, Bourne HR. Divergent signals and cytoskeletal assemblies regulate self-organizing polarity in neutrophils. Cell. 2003;114:201–214. doi: 10.1016/s0092-8674(03)00555-5. [DOI] [PubMed] [Google Scholar]
- Ziman M, Preuss D, Mulholland J, O’Brien JM, Botstein D, Johnson DI. Subcellular localization of Cdc42p, a Saccharomyces cerevisiae GTP-binding protein involved in the control of cell polarity. Mol Biol Cell. 1993;4:1307–1316. doi: 10.1091/mbc.4.12.1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.