Vibrational Probes and Determinants of the S = 0 ⇌ S = 2 Spin Crossover in Five-Coordinate [Fe(TPP)(CN)]⁻

Abstract

The low-frequency vibrational characterization of the spin crossover complex, five-coordinate cyano(tetraphenylporpyrinato)iron(II), [Fe(TPP)(CN)]⁻, is reported. Nuclear resonance vibrational spectroscopy has been used to measure all low-frequency vibrations involving iron at several temperatures; this yields vibrational spectra of both the low- (S = 0) and high-spin (S = 2) states. Multi-temperature oriented single-crystal measurements facilitate assignments of the vibrational character of all modes and are consistent with the DFT-predicted spectra. The availability of the entire iron vibrational spectrum allows for the complete correlation of the modes between the two spin states. These data demonstrate that not only do the frequencies of the vibrations shift to lower values for the high-spin species as would be expected owing to the weaker bonds in the high-spin state but that the mixing of iron modes with ligand modes changes substantially. Diagrams illustrating the changing character of the modes and their correlation is given. The reduced iron-ligand frequencies are the primary factor in the entropic stabilization of the high-spin state responsible for the spin crossover.

Introduction

We have previously reported the synthesis, multi-temperature structural, IR and Mössbauer spectroscopic, and magnetic characterization of the five-coordinate complex, [K(222)][Fe(TPP)-(CN)].^{1, 2} In addition to the complex being the first cyanoiron(II) porphyrinate isolated, un-expectedly the complex is not a completely low-spin (LS) complex, rather the species is a thermally-induced S=0 ⇋ S=2 spin crossover complex.¹ Surprisingly, the axial ligand field of cyanide is insufficient to yield a low-spin (LS) complex at all temperatures and a high-spin state is seen at higher temperatures.³ The spin crossover transition for [K(222)][Fe(TPP)(CN)]⁴ is gradual, but reversible, with no hysteresis over the 2–400 K temperature range explored. To our knowledge, [K(222)][Fe(TPP)(CN)] is the first spin crossover complex reported for an iron(II) porphyrinate, which is also unusual for having a coordination number of five, rather than the more common value of six in pseudo-octahedral spin crossover species. Previously known iron porphyrinate spin crossover complexes are all iron(III) species.^6–11

There is a rich history of investigating spin crossover complexes, which are especially prominent for iron(II) and iron(III) species.¹² The two most studied features of the spin transition in such complexes are the temperature-dependent magnetic properties and metal–ligand distances, which arise from a change in relative occupancies of the t_2g and e_g orbitals.¹² Temperature-dependent Mössbauer spectroscopy can also be applied to iron crossover species, independent of whether the the crossover is slow or fast on the Mössbauer time scale. Spin populations as a function of temperature can be obtained when the crossover is slow on the Mössbauer time scale (~10⁻⁷ s).

Vibrational spectroscopy has also been used to study spin crossover species, typically this has been done by following a characteristic vibration of one of the ligands. Better yet would be to monitor metal–ligand vibrations that are most directly responsive to changes of spin state.¹³ These are at relatively low frequencies and are generally difficult to observe by conventional vibrational spectroscopy such as IR and Raman, partially due to their complex spectra in this energy region¹⁴ as well as selection rules. An early study of the classical complex [Fe(phen)₂(NCS)₂] utilized iron isotopes to assign iron–ligand stretches;15 some of the low-frequency assignments were later questioned.¹³ However, the low frequency vibrations of iron complexes are conveniently studied by the synchrotron-based method nuclear resonance vibrational spectroscopy (NRVS),^{16, 17} a method that is selective and sensitive only to Mössbauer active centers, and provides direct access to all Fe vibrations.¹⁸ Therefore, NRVS presents a unique method to study iron spin transitions by displaying the low–frequency vibrational displacement spectra. The method has been applied to spin crossover complexes.¹⁹

In this study, we apply NRVS to the spin crossover complex [K(222)][Fe(TPP)(CN)]. In addition to (isotropic) powder measurements, we have also utilized oriented single-crystal NRVS measurements at several temperatures to clarify the vibrations and their assignments. These assignments have also been confirmed with DFT calculations for the two spin states. The results have allowed, for the first time, to thoroughly correlate the changing vibrational character of the two spin states. The large differences in character in the present case is the result of different mixing of the iron modes with the ligand (porphyrin) modes. Vibrational entropy calculations based on these results confirm that the reduced iron-ligand frequencies entropically stabilize the high-spin state and unexpectedly suggest the possible importance of peripheral substituents.

Experimental Section

General Information

All reactions and manipulations were carried out under argon using a double-manifold vacuum line, Schlenkware and cannula techniques. THF and hexanes were distilled over sodium/benzophenone. Chlorobenzene was washed with concentrated sulfuric acid, then with water until the aqueous layer was neutral, dried with MgSO₄, and distilled twice over P₂O₅ under argon. KCN was recrystallized and purified by a literature procedure.²⁰ Ethanethiol and Kryptofix 222 (Aldrich) were used as received. The free-base porphyrin meso-tetraphenylporphyrin (H₂TPP) was prepared according to Adler et al.21 Metalation of 95% ⁵⁷Fe enriched samples was prepared by a method similar to that of Landergren.²² [⁵⁷Fe(TPP)]₂O was prepared according to a modified Fleischer preparation.²³

Synthesis of [K(222)][⁵⁷Fe(TPP)(CN)] (single crystal and powder)

The reaction procedures described previously were used for the sample preparation.¹ [⁵⁷Fe(II)(TPP)] was prepared by reduction of [⁵⁷Fe(TPP)]₂O (27.1 mg, 0.02 mmol) with ethanethiol (0.5 mL) in benzene (8 mL) for 24 hours. Vacuum evaporation of the solvent yielded a dark purple solid to which KCN (2.9 mg, 0.044 mmol) and Kryptofix 222 (16.6 mg, 0.044 mmol) in THF or PhCl (~4 mL) was added by cannula and the mixture was stirred overnight. X-ray quality crystals were obtained in 8 mm × 250 mm sealed glass tubes by liquid diffusion using hexanes as nonsolvent. IR ν (C–N): 2070 (strong) and 2105 cm⁻¹ (weak). A powder sample was prepared by crushing the crystals. The purity of all samples was confirmed by Mössbauer measurements that showed a single quadrupole doublet at all temperatures.

Crystal Alignment and NRVS measurements

A detailed crystal alignment and NRVS measurement program has been developed.²⁴ The previously described procedures were used for single-crystal alignment on a Bruker-Nonius Kappa CCD diffractometer. Crystals of [K(222)][Fe(TPP)((CN)] are in space group Cc with four porphyrin molecules in the unit cell (Z =4).¹ The porphyrin planes are precisely parallel to each other in two sets. The dihedral angle between the two pairs of porphyrin planes is 15.9° (See Figure S1 in the S.I.).²⁵

A pseudo porphyrin plane (mean plane bisecting the dihedral angle) was calculated to orientate the single crystal. The Miller indices of the pseudo porphyrin plane was determined to be (6, 0, −12) from the algebraic equations calculated in SHELXL²⁶ from crystal information. With this plane perpendicular to the X-ray beam, a 90° rotation of the aligned crystal will give both the in-plane (ip) and out-of-plane (oop) orientations with only minor alignment errors (approximately 8° max).

All NRVS measurements were made at Sector 3–ID of the Advanced Photon Source, Argonne National Laboratory. Crystal orientations were confirmed to remain valid after the NRVS measurements. Analysis of the NRVS data has been described previously.^{17, 27, 28}

Vibrational Predictions

The first set of calculations were performed using the Gaussian 03 program package.²⁹ The hybrid-GGA functional B3LYP³⁰ and the triple-ζ valence basis set without polarization (VTZ) for iron and 6–31G* were used for the H, C, and N atoms. Both high-spin (HS, S = 2) and low-spin (LS, S = 0) states are calculated. The reported structures¹ were used as the starting geometry for optimization. The second set of calculations including structure optimizations and frequency analysis has been performed on [Fe(TPP)(CN)]⁻ using the Gaussian 09 program package.³¹ B3LYP and VTZ for iron and 6–31G* for H and C atoms were used. To better predict the anion system [Fe(TPP)(CN)] ⁻, a basis set with diffuse function 6–31+G* was added to the more negatively-charged atoms (the N atoms in the porphyrin and the cyanide ligand). Frequency calculations were performed on the fully optimized structures at the same basis level to obtain the vibrational frequencies with ⁵⁷Fe isotope set.³² Comparisons of the optimized geometry and frequencies with the observed data are given in Table 1. The calculated frequencies are surely no more accurate than 1 cm⁻¹. However, we have sometimes given another digit that is required to distinguish the mode with other calculated modes.

Table 1.

Measured and calculated structural parameters and vibrational modes for [K(222)][Fe(TPP)(CN)].^a

	ΔN4b		Fe–CN		(Fe–Np)av
DFT	LS	HS	LS	HS	LS	HS
	0.163	0.618	1.887	2.113	2.012	2.154
X-ray	100 K	400 K	100 K	400 K	100 K	400 K
	0.17	0.45	1.8783(10)	2.108(3)	1.986(7)	2.089(8)
	νFe-C(CN)		δFe-C-N		Doming
DFT	LS	HS	LS	HS	LS	HS
	461	336	413	277	108	90
NRVSc	116 K	290 Kd	116 K	290 K	116 K	290 K
	461	459/322	413	405/277	130	125/108

^aDistance values in A, mode values in cm⁻¹.

^bΔN₄ is the displacement of iron from the mean plane of the four porphyrin nitrogen atoms.

^cν_Fe-C(CN) and doming modes are from OP measurements; δ_Fe-C-N is from IP measurement.

^d290 K measurement shows both LS and HS modes.

Predicted Mode Composition Factors and NRVS

The Gaussian09 output files from DFT calculation can be used to generated predicted Mode Composition Factors with our scripts.³³ ${\text{e}}_{j\alpha }^2$ for atom j and frequency a are the fraction of a modes total kinetic energy contributed by atom j and is readily obtained from the atomic displacement matrix together with the equation: where the sum over i runs over all atoms of the molecule, m_i is the atomic mass of atom i, and r_i is the absolute length of the Cartesian displacement vector for atom i. The polarized NRVS intensities are calculated relative to an averaged porphyrin plane. The out-of-plane atomic displacement perpendicular to the resulting porphyrin plane for a normal mode is obtained from a projection of the atomic displacement vector (z) of the NRVS active nuclei (here: ⁵⁷Fe). The in-plane atomic displacements are calculated from a projection of the atomic displacement vector (x and y) on the porphyrin plane, which can be written:

$$e_{j\alpha ,\mathit{outofplane}}^2=\frac{m_j{r}_{jz}^2}{\sum m_i{r}_i^2}\text{and}{e}_{j\alpha ,\mathit{inplane}}^2=\frac{m_j(r_{jx}^2+r_{jy}^2)}{\sum m_i{r}_i^2}$$ (1)

Finally, the directions of mode composition factors are calculated as described above using the in-plane and the out-of-plane projection vectors respectively (as will be shown in a later figure). In order to enable comparison of the directions, the coordinate systems used in the HS and LS states of [Fe(TPP)(CN)]⁻ are fixed along the same iron-nitrogen bond directions (4N-in-plane) by our coordinate-rotation script.³³ Vibrational Density of States (VDOS) intensities can be simulated from the mode composition factors using the Gaussian normal distributions function, where the full width at half height (FWHH) is defined by the user from MATLAB R2010a software (FWHH = 7.5 cm⁻¹ is set in this paper). The x, y and z components of iron normal mode energy for [Fe(TPP)(CN)]⁻ (LS) and [Fe(TPP)(CN)]⁻ (HS) with ${\text{e}}_{Fe}^2\ge 0.001$ are given in Tables S1 and S2.

Results

NRVS data for the spin crossover (or spin-equilibrium) complex [K(222)][Fe(TPP)(CN)] have been recorded at several temperatures. The powder spectrum was measured at ~17 K and oriented single-crystal spectra were obtained at 116 K, and between 222 and 290 K. The complex (in the solid-state) is known to be low spin at temperatures below ~175 K. Above this temperature, the complex undergoes a gradual transition to a high-spin state. At 400 K, the transition is still not complete and accordingly is halfway complete at >265 K. Thus the spectra measured at 17 and 116 K represent spectra from the pure low-spin species, whereas spectra obtained at the higher temperatures must contain contributions from both the high- and low-spin states of the anion.

Oriented crystal spectra obtained when the porphyrin planes are effectively perpendicular to the exciting X-ray beam reveal all iron vibrations where the iron moves in an out-of-plane direction. Spectra were also obtained when the porphyrin planes were parallel to the exciting beam and in-plane motion of iron is observed. In this case, components of both the x and y directions are observed. XXX No in-plane anisotropy is expected for the fourfold symmetric [Fe(TPP)(CN)]⁻ ion, in contrast to [Fe(OEP)(NO)].²⁴ The oriented single-crystal spectra provide useful information on the direction of iron motion that substantially aids in the spectral assignments. In addition, two series of DFT calculations have been performed to aid in the task of assignment. Both DFT calculations utilized the B3LYP functional with the second extended with the additional use of diffuse functions. Diffuse functions were included because of the negative charge on the complex in question. The vibrational predictions of the two calculations are briefly compared.

We have also studied the entropy of the system based on the predicted vibrational data. We present our results on the contributions of the vibrational entropy to the spin crossover.

Discussion

The low-spin to high-spin spin crossover complex [Fe(TPP)(CN)]⁻ is an unusual species on at least two counts. The first is the presence of the cyanide ion, long considered a strong field ligand and thus judged unlikely to be in the coordination group of a species displaying high-spin character.^{3, 34} The second is that the species is a five-coordinate iron(II) species, whereas most iron(II) species that exhibit spin crossover behavior are pseudo-octahedral six-coordinate complexes. The thermally induced spin crossover has been confirmed by both magnetic susceptibility measurements and by Mössbauer spectroscopy over a range of temperatures. The interconversion of spin states is very rapid and shows only a single quadrupole split doublet in the Mössbauer spectra.¹ Thus, the interconversion is faster than the Mössbauer time scale (10⁻⁷ s). Vibrational spectroscopy, when used to investigate spin crossover complexes, typically follows a select band that has differing frequencies in the two states. In this study, we have obtained the entire iron vibrational spectrum for the low-spin complex. At higher temperatures, the observed NRVS spectra show contributions from both the low- and high-spin forms. Accordingly, we are able to extract the complete spectrum for the high-spin form as well. This observation also makes clear that the spin interconversion rate is slow on the vibrational time scale.

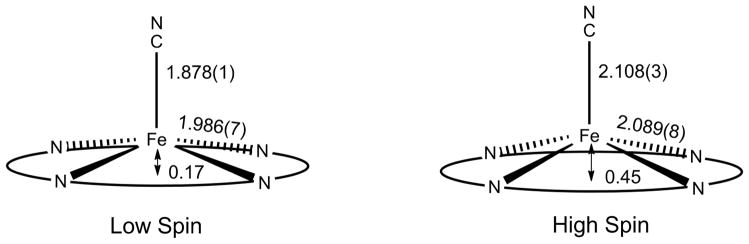
The differences in the structure of the two spin states have been obtained by multi-temperature X-ray structure studies.¹ The differences in structure are schematically depicted in Figure 1 and are consistent with known spin state correlations.³⁶

Figure 1.

Diagram illustrating the structural changes between the low-spin and high-spin states of [Fe(TPP)(CN)]⁻. The high-spin parameters are from the 400 K structure and may not reflect a complete conversion to the high-spin system.

Vibrational Analysis

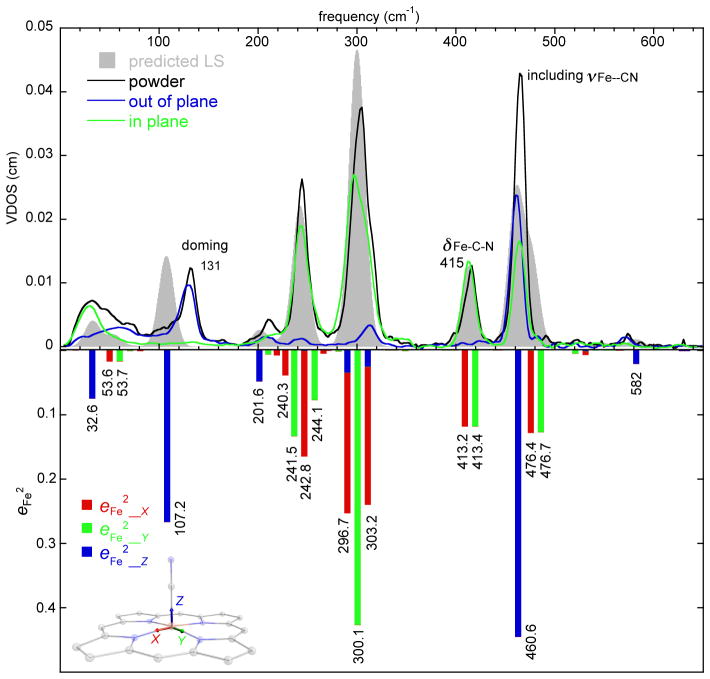
The iron vibrational spectrum of the low-spin state of [Fe(TPP)(CN)]⁻ is available from the NRVS spectra collected as both a powder (17 K) and as an oriented crystal specimen. The powder spectrum is shown in the upper panel of Figure 2 (solid black line) and consists of six major peaks. The powder spectrum is very well predicted by the DFT calculation with diffuse functions as shown by the predicted vibrational density of states (Figure 2, VDOS, filled gray envelope). The overall quality of the predicted fits to powder spectrum does provide confidence in the details of the prediction. The “standard” DFT calculation also shows good agreement (although not quite as good) and is provided in the Supporting Information (Figure S2) for comparison.

Figure 2.

(Upper panel) The measured VDOS for the powder sample (17 K), the single crystal sample (in-plane, 116 K; out-of-plane, 116 K) of [K(222)][Fe(TPP)(CN)], and predicted VDOS for the low spin state (grey shaded, G09). (Lower panel) The predicted directional characteristics of all modes with ${\text{e}}_{Fe}^2>0.001$ are shown. The tick marks are the values of the predicted frequencies, but the horizontal scale is only approximately linear in frequency to avoid overlaps. x, y and z are illustrated in the molecular structure and defined in text.

The available oriented crystal data are also shown in the top panel of Figure 2 (blue line, out-of-plane; green line, in-plane) and clearly demonstrate that several of the powder peaks are overlapped with in-plane and out-of-plane contributions unresolved in the powder. The lower panel of Figure 2 shows the predicted directional characteristics of each mode with ${\text{e}}_{Fe}^2>0.001$. As illustrated in the diagram, z is along the heme normal, equivalent to the measured oop spectrum; x and y directions correspond to the two ip Fe–N_p vectors. This bar graph provides details of directional contributions of the iron motions. Predictions of the directionality are well-correlated with the experimental orientational data. The modes can be described in terms of the well-known porphyrin mode classification by Abe et al.³⁷ as adapted for [Ni(P)]³⁸ and [Fe(P)].³⁹ Labels with ν_i denote modes with all atoms moving in the porphyrin plane and γ_i denotes modes with all atoms moving perpendicular to the porphyrin plane.

The strongest band in the powder spectrum is observed at 464 cm⁻¹. This might be expected to solely be the Fe–CN stretch but the oriented ip and oop measurements show that there are substantial ip contributions to the (overlapped) peak as well. The predicted character of the 476.4 and 476.7 cm⁻¹ ip peaks are the x and y components of ν₅₀ along with some contribution from the Fe–C–N bend. However, the predictions and experiment show that the bend primarily contributes to the in-plane peaks observed at 415 cm⁻¹ (powder) or 413 cm⁻¹ (in-plane). Thus there is significant mixing of the Fe–C–N bend with porphyrin vibrations; the two sets have nearly equivalent iron intensities. The predicted character of the two distinct bending components in the x direction is illustrated in Figure 3. There are thus three modes with overlapped frequencies; the third mode is indeed the very strong Fe–CN stretch. The observed peaks are at 464 cm⁻¹ (powder, overlapped), 464 cm⁻¹ (in-plane), and 461 cm⁻¹ (out-of-plane). The highest resolvable peak, which has modest intensity, is found at 572 cm⁻¹ (γ₅, pyrrole folding) and has not been previously seen by NRVS in porphyrins.

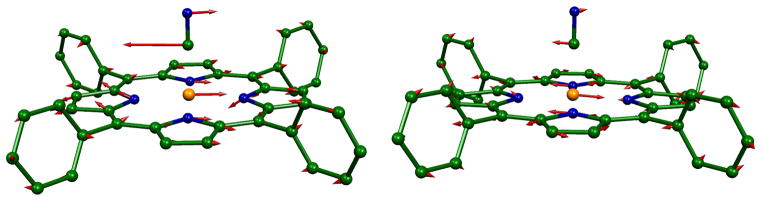
Figure 3.

The two FeCN bending modes in the x direction. The mode predicted at 413.2 cm⁻¹ is at the left and the mode predicted at 476.4 cm⁻¹ is at the right (with ν₅₀).

As in other low-spin iron porphyrinate complexes, the middle frequency range (220–360 cm⁻¹) of the spectrum is dominated by strong in-plane contributions. Two very strong bands are centered at 304 and 244 cm⁻¹; there are also modest (overlapped) contributions from out-of-plane motion that are unresolved in the powder. The band at 304 cm⁻¹ character has the in-plane motion analogous to the ν₅₃ modes predicted for [Fe(Porphine)].^{39, 40} The predicted mode in the y direction is illustrated in Figure 4. Unexpectedly, the DFT calculations predict two x in-plane modes, both with ν₅₃ character but also with a small amount of out-of-plane character as well (inverse doming: γ₆). It is the in-phase and and out-of-phase mixing of γ₆ that leads to the two predicted modes. The oriented crystal spectra show that there is modest out-of-plane iron motion in the region. Whether this is a separate mode or a component of the in-plane mode cannot be determined from our experimental data, but the predictions clearly suggest mixing. The differences in the total predicted motion are apparent in Figure 5. The total iron motion in these two modes is comparable to that for the mode with y character (as would be expected).

Figure 4.

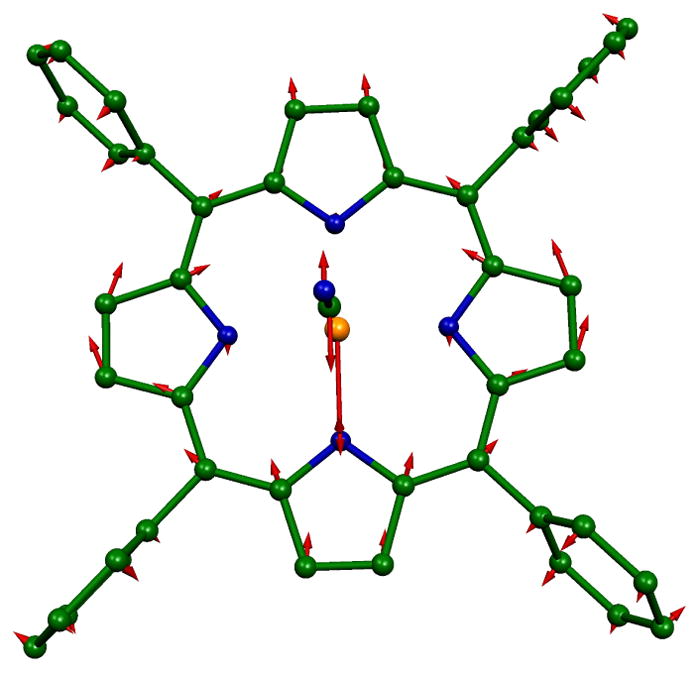
In-plane ν₅₃ in the y direction that is predicted at 300.1 cm⁻¹.

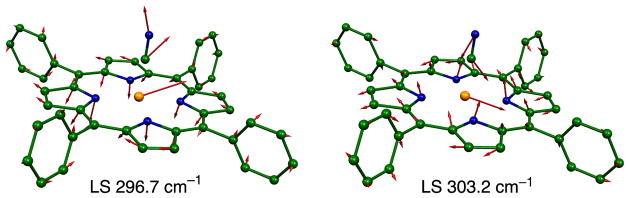
Figure 5.

The predicted modes at 296.7 and 303.2 cm⁻¹ showing the modest oop motion of iron.

The band observed at 244 cm⁻¹ is the result of the final (strong) in-plane set of iron motions. The DFT predictions show a set of four modes, with γ₂₃ and ν₄₉ character. The iron motion is all in ν₄₉. The four modes are illustrated in Figure S3.

The remaining observed peaks all display out-of-plane character. The band at 210 cm⁻¹ is predicted at 201.6 cm⁻¹ and can be described as motion of the Fe–C–N and porphyrinato atoms moving perpendicular to the heme plane with the four C_m atoms moving in the opposite motion (γ₇). The peak observed at 131 cm⁻¹ and predicted at 107.2 cm⁻¹ is the classical doming mode (γ₉). The final peak at the very low frequency of about 54 cm⁻¹ and predicted at 32.6 cm⁻¹ can be described as the motion of all porphyrin, iron, and cyanide atoms normal to the porphyrin plane with the peripheral phenyls moving in the opposite direction.

Spectra measured at higher temperatures will display features from both the high- and low-spin forms of the anion. In principle, at high enough temperatures the spectrum of the pure high-spin form of the anion could be obtained. However, the highest practical temperature for the NRVS measurements is ~290 K, where the transition is only about 70% complete. We have measured oriented crystal spectra at this temperature as well as an intermediate temperature, where the transition to high spin is about 40% complete. We thus have oriented crystal spectra that give spectra of the low-spin state as well as two spectra with differing amounts of the two spin states. DFT calculations and spectral predictions were also carried out for the high-spin state, which we believe provides an adequate depiction of the high-spin state. The out-of-plane spectra are simpler than those of the in-plane spectra; we consider the out-of-plane set first.

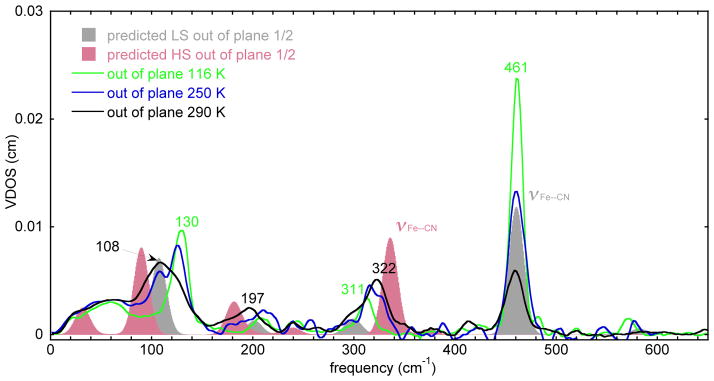
Figure 6 presents the out-of-plane spectra at three temperatures. Changes in four spectral regions are readily apparent. The stretching mode at 461 cm⁻¹ clearly becomes less intense while a peak at 322 cm⁻¹ increases in intensity with increasing temperature. In the 200 cm⁻¹ region, the peak at 197 cm⁻¹ increases in intensity as the temperature is increased. Finally the peak at 130 cm⁻¹ shifts to a peak at 108 cm⁻¹.

Figure 6.

The measured VDOS for a single-crystal sample of [K(222)][Fe(TPP)(CN)] (out-of-plane) at 116, 250, and 290 K and DFT predicted VDOS for the low-spin state (gray shaded) and the high-spin state (red shaded). To facilitate comparisons, the predicted out-of-plane VDOS for both spin states are shown at half height to give the approximate expected spectrum at the half conversion point.

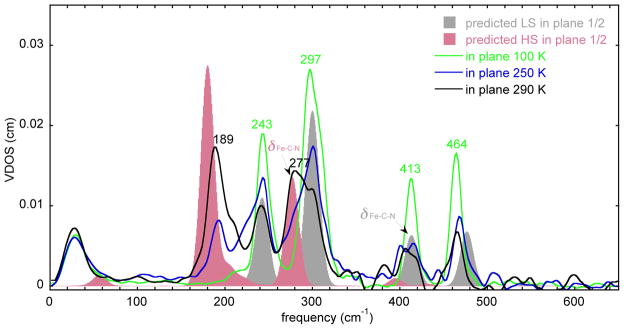
The changes in spectra in the in-plane region are shown in Figure 7. Peaks at 464, 413, 297, and 243 cm ⁻¹ all decrease in intensity, whereas increases in intensity are observed in only two regions, 280 and 189 cm ⁻¹. The 189 cm ⁻¹ peak also has a clear shoulder at higher frequency.

Figure 7.

The measured VDOS for single crystal sample of [K(222)][Fe(TPP)(CN)] (in-plane) at 116, 222, and 290 K and in-plane DFT predicted VDOS for the low-spin state (gray shaded) and the high-spin state (red shaded). To facilitate comparisons, the predicted VDOS for both spin states are shown at half height to give the expected spectrum at the half conversion point.

These spectral changes clearly show that the frequencies for the high-spin species are at lower frequency; there are also apparent significant changes in intensity. The shift to lower frequency in the high-spin complex is expected since the change in spin state leads to longer and weaker bonds for the high-spin state than those found for the low-spin state (Figure 1). Less anticipated features were the differing vibrational pattern and differing intensities. This appears to be the result of varying mixing of the iron motion with porphyrin motion, a reflection of the distinct structural features of the two states.

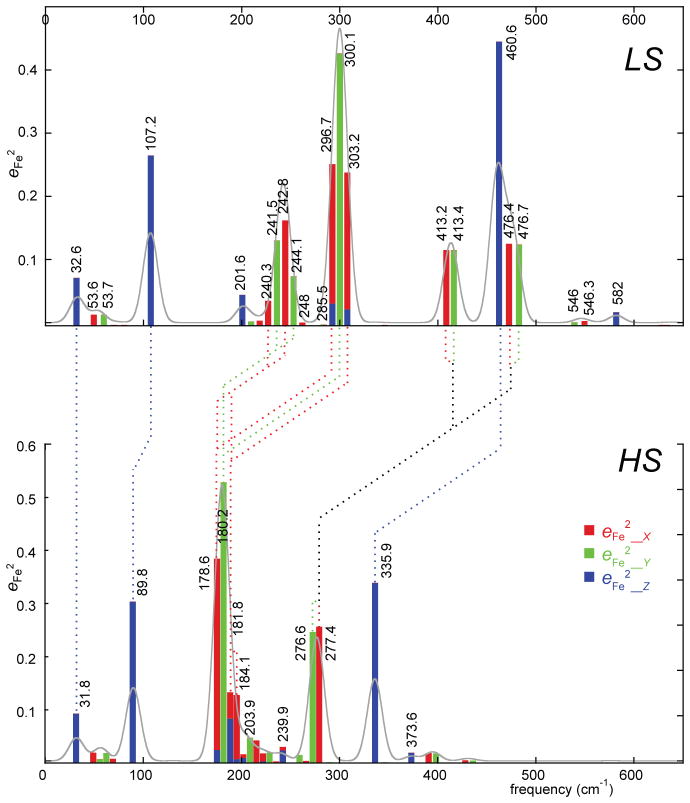
These features can be seen in Figure 8 where the lower frequencies for the high-spin state and the intensity pattern differences are clearly visible. The figure presents the predicted vibrational density of states (VDOS, gray shaded) and the predicted iron directional character of each node with frequencies. Given the strong agreement between the observed and predicted VDOS, we use the DFT-predicted spectral features since this gives us the most useful information on the character of the modes. The significant differences between the spectra are the result of the mixing of the iron motion with different porphyrin ring modes. Thus there is not a simple one to one correlation of modes in the two states. In the following sections showing the correlations of the modes between the two states, we use the predicted frequencies of the vibrations, but it is to be emphasized that there is always a corresponding observed mode. MOLEKEL depictions of the correlated LS and HS modes are given in the Supporting Information.⁴¹

Figure 8.

Diagram illustrating the correlations of iron motion in the high- and low-spin states of [K(222)]-[Fe(TPP)(CN)]. The horizontal axes are on the same linear scale, the positions of the predicted peaks are somewhat arbitrary in order to avoid overlaps.

The correlation of the out-of-plane modes is fairly straightforward as the amount of porphyrin ring mixing in the out-of-plane modes is minimal. The predicted Fe–C–N stretch down-shifts from 460.6 to 335.9 cm⁻¹ (Figure S4); the observed frequencies are 461 to 322 cm⁻¹. The doming mode downshifts from the observed value of 130 cm⁻¹ to 108 cm⁻¹ (Figure S5); the predicted values are 107.2 and 89.8 cm⁻¹.

The correlation of the in-plane modes is more complex owing to significant changes in the nature of mixing between porphyrin modes and iron modes. The Fe–C–N bending modes at 413.2 and 413.4 cm⁻¹ in the LS species are correlated with the modes predicted at 276.6 and 277.4 cm⁻¹. These two HS modes are mostly Fe–C–N bending, but there is some ν₅₃ character as well. However, these two HS modes are also correlated with the LS modes at 476.4 and 476.7 cm⁻¹ that are a combination of ν₅₀ and the Fe–CN bending mode; this mixing is minimal in the high-spin state. Thus, porphyrin modes mixed with Fe–C–N bending are very different in the two spin states and the number of modes with Fe–C–N bending character are also different.

Correlations of the modes involving the Fe–C–N bend in both the x and y directions are shown in Figures S6 and S7. In both spin states, there is the expected x and y degeneracy. The correlations of the iron mid-frequency modes are equally complicated; there are two groups of LS modes to be considered. The four LS modes between 240.3 and 244.1 cm⁻¹ have both γ₂₃ and ν₄₉ character with all iron motion arising from ν₄₉. The LS modes centered around 300 cm⁻¹ are primarily ν₅₃ with the x component also having in-phase and out-of-phase contributions from γ₆. Both the 240 and the 300 cm⁻¹ LS groups can be correlated with the four HS modes predicted between 178.6 and 184.1 cm⁻¹. These HS modes are a combination of ν₅₃ and ν₄₉; the major contributors to the two LS sets. This combination leads to effectively “destructive interference” of the rotation of the pyrrole rings and the two opposite pyrroles move in-phase with the in-plane iron motion. Thus the porphyrin modes mixed with the iron in-plane motion are again very different in the two spin states and the number of modes with substantial in-plane iron character are also different. The nature of the differences between the two spin states and the distinctions between the x and y directions is illustrated in Figures S8 and S9.

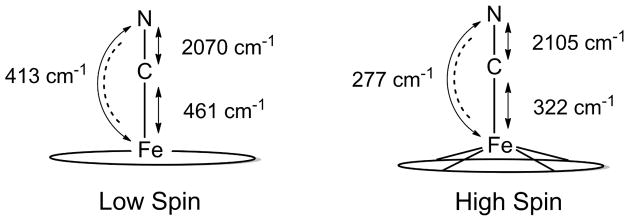
Figure 8 summarizes the correlations from the above analysis with the dashed lines connecting the HS and LS modes with similar iron motion. The CN stretch also shows a change in the frequency from the spin-state change; the experimental values for the Fe–CN and C–N stretches are shown in Figure 9. The data show that there is an inverse correlation between the strength of the Fe–C and C–N bonds. This pattern is reminiscent of the well-known correlation for isoelectronic heme carbonyls.⁴² The change in ν_CN frequency is a decrease in frequency by 35 cm⁻¹; the calculated differences in the two frequencies are 30 cm⁻¹. The data is thus consistent with π-back-bonding as a contributor to the Fe–C bonding in [Fe(TPP)CN)]⁻; however, π-bonding would certainly be much more significant for the low-spin state. The figure also shows the effects on the Fe–C–N bending mode as the Fe–C bond weakens and which shows the expected trend.

Figure 9.

Diagram illustrating changes in the Fe–C and C–N stretches and the Fe–C–N bend between the two spin states of [Fe(TPP)CN)]⁻. The C–N stretches were measured previously by IR¹ and the other vibrations by NRVS.

Vibrational Entropy

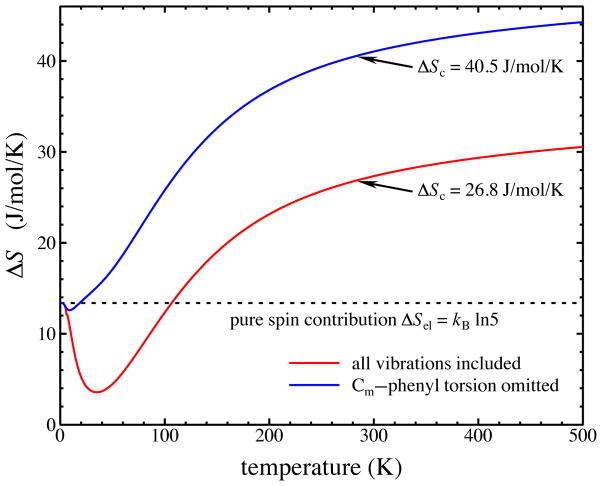
The preceding results demonstrate that Fe-ligand vibrations are sensitive reporters of the electronic state of [Fe(TPP)(CN)]⁻. These frequency changes also help to drive the spin crossover by entropically stabilizing the quintet state relative to the singlet, as commonly observed for other spin-crossover materials.^{43, 44, 45} A simple two-state model with temperature-independent quintet-singlet enthalpy and entropy differences yields a good fit to the previously published magnetic susceptibility measurements¹ (Figure S11) with a crossover temperature T_c = Δ H/ΔS = 286 K and an entropy increase ΔS = 46.6 J/mol/K for the high-spin state that is significantly larger than the electronic contribution (ΔS_el = k_B ln 5 = 13.4 J/mol/K) expected from the increased spin multiplicity alone.

The reduced Fe-ligand frequencies in the quintet state, as detailed above (Figure 8), will contribute to an increase in the vibrational entropy

$$S_{\mathit{vib}}=k_B\sum _{\alpha }[({\overline{n}}_{\alpha }+1)ln({\overline{n}}_{\alpha }+1)-{\overline{n}}_{\alpha }ln{\overline{n}}_{\alpha }],$$ (2)

because of the consequent increase in the vibrational occupation numbers n̄_α = [exp(hcν̄/k_BT) − 1]⁻¹. Calculation of the vibrational entropy change using all DFT-computed frequencies in Eq. 2 confirms a significant enhancement of the total entropy difference as the Fe-ligand frequencies become thermally excited with increasing temperature (red line Fig. 10). More specifically, each pair of corresponding singlet/quintet frequencies ν̄₁/ν̄₅ contributes a term that increases monotonically with temperature, reaching a maximum value

Figure 10.

Predicted entropy increase on crossover to the high-spin state of [Fe(TPP)(CN)]⁻ includes electronic and vibrational contributions. The blue trace indicates the entropy calculated by excluding the predicted frequencies of four torsional oscillations about the C_m-phenyl bonds, which increase significantly in the quintet state, while the red trace includes all vibrations. The dashed line indicates the temperature-independent electronic contribution ΔS = k_B ln 5 due to the increased spin multiplicity in the high-spin state. The difference between quintet and singlet vibrational entropies calculated from Eq. 2 using DFT-computed frequencies determines the additional vibrational contribution.

$$\mathrm{\Delta }{S}_{\mathit{max}}=k_{B}ln({\overline{\nu }}_1/{\overline{\nu }}_5)$$ (3)

when the thermal excitation energy exceeds the vibrational quantum (k_BT > hcν̄).⁴⁶ However, the ΔS = 27 J/mol/K entropy change calculated as the sum of electronic and vibrational contributions at the 286 K crossover temperature is more modest than that expected.

Examination of the vibrational calculations reveals that four vibrational frequencies involving torsional oscillations about the four C_m–C_phenyl bonds connecting the phenyl groups to the porphine nucleus also contribute significantly to the predicted vibrational entropy difference. In contrast with the Fe-ligand frequencies, the DFT calculation predicts these torsional frequencies to increase by approximately 40% from 27–30 cm⁻¹ in the singlet to 38–46 cm⁻¹ in the quintet state. Thermal excitation of these modes, visible as a prominent minimum near 35 K in the calculated entropy difference (red line Fig. 10), almost completely cancels the electronic contribution. Thermal excitation of the Fe-ligand contributions with further temperature increases ultimately enhances the entropic stabilization of the quintet state.

The relevance of these torsional frequencies to the experimental situation is difficult to assess, in part because calculations on an isolated molecule fail to account for intermolecular interactions that may strongly influence the motions of the phenyl groups on the molecular periphery. Moreover, these vibrations do not contribute significantly to the NRVS signal and this frequency region is also difficult to probe with infrared or Raman spectroscopy. However, explicit exclusion of the latter vibrations from the sums in Eq. 2 yields a value ΔS = 40 J/mol/K for the entropic stabilization of the quintet at 286 K that is closer to our experimental estimate.

Changes in the electronic state also lead to changes in the predicted frequencies of the heme distortion modes involving torsional motion of the bonds connecting the rigid pyrrole rings. The observed decrease of the doming (γ₉) frequency from 130 to 108 cm⁻¹ (see above) in the high-spin state is consistent with the predicted 107 to 90 cm⁻¹ decrease. In contrast, the calculation predicts an increase of the saddling (γ₁₉) frequency of the porphyrin from 48 to 66 cm⁻¹. Changes of the predicted ruffling (γ₁₄) frequency from 98 to 105 cm⁻¹ and the waving frequencies (γ₂₆) from 137 to 131 cm⁻¹ are less significant. Although difficult to detect in frequency-domain IR or Raman spectroscopy, saddling and ruffling frequencies have been reported to contribute to the time-domain vibrational coherences observed following femtosecond laser excitation.^{47, 48}

Summary

We have provided a detailed comparison of the vibrational character changes in the spin crossover complex [K(222)]Fe(TPP)(CN)] as the spin state changes. The mode character changes significantly owing to the strong mixing of the iron motion with porphyrin modes. This mixing differs substantially between the two spin states because of the large change in the force constants of similar iron vibrations in the two electronic states. The calculation of the vibrational entropy (the major driving force for the spin state change) based on the DFT predicted modes has been examined. The calculations show that some vibrations involving the peripheral groups of the porphyrin may in fact stabilize the less favored state. This result is in keeping with the observation that subtle molecular changes can have big effects on the occurrence (or not) of the spin crossover phenomenon.