The Element Effect Revisited: Factors Determining Leaving Group Ability in Activated Nucleophilic Aromatic Substitution Reactions

Abstract

The “element effect” in nucleophilic aromatic substitution reactions (S_NAr) is characterized by the leaving group order, F > NO₂ > Cl ≈ Br > I, in activated aryl halides. Multiple causes for this result have been proposed. Experimental evidence shows that the element effect order in the reaction of piperidine with 2,4-dinitrophenyl halides in methanol is governed by the differences in enthalpies of activation. Computational studies of the reaction of piperidine and dimethylamine with the same aryl halides using the polarizable continuum model (PCM) for solvation indicate that polar, polarizability, solvation, and negative hyperconjugative effects are all of some importance in producing the element effect in methanol. In addition, a reversal of polarity of the C–X bond from reactant to transition state in the case of ArCl and ArBr compared to ArF also contributes to their difference in reactivity. The polarity reversal, and hyperconjugative influences have received little or no attention in the past. Nor has differential solvation of the different transition states been strongly emphasized. An anionic nucleophile, thiolate, gives very early transition states and negative activation enthalpies with activated aryl halides. The element effect is not established for these reactions. We suggest that the leaving group order in the gas phase will be dependent on the exact combination of nucleophile, leaving group, and substrate framework. The geometry of the S_NAr transition state permits useful, qualitative conceptual distinctions to be made between this reaction and other modes of nucleophilic attack.

INTRODUCTION

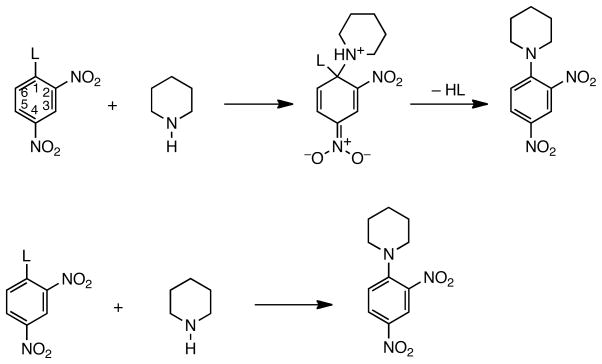
The nucleophilic aromatic substitution (S_NAr) reactions of activated substrates and their reaction mechanisms have been well investigated.^1–6 The reaction follows a two-step, addition-elimination mechanism as depicted in Figure 1 with piperidine as the nucleophile.

Figure 1.

Top: The S_NAr mechanism. L = leaving group. Bottom: The overall result for reaction of piperidine with 2,4-dinitrophenyl substrates.

Compared with S_N2 reactions of aliphatic halides, an inverted order of halide leaving group abilities, F > Cl ≈ Br > I is often found in studies of rates of S_NAr reactions of activated aromatic halides, e.g., substrates substituted at ortho and/or para positions on the ring with strong electron withdrawing groups (EWGs), commonly nitro, cyano, acyl, and even metal-substituted aryl halides in which vacant metal orbitals are available, e.g., para-tricarbonylchromiumphenyl halides.³ This result, called the “element effect”⁷ is found for a number of nucleophilic types including oxy-anions, amines, and sulfur anions, and is especially prominent for smaller, less polarizable nucleophiles in protic solvents. Where found it establishes the addition-elimination mechanism for S_NAr reactions in which step 1, addition of the nucleophile to form a tetrahedral Meisenheimer complex (a substituted cyclohexadienide anion), is rate determining.⁷

A number of explanations have been given for the element effect. In some advanced organic texts one finds, unattributed, the statement that the greater polarity of the C–F bond allows an attraction between nucleophile and carbon,^8,9 an attraction which is presumably considered to exist in the transition state (ts) of step 1 as well. This explanation, with references, is also given as one of several pertinent factors in Miller’s 1968 monograph on aromatic nucleophilic substitution.¹⁰

However, the number of factors governing reactivity in S_NAr reactions is large. Also to be considered are the polarizabilities of both nucleophile and leaving group.¹¹ Additionally, as made clear by Bartoli and Todesco,¹² reactivity in these S_NAr processes can be influenced by the size of the leaving group, by the basicity and size of the nucleophile, by interactions between nucleophile and leaving group, by the substrate framework (Miller’s term for the ring and its substituents), and by solvent effects, particularly on the nucleophile and leaving group. Bartoli and Todescu summarize their studies as 2-, 3- and 4-parameter equations which, depending on the individual magnitudes of the various parameters, correlate the rates of a wide range of S_NAr reactions. The 4-parameter equation is formally similar to the Edwards equation governing nucleophilicity.^13,14

We have recently reported that the same mechanism may be at play in substitution reactions of pyridinium.^15,16 In this paper, we re-examine S_NAr reactions of 2,4-dinitrophenyl halides experimentally, and provide computational results aimed at elucidating the reasons for the element effect.

EXPERIMENTAL RESULTS

Rate constants and activation parameters for the reaction of nucleophilic piperidine with 2,4-dinitrophenyl fluoride, chloride, bromide and iodide, as well as with 1,2,4-trinitrobenzene, in methanol are listed in Table 1.

Table 1.

Kinetic parameters for nucleophilic aromatic substitution reactions of 1-substituted-2,4-dinitrobenzenes with piperidine in methanol.^a

Substrates (L=)	Overall rate constant (20° C, M−1s−1)	Relative rate at 20 °C	ΔG‡ (kcal/mol)	ΔH‡ (kcal/mol)	ΔS‡ (cal/mol/K)
Fluoro	3.50	1613	16.6	5.3	−37.7
Nitro	1.00	461	17.3	5.9	−38.4
Chloro	0.00970	4	20.0	8.6	−38.4
Bromo	0.00928	4	20.0	8.9	−37.3
Iodo	0.00217	1	20.9	9.7	−37.6

^aKinetic parameters were calculated from temperature dependent studies using the Eyring equation.

All values are in satisfactory agreement with the benchmark values determined by Bunnett, Garbisch and Pruitt in their original “element effect” paper.⁷ As can be seen the large negative entropies of activation are almost constant throughout the series, the −TΔS^‡ term averaging about 11 kcal/mol. However the differences in this term contribute less than 1 kcal/mol to the differences in the free energies of activation. Rate constant differences are therefore determined by ΔH^‡. Both observations, along with the element effect itself, argue for the two-step addition-elimination mechanism, with the addition step rate controlling, as shown in Figure 1.

COMPUTATIONAL RESULTS

Our computations focus on the reactions of piperidine and dimethylamine with 2,4-dinitrophenyl fluoride, chloride and bromide. Additional computations were carried out on reactions of the same substrates with thiolate and chloride anions, and of other substrates, including unactivated fluorobenzene, with fluoride anion. We call attention here to the recent experimental and computational study of George and coworkers, where pertinent references to previous computational work on S_NAr reactions can be found.¹⁷

The ortho-nitro group in the 2,4-dinitrophenyl substrates is somewhat twisted with respect to the aromatic ring. In the transition states for these reactions the twist of the o-nitro group is less pronounced than in the substrates, and the amino group occupies a very slightly pseudoaxial position with a tilt at C1 of 6–8°. In each transition state an N–H bond is positioned for hydrogen bonding with the nearer oxygen of the ortho-nitro group with H^···O distances of 2.17 – 2.25 Å. This feature has also been observed computationally by George and coworkers.¹⁷

Table 2 shows calculated enthalpies of activation for the addition of the amine nucleophiles to the 2,4-dinitrophenyl halides, both for the gas and solution (methanol) phases. Table 3 lists calculated npa charges for the carbon center (C1) and the attached halogens, both for the substrates and transition states of these reactions.

Table 2.

Calculated enthalpies of activation (kcal/mol) for addition of dimethylamine and piperidine to C1 of the 2,4-dinitrophenyl halides: MP2/6-31+G*//HF/6-31+G* (gas phase) and MP2/6-31+G*//HF/6-31+G* (methanol).^a

halide	MP2/6-31+G*//HF/6-31+G* (gas phase)	MP2/6-31+G*//HF/6-31+G* (methanol)	iν (cm−1)b
dimethylamine
fluoride	1.2	1.4	424 (238)c
chloride	6.1	5.1	445
bromide	2.2	1.4	450
piperidine
fluoride	6.6	6.7	387
chloride	11.0	9.9	408
bromide	5.9	5.2	411

^aZero point energies were calculated at the HF/6-31+G* level and corrected according to the recommendations of Scott, A. P.; Radom, L. J. Phys. Chem. 1996, 100, 16502.¹⁸ Thermal corrections were not made. Gas phase geometries were used for the solvent calculations using the polarizable continuum model (PCM).

^bEach transition state had just one imaginary frequency; it corresponded to the reaction coordinate motion for addition of the nucleophile to the substrate.

^cAt MP2/6-31+G*.

Table 3.

Calculated npa charges on selected atoms in the 2,4-dinitrophenyl halide substrates and their transition states (ts) formed by reaction with dimethylamine and piperidine at carbon-1 (C1).

charge at indicated atom	ArF	ArCl	ArBr
nucleophile = dimethylamine, MP2/6-31+G*//HF/6-31+G* (gas phase)
C1, substrate		−0.073	−0.150
C1, ts	0.459	0.012	−0.047
halogen, substrate		0.088	0.144
halogen, ts	−0.350	0.018	0.063
nucleophile = dimethylamine, MP2/6-31+G*//HF/6-31+G* (methanol)a
C1, substrate	0.420	−0.076	−0.148
C1, ts	0.465	0.017	−0.041
halogen, substrate	−0.325	0.080	0.149
halogen, ts	−0.354	−0.016	−0.060
nucleophile = piperidine, MP2/6-31+G*//HF/6-31+G* (gas phase)
C1, substrate		−0.073	−0.150
C1, ts	0.455	0.005	−0.053
halogen, substrate		0.088	0.144
halogen, ts	−0.347	0.021	0.066
nucleophile = piperidine, MP2/6-31+G*//HF/6-31+G* (methanol)a
C1, substrate	0.420	−0.076	−0.148
C1, ts	0.460	0.010	−0.048
halogen, substrate	−0.325	0.080	0.149
halogen, ts	−0.352	0.017	0.062

^aSolvent calculations used the polarizable continuum model (PCM) applied to the optimized HF/6-31+G* gas phase geometry.

Table 4 shows the carbon–halogen bond lengths in the 2,4-dintrophenyl halides and in the transition states of their reactions with ammonia. Additionally the C–N bond lengths in the transition states are listed. Table 5 gives carbon–fluoride bond lengths as well as npa charges on fluorine for the Meisenheimer complexes formed by addition of fluoride anion to several aryl halide compounds including fluorobenzene.

Table 4.

Carbon-halogen and carbon-nitrogen bond lengths (Å) for substrates and transition states in the addition reactions of 2,4-dinitrophenyl halides with dimethylamine and piperidine (HF/6-31+G*).^a

halide	substrate (C-X)	transition state (C-X, C-N)
nucleophile = dimethylamine, HF/6-31+G*
fluoride	1.307	1.338, 1.899 (1.402, 1.880)b
chloride	1.722	1.782, 1.902
bromide	1.874	1.953, 1.914
nucleophile = piperidine, HF/6-31+G*
fluoride	1.307	1.336, 1.922
chloride	1.722	1.780, 1.923
bromide	1.874	1.951, 1.937

^aGeometries were optimized for the gas phase.

^bStructure optimized at MP2/6-31+G*.

Table 5.

C-F bond lengths and npa charges on fluorine in Meisenheimer complexes formed from several substrates reacting with fluoride at various positions (MP2/6-31+G*).

Meisenheimer complex (point group)a	C-F Bond Length, axial F (Å)	npa charge, axial Fb
Fluorobenzene
C1 adduct (C2v)c	1.498, 1.498	−0.470, −0.470
4-Nitrofluorobenzene
C1 adduct (C2v)c	1.447, 1.447	−0.428, −0.428
C3 adduct (C1)	1.540	−0.492
1,3-Dinitrobenzene
C6 adduct (C1)	1.497	−0.456
2,4-Dinitrofluorobenzene
C1 adduct (C1)c	1.421, 1.421	−0.397, −0.397
C3 adduct (C1)	1.488	−0.450
C5 adduct (C1)	1.495	−0.455
C6 adduct (C1)	1.771	−0.648

^aReaction at sites not listed in the table resulted not in covalent complex formation, but in hydrogen bonding between substrate and fluoride.

^bCharge and bond length are well correlated: npa charge = −0.70 CF length + 0.59, r² = 0.994.

^cThese complexes have flat rings and equivalent C–F bonds.

DISCUSSION

The calculated and experimental activation enthalpies (ΔH^‡) for the entries in Tables 1 and 2 are ordered similarly. In particular the computational data capture a key aspect of the element effect, namely the significantly greater reactivity of the fluoride relative to the chloride as leaving groups both in the gas phase and in methanol. Moreover the magnitudes of the activation enthalpies for those substrates in methanol agree well with experiment. However the fluoride and bromide substrates have similar calculated ΔH^‡ values in both media and with both nucleophiles, the bromide actually slightly more reactive toward piperidine. This result is consistent with Bunnett’s proposal that polarizability interactions between nucleophile and leaving group can provide extra stabilization of the transition state, the more so the greater the size of these moieties.¹¹ These results allow discussion of other calculated results, namely npa charge distributions and structural and geometric features. The most notable results of npa charge calculations (Table 3) are the high polarity of the C–F bond and the low polarities of the C–Cl and C–Br bonds. In fact the polarities of the C–Cl and C–Br bonds in the substrates are “reversed” with weakly negative carbons and weakly positive halogens. In the transition states the C–F bond is even more polar than in the substrate while the C–Cl and C–Br bonds are weakly polarized in the “normal” sense.

The two nitro groups in this set handle almost all the negative charge in the chloro and bromo transition states, but in the fluoro transition state the C–F bond has a strong δ+δ− distribution of charge as well. This result allows at least four explanations for the enhanced reactivity of fluoro compounds in activated S_NAr reactions. One is the qualitative argument that nucleophiles will be more strongly attracted to the carbon of the C–F bond.^8–10 This effect must exist in the transition state as well as the reactant complex of the aryl fluoride reaction in order for the element effect to be manifest. A clue is offered by the observation of the large, but constant, negative entropies of activation throughout the series. The reactions occur between neutral reactants and lead to charge-separated transition states. Extensive solvent reorganization is implied in all cases. Such reorganization would accompany formation of a solvated reactant complex with a first solvent shell organized to enable the forthcoming covalency changes. Within this shell the fluoro reactant is most strongly stabilized by the bond polarity effect mentioned above. This interaction results in a decrease in the enthalpy of both the solvated reactant complex and the subsequent transition state. A second explanation, closely related to the first, considers the likely effect of solvation on the fluoro transition state relative to the reactants. We argue that the highly polar Nu–C–X end of the fluoro transition state is more strongly solvated than are the chloro and bromo transition states, and that this outcome is reflected in the lower enthalpy of activation for that case, though compensated in the bromo ts by a superior polarizability interaction between nucleophile and leaving group.¹¹ Because the PCM solvent model does not reveal specific interactions such as hydrogen bonding solvation, we further argue that under experimental conditions in protic solvents, H-bonding stabilization of the fluoro transition state will accelerate the reactions of activated Ar–F compounds relative to Ar–Cl and Ar–Br compounds. The magnitude of the element effect in activated SNAr reactions can be reduced or even reversed in some cases by varying reaction conditions so that the ratio of rates, step 2 vs. step −1, can be altered. The use of aprotic solvents is one such variable. This result has been ascribed to retardation of step 2 (relative to step −1) caused by lack of hydrogen bonding assistance to departure of the halide leaving group such that step 2 becomes partly or wholly rate determining.^19–21 Thus, solvation (and other forms of electrophilic aid) of the δ⁻ leaving group in the transition state of step 2 provides important stabilization, especially in protic solvents. From our npa charge results (see Table 3) we further infer that it is also important for the transition state of step 1, especially when the leaving group is fluoride.

A different H-bonding effect, again suggested to favor stabilization of the reactant complex and the transition state in step 1 is intramolecular hydrogen bonding between N–H bonds of primary and secondary amine nucleophiles and the δ⁻ fluorine leaving group.^17,19,22,23 In fact the distance between the N-H proton and the departing fluoride, 2.42 Å in our transition states, is 0.3 to 0.4 Å shorter than for the other halogen transition states and offers a further small advantage for the fluoro substrate. This conclusion underlines the propensity of partially negative fluorine to engage in stabilizing H-bonding interactions be they intramolecular or intermolecular, e.g., by solvation.

However, we also note that the calculated gas phase activation enthalpies (Table 2) are ordered much the same as in solution. Therefore whatever role solvation plays, there must be an intrinsic component to the element effect as well. We suggest this component to be, or to include, the superior electrostatic interaction between the amine and the carbon of the highly polar C–F bond in the transition state, an interaction greatly diminished in the chloro and bromo reactions.

A third advantage of Ar–F compounds has to do with the fact that some reversal of C–X bond polarity must occur in reaching the transition states for Ar–Cl and Ar–Br substrates, an effect which has been shown to increase barriers to reaction.²⁴

A fourth effect is suggested by the extended C–X bond lengths in the transition states, Table 4, and by the relation between C–X bond lengths and npa charges tabulated in Table 5. The two parameters are well correlated: npa charge = −0.70 C–F length + 0.59, r² = 0.994, including both unactivated and activated substrates. Much of the bond-lengthening effect is due to the change from sp² hybridization to nominally sp³ hybridization at carbon in the transition state. But in addition to rehybridization there are at least two other effects possibly at work here. One is stabilization through anionic (negative) hyperconjugation.^25,26 This effect will be greatest for fluorine and is associated with both the bond lengthening and increased partial negative charge results shown in Table 5. Another effect is incipient departure of the leaving group. However, this effect will be in the order Br > Cl > F, opposite to the element effect order. Negative hyperconjugation in fluorinated ethyl anions has been observed computationally by us²⁷ and by Saunders²⁸ who also noticed agreement between C–F bond elongation and an increase in negative (npa) charge. Negative hyperconjugation has also been identified by Karni, Bernasconi and Rappoport as an important factor affecting reactivity in a computational study of nucleophilic vinylic substitution (S_NV) chemistry in vinylic systems activated by electron withdrawing groups.²⁹ These authors also found that 1,3-steric interactions between entering and leaving groups could be important, but that anomeric interactions involving these groups are relatively small for their systems. In fact, they argue that the anomeric interaction is compromised by negative hyperconjugation. We suggest that the superior negative hyperconjugative ability of fluoride compared with chloride and bromide provides additional “hyperaromatic” stabilization of the fluoro transition state,³⁰ illustrated for example by the no-bond resonance structure depicted below.

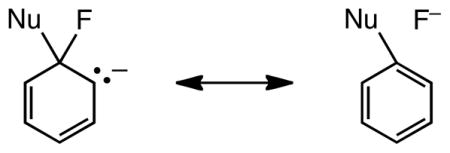
In Saunders’s fluorinated ethyl anions C–F hyperconjugation was associated with bond weakening by incipient departure of nucleofugic fluoride. In Meisenheimer complexes such hyperconjugation, always involving pseudoaxial C–F bonds, will result in stabilization by providing a measure of aromaticity, that is, “hyperaromaticity” to the anion.³⁰ In fact the longest C–F bond in Table 5 is found for addition of fluoride to C6 of 2,4-dinitrophenyl fluoride. That position is the only position not activated by ortho- or para-nitro groups. Addition at that position therefore requires the largest stabilizing response from the rest of the molecule including the hyperconjugating fluoride.

The possibility of steric effects on reactivity is indicated by the twist of the ortho-nitro group with respect to the ring. In the reactant 2,4-dinitrophenyl halides this twist amounts to 48°, 61° and 79° for the fluoro, chloro and bromo substrates as defined by the dihedral between the planar nitro moiety and the C2–C3 ring bond. This result might destabilize substrate according to the amount of twist, but since this effect opposes the element effect order, it must be small. In the transition states these dihedrals are reduced to an almost constant 17–20° as the ortho-nitro group moves toward greater coplanarity. Since the rings in the transition states are not planar it is difficult to assess precisely the effect of these changes on transition state stability. However the total npa charge on the ortho-nitro group is almost constant in these transition states, hence we judge there to be no differential effect on the ability of that group to accommodate negative charge, therefore to affect transition state stability. A different kind of steric effect could exist as a repulsion between nucleophile and leaving group.²⁹ Both calculated and experimental ΔH^‡ values for the chloro and bromo reactions (Tables 1 and 2) indicate that this effect is negligible, and that rather, there is a small, attractive 1,3-interaction enhancing reactivity of the bromo compound relative to the chloro substrate.¹¹ We suggest that overall, steric effects on reactivity are relatively unimportant in this series.

Our computational results also allow some comparisons with gas phase S_NAr reactions. As shown by the ΔH^‡ values in Table 2, computed reaction barriers are not much changed in methanol, compared with the gas phase, for the addition of neutral amines to activated arenes. Likewise, the calculated npa charges (Table 3) in solution are almost the same as in the gas phase for all substrates and transition states.

Table 6 gives results for addition of an anionic nucleophile, thiolate, to the 2,4-dinitrophenyl halides in the gas phase. The ΔH^‡ values are negative since considerable stability is gained by ion-molecule complexation of the negative nucleophile with the neutral substrate.

Table 6.

Enthalpies of activation for gas phase addition of thiolate anion to 2,4-dinitrophenyl halides, kcal/mol^{a, b} (MP2/6-31+G*//HF/6-31+G*).

Substrate	ΔH‡ (kcal/mol)	iν (cm−1)
ArF	−25.2	269
ArCl	−22.6	298
ArBr	−24.0	324

^aFrequencies and zero-point energies were calculated at the HF/6-31+G* level, the ZPVE values scaled by 0.9153 as recommended by Scott, A.P.; Radom, L. J. Phys. Chem. 1996, 100, 16502.¹⁸

^bTransition states calculated at the MP2 level did not hold the leaving group.

^cThe imaginary frequencies are associated with the reaction coordinate for addition of SH⁻ to carbon-1.

Addition of anionic nucleophiles will be highly exothermic, and the transition states found here are not good models for condensed phase structures. They occur very early along the reaction coordinate as may be inferred from the extended C–S partial bonds, averaging about 2.55 Å. Carbon-1 has become only slightly pyramidal in all transition states. The element effect has been overshadowed by a combination of electrostatic effects in which the fluoro substrate will be favored by the polarity of the C–F bond, countered by both polar and polarizability effects in which the nucleophile and the slightly positive Cl and Br atoms may interact attractively. Thus, the exact combination of anionic nucleophile, leaving group and substrate framework determines the reactivity order of the aryl halides. This conclusion, although based on only these few examples, is expected to hold for reactions of anionic nucleophiles with activated Ar–X compounds in the gas phase.

It is worthwhile to make some general remarks comparing some characteristics of the S_NAr reaction with other nucleophilic substitution mechanisms. In particular, one geometric aspect of the addition step of the S_NAr reaction offers conceptual utility, in that it allows qualitative distinctions to be made between the transition states for this reaction and that of the classic aliphatic S_N2 transition state. The angle formed by the nucleophilic center, carbon-1, and the leaving group runs from 92° to 96° in our computed S_NAr transition states whereas for the S_N2 ts this angle is close to 180°. This difference makes possible several of the influences on S_NAr reactivity discussed above: The polarity of the Nu–C–Lg portion of the ts is increased thereby enhancing solvation; The proximity of nucleophile and leaving group permits dipolar and polarizability interactions (and the possibility of steric interactions as well); And the π-σ* hyperaromaticity effect is enabled, for which there is no counterpart in the S_N2 ts.

Comparisons with the front-side S_N2 transition state are also possible. The geometry of the Nu–C–Lg triad for front-side attack is similar to that for the S_NAr addition step. However the carbon center in the S_N2 ts is 5-coordinate while that in the S_NAr ts is 4-coordinate, hence steric congestion is increased more in the S_N2 ts relative to its substrate than in the S_NAr addtion step. Additionally the orbital interaction between the nucleophile’s σ orbital and the σ* orbital of the substrate is poor in front-side attack, partly because of the low density of the σ* orbital between carbon and the leaving group, but mainly because there is a node in this region meaning that any bonding interaction is countered by an antibonding interaction.

CONCLUSIONS

Reactivity in nucleophilic aromatic substitution is subject to an impressive variety of influences.^7,11,12 The “element effect”, in which the reactivity order is F > Cl ≈ Br > I, is commonly observed in nucleophilic substitutions of activated aryl halides.⁷ This effect is here examined by a combination of experiment and computation. The experimental reactivity order is determined by enthalpies of activation, and this order is satisfactorily reproduced by calculations in which solvent is included, but with the aryl bromide relatively more reactive than by experiment, a result which can be ascribed to an attractive polarizability interaction between nucleophile and leaving group.¹¹ Among the possible factors leading to this order is the exalted polarity of the C–F bond, a factor cited in a number of texts (but only referring to the substrate). However transition state effects must also be important and these are revealed by computation. Polarity reversal of the C–Cl and C–Br bonds (but not the C–F bond) accompanies activation and is expected to increase the barrier to nucleophilic addition in solution.²⁴ Superior solvation of the reactant complex and the transition state is an expected consequence of the much greater polarity of the reaction center in the transition states of reactions of fluoro substrates. This effect should be magnified in hydrogen-bonding donor solvents. Additionally, negative hyperconjugation,^25–28 more effective for fluorine than for chlorine or bromine, provides stabilization according to the consequent contribution of a measure of aromatic character (hyperaromaticity)³⁰ to the transition state and addition complex. The polarity-reversal and hyperconjugation arguments have not previously been invoked as influences on S_NAr reactivity while the transition state solvation effect has not been strongly emphasized as a determinant of the element effect.

However, the element effect reactivity order is also displayed in gas phase calculations, thus there is an “intrinsic” component, probably a polar effect, to the element effect as well. Steric effects in the sets studied here are judged to be small.

Reactions of anionic nucleophiles with activated Ar–X substrates in the gas phase will probably not generally show an element effect but rather a jumbled order of reactivity, determined by the particular substrate-nucleophile combination.

EXPERIMENTAL SECTION

All chemicals are commercially available with the exception of 1,2,4-trinitrobenzene, which was prepared from the oxidation of 2,4-dinitroaniline as reported.³¹ However, a slightly modified procedure was employed due to the lack of availability of 90% hydrogen peroxide. Instead, a three-times larger volume of a 30% hydrogen peroxide solution in water was used and the reaction was run overnight to effect the oxidation of amino group to the nitro group.

The rate constants of the reactions were determined as reported.⁷ The reactions were followed by measuring the absorbance of the product at 380 nm. The sole product in each case was 1-piperidino-2,4-dinitrobenzene. No evidence for 2,4-dinitroanisole was found by NMR.

COMPUTATIONAL METHODS

Structures were built and optimized at lower levels using the MacSpartan Plus software package,³² then optimized at HF/6-31+G* and MP2/6-31+G* using the Gaussian 03 quantum mechanical software.³³ Frequency and zero-point energy values were calculated at the HF/6-31+G* level, and the ZPVE values scaled as recommended by Scott and Radom.¹⁸ All structures reported here represent electronic energy minima, and all structures identified as transition states (ts) have one imaginary frequency, that corresponding to the reaction coordinate for nucleophilic addition. The optimized MP2 geometries for substrates and transition states were used to obtain energies with the Polarizable Continuum Model (PCM), solvent = methanol.