Active Site Hydrophobic Residues Impact Hydrogen Tunneling Differently in a Thermophilic Alcohol Dehydrogenase at Optimal vs. Non-Optimal Temperatures

Abstract

A growing body of data suggests that protein motion plays an important role in enzyme catalysis. Two highly conserved hydrophobic active site residues in the cofactor-binding pocket of ht-ADH (Leu176 and V260) have been mutated to a series of hydrophobic side chains of smaller size, as well as one deletion mutant, L176Δ. Mutations decrease k_cat and increase K_M(NAD⁺). Most of the observed decreases in effects on kcat at pH 7.0 are due to an upward shift in the optimal pH for catalysis; a simple electrostatic model is invoked that relates the change in pK_a to the distance between the positively charged nicotinamide ring and bound substrate. Structural modeling of the L176Δ and V260A variants indicates the development of a cavity behind the nicotinamide ring without any significant perturbation of the secondary structure of the enzyme relative to the wild-type. Primary kinetic isotope effects (KIEs) are modestly increased for all mutants. Above the dynamical transition at 30 °C for ht-ADH (Kohen et al., Nature (1999) 399, 496), the temperature dependence of the KIE is seen to increase with decreasing side chain volume at positions 176 and 260. Additionally, the relative trends in the temperature dependence of the KIE above and below 30 °C appear reversed for the cofactor-binding pocket mutants in relation to wild-type protein. The aggregate results are interpreted in the context of a full tunneling model of enzymatic hydride transfer that incorporates both protein conformational sampling (preorganization) and active site optimization of tunneling (reorganization). The reduced temperature dependence of the KIE in the mutants below 30 °C indicates that at low temperature, the enzyme adopts conformations refractory to donor-acceptor distance sampling.

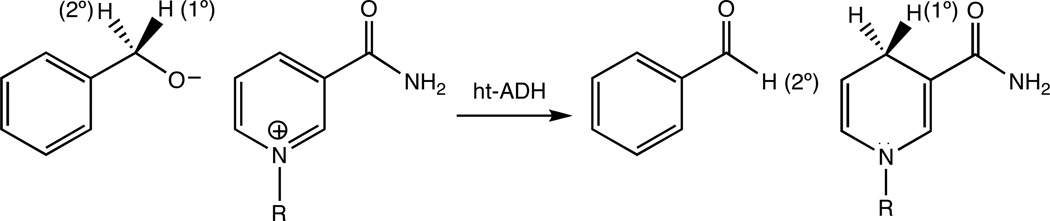
Current intensive research efforts aim to uncover the role of protein motion in the enormous rate accelerations achieved by enzymes (1–9). Enzymes that catalyze C−H bond activation have played an important role in these efforts due to the importance of hydrogen tunneling and the link of such tunneling to heavy atom environmental motions (10) (11) (12) (13). Alcohol dehydrogenases, which catalyze the stereospecific transfer of a hydride equivalent between a substrate alcohol and the nicotinamide ring of an NAD⁺ cofactor (Scheme 1), have become one of the paradigmatic systems for such studies. Early investigations of alcohol dehydrogenases yielded unexpected relationships between kinetic and equilibrium isotope effects, and conflicting interpretations of the transition state structure, pointing to a possible role for tunneling and coupled motion as the origin of the surprising isotope effects (14, 15). The first direct test for hydrogen tunneling in an enzyme-catalyzed reaction came from kinetic isotope effect (KIE) measurements in yeast alcohol dehydrogenase (16). According to semiclassical transition state theory, a comparison of reaction rates among protium (k_H), deuterium (k_D), or tritium (k_T) transfer should yield an exponential relationship, (k_H/k_T) = (k_D/k_T)^EXP (17) with an upper bound for EXP = 3 − 4 (18, 19). In contrast to these semiclassical expectations, highly-inflated values of EXP for alpha-secondary KIEs were first measured in the yeast alcohol dehydrogenase (16) and are now common place in the alcohol dehydrogenase family (20–22).

Scheme 1.

Reaction catalyzed by ht-ADH, in which a substrate-derived alkoxide ion is oxidized by NAD⁺. The primary and secondary hydrogens are labeled accordingly.

The inflated value for EXP in horse liver alcohol dehydrogenase (HLADH) was further interrogated using active site mutations and X-ray crystallography. Because tunneling is expected to be extremely sensitive to the distance over which hydrogen (in this case, a hydride ion) must move, it was hypothesized that the enzyme active site may be carefully packed so as to maintain a short donor-acceptor distance. To test this idea, a hydrophobic active site residue, V203, situated behind the nicotinamide ring of cofactor, was mutated mutated to smaller side chains. As bulk at position 203 was reduced, a regular trend was observed in which the Swain-Schaad exponent became progressively smaller, with the value of EXP for V203A exhibiting a semiclassical value of 3.3 (20). An X-ray structure of this mutant indicated that the nicotinamide ring of the cofactor had moved away from the substrate by approximately 0.8 Å, implicating a longer hydrogen transferring distance as the origin of the kinetic behavior.

Initially, the above result was interpreted in the context of a tunneling correction (23), leading to the conclusion that tunneling had become progressively less important in the mutant variants of HLADH. However, in recent years, the aggregate data for Swain-Schaad deviations in the alcohol dehydrogenase family indicate nonclassical behavior that cannot be described by a tunneling correction (24). This recognition, together with the phenomenon of nearly temperature-independent KIEs for wild-type forms of alcohol dehydrogenases (21, 25, 26), has contributed to mounting data consistent with full tunneling models in which the entire thermal barrier for reactions arises from heavy atom motions that carry the enzyme from an unreactive initial configuration to a reactive conformer which is “tunneling-ready” (11, 13, 25, 27–31). In the context of such models, the property of both temperature-independent KIEs and inflated values for EXP arises from tightly-packed active site conformations that are optimal for hydrogen tunneling (25, 32, 33).

A major focus of this laboratory in recent years has been on a homologous family of prokaryotic dehydrogenases that includes a thermophilic variant, ht-ADH. The behavior of ht-ADH has been shown to vary from temperature-independent KIEs and inflated values for EXP above 30 °C, to temperature-dependent KIEs and more “semiclassical” values for EXP below 30 °C. In addition, the enthalpy of activation for hydride transfer is increased by 7 kcal/mol, below 30 °C, resulting in a break in the Arrhenius plot for k_cat as a function of temperature. These results were the first evidence that a change in temperature could impact enzyme tunneling parameters in a manner similar to site directed mutagenesis. In more recent years, a trend from nearly temperature-independent KIEs toward an increased temperature-dependence of the KIEs has become the rule in a large number of different enzyme systems that have been perturbed away from their optimal structure/dynamics (27, 28, 34–37). It has been argued that such generic perturbants limit the ability of a given enzyme to achieve the subset of “tunneling- ready”, compacted active site conformers (1).

Direct examination of changes in the thermal fluctuation of ht-ADH above and below 30 °C has been carried out using hydrogen-deuterium exchange coupled to mass spectrometry (HDX) (38). A subset of five peptides, all localized to the substrate-binding domain of ht-ADH, was found to undergo a transition at 30 °C. Below this temperature, these peptides showed little variation in the rate or extent of deuterium incorporation as a function of temperature. However, above 30 °C, exchange was seen to increase regularly with temperature, leading to an almost 1:1 correlation between the temperature dependence for k_cat and the weighted average rate constant for deuterium incorporation into the five substrate domain-derived peptides. One important conclusion has been that the active site becomes more compacted above the temperature break (from the nearly temperature-independent KIE), despite an increase in overall protein flexibility. This initially counterintuitive result has been reconciled in the context of a model for enzyme catalysis that invokes two classes of motion, termed reorganization and conformational sampling (preorganization). According to this model, enzymes must be flexible and sample a large range of conformational space (preorganization) in order to reach catalytically active conformers, from which hydrogen tunneling can subsequently occur according to a modified Marcus-like reorganization barrier (25).

In direct analogy to the experiments in HLADH at position 203, we have now measured the effect of an active site mutation at the corresponding position, L176, as well as the adjacent V260 in ht-ADH (Figure 1), which was found to displace the NAD cofactor towards the substrate in a previous computational study of ht-ADH (39). Whereas, the HLADH data were collected only at 25 °C, the use of ht-ADH allows us to address the role of a proximal hydrophobic side chain on catalysis above and below a temperature-dependent change in protein flexibility. The data reveal an increase in the temperature dependence of the KIE relative to wild-type above the transition temperature of ca. 30 °C. This result adds to a trend in which site-directed mutagenesis increases the temperature dependence of KIEs for hydride transfer (34–37). Further, because of the proximity of the mutations in ht-ADH to the nicotinamide ring (hydrogen acceptor) and its measurable impact on an active site pK_a, the kinetic trends can be interpreted in the context of increased donor-acceptor distances, resulting in increased H-donor/acceptor distance sampling. Unexpectedly, the pattern in which KIEs become more temperature-dependent below 30 °C for the wild-type enzyme is reversed for the majority of the mutants. This contrasting behavior adds significant experimental weight to the critical role of a properly tuned protein conformational landscape in efficient enzyme catalysis, cf. (40). Furthermore, the aggregate data for ht-ADH variants also appear to be at odds with models for enzyme catalysis that attribute the temperature dependence of KIEs to conformational sampling alone (41, 42).

Figure 1.

Active site of ht-ADH. The NAD⁺ cofactor (blue) has been modeled into the X-ray structure for ht-ADH, which was solved previously in the presence of trifluoroethanol (red), a substrate analog (47). The side chains of mutated active site residues, L176 (yellow) and V260 (orange) are rendered in spheres.

Materials and Methods

Materials

Benzyl alcohol was purchased from Fisher Scientific, and purified by vacuum distillation prior to use. The α,α-d₂-benzyl alcohol was purchased from CDN isotopes, found to be chemically pure within the detection limits of GC-MS, and thus used without further purification. NAD⁺ and NADH were purchased from Sigma and Calbiochem respectively and used without further purification.

Preparation of Mutants

Site directed mutagenesis was carried out as previously described (43) using the QuikChange Stratagene kit for site-directed mutagenesis, with the following primers and their reverse complements (not shown).

• L176V: 5’-GGTATCGGCGGCGTTGGACACGTTGC-3’

• L176A: 5’-CAATTTACGGTATCGGCGGCGCAGGACACGTTGCCGTTCAATAC-3’

• L176G: 5’-CGGTATCGGCGGCGGTGGACACGTTGCCG-3’

• L176Δ: 5’-CAATTTACGGTATCGGCGGCGGACACGTTGCCGTTCAATAC-3’

• V260A: 5’-CTTGTGTGCTTGCCGGATTGCCACC-3’

Changes are underlined and shown in boldface type. For the deletion mutant, the codons flanking the deleted codon are both shown in boldface and underlined. Primers were designed using the program PrimerX (44) and purchased from Operon. Plasmids were isolated and sequenced to confirm the mutations and the intactness of the remainder of the gene.

Protein Purification

Purification was carried out as previously described (38) with some modifications: sonication replaced the treatment of cells with DNaseI, and dialysis was eliminated in favor of loading crude lysate directly to a DEAE ion exchange column. In addition, affinity chromatography was performed with 5'-AMP Sepharose 4B (GE Healthcare). Since affinity chromatography yielded homogenous protein, size exclusion chromatography could thus be eliminated for all mutants except L176Δ, which did not bind the affinity column. Enzyme stocks were concentrated to at least 10 mg/mL, flash frozen in liquid Nitrogen, and stored at −80 °C in 50 to 250 µL aliquots. Stocks stored in glycerol at −20 °C were found to lose activity over several months, while those stored without additives at −80 °C showed little or no activity loss over a comparable period. Protein concentrations were determined by the method of Bradford (45).

Kinetic Assays

Kinetic data were collected for the oxidation of benzyl alcohol (or its α,α-d₂ isotopolog) to benzaldehyde with concomitant reduction of NAD⁺ to NADH, as previously described (21), and activation parameters, KIEs, E_a(D) − E_a(H) and the parameter A_H/A_D were calculated as described previously (43). There was a small variation in the final ionic strength, between 110 and 160 mM, depending on the NAD⁺ concentration. The enzyme pK_a values were estimated by measuring k_cat as a function of pH, with ionic strength held constant at 500 mM. The resulting data could be fit to eq (1) to extract an estimated pK_a value.

$$k_{\text{cat}}(\text{pH})=\frac{k_{\text{cat}}({\text{pH}}_{\text{indep}})+{\mathrm{K}}_{\mathrm{a}}}{{\mathrm{K}}_{\mathrm{a}}+[{\mathrm{H}}^{+}]}$$ (1)

In this equation, k_cat(pH) is the estimate of k_cat at a given pH, k_cat(pH_indep) is for the fully ionized enzyme, and K_a is the acidity constant of the group that must be ionized for catalysis to occur.

Structural Modeling and in Silico Mutagenesis

A model of the ternary complex of ht-ADH bound to cofactor and trifluroethanol (a substrate analog) was prepared using the X-ray structure of alcohol dehydrogenase from Pseudomonas aeruginosa (pdb 1LLU) in complex with NAD⁺ and ethylene glycol (46) and the X-ray structure from ht-ADH with trifluoroethanol bound (pdb 1RJW) (47). The two enzymes share 62% sequence identity, and 73% sequence similarity. The peptide backbone of ht-ADH in complex with trifluoroethanol was modeled into the closed, ternary complex structure of the Pseudomonas enzyme using the program MODELLER (48) implemented in Python (49). MODELLER creates a structural model of an unknown protein (the ht-ADH ternary complex with NAD⁺ and trifluoroethanol) from a sequence alignment with a known protein structure, (the Pseudomonas structure) and by enforcing spatial constraints derived from the available structures, 1RJW and 1LLU (50). The sequence alignment was carried out in MODELLER (9v7), which uses a variable gap penalty that depends on the secondary structure of the template (51). A total of 100 models were generated for the wild-type ternary complex and each of the mutants. The models were subsequently subjected to an optimization using the variable target function method with conjugate gradients using the program automodel with a maximum of 300 iterations (50). Models were then refined using molecular dynamics with simulated annealing to allow the protein backbone and side chains to relax into an energy-minimized configuration. The relative energies of the models following optimization were assessed using the program DOPE (discrete optimized protein energy) (52), and the lowest energy models were further energy minimized with the program CNS (53). To predict the mutant structures, the residue of interest was replaced with the appropriate side chain in the PDB file, and then modeled as above.

Results

Steady-State Kinetics

All of the mutants that decrease bulk in the region behind the nicotinamide ring of the cofactor in the enzyme active site decrease k_cat at pH 7.0 and 30 °C between 5- and 50-fold, and lead to a modest increase in the magnitude of the KIE, from 3.1 for the wild-type enzyme to around 4 in the mutants (Table 1). An estimate has been made of the pK_a controlling a pH-dependent ionization that is required to obtain the active form of enzyme (Figure 2). Most of the effect of mutations on rate results from a shift in this pK_a between 0.3 and 1.2 pK_a units higher than the wild-type enzyme, giving a lower concentration of the active enzyme form at pH 7.0. When the limiting value of k_cat for fully ionized enzyme is determined at 30 °C, this is found to be diminished 2- to 4-fold for L176V, L176A, L176G and V260A, and around 28-fold for L176Δ (Table 1). Slightly diminished KIEs at pH 9.0 indicated that the chemical step was only partially rate-determining (data not shown), in contrast to data collected at pH 7.0 where hydride transfer controls k_cat (21). This is the reason for our extensive characterizations at pH 7.0, enabling the properties of the hydride transfer step to be directly studied.

Table 1.

Parameters for ht-ADH mutants at 30 °C.

Mutant	kcat, s−1a	Km(NAD+)a	Km(Alcohol)a	Dkcata	pKa	kcat optimum s−1b
WT	25 (±3)	1.1 (±0.1)	6.8 (±0.5)	3.1 (±0.2)	7.0 (±0.1)	50 (±1)
L176V	1.7 (±0.1)	1.2 (±0.2)	5.3 (±0.9)	4.1 (±0.4)	8.2 (±0.2)	16 (±1)
L176A	2.8 (±0.3)	2.6 (±0.6)	5.8 (±1.5)	4.1 (±0.6)	7.9 (±0.4)	13 (±1)
L176G	7.7 (±1.4)	25 (±8)	9.8 (±3.4)	4.0 (±1.1)	7.3(±0.2)	22 (±1)
L176Δ	0.43 (±0.1)	37 (±14)	7.4 (±3.5)	4.4 (±1.4)	7.6 (±0.8)	1.8 (±0.2)
V260A	2.4 (±0.2)	10 (±1.6)	4.2 (±0.8)	4.1 (±0.4)	7.8 (±0.1)	20 (±1)

^aAt pH 7.0.

^bThis is the value of k_cat estimated in the limit of fully ionized enzyme.

Figure 2.

The pH dependence of k_cat for the L176 mutant series of ht-ADH. Values for k_cat at pH values between 6.0 and 9.0 have been normalized to the limiting value of k_cat, obtained by fitting the data to eq (1). The normalized data have been fit to the same equation so that all mutants approach a limit of 100% activity at high pH. The trend toward elevated pK_a values for mutants (Table 1) can be seen qualitatively as the pH at which the enzyme reaches 50% activity increases from around 7.0 for wild-type to higher values in the mutants.

Temperature Dependence of KIEs

The comparative values for k_cat using deutero- as well as protio- substrates, together with the temperature dependence of the KIE, are shown in Figure 3. Kinetic parameters for all ht-ADH variants are available in Tables S2–S5. For the wild-type enzyme, H/D KIEs were calculated from high-precision, competitively measured H/T KIEs, using the Swain-Schaad relationship (17, 21), cf. Table S4. It has come to our attention that the two independent methods of determining the primary H/D KIE in reference 21 give estimates that differ somewhat in their magnitude (see Tables S3 and S4). In addition to their higher precision, the competitively measured KIEs (cf. Figure 2 of ref. 21) were taken as the reference for the wild-type enzyme here because they closely match values obtained more recently from steady-state kinetics using wild-type enzyme expressed and purified as described above in Materials and Methods ((38, 40, 43) and work herein). The differences between the two methods of measuring KIE in reference 21 could have resulted from the use of two separate enzyme preparations, which may have undergone different conditions during shipment from a collaborator. While the temperature dependence of the primary KIE below 30 °C in Figure 2 in reference 21 is smaller than that depicted in Figure 4 of the same reference, the overall trends in the data and conclusions drawn therefrom are unchanged.

Figure 3.

Temperature dependence of k_cat and KIE for wild-type and variant ht-ADH. KIEs are plotted on the right axis. Data collected above and below the Arrhenius break are indicated in red and blue, respectively. A linear best fit to the KIE data serves to guide the eye toward the “smiles” (wild-type and L176V) vs. “frowns” (the remaining mutants). The calculation of k_cat(D) for the wild type enzyme using k_cat(H) and k_H/k_T is to illustrate this trend, however error bounds have been omitted because the calculation introduces errors that are not representative of experimental data. The small error bounds for the calculated k_H/k_D are obscured by the data symbols.

Figure 4.

Models of active site for ht-ADH ternary complexes. The NAD⁺ cofactor is labeled NAD (a portion shown), and the substrate analog trifluoroethanol is labled TFE. Overlay of a model of the wild-type ht-ADH ternary complex with that of the V260A mutant (top) and the L176Δ mutant (bottom). The wild-type enzyme is shown in black, V260A in blue, and L176Δ in red. The models are virtually superimposable, with the exception of position L176 for L176Δ; which is occupied by a glycine residue (G177 in the wild-type structure).

Above the temperature break, [E_a(D) − E_a(H)] increases from 0.1 kcal/mol for the wild-type enzyme to between 1 and 2 kcal/mol in the mutants (Table 2); as a corollary, A_H/A_D decreases from significantly greater than unity for the wild-type enzyme to values less than unity in the mutants. Despite the size of the propagated errors, there are distinct patterns in the temperature dependence of the KIE above and below the break, Figure 3 and Tables S1 and S2. A trend is observed in which the plots of KIE as a function of temperature transition from concave upward ‘smiles’ (wild-type and L176V) to concave downward ‘frowns’ (L176A, L176G, L176 Δ, and V260A). The concave upward curves reflect KIEs that are more temperature-dependent below 30 °C than they are above 30 °C. The limiting values for the KIEs at low temperature are similar in all cases but the temperature regime where the KIE increases more strongly with decreasing temperature appears opposite for all of the mutants except L176V in relation to wild-type.

Table 2.

Temperature dependence of KIEs for ht-ADH mutants above the 30 °C break.

Enzyme	[Ea(D) – Ea(H)], high kcal/mol	Log(Aobs), lowc
WT	0.2 (±0.2)b	17.2 (±0.6)
L176V	1.3 (±1.1)	20.2 (±0.7)
L176A	1.4(±0.9)	19.6 (±0.2)
L176G	1.2 (±1.0)	20.6 (±0.8)
L176Δ	1.7 (±0.4)	25.2 (±1.6)
V260Aa	1.9 (±1.0)	24.1 (±1.0)

^aThe breakpoint for this mutant is at 40 °C.

^bE_a(T) – E_a(H); this parameter sets an upper limit on E_a(D) – E_a(H).

^cThese data are for the protio-substrate (40).

Structural Modeling

A model of the wild-type ht-ADH with cofactor and ethanol bound shows the nicotinamide ring of the NAD⁺ cofactor in van der Waals contact of both L176 and V260 side chains (Figure 1). Models of V260A and L176Δ in a ternary complex with NAD⁺ and a trifluoroethanol substrate analog have also been prepared to gauge whether this mutation can be expected to interfere with the overall structure of ht-ADH. Consistent with similar mutagenesis experiments in other proteins, no significant change is predicted in the secondary and tertiary structure for either of the variants (20, 27). Using molecular dynamics with simulated annealing and energy minimization (Materials and Methods), the only result of the changes at positions 260 and 176 is the creation of a hole/packing defect behind the nicotinamide ring of the cofactor. By this modeling method, no significant movement could be detected for the nicotinamide ring in V260A and L176Δ (Figure 4), in contrast to an earlier X-ray structure for the corresponding mutant (V203A) in HLADH that indicated a relaxation of cofactor into the cavity created in the active site upon mutation (20).

Discussion

Temperature Dependence of the KIE above the Arrhenius Break

The behavior of ht-ADH variants at elevated temperature (above 30 °C) contributes to a growing body of data that shows relatively temperature-independent KIEs for wild-type enzymes operating under physiological conditions, and more temperature-dependent isotope effects upon enzyme mutation (27, 29, 34–37). KIEs measured below the break will be discussed separately below. The KIE measured previously for the wild-type ht-ADH is nearly temperature-independent above the Arrhenius break, with E_a(D) − E_a(H) ~ 0, and the corresponding A_H/A_D = 2.6 (21), well in excess of the semiclassical value of 1.0 (54). As the bulk at position 176 is removed, E_a(D) − E_a(H) increases (Table 2). Very similar observations were made originally for the enzyme soybean lipoxygenase (SLO-1) (27, 29), and these were interpreted in the context of a full tunneling Marcus-like model for hydrogen transfer (25), discussed below. This model was originally introduced in the context of hydrogen atom transfer (13), and developed further to model the SLO-1 reaction (29). Although the hydride transfer reaction of ht-ADH has far more adiabatic character than the hydrogen atom transfer of SLO, the fact that an analogous trend in the temperature dependence of the KIE is seen in both systems supports the consideration of a similar underlying physical origin, as has been done in the context of similar very recent experiments in dihydroflate reductase (37).

The full tunneling model invoked for SLO-1 is given in eq (2),

$$k_{\text{tun}}=\mathrm{C}\times {\mathrm{e}}^{-{(\mathrm{\Delta }\mathrm{G}°+1)}^2/(4\mathrm{R}\mathrm{T})}{\displaystyle {\int }_{r_2}^{r_1}{\mathrm{e}}^{-m_{\mathrm{H}}{\omega }_{\mathrm{H}}{\mathrm{r}}^2\mathrm{H}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}\mathrm{d}\mathrm{X}(2)}$$ (2)

where C is the electronic coupling between the reactant and product states (in the present case, E•Alkoxide•NAD⁺ and E•Aldehyde•NADH), ΔG° is the driving force of the reaction on the enzyme, and λ is the energy required to reorganize the heavy atoms of the active site (enzyme and substrate) to facilitate wave function overlap between H-donor and acceptor atoms. Within the integral, the nuclear wave function overlap (dependent on the mass, m_H, frequency,ω_H, and distance traveled, r_H, for the transferred hydrogen) is sampled over a range of donor-acceptor distances. The potential energy governing distance sampling, E_x, can be approximated as a function of the donor-acceptor distance r_x via eq (3),

$${\mathrm{E}}_{\mathrm{x}}=\frac{1}{2}\hslash {\omega }_{\mathrm{x}}{\mathrm{X}}^2$$ (3)

where ω_x is the frequency of the donor-acceptor vibration, and X is a function of r_x as given in eq (4).

$$\mathrm{X}={\mathrm{r}}_{\mathrm{x}}\sqrt{\frac{m_{\mathrm{x}}{\omega }_{\mathrm{x}}}{\hslash }}$$ (4)

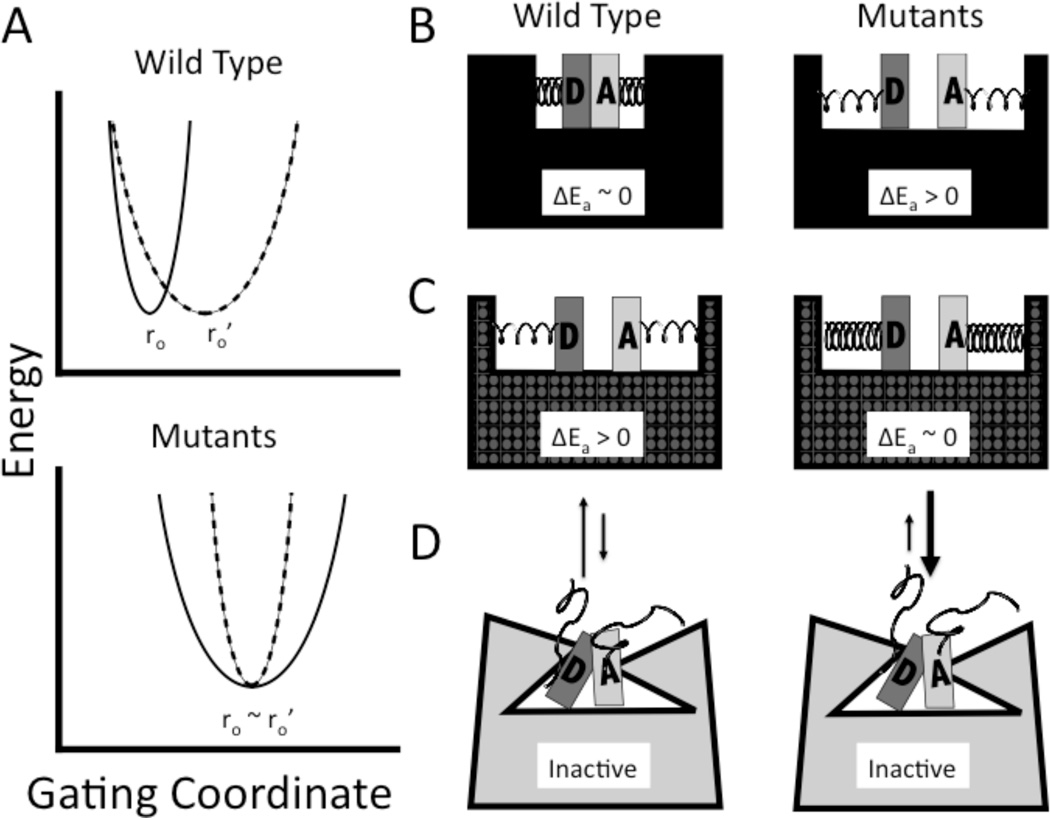
The collective mass of the atoms that are part of the donor-acceptor distance sampling motion is given by m_x. According to this model, the temperature dependence of the KIE is expected to reflect the extent of distance sampling between the donor and acceptor. For native enzymes with rigid, tightly-packed active sites, ω_x is large and E_x rises steeply with displacements away from the initial distance (r_o), leading to largely temperature-independent KIEs (25), cf. FIGURE 5, panel A. The short donor-acceptor distance (~ 2.8 Å) required for tunneling is achieved by sampling enzyme conformers that meet this condition (see below).

Figure 5.

Model for the physical origin of observed tunneling and kinetic parameters. (A) The top panel corresponds to the wild-type enzyme. Above 30 °C, the donor-acceptor distance sampling potential is shown as a heavy, solid line, with an equilibrium distance at r_o. The same potential surface for the low temperature regime is shown as a dashed line. The longer equilibrium donor-acceptor distance below 30 °C is reflected by r_o' and the softer potential is represented by the reduced curvature of the well. The combination of increased donor-acceptor distance and reduced force constant for distance sampling produces the temperature-dependent KIEs. The lower panel corresponds to the mutant enzymes. Note that the distance doesn’t change as a function of temperature, but the curvature has actually increased at low temperature (i.e., the combination of reduced temperature and mutation makes the protein especially rigid). (B) Illustrations of wild-type and mutant active sites above 30 °C. Increases in r₀ are represented by the gap between the donor D and acceptor A. Looser springs represent the softer distance sampling potential of the mutants. ΔE_a refers to E_a(D) − E_a(H). (C) For simplicity, we have illustrated the donor and acceptor distance and springs for wild-type at low temperature as similar to mutants at high temperature. Once again, on the right, the combination of low temperature and mutation is shown leading to very tight springs. (D) Low energy inactive conformers are represented by broken springs and a collapsed active site. The equilibrium between low temperature active site conformers (dotted pattern) and catalytically dead conformers (gray) gives rise to inflated Arrhenius parameters (30). Reproduced with modifications from (25).

In the case of mutations that introduce packing defects into the active site, two effects are expected. First, the donor and acceptor may relax to longer equilibrium distances, r_o', Figure 5. If the enzyme is unable to compensate for this with donor-acceptor distance sampling, this will be reflected in larger KIEs, as the shorter wavelength for deuterium makes its wave function overlap more sensitive to distance. Consistent with this picture, all of the mutants that expand the active site of ht-ADH result in a statistically significant increase in KIEs at 30 °C (Table 1). A second, related prediction that derives from the Marcus-like hydrogen tunneling model of eq (2) is that longer equilibrium donor-acceptor distances can be overcome by increased fluctuations at the active site (25). As illustrated in Figure 5, an increase in internuclear distance is expected to be accompanied by a decrease in ω_x (represented by shallower potential surfaces in panel A, and looser springs in the active site sketches in panels B and C), introducing a greater contribution for internuclear distance sampling. An important feature of such enhanced distance sampling is its mass dependence, with the more diffuse protium wavelength requiring less compensatory motion than deuterium.

Impact of Mutation on the pH Dependence of ht-ADH Reactivity

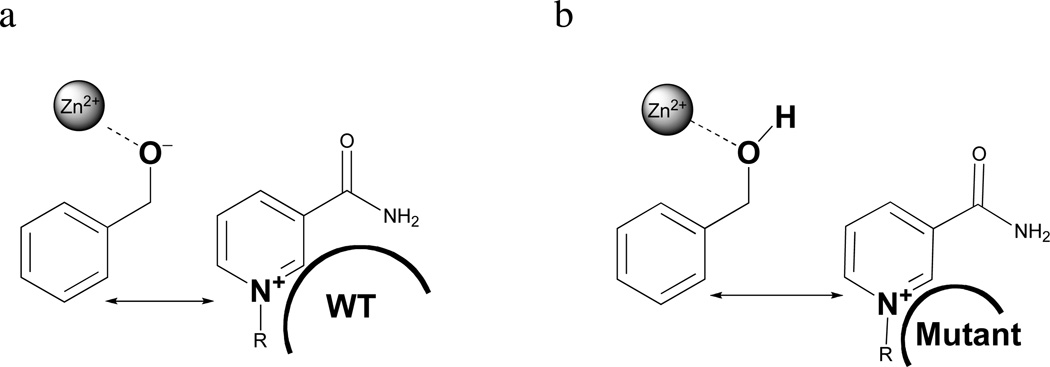
Although X-ray structures are not yet available for the cofactor site mutant forms of ht-ADH, it is possible to use the observed trends in pK_a (Table 1, Figure 2) to estimate the impact of mutation on the H-donor-acceptor distance. A trend is observed in which the decrease in bulk behind the nicotinamide ring of the cofactor leads to an increase in the apparent pK_a that controls catalysis (average pK_a for all mutants is 7.89 (0.25), with the exception of L176G. An analogous pK_a in other alcohol dehydrogenases has been attributed to the ionization of the zinc-bound alcohol to the corresponding alkoxide (Scheme 1), which occurs prior to hydride transfer (55). Perturbations to the pK_a for Zn²⁺ bound water have been detected previously upon cofactor binding in alcohol dehydrogenase (56), and the extent of this perturbation is expected to be sensitive to the distance between the stabilizing positive charge on the oxidized form of the cofactor, NAD⁺, and the negatively charged alkoxide (Figure 6). An alteration of pK_a arising from a temperature-dependent pK_a perturbation has been ruled out from the demonstration of similar pK_a shifts for V260A at high and low temperatures (40).

Figure 6.

Electrostatic stabilization of the alkoxide by NAD⁺. (A) Proximity of the positively charged nicotinamide ring of NAD⁺ is expected to lower the pK_a of the Zn-bound alcohol by forming a favorable interaction with the negatively charged alkoxide. (B) In the mutants, the stabilizing positive charge may relax to a longer distance, thus, raising the pK_a of the alcohol relative to wild-type.

A simple electrostatic model can be used to estimate enzyme active site pK_a values to within 1 pK unit, based on a point charge treatment of neighboring charge centers on the enzyme (57). The free energy (in Joules) for two point charges, q₁ and q₂, is given by eq (5):

$$\mathrm{\Delta }\omega =\frac{{\mathrm{q}}_1{\mathrm{q}}_2}{\epsilon (\mathrm{r}){\mathrm{r}}_{12}}$$ (5)

where ε(r) is the effective dielectric permittivity, and r₁₂ is the distance between the charges. As a frame of reference, we have used eq (5), and the expression for ε(r) obtained by Mehler and Eichele (57), to estimate the stabilization of the alkoxide resulting from the positive charge on the nicotinamide ring of the cofactor. In the ht-ADH ternary complex model, the distance between the oxygen of the alcohol and the nitrogen of the nicotinamide ring of the cofactor is 3.9 Å, corresponding to a stabilization of approximately 3.4 pK_a units in the wild-type enzyme. A similar value (3.0 pK_a units) was obtained when the same calculation was carried out for HLADH (58). This model indicates that a displacement of the nicotinamide ring between 0.2 and 0.8 Å away from the substrate alcohol would be sufficient to result in the range of pK_a perturbations (0.3–1.2 units) measured for the ht-ADH mutants. In the earlier X-ray structure of the ternary complex between HLADH containing the V203A mutation (corresponding to position 176 in ht-ADH), the displacement of the nicotinamide ring from the C-1 of substrate was estimated to be between 0.4 and 0.8 Å (20)(59). Although the pH dependence of the V203A mutant was not investigated in the earlier study, the magnitude of the observed displacement for HLADH is comparable to present estimates for ht-ADH based on the experimental pK_a perturbations.

Structural Modeling of ht-ADH Variants

While X-ray structures of the mutants in ht-ADH are not available at this time, our interpretation of the consequences of expanding the ht-ADH active site for catalysis is supported by structural models that have been generated for the ternary complex of V260A and L176Δ with trifluoroethanol and NAD⁺. Both models predict no significant structural rearrangements, except for the introduction of a packing defect behind the nicotinamide ring of the NAD⁺ cofactor. No major changes are seen in the positioning of the cofactor with respect to substrate. However, a cavity appears behind the nicotinamide ring, creating space for this moiety to move away from the alcohol substrate (Figure 4). While the present computational modeling does not generate a displacement of the nicotinamide ring away from the alcohol, it is highly likely that cofactor positioning will reflect an equilibrium distribution of several orientations, one of which was selected out preferentially upon crystallization [in the case of HLADH (20)] and another computationally (in the current study).

Temperature Dependence of KIEs for Reduced Bulk Mutants in the Context of Altered Conformational Sampling

In contrast to the increased temperature dependence of the KIEs for the mutants with reduced active site bulk at elevated temperature, these mutants show very little trend in the KIE at low temperature, with the maximum observable KIE achieved close to or at 30 °C for all but L176V, the most conservative mutant studied (Figure 3). This leads to a reversal of a key property of the wild-type enzyme, namely KIEs that are more temperature-dependent below 30 °C. We propose that active site mutation results in contrasting kinetic and tunneling properties above and below 30 °C because catalysis takes place in the context of different subsets of reactive conformers in the two temperature regimes (40).

Previous characterization by H/D exchange showed that wild-type ht-ADH undergoes a rigidification below 30 °C that introduces a restriction in the accessible conformational space and that this is linked to a need for greater donor-acceptor distance sampling (38). This conformational restriction has recently been invoked to account for the unusually large Arrhenius prefactors, A_obs, observed below 30°C for the same family of ht-ADH variants studied herein (40). In Table 2, the previously measured values for A_obs (< 30 °C) are included for comparison to the E_a(D) – E_a(H), measured above 30 °C. The two parameters are seen to increase together. By contrast, the values of A_obs above 30 °C were found to be largely unchanged from wild-type values (40), indicating the extent to which mutation is linked to temperature with regard to impaired conformational sampling. The apparent relationship in Table 2 indicates that rank of severity is largely preserved among the mutants across the breakpoint temperature, with a decrease in active site bulk resulting in increased local distance sampling above 30 °C, and impaired conformational sampling (preorganization) below 30 °C. We next consider mechanisms by which this could occur.

What is so unusual in the present study of ht-ADH is that the expected trend in the temperature dependence of the KIEs among the mutants is seen above 30 °C (see Discussion above), but with the exception of L176V, reverses itself below 30 °C. The low temperature regime in the mutant ht-ADH variants represents the first example from this laboratory in which a perturbation (in this case cooling a mutant enzyme below its optimal temperature) yields a smaller temperature dependence for the KIE than is observed under native conditions. In a recent study by Scrutton and co-workers, the generation of active site mutants with smaller side chains in morphinone reductase (MR) led to a series of proteins with a reduction in the sensitivity of the KIE to temperature when compared to wild-type (11). In the MR study, the distance between the hydride donor (NADH) and acceptor (FMN) was estimated based on the magnitude of absorbance for a charge transfer complex between a nonreactive NADH analog and the isoalloxazine ring of FMN. These measurements lead to an unexpected conclusion that the distance between the donor and acceptor had been reduced in the mutant proteins. While no X-ray structures were available for the mutant enzymes, it appears that the act of simply reducing the bulk of a side chain is not a guarantee that the distance between the hydride donor and acceptor will increase. Thus, a possible explanation for our data is that, in the mutants, the hydrogen donor and acceptor have relaxed (as expected) to a longer distance above 30 °C, but are forced into a shorter contact distance at low temperatures.

An alternate, and in our view far more plausible explanation is that the donor-acceptor distance is increased in the mutants at all temperatures, but that once the enzyme is restricted to a less optimal region of conformational space, its ability to correct the active site defect via distance sampling is severely impaired, as shown in Figure 5. A decrease in the temperature dependence of the KIE below a breakpoint temperature has been observed previously in protochlorophyllide reductase (60), indicating that a drop in temperature can freeze out motions that are required for donor-acceptor distance sampling. The anomalous low-temperature activation parameters discussed above for the mutant ht-ADH variants have been attributed to a skewing of the protein conformational landscape upon rigidification at 30 °C toward low energy, inactive states, from which the protein must exit before productive catalysis can proceed (40). The accessible catalytically active states populated at low temperature occur in the context of this severely altered conformational landscape, which imposes constraints on the active site that are not present in the more flexible/active conformers above 30 °C. We propose that the combination of a cofactor-binding site mutation with a temperature below its dynamical phase transition leads to proteins that have become too rigid, even among the subset of catalytically competent conformations, to support significant donor-acceptor distance sampling.

These data also present an opportunity to revisit an alternative hypothesis regarding the origins of temperature-dependent KIEs in ht-ADH at low temperature. It has been proposed that the temperature dependence of the primary KIE at low temperature could arise from the increased population of conformers with larger, but intrinsically temperature-independent KIEs (41). This model has also been proposed recently for additional enzyme systems (42). However, the data for mutant variants of ht-ADH at low temperature show an increase in the magnitude of the Arrhenius break [i.e., significantly larger activation energies below the break in relation to wild-type (40)] that occurs without an accompanying increase in the temperature dependence of the KIE; by contrast, if the temperature dependence of the KIE were arising from an increased population of conformers with larger (but only weakly temperature-dependent) KIEs, a significant increase in the temperature dependence for the KIE below the breakpoint temperature would have been expected for the L176 and V260 variants (cf. Figure 3). Similarly, the high-temperature data for ht-ADH indicate an increase in the temperature dependence of the KIE (Table 1) without a concomitant change in activation parameters (40). For these reasons, the data presented herein provide additional support for a Marcus-like model of hydrogen tunneling, which has been used successfully to replicate both the primary and secondary experimental KIEs for alcohol dehydrogenase (33). According to this model, the temperature dependence of the KIE arises from donor-acceptor distance sampling (25), and not from a temperature-dependent equilibration among conformers with intrinsically different KIEs.

Conclusions

Mounting experimental data indicate a role for at least two types of motion in enzymatic catalysis that involve large scale statistical sampling of a protein conformational landscape (preorganization), together with more local adjustments of the active site environment to support H-tunneling (reorganization). This paper presents evidence that both the reorganization and preorganization are optimized in wild-type enzymes for efficient catalysis under native conditions. The 30 °C break in ht-ADH provides valuable insight into both processes. First, a trend toward temperature-dependent KIEs at elevated temperature indicates an increased need for donor-acceptor distance sampling when bulky hydrophobic side chains are removed from the active site. This corroborates the expectation that enzymatic hydride transfer reactions will be subject to the same physical properties that underlie non-adiabatic hydrogen atom transfer with regard to donor-acceptor distance-sampling modes. Second, the observation of an opposing impact of mutation above and below the breakpoint temperature supports the hypothesis that a different conformational ensemble dominates at low temperature in the wild-type enzyme and that this is greatly exacerbated in the active site mutants.

Abbreviations

NAD⁺

nicotinamide adenine dinucleotide

ht-ADH

thermophilic alcohol dehydrogenase from B. stearothermophilus

HLADH

horse liver alcohol dehydrogenase

KIE

kinetic isotope effect

EXP

the Swain-Schaad exponent

^Dk_cat

the ratio of k_cat for the protio and deutero substrates

HDX

hydrogen-deuterium exchange

K_M(BnOH)

the K_M for ht-ADH with respect to the substrate benzyl alcohol