Understanding the recent colonization history of a plant pathogenic fungus using population genetic tools and Approximate Bayesian Computation

Abstract

Understanding the processes by which new diseases are introduced in previously healthy areas is of major interest in elaborating prevention and management policies, as well as in understanding the dynamics of pathogen diversity at large spatial scale. In this study, we aimed to decipher the dispersal processes that have led to the emergence of the plant pathogenic fungus Microcyclus ulei, which is responsible for the South American Leaf Blight (SALB). This fungus has devastated rubber tree plantations across Latin America since the beginning of the twentieth century. As only imprecise historical information is available, the study of population evolutionary history based on population genetics appeared most appropriate. The distribution of genetic diversity in a continental sampling of four countries (Brazil, Ecuador, Guatemala and French Guiana) was studied using a set of 16 microsatellite markers developed specifically for this purpose. A very strong genetic structure was found (F_st=0.70), demonstrating that there has been no regular gene flow between Latin American M. ulei populations. Strong bottlenecks probably occurred at the foundation of each population. The most likely scenario of colonization identified by the Approximate Bayesian Computation (ABC) method implemented in 𝒟ℐ𝒴𝒜ℬ𝒞 suggested two independent sources from the Amazonian endemic area. The Brazilian, Ecuadorian and Guatemalan populations might stem from serial introductions through human-mediated movement of infected plant material from an unsampled source population, whereas the French Guiana population seems to have arisen from an independent colonization event through spore dispersal.

Introduction

Understanding the dispersal processes involved in the introduction of invasive species is of major interest from a fundamental perspective as such processes affect the distribution and evolution of diversity. It is also relevant from a more applied point of view. First, introduction processes should be taken into account in the design of quarantine politics. Second, even after successful introduction, knowledge of the dispersal mode of invasive species remains crucial to limit multiple introductions, which may result in the admixture of individuals from differentiated populations, and possibly boost the evolutionary potential of introduced populations (Dlugosch and Parker, 2008). This is particularly true in plant–pathogen systems, where the successful introduction of a new species may often result in the emergence of a new disease (Anderson et al., 2004). Introductions of fungal plant pathogens are generally considered to stem from two main mechanisms. The first is the transport of infected plant material. For instance, the historical epidemic of potato late blight (Phytophthora infestans, Goodwin et al., 1994) resulted from human-mediated introduction of infected plant material. In addition, dispersal abilities of airborne plant pathogens are often suspected to be considerable. For instance, the natural dispersal of Puccinia striiformis f. sp. tritici—the causal agent of wheat stripe rust—has led to the dissemination of a single clone across Europe (Hovmøller et al., 2002). Exceptional climatic phenomena could also result in long-distance dispersal events, as for instance with Asian soybean rust (Phakopsora pachyrhizi), which was introduced into the United States by a hurricane (Pan et al., 2006).

Distinguishing between human-mediated and natural dispersal at different geographic scales is important and essentially requires identifying source pathogen populations and retracing colonization history. Studies of recent colonization events using extensive and precise monitoring of disease spread at large scales (continental or global) are possible. For instance, the diffusion of new strains of wheat pathogens P. striiformis f. sp. tritici and Puccinia graminis f. sp. tritici have recently been described in detail by means of molecular and phenotypic (virulence) markers (Hovmøller et al., 2008). Such epidemiological data describing the spatio-temporal progression of diseases may provide interesting clues on the mechanisms of propagation (Mundt et al., 2009). The above studies benefit from a wide monitoring network, looking for relatively easily detectable events, that is, the overcoming of resistance in crop fields. In most cases, however, accurate tracking of individual spores or infected plant fragments is almost impossible at the spatial scales considered, notably because of the stochastic nature of long-distance dispersal events (Aylor, 2003). In most biological systems, and in the special case of recent (tens of years) introductions of new species following long-distance dispersal, epidemiological information is partial, or at best imprecise (for example, there may be a significant lag time between introduction and the first report of the pathogen), disqualifying this type of approach in inferring the colonization history of a species.

Alternatively, identifying source populations and propagation routes may benefit from indirect methods, such as population genetics studies. Classical population genetics studies may already provide important clues by describing the genetic similarity between pairs of populations by means of differentiation indices and genetic distance trees. However, in many cases, this may not be sufficient. First, during the colonization of a continent, one may expect populations to be founded through strong genetic bottlenecks followed by rapid population expansion (Raboin et al., 2007). Such demographic events typically result in high levels of genetic differentiation between source and newly founded populations, making it difficult to clearly establish the links between populations based on population differentiation. Second, the colonization history of an entire continent may rely on relatively complex scenarios involving, for example, admixture between several differentiated source populations (Frankham, 2005), which is not compatible with trees based on pure divergence. Finally, in many plant pathogen species, most native populations are unknown at the time of emergence, for example, because the disease, initially restricted to a wild compartment, went unnoticed until it jumped on a crop and caused yield losses (for example, Brunner et al., 2007). Thus, sampling of native areas is generally unlikely to be sufficient for a solid reconstruction of propagation routes.

In the past few years, a new set of methodologies has emerged that, in principle, allow the analysis of complex demographic and evolutionary scenarios, in particular when some populations cannot be sampled (Estoup et al., 2010). These are based on Approximate Bayesian Computation (ABC). In ABC, the limiting step of very complex likelihood computations is replaced by an approximation of the likelihood, which is obtained by simulating data sets under considered scenarios and selecting the simulated data sets that are closest to the observed data using a regressive approach on summary statistics (Beaumont et al., 2002). Both the Bayesian nature of ABC and the approximation at the core of the technique require that it be used with caution and properly validated, as stressed by several authors (Bertorelle et al., 2010, Robert et al., 2011). It has nevertheless already been used to study the introduction of diploid invasive species, such as amphibians or insects (for example, Estoup et al., 2010; Guillemaud et al., 2010).

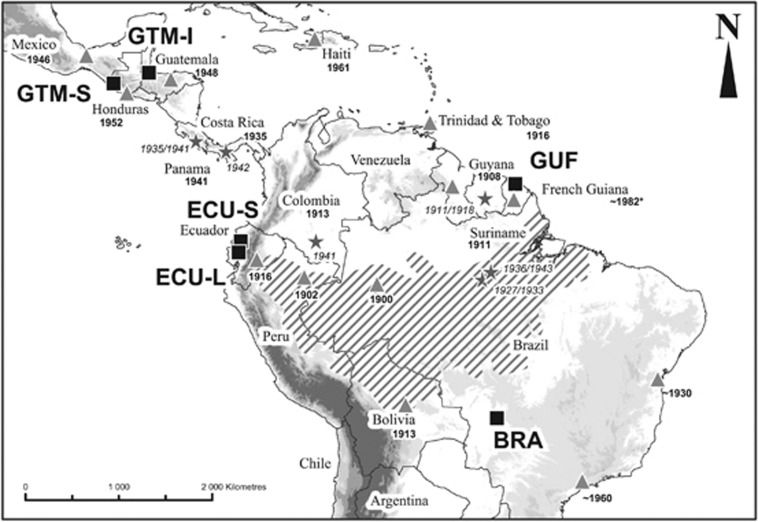
The South American Leaf Blight (SALB) disease caused on rubber trees (Hevea brasiliensis) by Microcyclus ulei (P. Henn), a Ascomycota fungus of the Mycosphaerellaceae family, is a striking example of the recent emergence of a fungal plant disease. This haploid fungus, originating from the Amazonian forest, was first reported in the Rio Jurua valley (Brazil) in 1900 (Ule, 1905, Figure 1). It then spread across the Central and South American plantations of H. brasiliensis only a few years after the development of rubber tree plantations (reviewed in Hilton, 1955; Guyot, 2007; Lieberei, 2007). Little is known about the life cycle of this species. By analogy to other Mycosphaerellaceae, this fungus is thought to alternate between asexual and sexual phases. It can only infect young rubber tree leaves and the mass production of asexual spores (named conidiospores) is responsible for epidemics in flushing rubber trees canopies (Lieberei, 2007). For other Ascomycota, spores produced during the sexual stage (named ascospores) generally act as primary inoculum and/or are implicated in long-distance dispersal, as for example for the tropical plant pathogens Mycosphaerella fijiensis or Mycosphaerella musicola (Marin et al., 2003). M. ulei sexual structures (stromata) have been described extensively (Holliday, 1970). Sexual spores (ascopores) have been rarely observed in stromata so that the process of ascospores production remains unclear (Guyot et al., 2008). Ascospores have been suspected to initiate epidemics (Guyot, 2007) but their precise role and dispersal capacities remain unknown. M. ulei dispersal over long distances has been attributed to either human-mediated transport (Holliday, 1970) or occasional natural long-distance dispersal (Liyanage, 1981). Rubber tree plantations in Central and South America are not continuous, and exchange of cuttings between countries has probably been intense in the recent past, potentially leading to extensive mixing of inoculums and strong foundation effects, which may complicate the interpretation of standard genetic data analyses. Dates of first mention are available in all locations infected by the pathogen but such historical data is insufficient to reconstruct the history of colonization of Latin America and thereby infer source populations as well as dispersal modes, from a classical epidemic viewpoint. Thus the use of population genetic methods seems particularly relevant to elucidate this history. From an applied point of view, knowledge of the history of dissemination of this pathogen at the scale of Latin America is important in order to limit its dispersal. SALB disease has not yet reached Asia, which is by far the largest production area for natural rubber (Lieberei, 2007). M. ulei, therefore, represents a major threat for H. brasiliensis plantations in this part of the world.

Figure 1.

Map of the recent history of M. ulei in Latin America. Gray triangles represent the country/region where M. ulei was identified, with the date of the first report. (*: Because no first report of M. ulei on H. brasiliensis in French Guiana has been published, we report here the date of first plantation tests of H. brasiliensis in French Guiana, since emergence of SALB disease has probably occurred only a few years after the introduction of the host (Le Guen et al., 2002).) Gray stars indicate notable SALB epidemics reported in the literature. The dashed area shows the approximate distribution area of natural H. brasiliensis trees. Black squares represent sampling sites.

Our objectives were to decipher the colonization history of M. ulei across Latin America and to infer the dispersal modes implicated in this spread (human-mediated versus natural dispersal) from population genetic structures. To achieve these goals, we genotyped isolates of M. ulei from different Latin American locations using a newly developed set of microsatellite molecular makers. These data were analyzed by combining classical population genetics tools and ABC analysis using 𝒟ℐ𝒴𝒜ℬ𝒞 (v1.0) software (Cornuet et al., 2010). We confirm the existence of sexual reproduction as well as the very low level of gene exchange between current M. ulei populations. Based on ABC results, we propose a scenario of colonization from two independent Amazonian sources, and discuss the implications and validity of these findings.

Materials and Methods

Sampling

Sampled individuals were collected from H. brasiliensis tree plantations in four countries: one location in Brazil (BRA, Plantações E. Michelin Ltda, Mato Grosso, Itiquira, 17°21′S 54°43′W), one location in French Guiana (GUF, CIRAD test plantation, Pointe Combi, 05°17′N 52°55′W), two locations in Ecuador (ECU-S, Santo Domingo, Pichincha, 00°01′N 79°22′W and ECU-L, Quevedo, Los Ríos, 01°05′S 79°27′W) and two locations in Guatemala (GTM-I, Livingstone, Izabal, 15°49′N 88°45′W and GTM-S, Santa Ana, San Marcos, 14°48′N 91°56′W). Each plantation contains different rubber tree clones. All samples were collected on rubber tree clones without any qualitative resistance, most samples coming from the rubber tree clone FX3864.

Sampling was conducted in 1999, 2003, 2004 and 2008, in French Guiana, Brazil, Ecuador and Guatemala, respectively. In each plantation, one H. brasiliensis leaf with M. ulei conidial lesions was collected from each of 30 rubber trees. Except in Guatemala, strain purifications were performed following the protocol described in Lespinasse et al. (2000). Briefly, conidial (asexual) spores were collected on a single lesion per leaf, placed in water and sprayed at low density on healthy rubber tree leaves in order to obtain lesions resulting from a single spore. A second round of inoculation was performed to ensure good purification. These two steps of multiplication and purification of strains were performed in order to obtain a sufficient amount of identical conidiospores for cultivation of mycelium, as the growth of M. ulei on medium is very slow and difficult. Spores were grown on M4 culture medium (Junqueira et al., 1984), and 20 mg of the resulting mycelium was collected and stored at −20 °C until DNA extraction. For Guatemalan populations, one conidial lesion per leaf was cut directly from leaves (∼3 mm²) and stored at −20 °C until DNA extraction.

Microsatellite development

Nine polymorphic microsatellite markers had already been developed for M. ulei (Le Guen et al., 2004). In order to increase the power of the population genetics analysis, supplementary microsatellite markers were designed (Supplementary Table S1). New DNA sequences were obtained from the microsatellite-enriched library used by Le Guen et al. (2004). Forty-two primers pairs were defined using 𝒫ℛℐℳℰℛ3 (Rozen and Skaletsky 2000). In order to allow size multiplexing, four classes of product size were defined: 100–140, 180–220, 260–300 and 340–380 base pairs, and annealing temperatures were fixed at 60 °C for each primer pair. The 42 primer pairs were tested on the four sampled populations. PCR was carried out in final reaction volumes of 20 μl containing 15 ng template DNA, 2 μl of 10 × reaction buffer, 1.5 mℳ MgCl₂, 0.2 mℳ dNTP, 0.5 U Taq polymerase (Eurobio, Les Ulis, France) and 0.2 μm forward and reverse primers. Reactions were performed in a PTC-200 Peltier Thermal Cycler (MJ Research, Waltham, MA, USA) with 5 min at 95 °C followed by 40 cycles of 60 s at 94 °C, 90 s at 60 °C and 60 s at 72 °C and a final extension step of 30 min at 60 °C. Of the 42 loci tested, 10 failed to have an interpretable pattern of migration on a 2% agarose gel because of multiple bands or unexpected allele size. Forward primers of the remaining 32 loci were labeled to allow size and dye multiplexing. PCR products were pooled in eight sets of four markers with each locus carrying a different dye (FAM, VIC, NED and PET) and were separated, sized and analyzed on a Applied ABI Prism 3130 XL apparatus (Applied Biosystems, Carlsbad, CA, USA). 𝒢ℰ𝒩ℰℳ𝒜𝒫𝒫ℰℛ software (Applied Biosystems) was used to score alleles.

DNA extraction

Mycelium DNA was extracted following Rivas et al. (2004). This protocol consists of a mycelial wall digestion step, followed by lysis of the cell wall with an extraction buffer containing cetyltrimethylammonium bromide , extraction of proteins using chloroform:isoamyl alcohol (24:1), and precipitation of DNA using absolute ethanol. A few slight modifications to the original protocol were made: RNAse A (Qiagen, Hilden, Germany) was added directly to the extraction buffer at a final concentration of 100 μg ml⁻¹, and DNA was suspended in 100 μl of ultra-pure water instead of an alkaline buffer.

For the Guatemalan population, DNA was extracted from single conidial lesions obtained from infected leaves as described by Bourassa et al. (2005), using a DNeasy Plant Mini Kit (Qiagen). We followed the ‘Fresh Leaves' protocol (DNeasy Plant Handbook, July 2006) except that samples were disrupted with one tungsten carbide bead for 2 × 1 min instead of 2 × 1.5 min at 30 Hz. DNA was eluted in a final volume of 200 μl. DNA from the host and the pathogen were therefore mixed together within each DNA extract, but as microsatellites are species specific, they allow direct genotyping of M. ulei only. DNA from healthy H. brasiliensis clone FX3864 was also extracted following the same procedure and used as a negative control to ensure that microsatellites did not cross-amplify the host DNA.

General data analyses

Identification and management of identical multilocus genotypes

Because M. ulei is capable of asexual reproduction, it is important to identify individuals that result from asexual multiplication, as this could greatly impact on measurement of genetic diversity and structure (Chen and McDonald, 1996). With this aim in mind, we constructed two different clone-corrected data sets. In the first, we assessed the likelihood that individuals with the same multilocus genotype (MLG) are indeed the result of asexual multiplication using 𝒢ℰ𝒩𝒞ℒ𝒪𝒩ℰ2.0 (Arnaud-Haond and Belkhir, 2007): the probability of observing a given MLG assuming random mating (P_sex) n times was computed in each population for each group of identical MLG. When P_sex was <0.01, we considered that the corresponding MLG was overrepresented and individuals were removed one by one from the MLG group until the probability became >0.01 or until only one individual remained in the MLG group. The second clone-corrected data set was built by keeping a single individual by MLG group in each sampled location. All subsequent analyses were performed on the three data sets (the complete set and the two different clone-corrected data sets) but as all the results were similar, we present only the output of the latter clone-corrected data set (the most drastic in terms of clone-correction).

Defining genetic clusters

We used two individual-centered approaches to describe the genetic structure of populations without a priori geographic knowledge. First, we applied a Bayesian clustering method using 𝒮𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ v2.3.3 software (Falush et al., 2003). 𝒮𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ uses individual MLG data to cluster individuals into an a priori given number of groups K while minimizing linkage disequilibrium between loci within groups. The underlying model authorized admixture and correlation of allele frequencies as advised by Hubisz et al. (2009). Each run of the software consisted of a burn-in period of 100 000 iterations followed by 500 000 simulations. Eight repetitions of each run were performed in order to verify the convergence of Monte Carlo Markov Chains for K ranging from 1 to 11. Different values of K can represent different organizational levels of genetic structure, and particularly hierarchical genetic structures (see, for an example, Vercken et al., 2011). Only K values that significantly increase the probability of the data given a number of groups K (Pr(X|K)) convey biologically meaningful information. To assess these values of interest, we both used the classical approach of Pritchard et al. (2000) based on the maximization of Pr(X|K), and the Delta-K method described in Evanno et al. (2005) based on the second-order rate of change of Pr(X|K) when K increases. As this clustering method relies on assumptions that may be expected to be violated in a recently introduced ascomycete fungus (for example, demographic and genetic equilibrium state of all populations), we also used a non-parametric method to describe genetic structure at the individual level. Shared allele distances between individuals were computed using 𝒫𝒪𝒫𝒰ℒ𝒜𝒯ℐ𝒪𝒩𝒮 v1.2.30 software (O. Langella, http://bioinformatics.org/~tryphon/populations/). We then performed a principal coordinate decomposition on the genetic distance between individuals using ℛ software package ‘ape' (Paradis et al., 2004, R Development Core Team, 2004).

Measures of genetic structure and diversity

Based on the results of the individual-centered approaches described above, individuals belonging to a country were grouped together and considered as a population. Genotypic linkage disequilibrium between all pairs of microsatellites markers in each population was computed using 𝒢ℰ𝒩ℰ𝒫𝒪𝒫 v4 (Rousset, 2008). In order to reduce Type I error, we applied the false discovery rate procedure (Benjamini and Hochberg, 1995) to P-values obtained for genotypic linkage disequilibrium tests. The resulting so-called Q-values were computed using the 𝒬𝒱𝒜ℒ𝒰ℰ package in ℛ (Storey, 2002). Allelic richness (A_r), estimated in each population with a rarefaction method (El Mousadik and Petit, 1996), and mean number of alleles (N_a) were computed using ℛ (R Development Core Team, 2004). Pairwise F_𝒮𝒯 values between populations were estimated using the method of Weir and Cockerham (1984), and the significance of genotypic differentiation was assessed from exact tests conducted with 𝒢ℰ𝒩ℰ𝒫𝒪𝒫 v4.

ABC analyses with 𝒟ℐ𝒴𝒜ℬ𝒞

To compare concurrent scenarios of colonization history, we used an ABC approach as implemented in the software 𝒟ℐ𝒴𝒜ℬ𝒞, which has been recently adapted to allow the study of haploid species (Cornuet et al., 2008, 2010). ABC allows ranking scenarios based on their approximate posterior probabilities. To do this, a large number of simulated data sets is produced under each scenario, sampling parameter values into prior distributions. Then the occurrence of each scenario among the simulated data sets that are closest to the observed data gives an estimate of its posterior probability using a logistic regression procedure (Fagundes et al., 2007).

Definition of scenarios

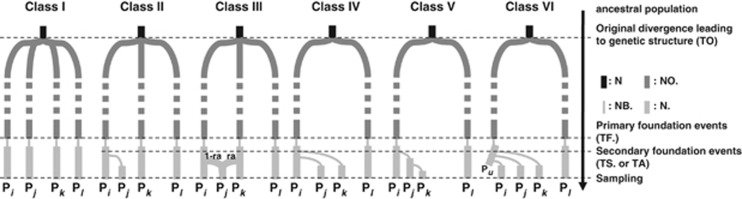
𝒟ℐ𝒴𝒜ℬ𝒞 simulates population divergence for unlinked markers, such as microsatellites (Cornuet et al., 2008, 2010). Even with only four sampled populations, the number of possible evolutionary scenarios is exceedingly large, taking into account bottlenecks, admixture events, multifurcations and the existence of unsampled (ghost) populations. It was therefore necessary to find a way to select a reasonable number of scenarios to compare. This is a critical step of ABC analysis and no general method can be applied to achieve the design of necessary and sufficient scenarios. In the present study, the definition of scenarios was carried out based on both basic historical information and the results of clustering analysis and is detailed in Figure 2 (that is, scenarios obviously unsupported by historical data and observed genetic structure were not considered). Six classes of scenarios were constructed (Figure 2), with each scenario class referring to a given topology. We know from historical data that studied in plantations have been installed during the twentieth century. The first epidemics occurred very soon after plantation creation (early twentieth century in Brazil, 1950s in Guatemala and 1970s in Ecuador). Whether the four sampled plantations were contaminated independently by strains from the Amazonian forest or by subsequent between-plantation exchanges is unknown. Scenarios likely to produce the present data all account for the existence of four ‘recently founded' populations (that is, within the past hundred years, light gray in Figure 2) with at least one such population originating in the endemism area. No sample of a natural population of M. ulei from the Amazonian forest was available, thus the genetic structure of the forest source populations was unknown. Depending on population dynamics and history in the endemism area, source populations may be more or less differentiated. As this may impact on the genetic composition of current samples, possible structure in the native area had to be simulated as the result of a more ancient divergence (dark gray in Figure 2) from an initial common pool (black in Figure 2). During colonization, the founding of new populations may be accompanied by a founder effect (Sakai et al., 2001). Because of the existence of a low genetic diversity within populations with several private alleles and of a high differentiation between populations (see the Results section), each founder event was assumed to be associated with a bottleneck (thin light gray lines). Importantly, scenarios without bottlenecks have systematically been tested and appeared unable to produce data sets close to the observed one (Supplementary Table S2, Supplementary Figure S3 and Supplementary Figure S4).

Figure 2.

Classes of evolutionary scenarios under comparison using ABC analyses. P_i, P_j, P_k and P_l represent the four sampled populations. Within each class different scenarios were obtained by permuting the four sampled populations at branch tips (P_x) (see Table 4). P_u stands for an unsampled population. The ‘ancestral population', with an effective population size of N, is represented in black. At time TO, it gave rise to diverging source populations in the endemic area with an effective population size of NO. (dark gray). At time TF., primary foundations occurred, that is, the source populations contaminated plantations (light gray) through a genetic bottleneck (of intensity NB., thin light-gray lines). Class II to Class VI scenarios involve secondary foundation events, where recently founded populations contaminated new localities, at time TS.; N. holds for the effective population sizes of sampled populations. ra stands for the admixture rate in the scenario Class III (see Table 1 for details).

Scenario classes differ in the number of independent introductions and in the recent history of contaminations between plantations (light gray). Within each class, several scenarios differing in the identity of populations at branch tips were tested. A total of 25 scenarios were designed. The unique Class I scenario assumes four independent founder events. The four sampled populations (light gray in Figure 2) would be independently founded by four differentiated source populations located in the endemic area (dark gray in Figure 2) through a genetic bottleneck (thin lines in Figure 2). Class II and III scenarios consider that three sampled populations stemmed from the native area (three dark gray source populations in Figure 2), the fourth sampled population being either founded by one of the three others (Class II) or the result of an admixture between two other populations (Class III), as suggested by some results of clustering analyses below (see the Results section). Finally, Classes IV to VI consider two independent foundations by source populations located in the native area, the other foundations being attributable to between-plantation exchanges. Class IV and V scenarios consider that an initial sampled population either spread to two other localities (Class IV) or contaminated only one other locality that subsequently contaminated another one (Class V). Class VI scenarios consider the case where this initial population that was not directly sampled.

Prior distributions and summary statistics

Defining the prior distribution of parameters is an essential step of ABC analyses (Bertorelle et al., 2010) as it may impact greatly on results. A list of all parameters and prior distributions used to model scenarios is summarized in Table 1. Because of the lack of knowledge of natural and plantation population sizes of M. ulei, a uniform distribution with large interval (10–100 000) was chosen as the prior distribution for effective population sizes of the ancestral population (N, black in Figure 2), of the different source populations in the endemism area (NO., dark gray in Figure 2) and of the sampled populations (N., light gray in Figure 2). Other distributions (a log-uniform distribution on interval (10–100 000) and a normal distribution with mean 10 000 and standard deviation 20 000) were tested and all results were similar (not shown). In addition, the list of first reports of M. ulei across Latin America enables us to delimit the range of the times of founding events (that is, plantation contamination). However, historical information may be imprecise. In some cases, the first report of a disease may appear several years after the real introduction of the pathogen. Furthermore, the life cycle of M. ulei is still poorly known and it cannot be excluded that it goes through several rounds of sexual reproduction per year. For these reasons, times of founding of sampled populations were drawn in a log-uniform distribution on interval (16–500) (expressed in numbers of generations). A condition was set in prior definition to ensure that the times of direct contaminations from the forest (TF. in Figure 2) be greater than times of subsequent plantation-to-plantation contamination (TS. in Figure 2). Bottleneck population sizes were drawn from a log-uniform distribution ranging from 1 to 100 (NB., thin light gray lines in Figure 2). The duration of all bottleneck events was fixed to five generations to reflect the fact that introduced populations might take several generations to reach their equilibrium population size. As mentioned above, no information was available on the genetic structure and evolutionary history of natural populations of M. ulei. We thus assumed that source populations could have diverged during a time drawn from a large uniform distribution on interval (600–100 000) (also called ‘original divergence', TO in Figure 2). Finally, when necessary, the rate of admixture between two populations was drawn in a uniform distribution (0.001–0.999). Parameters for microsatellite mutation models were set by default following a generalized stepwise mutation model (Cornuet et al., 2010). Furthermore, single nucleotide insertion/deletion (indel) mutations were allowed with a mean rate of mutation Mμsni as in Table 1 and 5 drawn in a log-uniform distribution [10⁻⁸–10⁻⁴]. Each locus was characterized by an individual rate of indel mutations drawn from a Gamma distribution with mean=Mμsni and shape=2. Summary statistics were the mean number of alleles per population, the mean allele size variance per population, as well as mean gene diversity, F_𝒮𝒯 and classification index—all three taken between pairs of populations (see Cornuet et al., 2008 for details).

Table 1. Definition and prior distribution of parameters used in the definition of the 25 tested scenarios.

	Parameter name	Distribution
		Type	Interval
Population effective sizes of the ancestral population	N	Uniform	{10–100 000}
Population leading to Brazilian population founder event	NOb	Uniform	{10–100 000}
Population leading to Equatorian population founder event	NOe	Uniform	{10–100 000}
Population leading to Guatemalan population founder event	NOgt	Uniform	{10–100 000}
Population leading to French Guyanian population founder event	NOgy	Uniform	{10–100 000}
Population leading to unsampled population founder event	NOu	Uniform	{10–100 000}
Bottleneck during founder event of Brazilian population	NBb	Log-uniform	{1–100}
Bottleneck during founder event of Equatorian population	NBe	Log-uniform	{1–100}
Bottleneck during founder event of Guatemalan population	NBgt	Log-uniform	{1–100}
Bottleneck during founder event of French Guiana population	NBgy	Log-uniform	{1–100}
Bottleneck during founder event of unsampled population	NBu	Log-uniform	{1–100}
Brazilian population	Nb	Uniform	{10–100 000}
Equatorian population	Ne	Uniform	{10–100 000}
Guatemalan population	Ngt	Uniform	{10–100 000}
French Guiana population	Ngy	Uniform	{10–100 000}
Unsampled population	Nu	Uniform	{10–100 000}
Time of the ancestral divergence in source population	TO	Uniform	{600–100 000}
Founder event of the Brazilian population	TFb	Log-uniform	{16–500}
Founder event of the Equatorian population	TFe	Log-uniform	{16–500}
Founder event of the Guatemalan population	TFgt	Log-uniform	{16–500}
Founder event of the French Guiana population	TFgy	Log-uniform	{16–500}
Founder event of the unsampled population	TFu	Log-uniform	{16–500}
Secondary founder event of Brazilian population	TSb	Log-uniform	{16–500}
Secondary founder event of Equatorian population	TSe	Log-uniform	{16–500}
Secondary founder event of Guatemalan population	TSgt	Log-uniform	{16–500}
Secondary founder event of French Guiana population	TSgy	Log-uniform	{16–500}
Admixture event	TA	Log-uniform	{16–500}
Rate of admixture	ra	Uniform	{0.001–0.999}
Mutation model parameters
Mean mutation rate	Mμmic	Uniform	{10−4–10−3}
Mean parameter of the geometric distribution of the number of repeats	MP	Uniform	{0.1–0.3}
Mean single nucleotide insertion/deletion mutation rate	Mμsni	Log-uniform	{10−8–10−4}

Simulations and posterior probability estimation

One million data sets were simulated for each scenario (as recommended in Cornuet et al., 2008, 2010). The choice of the best scenario was made in two steps. First, scenarios with the same typology and differing only by the identity of populations according to topology were grouped (in a total of six classes, see Figure 2). Posterior probabilities of each scenario within each class were computed by performing a polychotomous weighted logistic regression on the 1% of simulated data sets closest to the observed data set (Cornuet et al., 2008, 2010). Second, the best scenario of each group was kept and the six remaining scenarios (hereafter second-round scenarios) were compared using the same method. Posterior distributions of parameters were evaluated under this scenario using a local linear regression on the 1% closest simulated data sets with a logit transformation.

Confidence in scenario choice and model checking

Confidence in scenario choice was first assessed by evaluating Type I and Type II error rates, following the method described in Cornuet et al. (2010). One hundred test data sets (that is, pseudo-observed data sets) were simulated using each of the six second-round scenarios (representing the six classes of scenario). The posterior probability of the six competing scenarios was then evaluated for each of the pseudo-observed data sets. Type I error was estimated by counting the proportion of data sets simulated under the best scenario (Class VI scenario) that resulted in highest posterior probability for other scenarios (Classes I–V). Type II error was estimated by the proportion of data sets that resulted in highest posterior probability of the best scenario (Class VI scenario in this study), although simulated with other scenarios (Classes I–V).

Second, we tested the adequacy of secound-round scenarios using the model checking option of 𝒟ℐ𝒴𝒜ℬ𝒞 (v1.0). Adequacy is the ability of a given scenario to produce data sets similar to the real data set. For each of the six second-round scenarios, 1000 data sets were simulated by drawing with replacement parameter values among the data sets used to compute the posterior distribution of the parameters. The similarity between simulated and real data was estimated using summary statistics differing from the summary statistics used to conduct model choice. This precaution was taken in order to avoid overestimating the fit of the scenario (Cornuet et al., 2010). These summary statistics were chosen among those provided with the software: mean gene diversity and mean Garza-Williamson's M index for each population, as well as the mean number of alleles, the mean allele size variance and the shared allele distance (DAS) between all pairs of populations (Cornuet et al., 2008). For each summary statistics, the discrepancy between simulated and observed data was then assessed by ranking the observed value among the values obtained with the simulated data sets. This provided an estimation of the P-value for the considered summary statistics. Because many P-values are computed, the false discovery rate was controlled using the method of Benjamini and Hochberg (1995).

Finally, precision of parameter estimation was assessed by computing the relative median of the absolute error on 300 pseudo-observed data sets (that is, data sets simulated with known parameters) simulated with the best scenario. Relative median of the absolute error is the 50% quantile (over the 300 pseudo-observed data sets) of the absolute value of the difference between the median value of the posterior distribution sample (in each data set) and the true value, divided by the true value (Cornuet et al., 2010).

Results

Microsatellite markers

A new set of markers, well suited to perform studies on the genetic diversity and structure of M. ulei populations, was developed. Out of 32 loci tested, 16 were found to be polymorphic with two to eight alleles (Supplementary Table S1). Seven of these polymorphic markers were identical to the previously described microsatellites (Le Guen et al., 2004), and among these, most (Mu01, Mu02, Mu07, Mu08 and Mu12) have different primer sequences in order to allow size multiplexing. Furthermore, identical annealing temperatures were chosen for all primer pairs in order to allow multiplexed PCRs. The number of alleles ranged from 2 (μMU05) to 8 (μMU13 and μMU24). With the exception of μMU05, gene diversity indexes for all loci were found to be high, ranging from 0.39 to 0.79.

Characterization of M. ulei populations

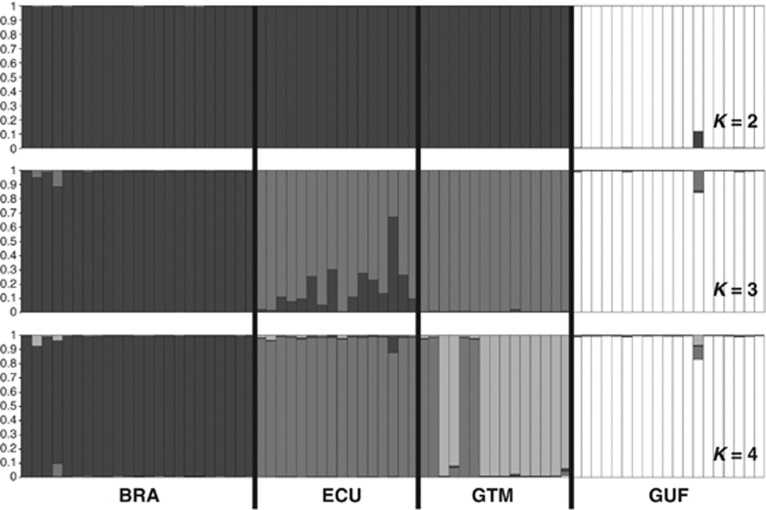
Both genetic clustering analyses with 𝒮𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ software and a principal coordinate decomposition on genetic distances between individuals revealed a hierarchical structure of studied samples (Figure 3 and Supplementary Figure S2). 𝒮𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ detected at most K=4 biologically meaningful genetic clusters as the likelihood of the data reached a plateau at K=4 (ln(Pr(X|K))=−456, with a small peak in the delta K profile, Supplementary Figure S1). These four clusters corresponded to the sampled countries. Further, both analyses suggested that these populations, defined on the basis of geographic and genetic information, could also be clustered into two higher order groups as the likelihood of the data (Pr(X|K)) significantly increased for K=2 and K=3 (Supplementary Figure S2). Western populations (Brazil, Ecuador and Guatemala) form a cluster that is clearly distinct from French Guiana individuals (K=2 in Figure 3 and Supplementary Figure S2). Interestingly, when assuming K=3, 𝒮𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ suggested that Ecuadorian samples could be assigned to either the Brazilian or the Guatemalan genetics clusters, or to both of them in varying proportions (K=3 in Figure 3). Congruently, Ecuadorian samples lied between the Brazilian and Guatemalan samples in the principal coordinate analysis (Supplementary Figure S2). This is the reason why scenarios with admixture were included in the ABC analysis.

Figure 3.

Population structure of M. ulei inferred with 𝒮𝒯ℛ𝒰𝒞𝒯𝒰ℛℰ (v2.3.3) software from the clone-corrected data set including 73 multilocus microsatellite haplotypes. The best number of clusters K was determined using the ΔK method (Evanno et al., 2005). K=2, K=3 and K=4 are the cluster numbers that are most supported considering the model described in the text. BRA, Brazil; ECU, Ecuador; GTM, Guatemala; GUF, French Guiana.

Within each of the four populations, out of 109 possible genotypic disequilibrium tests, none was significant (Q<0.05). Furthermore, a low number of identical MLGs were identified, which translates in a high relative genotypic diversity (Table 2). Most of these identical MLGs were probably a consequence of the low genetic diversity observed within populations. Based on this diversity, in the Guatemalan population for instance, only three out of the 12 identical MLGs were found to be more frequent than expected under purely sexual reproduction (P_sex<0.01), and may therefore be attributed to asexual reproduction. These results are indicative of the high frequency of recombination events within M. ulei populations. High levels of genetic differentiation between pairs of populations were detected with F_𝒮𝒯 values ranging from 0.44 to 0.79 (Table 3), suggesting an absence of regular gene flow between populations of M. ulei at the studied geographical scale. The presence of sexual reproduction within M. ulei populations and absence of gene flow between them were both pre-requisite for the use of 𝒟ℐ𝒴𝒜ℬ𝒞 (Cornuet et al., 2010), which assumes random mating and pure divergence.

Table 2. Indices of genetic diversity of the M. ulei populations.

Population ID	Number of isolates (N)	Number of genotypes (Ng)	Relative genotypic diversity (Ng/N)	Mean number of alleles (Na±s.d.)	Allelic richness (Ar±s.d., n=13)a
Brazil	29	23	0.79	2.12±0.96	1.87±0.76
Ecuador	17	16	0.94	1.62±0.62	1.62±0.61
Guatemala	24	15	0.63	1.56±0.73	1.54±0.70
French Guiana	26	19	0.73	2.06±0.85	1.89±0.75
Total	96	73	0.76	4.44±1.59	3.22±0.99

^aSamples were standardized to the size of the smallest sample (that is, the locus for which the number of individuals genotyped in a population was smallest).

Table 3. Pairwise population F_𝒮𝒯, estimated with Weir and Cockerham's θ (1984) between the four M. ulei populationsa.

	Brazil	Ecuador	Guatemala
Ecuador	0.44***
Guatemala	0.66***	0.46***
French Guiana	0.72***	0.71***	0.79***

^***Highly significant levels (P<0.001).

^aUnbiased estimate of the P-value of log-likelihood-based exact test on genotypic distribution using a Markov chain method (dememorization=10 000, batches=100, iterations=5000) in 𝒢ℰ𝒩ℰ𝒫𝒪𝒫 version 4.

Unraveling colonization scenarios of M. ulei by means of the ABC method

Within each scenario class, a single scenario clearly dominated the others in terms of posterior probability, always in accordance with classical population genetics analyses (Table 4). Of the six best scenarios (each belonging to a different scenario class), the scenario with the highest posterior probability was Class VI (P=0.869, 95% CI (0.833–0.905), Table 4 and Figure 4). This scenario consists of two independent founder events leading to the formation of the French Guiana population on the one hand and an unsampled population on the other. According to this scenario, this unsampled population would then have led to the successive and independent founding of the three other populations (Brazil, Ecuador and Guatemala).

Table 4. Comparison between scenarios belonging to a predefined class.

Scenario class	Pi	Pj	Pk	Pl	Probability of scenario (logistic regression)	Confidence interval
First-round scenarios
Class I	Brazil	Ecuador	Guatemala	French Guiana	—	—
Class II	Ecuador	Guatemala	Brazil	French Guiana	0.940	(0.865–1.000)
	Ecuador	Brazil	Guatemala	French Guiana	0.001	(0.000–0.033)
	Guatemala	Brazil	Ecuador	French Guiana	0.000	(0.000–0.000)
	Brazil	Guatemala	Ecuador	French Guiana	0.000	(0.000–0.000)
	Guatemala	Ecuador	Brazil	French Guiana	0.060	(0.000–0.122)
	Brazil	Ecuador	Guatemala	French Guiana	0.000	(0.000–0.012))
Class III	Brazil	Ecuador	Guatemala	French Guiana	1.000	(0.996–1.000)
	Brazil	Guatemala	Ecuador	French Guiana	0.000	(0.000–0.004)
	Ecuador	Brazil	Guatemala	French Guiana	0.000	(0.000–0.000)
	Ecuador	Brazil	French Guiana	Guatemala	0.000	(0.000–0.000)
Class IV	Ecuador	Brazil	Guatemala	French Guiana	0.974	(0.963–0.984)
	Brazil	Ecuador	Guatemala	French Guiana	0.005	(0.003–0.006)
	Guatemala	Brazil	Ecuador	French Guiana	0.022	(0.012–0.032)
	Ecuador	Brazil	French Guiana	Guatemala	0.000	(0.000–0.000)
Class V	Brazil	Ecuador	Guatemala	French Guiana	0.945	(0.921–0.969)
	Ecuador	Brazil	Guatemala	French Guiana	0.000	(0.000–0.000)
	Ecuador	Guatemala	Brazil	French Guiana	0.000	(0.000–0.000)
	Brazil	Guatemala	Ecuador	French Guiana	0.053	(0.029–0.077)
	Guatemala	Ecuador	Brazil	French Guiana	0.001	(0.000–0.002)
	Guatemala	Brazil	Ecuador	French Guiana	0.001	(0.000–0.001)
Class VI	Ecuador	Guatemala	Brazil	French Guiana	1.000	(1.000–1.000)
	Ecuador	French Guiana	Brazil	Guatemala	0.000	(0.000–0.000)
	French Guiana	Guatemala	Brazil	Ecuador	0.000	(0.000–0.000)
	Ecuador	Guatemala	French Guiana	Brazil	0.000	(0.000–0.000)
Second-round scenarios
Class I	Brazil	Ecuador	Guatemala	French Guiana	0.000	(0.000–0.000)
Class II	Ecuador	Guatemala	Brazil	French Guiana	0.000	(0.000–0.000)
Class III	Brazil	Ecuador	Guatemala	French Guiana	0.000	(0.000–0.000)
Class IV	Ecuador	Brazil	Guatemala	French Guiana	0.014	(0.011–0.017)
Class V	Brazil	Ecuador	Guatemala	French Guiana	0.118	(0.082–0.154)
Class VI	Ecuador	Guatemala	Brazil	French Guiana	0.869	(0.833–0.905)

P_i, P_j, P_k and P_l are the populations represented in Figure 2. Probability of scenario was computed on 1% closest simulated data sets. For each class of the first-round scenarios, the scenario with the best posterior probability is in bold. For the second-round scenarios, the best scenarios of each class are compared and the scenario with the best posterior probability is in bold.

Figure 4.

Most probable scenario based on ABC results. Each tip of the tree represents a sampled population. Divergence times between populations in number of generations are indicated in the right margin. They were estimated by the median value of the posterior distribution of the parameter. Estimates of effective population sizes are given in Table 5.

Assessment of the confidence in scenario choice

Type II error rate (that is, probability that data sets simulated under the other scenarios were assigned to the best scenario) was found to be very low with only 1.8% of wrong assignment. Type I error rate (that is, probability that data sets simulated under the best scenario were assigned to other scenarios) was reasonable and amounted to 21%. It is important to note that all these errors were due to the misclassification of data sets simulated using the Class VI scenario into the Class IV and Class V scenarios. The reason is probably the obvious proximity of the three scenario classes, which differ only in the existence of an unsampled population at the origin of the three Western populations.

Model adequacy was assessed for the six second-round scenarios by measuring the similarity between the real data set and data sets simulated with each considered scenario under the posterior distribution of parameter values. Similarity was assessed using 26 test summary statistics. For the best scenario (VI) only three observed summary statistics deviated significantly from its simulated distribution (P-value<0.05). For the other scenarios, the number of significant discrepancies ranged from 2 to 11 (Supplementary Table S3).

Parameter estimates gave reasonable values but cannot be considered fully reliable because of large relative median of the absolute errors ranging from 0.235 to 0.949 (Table 5). For instance, the estimation of current population effective sizes were similar for all populations ranging from ∼49 000 to ∼57 000. More interestingly, the estimated bottleneck sizes were found to be very low (ranging from 3.1 to 14.5, Table 5), likely reflecting the low number of individuals that has led to the foundation of the four populations.

Table 5. Estimation of parameters based on local linear regression on the 10 000 closest to the observed data set simulations using the best scenario (see Figure 4).

Parameter	Mean of the posterior distribution	Median of the posterior distribution	RMAE
N	3.82E+04	3.31E+04	0.420
NOgy	6.10E+04	6.65E+04	0.405
NOu	2.90E+04	1.98E+04	0.419
NBb	7.82E+00	5.66E+00	0.341
NBe	1.89E+01	1.45E+01	0.296
NBgt	5.47E+00	3.86E+00	0.281
NBgy	4.61E+00	3.10E+00	0.287
NBu	1.85E+01	1.44E+01	0.317
Nb	5.33E+04	5.50E+04	0.423
Ne	5.33E+04	5.45E+04	0.393
Ngt	4.93E+04	4.92E+04	0.434
Ngy	5.48E+04	5.74E+04	0.402
Nu	4.91E+04	4.89E+04	0.418
TO	2.86E+04	2.07E+04	0.339
TFgy	1.83E+02	1.55E+02	0.276
TFu	2.44E+02	2.26E+02	0.323
TSb	1.01E+02	8.39E+01	0.340
TSe	2.62E+01	2.18E+01	0.387
TSgt	5.20E+01	4.01E+01	0.405
Mμmic	2.48E−04	1.88E−04	0.282
MP	1.80E−01	1.69E−01	0.235
Mμsni	3.89E−06	2.40E−07	0.949

Abbreviation: RMAE, relative median of the absolute error.

RMAE taking the median of the posterior distribution as point estimates was computed on 300 pseudo-observed data sets simulated using the best scenario. Parameter names are the same as in Table 1.

Discussion

A scenario of colonization of Latin America by M. ulei

Using a combination of classical population genetics tools and more recent ABC model choice techniques, we found that the most likely scenario of colonization of M. ulei in Latin America involves two independent founder events. On the one hand, a population was founded in French Guiana and, on the other, independent serial introductions from another source population gave rise to the three other sampled populations in Brazil, Ecuador and Guatemala. The identification of this scenario has implications as to the dispersal processes in M. ulei.

According to this scenario, the French Guiana population did not originate in the same source population as the other three populations studied. From an agro-ecological perspective, three essential characteristics of the host population of H. brasiliensis distinguish the French Guiana context from that of Brazil, Ecuador and Guatemala. First, the implantation of H. brasiliensis in French Guiana is much more recent (about 30 years) than in the other three countries. Second, there are no industrial/commercial rubber tree plantations in French Guiana. The H. brasiliensis population in this region consists of a series of small scientific assays and of a collection of clones. Third, exchange of cuttings has been limited and strictly controlled since the beginning of planting experiments. Among the studied localities, French Guiana is nearest the SALB disease endemic area. Therefore, the chances that primary inoculums leading to the formation of the French Guiana population originate straight from the Amazonian forest, as hypothesized by Guyot (2007), are high.

We further confirm here that sexual reproduction exists and is frequent in the studied M. ulei populations by a population genetics approach. The DNA samples available for this study stem from conidial lesions collected at random. Conidial lesions do produce asexual spores called conidia but they may result from leaf infection by either sexual (ascospores) or asexual (conidia) spores. Both the low level of identical MLGs in the data set and the absence of linkage disequilibrium within populations are congruent with frequent sexual reproduction in plantations. This suggests that the lack of ascospores often noted in sexual structures can be attributed to a problem of timing of observation (that is, ascospores have not yet been produced, or have been produced but already emitted) rather than to low sexual spores production. This also supports the hypothesis that ascospores have an important role in M. ulei epidemics (Guyot, 2007). In particular, this suggests that the French Guiana population may stem from primary inoculums constituted with ascospores, as already described in related species (for example, Marin et al., 2003).

According to ABC analysis, Brazil, Ecuador and Guatemala populations stem from independent introductions from a common pool. Two colonization histories may be formulated to explain such a pattern. The first is that the three populations were founded by independent natural long-distance dispersal events originating from the same, still unsampled, region of the endemic area. This implies that spores would have dispersed and initiated epidemics in three distinct plantations distant by several thousand kilometers. The alternative hypothesis is that cutting exchanges led to the dissemination of related M. ulei strains. For instance, the common source could be a set of H. brasiliensis nurseries, which could have spread the disease by trading infected cuttings. Considering the strategic and economic importance that rubber tree cultivation has had from the late nineteenth century to the Second World War in Latin America, such cutting exchanges between countries are rather likely to have taken place (Hilton, 1955). At the continental scale, ascospores might be implicated in long-distance dispersal events (Aylor, 2003). But when such distances (several thousand kilometers) are implicated, human-mediated transport must be considered more parsimonious.

Confidence in the identified scenario

The analysis presented here mostly relies on a model-based approach. As a consequence, a cautious use of the method requires that the biology of the studied organism conform to model assumptions. Specifically, 𝒟ℐ𝒴𝒜ℬ𝒞 implements a model of population evolution with random mating within populations (that is, samples) and an absence of regular gene flow between populations. None of these assumptions was strongly violated in the present data set. First, we have shown that M. ulei reproduces both sexually and asexually. The impact of asexual reproduction on the efficiency of the method could be more extensively tested, but in the present study, scenario choice led to the same conclusion using either a complete or two different clone-corrected data sets. So it seems that scenario choice was not greatly impeded by the observed moderate occurrence of clonal copies. Second, genetic differentiation between the sampled populations was very high (pairwise F_𝒮𝒯 ranging from 0.44 to 0.79), which is consistent with the assumption that migration at the continental scale was almost nonexistent. If such conditions were not fulfilled, more appropriate simulation software should have been used (for a review of existing softwares, see Bertorelle et al., 2010).

In addition to these a priori elements of validation of the method used, we conducted a number of a posteriori tests to assess the confidence that one can have in the present scenario choice. This is an essential step of any ABC analysis, as it has recently been shown that on some specific statistical models ABC could lead to inaccurate estimates of Bayes factors due to an uncontrolled loss of information induced by the use of summary statistics (Robert et al., 2011). This problem seems less critical for population genetics analyses than for other types of data. One reason is that ABC leads to a correct ranking of Bayes factors if the chosen combination of summary statistics differs between the scenarios under comparison (Marin et al., 2011). Summary statistics used in population genetics are not chosen at random but generally because they are suspected to allow distinguishing scenarios, so that in practice erroneous model choice is not frequent in such analyses (Robert et al., 2011). Choosing the correct summary statistics may however reveal difficult and other technical issues exist in ABC, so that in all cases, reliability of the results must be properly checked. In the present study, the posterior probability of the best scenario (scenario VI) was extremely high (0.869, CI (0.833–0.905)). Its ability to generate data sets similar to the real one (adequacy) was good and better than scenarios I–IV. Accordingly, Type II error rate was found very low (1.8%). In other words, among all pseudo-observed data sets generated under one of the five other best scenarios tested, only 1.8% were erroneously attributed to scenario VI. This implies that the colonization histories formalized under scenarios I–V can be rejected. In particular, an admixture event between Brazilian and Guatemalan populations leading to the foundation of the Ecuadorian population, that could seem plausible at first sight based on descriptive population genetics analyses, is rejected.

Modeling unsampled populations

When trying to infer the colonization history of an invasive species, accounting for unsampled populations may be very important, especially to avoid the misidentification of source populations (Guillemaud et al., 2010). In the present study, without the possibility of modeling an unsampled population, we would have selected scenario V with considerable support. Scenario V assumes that the Brazilian population gives birth to the Ecuadorian one, which is subsequently introduced into Guatemala. Model checking would also have been better for this scenario than for scenarios I–IV. And so the conclusions would have been sensibly different. This illustrates that building the set of scenarios under comparison is a crucial step of ABC analyses. The lack of samples for populations important for the reconstruction of colonization history may be particularly frequent in such emerging pathogens. Pathogens such as M. ulei have generally not been studied before their emergence; their native area (including location, natural host and so on) is often unknown. In the present case, it is also very difficult to access to the natural compartment, as it implies sampling, at the top of the canopy within the Amazonian forest, rubber trees that occur at low density. In addition, agricultural plots are sometimes installed at the detriment of native environments, possibly leading to an extinction of source populations. The history of plantations themselves has been punctuated with field plantings and abandonments and finally nurseries that existed a few decades ago may have closed since then. The effect of unsampled populations is no longer a neglected issue in population genetics. For instance, it has been assessed on a model migration-drift equilibrium (that is, ℳℐ𝒢ℛ𝒜𝒯ℰ software; Beerli, 2004). Inference of bottleneck and migration intensities appeared to be robust to migration from the unsampled population so long as migration rate remained low (Beerli, 2004). However, during colonization new populations may be founded with all individuals coming from a single unsampled population. The effect of unsampled populations should thus be properly tested de novo depending on the peculiarity of the studied biological model and the scenario tested (Guillemaud et al., 2010).

Insights from parameter estimates

Evaluation of biological parameters of interest can be considered as the final step of the ABC approach (Bertorelle et al., 2010). In our study, parameter estimates are too inaccurately estimated for subtle interpretations to be drawn. In principle, this should not affect much scenario choice as recently been advocated, although not properly evaluated (Bertorelle et al., 2010). We argue that this is likely to be true here as the ability of the three best scenarios (IV–VI) to mimic the observed data (adequacy) was good and that scenarios IV and V were nevertheless clearly rejected in front of scenario VI (low Type II error rate). Furthermore all parameter estimates seemed reasonable and some of them shed light on the population biology of M. ulei. For instance, times of divergence are compatible with the ordering of the dates of first reports in plantations (early twentieth century in Brazil, 1950s in Guatemala and 1970s in Ecuador). It is also remarkable that the present data convey the signature of very strong bottlenecks. As shown in Supplementary data, (Supplementary Table S2, Supplementary Figure S3 and Supplementary Figure S4), scenarios without bottlenecks appeared unable to produce summary statistics resembling the observed ones, even with very large priors, which, in principle, would have permitted differences to accumulate over long periods in low-size populations. The distribution of summary statistics simulated in absence of bottlenecks reveals a lack of differentiation and an excess of allelic richness as compared with observed data, both of which can be explained by recent and intense drift events. This strongly suggests that sampled populations experienced such a drift episode, but it is not possible to distinguish from the present study whether populations have passed through a mild bottleneck for a larger number of generations or through a severe bottleneck during a smaller number of generations. Focusing on the order of magnitude of parameters, one can also observe that both effective population sizes of native and current invasive populations were estimated large (above 10 000). This is interesting in two respects. First, so large effective population sizes, if confirmed, suggest that drift has a low impact on current invasive populations, which constitutes a challenge for H. brasiliensis breeders. Second, in its native area, the pathogen infects trees occurring at low densities in the Amazonian forest. Large effective population sizes therefore imply either large populations on each tree or gene flow between trees. Validating these estimates, either using larger sampling and more precise historical information (Estoup and Guillemaud, 2010) or through dedicated studies, would certainly allow gaining a better understanding on the population biology in the pathogen native conditions.

Conclusion

Using population genetic analyses of M. ulei populations from Latin American H. brasiliensis plantations, the present study progresses our understanding of the biology of this pathogen. The use of ABC allowed us to partially retrace the history of colonization of M. ulei at the continental scale, and to suggest a role of human activities in disseminating this disease across Latin America. Up to now, the disease has not emerged in Asia, where susceptible H. brasiliensis varieties are used. The rubber tree cuttings initially used to propagate H. brasiliensis in Asia had been raised in England, where the pathogen cannot survive, and were therefore disease free. It has since then never been introduced owing to a very strict quarantine strategy. These results support the importance of quarantine politics in order to confine SALB disease to the Latin American area. We finally have shown that the pathogen is likely capable of recombination through sexual reproduction. This may suggest that the SALB fungus has a strong evolutionary potential (McDonald and Linde, 2002) and justifies the effort toward the development of a durable strategy for rubber tree resistance to M. ulei.

Data archiving

DNA sequences: Genbank accessions GQ420355, GQ420356, GQ420357, GQ420358,GQ420359, GQ420360, GQ420361, GQ420362, GQ420363, GQ420364, GQ420365, GQ420366, GQ420367 and GQ420368.

Microsatellite data have been deposited at Dryad:doi:10.5061/dryad.5s260

The authors declare no conflict of interest.