Identifying therapeutic targets in a combined EGFR–TGFβR signalling cascade using a multiscale agent-based cancer model

Abstract

Applying a previously developed non-small cell lung cancer model, we assess ‘cross-scale’ the therapeutic efficacy of targeting a variety of molecular components of the epidermal growth factor receptor (EGFR) signalling pathway. Simulation of therapeutic inhibition and amplification allows for the ranking of the implemented downstream EGFR signalling molecules according to their therapeutic values or indices. Analysis identifies mitogen-activated protein kinase and extracellular signal-regulated kinase as top therapeutic targets for both inhibition and amplification-based treatment regimen but indicates that combined parameter perturbations do not necessarily improve the therapeutic effect of the separate parameter treatments as much as might be expected. Potential future strategies using this in silico model to tailor molecular treatment regimen are discussed.

1. Introduction

Epidermal growth factor receptor (EGFR) is a transmembrane signalling receptor that is frequently over-expressed in many cancers, including non-small cell lung cancer (NSCLC) (Hirsch et al., 2003). Ligand binding to EGFR leads to receptor tyrosine kinase activation as well as a series of downstream signalling events that stimulate cell proliferation, motility, adhesion and invasion, and the overexpression of EGFR causes cell apoptosis inhibition and resistance to chemotherapy (Mendelsohn & Baselga, 2000). Tyrosine kinase inhibitors (TKIs) of EGFR, such as erlotinib and gefitinib, have thus emerged as therapeutic option for patients with advanced NSCLC (Siegel-Lakhai et al., 2005). Although treatment with these drugs so far has resulted in significant tumour regressions in only 10–20% of NSCLC patients (Janne et al., 2005), the development of novel therapeutic targets continues to be a very active topic in current cancer research.

In recent years, interdisciplinary cancer systems biology has drawn much attention in exploring the quantitative relationship between complicated intra- and intercellular signalling processes and the behaviour they trigger on the microscopic and macroscopic scales (Anderson & Quaranta, 2008; Sanga et al., 2007; Wang & Deisboeck, 2008). Many data-driven mathematical and computational models and analysis methods have been developed, but so far the focus is still mostly on the single-cell level (Aldridge et al., 2006). As demonstrated elsewhere in systems biology (Swameye et al., 2003), sensitivity analysis has been widely accepted as a useful tool for studying pathway parameters and signalling events, which have significant effects on system behaviour. Such in silico methods are especially useful when it is not possible or practical to conduct experiments on the living system itself (van Riel, 2006). However, different sensitivity analysis methods may produce different parameter rankings for a specific system outcome (Zhang & Rundell, 2006). Moreover, it is quite common that a parameter that is significant to one specific system outcome may not be significant to others. For example, in a mitogen-activated protein kinase (MAPK) signalling pathway study, MAPK kinase (MEK) dephosphorylation was found to have significant impact on the duration and integrated output, but not the amplitude, of extracellular signal-regulated kinase (ERK) activation (Hornberg et al., 2005). Hence, in some cases, an evaluation function that creates a ‘composite ranking’ indicating the importance of parameters in multiple system outcomes at one time would be more appropriate. In the case of molecular oncology therapy, we believe that the optimal target should lead to tumour control; i.e. it should reduce the ability of cancer cells to grow (and/or cause them to die) as well as diminish cancer cell motility (i.e. reduce invasion and contain metastasis) as much as possible.

We have previously developed a set of multiscale agent-based lung cancer models integrating both molecular and microscopic levels to examine NSCLC growth dynamics in 2D and 3D microenvironments (Wang et al., 2007, 2009). Using the 2D model as the computational platform, we also presented a novel ‘cross-scale’ sensitivity analysis method to identify model parameters that have significant effect on the tumour’s expansion rate (Wang et al., 2008). Here, we introduce a new evaluation measure, termed the ‘therapeutic index (TI)’ function. The main purpose of this formula is to help identify key parameters that are critical in affecting the two main tumour phenotypic traits or ‘outcomes’: on-site tumour growth and spatiotemporal expansion. We employed the 3D model as the simulation platform to evaluate the TI function and then compared current results with those from the previously developed sensitivity analysis. Analysis and comparison results showed that the TI function allows for the ranking of the critical parameters according to their therapeutic values by assessing the influence of changes in parameters on multiple tumour outcomes and thus demonstrate that this function is a more powerful tool for target evaluation.

2. Methods

2.1. Multiscale cancer model

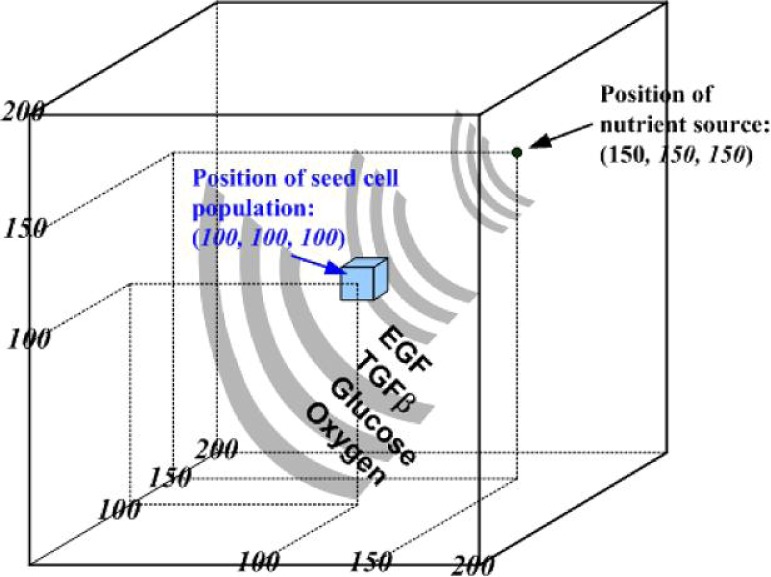
We briefly reintroduce the main features of the multiscale 3D agent-based NSCLC model (Wang et al., 2009), which encompasses both molecular (signalling pathway) and microscopic (multicellular) scales. At the molecular level, two stimuli, epidermal growth factor (EGF) and transforming growth factor β (TGFβ), trigger downstream signalling through different routes but converge at the activation of the Raf signal. This process then initiates the ERK signalling cascade. Figure 1 shows, in brief, the implemented signalling scheme (see Wang et al., 2009 for detailed pathway kinetics). At the microscopic level, we construct a 3D microenvironment consisting of a discrete cube with 200 × 200 × 200 grid points (Fig. 2); a single distant nutrient source representing a blood vessel is located at grid point (150, 150, 150). A heterogeneous biochemical environment is attained by normally distributing external diffusive chemical cues (EGF, TGFβ, glucose and oxygen tension) throughout the 3D microenvironment. The assigned initial values of these chemical cues are weighted by the distance of a grid point from the nutrient source. Hence, the nutrient source is the most attractive location for the chemotactically acting tumour cells because it maintains the highest weight for each of the aforementioned four cues. Moreover, throughout the simulation, the concentrations of these four chemical cues are continuously updated at a fixed rate (see Wang et al., 2009 for corresponding equations).

Fig. 1.

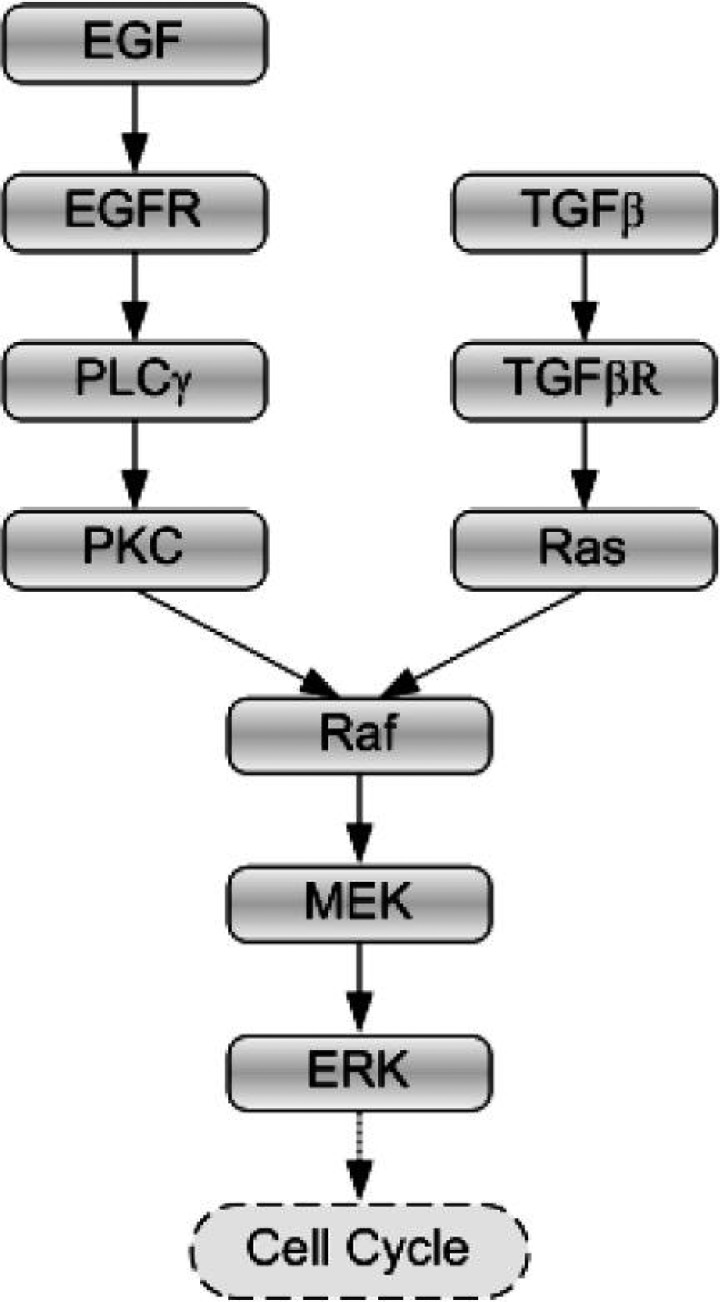
Signalling schematic of the integrated pathway, with EGF and TGFβ as the two external stimuli.

Fig. 2.

Setup of the 3D virtual biochemical microenvironment.

Each cell (agent) carries a self-maintained signalling network, and the computer model records the molecular profile for each cell at every time step. In an earlier work, we proposed an experimentally supported molecularly driven cellular phenotypic decision algorithm (Wang et al., 2007). In brief, phospholipase Cγ (PLCγ) and ERK (two downstream signalling molecules of EGFR) are used to determine the emergence of two important phenotypic traits: migration and proliferation, respectively. Experimental studies have shown that transient acceleration of accumulating PLCγ levels leads to cell migration (Dittmar et al., 2002), while that of ERK leads to cell replication (Santos et al., 2007). Therefore, in our model, the rate of change of PLCγ determines the cellular migration decision, and the rate of change of ERK dictates a cellular proliferation fate. If a cell decides to migrate or proliferate, it will search for a neighbourhood location to move to or for its offspring to occupy. If there are two or more locations available, the cell will select the one with the highest glucose concentration (this location is referred to as the appropriate location); if there are two or more appropriate locations available, the cell will simply randomly pick one. Generally, tumour cells expand towards the nutrient source since these sites are more permissive with regard to the chemical cues. A simulation run is terminated when the first cell reaches the nutrient source since at this point a tumour is able to metastasize (as the nutrient source represents a blood vessel) and consequently is more difficult to contain and treat. Tumour growth and invasion patterns due to cell proliferation and migration are neither predefined nor intuitive: they emerge as a result of intracellular signalling of individual cells and the dynamic cellular interactions within the framework of the 3D biochemical microenvironment.

2.2. Sensitivity analysis and TI function

In a previous cross-scale sensitivity analysis study (Wang et al., 2008), we used a sensitivity coefficient as an index to evaluate how a change in a single sub-cellular model component affects the overall system response at the microscopic level. This coefficient is calculated by the following equation:

$$S_p^M=\frac{\left(M_i-M_0\right)/M_0}{\left(p_i-p_0\right)/p_0},$$ (1)

where p represents the parameter that is varied in a simulation and M the response of the system; M₀ is obtained by setting all parameters to their reference values, and thus (M_i – M₀) is the change in M due to the change in p, i.e. (p_i – p₀). It is worth noting that this type of sensitivity analysis belongs to the ‘local’ sensitivity analysis category (Rabitz et al., 1983), i.e. quantifying the influence of individual parameters by varying only one parameter at the same time. Equation 1 will be used here again for our sensitivity analysis in this study. The system response M now corresponds to either tumour volume (indicated by the final number of viable cancer cells at the time of termination of the simulation run) or tumour expansion rate (represented by the total simulation steps; however, a simulation that terminates after a greater number of time steps has a slower tumour expansion rate).

There are, however, some drawbacks in applying this local sensitivity analysis to target discovery since (1) can show a parameter’s sensitivity to only ‘one’ tumour outcome at a time, i.e. either tumour volume or tumour expansion rate. The equation therefore has to be revised especially with respect to the system output term, M, to concurrently evaluate ‘two or more’ tumour outcomes. Moreover, the sensitivity coefficient is a relative value showing the correlative relationship between changes in parameters and tumour outcome, which means that this value cannot be independently used to evaluate tumour outcomes (in our case, to determine the final number of alive cells and simulation steps). We thus seek to solve this problem and present here a TI function that incorporates tumour outcome terms directly:

$$\text{TI}\left(x_i,y_i\right)=k_x\left(x_i/x_0\right)-k_y\left(y_i/y_0\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n,$$ (2)

where x and y represent the two tumour outcomes, i.e. simulation steps and the final number of alive cells, respectively; x_i and y_i indicate their corresponding values for the ith simulation run; x₀ and y₀ are their corresponding values for the ‘standard’ simulation (when all model parameters are set to their reference values); k_x and k_y are weights for x and y and are both greater than or equal to 0. Hence, the value of TI increases with x_i and decreases with y_i ; k_x and k_y simply indicate which tumour outcome (simulation steps or cell number) is more important for the evaluation. In the absence of specific data, we set k_x = k_y = 1, meaning that the two types of tumour outcome are equally important. Future works can specify these coefficients with regard to tumour type, grade and stage or potentially account for the particular strengths and weaknesses of the drug under consideration.

The goal of our simulations, aimed at uncovering high-value therapeutic targets, is clear: by changing parameters separately, we attempt to reduce the cell number (corresponding to tumour growth inhibition) while increasing the number of simulation steps (corresponding to tumour expansion inhibition). Parameters that produce high TIs merit particular attention since, generally, they will produce favourable anti-tumour outcomes and hence will be valuable therapeutic targets. However, when changing a parameter leads to a simulation result with (x_i > x₀ and y_i > y₀) or (x_i < x₀ and y_i < y₀) and thus a large value of TI, the particular parameter does not produce a desirable therapeutic outcome because the tumour still grows in cell number in the former case or spreads faster in the latter. Hence, we further distinguish between the following two groups:

• Group I: (x_i, y_i) ∈ {x_i ⩽ x₀, y_i ⩽ y₀, (x_i, y_i) ≠ (x₀, y₀)} and

• Group II: (x_i, y_i) ∉ {x_i ⩾ x₀, y_i ⩽ y₀, (x_i, y_i) ≠ (x₀, y₀)}.

Figure 3 schematically shows the distribution of the two groups. Tumour outcome values in Group I fulfill the requirements that we set for a therapeutic target. Using these definitions, parameters (along with their variations) will first be classified into these groups before a parameter ranking is produced through (2) for each group. The evaluation process also implies that a parameter that produces an (x, y) pair in Group II with a large TI value cannot be accepted as a promising therapeutic target because changing the component either decreases simulation steps, increases cell number or both.

Fig. 3.

Distribution of Group I and Group II. Only parameter variations resulting in a larger simulation step and a smaller cell number, when compared to standard simulation results, belong to Group I.

3. Results

The 3D agent-based model was implemented in C/C++. A total of 27 seed cells arranged in a 3 × 3 × 3 cube were initially positioned in the center of the 3D environment. Due to computation intensity, the maximum number of simulation steps for all runs is set to 250, with each time step corresponding to 2.4 h. It takes 10–12 steps for a cell to complete a proliferation process, which is in agreement with experimental data (Hegedus et al., 2000). The diameter of each cell is 10 μm, and in our model, the cell shape has been approximated as a cube so that the volume of each cell is 1000 μm³. For the standard simulation case (the final cell number = 16773; the number of elapsed time steps = 222), the resultant volume (made up of live tumour cells, dead tumour cells and interstitial fractions within the tumour mass) is approximately 3.75 × 10⁻² mm³. The variation ranges for individual parameters were set to (1) [0.1–0.9]-fold for parameter inhibition and (2) [1.1–2, 3–10]-fold for parameter amplification of their corresponding reference values. Note that we only considered variations of pathway component concentrations in this study. Each of the variations in the parameters was used as the only change of input when running a simulation, and all other parameters were held fixed at their reference values. This process was repeated for all parameter values, and the resulting tumour growth indices (i.e. simulation steps and the final number of live cells) were compiled for further analysis.

3.1. Parameter sensitivity rankings

Using (1), we calculated sensitivity coefficients for all of the pathway components over the entire predefined variation range for each of the two tumour growth indices. Table 1 shows the parameter sensitivity rankings. As described before, a sensitivity coefficient value only reports how sensitive the system outcome is to a particular parameter and is a relative measure. From Table 1, one cannot determine what variation of which parameter produces a particular tumour outcome because a coefficient value is calculated specific to only one tumour outcome, ignoring others. For example, although EGFR is the most sensitive parameter in both simulation steps and cell number, a 0.9-fold variation in EGFR concentration results in an increase in both tumour outcomes, which does not qualify it to be a therapeutic target. Note that the same 0.9-fold variation in EGFR results in distinct sensitivity coefficient values for different tumour outcomes.

Table 1.

Sensitivity rankings with respect to simulation step and cell number; SC standards for sensitivity coefficient (calculated according to (1)); * indicates that multiple values exist. For a specific parameter, only the variation resulting in the maximum absolute value of SCs with respect to simulation step and cell number, respectively, is listed

Rankings	Parameter	Variation	SC	Cell number		Simulation step
Tumour output: simulation step
1	EGFR	0.9	− 0.8108	20102	↑	240	↑
2	ERK	0.9	0.6306	15079	↓	208	↓
3	PLCγ	0.7	− 0.4054	17449	↑	240	↑
4	MEK	1.2	− 0.3153	11417	↓	208	↓
4	TGFβR	0.8	0.3153	15224	↓	208	↓
6	Raf	0.5	0.1261	14787	↓	208	↓
7	PKC	3	0.018	19058	↑	230	↑
8	Ras	0.1–10.0	0	*	*	222	—
Tumour output: cell number
1	EGFR	0.9	− 1.9847	20102	↑	240	↑
2	ERK	1.1	− 1.8428	13682	↓	222	—
3	PLCγ	1.4	− 1.662	5,622	↓	188	↓
4	TGFβR	1.1	0.6296	17829	↑	222	↑
5	MEK	0.7	0.5678	13916	↓	220	↓
6	Raf	0.9	− 0.4561	17538	↑	222	—
7	PKC	3	0.0681	19058	↑	230	↑
8	Ras	0.2	− 0.0581	17552	↑	222	—

3.2. Parameter TI rankings

The parameter rankings based on the value of TI for parameter inhibition and amplification are presented in Tables 2 and 3, respectively. Under parameter inhibition, MEK with a 0.5-fold variation results in the maximum value in TI, and thus MEK emerges as the number one therapeutic target for this treatment strategy. However, further decreasing the MEK concentration fails to add therapeutic value.

Table 2.

Rankings with respect to TI for parameter inhibition ([0.1–0.9]-fold of each parameter’s reference value)

Rankings	Parameter	Variation	TI	Cell number		Simulation step
Group I
1	MEK	0.5	0.1308	15184	↓	230	↑
2	PLCγ	0.8	0.1004	16449	↓	240	↑
3	Ras	0.4	0.0138	16542	↓	222	—
4	PKC	0.7	0.0007	16762	↓	222	—
Group II
1	ERK	0.1	0.7517	1444	↓	186	↓
2	MEK	0.4	0.252	11413	↓	207	↓
3	EGFR	0.1–0.5	0.1142	16897	↑	249	↑
3	PLCγ	0.1–0.4	0.1142	16897	↑	249	↑
5	TGFβR	0.1	0.0874	14249	↓	208	↓
6	Raf	0.1	0.0805	14365	↓	208	↓
7	PKC	0.9	0	16773	—	222	—
8	Ras	0.8	− 0.0002	16777	↑	222	—

Table 3.

Rankings with respect to TI for parameter amplification ([1.1–2, 3–10]-fold of each parameter’s reference value)

Rankings	Parameter	Variation	TI	Cell number		Simulation step
Group I
1	ERK	1.1	0.1843	13682	↓	222	—
2	TGFβR	3	0.1756	13828	↓	222	—
3	Ras	4	0.0161	16503	↓	222	—
4	PKC	2	0.0024	16732	↓	222	—
Group II
1	PLCγ	6	0.7395	214	↓	167	↓
2	EGFR	10	0.7111	766	↓	168	↓
3	MEK	10	0.4678	5829	↓	181	↓
4	ERK	1.2	0.2518	11417	↓	207	↓
5	TGFβR	10	0.184	13535	↓	220	↓
6	Raf	3	0.0253	16198	↓	220	↓
7	PKC	1.2–1.3	− 0.0001	16775	↑	222	—

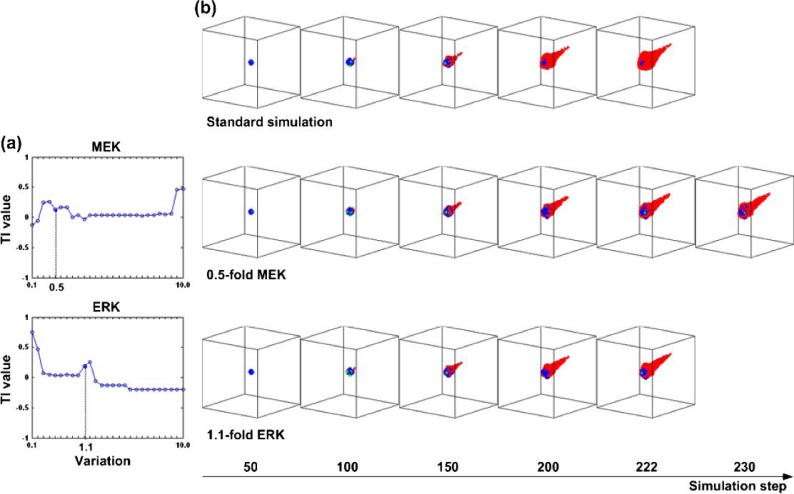
For example, while a variation of 0.4-fold in MEK (Group II section in Table 2) results in an even smaller cell number, it is also accompanied by the ‘adverse effect’ of faster tumour expansion (a smaller number of simulation steps in the standard simulation). Under parameter amplification, ERK with a 1.1-fold variation results in the maximum TI, which implies that increasing the concentration of ERK contributes to an increase in the number of simulation steps and a reduction in the cancer cell number. However, similar to the result for MEK inhibition, further increasing the ERK concentration (e.g. to 1.2-fold) causes faster tumour expansion, thus putting ERK with a 1.2-fold variation into Group II. Figure 4 displays the overall change in TI values for MEK and ERK and depicts a series of selected simulation snapshots for the standard simulation, with MEK set to a variation of 0.4-fold and ERK to a variation of 1.1-fold. As can be seen, the MEK treatment simulation takes longer to finish, and both MEK and ERK treatment cases exhibit a smaller tumour volume than that produced by the standard simulation.

Fig. 4.

(a) Plot of TI values for all variations in MEK and ERK. (b) Selected simulation snapshots for the standard simulation (upper panel), MEK with a variation of 0.5-fold (middle panel) and ERK with a variation of 1.1-fold (lower panel). In the snapshots, migrating cells are indicated in ‘red’, proliferating cells in ‘blue’ and quiescent cells in ‘green’. A colour version of this figure is available at www.imammb.oxfordjournals.org.

3.3. Combined parameter perturbations

We next sought to gain an understanding of the influence of combined parameter perturbations on tumour outcome, using our cross-scale computer simulation and applying the TI method. The parameters and their variations that we use for this analysis are those in Group I of Tables 2 and 3 for a total of eight parameter variation elements. There are 26 combinations of these elements (note: variation pairs of Ras (0.4-fold) and Ras (4.0-fold), and PKC (0.7-fold) and PKC (2.0-fold) are impossible, and thus are eliminated). Table 4 shows the analysis results. It is somewhat surprising that only 15 out of the 26 variation pairs (about 58%) show a therapeutic gain. Of these 15 pairs, the variation pair of TGFβR (3.0-fold) and PKC (2.0-fold) results in the biggest TI value. More surprisingly, only in two of the variation pairs, PLCγ (0.8-fold) and Ras (0.4-fold), and PLCγ (0.8-fold) and Ras (4.0-fold), does the simulation obtain a greater TI value than when the parameters of the variation pair were varied individually.

Table 4.

Systematic analysis of combined parameter perturbations

Parameter 1	Variation 1	Parameter 2	Variation 2	TI	Cell number	Simulation step
Group I
PLCγ	0.8	PKC	0.7	0.0932	16569	240
PLCγ	0.8	PKC	2	0.0998	16459	240
PLCγ	0.8	ERK	1.1	0.1216	16093	240
PLCγ	0.8	TGFβR	3	0.1243	16048	240
PLCγ	0.8	Ras	0.4	0.1281	15984	240
PLCγ	0.8	Ras	4	0.1209	16105	240
PKC	0.7	ERK	1.1	0.1432	14371	222
PKC	0.7	TGFβR	3	0.1609	14075	222
MEK	0.5	PLCγ	0.8	0.1098	16064	237
ERK	1.1	PKC	2	0.1442	14354	222
ERK	1.1	Ras	4	0.1443	14352	222
TGFβR	3	PKC	2	0.1696	13929	222
TGFβR	3	Ras	4	0.1527	14211	222
Ras	0.4	ERK	1.1	0.1259	14662	222
Ras	0.4	TGFβR	3	0.1601	14088	222
Group II
PKC	0.7	Ras	4	− 0.0178	17071	222
MEK	0.5	PKC	0.7	0.1882	13466	220
MEK	0.5	PKC	2	0.1899	13436	220
MEK	0.5	ERK	1.1	− 0.0488	19631	249
MEK	0.5	TGFβR	3	0.1895	13142	216
MEK	0.5	Ras	0.4	0.1899	13436	220
MEK	0.5	Ras	4	0.1847	13524	220
ERK	1.1	TGFβR	3	0.2439	11549	207
Ras	0.4	PKC	0.7	− 0.0136	17001	222
Ras	0.4	PKC	2	− 0.0073	16896	222
Ras	4	PKC	2	− 0.0153	17030	222

4. Discussion

Despite advances in molecular therapies, only modest improvements have been made in the treatment of patients with advanced NSCLC (Horn & Sandler, 2009). We have presented here a new method for evaluating therapeutic NSCLC targets by applying a previously developed multiscale model. Because this computational model links molecular and microscopic scales, we are able to assess the influence of parameters at the molecular level on the tumour’s spatiotemporal behaviour at the microscopic and multicellular level. The most important feature of the method is that it takes both tumour growth measures (simulation steps and cell number) into account, while general local sensitivity analysis only focuses on one system output (Rabitz et al., 1983). Hence, the model presented in this paper is more appropriate for evaluating therapeutic targets when two or more tumour outcomes are involved (as is realistic) than is the general sensitivity analysis method, which only yields the relative information between the system input and output. The comparison results confirm the effectiveness of the new method in yielding parameter rankings based on both main tumour features (growth and motility), which is a significant improvement over local sensitivity analysis.

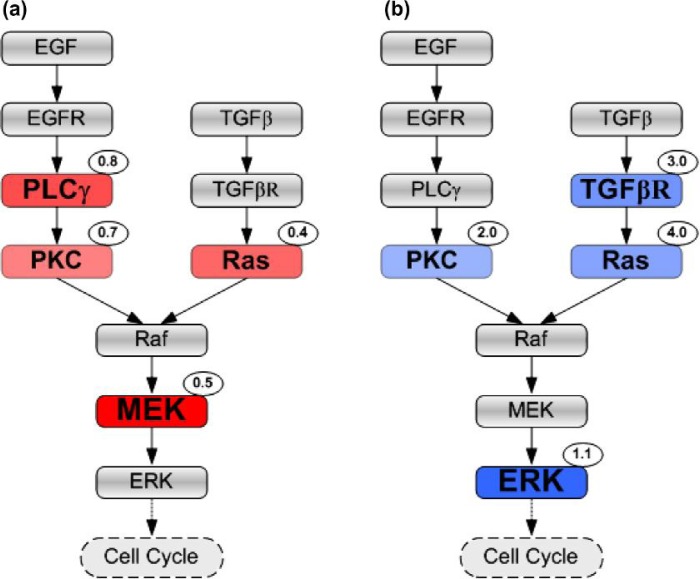
Since PLCγ and ERK have been experimentally proven to play significant roles in cancer cell growth and invasion (Dittmar et al., 2002; Santos et al., 2007), they have been implemented as ‘decision’ molecules in determining a cell’s migration and proliferation fates in this 3D model (Wang et al., 2009). It is thus reasonable to expect them to be more prominent than other parameters in the therapeutic value rankings. Indeed, based on our analysis, PLCγ is a therapeutic target under parameter inhibition strategy (Table 2), while ERK qualifies as a valuable target in an amplification regimen (Table 3). What is unexpected, however, is that MEK exceeds PLCγ as the most important parameter in the inhibition regimen. We note that it has already been demonstrated experimentally that MEK plays a significant role in the MAPK cascade (Wakeling, 2005). Overall, our result is also in good agreement with another control analysis study on a more complex kinetic model of EGF-induced MAPK signalling where both MEK and ERK have been identified to be critical for cellular signal transduction (Hornberg et al., 2005). It is then straightforward to modify the representation of the signalling pathway (Fig. 1) using parameter rankings provided in Tables 2 and 3 in an effort to graphically represent therapeutic target information. A tentative way to achieve this is shown in Fig. 5 from which one can easily identify which components can serve as therapeutic targets as well as their positions relative to other molecules in the downstream EGFR signalling cascade. For example, it is easy to observe that PKC and Ras can serve as therapeutic targets for both parameter inhibition and amplification treatments.

Fig. 5.

Signalling pathway with encoded therapeutic value information. Therapeutic targets are presented with a different colour (red for pathway inhibition (a) and blue for parameter amplification (b)) and font size according to their TI rankings; a target with a higher ranking has a deeper colour and larger font size. The number at the top-right corner of each target indicates the variation that leads to a favourable tumour outcome. A colour version of this figure is available at www.imammb.oxfordjournals.org.

It can also be deduced from our analysis that targeting a parameter should be conducted in a cautious manner. As shown in Fig. 2a, MEK and ERK can only be considered as therapeutic targets when they are at a variation of 0.5-fold and 1.1-fold, respectively. Other variations in these two parameters do not satisfy the requirements for a therapeutic target; i.e. although some variations result in bigger TIs, the adverse effects preclude them from being effective targets. This finding thus suggests that the amount of molecular-targeted drugs on site represents a significantly important factor where minor fluctuations can quickly change a therapeutic gain into a loss and vice versa.

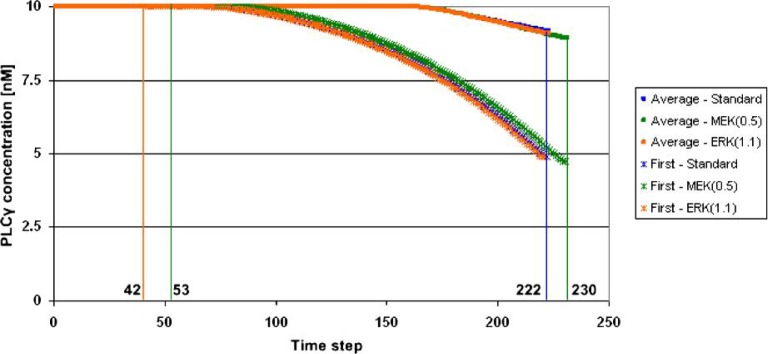
Because it can track molecular signalling dynamics on a single-cell level, the multiscale computational platform employed in this study can potentially help us understand why MEK with a variation of 0.5-fold and ERK with a variation of 1.1-fold are on the top of the therapeutic target list. We only present some preliminary results here. Figure 6 shows changes in concentration of PLCγ over time at both population and single-cell levels for three simulations: the standard simulation, MEK (0.5-fold) and ERK (1.1-fold), respectively. We chose to investigate PLCγ because it is the molecular determinant for cell migration in our setup. The cancer cell reaching the nutrient source first is of particular interest because it represents how fast the tumour system expands. From Fig. 6, one sees that this particular cell experiences a greater change in PLCγ concentration than does the entire cell population in all three simulations, which may explain why this cell reaches the nutrient source first. Moreover, there is a clear difference between the graphs for MEK (0.5-fold) and the standard simulation, but only a small difference between the graphs for ERK (1.1-fold) and the standard simulation. This result confirms our simulation results on tumour expansion rate (the number of simulation steps): 222 steps for both the standard simulation and ERK (1.1-fold) and 230 steps for MEK (0.5-fold). Furthermore, the emergence of the first new cell in the simulation via proliferation happens later in MEK (0.5-fold) than in the other two simulation cases, which shows the effect MEK inhibition has, at this variation, on suppressing tumour expansion.

Fig. 6.

Preliminary results of changes in concentration of PLCγ over time for three representative simulations: the standard simulation (blue), MEK with a variation of 0.5-fold (green) and ERK with a variation of 1.1-fold (brown). Both the average concentration values of all live cancer cells and the signalling dynamics for the first mobile cancer cell reaching the nutrient source are depicted. The emergence of the first new cell via proliferation in the standard simulation and ERK (1.1-fold) occurs during Step no. 42 and that of MEK (0.5-fold) in Step no. 53. A colour version of this figure is available at www.imammb.oxfordjournals.org.

The success of molecular-targeted therapeutics is often hindered by the capacity of tumour cells to acquire resistance (Bublil & Yarden, 2007), the onset of which may be delayed by the ‘combination’ of more than one inhibitor. Clinical investigators have begun to evaluate the benefit and efficacy of various drug combinations, e.g. monoclonal antibodies and tyrosine kinase inhibitors (Guarino et al., 2009), anti-receptor therapy with EGFR downstream signalling inhibitors (Milton et al., 2007) and angiogenesis inhibitors (Morabito et al., 2009). Hence, we conducted a set of pilot systemic analyses investigating the effects of combined parameter perturbations on tumour growth and expansion (Table 4). We hypothesized that such a theoretical ‘combination therapy’ would produce a greater decrease in cell number and increase in simulation steps in the tumour system (reflected in a greater TI value) than would individual therapies with the parameters involved in the particular combination therapy. However, only 2 out of 26 variation pairs showed such an improved effect (a 21.6% increase in TI for PLCγ [0.8-fold] and Ras [0.4-fold] variation pair and 17.0% increase for PLCγ [0.8-fold] and Ras [0.4-fold], compared to the individual parameter perturbation: PLCγ [0.8-fold] with TI = 0.1004 [see Table 2]). Hence, in this model, most of the combined parameter perturbations did not show improvement when compared to individual parameter inhibition or amplification treatments. One explanation for this is that the underlying signalling system, represented by a system of differential equations in the model, is a non-linear system, i.e. a change in the cellular responses (output) is not directly proportional to molecular changes (input). Regardless, current clinical trials of multitargeted therapy in NSCLC treatment have indeed only benefited a small percentage of patients who have been treated with chemotherapy and monoclonal antibody therapy (Felip et al., 2007), which, to some degree, confirms our finding where most of the combination therapy examinations failed to show additional therapeutic gain.

In summary, we have presented a new method for evaluating the effect of parameter variations on two or more cancer traits or system outputs at the same time. This TI ranked the pathway components according to their target value in order to achieve tumour control. In the future, other relevant output factors, e.g. cell density and tumour diameter, will be incorporated into the TI equation form as well. We note that TIs can also be used to examine which pathway mutations (to pathway components or their association and dissociation kinetic rates) can be the leading causes of the cancer type implemented in silico. Moreover, to facilitate ‘computational target discovery’, we plan to (1) integrate more interconnected signalling pathways that play key roles in cancer initiation and progression and (2) revise the current model to understand tumour responses to different drug dosing regimen, e.g. continuous and periodic drug infusion. We argue that the TI method paired with the cross-scale capacities of such advanced agent-based modelling lend themselves to a more integrated approach of studying the therapeutic susceptibility of signalling pathways in cancer.