Abstract
The disruption of tissue epithelial architecture is thought to be involved in the initiation of cancer; however, little is known about the cell biology of early neoplastic lesions. Computational models can facilitate in the study of early cancer stagesby simulating different scenarios of tumour inception and by testing in silico the influence of various intrinsic and extrinsic factors on the emerging multicellular morphologies. Here, we have used a computational model to create 3D morphocharts, collections of multicellular morphologies arising from systematic modification of three model parameters defining cell sensitivity to external cues for cell growth, death and adhesion to the extracellular matrix. This systematic search revealed the ranges of parameter values for which robust epithelial structures formed and those that led to abnormal geometrical forms resembling tumour-like morphologies. We also showed how our model can be used to map morphologies of experimental multicellular systems onto their in silico counterpart via the cell sensitivity parameter space that may in turn allow us to identify genetic or epigenetic changes responsible for these morphological distortions.
Keywords: development of epithelial tumours, formation of mutant acini, single-cell-based models, immersed boundary method, self-organization, robustness, morphology classification
1. Introduction
Most tumours arise from epithelial tissues that form sheets of tightly packed cells separating different body compartments. These epithelia cover various glandular structures, such as the breast ducts producing milk or the lung ducts forming bronchial arteries. A disruption of tissue epithelial architecture is thought to be involved in the initiation of cancer. However, little is known about the cell biology of these early neoplastic lesions. In order to shed light on interactions between the epithelial cells and their micro-environment during the formation and maintenance of epithelial structures, 3D culture systems have been introduced (Debnath et al., 2003; Wang et al., 1990a,b) that allow for in vitro growth of multicellular forms resembling normal epithelial glands. Several different cell lines have been successfully cultured on adequate 3D matrices forming spherical shells of tightly packed cells enclosing the hollow lumen (acini). These culture systems include MCF10A breast cell line (Debnath et al., 2003), RWPE-1 prostate cell line (Tyson et al., 2007), MDCK kidney cell line (Wang et al., 1990a) and pancreas cells (Chen et al., 2002).
It is widely believed that the extent to which acinar structures depart from the normal architecture formed in 3D culture is an indication of various cancerous changes that a particular cancer cell line has acquired. Therefore, some genetic modifications of these cell lines have also been investigated to examine the correlation between cancer-related gene mutations and the morphogenesis of early neoplastic lesions (Debnath & Brugge, 2005; Nelson & Bissell, 2005; Muthuswamy et al., 2001; Wang et al., 2006; Inokuchi et al., 2009). Experimentally, it is common to modify the genetic make-up of a cell line by overexpression or knock-down of a particular gene. The subsequent phenotype, or in this case the dysmorphic acinus, is then investigated biochemically to connect altered gene expression with altered signalling network. However, it is not obvious how these gene, protein and pathway changes translate into alterations of specific cell core processes (e.g. proliferation, adhesion, death) and how these impact the morphogenetic outcome. Cell sensitivity to extrinsic factors, such as composition of the extracellular matrix (ECM) or homogeneous concentration of nutrients, is even more difficult to manipulate experimentally in order to determine their impact on the final tissue architecture and function. However, the role of the micro-environment in aiding and controlling the development of early cancers is currently of great interest to both modellers and experimentalists. Computational models can facilitate the study of early cancer lesions by simulating different scenarios of tumor inception and by testing in silico the influence of various intrinsic and extrinsic factors on the emerging multicellular morphologies.
The computational framework for our study will be a modified version of the previously developed IBCell model (Section 2), capable of reproducing the formation of normal hollow acini (Section 3.1). Using this model, we will investigate how cell sensitivity to extrinsic signals sensed from the cell micro-environment via cell membrane receptors influences final cluster morphologies (Section 3.2). We will introduce 3D morphocharts, i.e. collections of multicellular morphologies arising from systematic modification of three model parameters defining cell sensitivity to external cues for cell growth, death and ECM adhesion. These morphocharts enable us to investigate the mapping between molecular and cellular processes via multicellular organization by projecting morphologies of experimental multicellular culture systems onto the model parameter space (Section 3.3). By identifying which cellular processes are down- or up-regulated in the morphocharts, we may be able to suggest area of further experimentation in order to determine key genetic or epigenetic changes responsible for these morphological distortions. This systematic search will reveal the ranges of parameter values for which robust epithelial structures can emerge and those that can lead to abnormal geometrical forms resembling tumour-like morphologies (Section 3.4). Since these dysmorphic IBCell mammospheres reproduce observed abnormal morphologies caused by changes in cancer-related genes, our model can establish an important multiscale link between molecular and cell/tissue scales that can inform further experimental studies.
2. The mathematical model
The biomechanical model of fully deformable eukaryotic cells (named IBCell, an immersed boundary model of a cell) has been applied previously to simulate the development of epithelial acini and to investigate the necessary and sufficient conditions for acini formation and stability (Rejniak & Anderson, 2008a; Rejniak & Anderson, 2008b). Here, we present a modified version of IBCell in which we introduce a new mechanism of cell growth arrest based on the negative feedback between cell proliferation and ECM accumulation. This modification brings the following advantages: (1) it allows for simulations of non-stabilized continuously growing morphologies that were not previously possible; (2) it enables a more natural emergence of growth-arrested cells as a continuous process depending on the number of different cell receptors, instead of a switch between two modes of cell polarity: partial in which cells were allowed to proliferate and full in which cells were growth arrested; (3) it simplifies the model in terms of the cell cycle flowchart and (4) it unifies the initiation and progression of all cell life processes making them entirely dependent on cell intrinsic sensitivity to extrinsic stimuli from the micro-environment. We now briefly describe the model equations (Section 2.1), then discuss the dynamics of cell membrane receptors (Section 2.2) and finally the evolution of cell phenotypes (Section 2.3) in this new version of IBCell.
2.1. Model equations
To define the mathematical basis of our model, we follow the computational framework of the immersed boundary method (Peskin, 2002; Rejniak & Anderson, 2008a; Rejniak, 2007a) that captures interactions between individual elastic cells and a viscous incompressible fluid representing the cytoplasm inside the cells, the ECM outside the tissue and the lumen inside the hollow acinar structure. The fluid flow is influenced by point sources and sinks used to model transport of fluid across the membrane of growing and dying cells, as well as forces generated by cell membranes (arising from cell elastic membrane, cell contractile ring and cell–cell adhesion), while at the same time the elastic structures move at the local fluid velocity. The ECM proteins are produced, accumulated and degraded along the cell membranes.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Equations (1–7) describe motion of the fluid and all interactions between cells, the fluid and the ECM density. In this system, (1) is the Navier–Stokes equation of a viscous incompressible fluid defined on the Cartesian grid x = (x1, x2), where p is the fluid pressure, μ is the fluid viscosity, ρ is the fluid density, s is the local fluid expansion and f is the external force density. Equation (2) is the law of mass balance. Interactions between the fluid and the material points X(l, t) on cell boundaries Γ and at point sources Yk and sinks Zm placed in the cell local micro-environment are defined in (3–6). Here, the force density F(l, t) defined on cell boundaries, as well as sources S+(Yk, t) and sinks S−(Zm, t) defined in the cell micro-environment are applied to the fluid using the 2D Dirac delta function δ, while all material boundary points X(l, t) are carried along with the fluid. The boundary forces F(l, t) arise from elastic properties of cell membranes, from cell–cell adhesion and from contractile forces splitting a cell during its division and are represented by short linear Hooks springs in (4), where ℱ* is the spring stiffness, ℒ* is the spring resting length and X(l*, t) is the adjacent, opposite or neighbouring point for either the elastic, contractile or adhesive force, respectively. The sources S+(Yk, t) and sinks S−(Zm, t) are chosen such that they balance around each cell separately. The kinetics of the ECM protein concentration γ is described at the material points X(l, t) on the cell boundaries. It includes a constant rate of ECM secretion at the free growth receptors and decay proportional to the local concentration at each boundary point. This simple equation of ECM kinetics is coupled with the dynamics of cell membrane receptors described in more detail in Section 2.2. In brief, the ECM accumulation level determines the switch in receptor function from the growth to ECM receptor, whereas the decay rate diminishes ECM concentration at all cell boundary points, in particular at the adhesive and apical receptors. Because we model a generic ECM protein, an arbitrary small value has been chosen as the receptor secretion rate κ1. The decay rate κ2 has been defined in such a way as to allow for the natural decay of ECM around the receptors in which protein secretion was stopped due to a change in receptor function (such as adhesive or apical receptors) but still allow for the steady accumulation of ECM around the free growth receptors. Provided this parameter is chosen to be small, it will only influence the time to receptor transition and not their overall dynamics. All other physical parameters are identical with those used in the previous model (Rejniak & Anderson, 2008a) but are listed in Table 1 for completeness.
Table 1.
Physical parameters of the IBCell model of acinar morphogenesis
| Model parameter | Value | Units | References |
|---|---|---|---|
| Fluid density | ρ = 1.35 | g/cm3 | Dembo & Harlow (1986) |
| Laurent et al. (2003) | |||
| Fluid viscosity | μ = 100 | g/(cm · s) | Dembo & Harlow (1986) |
| Laurent et al. (2003) | |||
| Elastic membrane force stiffness | ℱelastic = 500 | g/(cm · s) | Laurent et al. (2003) |
| Adhesive force stiffness | ℱadhesive = ℱelastic | g/(cm · s) | Rejniak & Anderson (2008a) |
| Contractile force stiffness | ℱcontractile = 50 × ℱelastic | g/(cm · s) | Rejniak & Anderson (2008a) |
| Fluid sources and sinks | 𝒮+ = 𝒮− =5 × 10−10 | g/s | Rejniak & Anderson (2008a) |
| Elastic spring resting length | ℒelastic = 0.5 | μm | Rejniak & Anderson (2008a) |
| Adhesive spring resting length | ℒadhesive = 0.5 | μm | Rejniak & Anderson (2008a) |
| Contractile spring resting length | ℒcontractile = 2.5 | μm | Rejniak & Anderson (2008a) |
| ECM secretion rate (at the growth receptors) | κ1 = 1 × 10−10 | mM/s | This text |
| ECM decay rate | κ2 = 0.05 × κ1 | 1/s | This text |
2.2. Model of cell membrane receptor dynamics
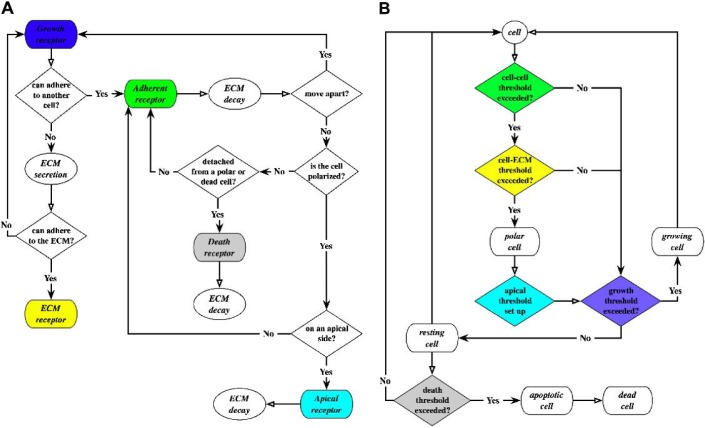
In the IBCell model, all material points on cell boundaries are considered to be cell membrane sensors/receptors (colour coded in Fig. 2(A)) and are used to sense the presence of other cells or the ECM in their immediate neighbourhood. This is similar to the biological function of cell surface receptors. However, in contrast to biological receptors that can be created or relocated depending on extrinsic signals sensed by the cell, locations of the IBCell abstract receptors are preserved along the cell boundary, but their status and function will be dynamically modified in response to local environmental cues. A flowchart showing the dynamics of cell membrane receptors is presented in Fig. 1(A), and the rules of receptor emergence and activation together with a link to the corresponding model equations are summarized in Table 2.
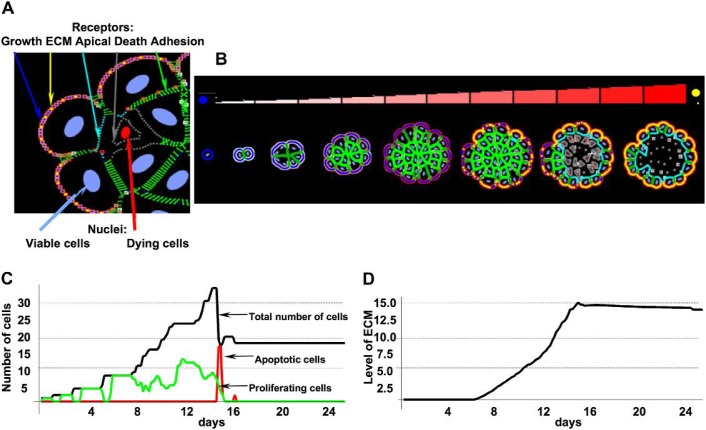
Fig. 2.
(A) Colour-coded cell membrane receptors: cell–cell adhesion (green), cell–ECM adhesion (yellow), apical (cyan), growth (blue), death (grey). (B) A sequence of consecutive stages in the development of a hollow acinus starting from a single cell and ending with a monolayer structure enclosing the hollow lumen. Accumulating ECM proteins are indicated by different shades of red (see colour bar) and the change of receptors from growth (blue) to ECM (yellow). (C) Evolution of different cell subpopulations: proliferating (green), apoptotic (red) and total (black) over the time course of acinar formation. (D) Dynamics of ECM secretion and accumulation along the perimeter of an emerging acinus. Both data sets correspond to the morphologies shown in panel (B). Model parameters: growth threshold: 15%, death threshold: 25%, ECM threshold: 15×103κ1.
Fig. 1.
(A) Flowchart describing the dynamics of cell membrane receptors; the default state is growth; transition to another state (ECM, adherent, apical or death) depends on cues sensed from other cells and from the micro-environment. (B) Flowchart describing the evolution of phenotypically different subpopulations of resting, growing, polarized, apoptotic and dead cells; the initiation of cell life processes depends on the distribution of all cell membrane receptors and the predefined receptor thresholds.
Table 2.
Rules for the emergence and activation of cell membrane receptors in the IBCell model and their link to model equations. Cell membrane receptors are colour coded as in Fig. 2A
| Cell receptors | Receptor activation/emergence | Model equations |
|---|---|---|
| Adhesion (green) | Activated when two receptors from distinct cells are close enough | Adhesive forces F(l, t) in (3) and (4) |
| ECM (yellow) | Activated when the expression of ECM proteins exceeds the threshold | ECM γ (X(l, t)) kinetics in (7) |
| Growth (blue) | All receptors free from any cell–cell or cell–ECM contacts (a default state) | Sources S+(Yk, t) inside and sinks S−(Zm, t) outside the growing cell, (5) |
| Death (grey) | Emerge after detachment from a polarized or from another dying cell | Sinks S− (Zm, t) inside and sources S+(Yk, t) outside the dying cell, (5) |
| Apical (cyan) | Emerge during the development of a cell’s apical membrane domain | Adhesive forces F(l, t) in (3) and (4) are disassembled; all extrinsic signals are blocked |
The default state of each receptor is ‘growth’, and if the host cell is capable of proliferation (see Section 2.3 for details), the balancing sources and sinks of fluid are placed around each growth receptor, inside and outside of the cell, respectively. This creates a flow pushing on the cell membrane and expanding its area. Each growth receptor is also a site of ECM protein secretion (at rate κ1; Table 1). Since the cell membrane is stretched during its growth, new boundary points are added halfway between the existing receptors (following rules of the immersed boundary method; Peskin, 2002). ECM concentration at these new receptors is assumed to take an average value of their two immediate neighbours. When ECM accumulation at a given receptor exceeds a predefined threshold (see Section 2.3), this receptor becomes an ‘ECM’ receptor. When two receptors from two distinct cells fall within a pre-defined distance (ℒadhesive; Table 1), an adhesive spring is created between them, (4), and the receptor function is switched to ‘adhesive’. If adhesive receptors move apart due to dynamical interactions between neighbouring cells, the adhesive springs between them are disassembled and the receptor function is changed back to ‘growth’. When the host cell becomes polarized, all receptors located on cell apical side (see Section 2.3) acquire an ‘apical’ status. All existing adhesive springs between apical receptors and their neighbours are disassembled and all apical receptors are blocked from sensing any extrinsic signal. When the adhesive spring is broken (due to either the development of an apical side in the polarized cell or the initiation of cell death, see Section 2.3), the function of adhesive receptors in the inner cells is changed to ‘death’ receptors. When the host cell is in a process of apoptotic death (see Section 2.3), the balancing sinks and sources of fluid are placed in the receptor neighbourhood, inside and outside the cell, respectively, to create a flow that diminishes cell area. The cell membrane shrinks and overcrowded boundary points are removed. In addition, all adherent, apical, growth and death receptors are sites of ECM protein decay (at a rate κ2; Table 1).
2.3. Model of cell life processes
The initiation of a specific cell life process is determined by a current distribution of cell membrane receptors and a set of predefined critical thresholds. For example, when the cell senses sufficient free space in its micro-environment (i.e. when a certain percent of cell membrane receptors are in contact neither with other cells nor with the ECM), this cell may enter into the process of cell proliferation. In contrast, if the percentage of cell-free receptors does not meet the growth threshold, the host cell remains in a resting (growth-arrested) state. Similarly, when the number of cell death receptors reaches a prescribed threshold, the host cell starts a process of an apoptotic death. Therefore, by changing the membrane receptor thresholds, we can impose various physiological properties on the host cell. For instance, by increasing the death receptor threshold of the host cell, more death receptors must be accumulated before entering into the apoptotic processes, thus we force the cell to become more resistant to death. By diminishing the growth receptor threshold, we allow the host cell to grow even if the percentage of their receptors engaged in cell–cell and cell–ECM contacts is large, therefore allowing the host cell to be less sensitive to contact inhibition. A new feature of our model is the emergence of ECM receptors in relation to the concentration of ECM proteins. By setting the ECM receptor threshold (in terms of an ECM concentration level, α × κ1, at which a free growth receptor function is changed), we can impose the cell sensitivity to ECM adhesion. Intuitively, an increased number of ECM membrane receptors diminishes the number of growth receptors leading naturally to cell growth arrest and to acini stabilization. The accumulated concentration of ECM acts thus as an inhibitory mechanism on cell proliferation via a negative feedback loop. In our previous model (Rejniak & Anderson, 2008a; Rejniak & Anderson, 2008b), the conditions for cell epithelial polarization were specified in terms of the length of three cell membrane domains: basal (in contact with the ECM), lateral (in contact with other cells) and apical (in contact with the lumen), and the number of assembled tight junctions along cell lateral sides. Moreover, we modelled the process of cell epithelial polarization by introducing two cell states: partially polarized in which the cells are still capable of growing and fully polarized in which the cells are in permanent growth arrest. Here we relate cell polarization only to the presence of cell–cell and cell–ECM adhesion receptors, and the inhibition of cell growth is a natural consequence of the cell receptor dynamics. In addition, by using this negative feedback loop based on an extrinsic factor (ECM accumulation), we were able to greatly simplify the cell cycle flowchart (there is no need now for two polarization states; Fig. 1(B)) and to unify the initiation of cell life processes making them entirely dependent on the cell membrane receptor distribution.
In summary, every cell in the simulated system is equipped with a decision mechanism that modifies its state by initiating certain life processes based on the configuration of cell receptors. Figure 1(B) depicts a flowchart showing the evolution of five phenotypically distinct subpopulations of cells in our model: resting, growing, polarized, apoptotic and dead. Each cell phenotype (except the death cells) can make decisions based on the configuration of cell membrane receptors (growth, death, apical, cell–cell and cell–ECM) to enter the associated cell life processes (growth, polarization, apoptotic death, rest) that are responsible for movement through the flowchart.
The first cell in the system spontaneously executes cell proliferation since all its receptors are growth receptors. This is modelled by introducing fluid sources inside the host cell in a close neighbourhood of each growth receptor and the balancing fluid sinks outside the host cell, (5). As a result, the amount of fluid inside the cell increases pushing on the cell boundary points that are moved on the local fluid velocity, (6). When the boundary points move apart a distance larger than the prescribed resting length (ℒelastic; Table 1), new points (growth receptors) and springs are added halfway between the existing points. Once the cell area is doubled, the contractile springs are introduced on opposite sides of cell membrane pushing cell boundaries towards each other until they reach the prescribed distance (ℒcontractile; Table 1). At this point, the host cell is split into two daughter cells. Since they are in a close proximity to one another, the adhesive connections and adhesive springs are defined between boundary points on both cells, (4), and the function of these boundary points is changed from growth to adhesive receptors. Thereafter, the context becomes ever changing and the receptors react accordingly (as described by the flowchart in Fig. 1(A)). As the number of adhesive receptors increases, the percentage of free growth receptors is diminished which directly influences the cell decision to initiate a new proliferation process (if the growth receptors threshold is exceeded) or to remain in a growth arrest state, otherwise. The development of both adhesive and ECM receptors (upon accumulation of ECM proteins, (7)) leads to a change in cell phenotype, i.e. the host cell becomes epithelially polarized. This is followed by the emergence of an apical side that is disjoint from the lateral sides of the cell and is located opposite to the ECM receptors. This process requires the disassembly of all adhesive springs between the polarized host cell and its neighbouring inner cells that in turn leads to the change of receptor function from adhesive to apical in the polarized cell and from adhesive to death receptors in the inner cells. The polarized cells can still proliferate if they meet the growth receptor threshold; however, by increasing the number of ECM receptors, the overall percentage of growth receptors is diminished and generally leads to cell growth arrest. The inner cells will initiate the process of apoptotic death if the percentage of their death receptors meets the predefined threshold. This is modelled by introducing fluid sinks inside the host cell in a close neighbourhood of each death receptor and balancing fluid sources outside the host cells, (5). As a result, the amount of fluid inside the cell decreases and the cell boundaries shrink. More details on the IBCell model implementation, solution and model parameters can be found in Rejniak & Anderson (2008a) and Rejniak (2007a,b).
3. Computational results
Our overall goal is to investigate how cell intrinsic sensitivity to extrinsic factors influences the disruption of normal acinar architecture and the emergence of mutant-like multicellular morphologies. Because we compare how changes in model parameters translate to altered morphogenesis, we first need to ensure that the modified IBCell model is capable of generating stable self-organizing acinar structures, comparable to those produced by our previous model (Section 3.1). We will then discuss the concept of multidimensional morphocharts, i.e. collections of final acinar morphologies arising from simulations with systematically varied parameter combinations that define cell sensitivity to extrinsic factors (Section 3.2). Utilizing these morphocharts, we will classify different tissue architectures (including various forms resembling tumors) and map the morphologies observed in experimental multicellular systems onto the corresponding set of cell intrinsic properties (Section 3.3). Finally, we discuss the robustness of normal and mutant-like morphologies with respect to some intrinsic and extrinsic perturbations (Section 3.4).
3.1. Cells self-organization into a stable epithelial acinus
The new mechanism for cell growth arrest that relies on the concentration of an extrinsic factor sensed by the cells through their membrane receptors allows us to simplify certain model assumptions without loosing the ability to reproduce stable self-organizing acinar structures, comparable to those produced by our previous model (see Fig. 10 in Rejniak & Anderson (2008a) and Fig. 3 in Rejniak & Anderson (2008b)). We initiate all simulations with a single cell (Fig. 2(B)) that, upon consecutive divisions, gives rise to a cluster of randomly oriented cells that adhere to their immediate neighbours (green receptors, Fig. 2(B)). All cells secrete ECM proteins in the vicinity of those membrane receptors that are not engaged in cell–cell adhesion, i.e. initially along the whole cell boundary. However, with the increased number of adhesive receptors, the ECM secretion remains confined only to the outer part of the cell membrane that is in direct contact with the external medium. Moreover, upon accumulation of the ECM (increased intensity of pink-red staining around cell receptors, Fig. 2B), the free growth receptors (blue, Fig. 2(B)) will change their function to the ECM receptors (yellow, Fig. 2(B)) subsequently leading to the differentiation of all outer cells and their epithelial polarization. These polarized cells will eventually develop apical membrane domains (cyan receptors, Fig. 2(B)) by breaking all adhesive connections with inner cells. This will subsequently increase the number of death receptors (grey receptors, Fig. 2(B)) on the boundaries of inner cells and trigger their apoptotic death.
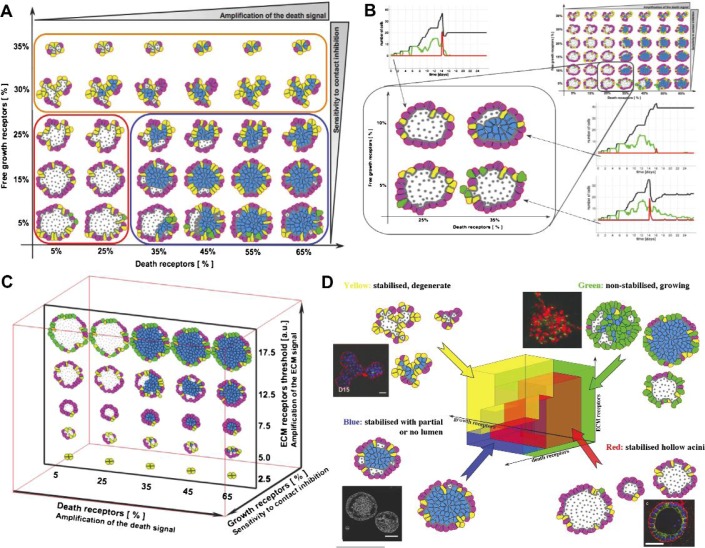
Fig. 3.
(A) A 2D morphochart of final acinar structures produced for different combinations of growth and death receptor thresholds and the ECM threshold fixed at 15×103κ1. (B) A morphochart in which the change of a single threshold (growth or death) still produces a hollow acinus, whereas the simultaneous change of both thresholds results in a partially filled lumen (the ECM threshold fixed at 10×103κ1). (C) A morphochart showing acinar structures produced for the growth receptor threshold fixed at 20% and varied thresholds for death and ECM receptors. (D) A 3D IBCell parameter space defining cell sensitivity to growth, death and ECM signals divided into four colour-coded morphology classes: normal hollow acini (red), filled lumen acini (blue), small degenerated acini (yellow) and non-stabilized acini (green). Insets show examples of similar morphologies observed in 3D in vitro cultures; clockwise: MCF10A-Ras-Scribble (green) from Dow et al. (2008, Fig. 4d); MCF10A (red) from Debnath et al. (2003, Fig. 5C); RWPE-1/rA1 (blue) from Inokuchi et al. (2009, Fig. 2A) and MCF10A/Mek2-DD (yellow) from (Reginato et al., 2005, Fig. 7B). All figures reproduced with permission.
Figure 2(C) shows the evolution of different cell subpopulations (proliferating, apoptotic, total) over the time course of acinar formation presented in Fig. 2(B). In this simulation, the following three receptor thresholds have been chosen: the growth receptors threshold is equal to 15%, the death receptors threshold to 25% and the ECM threshold to 15 × 103κ1. The proliferating cells are observed continuously over the period of the simulation equal to about 15 days of real time, and in the first phase (Days 1–7), almost all cells are growing. After about 2 weeks, the growth of all cells is suppressed. Around Days 15–16, there is a massive death of inner cells that leads to the formation of the hollow lumen. After Day 16, the whole multicellular system reaches an equilibrium. The dynamics of ECM secretion and its accumulation along the perimeter of an emerging acinus is shown in Fig. 2(D). Initially (up to Day 6), the amounts of secreted and accumulated ECM proteins are very small (undetectable), but subsequently (Days 6–14) the concentration of ECM is steadily increasing and reaches a plateau at Day 14. Similar dynamics of real acini formation have been observed in 3D in vitro experiments. For instance, the non-tumorigenic MCF10A cell line when grown in Matrigel forms hollow multicellular spheroids over a period of 15 days (Debnath et al., 2002). Cell polarization in the outer layer is detectable as soon as at Day 3 (Debnath et al., 2003), and the acinar diameter stabilizes around Day 12 (Debnath et al., 2002). The inner lumen becomes completely empty in the period of 2–3 days (Debnath et al., 2003), and cell apoptosis has been shown to be one of the contributing factors (Debnath et al., 2002).
The acinar morphogenesis shown in Fig. 2 is an example simulated for one particular set of receptor thresholds. However, by changing these parameters, several distinct acinar architectures of various sizes and dynamics may be produced. We will discuss the full multidimensional parameter space of model outcomes in Sections 3.2 and 3.3. In general, the spatial self-arrangement of proliferating cells into a hollow acinus is achieved solely due to local interactions among individual cells and local information sensed through the cell membrane receptors, without any predefined blueprint to build an acinar structure or any other given a priori pattern. Moreover, the expanding multicellular structure becomes and remains stable via a self-inhibition mechanism of proliferation. This is accomplished due to the emergence of ECM receptors diminishing the number of free growth receptors that contribute to cell growth arrest. In the previously published model (Rejniak & Anderson, 2008a), the stability of an acinar structure was achieved by introducing two types of cell polarity: partial, when the cells were still allowed to proliferate, and full, when the cells were assumed to be in a permanent growth arrest. We used these two different modes of cell polarity to represent a gradual transformation in cell phenotype from sporadically proliferating to growth suppressed. Such a change in cell behaviour has been observed in experimentally grown acini where the outer cells were proliferating sporadically just before the whole acinar structure became stabilized. However, there are no clear molecular markers for identifying cell epithelial polarity. The introduction of an extrinsic factor, such as ECM density, allows us to avoid the use of an additional cell phenotype and the process of cell growth arrest now becomes an emergent property due to insufficient free membrane receptors. It has been observed experimentally that ECM proteins, such as laminin-332, form a basal membrane surrounding the growth-arrested acinus (Debnath et al., 2002) and that the ECM receptors, such as integrin-α6, are expressed differently in normal and tumour-like cells (Liu et al., 2005).
3.2. IBCell morphocharts as a tool for multicellular morphology classification
During IBCell simulations, the actions of all cells depend on their current membrane receptor configuration. Individual cells undergo receptor-dependent state switching that changes interactions between cells and their micro-environment and in turn modulates cell behaviour. Central to this process are the thresholds defining the switch between cell states and determining which cell life process will be initiated. By varying these thresholds, we can modify cell intrinsic responses to environmental cues, i.e. specify whether the cell is more resistant or more sensitive to a specific extrinsic cue. In addition, by systematically exploring the whole threshold parameter space we can produce multidimensional simulation charts (morphocharts), which plot collections of final acinar morphologies arising from simulations with different combinations of receptor thresholds. This in turn enables us to classify final acinar morphologies with respect to the imposed cell sensitivity.
We use the simulation presented in Section 3.1 as a seed for varying the three receptor thresholds and examine emerging multicellular morphologies. Figure 3(A) shows a 2D morphochart created for different combinations of growth and death receptor thresholds and the fixed ECM threshold equal to 12.5 × 103κ1. Note that by increasing the death receptor threshold, we impose on the host cell a requirement to accumulate more death receptors before it can begin the process of apoptotic death; thus, we make the cell more resistant to death signals. For example, the cells in the left part of the morphochart, that require only 5–25% of death receptors to trigger their apoptotic death, produce hollow structures. Whereas acini in the right part of the panel will remain partially or fully filled since these cells need to accumulate many more death receptors (35–65%) to start the apoptotic process, making it much more difficult to achieve. Similarly, by decreasing the growth receptor threshold, we lower the requirement on how much free space a cell needs to sense in order to start growing. Therefore, we enable cell proliferation even in the presence of large numbers of cell–cell and cell–ECM contacts; thus, we make the cell more resistant to contact inhibition signals. For example, the cells in the lower part of the morphochart require only 5–15% of its membrane receptors to be free from cell–cell and cell–ECM contacts to start proliferating, i.e. potentially about 85–95% of cell membrane receptors can be engaged in cell–cell contacts and the cell will still start growing. In contrast, the upper part of the panel shows degenerate acini characterized by very irregular shapes which is a consequence of the fact that some cells have entered into a growth arrest state early, not having sufficient free growth receptors (30–35%) to continue the process of cell growth, whereas other cells were still capable of growing; in combination this leads to abnormal folding and irregularities in acinar structure.
Different biological cell lines may be characterized by distinct levels of cell sensitivity to a particular external factor. Moreover, cells derived from the same cell line may respond differently to similar external conditions depending on whether or not they are exposed to specific drugs or oncogenes. One such case has been reported in Debnath et al. (2002), where the authors used the 3D cultures of MCF-10A cells, a non-transformed, non-tumorigenic mammary epithelial cell line. By growing them on a reconstituted basement membrane (Matrigel), they formed growth-arrested acini-like hollow spheroids. Interestingly, the normal hollow acinar morphology was still achieved when either inner cell apoptosis was inhibited (by overexpressing the anti-apoptotic proteins Bcl-2 or Bcl-XL) or cell proliferation rate was increased (by overexpressing cyclin D1 or oncoprotein HPV16E7). However, by combining both kinds of molecular insults, the normal hollow morphology was disrupted resulting in acinar morphologies with the filled lumen. Thus, inhibition of luminal apoptosis alone delayed but did not prevent formation of the lumen. Similarly, increased proliferation was insufficient to disrupt acinar morphology. Luminal filling was only observed when an anti-apoptotic signal was combined with a pro-proliferative signal. This phenomenon naturally emerges in our model. Figure 3(B) shows that the change in the threshold of a single process (either growth from 5% to 10% of cell membrane receptors or death from 25% to 35%) still produced normal hollow acini, but when the thresholds of both processes were changed simultaneously, the lumen remained partially filled. Note differences in the dynamics of emerging cell subpopulations for each of the four featured morphologies, especially after Days 14–16: a stable hollow and growth-arrested structure (top left, death threshold D = 25%, growth threshold G = 10%), a stable hollow structure with sporadic growth events accompanied by apoptosis producing a dynamic equilibrium (right bottom, with thresholds D = 35%, G = 5%) and a stable structure with partially filled lumen (right top, D = 35%, G = 10%).
3.3. Mapping experimental morphologies onto multidimensional morphocharts
By altering various receptor thresholds, IBCell can produce different acinar and tumour-like morphologies (Fig. 3(A–C)). We here discussed in the previous section how changing the thresholds for growth and death receptors resulted in the emergence of either normal hollow acini or epithelial ducts with partially or fully filled lumen (Fig. 3(A and B)). When, in turn, the ECM threshold is varied, the model generates acini of various sizes (Fig. 3(C)). For low values of the ECM threshold (bottom of the ECM plane, Fig. 3(C)), the ECM receptors emerge early leading to early cell growth suppression and the formation of smaller growth-arrested acini. With increased values of the ECM threshold, the acinar clusters grow larger before stabilizing. For high values of the ECM threshold (top row in Fig. 3(C)), the acini never stabilize and the outer cells (green) continue to proliferate. By systematically exploring the whole 3D parameter space of growth, death and ECM receptor thresholds, we can classify the final acinar structures into four broad morphologically distinct categories (Fig. 3(D)): normal hollow acini of various sizes (red region), acini with partially or fully filled lumen (blue region), degenerate acini with small irregular shapes (yellow region) and continuously growing, non-stabilized acini (green region). Further subclassification may take into consideration acinar size, regularity of its final shape or the extent of lumen filling. Examples of four experimental morphologies matching the four classes determined by IBCell analysis are shown in the insets in Fig. 3(D). Other examples are discussed in Rejniak et al. (2010).
Carcinogenesis is a complex process that involves multiple cellular and micro-environmental changes. Often mammary acini are used to investigate the impact that certain intrinsic and extrinsic factors have on the final multicellular structure. However, it is very difficult to quantify how these factors alter individual cell behaviour, especially in terms of multiple processes. By utilizing our computational morphocharts, we can dynamically inspect multiple processes in a systematic manner teasing out which ones have been altered and how, thus guiding further experimentation. This can be done by mapping a particular experimental morphology onto a set of semi-quantitative model parameters in order to quantify the range of possible changes in cell sensitivities defined by the thresholds of cell membrane receptors under consideration. For example, the multicellular structure with morphology matching patterns from the blue region may be simulated by our model by increasing the thresholds for both cell proliferation and death sensitivities, with possibly reduced signalling from ECM. The multicellular pattern resembling shapes from the yellow region may emerge when cells are resistant to growth signals and sensitive to contact inhibition. The morphology corresponding to shapes generated in the green region may arise by either a high resistance to ECM adhesion signals or elevated cell proliferation accompanied by changes in cell response to accumulated ECM. By comparing model parameters in simulations leading to normal acinar morphologies with those from mutant like, one can gain information about the underlying differences in cell sensitivities to extrinsic signals (Rejniak et al., 2010). These multidimensional morphocharts can highlight which combinations of cellular modifications drive a given acini structure and therefore guide further experimentation to confirm or rule out model predictions. If other sensitivity parameters are indicated by experiments, the corresponding morphocharts can be constructed and final in silico morphologies compared to experimental patterns.
3.4. Robustness of acinar and tumor-like morphologies as revealed by IBCell
Another important result of IBCell simulations is that they capture robustness of the self-organizing multicellular system, i.e. the capability of acini to maintain or repair their structure in response to some intrinsic or extrinsic perturbations. This is manifested in our model by the quite vast regions of similar morphologies that arise in response to variation in receptor thresholds. For example, changes in proliferation or death sensitivity thresholds from 5% to 25% still resulted in stable hollow acini. Similar robust results in generating hollow round acini were achieved when the ECM sensitivity threshold was increased threefold. The morphocharts nicely capture and represent this variance and define a parameter space for normalcy. This kind of robustness has also been observed experimentally. We described in Section 3.2 the case reported in Debnath et al. (2002) in which normal acinar structures were created even when the baseline cells were manipulated to overexpress the anti-apoptotic or pro-proliferative proteins. In the same paper, the authors reported that due to intrinsic cell variability the diameter of hollow acini derived from the MCF10A cell line can vary almost twofold. Therefore, our model indicates that a self-organizing process such as acinar morphogenesis endowed with sufficient robustness will generate reproducible patterns. Moreover, each of the four broad classes of multicellular morphologies generated by IBCell, either normal or mutant like, are robust to (a certain degree) alterations in cell sensitivity to each of the three cellular processes: cell growth, death and ECM accumulation (see also Rejniak et al., 2010). This also corresponds to the view that acinar mutants that resemble cancers form highly robust systems (Kitano, 2004).
4. Discussion
In this paper, we introduced a modified version of the IBCell computational model capable of simulating the biomechanics of life processes of eukaryotic cells and local interactions between cells and their micro-environment. This model has no built-in knowledge about the type of tissue architecture that cells may construct. In contrast, the shape and form of final multicellular structures produced by the model are derived exclusively from the local interactions between cells. In particular, the change of cell phenotype, the initiation and progression of all cell life processes and cell responses to extrinsic cues are all dependent, in our model, on the distribution and dynamics of cell membrane receptors. The novelty of this version of IBCell is introduction of an extrinsic factor, such as ECM proteins, that upon secretion and accumulation lead to the emergence of ECM receptors that inhibit cell growth resulting in stabilization of the whole developing structure.
The five kinds of cell membrane receptors/sensors: growth, death, apical, cell–cell and cell–ECM adhesion considered in our model have their counterparts in biology. Adhesive receptors which are activated when sensors from two distinct cells are sufficiently close to one another enable both cells to stay in a close contact which is similar to the homotypic nature of cadherins (Gumbiner, 1996). ECM receptors that are specified by the boundary point positioned at the outer segments of the plasma membrane being in contact with extracellular medium reflect the biological function of integrins (Tarone et al., 2000). Apical receptors (markers) (Wang et al., 1990a) are activated in the outer polarized cells by disassembling existing cell–cell adhesive links with inner cells. Death receptors (Jung et al., 2001) are created in the inner cells upon their detachment from the polarized or from other dying cells. Polarized cells are by necessity on the outer rim of the acinus, due to ECM contacts (Liu et al., 2005). Upon the assembly of ECM receptors, the number of free growth receptors is reduced resulting in cell growth arrest that is linked to secretion of ECM. This is biologically realistic because certain ECM proteins, such as laminins, are known to be a major component of epithelial basement membrane, a thin, dense ring of the ECM that surrounds and encapsulates acini or epithelial ducts, but may be dysregulated in cancers (Guess & Quaranta, 2009).
To our knowledge, there are no other models (except two other implementations of the immersed boundary method by Dillon (Rejniak & Dillon, 2007; Dillon et al., 2008) and Dallon (Dallon et al., 2009; Dallon, 2010)) that couple the mechanics of elastic deformable cells with the dynamics of their membrane receptors allowing for simulations of morphological changes on both cell and tissue scales. The computational framework of Glazier–Graner–Hogeweg (cellular Potts) model (Shirinifard et al., 2009; Merks et al., 2008) enables one to model 3D deformable cells and to define cell adhesion to be proportional to the cell surface area, but the individual receptors or receptor clusters are not represented in this model. The mechanical framework of the subcellular element model (Sandersius & Newman, 2008; Newman, 2007) has no explicit representation of the cell membrane but models cell–cell adhesion directly between subcellular element representing cell cytoskeleton. Several mathematical models have addressed the dynamics of various receptors, such as integrins clustering (Paszek et al., 2009), integrin-mediated cell migration (Cirit et al., 2010), E-cadherins signalling in cancer invasion (Ramis-Conde et al., 2008) and colorectal cancer development (van Leeuwen et al., 2009). Other models have handled cell adhesion in a more simplified way as an average adhesion strength between individual point cells (in both lattice-based (Anderson, 2005; Deutsch, 2007; Kim et al., 2009) and lattice-free (Drasdo & Hoehme, 2005; Galle et al., 2006; Norton et al., 2010) models) or as a mean value taken over a patch of tissue modelled as a continuum (Byrne & Chaplain, 1996; Armstrong et al., 2006).
The mechanism of ECM-density-dependent self-inhibition of cell proliferation introduced in our model of acinar morphogenesis constitutes a typical negative feedback. This inhibition process is self-generated and proportional to proliferation itself since the larger the number of cells in the cluster the higher the accumulation of ECM along the acinar perimeter which in turn will increase the number of ECM membrane receptors diminishing the ratio of free growth receptors leading to cell growth arrest. Biologically, contact inhibition resembles this kind of behaviour, and it is generally observed in 2D tissue cultures leading to cells growing to confluence. Though the molecular details of contact inhibition are not entirely understood, it is believed that as the number of adherens junctions on the plasma membrane increases, proliferation decreases proportionally. In a 3D setting, contact inhibition is likely more closely related to epithelial polarization, whereby plasma membranes become committed to basolateral and apical domains. Both processes, contact inhibition and cell polarization, are represented in IBCell by assembling cell–cell and cell–ECM contacts, respectively. We have hypothesized here that the ECM-density-dependent inhibition of cell proliferation is a mechanism for the stability and growth arrest of the developing acinar structure. It has been observed experimentally that ECM proteins, such as laminin-332, form a basal membrane surrounding the growth-arrested acinus (Debnath et al., 2003) and that the ECM receptors, such as integrins-α6, are expressed differently in normal and tumour-like cells (Liu et al., 2005). However, further experimentation is needed to prove or disprove this mechanism.
The cell membrane receptors configuration and the predefined thresholds regulate the initiation of cell proliferation, apoptosis and cell–ECM adhesion. Thus, cells undergo receptor-dependent state switching that changes interactions between cells and their micro-environment. This in turn modulates cell behaviour and ultimately leads to the emergence of an epithelial acinus. Systematic changes in these thresholds allow us to construct the IBCell morphocharts and classify the final acinar morphologies into normal and various tumour-like or mutant-like structures. We have shown in Fig. 3(D) four distinct experimental morphologies to highlight that the computationally developed architectures have their experimental equivalent. These include the non-tumorigenic MCF10A (Debnath et al., 2003) cells that form normal hollow acini; MCF10A-Ras-Scrible (Dow et al., 2008) mutants producing non-stabilized spheroids without detectable lumen; MCF10A-Mek2-DD (Reginato et al., 2005) mutant forming multiacinar structures of irregular shapes and RWPE-1/rA1 (Inokuchi et al., 2009) mutant producing acini with partially filled lumen. However, without detailed time lapse of the development of these structures, we cannot claim that the computational acini are direct equivalents as we have no means of quantifying the computationally determined thresholds (at least from a single static image). Further experimentation (that is outside the scope of this manuscript) is needed in order to dissect whether cell phenotypes or receptor characteristics of these experimental cell lines are in agreement with those predicted by our model.
Since carcinogenesis is a complex process involving multiple cellular and micro-environmental modifications, it is difficult to dissect changes in individual cellular processes. Computational morphocharts can inspect these processes systematically and determine key intrinsic or extrinsic factors that govern the transition in cellular morphologies from one class in parameter space to another. This will reduce the number of possible processes that can lead to a particular morphological structure guiding further experimentation. In this manuscript, we have focused on three cell processes and their corresponding receptors: growth, death and ECM because proliferation and apoptosis are known to be dys-regulated in tumours. The ECM contribution to tumour initiation is not widely investigated, but using a systematic search of IBCell model parameters, we have suggested a possible mechanism concerning the impact of ECM concentration on acinar size and stability. Other processes and membrane receptors, such as cell–cell adhesion, can be considered and corresponding morphocharts constructed.
There is a wealth of information on genes and pathways that may be responsible for early carcinoma lesions. However, a general theory linking cancer-related gene mutations to the emerging morphology of the lesion is lacking. Computational models, such as IBCell, can facilitate this task by defining the parameter space of normal epithelial acini morphogenesis and comparing them with the equivalent space for pre-neoplastic mutant morphologies. This will allow us to link the underlying cellular and molecular defects in relation to morphology. Thus, IBCell can map from genetic change to phenotypic change via morphological change. Finally, by reversing this process, by identifying which cellular processes are down- or up-regulated in the morphocharts, we may suggest the areas of further experimentation in order to determine the molecular or genetic changes responsible for such morphological distortions.
Acknowledgments
We would like to thank Dr Scott Camazine for fruitful discussions. We thank the members of the Vanderbilt Integrative Cancer Biology Center (ViCBC) for crucial biological insight. We also would like to thank two anonymous reviewers for all invaluable comments and critics.
Footnotes
Funding
National Cancer Institute Integrative Cancer Biology Program (U54 CA113007).
REFERENCES
- Anderson ARA. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math Med Biol. 2005;22:163–186. doi: 10.1093/imammb/dqi005. [DOI] [PubMed] [Google Scholar]
- Armstrong NJ, Painter KJ, Sherratt JA. A continuum approach to modelling cell-cell adhesion. J Theor Biol. 2006;243:98–113. doi: 10.1016/j.jtbi.2006.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrne HM, Chaplain M. Modelling the role of cell-cell adhesion in the growth and development of carcinoma. Math Comput Model. 1996;24:1–17. [Google Scholar]
- Chen X, Edwards JAS, Logsdon CD, Ernst SA, Williams JA. Dominant negative Rab3D inhibits amylase release from mouse pancreatic acini. J Biol Chem. 2002;277:18002–18009. doi: 10.1074/jbc.M201248200. [DOI] [PubMed] [Google Scholar]
- Cirit M, Krajcovic M, Choi CK, Welf ES, Horowitz AF, Haugh JM. Stochastic model of integrin-mediated signaling and adhesion dynamics at the leading edges of migrating cells. PLoS Comput Biol. 2010;6:e1000688. doi: 10.1371/journal.pcbi.1000688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dallon JC. Multiscale modelling of cellular systems in biology. Curr Opin Colloid Interface Sci. 2010;15:24–31. [Google Scholar]
- Dallon JC, Newren E, Hansen MDH. Using a mathematical model of cadherin-based adhesion to understand the function of the actin cytoskeleton. Phys Rev E. 2009;79:031918. doi: 10.1103/PhysRevE.79.031918. [DOI] [PubMed] [Google Scholar]
- Debnath J, Brugge JS. Modeling glandular epithelial cancers in three-dimensional cultures. Nat Rev Cancer. 2005;5:675–688. doi: 10.1038/nrc1695. [DOI] [PubMed] [Google Scholar]
- Debnath J, Mills KR, Collins NL, Reginato MJ, Muthuswamy SK, Brugge JS. The role of apoptosis in creating and maintaining luminal space within normal and oncogene-expressing mammary acini. Cell. 2002;111:29–40. doi: 10.1016/s0092-8674(02)01001-2. [DOI] [PubMed] [Google Scholar]
- Debnath J, Muthuswamy SK, Brugge JS. Morphogenesis and oncogenesis of MCF-10A mammary epithelial acini grown in three-dimensional basement membrane cultures. Methods. 2003;30:256–268. doi: 10.1016/s1046-2023(03)00032-x. [DOI] [PubMed] [Google Scholar]
- Dembo M, Harlow F. Cell motion, contractile networks, and the physics of interpenetrating reactive flow. Biophys J. 1986;50:109–121. doi: 10.1016/S0006-3495(86)83444-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deutsch A. Lattice-gas cellular automata modeling of developing cell systems. In: Anderson A, Chaplain M, Rejniak KA, editors. Single-Cell-Based Models in Biology and Medicine. Basel, Switzerland: Birkhauser; 2007. pp. 29–51. [Google Scholar]
- Dillon RH, Owen M, Painter K. A single-cell-based model of multicellular growth using the immersed boundary method. AMS Contemp Math. 2008;466:1–15. [Google Scholar]
- Dow LE, Elsum IA, King CL, Kinross KM, Richardson HE, Humbert PO. Loss of human Scribble cooperates with H-Ras to promote cell invasion through deregulation of MAPK signalling. Oncogene. 2008;27:5988–6001. doi: 10.1038/onc.2008.219. [DOI] [PubMed] [Google Scholar]
- Drasdo D, Hoehme S. A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys Biol. 2005;2:133–147. doi: 10.1088/1478-3975/2/3/001. [DOI] [PubMed] [Google Scholar]
- Galle J, Sittig D, Hanisch I, Wobus M, Wandel E, Loeffler M, Aust G. Individual cell-based models of tumor-environment interactions: multiple effects of CD97 on tumor invasion. Am J Pathol. 2006;169:1802–1811. doi: 10.2353/ajpath.2006.060006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guess CM, Quaranta V. Defining the role of laminin-332 in carcinoma. Matrix Biol. 2009;28:445–455. doi: 10.1016/j.matbio.2009.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gumbiner BM. Cell adhesion: the molecular basis of tissue architecture and morphogenesis. Cell. 1996;84:345–357. doi: 10.1016/s0092-8674(00)81279-9. [DOI] [PubMed] [Google Scholar]
- Inokuchi J, Lau A, Tyson DR, Ornstein DK. Loss of annexin A1 disrupts normal prostate glandular structure by inducing autocrine IL-6 signaling. Carcinogenesis. 2009;30:1082–1088. doi: 10.1093/carcin/bgp078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung YS, Kim KS, Kim KD, Lim JS, Kim JW, Kim E. Apoptosis-linked gene 2 binds to the death domain of Fas and dissociates from Fas during Fas-mediated apoptosis in Jurkat cells. Biochem Biophys Res Commun. 2001;288:420–426. doi: 10.1006/bbrc.2001.5769. [DOI] [PubMed] [Google Scholar]
- Kim SHJ, Debnath J, Mostov K, Park S, Hunt CA. A computational approach to resolve cell level contributions to early glandular epithelial cancer progression. BMC Syst Biol. 2009;3:122. doi: 10.1186/1752-0509-3-122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitano H. Cancer as a robust system: implications for anticancer therapy. Nat Rev Cancer. 2004;4:227–235. doi: 10.1038/nrc1300. [DOI] [PubMed] [Google Scholar]
- Laurent VM, Planus E, Fodil R, Isabey D. Mechanical assessment by magnetocytometry of the cytosolic and cortical cytoskeletal compartments in adherent epithelial cells. Biorheology. 2003;40:235–240. [PubMed] [Google Scholar]
- Liu H, Radisky DC, Bissell MJ. Proliferation and polarity in breast cancer: untying the Gordian knot. Cell Cycle. 2005;4:646–649. doi: 10.4161/cc.4.5.1674. [DOI] [PubMed] [Google Scholar]
- Merks RMH, Perryn ED, Shirinifard A, Glazier JA. Contact-inhibited chemotaxis in de novo and sprouting blood-vessel growth. PLoS Comput Biol. 2008;4:e1000163. doi: 10.1371/journal.pcbi.1000163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthuswamy SK, Li D, Lelievre S, Bissell MJ, Brugge JS. ErbB2, but not ErbB1, reinitiates proliferation and induces luminal repopulation in epithelial acini. Nat Cell Biol. 2001;3:785–795. doi: 10.1038/ncb0901-785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson CM, Bissell MJ. Modeling dynamic reciprocity: engineering three-dimensional culture models of breast architecture, function, and neoplastic transformation. Semin Cancer Biol. 2005;15:342–352. doi: 10.1016/j.semcancer.2005.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman TJ. Modeling multicellular structures using the subcellular element model. In: Anderson ARA, Chaplain MAJ, Rejniak KA, editors. Single-Cell-Based Models in Biology and Medicine. Basel, Switzerland: Birkhauser; 2007. pp. 221–239. [Google Scholar]
- Norton K-A, Wininger M, Bhanot G, Ganesan S, Barnard N, Shinbrot T. A 2D mechanistic model of breast ductal carcinoma in situ (DCIS) morphology and progression. J Theor Biol. 2010;263:393–406. doi: 10.1016/j.jtbi.2009.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paszek MJ, Boettiger D, Weaver VM, Hammer DA. Integrin clustering is driven by mechanical resistance from glycocalyx and the substrate. PLoS Comput Biol. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- Ramis-Conde I, Drasdo D, Anderson A, Chaplain M. Modeling the influence of the E-cadherin-ß-catenin pathway in cancer cell invasion: a multiscale approach. Biophys J. 2008;95:155–165. doi: 10.1529/biophysj.107.114678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reginato MJ, Mills KR, Becker EBE, Lynch DK, Bonni A, Muthuswamy SK, Brugge JS. Bim regulation of lumen formation in cultured mammary epithelial acini is targeted by oncogenes. Mol Cell Biol. 2005;25:4591–4601. doi: 10.1128/MCB.25.11.4591-4601.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rejniak KA. An immersed boundary framework for modelling the growth of individual cells: an application to the early tumour development. J Theor Biol. 2007a;247:186–204. doi: 10.1016/j.jtbi.2007.02.019. [DOI] [PubMed] [Google Scholar]
- Rejniak KA. Modelling the development of complex tissues using individual viscoelastic cells. In: Anderson ARA, Chaplain MAJ, Rejniak KA, editors. Single-Cell-Based Models in Biology and Medicine. Basel, Switzerland: Birkhauser; 2007b. pp. 301–323. [Google Scholar]
- Rejniak KA, Anderson ARA. A computational study of the development of epithelial acini. I. Sufficient conditions for the formation of a hollow structure. Bull Math Biol. 2008a;70:677–712. doi: 10.1007/s11538-007-9274-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rejniak KA, Anderson ARA. A computational study of the development of epithelial acini. II. Necessary conditions for structure and lumen stability. Bull Math Biol. 2008b;70:1450–1479. doi: 10.1007/s11538-008-9308-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rejniak KA, Dillon RH. A single cell based model of the ductal tumour microarchitecture. Comput Math Methods Med. 2007;8:51–69. [Google Scholar]
- Rejniak KA, Wang SE, Bryce NS, Chang H, Parvin B, Jourquin J, Estrada L, Gray JW, Arteaga CL, Weaver AM, Quaranta V, Anderson ARA. Linking changes in epithelial morphogenesis to cancer mutations using computational modeling. PLoS Comput Biol. 2010;6:e1000900. doi: 10.1371/journal.pcbi.1000900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandersius SA, Newman TJ. Modeling cell rheology with the subcellular element model. Phys Biol. 2008;5:e015002. doi: 10.1088/1478-3975/5/1/015002. [DOI] [PubMed] [Google Scholar]
- Shirinifard A, Gens JS, Zaitlen BL, Poplawski NJ, Swat M, Glazier JA. 3D Multi-cell simulation of tumor growth and angiogenesis. PLoS One. 2009;4:e7190. doi: 10.1371/journal.pone.0007190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarone G, Hirsch E, Brancaccio M, De Acetis M, Barberis L, Balzac F, Retta F, Botta C, Altruda F, Silengo L. Integrin function and regulation in development. Int J Dev Biol. 2000;44:725–731. [PubMed] [Google Scholar]
- Tyson DR, Inokuchi J, Tsunoda T, Lau A, Ornstein DK. Culture requirements of prostatic epithelial cell lines for acinar morphogenesis and lumen formation in vitro: role of extracellular calcium. Prostate. 2007;67:1601–1613. doi: 10.1002/pros.20628. [DOI] [PubMed] [Google Scholar]
- van Leeuwen IMM, Mirams GR, Walter A, Fletcher A, Murray P, Osborne J, Varma S, Young SJ, Cooper J, Doyle B, Pitt-Francis JP, Momtahan L, Pathmanathan P, Whiteley JP, Chapman SJ, Gavaghan DJ, Jensen OE, King JR, Maini PK, Waters SL, Byrne HM. An integrative computational model for intestinal tissue renewal. Cell Prolif. 2009;42:617–636. doi: 10.1111/j.1365-2184.2009.00627.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang AZ, Ojakian GK, Nelson WJ. Steps in the morphogenesis of a polarized epithelium I. Uncoupling the roles of cell-cell and cell-substratum contact in establishing plasma membrane polarity in multicellular epithelial (MDCK) cysts. J Cell Sci. 1990a;95:137–151. doi: 10.1242/jcs.95.1.137. [DOI] [PubMed] [Google Scholar]
- Wang AZ, Ojakian GK, Nelson WJ. Steps in the morphogenesis of a polarized epithelium. II. Disassembly and assembly of plasma membrane domains during reversal of epithelial cell polarity in multicellular epithelial (MDCK) cysts. J Cell Sci. 1990b;95:153–165. doi: 10.1242/jcs.95.1.153. [DOI] [PubMed] [Google Scholar]
- Wang SE, Narasanna A, Perez-Torres M, Xiang B, Wu FY, Yang S, Carpenter G, Gazdar AF, Muthuswamy SK, Arteaga CL. HER2 kinase domain mutation results in constitutive phosphorylation and activation of HER2 and EGFR and resistance to EGFR tyrosine kinase inhibitors. Cancer Cell. 2006;10:25–38. doi: 10.1016/j.ccr.2006.05.023. [DOI] [PubMed] [Google Scholar]